Electric Power Generation Optimization With Markowitz Model

Ticoh, J. D

, Laloan, C. F

Department of Electrical Engineering Education, Universitas Negeri Manado, Sulawesi Utara, Indonesia

Department of Economics Education, Universitas Negeri Manado, Sulawesi Utara, Indonesia

Keywords: Power Generation, Optimization, Efficient Frontier, Markowitz Model.

Abstract: Factors of economic growth, the growth of the population and the global warming issue require that electricity

providers must be able to provide electrical power energy with a high-reliability factor. The duration of

extinguishing and how often blackouts are a measure of the reliability of an electric power system.

Diversification of the types and sources of electrical energy as a way to ensure the availability of electrical

energy in the form of parallel work of power generation systems. The existence of a variety of constraints on

each generation system so that a special method is needed to be able to regulate the operation

variation/scheduling to provide electricity for consumers. This journal discusses the optimization method of

the portfolio of electric energy generation systems using the Markowitz model. This model provides an

optimum value for the variation of the power plant system at each time indicated by an efficient frontier curve.

Every optimum combination of plants that might be on the frontier efficient curve line.

1 INTRODUCTION

Diversification is the act of spreading investment into

several forms of investment projects and if it is

appropriate to choose the characteristics of each

project, the effects of the portfolio will reduce the

overall risk. ( Acemoglu,1997)

This portfolio is essentially a combination or

combination or set of assets / projects, both in the

form of real assets and financial assets owned by

companies / investors, formed to reduce risk.

Markowitz, 1952 and Bodie, 2009).

In the process of forming this portfolio must go

through an investment process consisting of a policy

determination process, investment analysis, portfolio

formation, portfolio performance evaluation, and

portfolio revision process.(Chandra, 2017)

At least there are two things that underlie this:

first if one is wrong in planning and decision making

will have severe and long consequences for the

company, considering the number of funds spent is

quite large and tied for a long time, and secondly if

there is wrong in estimating their needs, for example,

investment is too large (over investment) there will be

burdens which should not be necessary. Conversely,

if the investment is too small (under investment) the

company will lack production capacity. (Sovic, 2016;

Brook, 2016; Hult, 2017)

From the description above shows how

important the management process is to risk, its

relationship with how to avoid, prevent and reduce or

in other words the process of maximizing

opportunities and minimizing failure. For this reason,

it is very necessary to seek, build, implement realistic

best strategies, and allocate limited resources into the

most productive areas. This is a very challenging task

for executives of any company in any industry and

even more challenging for executives who manage

business portfolios.

Electricity generation nowadays presents a greater

number of challenges related to reliability,

sustainability and security of supply. The use of

renewable resources in power generation has been

adopted in most OECD (Organization for Economic

Cooperation and Development) countries as an

answer to the climate change problems originated by

the burning of fossil fuels in the traditional thermal

plants to supply the ongoing increase in electricity

demand. (Eusébio et al., 2015).

In terms of the economic model, the electricity

industry has evolved from a vertically integrated

state-owned monopoly company (not subjected to the

Ticoh, J. and Laloan, C.

Electric Power Generation Optimization with Markowitz Model.

DOI: 10.5220/0009009702730279

In Proceedings of the 7th Engineering International Conference on Education, Concept and Application on Green Technology (EIC 2018), pages 273-279

ISBN: 978-989-758-411-4

273

normal rules of competition) to a liberalized market

where generators and consumers have the opportunity

to freely negotiate the purchase and sale of electricity.

Usually the liberalization of the electricity market

allows entry of independent power producers with

long term contracts and the creation of active

wholesale and retail markets came in a later stage.

Nowadays the actual economic situation affects all

the participants in the sector, consumers, producers

and “prosumers”, many hypotheses to decrease the

bill to pay for electricity are considered, such as

different energy suppliers, control load programs,

load forecasting, smart-grid, smart-metering and

smart-box.

In terms of the economic model, the electricity

industry has evolved from a vertically integrated

state-owned monopoly company (not subjected to the

normal rules of competition) to a liberalized market

where generators and consumers have the opportunity

to freely negotiate the purchase and sale of electricity.

The energy sector is in transition to a flexible and

sustainable energy system based on renewable

energy sources. This complex transition is affecting

multiple levels in the sociotechnical system. One

driver of the transition is climate change that

enforces the policy push from the macro level to

change the way energy is produced, delivered, and

used. As part of the energy system evolution, the

role of the end user in the energy sector is

undergoing profound changes, and consumers are

increasingly being empowered to participate

actively in the production and use of energy.

(mesaric et all, 2017: Kotilainen, 2018)

The small passive consumer evolves to an active

player, participating in the generation of electricity

and the provision of network services. In this context,

both aggregators and companies can bring their

customers, consumers, producers, consumers and

traders to market (Lampropoulos et al., 2010) (Stern,

1999)

With the new paradigm of the distributed generation

of electrical models allows the medium, small

consumers and producers to integrate the satisfaction

of the power system because they adopted opposed to

the traditional power system, composed by medium

and large power plants. (Markovis, 2013)

The optimization method of the portfolio of electric

energy generation systems using the Markowitz

model is the main objective in this research.

2 METHOD

This research is a descriptive research which

describes the determination of the optimal Portfolio

model with the Markowitz model chosen from the

many efficient portfolio alternatives that can provide

a certain level of return in accordance with the risk

dared to be borne by the manager, the optimal

combination is shown on Markowitz's efficient curve.

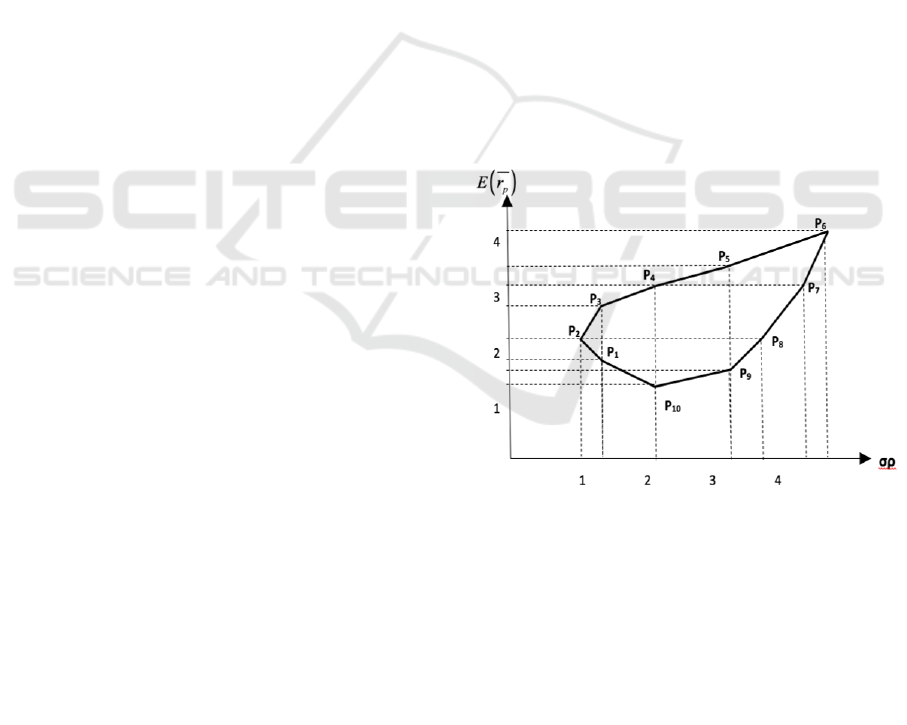
Figure 1 shows the efficient curve where P1 until P10

are possible portfolio combinations, Markowitz states

that efficient frontiers are all efficient portfolios that

may be from a combination of risk and return P2, P3,

P4, P5, P6. According to Markowitz (Xu et al, 2017),

the key why investors / companies only need to look

at some portfolios is located in the efficient set

theorem, which states that (Sharpe et al, 2005):

Manager will choose an optimal portfolio from a

number of portfolios that: 1) Offering maximum

expected return for various levels of risk and 2) Offer

minimum risk for various levels of expected return.

Figure 1: Markowitz efficiency curve

Concept of Expected Value is one method of how we

Figure 1: Markowitz efficiency curve

combine probability quantitatively with investment

opportunities, while the risk in an investment project

is shown by the size of the expected rate of return that

deviates from the actual rate of return where the

greater the deviation means the higher the level of

risk. Standard deviation (SD) as a measurement of the

variability of distribution based on this statistical

science. The optimal Portfolio model with the

Markowitz model chosen from the many efficient

portfolio alternatives that can provide a certain level

of return in accordance with the risk dared to be borne

EIC 2018 - The 7th Engineering International Conference (EIC), Engineering International Conference on Education, Concept and

Application on Green Technology

274

by the manager, the optimal combination is shown on

Markowitz's efficient curve (Halim, 1995; Jogiyanto,

2003).

! " #$ %

' ()#$

+,%

& /0

" #$ %

' ()#$

+,%

& /0

(1)

where ; ! = Deviation standard;!

=Varians;

(CF)xi= Cash flows obtained in the case of i;

EVCF=Expected value of cash flow; P(xi) = The

probability of the occurrence of cash flows in

conditions i and ; n =Frequency of cash flows

received.

According to Markowitz the expected return of a

project portfolio is a weighted average of expected

returns for each individual project (Gao, 2003) so that

the expected value of a project portfolio is;

( ) ( )

pp i

Er E XEr

(2)

With Xi expressed as;

23.456&.7859859846&.69:86;<=>8?9

Total Invsetment Fund in Portofolio

(3)

Where:

( )

= Expected portfolio return from the

project; Xi = Proportion of funds invested in the project I;

( )

= Returns expected from the project I;

N=Returns expected from the project i.

Whereas to calculate the standard deviation (standard

deviation) the Markowitz model portfolio consisting

of N projects includes multiple addition actions

shown in equation (2) to N projects.

PP ijij

SD X X

åå

(4)

if there are three projects in the portfolio, then the

portfolio risk equation (2) will become;

PP ijij

SD X X

åå

11 1212 1313

2121 2 2 2323

3131 3232 3 3

[

]

XXXXX

XX X XX

XX XX X

sss

ss s

sss

=+++

++ +

(5)

with

ij i j ij

sssr

and portofolio varian

P i j ij

VXX

åå

where ; @

= Portfolio deviation; 1

B 1

= Proportion

of funds invested in i & j projects; @

B @

=Standard

deviation of projects i and j;

B C

= Coefficient of correlation between two

random variables; @

= Return covariance between

two random variables i and j.

3 RESULTS AND DISCUSSION

Table 1 shows examples of Expected Monetary Value

(EMV), standard deviations and covariance for each

generation system or customer variation.

Nowadays there are various kinds of energy

sources that are trying to be used to ensure the

availability of electricity that tends to change, such as

gas, wind, coal, oil, biomass, sunlight and much

more. Each generation system has its own character,

starting from investment, the size of the energy

potential, risk to the environment, environmental

conditions that can interfere with normal operation,

operating costs, to the load variation. (Calvo, 2017).

To reach these goals they research and develop new

technologies which could better meet the needs of

their consumers and to adjust to changes in the energy

industry. The intense changes in worldwide energy

industry are the results of a number of factors, such as

the increase in energy demand, growing

industrialization processes, and resources limitations.

Many countries and energy providers are obligated to

reconstruct their power generation mix and to develop

new possibilities for producing energy. One reason is

that their existing power plants are often old, not very

energy-efficient and not very eco-friendly (e.g.

featuring high CO2 emissions). Moreover, present

energy utilities are heavily involved to develop CO2-

free or CO2-low technologies. The construction of

power portfolios is a process where energy utilities

have to consider a number of factors and goals,

including the following: minimizing the impact on the

environment, keeping the cost of generation as low as

possible and, from a power supplier’s point of view,

achieving the best profit for a given risk level.

(Madlener).

EMV of an outcome is a combination of

profitability and risk measure (with numerical

probability) that adjusts to the value. In other words

EMV is the result of multiplication between the

Electric Power Generation Optimization with Markowitz Model

275

probability of the outcome and the conditional value

received if the outcome occurs; Standard deviation is

a statistical value that is used to determine how the

data is distributed in the sample, and how close the

individual data points are to the mean or average

sample value; and Covariance is a statistical measure

of the relationship between two random variables.

(Moore, 1983).

Table 1 shows examples of Expected Monetary

Value, standard deviations and covariance for each

generation system or customer variation.

Based on Table 1, it can be seen that 3 (three) systems

of dissemination may be developed, namely the

optimal project portfolio selected "CDH", so that the

company will be faced with the problem of funding

the project / determining the capacity of the power to

be raised, ie how many parts / variations of money

will be place it in each plant in the "CDH" project

portfolio.

Using the Markowitz theory, the problem can be

solved by forming a portfolio distribution that

consists of variations in investment weights for each

project which will also provide an expected portfolio

return and standard portfolio deviation (a variety of

efficient set theorems. For the case of the "CDH"

project portfolio, A curve can be made attainable set

or feasible set or possible combination of "CDH"

portfolios as shown in Figure 24, which consists of

1000 portfolio combinations of the project "CDH"

with a fraction / weight of each particular project

(although basically this number of attainable sets can

not countless or more than 1000 variations)

Table 1: Expected Monetary Value Standard deviation and

Covariance, (Ticoh, 2012)

Power

Pant

EMV (US$)

COV(%)

5.889.036

13.432.690,11

228

11.234.202

17.703.410,90

157

31.666.278

62.470.393,51

197

CDH

16.297.952,20

21.532.936,78

132

by using Matlab software optimizer (listening

program in Appendix 6). Calculation of each possible

portfolio combination (attainable set portfolio) in

Appendix 7 using equation (1) to (5) each portfolio

standard deviation and expected portfolio return can

be obtained

Figure 2: Curve combination of 1000 feasible sets of

project portfolio "CDH" by using the help of Optimizer

Matlab .

So that from this efficient frontier theorem (figure

1), a number of portfolios that meet both conditions

are expressed as efficient set or efficient frontier, in

which efficient portfolios are located, and according

to Markowitz the combination under the curve can be

ignored. Based on this, the portfolio is at the efficient

frontier for the "CDH" project portfolio.

Below is listening program with matlab to

produce 1000 combinations of 3 projects “CDH”.

%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%

% Filename JanneD_Ticoh.M

% OPTIMALISASI PORTOFOLIO " ":

% Plotting an Efficient Frontier

%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%

% Specify the expected returns, standard

deviations, and

% correlation matrix for a hypothetical 3-asset

portfolio.

returns = [5902995 11252120 31700830];

STDs = [13425504.28 17698112.37

62454711.32];

correlations = [ 1 0 0

0 1 0

EIC 2018 - The 7th Engineering International Conference (EIC), Engineering International Conference on Education, Concept and

Application on Green Technology

276

0 0 1 ];%

% Convert the standard deviations and

correlation

% matrix into a variance-covariance matrix.

% covariances = corr2cov(STDs ,

correlations);

% Compute and plot the efficient frontier for

% 100 portfolios along the frontier.

portopt(returns , covariances , 20)

% Randomly generate the asset weights for

1000

% portfolios starting from the MATLAB initial

state.

rand('state' , 0)

weights = rand(1000 , 3);

% Normalize the weights of each portfolio so

that the sum = 1.

total = sum(weights , 2);

total = total(:,ones(3,1));

weights = weights./total;

% Compute the expected return and risk of each

portfolio.

[portRisk , portReturn] = portstats(returns ,

covariances , weights);

% Now plot the returns and risks of each

portfolio

% on top of the existing efficient frontier for

comparison.

hold on

plot (portRisk , portReturn , '.r')

title('Mean-Variance Efficient Frontier and

Random Portfolios')

hold off

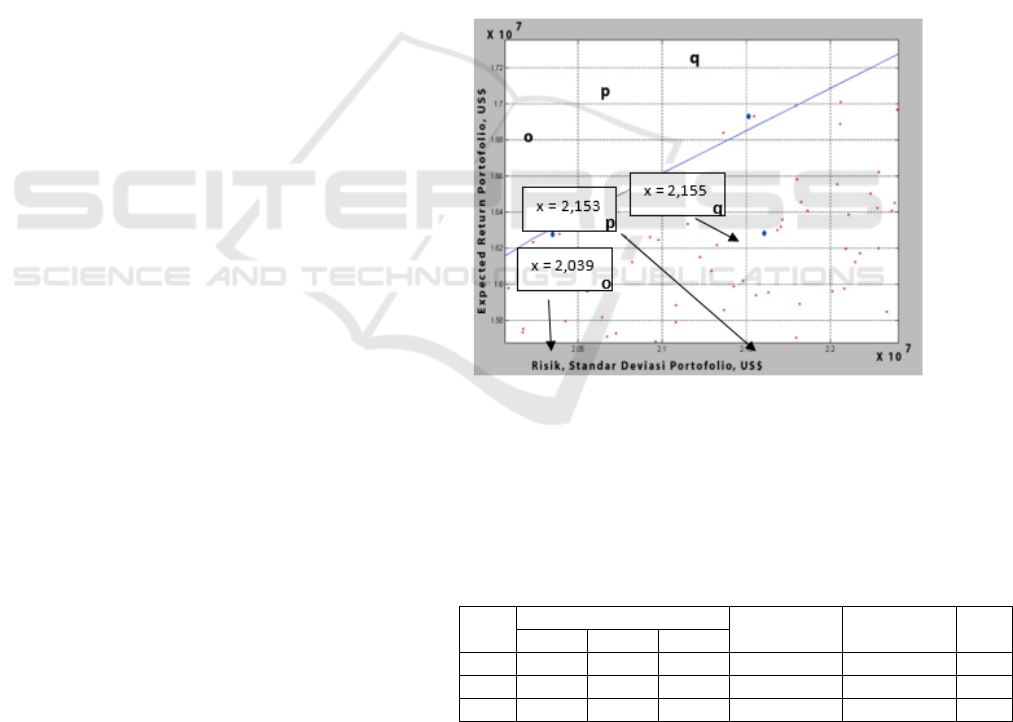
If the company has an investment policy to fund all

projects in the "CDH" portfolio, then the portfolio for

the company lies in the "p" point in Figure 3 clicked

from Figure 2. This "CDH" portfolio has the expected

value and a standard deviation of US $ 16,297,952.20

and US $ 21,532,936.78 .

According to the efficient frontier theorem, it is

inappropriate to choose a portfolio that is not at the

efficient frontier or in other words the portfolio is not

included in an efficient portfolio. This is clear

because when compared with the "CDH" portfolio

which is at the frontier efficient frontier around the

point "o" and "q" is more efficient than the portfolio

at the point “p”.

Figure 3: Location of the "CDH" project portfolio in the

sample of 1000 portfolio combinations in Figure 2. If the

company decides to fund the three projects in its overall

portfolio "CDH"

Table 2: Comparison of the "CDH" portfolio if the company

decides to fund the entire project and "CDH" portfolio that

is at the efficient frontier if the company wants to fund a

project with a certain weight

Porto

folio

Project weight

Portofolio Risk

Portofolio

Return

COV

(%)

“o”

0,118

0,6054

0,2766

20.390.176,19

16.277.380,26

125

“p”

0,28

0,4

0,32

21.532.936,78

16.297.952,20

132

“q”

0,0074

0,7129

0,2797

21.547.188,01

16.931.232,28

127

Based on this analysis, then to get an optimal

portfolio, the company must choose one of the

optimal portfolios from a number of portfolios that

Electric Power Generation Optimization with Markowitz Model

277

are in figure 4 efficient frontier. This is very

important for the company because if the company

has limited investment funds, then the company can

make the policy to invest funds with optimal variation

and can provide opportunities for parties from outside

the company to invest in each project in the "CDH"

portfolio. According to the efficient set theorem,

companies can choose the optimal portfolio "CDH"

that is located along the efficient frontier, depending

on how the company prefers risk.

Figure 4: Various optimal portfolios of "CDH" based on

investor preferences on the efficient frontier curve

4 CONCLUSIONS

The electricity industry has evolved from a

vertically integrated state-owned monopoly company

(not subjected to the normal rules of competition) to

a liberalized market where generators and consumers

have the opportunity to freely negotiate the purchase

and sale of electricity.

With the shift in the paradigm of electricity

supply, producers are faced with variations in the

choice of generation systems and character loads /

customers that are always dynamic.

Risks and Expected Economic returns are to be a

measure for producers to choose a combination /

portfolio of power plant systems to be operated.

By using the Markowitz efficient curve portfolio,

the optimal portfolio combination can be

determination. The optimal Portfolio model with the

Markowitz model chosen from the many efficient

portfolio alternatives that can provide a certain level

of return in accordance with the risk dared to be borne

by the manager.

Producers who dare to face risks will choose a

portfolio combination that is on the rightmost

efficient curve, and if you want to avoid risk the

producer will choose a portfolio combination that is

left most on the efficient curve

REFERENCES

Acemoglu, D., & Zilibotti, F. (1997). Was

Prometheus unbound by chance? Risk,

diversification, and growth. Journal of political

economy, 105(4), 709-751.

Bodie, Z. (2009). Investments. Tata McGraw-Hill

Educatio

Brook, M., 2016. Estimating and tendering for

construction work. Routledge.

Chandra, P. 2017. Investment analysis and portfolio

management. McGraw-Hill Education.

Calvo-Silvosa, A., Antelo, S.I. and Soares, I., 2017.

Energy planning and modern portfolio theory: A

review. Renewable and Sustainable Energy

Reviews, 77, pp.636-651.

Dhrymes, P.J., 2017. Portfolio Theory: Origins,

Markowitz and CAPM Based Selection. In

Portfolio Construction, Measurement, and

Efficiency (pp. 39-48). Springer, Cham.

Eusébio, E., de Sousa, J., & Neves, M. V. 2015, April.

Risk analysis and behavior of electricity portfolio

aggregator. In Doctoral Conference on

Computing, Electrical and Industrial Systems (pp.

365-373). Springer, Cham.

Hult, G.T.M., Morgeson, F.V., Morgan, N.A.,

Mithas, S. and Fornell, C., 2017. Do managers

know what their customers think and

why?. Journal of the Academy of Marketing

Science, 45(1), pp.37-54.

Kotilainen, K. and Saari, U.A., 2018. Policy

Influence on Consumers’ Evolution into

Prosumers—Empirical Findings from an

Exploratory Survey in

Europe. Sustainability, 10(1), p.186.

Lampropoulos, I., Vanalme, G. M., & Kling, W. L.

(2010, October). A methodology for modeling the

behavior of electricity prosumers within the smart

grid. In Innovative Smart Grid Technologies

Conference Europe (ISGT Europe), 2010 IEEE

PES (pp. 1-8). IEEE.

Madlener, R. and Glensk, B., Use of Modern

Portfolio Theory to Optimize the Power

Generation Mix at the Company Level: Impact of

Investments in New Renewable Energy

Technologies. In Energy Economy, Policies and

Supply Security: Surviving the Global Economic

Crisis,,. International Association for Energy

Economics.

Markowitz, H. 1952. Portfolio selection. The journal

of finance, 7(1), 77-91.

Mesarić, P., Đukec, D., & Krajcar, S. 2017. Exploring

the potential of energy consumers in smart grid

using focus group

methodology. Sustainability, 9(8), 1463.

EIC 2018 - The 7th Engineering International Conference (EIC), Engineering International Conference on Education, Concept and

Application on Green Technology

278

Sharpe, F. W., Alexander, J. G. dan Bailey, J. V.

2005. Investasi Jilid 1& Jilid 2. Edisi Ke-6.

Jakarta: PT Indeks Kelompok Gramedia.

Ticoh, J.D., 2010. Optimalisasi Portofolio Proyek

dengan Menggunakan Kurva Efisien Markowitz.

Ed Vokasi. Jurnal Pendidikan Teknologi dan

Kejuruan, 1(1), pp.36-57.

Slovic, P., 2016. The perception of risk. Routledge.

Xu, G., Markowitz, H., Wang, M. and Guerard, J.B.,

2017. Constructing Mean Variance Efficient

Frontiers Using Foreign Large Blend Mutual

Funds. In Portfolio Construction, Measurement,

and Efficiency (pp. 315-329). Springer, Cham.

Moore, P.G. and Moore, P.G., 1983. The business of

risk. Cambridge university press.

Electric Power Generation Optimization with Markowitz Model

279