Print-cam Resilient Watermarking based on Fourier Transform

Khadija Gourrame

1,2,*

Hassan Douzi

, Rachid Harba

, Frederic Ros

, Rabia Riad

, Mohamed Elhajji

IRF-SIC Laboratory, Ibn Zohr University, BP 8106 - Cite Dakhla, 80000 Agadir, Morocco

PRISME Laboratory, Orleans University, 12 Blois street, 45067 Orleans, France

Keywords: Resynchronization, projective distortions, image watermarking, Fourier transform, Print-cam.

Abstract: Synchronization problems are still challenging issues in image watermarking field. In this paper, we present

a robust image watermarking for projective deformations produced by print-cam system. The approach

associates watermark insertion in invariant domain based on Fourier transform with correction pre-process

for projective distortions, blur and color degradations. The robustness of the proposed method is tested and

compared with different existing approaches. The comparison test is presented with simulated projective

distortions and with real print-cam system using two different smartphones (iPhone6 and Samsung S5). The

results show better performance of the proposed method in term of robustness, compared with other tested

methods.

1 INTRODUCTION

Image watermarking is the process of embedding

digital information called watermark into an image

that can later be detected or extracted. With the rise

of using smartphones, print-cam image

watermarking comes as a convenient procedure to

detect watermarks from printed and captured

images. In general, image watermarking should

satisfy three main requirements (Cox et al., 2008),

imperceptibility or the invisibility of the watermark

in the image, capacity or the quantity of the

information that can be inserted and robustness that

indicates how well the watermarking technique

resists attacks. Here, attacks and distortions are any

type of manipulations that make the detection

process fails to find the watermark in the image.

Although print-cam scheme has the advantage of

place-free and time-free conditions, it suffers from

many attacks compared with other existing schemes

like print-scan watermarking system (Riad et al.,

2015).

Print-cam system produces several attacks

including; image blur from the used materials

(printer and smartphone), color degradation, lighting

variation including light reflection and geometric

distortions from the freehandedly use of the

smartphone (Pramila et al., 2007). Geometric

distortions in this case are precisely called

perspective or projective distortions that are

combinations of rotation, translation, scaling and

tilting of the optical axis (Hartley and Zisserman,

2003). Robustness against geometric distortions is

crucial in every design of image watermarking

method. “Invariant domains”, “template based

methods” and “feature based methods” are the main

strategies dealing with geometric problem in

watermarking field. They have been widely used to

face print-scan attacks but they afford only a partial

response to the problematic of projective distortions

that combines Rotation Scale Translation (RST)

attacks and the tilting of the optical axis. Projective

deformations are still a challenging problem.

In this paper we adapt print-cam image

watermarking method to be robust against projective

distortions, using Fourier transform as watermarking

based domain, with a set of pre-process corrections

including projective, blur and color corrections. The

proposed method combines frequency domain with

spatial frame based approach to provide better

robustness against projective distortions. The

proposed method is tested with simulated projective

distortions for 500 ID images. In addition, it is tested

with real print-cam system using two smartphones

iPhone 6 and Samsung S5. The results are compared

with existing watermarking method based on spatial,

wavelet and Fourier-Mellin domains.

The paper is organized as follow: section 2

describes the print-cam attacks, section 3 reviews

the state of the art regarding geometric solutions in

Gourrame, K., Douzi, H., Harba, R., Ros, F., Riad, R. and Elhajji, M.

Print-cam Resilient Watermarking based on Fourier Transform.

DOI: 10.5220/0009771403170325

In Proceedings of the 1st International Conference of Computer Science and Renewable Energies (ICCSRE 2018), pages 317-325

ISBN: 978-989-758-431-2

317

watermarking field, section 4 is devoted to our

proposal method. The experimental results are

presented in section 5. Finally, section 6 is for the

conclusion of the study.

2 PRINT-CAM ATTACKS

Print-cam image watermarking is a

watermarking system where the watermarked image

is printed out then captured with a mobile phone’s

camera to detect and/or extract the watermark. In

this case image watermarking system has four main

processes; process of inserting the mark into the

image, this operation can be applied on different

domains (spatial, Fourier, Wavelet) depends on the

used method for the insertion. Then printing process

where the watermarked image is transformed from

the digital form to analog form using the printer as

one of the system materials. Capturing process,

where smartphone's camera is considered as another

material of the system to transform the watermarked

image from the analog to the digital form, where the

user take a picture of the printed image

freehandedly. Finally, detection process to search for

the inserted watermark on the image to verify its

authentication. This operation should be done on the

same domain used on the embedding process.

Attacks or problems are every deformations

and/or actions that occur to the watermarked image

and harm the mark, in a way to make the

detection/extraction operation fails to find the mark

in the image. The following explains different

attacks and problems in form of three main

categories; problems related to the materials of the

print-cam system, problems related to the user, and

problems related to the environment.

2.1 Attacks Related to the Printer and

Camera’s Smartphone

The materials of the system are the printer and the

camera, as we mention before the printer is used to

convert the digital form of the image into analog

form, and the camera is responsible to convert the

image from analog to digital form. These

transformations produce many changes on the

original watermarked image.

For printers, in market, there are various types as

Laser printer, Ink-jet printer, Dye-sub printer and

others; each one has its complex operations, which

introduce different kinds of attacks and distortions.

Also the same printer may give different results at

different times due to the printer properties or ink

qualities (Pramila et al., 2007). However, the

common attacks related to almost all the printers are

noise and blurring of the pixels, which it can be

visual by human eyes or not depending on the

quality of the printer. In addition, Paper quality, the

printing quality is related directly to the properties of

the used printing paper. The same for cameras, as

printers, there are many types but all work with one

basic concept, which is mapping 3D world into a 2D

image, coordinates. The camera system in general

characterized by two types of parameters, and any

change of them have a significant impact on the

produced image. The parameters are extrinsic

parameters and intrinsic parameters (Hartley and

Zisserman, 2003), where the first ones are related to

the position of the camera along with the object, and

the second ones are internal and fixed to a particular

camera/digitization setup, which allow a mapping

between cameras coordinates and pixel coordinates

in the image frame. Therefore, the problems related

to this part of camera system are lens distortions,

which is caused by the optical design of the lenses.

In general there are three known types of optical

distortion – barrel, pincushion and mustache/

moustache (also known as wavy and complex)

(Wang et al., 2013). Likewise camera resolution is

one of the camera quality that determines how many

pixels camera can produce, The less megapixels the

camera offers, the less information is being recorded

in the image is. Usually the smartphone camera has

low resolution than for example DSLR camera (Seo,

2016). Moreover in this category of print-cam

attacks any problem concerns the mechanical part of

the materials will damage the image and so the

watermark.

2.2 Attacks Related to the User

In print-cam process, the user interferes only while

taking a picture of the printed image. So the

problems related to the external parameter of the

camera are done mostly by the user, we can call

those attacks as: Perspective distortions which is

caused by the camera relative to the subject, it is a

combination of four main geometric distortions;

rotation, translation, scale, and tilt of the optical

axis, therefore it is known as 3D geometric

distortions. For Motion blur, mostly the shaking of

the user’s hand while taking the picture causes it. It

is difficult to detect the watermark in this kind of

images.

ICCSRE 2018 - International Conference of Computer Science and Renewable Energies

318

2.3 Attacks Related to the

Environment

Other kind of attacks are related the environment or

the place where the capturing process is done, like

light or changes of luminance that can destroy the

watermark. Also multiple light sources, direction of

the light, shadows, flashlight, flatness and color of

the light, all have an impact to detection failure of

the watermark (Pramila et al., 2007). As well as

Light reflection with the presence of glass kind

material, between the printed image and the camera.

Moreover, other Noises due to the air interface will

degrade the quality of the image.

All the previous attacks can be classified under

controlled and uncontrolled attacks. In such way that

the controlled attacks, as attacks related to materials,

can be predicted and fixed. However, uncontrolled

attacks, like 3D geometric distortions and light, are

hard to predict and fix. In the following, we focus on

the 3D geometric distortions.

3 STATE OF THE ART

There are three main followed strategies to deal

with geometric problem in watermarking filed:

Invariant domains; they are spaces with specific

geometric invariance that can be used for watermark

insertion. For example, the magnitude of Fourier

transform is invariant to translation. In case of

rotation, the Fourier magnitude is rotated with the

same angle and for scaling it is scaled with the

inverse scaling factor. (Poljicak et al., 2011) and

(Riad, et al., 2016) proposed a Fourier based

watermarking method using circular insertion in the

frequency domain. The method is invariant to

translation and rotation, however it is not invariant

to scaling if the size of the original image in

unknown. With (Xiao et al., 2012), RST invariant

watermarking domain was proposed based on

Fourier-Mellin transform. In practical, the proposed

domain has approximate invariance to RST

distortions. Moreover, other invariant watermarking

method were proposed based on geometric moment

invariants, such as; complex moments and Zernike

moments (Zhu et al., 2010) and (Singh and Ranade,

2014). Nevertheless, they suffer from poor

reconstruction quality.

Template based methods; templates with known

structure helps to reflect the geometric distortion

applied on the image. In (Kutter, 1999),

watermarking method is proposed invariant to RST

using template in Fourier domain. In this case,

template embedding should be careful in form of

embedding position and strength. In (Pramila and

Keskinarkaus, 2008), a frame based watermarking

method was proposed to correct the projective

distortions before the detection phase using four

corners detection of the frame on the ID image. In

(Thongkor and Amornraksa, 2014), watermarking

method for Thai ID cards is proposed, where the

projective distortions are rectified using feature

points from both the watermarked image and the

original image. Yet, their method is a non-blind

method. The robustness of template based

watermarking methods against geometric attacks

relies on the successful detection of the template.

Feature based methods; feature or interest

points are used to create regions for watermark

insertion and detection. This technique uses

geometrical stable feature points to localize the

watermark in the image. In (Bas et al., 2002), feature

points are extracted using Harris detector to create

triangular regions for watermark insertion. However,

this approach is not invariant to the scaling. With

(Ye et al., 2014), scale invariant feature transform

(SIFT) is used to produce circular regions for

watermark insertion. This type of watermarking

method requires that the group of feature points used

for insertion process should be found the same in the

detection process, which is non-trivial especially in

the case of capturing image with smartphones.

4 PROPOSED METHOD

The watermark is first embedded in the input image.

After the print-cam process, three different

correction steps process the captured image: a

frame-based perspective correction, a Wiener filter

to decrease image blurring and adjustment to

eliminate color degradations. Finally, the decision is

taken, during the detection process, whether the pre-

processed image is watermarked or not according to

a given threshold value.

4.1 Watermarking Technique

In this section, the proposed watermark insertion and

detection techniques are detailed.

4.1.1 Watermark Insertion

Watermark embedding is performed in the DFT

magnitude of the colored image luminance

(chrominance components are not modified). A

symmetric watermark is inserted along a circle of

radius r in the DFT magnitude. The watermark W of

Print-cam Resilient Watermarking based on Fourier Transform

319

N elements is inserted in the mid coefficients as

follows:









,

(1)

where 



the magnitude of the watermarked DFT

coefficient is, 



is the original one after filtering

the embeddable coefficients using a Gaussian filter,

and α is the strength parameter. The choice of α is

related to the invisibility of the watermark. The

adaptive strength α is determined to obtain the

desired value of PSNR, in general equal to 40dB

(Riad et al. 2016). The final watermarked image is

reconstructed by applying the inverse DFT to obtain

the luminance of the watermarked image from which

color image is recovered using the unmodified

chrominance components.

4.1.2 Watermark Detection

The blind decoder needs only the captured image

and the watermark. First, the DFT is applied to

the luminance of the captured image. Then, the

coefficients are extracted from the magnitude along

the radius . The maximum of the normalized cross-

correlation 



is computed between the extracted

coefficients F and the sequence  of the watermark,

as shown in equation (2):





max



∑





































∑

















∑



























(2)

Where  is the sequence length, 



and 



are the

means of the watermark and extracted Fourier

coefficients respectively. The watermark is said to

be present if the maximum value of the normalized

cross-correlation exceeds a threshold.

4.1.3 Threshold Estimation

To estimate the threshold, detection theory problems

are often formulated as a classical hypothesis testing

problem; with the null hypothesis (0) for images

without watermark, and the alternative hypothesis

(1) for images containing the watermark (Nguyen

et al., 2009). The threshold decision or the criterion

response must be taken based on observations of a

set of watermarked and non-watermarked images. It

is chosen according to some application-dependent

criteria, either to minimize the false rejection (when

the watermarked image detected as non-

watermarked) and false alarm (when the non-

watermarked image detected as watermarked) or to

find a trade-off between them. For many

applications, the threshold is defined by placing a

constraint on the false alarm (also called Neyman-

Pearson criterion) (Yan et al., 2001). The probability

of false alarm is defined as:





\



 













(3)

where 



is the probability false alarm. For Fourier

watermarking domain, we used theoretical model for

the calculation of pdf mentioned in (Riad et al.,

2016). Depending on cross correlation coefficient 

of a watermark with size, and non-watermarked

image, the pdf in this model can be modelled as:









\









































(4)

For the testing part of this study, we fix the value

of the false alarm, so that each tested domain will

have its own specific threshold value for the sake of

the objectivity of the experiment.

4.2 Correction Pre-process

4.2.1 Geometric Correction

The operation of transforming coordinate points

from a 3D world to the 2D image plane is called

projective transformation. The projective

transformation of 2D ID cards coordinates into 2D

image coordinates can be presented in the form of a

matrix relation (equation (5)):













,

(5)

where ,



are real coordinates, ,



are image

coordinates and is the 3×3 Projective matrix

(Hartley and Zisserman, 2003).

For the projective correction, we have to estimate

the matrix . It have 8 degree of freedom, hence, 4

known corresponding pair points are needed to solve

the system equation (6):





























1























1

(6)

With frame synchronization method based on Hough

transform in (Gourrame et al., 2016), the 4 corners

of distorted image are detected and the image is

geometrically corrected by applying the inverse of

the estimated projective matrix as the following

steps show:

Step 1: Detect the four corners: we use Hough line

to detect the frame of ID image, and then we get the

four points from the intersections of those lines.

ICCSRE 2018 - International Conference of Computer Science and Renewable Energies

320

Step 2: Estimate the projective matrix: with

corresponding four points, we solve the system

equation in (4).

Step 3: Apply the invert transformation in the whole

image, to remap the rectified image.

Figure 1: Projective correction process.

4.2.2 Blur Correction

Image blurring process is commonly modelled as the

convolution of a clear image with a blur kernel

(Point Spread Function PSF) plus noise. Non-blind

image deblurring is dependent on prior knowledge

of the system and of its parameters. Wiener filter

minimizes the mean square error between the

degraded and the estimated images, it is expressed in

the frequency domain by the following equation:



I

∗

H∗H

∗



SNR

(7)

where  is the Fourier transform of the impulse

response of the system. 

∗

Is the complex conjugate

of,  and 



are the Fourier transforms of the

degraded and estimated images, respectively. The

SNR represents the signal to noise ratio. In this

work, we used a Wiener filter (Riad et al., 2015)

since the print-cam watermarking system is known.

The PSF of the system and its noise variance must

first be estimated [20]. Noise variance was

estimated from four printed and captured images of

uniform gray level, respectively 50, 100, 150, 200.

Image variance was computed for each tested gray

level. The mean of the image variance is the final

noise variance.

4.2.3 Color Correction

Color distortion is a result of many factors occurring

during the print-cam process. The correction is

established first by estimating the color distortion

function then applying the inverse of this function to

the distorted image in a given color domain (RGB,

HSV,…). Polynomial 4



order correction method is

used by solving the following equation in the RGB

domain:















































































































(8)

The,  and denote the original Red, Green and

Blue color pixel value and’, ’ and ’ denote the

distorted output color pixel value. To estimate the

function a color palette in (Riad et al., 2016) with

specific color collections is used.

5 EXPERIMENTAL RESULTS

In this section, the Fourier watermarking method is

compared to two other existing methods in print-

cam state of art. The first is discrete Wavelet

transform (DWT) based method inspired from

(Pramila et al., 2008), and the second is spatial

based method in (Thongkor and Amornraksa,

2014).

We present two tests: a first simulated test where

we apply only simulated perspective deformations

on ID images as mentioned in (Gourrame et al.,

2016). Only the frame-based perspective correction

is applied. In the second test, we apply real print-

cam attacks on ID watermarked images printed on a

paper and digitized using smartphones freehandedly

(iPhone 6 and Samsung S5) (Gourrame et al., 2018).

Perspective correction is associated to the blur and

color corrections. Additional results are also shown.

5.1 Simulated Test

For the first test, we used 500 ID digital images

from the PICS database (Hancock, 2008).

Perspective attacks were simulated and the frame-

based perspective correction was applied. All

watermarking methods were implemented under the

same protocols and conditions. The steps of the test

are shown in the following figure:

Figure 2: Simulated testing process.

For perspective distortions, the simulation of 3D

rotation of the image (3 rotations around the x, y,

and z-axes) is used simultaneously with the

simulation of camera position (viewpoint position)

that defines the polar angles θ and φ (polar angle in

the x-y plane, polar angle above or below the x-y

plane). These angles are measured in degrees.

Print-cam Resilient Watermarking based on Fourier Transform

321

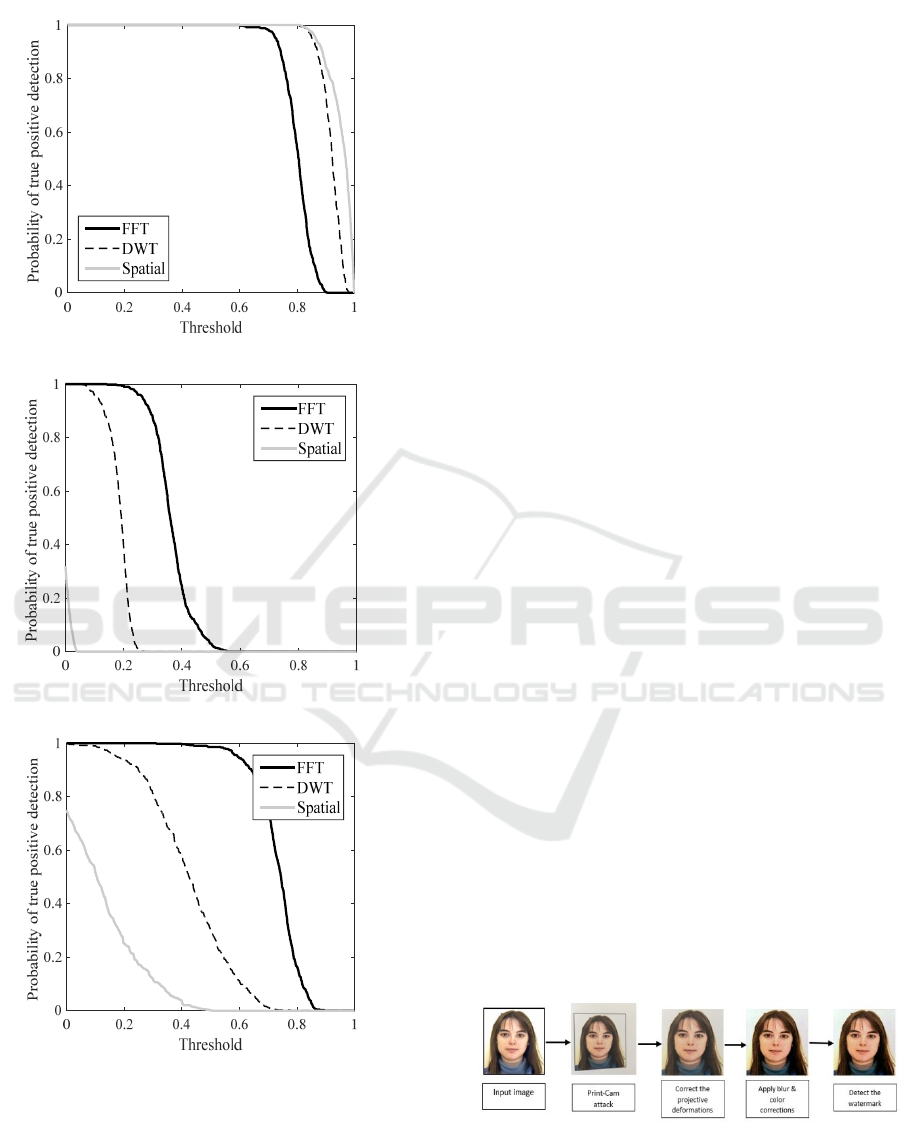
The 500 ID images were deformed under random

values of perspective attacks similar to those

occurring when taking an image freehandedly with a

smartphone. The rotation values around the, , and

 axes were respectively taken from the intervals [-

5°, 5°], [-5°, 5°], and [-10°, 10°]. View point values

of θ and φ were respectively between [0°, 10°] and

[60°, 90°]. We corrected the geometric deformation

using frame-based perspective correction.

Figure 3: Probability of true positive detection as a

function of the threshold values before (a), after (b) the

perspective attacks and (c) after the perspective

corrections.

The probability of true positive detection as a

function of the detection threshold is shown in

Figure 3.

Results show that the DWT and spatial based

methods are better than the Fourier one in the case

where no perspective or projective attack occurs.

The probability of true positive detection of the

Fourier method outperforms the other tested methods

in the case of perspective attacks. Finally, the quality

of the detection after geometrical correction for

Fourier is almost identical to the quality when no

attack was present. This is not the case for the other

methods. This can be explained as follows: The

geometric correction is not perfect and some residual

rotations and translation still survived. The Fourier

method is naturally adapted to rotation and

translation attacks and is less sensitive than DWT or

spatial methods to these residual attacks.

To confirm these preliminary results, test in real

situations will be conducted in the next section.

5.2 Real Test

The three methods were tested in real conditions. 480

ID images (240 are marked and 240 are not marked)

were printed on a paper support with a Konica

Minolta C284 printer (Dot-Matrix type) with a

resolution of 300 dpi and size 43x43 mm

for the

printed ID image.

Then captured freehandedly with iPhone 6 and

Samsung S5 with a resolution of 8 megapixels and

16 megapixels respectively (remember that the

acquisition is freehandedly). The camera of the two

devices are set by default parameters: no filter, no

flashlight during the capturing process. The pictures

have been captured under daylight illumination

(Gourrame et al., 2018). The steps of this test are

shown in the following figure:

Figure 4: Process of the test.

In Figure 5, the proposed Fourier watermarking

method, with the complete correction process, is

compared with the other two tested methods in

terms of ROC curves.

(a)

(b)

(c)

ICCSRE 2018 - International Conference of Computer Science and Renewable Energies

322

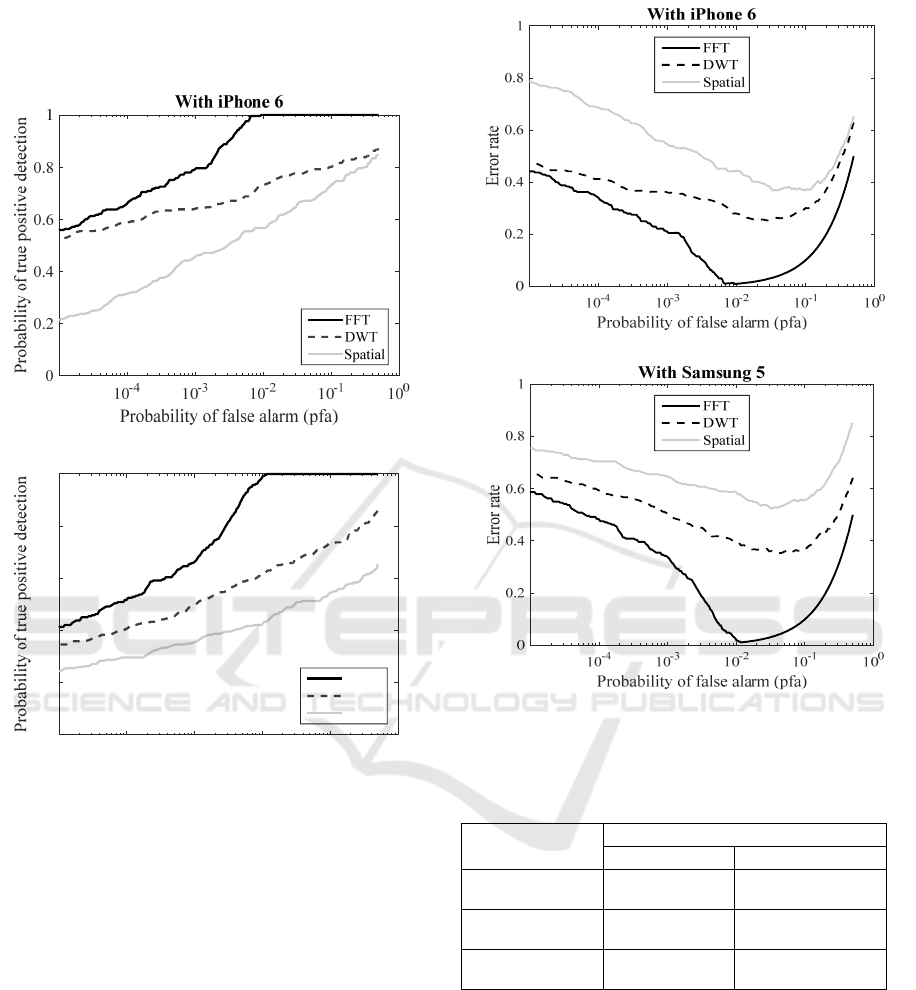
The performance of the watermarking method in

the FFT domain is better than those watermarking

methods in other domains. These results confirm the

results obtained during the simulated test.

Figure 5: Comparison of ROC curves between the three

methods with corrections for (a) iPhone 6 and (b)

Samsung S5.

As a result, the following Figure 6 represents the

total errors according to different pfa values of the

three tested methods.

According to Figure.6, the minimum error rates

are found for the Fourier method. It corresponds to a

pfa value of 10

-2

. The following table shows the

minimal errors for the three methods and for the two

smartphones.

(a)

(b)

Figure 6. Comparison of total error variation between the

three methods with (a) iPhone 6 and (b) Samsung S5.

Table 1. Minimal error rate for the three methods and the

two smartphones

Methods

Minimal error rate

iPhone6 Samsun

FFT 1.02% 1.07%

DWT 25.52% 35.31%

Spatial 36.77% 52.35%

The results show the outstanding performances

of the proposed method with a minimal error rate of

1.02% and 1.07% for respectively iPhone 6 and

Samsung S5. These numbers are to be compared

with the other results (25.52% in the best case).

Lastly, few differences were found between the two

smartphones (iPhone6 and Samsung S5), although

the former led to fewer errors when considering the

Fourier method.

(a)

(b)

Probabilit

of false alarm

)

-4

-3

-2

-1

0.2

0.4

0.6

0.8

With Samsung S5

FFT

DWT

Spatial

Print-cam Resilient Watermarking based on Fourier Transform

323

6 CONCLUSIONS

This paper presents a resilient image-watermarking

scheme based on Fourier transform for print-cam

attacks that can be implemented on a smartphone.

The method contains a pre-process stage to correct

the projective deformations of images taken

freehandedly as well as blur and color correction.

The idea behind these corrections is to use prior

knowledge of the devices involved in the process.

The results show better performance of the proposed

method, in term of detection rate, compared with

other competitive methods. Which demonstrate the

robustness against print-cam attacks.

REFERENCES

Bas, P., Chassery, J.M. and Macq, B., 2002. Geometrically

invariant watermarking using feature points. IEEE

transactions on image Processing, 11(9), pp.1014-

1028.

Cox, I.J., Miller, M.L. and Bloom, J.A., 2008. J. Fridrich,

T. Kalker, Digital Watermarking and Steganography.

Gourrame, K., Douzi, H., Harba, R., Riad, R., Ros, F.,

Amar, M. and Elhajji, M., 2019. A zero-bit Fourier

image watermarking for print-cam

process. Multimedia Tools and Applications, 78(2),

pp.2621-2638.

Gourrame, K., Douzi, H., Harba, R., Ros, F., El Hajji, M.,

Riad, R. and Amar, M., 2016, May. Robust Print-cam

Image Watermarking in Fourier Domain.

In International Conference on Image and Signal

Processing (pp. 356-365). Springer, Cham.

Hancock, P., 2008. Psychological image collection at

stirling (pics). Web address: http://pics. psych. stir. ac.

Hartley, R. and Zisserman, A., 2003. Multiple view

geometry in computer vision. Cambridge university

press.

Kutter, M., 1999, January. Watermarking resistance to

translation, rotation, and scaling. In Multimedia

Systems and Applications (Vol. 3528, pp. 423-432).

International Society for Optics and Photonics.

Moore, R., Lopes, J., 1999. Paper templates. In

TEMPLATE’06, 1st International Conference on

Template Production. SCITEPRESS.

Nguyen, P.B., Beghdadi, A. and Luong, M., 2009,

December. Robust watermarking in DOG scale space

using a multi-scale JND model. In Pacific-Rim

Conference on Multimedia (pp. 561-573). Springer,

Berlin, Heidelberg.

Poljicak, A., Mandic, L. and Agic, D., 2011. Discrete

Fourier transform-based watermarking method with an

optimal implementation radius. Journal of Electronic

Imaging, 20(3), p.033008.

Pramila, A., Keskinarkaus, A. and Seppänen, T., 2007.

Camera based watermark extraction-problems and

examples. In Proceedings of the finnish signal

processing symposium.

Pramila, A., Keskinarkaus, A. and Seppänen, T., 2008.

Watermark robustness in the print-cam process. Proc.

IASTED Signal processing, pattern recognition, and

applications (SPPRA 2008), pp.60-65.

Riad, R., Douzi, H., El Hajji, M., Harba, R. and Ros, F.,

2015. A Print-Scan Resilient Watermarking based on

Fourier Transform and Image

Restoration. International Journal of Computer

Applications, 975, p.8887.

Riad, R., Harba, R., Douzi, H., El-hajji, M. and Ros, F.,

2014, June. Print-and-scan counterattacks for plastic

card supports Fourier watermarking. In

2014 IEEE

23rd International Symposium on Industrial

Electronics (ISIE) (pp. 1036-1041). IEEE.

Riad, R., Harba, R., Douzi, H., Ros, F. and Elhajji, M.,

2016. Robust fourier watermarking for id images on

smart card plastic supports. Advances In Electrical

and Computer Engineering, 16(4), pp.23-30.

Seo, S., 2016. Investigation on Image Quality of

Smartphone Cameras as Compared with a DSLR

Camera by Using Target Image Edges. Korean

Journal of Remote Sensing, 32(1), pp.49-60.

Singh, C. and Ranade, S.K., 2014. Image adaptive and

high-capacity watermarking system using accurate

Zernike moments. IET Image Processing, 8(7),

pp.373-382.

Smith, J., 1998. The book, The publishing company.

London, 2

edition.

Thongkor, K. and Amornraksa, T., 2014, September.

Robust image watermarking for camera-captured

image using image registration technique. In 2014

14th International Symposium on Communications

and Information Technologies (ISCIT)(pp. 479-483).

IEEE.

Wang, Q., Desai, V.N., Ngo, Y.Z., Cheng, W.C. and

Pfefer, J., 2013, December. Towards standardized

assessment of endoscope optical performance:

geometric distortion. In 2013 International

Conference on Optical Instruments and Technology:

Optical Systems and Modern Optoelectronic

Instruments (Vol. 9042, p. 904205). International

Society for Optics and Photonics.

Xiao, B., Ma, J.F. and Cui, J.T., 2012. Combined blur,

translation, scale and rotation invariant image

recognition by Radon and pseudo-Fourier–Mellin

transforms. Pattern Recognition, 45(1), pp.314-321.

Yan, Q. and Blum, R.S., 2001. Distributed signal detection

under the Neyman-Pearson criterion. IEEE

Transactions on Information Theory, 47(4), pp.1368-

1377.

Ye, X., Chen, X., Deng, M. and Wang, Y., 2014, October.

A SIFT-based DWT-SVD blind watermark method

against geometrical attacks. In 2014 7th International

Congress on Image and Signal Processing (pp. 323-

329). IEEE.

ICCSRE 2018 - International Conference of Computer Science and Renewable Energies

324

Zhu, H., Liu, M. and Li, Y., 2010. The RST invariant

digital image watermarking using Radon transforms

and complex moments. Digital Signal

Processing, 20(6), pp.1612-1628.

Print-cam Resilient Watermarking based on Fourier Transform

325