A Sub-1V Bandgap Voltage Reference with Improved PSRR Scheme

Anass Slamti and Zakia Lakhliai

Computer and Interdisciplinary Physics Laboratory (L.I.P.I.), USMBA, Fez, Morocco

Keywords: Bandgap reference, power supply rejection ratio, temperature coefficient, error amplifier.

Abstract: A High performance sub-1V bandgap voltage reference (BGVR) with high power supply rejection ratio

(PSRR) and low temperature coefficient (TC) is proposed in this paper. An improved PSRR scheme is

inserted to isolate the supply voltage of the error amplifier and the supply voltage of BGVR core from a

power supply source in order to achieve a high PSRR. The proposed circuit is designed and simulated in

0.18μm CMOS 1.8V/3.3V technology. The proposed BGVR deliver an output voltage of 0.6346V at 27°C

and the measurement temperature coefficient is 22,3ppm/°C over temperature range -40°C to 140°C, the DC

value of PSRR is -93dB at 10kHz and -71dB of PSRR is achieved at 1MHz and a line regulation of

104μV/V is achieve over supply voltage range 1.2V to 1.8V. The area of layout is 0.0337 mm

2

. The

proposed sub-1V bandgap voltage reference is suitable for low power LDO regulators and switching

regulators.

1 INTRODUCTION

Bandgap voltage reference is a circuit used to

generate a fixed voltage, V

REF

, that in theory is

independent of the power supply voltage V

DD

(where

V

REF

<V

DD

), temperature, and process variations. In

other words, the ideal reference voltage is

independent of PVT. Voltage reference is among the

most important subcircuit in analog integrated

circuits and is used as an internal voltage reference

in linear regulator (LDO), switching regulator,

analog-to-digital converter (ADC) and digital-to-

analog converter (DAC) and other analog integrated

circuits. This is achieved by adding a voltage, which

is proportional to the absolute temperature (PTAT),

to a base-emitter voltage of diode connected Bipolar

Junction Transistor (BJT) NPN or PNP type which

is a complementary to the absolute temperature

(CTAT) in order to compensate for its first-order

temperature dependency (Razavi, 2017).

The classical design of BGVR circuits

commonly has an output voltage V

REF

around 1.25V

(close to the theoretical 1.206V bandgap

voltage of silicon at 0 K) (Widlar, 1971; Kujik,

1973; Brokaw, 1974; Tzanateas et al., 1979; Song

and Gray, 1983).

As the technology scales less than 350

nanometers, so do to supply voltages. The supply

voltages recently tend to be in the range of 0.6-1.2V.

The supply voltage scales with the technology, but

the threshold voltage of the transistors does not scale

at the same rate. This makes it difficult to

incorporate conventional design of bandgap voltage

reference to operates properly in the low supply

voltages. For the low voltage bandgap reference

design many approaches have been proposed;

resistive divider networks (Banba et al., 1999; Leung

and Mok, 2002; Ker et al., 2006), Current summing

and a voltage summing circuits (Ripamonti et al.,

1999), transimpedance amplifier (Jiang and Lee,

2000), dynamic threshold mosfets (Annema, 1999).

Other circuits have been proposed for the design of

sub-1V BGVR to have a low temperature coefficient

and at the same time a high PSRR (Andreou et al.,

2012; Xin et al., 2009), but they have always limited

by the short channel effects existing in nanometer

technologies which has a very low supply voltage,

and especially in the design of the opamp with very

low input offset voltage which remains an important

element in the BGVR circuit to provide a precise

voltage (or current) proportional to the absolute

temperature V

PTAT

(or I

PTAT

) because a very low

offset guarantees the obtaining of this voltage (or

this current).

This work propose a novel design for sub-1V

bandgap voltage reference generator while provide

an output voltage reference V

REF

with low TC and

high PSRR and good line regulation. In section 2,

Slamti, A. and Lakhliai, Z.

A Sub-1V Bandgap Voltage Reference with Improved PSRR Scheme.

DOI: 10.5220/0009772701850193

In Proceedings of the 1st International Conference of Computer Science and Renewable Energies (ICCSRE 2018), pages 185-193

ISBN: 978-989-758-431-2

Copyright

c

185

the conventional scheme of the sub-1V bandgap

voltage reference is analyzed to show the limits of

its performance. In section 3 a related work of high

PSRR structure of bandgap voltage reference is

presented. In section 4, the scheme of the proposed

circuit is given and a detailed analysis of BGVR

core generator is presented and the literal expression

of the output voltage reference is established in

order to show the design method of this block, also

the small high frequency signal model of the

proposed circuit is presented in order to calculate the

lateral expression of the PSRR. In section 5, the

simulation results are given to show the performance

of the proposed circuits and a comparison with

related works is presented. Finally in section 6 a

conclusion is given to show the contribution of the

proposed circuit.

2 CONVENTIONAL SUB-1V

BANDGAP VOLTAGE

REFERENCE

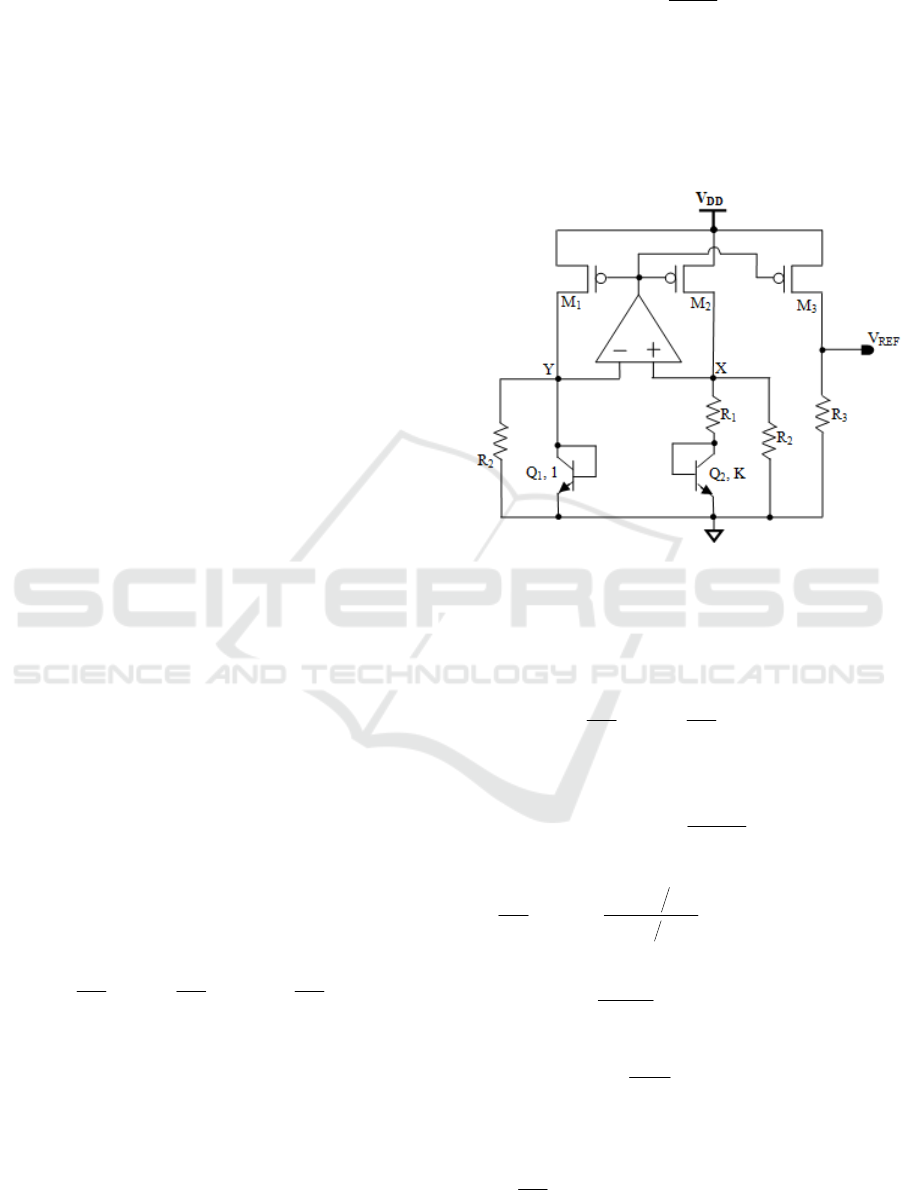
The conventional sub-1V bandgap voltage reference

suitable for low power supply is shown in Figure 1

(Banba et al., 1999). He use an opamp based β-

multiplier architecture with resistive division, where

an opamp works as an error amplifier will form an

inverted feedback loop to enforce the two input

nodes X and Y of the opamp having the same

voltages.

The current mirror is formed by the PMOS

transistors M

1

, M

2

and M

3

having identical size, such

that the currents flowing through this three

transistors are the same. The β-multiplier consists of

two diode connected NPN transistors Q

1

and Q

2

,

with their emitter area ration being 1:K to provide

the required temperature dependent voltages to

construct the voltage reference circuit.

The output voltage reference V

REF

is expressed

as:

)V

R

V.lnK.

R

.(V

R

V

OS

1

2

T

1

2

BE

2

3

REF

1

 (1)

Where,

1

BE

V

is the base-emitter voltage of BJT

Q

1

witch it’s had a negative temperature coefficient

and represents the CTAT voltage.

And V

T

is the thermal voltage (V

T

=25,9mV at

300K) expressed as,

q

T.k

V

B

T

 (2)

Where k

B

is the Boltzmann’s Constant

(k

B

=1,381.10

-23

J.K

-1

), q is the electron’s charge

(q=1,602.10-19C) and T is the absolute temperature.

V

OS

present the input offset voltage of the

opamp.

Figure 1: Schematic of Conventional sub-1V BGVR.

V

T

has a positive temperature coefficient and

represents the PTAT voltage. If we neglect the value

of V

OS

, the Equation 1 becomes:

)V.lnK.

R

.(V

R

V

T

1

2

BE

2

3

REF

1

 (3)

A voltage reference independent of the absolute

temperature is obtained if 0

T

V

REF





, then:

TV

lnK.

R

T

BE

1

2

1





(4)

Noted that

0

T

V

1

BE





and its value depends on

the CMOS technology used and can be extracted by

simulation, while 0

T

V

T





and it value can easily

calculated.

The value of K is usually set to 8, so the resistor

ratio

1

2

R

can be calculated from Equation 4.

ICCSRE 2018 - International Conference of Computer Science and Renewable Energies

186

For a fixed value of V

REF

less than 1V, the value

of the resistance R

3

can be obtained from the

Equation 3. Noted that the V

REF

can be scaled by the

resistor ratio

2

3

R

, and thus achieve an arbitrary

V

REF

.

The conventional sub-1V BGVR using opamp β-

multiplier architecture ensures a low temperature

coefficient for V

REF

but remains very limited in

terms of PSRR caused by the input offset voltage

problem of the error amplifier, although some

modifications have been proposed to improve the

PSRR.

3 RELATED WORK

In order to achieve a high PSRR of the bandgap

voltage reference, a pre-regulator scheme and low

pass filter are added to a main circuit as shown in

Figure 2 (Li and Zhang, 2014). The pre-regulator

bloc improves a DC PSRR at low frequencies while

the low pass filter improves a little the value of

PSRR at high frequencies.

Figure 2: High PSRR structure of bandgap voltage

reference proposed in (Li and Zhang, 2014).

The disadvantage of this structure is the use of large

resistor to achieve a high PSRR and a low

temperature coefficient.

4 PROPOSED SUB-1V BANDGAP

VOLTAGE REFERENCE

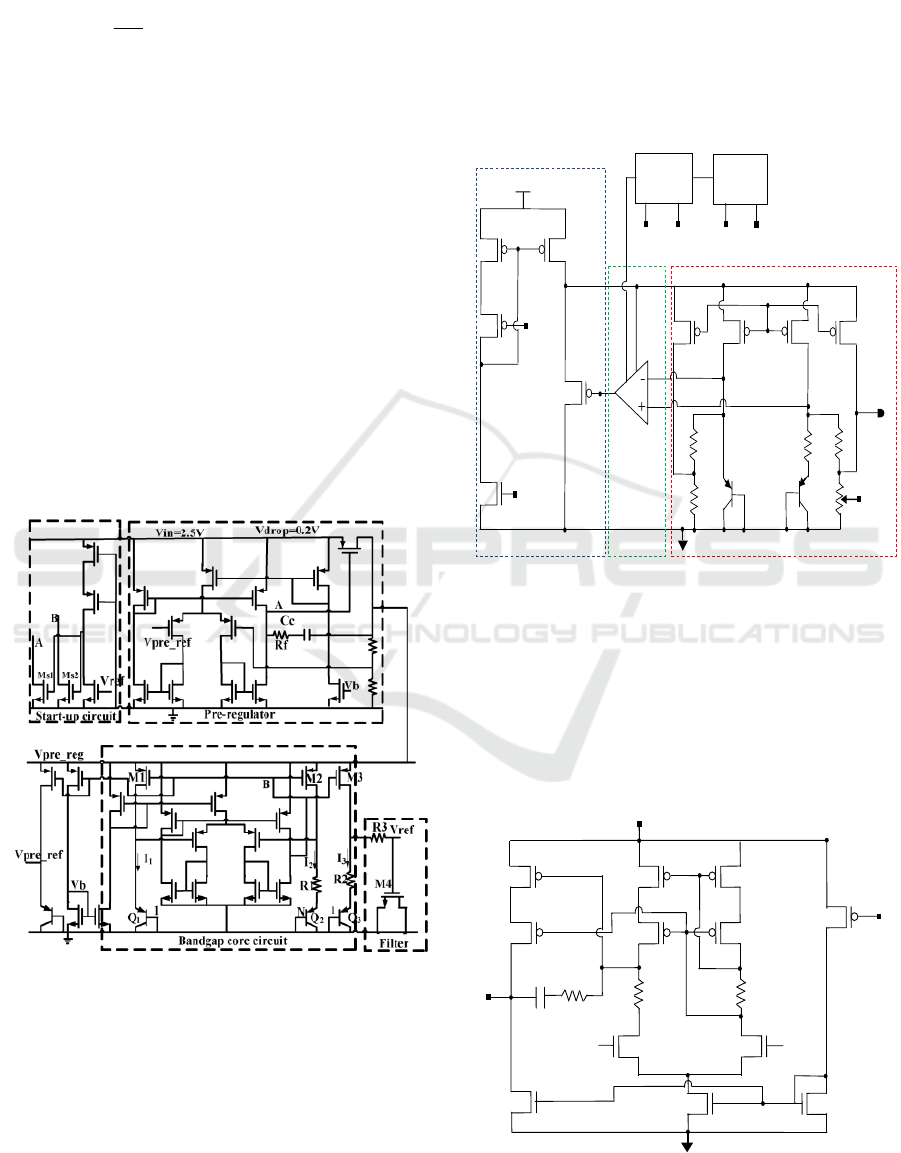
The schematic of proposed sub-1V BGVR is shown

in Figure 3. A current mode regulator scheme is

inserted to improve the performance of the PSRR by

isolating a supply voltage of the error amplifier and

supply voltage of the BGVR core from a power

supply source VDD.

Figure 3: Schematic of proposed sub-1V BGVR

The schematic of the error amplifier used is

shown in Figure 4, a self biased cascode current

mirror load is adopted to achieve a high gain (Allen

and Holberg, 2002). This opamp need a network

compensation to achieve a sufficient phase margin to

guarantee closed-loop stability.

Figure 4: Schematic of error amplifier and his Bias circuit

M

7

M

6

M

5

M

21

M

8

V

bp

V

bn

R

2

V

REF

M

1

M

2

M

4

M

3

Q

1

, K

Q

2

R

1

R

2

R

3

R

3

OA

V

REG

V

bp

Startup

Circuit

Bias

Circuit

V

bp

V

DD

V

G6,7

V

REG

V

G6,7

V

bp

V

bn

Improved PSRR stage:

Current mode regulator

OpAmp

BVR generator core

V

G5

Y

X

M

11

M

20

M

12

M

14

M

15

X

V

REG

V

bp

M

16

M

13

Y

C

M

10

M

9

M

19

M

18

M

17

R

Z

V

bn

R

B

R

B

V

G5

A Sub-1V Bandgap Voltage Reference with Improved PSRR Scheme

187

Figure 5: Schematic of Start-up circuit

The supply voltage of the opamp is V

REG

which

equal to regulate source-drain voltage of M

5

. The

proposed sub-1V BGVR needs a start-up circuit

shown in Figure 5 to fix at the proper operation

point.

4.1. Analysis and Design of Proposed

BGVR Core

The core of the proposed BGVR uses the same

principle of the conventional scheme with some

modifications on the resistive voltage divider in

order to compensate the error introduced by the

input offset voltage of the error amplifier and

consequently to have the same voltage level in the X

and Y nodes.

The PMOS transistors M

1

, M

2

, M

3

and M

4

have

identical size, such that the currents flowing through

this four transistors are the same as

DDDD

IIII

321



. The β-multiplier consists of

two diode connected PNP transistors Q

1

and Q

2

,

with their emitter area ratio being K:1 to provide the

required temperature dependent voltages to construct

the voltage reference circuit.

The expression of the output voltage reference

V

REF

is given by:

)V.

R2

R

lnK.U.

R2

R

.(VKV

OS

1

2

T

1

2

EBRREF

2



(5)

With,

32

3

R

R2R

R2

K





(6)

lnK).U.

R2

R

.(VKV

T

1

2

EBRREF

2

 (7)

If we take into account the input offset voltage

V

OS

, we have V

X

=V

Y

+V

OS

,

Thus the expression of V

REF

becomes:

)V.

R2

R

lnK.U.

R2

R

.(VKV

OS

1

2

T

1

2

EBRREF

2



(8)

Equation 9 shows that the factor amplifying the

input offset voltage is reduced in half in proposed

circuit compared to that of the conventional scheme

(see equation 1).

Differentiating equation 8 with respect to

absolute temperature yields:

)

T

V

.lnK.

R2

R

T

V

.(K

T

V

T

1

2

EB

R

REF

2











(9)

To achieve a near-zero TC of V

REF

, 0

T

V

REF





.

Thus,

TV

lnK.

R2

R

T

EB

1

2

1





(10)

For the CMOS technology used in our design,

CmV/1.89

T

V

2

EB





, and by using Equation 2, we

have

CmV/0.0862

q

k

T

V

BT





, from where we

get:

9.21lnK.

R2

R

1

2

 (11)

The value of K is close to 8, thus:

12

R.21R  (12)

The value of R

1

is calculated from the following

equation:

PTAT

T

1

I

lnK.U

R 

(13)

A reasonable current I

PTAT

is designed to bias

transistor Q

1

in the active region. The value of R

3

is

ICCSRE 2018 - International Conference of Computer Science and Renewable Energies

188

calculated from Equation 7 for a desired output

voltage reference V

REF

.

Design resistor example:

I

PTAT

=10μA,

V0.6V

2

EB



, V

REF

=0.65V.

We have:

PTAT

T

1

I

lnK.U

R 

We get: R

1

=5.4 kΩ

From equation 12, we obtain: R

2

=113.4 kΩ.

From equation 6 and 7, we have:

)U21.(V

V

K

TEB

REF

R

2





We get: K

R

≈0.56

Frome equation 6, we obtain: R

3

=0.64.R

2

Thus: R

3

=72.6 kΩ

Note that the final values of the resistances

calculated by the hand must be adjusted during the

design of the circuit to obtain an optimal value of the

temperature coefficient of V

REF

over the required

temperature range.

The minimum supply voltage to ensure proper

operation of the proposed circuit and obtain an

output voltage reference V

REF

less than 1 V with a

small variation in the required temperature range is

such that the following two constraints are met:

6,7sat3,4sat

SDSDREFDD

VVVV  (14)

And,

6,7sat1,2sat

SDSDEBDD

VVVV

2

 (15)

Where

3,4sat

SD

V is the overdrive voltage of M

3

and M

4

,

1,2sat

SD

V is the overdrive voltage of M

1

and

M

2

and

6,7sat

SD

V is the overdrive voltage of M

6

and

M

7

.

4.2. PSRR Analysis

In order to reduce noise from the supply voltage

which directly influences the performance of the

PSRR, a pre-regulation stage is added to isolate the

supply voltage V

DD

from the supply voltage of the

operational amplifier and also the supply voltage of

the BGVR core generator.

To establish the expression of the PSRR, the

high frequency small signal model of the proposed

circuit is realised (see Figure 6). For the calculation

of the PSRR, a similar method to that adopted in

(Giustolisi and Palumbo, 2003) is applied. The body

effect is ignored and both Q

1

and Q

2

BJT transistors

can be considered as short-circuited.

The voltage v

dif

shown in Figure 5 is the small

signal part of the differential input voltage of the

opamp.

We have:

(s)v

PSRR(s)

ref

dd

 (16)

Where v

dd

(s) is the high frequency small signal

part of V

DD

, v

ref

(s) is the high frequency small signal

part of V

REF

and s is the complex variable of

Laplace.

We can write that:

(s)v

PSRR(s)

ref

reg

dd



(17)

Where v

reg

(s) is the high frequency small signal

part of V

REG

.

For a simple notation the variable s is omitted in

the voltages symbols.

Figure 6: High frequency small signal model of proposed

sub-1V BGVR

A Sub-1V Bandgap Voltage Reference with Improved PSRR Scheme

189

In the node D

3

, the Kirchhoff’s Current Law

gives:

ref

1

21131d

1

2reg3m

v).RY(Yv.Rv).Y(g

3





(18)

Where,

s.CgY

3ds033



 (19)

s.CRY

3gd

1

311





(20)

v

d1

is the high frequency small signal part of V

D1

.

In the node D

1

, Kirchhoff’s Current Law gives:

ref

1

2011

1

2

reg

1

2011

1m

1d

v.

)RY(Y

R

v.

)RY(Y

)Y(g

v

1













(21)

Where,

s.CgY

1ds011



 (22)

s.CRY

1gd

1

110





(23)

By substituting equation 21 in equation 18, we

obtain:

(s)D

(s)N

v

1

ref

reg



(24)

Where,

)Y.(gR)RY).(YY(g(s)N

11m

1

2

1

210133m1





(25)

)Y.(YR)RY).(YY(Y(s)D

111

1

2

1

21011131





(26)

In the node D

6

, the Kirchhoff’s Current Law

gives:









dd65mref31d14d4reg4

v).Y(gv.Yv.Yv.Yv(s).N

5g5gs5m6g6gd6m

vs)..C(gvs)..C(g 



(27)

Where,

s]).CC(CYYgY[g(s)N

45gs6gd655mTmT4



(28)

4m3m2m1mmT

ggggg 



 (29)

4321T

YYYYY 



 (30)

s.CgY

2ds022





(31)

s.CgY

4ds044





(32)

s.CgY

5ds055





(33)

s.CgY

6ds046





(34)

4bs3bs2bs1bs4gs3gs2gs1gs4

CCCCCCCCC 





(35)

And, v

d4

is the high frequency small signal part

of V

D4

, v

g5

is the high frequency small signal part of

V

G5

and v

g6

is the high frequency small signal part of

V

G6

.

In the node D

4

, the Kirchhoff’s Current Law gives:

reg

91

4m

4d

v.

)Y(Y

)Y(g

v

4





(36)

Where,

s.C)//R(RY

4gd

1

329





(37)

In the node G

5

, Kirchhoff’s Current Law gives:







1d

5gs5gdoutout

v

5g

v.

s]).C(C.[Yr

A

v

reg

5gs5gdout

5gs

v.

s]).C(C[Y

s.C



(38)

Where,

s.CrY

out

1

outout





(39)

A

v

is the open-loop gain of the opamp and r

out

is

its output resistance.

C

out

is all capacitance connected from the output

of the opamp to ground.

In the node G

6

, the Kirchhoff’s Current Law

gives:







reggddd1ggd1b

v.Cv.s.Cvs].).C(C[Y

666

888 sm

v).Y(g  (40)

Where, v

s8

is the high frequency small signal part

of V

S8

and,

s.CRY

8gd

1

bb





(41)

ICCSRE 2018 - International Conference of Computer Science and Renewable Energies

190

Where R

b

represent the output resistance of

current source bias network and,

7bs6bs7gs6gs1

CCCCC 





(42)

s.CgY

3088

 (43)

7gd8ds3

CCC 

(44)

In the node S

8

, the Kirchhoff’s Current Law

gives:









dd

2788m

77m

s

v.

s).CYY(g

)Y(g

v

8

6g

2788m

7m8

v.

s).CYY(g

)g(Y





(45)

Where,

8ds8gs2

CCC 

(46)

By substituting equation 45 in equation 40, we

obtain:

reg

2

3

dd

2

g

v.

(s)D

(s)N

v.

(s)D

(s)N

v

6

 (47)

Where,







 s).CYYs(g.C(s)N

2878m12

)Y).(gY(g

77m88m

 (48)

s).CYYs(g.C(s)N

2878m6gd3







(49)



 s).CYYs)].(g).C(C[Y(s)D

2788m6gd1b2

)Y).(gY(g

78m87m

 (50)

By substituting equations 21, 36, 38 and 47 in

equation 27, we obtain:

(s)]D(s)D(s)D(s)[D(s)D

(s)D(s).D(s).Ns)..CYg(g

v

87654

1326gd66m5m

dd

reg







(51)

Where,

(s)D(s).D(s).D(s).N(s)D

21344

 (52)

(s).D(s).D(s)D

315



















s).C(s).(gN

)Y(Y

)Y.(gY(s).D

5gd6m3

94

44m42

(53)

.r).Y.(gY(s).D(s).D(s)D

out11m1216





s]).C(C[Y

45gdout



(54)

s)..C(s).(gD(s).D(s)D

45m217





s].C).RY.(Yr)Y.(g[A

4

1

2101out11mv





(55)

(s).D(s).N(s)D

218







1

2v45m3345gdout

1

21out

R.As)..C(g(s)D.Ys]).C(C.[YR.Y.r





(56)

Note that g

0i

represents the small signal source-

drain conductance of the MOSFET M

i

and Y

i

represents the equivalent admittance for the shunt

connection of the impedance of the capacitor and a

resistor.

By substituting equations 24 and 51 in equation

17, we obtain:

(s)]D(s)D(s)D(s)[D(s)D

(s)N(s).D(s).Ns)..CYg(g

PSRR(s)

87654

1326gd66m5m







(57)

The expression of the PSRR(s) shows that its

transfer function has 7 poles and 7 zeros, and

consequently the frequency response is convergent

and the proposed circuit system is stable.

The expression of DC value (zero frequency) of

the PSRR is obtained by replacing s=0 in all the

terms containing the complex variable s. Thus,

)]0(D)0(D)0(D)0([D)0(D

)0(N).0(D).0(N).gg(g

)0PSRR(

87654

132066m5m







(58)

The equation 58 shows that the DC value of

PSSR can be improved by more than 20dB in

comparison to the previous high PSRR structures in

related work (Li and Zhang, 2014; Tham and

Nagaraj, 1995; Francisco and Hora, 2012).

5 SIMULATION RESULTS AND

LAYOUT

The proposed design of sub-1V bandgap voltage

reference was simulated in 0.18-μm CMOS

1.8V/3.3V technology using Cadence Virtuoso

Spectre Simulator. The proposed circuit generates an

output voltage reference V

REF

of 0.6346 V at 27°C

when the supply voltage is set to 1.8V. As it is

shown in Figure 7, the measurement temperature

coefficient of V

REF

is 22,3ppm/°C over temperature

range -40°C to 140°C.

A Sub-1V Bandgap Voltage Reference with Improved PSRR Scheme

191

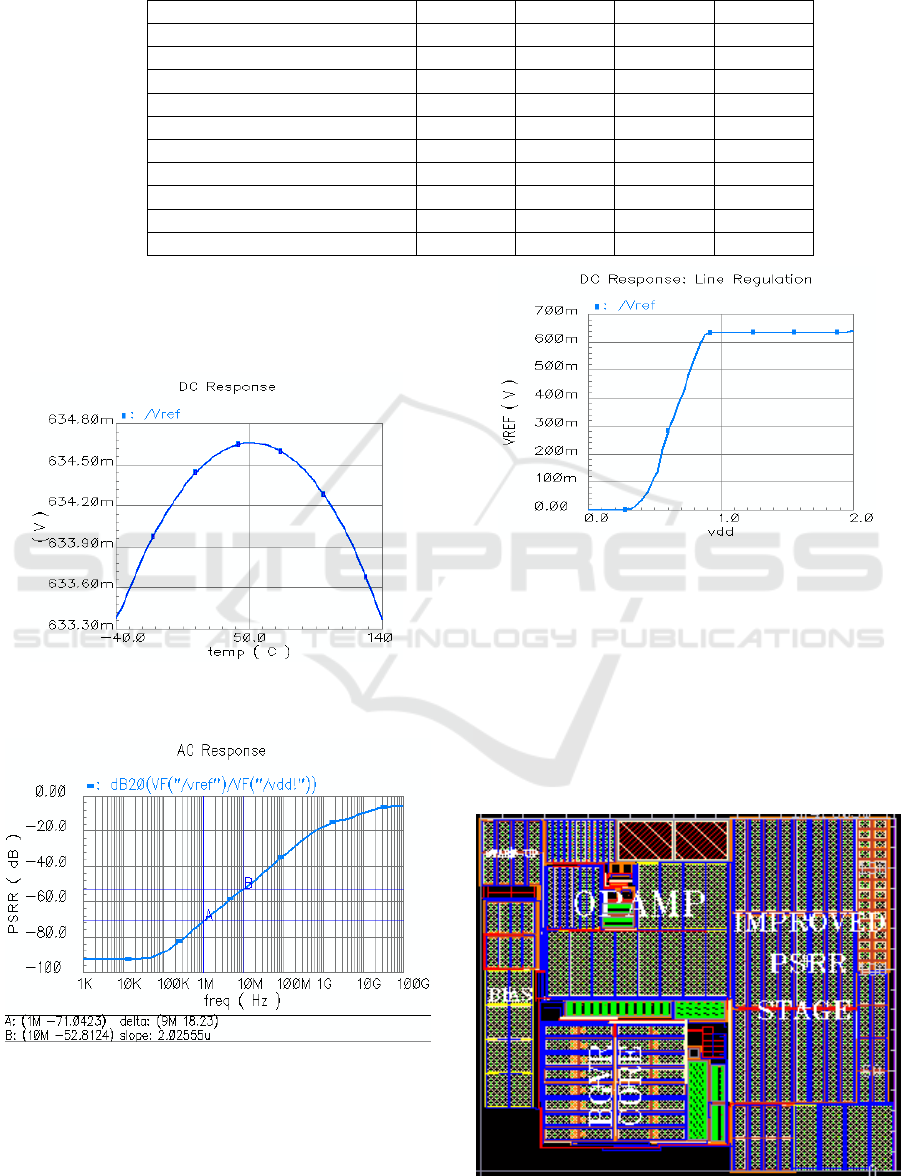
As it is shown in Figure 8 the DC value of PSRR is

-93dB at 10 kHz and -71dB at 1MHz is achieved.

The measurement line regulation of V

REF

is

104μV/V as it is shown in Figure 9.

Figure 7: Simulated temperature dependence of the output

voltage reference at 1.8 supply voltage.

Figure 8: Simulated PSRR of the proposed sub-1V BGVR.

Figure 9: Simulated line regulation of the proposed sub-

1V BGVR.

Table 1 summarizes performance characteristics

of the proposed sub-1V BGVR and comparison with

related works is given. As shown in Table I, the

proposed circuit satisfied the high performance of a

voltage reference and especially for the PSRR value

in the 1MHz to 10MHz frequency range which is

significantly higher than the value found in the

related works (see Table 1).

Table 1: Simulation results summary and comparison

Performance [17] [18] [19] This work

Technology (CMOS) 0,9 μm 0.09 μm 0.18 μm 0.18 μm

V

DD,min

(V) 2.7 2.6 2.5 1.2

V

DD,max

(V) 5.5 3.6 6 1.8

V

REF

(V) 1.236 0.21398 1.194 0.6346

TC (ppm/°C) 85 6.07 6.51 22.3

Temperature operation range (°C) -50 to 125 -20 to 120 -25 to 80 -40 to 140

Line regulation 20μV/V 1143μV/V 104μV/V

PSRR DC (dB) -80 -82.7 -125 -93

PSRR@ 1MHz -40 -40 -71

PSRR@ 10MHz -52.8

ICCSRE 2018 - International Conference of Computer Science and Renewable Energies

192

Figure 10: Layout of proposed sub-1V BGVR reference

The layout of the proposed sub-1V bandgap

voltage reference is shown in Figure 10, the area is

0.0337 mm

2

.

6 CONCLUSIONS

In this paper a novel design of sub-1V bandgap

voltage reference circuit with opamp base β-

multiplier and resistive divider architecture is

proposed. The important contribution of this work is

the obtaining of an accurate voltage reference value

with a high value of the PSRR in a very wide

frequency range from 1kHz up to 10MHz.

The proposed architecture of the voltage divider

has made it possible to minimize the undesirable

effect of the input offset voltage of the opamp and

consequently to obtain a very accurate value of the

output voltage and to improve the dc value of the

PSRR.

In order to reduce noise from the supply voltage

which directly influences the performance of the

PSRR, a pre-regulation stage is added to isolate the

supply voltage source from the supply voltage of the

operational amplifier and also the supply voltage of

the BGVR core generator which allows improving

the value of the PSRR in high frequency.

REFERENCES

Razavi, B., 2017. Design of Analog CMOS Integrated

Circuits. McGraw-Hill Education. Los Angeles, 2

nd

edition.

Widlar, R.J., 1971. New Developments in IC Voltage

Regulators. IEEE Journal of Solid State Circuits,

Vol. SC-6, p 2-7.

Kujik, K.E., 1973. A precision reference voltage source.

IEEE Journal of Solid State Circuits, 8 (3) p 222-226.

Brokaw, A.P., 1974. A Simple three-terminal IC Bandgap

Reference. IEEE Journal of Solid State Circuits, 9 (6)

p 388–393.

Tzanateas, G., et al., 1979. A CMOS BG Reference. IEEE

Journal of solid-State Circuits, 14 (3) p 655-657.

Song, Bang-Sup and Gray, P., 1983. A Precision

Curvative-compensated CMOS BG Reference. IEEE

Journal of Solid State Circuits, 18 (6) p 634-643.

Banba, H., et al., 1999. A CMOS Bandgap Reference with

Sub-1-V Operation. IEEE Journal of Solid State

Circuits, Vol 34, pp. 670-674.

Leung, Ka Nang and Mok, P.K.T., 2002. Sub-1-V

15ppm/°C CMOS Bandgap Voltage Reference without

Requiring low Threshold Voltage Device. IEEE

Journal of Solid State Circuits, 37 (4), pp. 526-529.

Ker, M.D. et al., 2006. New Curvative-Compensation

Technique for CMOS Bandgap Reference with Sub-1-

V Operation. IEEE Journal of Solid State Circuits and

Systems-II:Express Briefs, 53 (8), pp. 667-671.

Ripamonti, G., et al., 1999. Low Power – Low Voltage

Bandgap Refrences for Flash EEPROM Integrated

Circuits: Design Alternatives and Experiments. In

Proceedings of ICECS 1999, Vol. 2, pp. 635-638.

Jiang, Yueming, and Lee, E.K.F., 2000. Design of Low-

Voltage Bandgap Refrence Using Transimpedance

Amplifier. IEEE Transactions on Circuits and

Systems-II, Vol. 47, pp. 552-555.

Annema, Anne-Johan, 1999. Low-Power Bandgap

References Future DTMOST’s. IEEE Journal of Solid

State Circuits, Vol 34, pp. 949-955.

Andreou, C.M., et al., 2012. A Novel Wide-Temperature-

Range, 3.9ppm/oC CMOS Bandgap Reference Circuit.

IEEE Journal of Solid-State Circuits, vol.47, no. 2, pp.

574–581.

Xin, Ming, et al., 2009. A 2.8 ppm/◦C high PSRR

BiCMOS bandgap voltage reference. Journal of

Semiconductors, Vol.30, No. 9.

Li, Xiuhan, and Zhang, Hanru, 2014. A High PSRR

Voltage Reference for High Efficiency Power

Management Circuits of MEMS Energy Harvesters,’’

Journal of Applied Science and Engineering, Vol. 17,

No.2, pp. 111-116.

Allen, Phillip E. and Holberg, Douglas R., 2002. CMOS

Analog Circuit Design. Oxford University Press. New

York, 2

nd

edition.

Giustolisi, G. and Palumbo, G. 2003. A Detailed Analysis

of Power Supply Noise Attenuation in Bandgap

Voltage References. IEEE Transactions On Circuits

and System-I: Fundamental Theory and Applications,

vol. 50, No. 2, p. 185-197.

Tham, Khong-Meng and Nagaraj, K., 1995. A Low

Supply Voltage High PSRR Voltage Reference in

CMOS Process. IEEE Journal of Solid State Circuits,

vol. 30, No. 5, pp. 586-590.

Francisco, Keith R. and Hora, Jefferson A., 2012. Very

Low Bandgap Voltage Reference With High PSRR

Enhancement Stage Implemented in 90nm CMOS

Process Technology for LDO Application. IEEE

International Conference on Electronics Design

Systems and Applications.

A Sub-1V Bandgap Voltage Reference with Improved PSRR Scheme

193