
MPPT and Pitch Angle Control of a Permanent Magnet Synchronous
Generator based Wind Emulator
Rania Moutchou* and Ahmed Abbou
Mohammadia School of Engineers (EMI), Research team in Electrical Energy and Control (RTEEC)
Mohammed V University, Rabat, Morocco
Keywords: MPPT, pitch angle, DC machine, wind turbine emulator, PMSG.
Abstract: This work aims at studying the interconnection characteristics of a wind turbine based on a permanent
magnet synchronous generator (PMSG) from a wind turbine emulator. The goal is to make a maximum
power point tracking (MPPT) analysis and pitch angle control. In first place, wind turbine modeling is done
using a DC machine. Then, a maximum power technique MPPT and a wedging angle control strategy will
be developed in order to adapt turbine speed to wind speed to maximize and limit power output of the wind
turbine (WT). Results of simulation are given to show the performance and the effectiveness of the
proposed controls, regarding reference tracking, sensibility to high wind speed variations and unavailability
of turbine parameters. The complete system model will be developed in the Matlab/Simulink environment.
1. INTRODUCTION
Recently, the global energy consumption has
seen an enormous increase due to the massive
industrial development, which tends to increase in
size. China is one of the world’s countries which
represent a remarkable case of this increased
consumption of energy. The risks of scarcity of
fossil fuels and their effects on climate change once
again highlight the importance of renewable
energies, particularly the wind turbine which has
been identified as one of the most promising.
The evolution of the wind turbine has grown in
recent years, which has been given enormous
attention as a privileged technology that represents
an interesting alternative especially for the
production of electrical energy. In this paper, we
focus on the variable speed wind energy conversion
system (WECS) due to its many advantages, such as
a reduced torque oscillations and mechanical stress
and a better exploitation of available wind energy
compared to the fixed speed WECS.
In this paper, we aim to study the
interconnection characteristics of a permanent
magnet synchronous generator based wind turbine
from a wind turbine emulator based on the principle
of control of a DC machine. The main objective is to
develop a MPPT control method in order to adapt
the speed of the turbine with respect to the wind
speed, in order to maximize the converted power,
this will improve their integration to the electrical
networks. On the other hand, the pitch angle control
is employed to protect the WT against overloading
in the case of high wind speed. The performances of
the proposed controllers system were tested,
analyzed using Matlab/Simulink Software.
2. CONVERSION OF WIND
ENERGY
The WECS proposed is represented on the
Fig. 1. A wind turbine is a device that captures
the kinetic energy of the wind and converts it
into mechanical energy.
Moutchou, R. and Abbou, A.
MPPT and Pitch Angle Control of a Permanent Magnet Synchronous Generator based Wind Emulator.
DOI: 10.5220/0009774503830390
In Proceedings of the 1st International Conference of Computer Science and Renewable Energies (ICCSRE 2018), pages 383-390
ISBN: 978-989-758-431-2
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
383

Figure 1: Wind energy conversion system (WECS).
A. Wind modeling
The wind speed at a point can be broken down
into two components: a slowly varying average, and
the other with fluctuations such as:
(1)
With,
is the average value of the slow component,
and
is the fluctuations caused by turbulence.
Fluctuations in wind speed must be treated
statistically. The standard deviation describes the
variability of the wind and is defined as follows:
∆
∆
∆
(2)
It has been demonstrated experimentally that
only the slow component introduces in the
production of the pair at the level of the pale. To
correct the effect of the turbulence component, a low
pass filter is introduced in Fig .2.
Figure 2: Synoptic diagram of wind reconstruction.
B. Wind turbine system modeling
The modeling of the wind turbine is the
greatest part for a WECS. The modeling of the
turbine must be made to collect the maximum
kinetic energy of the wind with lower costs.
The captured aerodynamic power can expressed
as:
...
.
ʎ, (3)
And, the torque collected by the wind turbine is
given by the following relation:
Ω
ʎ
...
.
.
ʎ, (4)
Where,
ρ
,
S
and
V
represent respectively the
density of air, the surface swept by the blades and
the wind speed.
In our case, the variations of
),(
p
C
are
modeled by the following exponential
approximation:
ʎ,
ʎ
ʎ
ʎ (5)
With:
1β
0.035
β0.08λ
1
λ
1
3
i
And
is the pitch angle of the blades.
Where, ʎ present the relationship between
the linear velocity of pale and the speed of the
wind which can be expressed as follows:
Ω
(6)
With R the ray of pale of the wind,
reactivity power coefficient and Ω
t
he angular
a velocity of the turbine.
,
,
,
,
,
-depend on the particular
turbine and the values are given in table 1.
T
ABLE
1:
C
OEFFICIENT DEFINING THE EVOLUTION OF CP
.
COEFFICIENT
VALUE
0.5109
116
0.4
5
1
1.
V
White
Noise
Gaussian
Low Pass
Filter
Avera
g
e S
p
ee
d
V0
ICCSRE 2018 - International Conference of Computer Science and Renewable Energies
384

21
0.0068
Fig. 3 represents the power coefficient curves as
a function of λ for different values of β. The
maximum value of
p
C
(
maxp
C
=0.48) is achieved
for
opt
λ
=0.014 and
0
.
Figure 3: Power coefficient as a function of λ.
The characteristic of the optimum power of a
wind turbine is strongly nonlinear. For each wind
speed, the system should always find the maximum
power, which requires controlling the speed of the
WT to be equal to its optimum one. It is clear from
Fig. 4 that the mechanical power is maximized at
particular rotational speed for each wind speed.
Figure 4: The power of the wind turbine.
We take the aerodynamic torque in this case is
equal to the torque of the fast shaft:
(7)
The fundamental equation of the dynamic makes
it possible to determine the development of the
rotational speed from the mechanical torque
mec
C
available on the rotor of the machine.
Ω
(8)
m
and
J
represent respectively the mechanical
speed and moment of inertia.
The mechanical torque is given by the following
relation:
Ω
(9)
Where,
em
C
is the electromagnetic torque and
f
is a
viscous friction coefficient.
3. EMULATION BY
ASSOCIATION OF THE DC
MACHINE
The DC machine is reversible; it works as a
motor if the torque and speed are of the same sign
and generator if the torque and speed are contrary
signs. Fig. 5 shows the association of the MCC with
the system.
Figure 5: The MCC with the system.
From a methodological point of view, the control
of the DC motor is very important and it is done by a
chopper + regulator shown in Fig. 6.
λ
MPPT and Pitch Angle Control of a Permanent Magnet Synchronous Generator based Wind Emulator
385
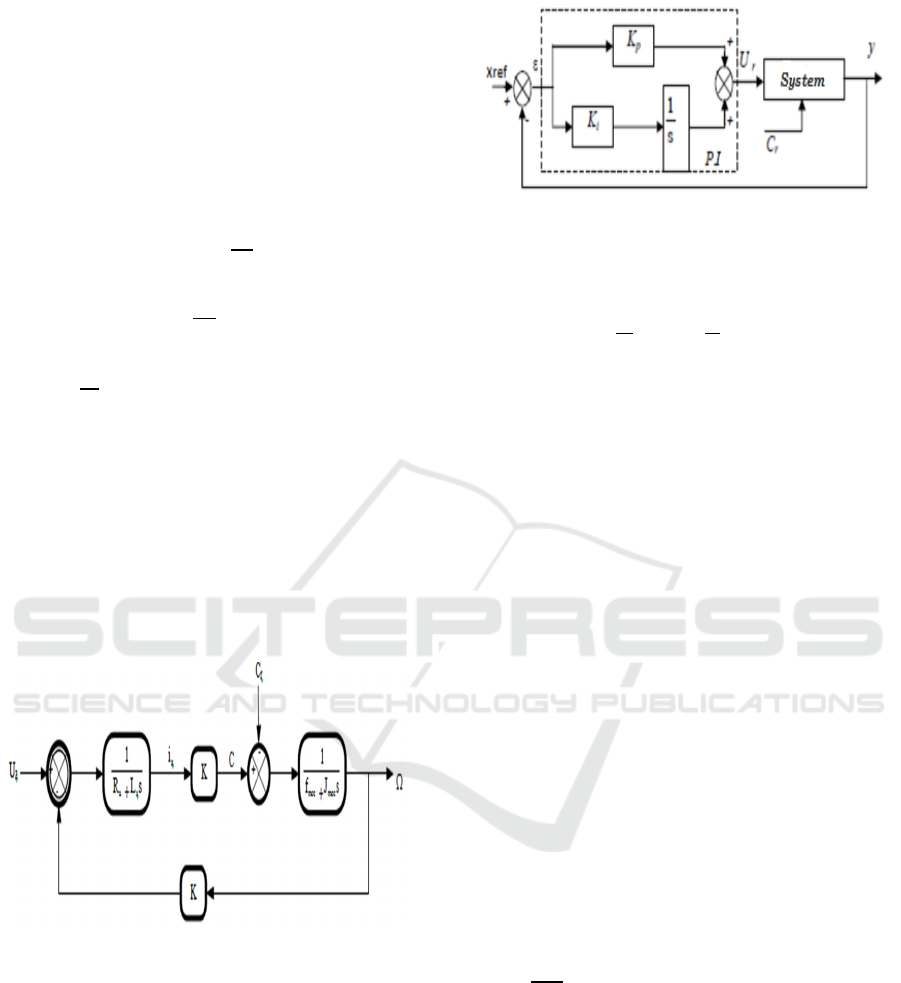
Figure 6: Block diagram of the MCC regulated by a
PI.
A. Modeling of the DC machine
The DC machine can be modeled through
electrical, electromechanical and mechanical
equations.
The electrical equations of the machine are:
For the excitation circuit
.
.
(10)
For the armature circuit
.
.
.
.Ω (11)
The mechanical equation is given by:
.
Ω
.
.
.Ω
(12)
With
the resistant torque,
the coefficient
of friction,
the Moment of inertia.
In our case, the machine is separate excitation,
the flux created by the inductor winding is constant.
We then have:
∅
.
(13)
From the electrical (armature) and mechanical
equations, the block diagram of the model of the DC
machine is shown in Fig. 7.
Figure 7: Block diagram of the MCC with constant
flow.
B. Synthesis of the integrated proportional
regulator (PI)
After modeling the DC machine, we will then
develop the synthesis of the proportional-integral
(PI) controller used to control the DC machine.
The regulator (PI) is given by the following
Fig. 8:
Figure 8: Regulator P.I.
The transfer function will be:
(14)
4. MPPT CONTROL WITHOUT
MECHANICAL SPEED
CONTROL
The purpose of variable speed control is to
extract the maximum power of the wind turbine. For
that, we need algorithm acting on set point variables
to get the best return possible of the device. Through
the bibliography study, we distinguished two
families control structures for maximizing extracted
power:
MPPT control without mechanical speed
control;
MPPT control with mechanical speed
control.
In our case, the technique used for extracting the
maximum power is MPPT without mechanical speed
control, this mode of control is based on the
assumption that the wind speed varies very little
steady state in front of the system's electrical time
constants wind turbine, which implies that the
acceleration torque of the turbine can be considered
like no one. In this case, from the mechanical
equation, we can write:
Ω
0
Ω
(15)
Moreover, if we neglect the effect of torque due
to viscous friction Ω
0 compared to the
mechanical torque
, we can then write:
(16)
The electromagnetic torque is determined from
an estimate of the torque wind turbine:
∗
(17)
ICCSRE 2018 - International Conference of Computer Science and Renewable Energies
386

The wind turbine torque is itself estimated
according to the wind speed and the speed of the
turbine:
Ω
...
.
,
.
.
Ω
(18)
An estimate of the speed of the turbine is
calculated from the speed mechanical:
Ω
(19)
The estimate of the wind speed is then expressed
by:
Ω
(20)
From these relationships we have:
∗
...
.Ω
(21)
To extract the maximum power generated, it is
necessary to set the speed ratio at
which
corresponds to the maximum of the power
coefficient
.
The estimated electromagnetic torque must then
be set to the following value:
∗
...
.Ω
.
(22)
Fig. 9 shows the principle of MPPT control of the
wind turbine without slaving of the speed of
rotation:
Figure 9: Block diagram of the maximization of the
power extracted without servo of speed.
5. SIMULATION RESULTS AND
DISCUSSIONS
The wind profile illustrated in Fig. 10, that
varies considerably, is applied to the wind turbine
system. A simulation is performed considering
the operation of the vacuum turbine, (no resisting
torque and no power generation).
For a wind speed of
= 10 m/s:
Figure 2: Wind speed’s profile.
Different wedging angle and a fixed
speed
V = 10 m /s
Figure 11: Evolution of the speed of the turbine.
MPPT and Pitch Angle Control of a Permanent Magnet Synchronous Generator based Wind Emulator
387
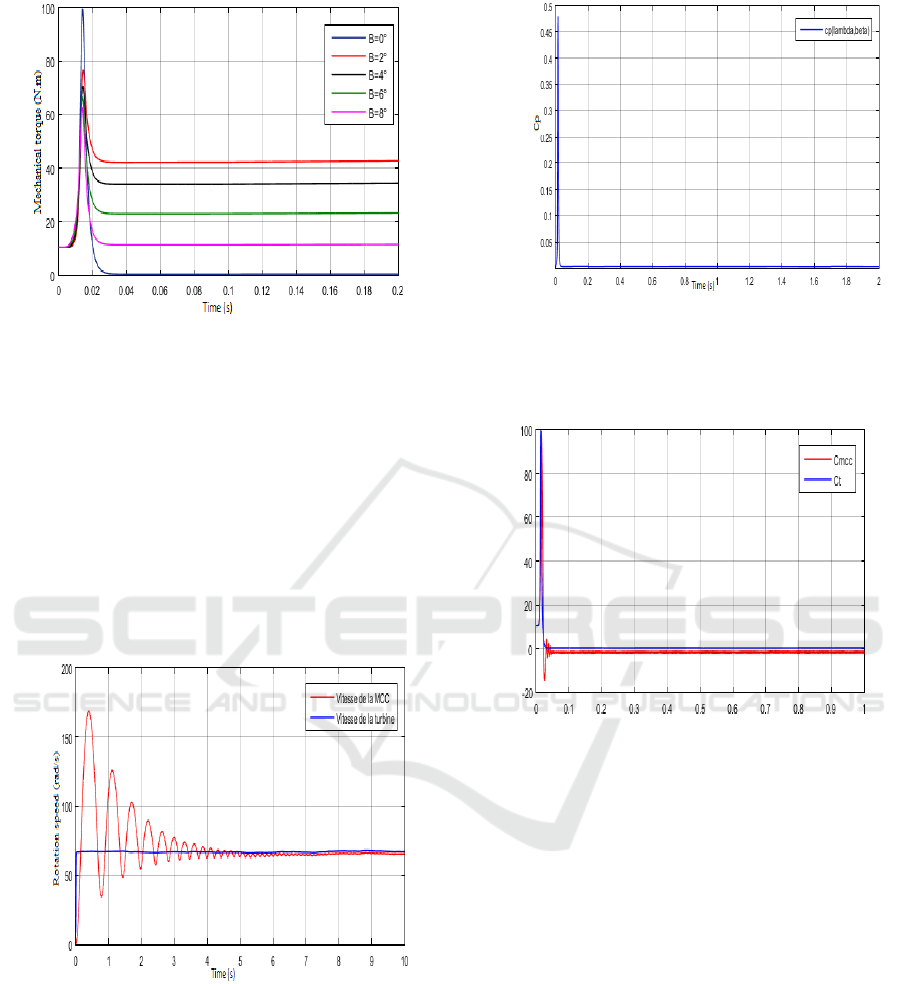
Figure 12: Evolution of turbine torque.
From the results presented in Figs. 11 and
Fig. 12, we see that for low speeds, the increase in
wedging angle causes good dynamics at the
turbine due to the large torque developed. On the
other hand, concerning the high-speed operation
where the small angles of rigging are more
effective.
The application of the model of the wind
given by Fig. 10 , shows the shape of the
rotational speed variation of the direct current
machine Fig. 13 and the power coefficient Cp,
Fig. 14.
Figure 13: Reference speed and measured speed
of the MCC.
Fig. 13 shows respectively the speed of the
turbine which is the reference speed at which one
wants to control the MCC and the speed of the
MCC. It is clear that the speed of the turbine is
not adapted to that of the wind, however there is a
good continuation of the reference value.
Figure 14: Variation of the power coefficient.
The value of the power coefficient does not
reach the maximum theoretical value declared by
Betz (0.59) as shown in Fig. 14.
Figure 15: Reference torque generated by the
turbine and measured torque produced by the DC
motor.
It can be seen that the measured torque is
very well the variations of the reference torque
imposed on it by the model of the wind turbine
Fig. 15, which shows the efficiency of the
proportional integral regulator in terms of
trajectory tracking.
The MPPT control structure without speed
control was simulated with a mean wind profile
around 10m /s.
ICCSRE 2018 - International Conference of Computer Science and Renewable Energies
388

Figure 16: Relative speed with MPPT.
Figure 17: Power coefficient with MPPT.
Figure 18: Wind turbine power with MPPT.
Figure 19: Wind turbine torque with MPPT.
From the results Fig. 16, Fig. 17, Fig. 18 and
Fig. 19, we see that the power, the aerodynamic
torque and mechanical speed vary proportionally
with the variation of the wind profile. Note also
that the relative speed λ and the power coefficient
Cp follow their references with a non-nule static
error. This amounts to the absence of regulation
of the speed of the turbine.
6. CONCLUSION
This paper discusses the modeling steps of a
wind turbine to drive a DC machine to reproduce
the torque and speed variations of the wind
turbine. We first established a model to reproduce
variations in wind speed. Torque and rotational
speed are imposed as references to a DC machine.
The MCC was modeled in turn and was
controlled by a PI regulator for its simplicity and
to reduce static error.
In a second step, by adapting the speed of the
turbine to that of the wind one can extract the
maximum power of the turbine using the
technique MPPT. The simulation results show a
good speed reference tracking of the optimal
operating point.
As a perspective for the rest of this work, to
model each component of the proposed system to
study the reactions of the permanent magnet
synchronous generator in the presence of network
imbalance, voltage dips and fluctuations.
MPPT and Pitch Angle Control of a Permanent Magnet Synchronous Generator based Wind Emulator
389

ACKNOWLEDGEMENT
This work has been supported by National
Center for
Scientific and Technical Research (CNRST), Rabat,
Morocco.
REFERENCES
I. Colak, G. Fulli, S. Bayhan, S. Chondrogiannis and S.
Demirbas, “Critical aspects of wind energy systems in
smart grid applications,” Renewable and Sustainable
Energy Reviews, vol. 52, pp. 155–171, December
2015.
X. Zhao and D. Luo, “Driving force of rising renewable
energy in China: Environment, regulation and
employment,” Renewable and Sustainable Energy
Reviews, vol. 68, pp. 48-56, September 2016.
A. El Yaakoubi, A. Asselman, A. Djebli and E. H.
Aroudam, “A MPPT strategy based on fuzzy control
for a wind energy conversion system ,” 9th
International Conference Interdisciplinarity in
Engineering, INTER-ENG, vol. 22, pp. 697-704,
Tirgu-Mures Romania, 8-9 October 2015.
R. Tiwari and N. R. Babu, “Fuzzy logic based MPPT for
permanent magnet synchronous generator in wind
energy conversion system,” IFAC, vol. 49, pp. 462-
467, April 2016.
S. Chekkal, N. A. Lahaçani, D. Aouzellag and K.
Ghedamsi, “Fuzzy logic control strategy of wind
generator based on the dual-stator induction
generator,” Electrical Power and Energy Systems, vol.
59, pp. 166-175, March 2014.
S. El Aimani. Modélisation de Différentes Technologies
d’Eoliennes Intégrées dans un Réseau de Moyenne
Tension ,Thèse présentée pour l’obtention du diplôme
de Doctorat en Génie Electrique, Université des
Sciences et Technologies de Lille. 2004.
A. Dahbi, N. Nait-Said, and M. S. Nait-Said, “A novel
combined MPPT-pitch angle control for wide range
variable speed wind turbine based on neural network,”
International Journal of Hydrogen Energy, vol. 41, pp.
9427-9442, June 2016.
A. Mechter, K. Kemih, and M. Ghanes, “Sliding Mode
Control of a Wind Turbine with Exponential Reaching
Law,” Acta Polytechnica Hungaria, vol. 12, pp. 167-
183, 2015.
AKEL Fethi, “ETUDE ET REALISATION D’UN
EMULATEUR DE TURBINE EOLIENNE “, thèse de
magister, école militaire polytechnique, Algerie 2009.
I. Nouira, and A. Khedher, “A contribution to the design
and the installation of an universal platform of a wind
emulator using a DC motor”, International Journal of
Renewable Energy Research, vol. 2, pp. 797-804,
October 2012.
M. Reddak, A. Berdai, A. Gourma, and A. Belfqih,
“Integral backstepping control based maximum power
point tracking strategy for wind turbine systems driven
DFIG,” IEEE, 2
nd
International Conference on
Electrical and Information Technologies, pp. 84-88, 4-
7 May 2016.
APPENDIX
TABLE 2: TURBINE AND MCC PARAMETERS.
Parameters of the Wind Turbine and MCC
PARAME
TER
VALUE PARAME
TER
VALUE
Nominal
power
130
Turbine
radius
2
Moment
of inertia
0.0089
/²
Armature
resistance
0.5 Ω
Coefficien
t of
friction
0.02 ..
Inductance
of
armature
0.001
Moment
of inertia
0.05
/²
Constant
torque
0.7
/A
ICCSRE 2018 - International Conference of Computer Science and Renewable Energies
390
