
Daily Time Series Estimation of Global Horizontal Solar Radiation
from Artificial Neural Networks
M. Bellaoui, K. Bouchouicha, N. Aoun, B. Oulimar and A. Babahadj
Unité de Recherche en Energies renouvelables en Milieu Saharien, UERMS, Centre de Développement des Energies
Renouvelables, CDER, 01000, Adrar, Algeria
Keywords: Database, Solar Radiation, Neural Networks, Estimation.
Abstract: Obtaining a complete and efficient database is necessary for the sizing of photovoltaic systems. Despite the
existence of the unit-level radiometric chain, the acquisition of data from different radiation components has
problems, and thus gaps in the radiometric database. Thus, good sizing is possible only if the measurements
are available continuously in space and time. The purpose of our work is to use the insolation basis for the
estimation of the global daily radiation at the URER-MS research unit (Latitude 27.87 Longitude -0.272)
using neuronal techniques. The efficiency of using neural networks as a global solar irradiation modeling
tool.
1 INTRODUCTION
Energy assessment requires measurements and
comprehensive data collection in the best conditions.
Several studies have been conducted on the
evaluation of solar radiation by models in order to
generate artificial sequences of radiometric data.
Artificial intelligence is a term, in its broadest
sense, the ability of a machine to perform functions
similar to those that characterize human thought.
Artificial Intelligence techniques are grouped into
five branches: neural networks, fuzzy logic, genetic
algorithms, expert system and hybrid systems
(Mohandes, 1998), ( Mubiru and Banda, 2008).
The aim of our work is to use neural models to
estimate the global daily radiation at the Renewable
Energy Research Unit station in the Saharan
environment, in order to obtain a reliable database.
2 MODEL DESCRIPTION
2.1 Artificial Neural Network (ANN)
Is a system inspired by theories and observation of
the neural structure and functioning of the human
nervous system. ANN is a programmed
computational nonlinear model which is widely used
in the field of solar energy for design, modeling and
optimization solar projects.
The Artificial Neural Network is a part of
Artificial Intelligence (AI) which represents
computational model that have the capability to learn
from observational data. ANN model usually can be
divided into three parts, named layers, the input layer
which is responsible for receiving the input data, these
data must be normalized before being used, the
second layer is hidden layer that contains a nonlinear
transfer function and the third layer produces the
output (Mellit, 2005; Mellit et al 2009).
Learning an artificial neural network being
reduced to an optimization problem: find the
minimum of an error function, so we can build on
this method of universal optimization gradient
descent, which will be the gradient backpropagation
rule for multilayer networks, studied after (Azadeh
et al 2009).
Figure 1: Neuronal network model.
Bellaoui, M., Bouchouicha, K., Aoun, N., Oulimar, B. and Babahadj, A.
Daily Time Series Estimation of Global Horizontal Solar Radiation from Artificial Neural Networks.
DOI: 10.5220/0009775204050408
In Proceedings of the 1st International Conference of Computer Science and Renewable Energies (ICCSRE 2018), pages 405-408
ISBN: 978-989-758-431-2
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
405

2.2 Learning Algorithm
Let p and t be the target input and output vectors
used for network learning and a, is the network
response. The objective is to minimize the cost
function F (mean squared error between inputs and
network responses) (Rahimikhoob, 2010) (CYRIL,
2011) defined as:
(1)
Q is the number of examples. This minimization
is done according to a delta rule:
(2)
The Least Mean Squared (LMS) algorithm
estimates the kth iteration of the mean squared error
e2 by calculating the derivative of the mean squared
errors in relation to the network weight and bias, So:
(3)
Or
Simplified:
(4)
This means that the weights and biases of the
network must change
(5)
Where α is the learning rate. For the case of
several neurons, we can write:
(6)
Multi-layer perceptron (MLP), or layered
networks, form the vast majority of networks. They
are timeless (static and not dynamic networks).
3 DATABASE PRESENTATION
The data we used in our application are global
insolation measurements of the Adrar site (Latitude
27.87 Longitude -0.272).
The geographical coordinates of Adrar are:
- Altitude: 278 m
- Latitude: 27 ° 52 North
- Longitude: 00 ° 17 West.
The database has been divided into two subsets,
the first is used to perform the learning and the other
set to do the test. The first contains four years from
2000 to 2003, and the second two-year set from June
2003 to June 2005 to test. As shown in the following
figures:
Figure 2: Daily data of global solar irradiation Horizontal
2000-2003, ADRAR area.
Figure 3: Daily data of global solar irradiation Horizontal
2003-2005, ADRAR. area.
Figure 1 : neurone network Model
ICCSRE 2018 - International Conference of Computer Science and Renewable Energies
406

4 MODEL USED
The model used to estimate global solar radiation on
a horizontal plane is the modified form of the
Angstrom equation. This regression equation relates
the average fraction of daily radiation by the
radiation in a clear sky and the average fraction of
duration of sunshine (Angstrom, 924), (Prescott,
940), (Page, 1961), (Duffie and Beckman, 1991).
(7)
H: daily global solar radiation.
H
0
: extra-terrestrial solar radiation.
S: sunshine durations.
S
0
: astronomical duration of the day.
a and b empirical coefficients.
Isc: The solar constant (= 1367 Wm2).
φ latitude of site, δ solar declination,
ω sunrise angle,
(9)
(10)
The maximum sunshine duration S
0
can be
calculated as follows:
(11)
5 SIMUATION RESULTS
For learning we used the measured data during the
period 2000-2003.
The correlation coefficient for the forecast R =
0.81651.
Figure 4: Learning phase (First step).
The correlation coefficient for the forecast R =
0.76259.
The mean squared error graph shows that the
Lavenberg-Marquardt algorithm gives satisfactory
results and the error is less than 0.7.
The correlation coefficient for the forecast R =
0.73512.
Figure 5: Quadratic Mean Error. Curves red green blue
Learning, validation, test respectively.
Figure 6: Gradient = 4.8735
e
-005 for 12 iteration.
Daily Time Series Estimation of Global Horizontal Solar Radiation from Artificial Neural Networks
407
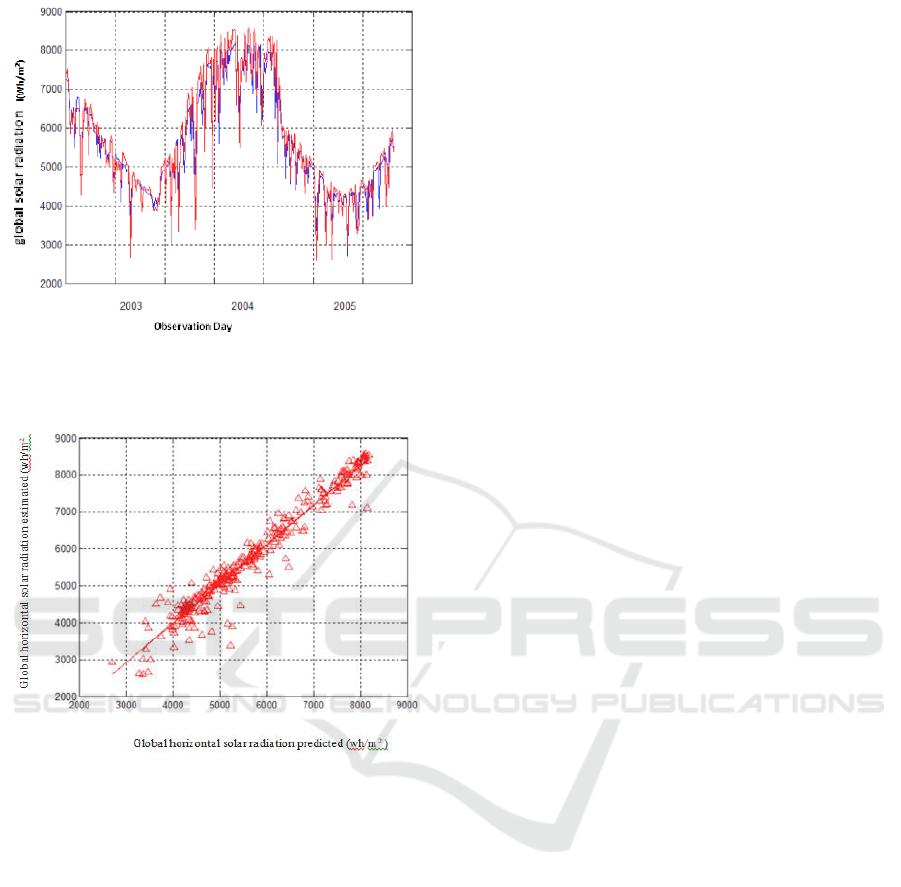
Figure 7: Global horizontal solar radiation estimated from
a sunshine duration of the 2003-2005 period, in red the
desired outputs, in blue the predicted outputs (simulated).
Figure 8: The correlation between the desired outputs and
predicted outputs of global horizontal solar radiation.
The function represents an approximation of the
correlation between predicted and desired outputs;
according to the data used the coefficient is
approximately 0.78 so make improvements on the
model to get better results.
6 CONCLUSIONS
In our study we were interested in the neural
network prediction method, in particular the multi-
layer perceptron method.
For learning has used the Levenberg-Marquardt
algorithm to calculate the approximation weights.
For this network the inputs propagate to the output
without return.
For the learning used the database 2000-2003,
for the test used the data of 2003-2005, the
simulation with these databases gives results of
correlation coefficient equal 0.81651for learning;
and 0.76259 for validation. According to the
correlation graphs between the desired and predicted
outputs on the one hand, and the mean square error
on the other, we can use this neural model to
estimate daily global solar irradiations.
Improving the model with the use of data from the
Adrar URERMS research unit station remains a
work of the future.
REFERENCES
Angstrom, A., 1924. Solar and terrestrial radiation, Quart
J Roy Met Soc, 50:121–5.
Azadeh, A., Maghsoudi, A., Sohrabkhani, S., 2009 An
integrated artificial neural networks approach for
predicting global radiation, Energy Conversion and
Management 50.
CYRIL v., 2011. Prédiction de séries temporelles de
rayonnement solaire global et de production d’énergie
photovoltaïque à partir de réseaux de neurones
artificiels, Université de corse-pascal paoli. Thèse
doctorat
Duffie JA, Beckman WA. Solar engineering of thermal
process. New York: Wiley; 1991.
Mellit, A., 2008. Artificial Intelligence technique for
modelling and forecasting of solar radiation data, Int.
J. Art. Int and Soft Computing, Vol. 1, No. 1.
Mellit, A., Benghanem, M., Hadj Arab, c, A., Guessoum,
d. 2005 A simplified model for generating sequences
of global solar radiation data for isolated sites :Using
artificial neural network and a library of Markov
transition matrices approach, Solar Energy 79 469–
482.
Mohandes, M., Rehman, S., and Halawani, T. O., 1998.
Estimation of global solar radiation using artificial
neural networks, Renewable Energy, Vol. 14.
Mubiru, J., Banda, E. J. K. B., 2008. Estimation of
monthly average daily global solar irradiation using
artificial neural networks, Solar Energy, 82.
Prescott, JA., 1940. Evaporation from water surface in
relation to solar radiation. Trans Roy Soc Austrn
46:114–8.
Page, JK., 1961.The estimation of monthly mean values of
daily total short wave radiation on vertical and
inclined surfaces from sunshine records for latitudes
40N–40S. In: Proceedings of UN conference on new
sources of energy, 78–90.
Rahimikhoob, A., 2010. Estimating global solar radiation
using artificial neural network and air temperature data
in a semi-arid environment, Renewable Energy 35.
ICCSRE 2018 - International Conference of Computer Science and Renewable Energies
408
