
The Finite Volume Method Applied to The Patlak-Keller-Segel
Chemotaxis Model in a General Mesh
Ouafa Soualhi
1
and Mohamed Rhoudaf
2
1
Department of Mathematics, Moulay Ismail University, Meknes, Morocco
2
Department of Mathematics, Moulay Ismail University, Meknes, Morocco
Keywords:
chemotaxis; finite volume; numerical simulation.
Abstract:
In this paper, we present the discrete duality finite volume method (DDFV) applied to a model of (Patlak)
Keller-Segel modeling chemosensitive movements, this model consists of a coupled system of elliptic and
parabolic equations. Firstly, we prove the existence and uniqueness of the numerical solution to the proposed
scheme. Next, numerical simulations are performed to verify accuracy.
1 INTRODUCTION
Chemotaxis is the characteristic movement or orienta-
tion of cells, organisms or bacteria along chemical con-
centration gradient towards chemoattractant or away from
chemorepellant, it is very essential for organisms to search
food around them. Well-known examples, the first is the
bacteria Escherichia Coli such that there cells are known to
swim towards the amino acids serine and aspartic acid and
towards sugars such as maltose, ribose, galactose and glu-
cose, the second is the amoeba Dycliostelium discoideum
,where it has been used as a model organism in molecu-
lar biology and genetics, and is studied as an example of
cell communication, differentiation, and programmed cell
death.
There are two types of chemotaxis:
1) Positive chemotaxis: the movement of organisms to-
wards a chemical.
2) Negative chemotaxis: the movement of organisms away
from a chemical.
Patlak in 1953 (Patlak, 2953) and Keller and Segel in
1970 (Keller and Segel, 1970), were created as a classical
model to describe the evolution over time of the cell den-
sity n(x,t) and the chemical signal concentration variable
S(x,t) assuming that the cells emit directly the chemoat-
tractant which is directly diffused. A lot of theoretical and
mathematical model chemotaxis phenomena but the most
famous model is the following the classical Paltak-Keller-
Segel(PKS) system:
(
∂n
∂t
− div(∇n − χn∇S) = 0, on Ω × [0,T ],
−div(∇S) − µn + S = 0, on Ω × [0,T ],
(1)
where
χ : The chemotactic sensitivity function.
µ : The secretion rate at which the chemical substance is
emitted by the cells, let µ > 0.
Ω is a Convex, bounded and open set of R
2
and T > 0.
The initial conditions on Ω are given by
n(x,0) = n
0
(x), in Ω. (2)
Therefore, the system (1) is supplemented by the following
boundary conditions on ∂Ω × [0,T ].
∇n.ν = 0, in ∂Ω × [0, T ], (3)
∇S.ν = 0, in ∂Ω × [0, T ], (4)
with ν is the unite vector.
This model is very successful for describing the aggre-
gation of the population in a finite time point-wise blowup
(in a single point).
In the literature, there exist several works present
some numerical method to solve the classical Keller-Segel
system, let us set: F. Filbet prove the existence and
uniqueness of a numerical solution to the scheme finite
volume schemes in (G.Chamoun and R.TalhoukF.Filbet,
2006) and the authors present the finite volume scheme
for a Keller-Segel model with additional cross-diffusion in
(Bessemoulin-Chatard and Jungel, 2014). In (A.J.Carrillo,
2012) the authors present the cross diffusion and nonlinear
diffusion preventing blow up in the Keller-Segel model.
A second-order positivity preserving central-upwind
scheme is presented by A. Chertock and A. Kurganov in
(A.Chertock and A.Kurganov, 2008) for chemotaxis and
haptotaxis models. Noted that, the fully discrete analysis
of a discontinuous finite element method in (Ref, a) and
the new interior penalty discontinuous Galerkin methods
in (Ref, b). Moreover, (Ha
b
skovec and Schmeiser, 2009;
Ha
b
skovec and Schmeiser, 2011) propose the numerical
and theoretical study of the stochastic particle approxi-
mation and the paper (A.Marrocco, 2003) concerned the
numerical simulation of chemotactic using the mixed finite
elements method. Finite-element method for a simplified
Keller-Segel system in (N.Saito, 2007; N.Saito, 2012) and
finite difference schemes to a parabolic-elliptic system
modelling chemotaxis in (N.Saito and T.Suzuki, 2005). An
42
Soualhi, O. and Rhoudaf, M.
The Finite Volume Method Applied to The Patlak-Keller-Segel Chemotaxis Model in a General Mesh.
DOI: 10.5220/0009775800420049
In Proceedings of the 1st International Conference of Computer Science and Renewable Energies (ICCSRE 2018), pages 42-49
ISBN: 978-989-758-431-2
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

implicit flux-corrected transport (FCT) algorithm has been
developed for a class of chemotaxis models in (R. Strehl
and Turek, 2010). Fractional step methods applied to a
chemotaxis model in (Ref, c).
Four-point scheme on triangles are not easily adapted
to obtain consistent diffusive flow in case in unstructured
meshes.
In what follows, we are interested in a finite volume method,
called the discrete duality finite volume (DDFV) method
the interest of this method is its ability to deal with arbi-
trary polygonal meshes such as nonconforming meshes or
unstructured meshes without constraints of orthogonality.
The DDFV (Discrete Duality Finite Volume ) method
presented by Hermeline (F.Hermeline, 2000), Domelevo,
Omnes (AK.Domelevo, 2005) and Andreianov, Boyer,
Hubert (B.Andreianov and F.Hubert, 2007), the DDFV
method was extended to convection-diffusion (Y.Coudi
`
ere
and G.Manzini, 2010), nonlinear diffusion (Y.Coudi
`
ere and
F.Hubert, 2011; Boyer and Hubert, 2008; B.Andreianov and
F.Hubert, 2007), electro and magnetostatics (S.Delcourte
and P.Omnes, 2007), miscible fluid flows in porous me-
dia (C. Chainais-Hillairet and Mouton, 2013; C.Chainais-
Hillairet and Mouton, 2015), drift-diffusion and energy-
transport models (C.Chainais-Hillairet, 2009), Stokes flows
(Krell, 2011; Krell, 2012; Krell and Manzini, 2012; Del-
courte, 2007), electromagnetism (F. Hermeline and Omnes,
2008).
Our purpose is to introduce and analyse the finite vol-
ume scheme DDFV for the classical model of PKS in gen-
eral triangular mesh (without orthogonality condition), we
demonstrate the existence and uniqueness of the solution of
the DDFV schemes using Brouwer’s fixed point theorem,
and also we presented numerical tests to show the efficiency
of the schemes and to observe the blow-up phenomenon.
The paper is organized as follows : In Section 2 we
detail the DDFV formulation. The demonstrate of the ex-
istence and uniqueness of the DDFV solutions and number
of numerical results obtained on different two-dimensional
meshes are realized in section 3 .
2 DISCRETE DUALITY FINITE
VOLUME SCHEMES FOR
MODIFIED KELLER-SEGEL
MODEL
2.1 Meshes and Notations
Let Ω be a polygonal open bounded connected subset of R
d
with d ∈ N
∗
, and ∂Ω = Ω\Ω its boundary .
Following Hermeline (F.Hermeline, 2000), Domelevo,
Omnes (AK.Domelevo, 2005) and Andreianov, Boyer, Hu-
bert (B.Andreianov and F.Hubert, 2007), we consider a
DDFV mesh which is a triple T = (M , M
∗
,D) described
below.
The primal mesh M is defined as the triplet (M,E,P),
where M is a finite family of nonempty open disjoint sub-
set K of Ω (the control volume primal) such that Ω =
∪
K ∈M
K , with ∂K = K \K be the boundary of K , let
m
K
= |K | > 0 is the measure of K and let d
K
the diam-
eter of K , E is the set of edges σ of the mesh, m
σ
is the
measure of σ, E
int
is the subset of interior edges of Ω. For
all K ∈ M and σ ∈ E
K
(subset of edges of K ) , we de-
note by ν
K ,σ
the unite vector normal to σ outward to K .
P is the subset of points of Ω indexed by M, we denote
P = {(x
K
)
K ∈M
;x
K
∈ K }, (x
K
is the barycentre of K ) we
than denote by D
K ,σ
the cone with vertex x
K
and basis K .
Then, the dual mesh M
∗
is defined as the triplet
(M
∗
,E
∗
,P
∗
), with M
∗
is a finite family of nonempty open
disjoint subset K
∗
of Ω (the control volume dual) such that
Ω = ∪
K
∗
∈M
∗
K
∗
, for all K
∗
∈ M
∗
,with ∂K
∗
= K
∗
\K
∗
be the boundary of K
∗
, let m
K
∗
= |K
∗
| > 0 is the mea-
sure of K
∗
and let d
K
∗
the diameter of K
∗
, E
∗
is the set
of the edges σ
∗
of this mesh, m
σ
∗
is the measure of σ
∗
,
E
∗
int
is the subset of interior edges of Ω. For all K
∗
∈ M
∗
and σ
∗
∈ E
K
∗
(subset of edges of K
∗
) , we denote by
ν
σ
∗
,K
∗
the unite vector normal to σ
∗
outward to K
∗
. P
∗
is the subset of points of Ω indexed by M
∗
, we denote
{P
∗
= (x
K
∗
)
K
∗
∈M
∗
;x
K
∗
∈ K
∗
}, we than note by D
K
∗
,σ
∗
the cone with vertex x
K
∗
and basis K
∗
Finally, We denote by D the sets of all diamonds D, let:
• D
K
= {D ∈ D/σ ∈ E
K
}.
• D
K
∗
= {D ∈ D/σ
∗
∈ E
K
∗
}.
• D
int
= {D ∈ D/σ ∈ E
int
}.
• D
ext
= {D ∈ D/σ ∈ E
ext
}.
• M
D
= {K ∈ M such that σ ∈ E
K
}.
• M
∗
D
= {K
∗
∈ M
∗
such that σ
∗
∈ E
K
∗
}.
• m
D
measure of the diamond.
• For a diamond cell D recall that (x
K
,x
K
∗
,x
L
,x
L
∗
) are
the vertices of D
σ,σ
∗
.
• τ the unite vector parallel to σ, oriented from K
∗
to L
∗
.
• τ
∗
the unite vector parallel to σ
∗
, oriented from K to L.
• α
D
the angle between τ and τ
∗
.
• ν
K ,σ
= −cosα
D
ν
σ
∗
,K
∗
+ sinα
D
τ
K ,σ
.
• d
D
the diameter of D
σ,σ
∗
.
We consider the following property:
m
σ
m
σ
∗
2m
D
≤
mes(D
K ,σ
)
3
. (5)
Finally, the size of the mesh: size(T ) = max
D∈D
d
D
.
2.2 Discrete Operators and Duality
Formula
We define the spaces:
• R
T
is a linear space of scalar fields constant on the cells
of M and M
∗
.
R
T
= {u
T
= ((u
K
)
K ∈M
,(u
K
∗
)
K
∗
∈M
∗
),
with u
K
∈ R, for all K ∈
M
and u
K
∗
∈ R; for all K
∗
∈ M
∗
}.
The Finite Volume Method Applied to The Patlak-Keller-Segel Chemotaxis Model in a General Mesh
43

• (R
2
)
D
is a linear space of vector fields constant on the
cells of D.
(R
2
)
D
= {ξ
D
= (ξ
D
)
D∈D
; with ξ
D
∈ R
2
;
for all D ∈ D}.
Now, we recall the definition of the discrete gradient and
the discrete divergence have been introduced respectively
in (Y. Coudiere and Villedieu, 1999) and (AK.Domelevo,
2005). We also introduce some trace operators and scalar
products
Definition 2.1. Let
∇
D
:R
T
→ (R
2
)
D
,
u
T
→ ∇
D
u
T
= (∇
D
u
T
)
D∈D
,
the discrete gradient, such that for all D ∈ D
(
∇
D
u
T
.τ
K
∗
,L
∗
=
u
L
∗
−u
K
∗
m
σ
,
∇
D
u
T
.τ
K ,L
=
u
L
−u
K
m
σ
∗
,
equivalent to
∇
D
u
T
=
1
sin(α
D
)
u
L
− u
K
m
σ
∗
ν
σ,K
+
u
L
∗
− u
K
∗
m
σ
ν
σ
∗
,K
∗
,
using the propriety m
D
=
1
2
m
σ
m
σ
∗
sin(α
D
), we have
∇
D
u
T
=
1
2m
D
(u
L
− u
K
)m
σ
ν
σ,K
+ (u
L
∗
− u
K
∗
)m
σ
∗
ν
σ
∗
,K
∗
.
Than the discrete divergence div
T
is defined by
Definition 2.2. The discrete divergence operator div
T
is a
mapping from (R
2
)
D
to R
T
defined for all ξ ∈ (R
2
)
D
by
div
T
ξ
D
=
div
M
ξ
D
,0,div
M
∗
ξ
D
,div
∂M
∗
ξ
D
,
such that
div
M
(ξ
D
) = (div
K
(ξ
D
))
K ∈M
,
div
M
∗
(ξ
D
) = (div
K
∗
(ξ
D
))
K
∗
∈M
∗
,
div
∂M
∗
(ξ
D
) = (div
K
∗
(ξ
D
))
K
∗
∈∂M
∗
,
with
div
K
ξ =
1
m
K
∑
D∈D
K
m
σ
ξ
D
.ν
σ,K
, for all K ∈ M,
div
K
∗
ξ =
1
m
K
∗
∑
D∈D
K
∗
m
σ
∗
ξ
D
.ν
σ
∗
,K
∗
, for all K
∗
∈ M
∗
,
div
K
∗
ξ =
1
m
K
∗
[
∑
D∈D
K
∗
m
σ
∗
ξ
D
.ν
σ
∗
,K
∗
+
∑
D∈D
K
∗
∩D
ext
m
σ
2
ξ
D
.ν
σ,K
], for all K
∗
∈ ∂M
∗
.
Let us now define the scalar products < ., . >
T
on R
T
and < ., . >
D
on (R
2
)
D
by
< v
T
,u
T
>
T
=
1
2
∑
K ∈M
m
K
u
K
v
K
+
∑
K
∗
∈M
∗
m
K
∗
u
K
∗
v
K
∗
!
,
for all u
T
,v
T
∈ R
T
.
< ξ
D
,ϕ
D
>
D
=
∑
D∈D
m
D
ξ
D
.ϕ
D
, for all ξ
D
,ϕ
D
∈
R
2
D
.
(6)
The corresponding norms are denoted by k.k
p,T
and k.k
p,D
for all 1 ≤ p ≤ +∞.
• For all u
T
∈ R
T
and for all 1 ≤ p < +∞
ku
T
k
p,T
=
1
2
∑
K ∈M
m
K
|u
K
|
p
+
1
2
∑
K
∗
∈M
∗
m
K
∗
|u
K
∗
|
p
!
1/p
. (7)
• For all ξ
D
∈
R
2
D
and for all 1 ≤ p < +∞.
kξ
D
k
p,D
=
∑
D∈D
m
D
|ξ
D
|
p
!
1/p
. (8)
• For all u
T
∈ R
T
ku
T
k
∞,T
= max
max
K ∈M
|u
K
|, max
K
∗
∈M
∗
|u
K
∗
|
!
. (9)
• For all ξ
D
∈ (R
2
)
D
kξ
D
k
∞,D
= max
D∈D
|ξ
D
|, (10)
Definition 2.3 (Convection term). Let divc
T
: (R
2
)
D
×
R
T
→ R
T
the convection operator defined for all ξ
D
∈
(R
2
)
D
and v
T
∈ R
T
by
divc
T
(ξ
D
,v
T
) = [divc
M
(ξ
D
,v
T
),0,
divc
M
∗
(ξ
D
,v
T
),divc
∂M
∗
(ξ
D
,v
T
)],
such that
divc
M
(ξ
D
,v
T
) = (divc
K
(ξ
D
,v
T
))
K ∈M
,
divc
M
∗
(ξ
D
,v
T
) = (divc
K
∗
(ξ
D
,v
T
))
K
∗
∈M
∗
,
divc
∂M
∗
(ξ
D
,v
T
) = (divc
K
∗
(ξ
D
,v
T
))
K
∗
∈∂M
∗
,
with
• For all K ∈ M,
divc
K
(ξ
D
,v
T
) =
1
m
K
∑
D∈D
K
σ=K /L
m
σ
[(ξ
D
.ν
σ,K
)
+
v
K
−
(ξ
D
.ν
σ,K
)
−
v
L
],
• For all K
∗
∈ M
∗
divc
K
∗
(ξ
D
,v
T
) =
1
m
K
∗
∑
D∈D
K
∗
σ
∗
=K
∗
/L
∗
m
σ
∗
[(ξ
D
.ν
σ
∗
,K
∗
)
+
v
K
∗
−
(ξ
D
.ν
σ
∗
,K
∗
)
−
v
L
∗
],
• For all K
∗
∈ ∂M
∗
divc
K
∗
(ξ
D
,v
T
) =
1
m
K
∗
(
∑
D∈D
K
∗
σ
∗
=K
∗
/L
∗
m
σ
∗
[(ξ
D
.ν
σ
∗
,K
∗
)
+
v
K
∗
− (ξ
D
.ν
σ
∗
,K
∗
)
−
v
L
∗
]
+
∑
D∈D
K
∗
∩D
ext
σ=K /L
m
σ
2
[(ξ
D
.ν
σ,K
)
+
v
K
− (ξ
D
.ν
σ,K
)
−
v
L
].
ICCSRE 2018 - International Conference of Computer Science and Renewable Energies
44

where x
+
= max(x, 0) and x
−
= max(0, −x).
2.3 The Numerical Scheme
A DDFV scheme for the the discretisation of the problem
(1) is given by the following set of equations:
For all K ∈ M and K
∗
∈ M
∗
, let
n
0
K
=
1
m
K
Z
K
u
0
(x)dx and n
0
K
∗
=
1
m
K
∗
Z
K
∗
u
0
(x)dx. (11)
At each time step k, the numerical solution will be given by
(n
k+1
T
,S
k+1
T
). Then, the scheme for (1) writes for all 0 <
k < N
T
− 1
n
k+1
T
−n
k
T
∆t
− div
T
(∇
D
n
k+1
T
) + divc
T
(n
k
T
∇
D
S
n+1
T
) = 0,
−div
T
(∇
D
S
k+1
T
) + µS
k+1
T
= n
k
T
.
∇
D
n
k
T
.ν = ∇
D
S
k
T
.ν = 0,∀D ∈ D
ext
.
(12)
Whith div
T
and ∇
D
are defined respectively by defini-
tion 2.2 and definition 2.1.
3 THE MAIN RESULTS
3.1 Existence of DDFV
Solutions
Theorem 3.1. Let Ω be an open, bonded, connected,
polygonal domain of R
2
and let T be a discretization of
Ω × (0,T ) such that
m
σ
m
σ
∗
2m
D
≤
mes(D
K ,σ
)
3
. (13)
Let n
0
∈ L
2
(Ω),n
0
≥ 0 in Ω. Then there exists a solution
{(n
k+1
T
,S
k+1
T
),0 ≤ k ≤ N
T
− 1} to (11) and (12) satisfying:
for all K ∈ M and K
∗
∈ M
∗
, for all 0 ≤ k ≤ N
T
.
n
k
K
≥ 0 and n
k
K
∗
≥ 0
1
2
∑
K ∈M
m
K
n
k
K
+
1
2
∑
K
∗
∈M
∗
m
K
∗
n
k
K
∗
=
1
2
∑
K ∈M
m
K
n
0
K
+
1
2
∑
K
∗
∈M
∗
m
K
∗
n
0
K
∗
= kn
0
k
L
1
(Ω)
,
for all 0 ≤ k ≤ N
T
.
Proof. Let k ∈ {0, 1, 2, 3,...,N
T
} and let (n
k
T
,S
k
T
) be a so-
lution to (1), we introduce the set:
X
T
= {v ∈ R
T
;v ≥ 0 in Ω,kvk
L
1
(Ω)
≤ kn
0
k
L
1
(Ω)
}.
Firstly we constructed n and S, then we demonstrate in the
first step the unicity of the solution, after in the second step
we using the Browr’s fixed point to proof the existance of
the solution.
We construct S ∈ X
T
using the following schemes
−
∑
σ∈E
K
m
σ
∇
D
S
T
.ν
σ,K
+ m
K
S
K
=
m
K
µn
k
K
, for all K ∈ M,
−
∑
σ
∗
∈E
K
∗
m
σ
∗
∇
D
S
T
.ν
σ
∗
,K
∗
+ m
K
∗
S
K
∗
=
m
K
∗
µn
k
K
∗
for all K
∗
∈ M
∗
,
(14)
and we comput n ∈ X
T
using the schemes
m
K
n
K
−n
k
K
∆t
−
∑
σ∈E
K
m
σ
∇
D
n
T
.ν
σ,K
+
∑
σ∈E
K
m
σ
[n
K
(∇
D
S
T
.ν
σ,K
)
+
−n
L
(∇
D
S
T
.ν
σ,K
)
−
] = 0, for all K ∈ M,
m
K
∗
n
K
∗
−n
k
K
∗
∆t
−
∑
σ
∗
∈E
K
∗
m
σ
∗
∇
D
n
T
.ν
σ
∗
,K
∗
+
∑
σ
∗
∈E
K
∗
m
σ
∗
[n
K
∗
(∇
D
S
T
.ν
σ
∗
,K
∗
)
+
−
n
L
∗
(∇
D
S
T
.ν
σ
∗
,K
∗
)
−
] = 0, for all K
∗
∈ M
∗
.
(15)
Step 1: The system (14) can be written as AS = b,
where for all K , L ∈ M such that σ = K |L and for all for
all K
∗
,L
∗
∈ M
∗
such that σ
∗
= K
∗
‘|L
∗
, A is defined by:
A
K ,K
=
∑
σ∈K
m
2
σ
2m
D
+ m
K
,
A
K
∗
,K
∗
=
∑
σ
∗
∈K
∗
m
∗
σ
2
2m
D
+ m
K
∗
.
A
K ,L
= −
m
2
σ
2m
D
,
A
K ,K
∗
= −
m
σ
m
σ
∗
2m
D
ν
K ,σ
.ν
K
∗
,σ
∗
,
A
K ,L
∗
=
m
σ
m
σ
∗
2m
D
ν
K ,σ
.ν
K
∗
,σ
∗
,
and
A
K
∗
,L
∗
= −
m
2
σ
∗
2m
D
,
A
K
∗
,K
= −
m
σ
m
σ
∗
2m
D
ν
K ,σ
.ν
K
∗
,σ
∗
,
A
K
∗
,L
=
m
σ
m
σ
∗
2m
D
ν
K ,σ
.ν
K
∗
,σ
∗
,
and b
K
= µm
K
n
k
K
., b
K
∗
= µm
K
∗
n
k
K
∗
. Since for all K ∈ M
and K
∗
∈ M
∗
:
|A
K ,K
| −
∑
σ∈E
K
[|A
K ,L
| + |A
K ,L
∗
|+
|A
K ,K
∗
|] = m
K
− 2
∑
σ∈E
K
m
σ
m
σ
∗
2m
D
|cos(α
D
|),
and
|A
K
∗
,K
∗
| −
∑
σ
∗
∈E
K
∗
[|A
K
∗
,L
∗
| + |A
K
∗
,L
|+
|A
K
∗
,K
|] = m
K
∗
− 2
∑
σ
∗
∈E
K
∗
m
σ
∗
m
σ
2m
D
|cos(α
D
|).
Using the hypothesis (13) we have
|A
K ,K
| −
∑
σ∈E
K
|A
K ,L
| + |A
K ,L
∗
| + |A
K ,K
∗
|
≥ 0
|A
K
∗
,K
∗
|−
∑
σ
∗
∈E
K
∗
|A
K
∗
,L
∗
| + |A
K
∗
,L
| + |A
K
∗
,K
|
≥ 0.
Then the matrix A is strictly diagonally dominant with re-
spect to the columns and hence, A is invertible. This shows
the unique solvability of (14).
Now, the system (15) equivalent to the system Bn = C,
with:
B
K ,K
=
∑
σ∈E
K
m
2
σ
2m
D
+
m
K
∆t
+
∑
σ∈E
K
m
σ
(∇
D
S.ν
σ,K
)
+
,
The Finite Volume Method Applied to The Patlak-Keller-Segel Chemotaxis Model in a General Mesh
45

and
B
K
∗
,K
∗
=
∑
σ
∗
∈E
K
∗
m
2
σ
∗
2m
D
+
m
K
∗
∆t
+
∑
σ
∗
∈E
K
∗
m
σ
∗
(∇
D
S.ν
σ
∗
,K
∗
)
+
.
B
K ,L
= −
m
2
σ
2m
D
− m
σ
(∇
D
S.ν
σ,K
)
−
,
B
K ,K
∗
=
m
σ
m
σ
∗
2m
D
ν
K ,σ
.ν
K
∗
,σ
∗
,
B
K ,L
∗
= −
m
σ
m
σ
∗
2m
D
ν
K ,σ
.ν
K
∗
,σ
∗
,
and
B
K
∗
,L
∗
= −
m
2
σ
∗
2m
D
− m
σ
∗
(∇
D
S.ν
σ
∗
,K
∗
)
−
,
B
K
∗
,K
=
m
σ
m
σ
∗
2m
D
ν
K ,σ
.ν
K
∗
,σ
∗
,
B
K
∗
,L
= −
m
σ
m
σ
∗
2m
D
ν
K ,σ
.ν
K
∗
,σ
∗
,
and c
K
=
m
K
n
k
K
∆t
, c
K
∗
=
m
K
∗
n
k
K
∗
∆t
. Since for all K ∈ M and
K
∗
∈ M
∗
:
|B
K ,K
| −
∑
σ∈E
K
|B
K ,L
| + |B
K ,L
∗
| + |B
K ,K
∗
|
=
m
K
∆t
+
∑
σ∈E
K
m
σ
|(∇
D
S.ν
σ,K
)
+
|
−
∑
σ∈E
K
m
σ
|(∇
D
S.ν
σ,K
)
−
|−
2
∑
σ∈E
K
m
σ
m
σ
∗
2m
D
|cos(α
D
|),
|B
K
∗
,K
∗
| −
∑
σ
∗
∈E
K
∗
|B
K
∗
,L
∗
| + |B
K
∗
,L
| + |B
K
∗
,K
|
=
m
K
∗
∆t
+
∑
σ
∗
∈E
K
∗
m
σ
∗
|(∇
D
S.ν
σ
∗
,K
∗
)
+
|
−
∑
σ
∗
∈E
K
∗
m
σ
∗
|(∇
D
S.ν
σ
∗
,K
∗
)
−
|−
2
∑
σ
∗
∈E
K
∗
m
σ
∗
m
σ
2m
D
|cos(α
D
|),
for all σ ∈ E
K
and σ
∗
∈ E
K
∗
we have
(
∇
D
S.ν
σ,K
= −∇
D
S.ν
σ,L
∇
D
S.ν
σ
∗
,K
∗
= −∇
D
S.ν
σ
∗
,L
∗
(16)
which yields
(
(∇
D
S.ν
σ,K
)
−
= (∇
D
S.ν
σ,L
)
+
,
(∇
D
S.ν
σ
∗
,K
∗
)
−
= (∇
D
S.ν
σ
∗
,L
∗
)
+
,
(17)
that’s give
|B
K ,K
| −
∑
σ∈E
K
|B
K ,L
| + |B
K ,L
∗
| + |B
K ,K
∗
|
=
m
K
∆t
− 2
∑
σ∈E
K
m
σ
m
σ
∗
2m
D
|cos(α
D
|)
|B
K
∗
,K
∗
| −
∑
σ
∗
∈E
K
∗
|B
K
∗
,L
∗
| + |B
K
∗
,L
| + |B
K
∗
,K
|
=
m
K
∗
∆t
− 2
∑
σ
∗
∈E
K
∗
m
σ
∗
m
σ
2m
D
|cos(α
D
|)
using the hypothesis (13) we have
|B
K ,K
| −
∑
σ∈E
K
|B
K ,L
| + |B
K ,L
∗
| + |B
K ,K
∗
|
≥ 0
|B
K
∗
,K
∗
| −
∑
σ
∗
∈E
K
∗
|B
K
∗
,L
∗
| + |B
K
∗
,L
| + |B
K
∗
,K
|
≥ 0.
Then the matrix B is strictly diagonally dominant with re-
spect to the columns and hence, B is invertible. This shows
the unique solvability of (15). Then n is nonnegative, im-
plies that n satisfies (14).
In (15), summing the first equation over K ∈ M and the
second equation over K
∗
∈ M
∗
, we obtain
∑
K ∈M
m
K
n
K
=
∑
K ∈M
m
K
n
k
K
.
∑
K
∗
∈M
∗
m
K
∗
n
K
∗
=
∑
K
∗
∈M
∗
m
K
∗
n
k
K
∗
.
(18)
That’s give
1
2
∑
K ∈M
m
K
n
K
+
1
2
∑
K
∗
∈M
∗
m
K
∗
n
K
∗
=
1
2
∑
K ∈M
m
K
n
k
K
+
1
2
∑
K
∗
∈M
∗
m
K
∗
n
k
K
∗
= kn
0
k
L
1
(Ω)
.
(19)
step 2: Let H : X
T
→ X
T
the operator define by the solution
to (14) and (15) such that H(n) = n, it must be shown that
the operator H is continuous to apply Brouwer fixed point
thm (i.e) we have to prove that n
β
→ n as β → ∞ such that:
(n
β
)
β∈N
N
N
⊂ X
T
be a sequence verified
n
β
→ n as β → ∞ in X
T
,
H(n
β
) = n
β
,
H(n) = n.
(20)
It easy to show that S
β
− S → 0 in X
T
as β → ∞,
since the map n → S is linear on the finite dimensional
space X
T
and continuous. Later, using (15) and an adap-
tation of the proof of theorem 2.1 in (G.Chamoun and
R.TalhoukF.Filbet, 2006) leads to:
∑
K ∈M
m
K
|n
β
K
− n
K
| ≤ 2∆t
∑
K ∈M
|n
K
|
2
!
1/2
∑
K ∈M
∑
σ∈E
K
m
σ
|∇
D
(S
β
− S).ν
σ,K
|
2
!
1/2
,
∑
K
∗
∈M
∗
m
K
∗
|n
β
K
∗
− n
K
∗
| ≤ 2∆t
∑
K
∗
∈M
∗
|n
K
∗
|
2
!
1/2
∑
K
∗
∈M
∗
∑
σ
∗
∈E
K
∗
m
σ
∗
|∇
D
(S
β
− S).ν
σ
∗
,K
∗
|
2
1/2
,
Let c
1
> 0 such that 2∆t
∑
K ∈M
|n
K
|
2
≤ c
1
kn
0
T
k
L
2
(Ω)
and
2∆t
∑
K
∗
∈M
∗
|n
K
∗
|
2
≤ c
1
kn
0
T
k
L
2
(Ω)
, then
∑
K ∈M
m
K
|n
β
K
− n
K
| ≤
c
1
kn
0
T
k
L
2
(Ω)
∑
K ∈M
∑
σ∈E
K
m
σ
|∇
D
(S
β
− S).ν
σ,K
|
2
1/2
,
∑
K
∗
∈M
∗
m
K
∗
|n
β
K
∗
− n
K
∗
| ≤
c
1
kn
0
T
k
L
2
(Ω)
∑
K
∗
∈M
∗
∑
σ
∗
∈E
K
∗
m
σ
∗
|∇
D
(S
β
− S).ν
σ
∗
,K
∗
|
2
1/2
,
ICCSRE 2018 - International Conference of Computer Science and Renewable Energies
46

then
1
2
∑
K ∈M
m
K
|n
β
K
− n
K
|
2
+
1
2
∑
K
∗
∈M
∗
m
K
∗
|n
β
K
∗
− n
K
∗
|
2
≤
c
2
1
kn
0
T
k
2
L
2
(Ω)
(
1
2
∑
K ∈M
∑
σ∈E
K
m
σ
|∇
D
(S
β
− S).ν
σ,K
|
2
+
1
2
∑
K
∗
∈M
∗
∑
σ
∗
∈E
K
∗
m
σ
∗
|∇
D
(S
β
− S).ν
σ
∗
,K
∗
|
2
),
using the poincare inequality, we have
1
2
∑
K ∈M
m
K
|n
β
K
− n
K
|
2
+
1
2
∑
K
∗
∈M
∗
m
K
∗
|n
β
K
∗
− n
K
∗
|
2
≤
c
2
1
kn
0
T
k
2
L
2
(Ω)
k∇
D
(S
β
− S)k
2
D
≤ c
1
)
2
kn
0
T
k
2
L
2
(Ω)
kS
β
− Sk
2
2,T
,
then
kn
β
K
− n
K
k
2
2,T
≤
c
2
1
kn
0
T
k
2
L
2
(Ω)
k∇
D
(S
β
− S)k
2
D
≤ c
2
1
kn
0
T
k
2
L
2
(Ω)
kS
β
− Sk
2
2,T
.
kn
0
T
k
L
2
(Ω)
is bounded and S
β
−S → 0 as β → ∞, then n
β
→
n in H
T
implies that H is a continuous operator.
Therefore using the Brouwer fixed point thm the opera-
tor H has a fixed point, hence the prove of thm.
3.2 Numerical Experiments
In this section, we show three numerical simulations of
model (1) in a two dimensional space to show the effi-
ciency of the DDFV scheme. the system (1) is describes
the evolution over time of the cell density n(x,t) and the
chemical signal concentration variable S(x,t), Some of the
tests cases come from the paper (Bessemoulin-Chatard and
Jungel, 2014) where a finite volume scheme is used, and
our results compare very well to the ones in this refer-
ence. We simulate the model in a two dimensional domain
Ω = (0; 5) × (0; 5) for which we consider a nonuniform and
non-admissible grid figure.1,
Figure 1: The mesh supported in the numerical tests with
h = 0.0471
3.2.1 Test 1
Firstly, we chose the nonsymmetric initial data on a square
(0;5) × (0; 5) and we present the numerical solution of (1)
for different values of t. in this subsection, µ = 1, ξ = 1, the
time step is ∆t = 10
−3
, the number of triangles is 1296 and
the nonsymmetric initial functions is given by
n
0,1
(x,y) =
M
2πθ
exp
−
(x − x
0
)
2
+ (y − y
0
)
2
2θ
, (21)
with the total mass is M = 6π, θ = 10
−2
and x
0
= y
0
= 0.1.
Figure 2: Test 1: Time evolution of knk
L
∞
(Ω)
computed
from the radially non-symmetric initial datum n
0,1
with
M = 6π
Figure 3: Initial datum n
0,1
, t = 0 and t = 0.005
Figure 4: Initial datum n
0,1
, t = 0.015 and t = 1
3.2.2 Test 2
Next, we present the numerical solution of (1) for differ-
ent values of t. in this subsection, µ = 1, ξ = 1, the time
step is ∆t = 10
−3
, the number of triangles is 1296 and the
nonsymmetric initial functions is given by:
n
0,2
(x,y) =
4π
2πθ
exp
−
(x−x
0
)
2
+(y−y
0
)
2
2θ
+
2π
2πθ
exp
−
(x−x
1
)
2
+(y−y
1
)
2
2θ
,
(22)
with θ = 10
−2
, x
0
= y
0
= 0.1, and x
1
= y
1
= −0.2.
Test 2: Cell density computed from nonsymmetric ini-
tial data with M = 6π for different values of t.
The Finite Volume Method Applied to The Patlak-Keller-Segel Chemotaxis Model in a General Mesh
47
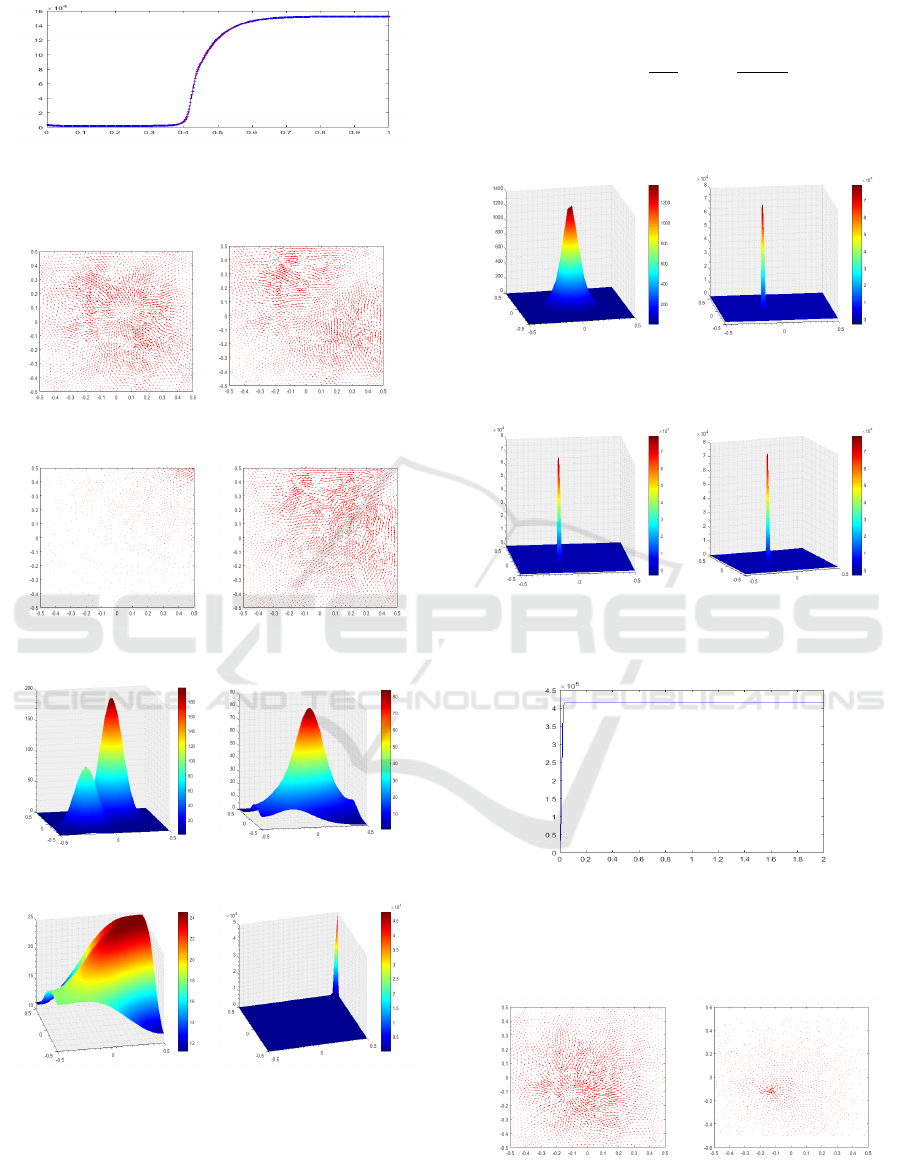
Figure 5: Test 2: Time evolution of knk
L
∞
(Ω)
computed
from the radially non-symmetric initial datum n
0,2
with the
total mass is M = 6π
Figure 6: Initial datum n
0,2
, t = 0.01 and t = 0.045
Figure 7: Initial datum n
0,2
, t = 0.55 and t = 0.15
Figure 8: Initial datum n
0,1
, t = 0 and t = 0.01.
Figure 9: Initial datum n
0,1
, t = 0.045 and t = 1
3.2.3 Test 3
We now consider the case of radially symmetric initial func-
tions, we present the numerical solution of (1) for different
values of δ. in this subsection, µ = 1, ∆t = 2 × 10
−2
and the
radially symmetric initial function is given by:
n
0,3
(x,y) =
M
2πθ
exp
−
x
2
+ y
2
2θ
, (23)
with the mass M = 20π, ξ = 1 and θ = 10
−2
.
Figure 10: Initial datum n
0,3
, t = 0 and t = 1.5
Figure 11: Initial datum n
0,3
, t = 3 and t = 5
Figure 12: Test 3 : Time evolution of knk
L
∞
(Ω)
computed
from the radially symmetric initial datum n
0,3
with M =
20π.
Figure 13: Test 3 : Chemical signal concentration computed
from symmetric initial data with M = 20π for t = 0 and
t = 5.5.
ICCSRE 2018 - International Conference of Computer Science and Renewable Energies
48

4 CONCLUSION
Our numerical results, in the case of radially non-
symmetrical initial data (test 1 and 2), show that the blow-
up occurs at the nearest corner of the point of inoculation
from the 0.1 instant for n
0;1
and 0.4 for n
0;2
, which is com-
patible with cellular dynamics. In the case where the initial
datum is radially symmetrical(test3, the figures show that
the explosion of the solution of Keller-Segel classical mod-
els occurs at the center of the domain.
REFERENCES
A.Chertock and A.Kurganov (2008). A second-order pos-
itivity preserving central-upwind scheme for chemo-
taxis and haptotaxis models. Numer. Math., 111:169–
205.
A.J.Carrillo, S.Hittmeir, A. u. (2012). Cross diffusion and
nonlinear diffusion preventing blow up in the keller-
segel model. Math. Mod. Meth. Appl. Sci.
AK.Domelevo, P. O. (2005). A finite volume method for the
laplace equation on almost arbitrary two-dimensional
grids. M2AN Math. Model. Numer. Anal., 39(6):1203–
1249.
A.Marrocco (2003). Numerical simulation of chemotactic
bacteria aggregation via mixed finite elements. Math.
Mod. Numer. Anal., 4:617–630.
B.Andreianov, F. and F.Hubert (2007). Discrete duality fi-
nite volume schemes for leray-lions type elliptic prob-
lems on general 2d-meshes. Num. Meth. for PDEs,
23:145–195.
Bessemoulin-Chatard, M. and Jungel, A. (2014). A fi-
nite volume scheme for a keller-segel model with ad-
ditional cross-diffusion. IMA Journal of Numerical
Analysis, 34:96–122.
Boyer, F. and Hubert, F. (2008). Finite volume method for
2d linear and nonlinear elliptic problems with discon-
tinuities. SIAM J Numer Anal, 46:3032—-3070.
C. Chainais-Hillairet, S. K. and Mouton, A. (2013).
Study of discrete duality finite volume schemes
for the peaceman model. SIAM J. Sci. Comput.,
35(6):A2928–A2952.
C.Chainais-Hillairet (2009). Discrete duality finite vol-
ume schemes for two-dimensional driftdiffusion and
energy-transport models. Internat J Numer Methods
Fluids, 59:239–57.
C.Chainais-Hillairet, S. Krell, A. and Mouton (2015). Con-
vergence analysis of a ddfv scheme for a system de-
scribing miscible fluid flows in porous media. Numer-
ical Methods for Partial Differential Equations, Wiley,
315(3):1098–2426.
Delcourte, S. (2007). D
´
eveloppement de m
´
ethodes de vol-
umes finis pour la m
´
ecanique des fluides. Ph.d. thesis
(in french), University of Toulouse III, France.
F. Hermeline, S. L. and Omnes, P. (2008). A finite volume
method for the approximation of maxwell’s equations
in two space dimensions on arbitrary meshes. J Com-
put Phys, 227:9365––9388.
F.Hermeline (2000). A finite volume method for the approx-
imation of diffusion operators on distorted meshes. J.
Comput. Phys., 160(2):481–499.
G.Chamoun, M. and R.TalhoukF.Filbet (2006). A finite
volume scheme for the patlak-keller-segel chemotaxis
model. Numer. Math., 104:457–488.
Ha
b
skovec, J. and Schmeiser, C. (2009). Stochastic particle
approximation for measure valued solutions of the 2d
keller-segel system. J. Stat. Phys., 135:133–151.
Ha
b
skovec, J. and Schmeiser, C. (2011). Convergence of
a stochastic particle approximation for measure solu-
tions of the 2d keller-segel system. Commun. Part.
Diff. Eqs., 36:940–960.
Keller, E. and Segel, L. (1970). Initiation of slime mold
aggregation viewed as an instability. J. Theor. Biol.,
26:399–415.
Krell, S. (2011). Stabilized ddfv schemes for stokes prob-
lem with variable viscosity on general 2d meshes.
Numer Methods Partial Differential Eq, pages 1666–
–1706.
Krell, S. (2012). Finite volume method for general multi-
fluid flows governed by the interface stokes problem.
Math Models Methods Appl Sci, 22(5):1150–025.
Krell, S. and Manzini, G. (2012). The discrete duality
finite volume method for stokes equations on three-
dimensional polyhedral meshes. SIAM J Numer Anal,
50:808—-837.
N.Saito (2007). Conservative upwind finite-element method
for a simplified keller-segel system modelling chemo-
taxis. IMA J. Numer. Anal., 27:332–365.
N.Saito (2012). Error analysis of a conservative finite-
element approximation for the keller-segel model of
chemotaxis. comm. Pure Appl. Anal., 11:339–364.
N.Saito and T.Suzuki (2005). Notes on finite differ-
ence schemes to a parabolic-elliptic system modelling
chemotaxis. Appl. Math. Comput., 171:72–90.
Patlak, C. (2953). Random walk with persistence and exter-
nal bias. Bull. Math. Biophys, 15:311–338.
R. Strehl, A. Sokolov, D. K. and Turek, S. (2010). A flux-
corrected finite element method for chemotaxis prob-
lems. Comput. Meth. Appl. Math., 10:219–232.
S.Delcourte, K. D. and P.Omnes (2007). A discrete du-
ality finite volume approach to hodge decomposi-
tion and div-curl problems on almost arbitrary two-
dimensional meshes. SIAM J Numer Anal, 45:1142—
-1174.
Y. Coudiere, J.-P. V. and Villedieu, P. (1999). Convergence
rate of a finite volume scheme for a two-dimensional
convection-diffusion problem. M2AN Math. Model.
Numer. Anal., 33:493–516.
Y.Coudi
`
ere and F.Hubert (2011). A 3d discrete duality finite
volume method for nonlinear elliptic equations. SIAM
J Sci Comput, 33:1739—-1764.
Y.Coudi
`
ere and G.Manzini (2010). The discrete duality fi-
nite volume method for convectiondiffusion problems.
SIAM J Sci Comput, 47:4163—-4192.
The Finite Volume Method Applied to The Patlak-Keller-Segel Chemotaxis Model in a General Mesh
49
