
Where Exactly for Enhance Critical and Creative Thinking: The
Use of Problem Posing or Contextual Learning
Toheri
1
and Widodo Winarso
1
1
I
nstitut Agama Islam Negeri Syekh Nurjati Cirebon, Indonesia
Keywords: Critical Thinking, Creative Thinking, problem posing, contextual learning.
Abstract: Critical and creative thinking are the two essential competencies of the four competencies required in the
21st century. However, both are still difficult to achieve well by students due to lack of training during the
course of mathematics learning. This study was conducted to determine what model of learning is
appropriate to develop students' critical and creative thinking skills. The study used three class samples from
class VIII. First class is given problem posing lesson, second class is given contextual learning and third
class as control class. The results of the study indicate that improving students' critical and creative thinking
skills are included in the moderate category for classes using contextual and contextual classroom posing
problems. In addition, it is also found that contextual learning is more effective for improving critical
thinking skills when compared with learning posing and exposure problems. Meanwhile, learning problem
posing is more effective to improve creative thinking skills compared with contextual and expository
learning.
1 INTRODUCTION
Critical and creative thinking is very important for
students in school and life going forward. Thinking
of this is necessary to face the 21st century (Center.
Pacific Policy Research, 2010; Koetzsch, 1997), as
the objective of mathematics learning (Mahmuzah,
2015), analyzing problems and synthesizing
(McCormick, Clark and Raines, 2015), make
decisions and make judgments (Paul and Linda,
2006). Both are essential for solving everyday
problems (Apino and Retnawati, 2017).
Results of the 2015 TIMSS Review show
Indonesian students are still weak in the content and
cognitive domains of mathematics. In line with the
findings of Indah Nurul Faizah and Budi Murtiyasa
which states that UN questions are still minimal in
the domain of cognitive reasoning such as generalize
and justify (Faizah, Budi and M., 2017). Lack of
linkage between creativity in the curriculum and
creativity taught by teachers (Aizikovitsh-Udi and
Diana, 2015), Feeling less ready to teach creativity
(Mullet et al., 2016).
The various notions of critical thinking are
presented by experts and researchers. Trend and
skills to engage in activities with reflective
skepticism (McPeck, 2016). A rational-reflective
thinking to decide what to believe or do (Ennis,
2015), a metacognitive process involving analysis,
evaluation, and inference (Dwyer, Hogan and
Stewart, 2014).
In this study, the critical thinking that we use is
adopting from Ennis with 4 indicators: 1)
formulating the main issues, 2) analyzing arguments,
3) determining the strategy, and 4) concluding.
Creative thinking refers to Torrance containing 4
cognitive processes, fluency, flexibility, authenticity,
and elaboration (Almeida et al., 2008), stated
creative thinking contained innovative creativity
(fluency, originality), and adaptive creativity
(flexibility, the abstractness of titles, and Resistance
to Premature Closure).
In this study, the creative thinking that we use is
adopted from Torrance with 4 aspects: 1) fluency, 2)
flexibility, 3) originality, and 4) elaboration.
Various efforts were made by teachers and
researchers to develop students' critical and creative
thinking in mathematics learning. Problem posing is
central to the nature of mathematical thinking (Silver
and Cai, 1996). Strategies for questions asked by
teachers in discussions and play roles in real-life
problem solving very well for developing critical
thinking (Abrami et al., 2015). Problem-based
learning affects the students' mathematical thinking
698
Toheri, . and Winarso, W.
Where Exactly for Enhance Critical and Creative Thinking: The Use of Problem Posing or Contextual Learning.
DOI: 10.5220/0009914806980705
In Proceedings of the 1st International Conference on Recent Innovations (ICRI 2018), pages 698-705
ISBN: 978-989-758-458-9
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

skills (Widyatiningtyas et al., 2015). At the same
time, Rifaatul Mahmuzah suggests Problem Posing
as an alternative to improving critical thinking
(Mahmuzah, 2015). State the importance of effective
learning so students become critical thinkers and
how students learn effectively, the role of students,
teachers and the context in teaching critical thinking,
In line with the traditional paradigm shift and the
transfer of information toward constructivism of
student activities for more meaningful learning
(Bonney and Sternberg, 2016). If the teacher
consistently and systematically encourages critical
thinking in their class by applying mathematics to
real-life problems, encouraging debate, and planning
investigative lessons, students tend to practice
critical thinking skills and develop critical thinking
languages (Aizikovitsh-Udi and Diana, 2015).
Creative thinking can be developed through
problem posing and problem-solving (Suastika and
Wahyuningtyas, 2017), MEAs with realistic
problems (Wessels, 2014).
According to Ranak Lince revealed that NHT is
more suitable to enhance students' creative thinking
mathematically (Lince, 2016). Apino and Retnawati
suggest the importance of providing a variety of
non-routine issues that enable students to practice
asking "why and How” (Apino and Retnawati,
2017). Huang, Ricci, and Mamikon Mnatsakanian
suggested that Students be taught how to: identify
the steps; evaluate; choose a troubleshooting
strategy; identify possible conclusions; choosing
logical conclusions; explains how solutions are
obtained; and shows how the solution can be applied
to wider mathematical problems (Huang, Ricci and
Mnatsakanian, 2016). The importance of student and
context analysis, the setting of learning objectives,
differences in strategy development or assessment
techniques in designing learning steps on problem-
based learning approaches to develop students'
critical and creative thinking (Birgili, 2015).
Another approach that teachers can use as an
effort to optimize students' critical and creative
thinking skills is a contextual approach called
Contextual Teaching Learning (CTL). Contextual
Teaching and Learning (CTL) is a learning strategy
that emphasizes the full process of student
involvement in order to find the material learned and
relate it to real life situations that encourage students
to apply it in their lives(Sanjaya, 2006). Johnson that
in Contextual Teaching and Learning (CTL) requires
a more empowering approach to students in the hope
that students are able to construct knowledge in their
minds rather than memorizing facts (Johnson, 2002).
This study uses learning posing and contextual
problems given to students with the aim of
developing critical thinking (analyzing arguments,
being able to ask, able, answering questions, solving
problems, determining strategies and making
conclusions) and thinking creatively (thinking
fluently, thinking flexible, thinking original, and
detailed thinking) students.
2 METHODS
The quantitative approach is done by quasi-
experimental method (Campbell and Stanley, 2015)
with Nonequivalent Control Group Design (Bryk
and Weisberg, 1977) in sample 3 class VIII MTs N 1
Cirebon-Indonesia. This research was conducted to
see the learning of the mathematical problem of
posing and contextual in improving critical and
creative thinking skill.
2.1 Procedure
The research procedure is done through the
determination of 3 class samples, where 2 classes
are given treatment and 1 class as a control. Class 1
is treated by learning problem posing, second class
is given contextual learning treatment, and third
class is controlled by traditional learning. Prior
learning was given preliminary tests with students'
critical and creative thinking skills for the three
groups.
Implementation of learning problem posing for
experiment class 1 refers to pre-positioning posing
activity (Leonard, 2017) with the learning stages
adopting Mathematical education research. While
contextual learning for experimental class 2 refers
to Elaine B Johnson which describes the stages of
Contextual Teaching Learning with student activity
and teacher activity (Johnson, 2002). while the
control class is given expository learning.
After the implementation of the learning, each
group is given a final test related to students'
critical and creative thinking skills related to the
topic of the circle in accordance with the
competencies contained in the 2013 curriculum at
the topic of the circle and their parts.
2.2 Data Collection
The technique of data collecting using description
test which amounted to 9 item, where 5 items about
which to measure a student's critical thinking ability
and 4 remaining matter to measure student's creative
thinking ability. The test will be done before
Where Exactly for Enhance Critical and Creative Thinking: The Use of Problem Posing or Contextual Learning
699

(pretest) and after learning (postest) in experiment
and control class. both of tests have similar
indicators, but are different in the question The
scoring to calculate the results of the description test
is by using Holistic Scoring Rubrics criteria
(Mertler, 2001).
Critical thinking tests using instruments with
indicators cover four aspects (Ennis, 2013), details
of this including at the table below;
Table 1: Instrument of critical thinking
Aspects Indicator
analyzing
arguments
Determining a problem and
identify reasons that match the
question
formulating
problems
Digging information by asking
and answering through various
alternative answers to solve a
problem
determining
strategies
Determining an alternative
action that is possible to solve
the problem
concluding the giving a meaningful idea
Examples of pretest and post for determining
strategies can be seen in the following figure 1 and 2
below;
Figure 1: Sample Pre-test of critical thinking
Figure 2: Sample Post-test of critical thinking.
The creative thinking test uses instruments with
indicators, including: 1) fluency, 2) flexibility, 3)
originality, and 4) elaboration (Torrance, 1972),
details of this including at the table bellow;
Table 2: Instrument of creative thinking
Aspects Indicator
Fluency Students can provide relevant
ideas to solve problems
Flexibility Students can express various
ways or approaches to a
problem
Originality Students can provide unique
answers to solve problems
Elaboration Students Able to develop ideas
or ideas and explain in detail
the problems resolved so that
they are more interesting
Examples of pretest and post for elaboration can
be seen in the following figure 1 and 2 below;
Figure 3: Sample Pre-test of Creative thinking
Figure 4: Sample Post-test of Creative thinking
This instrument is analysed in advance to see the
validity, reliability, indices of difficulty (easy and
middle) and distinguishing power (good and very
good) previously tested by experts.
ICRI 2018 - International Conference Recent Innovation
700

2.3 Data Analysis Technique
Data analysis techniques used to describe the
learning approach (problem posing, contextual, and
expository approach) in terms of students' critical
and creative thinking ability include normality test
by using Kolmogorov Smirnov test, homogeneity
test, and N-gain calculation for both thinking
variables (Creswell and Creswell, 2017). To test the
hypothesis done through One Way ANOVA (Kim
and Kohout, 1975). which compares the N-gain of
critical and creative thinking to the three groups.
Data analysis is continued by using the Scheffe Test
to determine which variable is better. All data
analysis is done by using SPPS software version 20.
3 RESULTS AND DISCUSSION
Overall, the critical and creative thinking for the
three groups can be presented in the following table;
Table 3 : Mean value of creative and critical Thinking
Critical Thinking Creative Thinking
Pretes Postest Pretes Postest
Eks. 1 38,82 77,37 35,36 79,44
Eks. 2 37,57 77,30 35,47 75,17
Control 36,25 65,14 33,85 63,19
The data in table 3 shows all groups have an
average increase from pretest to posttest. This
increase occurs in students' critical and creative
thinking skills in mathematics, especially with
regard to the topic of circle and theirs parts.
To achieve the intended objectives in this study, the
research findings will be presented in 3 sections,
namely: the difference in the increase of critical and
creative thinking, the best improvement of critical
thinking, and the best improvement of students'
creative thinking.
3.1 Differences in Improving the
Critical and Creative Thinking
Skills of Students
The students' critical and creative thinking skills
improved in the medium category as measured by
N-gain. This increase is experienced by all students
in experimental 1 (Problem Posing), experiment 2
(Contextual Problem), and the control group.
However, the N-gain value varies for both
capabilities and the three groups as shown in table 2
below.
Table 4: N-gain value of students' critical and creative
thinking skills
Class N-Gain Interpretation
Critical Creativ
e
Critical Creative
Exp. 1
0,63 0,68
Moderat
e
Moderat
e
Exp. 2
0,64 0,61
Moderat
e
Moderat
e
Control
0,45 0,44
Moderat
e
Moderat
e
The data in Table 4 shows that the N-gain of
experimental group 1 (who studied with probing
problem) and experiment 2 (who studied
contextually) were greater than the control group
either critical thinking or creative thinking in
mathematics.
For critical thinking, the n-gain value
of the posing's problem group is greater than the
contextual group. Conversely, n-gain creative
thinking posing problem groups are lower than
contextual groups. Although, all of treatment give as
same as criteria about n-gain.
The involvement of students in learning posing
and contextual problems is the cause of the
development of critical thinking (Abrami et al.,
2015; Widyatiningtyas et al., 2015) and creative
students
(Ayllón, Gómez and Ballesta-Claver, 2015).
The existence of mathematical problems presented
in learning posing and contextual problems make
learning more meaningful (Yen and Halili, 2015).
3.2 The Differences in Increasing
Critical Thinking
To answer the second question, first analysis used by
anova. The differences in critical thinking between
groups can be seen in Table 5 below;
Table 5: Anova the ability of creative thinking
Sum of
Squares
df Mean
Square
F Sig
Betwe
en
Group
s
1,127 2 ,564
22,12
8
,000
Within
Group
s
2,751 108 ,025
Total 3,879 110
Furthermore, we founded significant differences
in students' critical thinking skills between classes in
the learning process using problem posing,
contextual problem and expository approaches. The
Where Exactly for Enhance Critical and Creative Thinking: The Use of Problem Posing or Contextual Learning
701
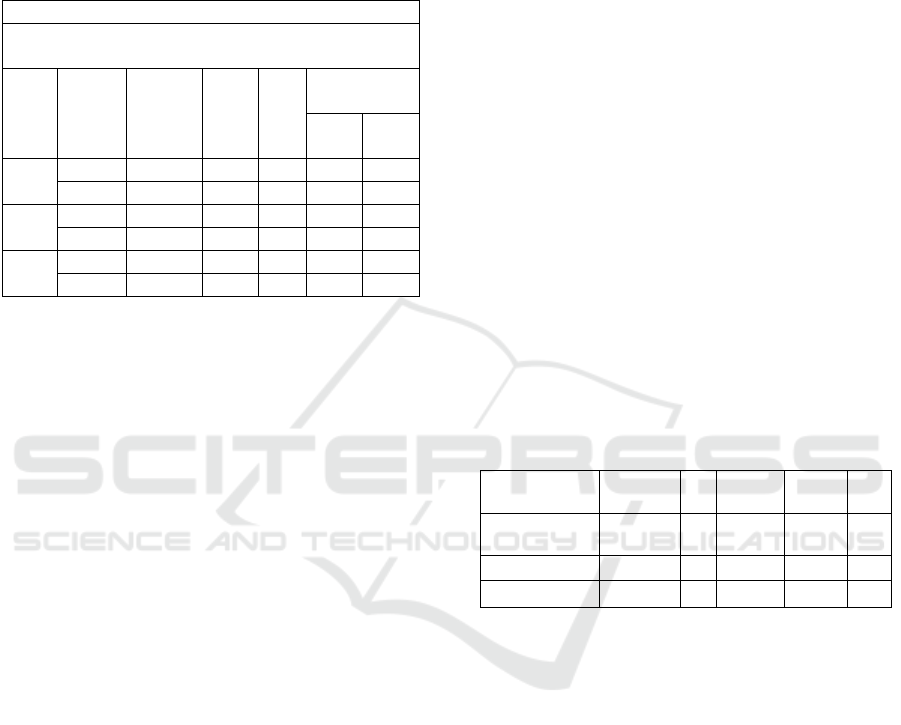
analysis used Scheffe test which is 95% significant
level to know the difference of significance at
treatment. The output results of this analysis can be
seen as follows:
Table 6: Scheffe test of critical thinking skill
Multiple Comparisons
Dependent Variable: Learning approaches
Scheffe
(I)
Learn
. App.
(J)
Learn.
App.
Mean
Diff. (I-
J)
Std.
Error
Sig.
95% Confidence
Interval
Lower
Bound
Upper
Bound
Exp.
1
Exp. 2 -,00753 ,0335 ,975 -,090 ,0756
Exp. 3 ,15240
*
,0338 ,000 ,0686 ,2362
Exp.
2
Exp. 1 ,00753 ,0335 ,975 -,075 ,0907
Exp. 3 ,15994
*
,0340 ,000 ,0756 ,2442
Exp,
3
Exp. 1 -,15240
*
,0338 ,000 -,236 -,068
Exp. 2 -,15994
*
,0340 ,000 -,244 -,076
Table 6 shows significant differences in students'
critical thinking skills between classes using
problem posing approaches (Experiments 1) and
those using a contextual approach (Experiment 2)
with a class using an expository learning approach.
However, there is no significant difference in
students' critical thinking skills between classes
using the problem-posing approach (Experiment 1)
with those using the contextual approach
(Experiment 2). Nonetheless, classes that acquire a
contextual learning approach are better than classes
using problem posing approaches the inability of
critical thinking.
Real issues related to the student's daily life in
contextual learning trigger student activities to
identify and analyze information logically, find
solutions and present them argumentatively.
Discussions of small groups and large groups trigger
them to argue with each other and reasoning that
train them to be more critical. As Sanjaya and
Hassoubah argue that Contextual Teaching and
Learning (CTL) is a learning strategy that
emphasizes the full process of student involvement
in order to find the material learned and relate it to
real life situations that encourage students to be able
to apply it in their lives, to empower students with
the hope that students are able to construct
knowledge in their minds, rather than memorizing
facts (Sanjaya, 2006; Paul and Linda, 2006).
This is in line with what suggests, Bonney and
Sternberg state the importance of effective learning
so that students become critical thinkers and how
students learn effectively, the roles of students,
teachers and the context in critical thinking teaching
(Bonney and Sternberg, 2016). Contextual learning
is a constructivism approach to student activity for
more meaningful learning (Yen and Halili, 2015).
The students who learn through contextual have
excellent abilities in identifying, formulating things
that are known and asked correctly and the results of
calculations are correct. However, the aspect of
determining the strategy for problem-solving is less
systematically and logically even though the results
are correct.
The aspects of critical thinking to analyze and
conclude are good. They can identify 5 to 6 elements
contained in a circle. They were able to provide a
good explanation of the results from the right
calculations, although in concluding there were still
a few mistakes.
3.3 Differences in Enhancing Creative
Thinking
Differences in creative thinking between groups can
be seen in table 5 below.
Tabel 7: Anova the ability of creative thinking
Sum of
Squares
df
Mean
Square
f Sig.
Between
Groups
1,127 2 ,564 22,128 ,000
Within Groups 2,751 108 ,025
Total 3,879 110
Table 7 shows that there is a significant
difference in students' creative thinking ability
between classes which in their learning process use
posing, contextual and expository approaches.
The next analysis used Scheffe test which is 95%
significant level to know the difference of
significance at treatment.
Table 8, shows significant differences in
students' creative thinking ability between classes
using problem posing approach (Experiment 1) and
using contextual approach (Experiment 2) with a
class using an expository learning approach.
However, there is no significant difference in
students' creative thinking ability between classes
using the problem-posing approach (Experiment 1)
with those using the contextual approach
(Experiment 2). Nonetheless, the class that acquired
the problem-posing learning approach is better than
the class using the contextual approach in ability of
creative thinking.
ICRI 2018 - International Conference Recent Innovation
702
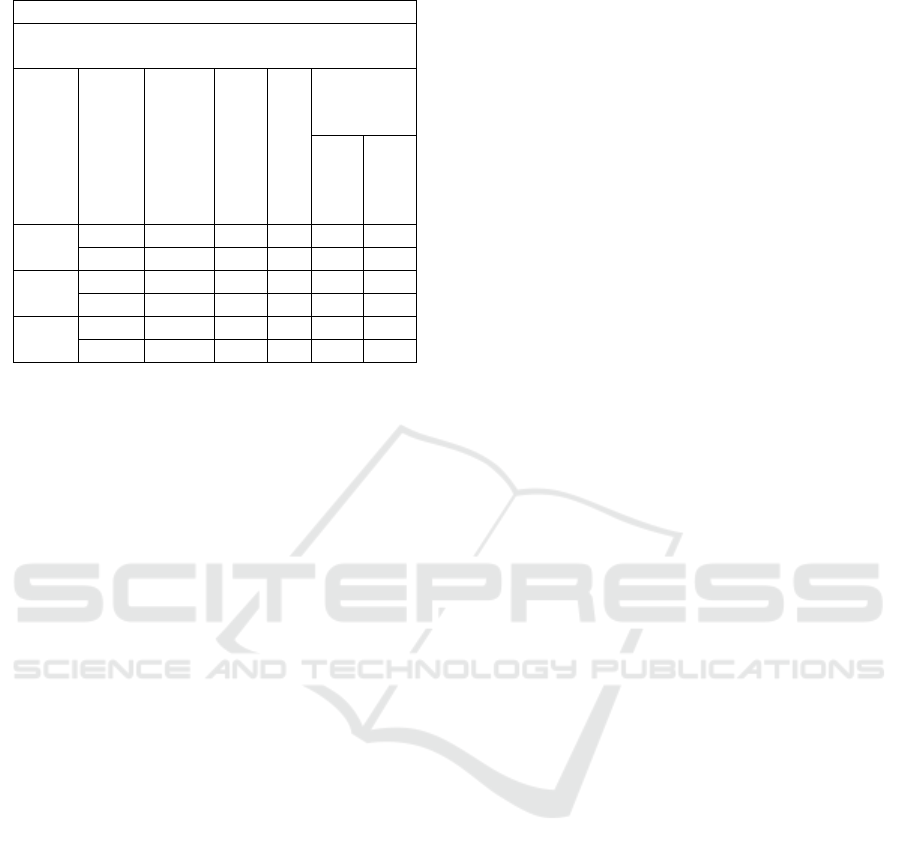
Tabel 8: Scheffe test-the ability of creative thinking
Multiple Comparisons
Dependent Variable: Learning approaches
Scheffe
(I)
Learn.
appr.
(J)
Learn.a
ppr.s
Mean
Differen
ce (I-J)
Std.
Erro
r
Sig.
95%
Confidence
Interval
Lowe
r
Boun
d
Uppe
r
Boun
d
Exp. 1
Exp. 2 ,068 ,0369 ,189
-
,0237 ,1593
Exp. 3 ,240
*
,0371 ,000 ,1482 ,3325
Exp. 2
Exp. 1 -,068 ,0369 ,189
-
,1593 ,0237
Exp. 3 ,173
*
,0374 ,000 ,0798 ,2653
Exp. 3
Exp. 1 -,240
*
,0371 ,000
-
,3325
-
,1482
Exp. 2 -,173
*
,0374 ,000
-
,2653
-
,0798
*. The mean difference is significant at the 0.05 level.
This findings reinforce the results of Ayllón's,
Gómez and Ballesta-Claver research, who argue that
posing problems can develop students' creative
thinking (Ayllón, Gómez and Ballesta-Claver,
2015), supporting also the results of Silver and Cai's
research that posing problems are at the core of
mathematical thinking, a problem that implies
students train to ask " why and how "through a
variety of problems, so students have various ways,
arguments, alternatives in identifying ways to solve
problems at hand (Silver and Cai, 1996).
The exercises to make sub-questions from the
main problem make them accustomed to finding
ideas, ideas in finding alternative solutions. Students
are also trained to complete their ideas so that they
are triggered to find new ideas or strategies for
finding more effective solutions. Sharing ideas in
posing problems is an important medium in finding
new ideas and revised old ideas.
Students who learn through problem posing have
excellent abilities in aspects of flexibility and
elaboration. This is characterized by the ability to
provide answers in more than one way, the
calculation process and the results are correct, and
resolve problems accompanied by reasons or
explanations in detail correctly and the results are
correct.
4 CONCLUSION
Based on the results and discussions conducted in
this study can be concluded that learning posing and
contextual problems more effectively used to
improve the ability of critical thinking and creative
thinking of students compared with expository
learning. Problem posing learning enables the
development of creative thinking better than
contextual learning. In line with the findings that
learning problem posing and problem-solving can
develop creative thinking (Ayllón, Gómez and
Ballesta-Claver, 2015). Conversely, contextual
learning is more instrumental in developing students'
critical thinking than learning problem posing. In
parallel with the traditional paradigm shift and the
transfer of information toward constructivism from
student activities for more meaningful learning (Yen
and Halili, 2015).
Critical and creative thinking can be improved
through thinking exercises during the learning
process (Bostic, Pape and Jacobbe, 2016). This
practice of thinking will be formed through the
context of problems that are close to their lives,
questions that have many ways to be solved.
To provide opportunities for them to share ideas
or opinion, give one or two trigger questions by the
teacher when they are deadlocked. Teachers should
make instruction how to talk or use talk to ask
questions, to explain their thinking, to analyze and
solve problems, explore and evaluate ideas, argue,
reason and justify (Gillies, 2016).
5 RECOMENDATIONS
Furthermore, the study needs to be done to see
which aspects of critical thinking and creative
thinking can be developed through learning of
posing and contextual problems. In addition, the
study also needs to be done through a mix method
approach to obtain more complete data again.
Innovations in learning posing and contextual
problems by utilizing technology and collaboration
with other subjects need to be done in order to
comprehensively the students can develop specially
to face the century 21 ahead. Teachers can
implement this method for any topic in mathematics.
Further studies can be conducted to identify 21st-
century character quality through contextual learning
and problem posing.
ACKNOWLEDGEMENTS
The authors wish to thank Faculty of Tarbiyah and
Teacher Science (FITK) IAIN Syekh Nurjati
Cirebon-Indonesia.
Where Exactly for Enhance Critical and Creative Thinking: The Use of Problem Posing or Contextual Learning
703

REFERENCES
Abrami, P. C. et al. (2015) ‘Strategies for teaching
students to think critically: A meta-analysis’, 85(2),
pp. 275–314.
Aizikovitsh-Udi, E. and Diana, C. (2015) ‘Developing
critical thinking skills from dispositions to abilities:
Mathematics education from early childhood to high
school’, Creative Education, 6(04), pp. 455–462.
Almeida, L. S. et al. (2008) ‘“Torrance Test of Creative
Thinking: The question of its construct validity.” 3,
no. 1 (2008)’, Thinking skills and creativity, 3(1), pp.
53–58.
Apino, E. and Retnawati, H. (2017) ‘Developing
instructional design to improve mathematical higher
order thinking skills of students’, Journal of Physics:
Conference Series. IOP Publishing, 812.(1), pp. 1–7.
Ayllón, M. F., Gómez, I. A. and Ballesta-Claver, J. (2015)
‘Mathematical Thinking and Creativity through
Mathematical Problem Posing and Solving’, Journal
of Educational Psychology-Propósitos y
Representaciones, 4(1), pp. 195–218.
Birgili, B. (2015) ‘Creative and Critical Thinking Skills in
Problem-Based Learning Environments’, Online
Submission, 2(2), pp. 71–80.
Bonney, C. N. R. and Sternberg, R. R. J. (2016) ‘Learning
to think critically’, in Handbook of research on
learning and instruction. England: Routledge, pp.
191–222.
Bostic, J. D., Pape, S. J. and Jacobbe, T. (2016)
‘Encouraging sixth-grade students’ problem-solving
performance by teaching through problem solving’,
Investigations in mathematics learning, 8(3), pp. 30–
38.
Bryk, A. S. and Weisberg, H. I. (1977) ‘Use of the
nonequivalent control group design when subjects are
growing’, Psychological Bulletin, 84(5), pp. 950–962.
Campbell, D. T. and Stanley, J. C. (2015) Experimental
and quasi-experimental designs for research. Ravenio
Books.
Center. Pacific Policy Research (2010) 21st century skills
for students and teachers. Honolulu, Hawai:
Kamehameha Schools reserach & Evaluation.
Creswell, J. W. and Creswell, J. D. (2017) Research
design: Qualitative, quantitative, and mixed methods
approaches. Los Angelas: Sage publications.
Dwyer, C. P., Hogan, M. J. and Stewart, I. (2014) ‘An
integrated critical thinking framework for the 21st
century’, Thinking Skills and Creativity, 12, pp. 43–
52.
Ennis, R. (2013) ‘Critical thinking across the curriculum:
the wisdom CTAC program’, Inquiry: Critical
Thinking across the Disciplines, 28(2), pp. 25–45.
Ennis, R. H. (2015) ‘Critical thinking: A streamlined
conception’, in The Palgrave handbook of critical
thinking in higher education. New York,: Falgrave
Macmillan, pp. 31–47.
Faizah, I. N., Budi, M. and M., K. (2017) Analisis Butir
Soal Ujian Sekolah/Madrasah Matematika SD/MI
Tahun Ajaran 2015/2016 Berdasarkan Domain Isi dan
Domain Kognitif TIMSS. Universitas Muhammadiyah
Surakarta.
Gillies, R. M. (2016) ‘Cooperative learning: Review of
research and practice’, Australian Journal of Teacher
Education, 41(3), pp. 39–54.
Huang, H. F., Ricci, F. A. and Mnatsakanian, M. (2016)
‘Mathematical teaching strategies: Pathways to critical
thinking and metacognition’, International Journal of
Research in Education and Science, 2(1), pp. 190–
200.
Johnson, E. B. (2002) Contextual teaching and learning:
What it is and why it’s here to stay. California: Corwin
Press.
Kim, J.-O. and Kohout, F. J. (1975) ‘Analysis of variance
and covariance: subprograms ANOVA and
ONEWAY’, Statistical package for the social
sciences, 2, pp. 398–433.
Koetzsch, R. E. (1997) The Parents’ Guide to Alternatives
in Education. Massachusetts Avenue, Boston:
Shambhala Publications, Inc., Horticultural Hall, 300.
Leonard, J. (2017) Culturally specific pedagogy in the
mathematics classroom: Strategies for teachers and
students. England: Routledge.
Lince, R. (2016) ‘Creative Thinking Ability to Increase
Student Mathematical of Junior High School by
Applying Models Numbered Heads Together’,
Journal of Education and Practice, 7(6), pp. 206–212.
Mahmuzah, R. (2015) ‘Peningkatan Kemampuan Berpikir
Kritis Matematis Siswa SMP melalui Pendekatan
Problem Posing’, Jurnal Peluang, 4(1), pp. 64–72.
McCormick, N. J., Clark, L. M. and Raines, J. M. (2015)
‘Engaging students in critical thinking and problem
solving: A brief review of the literature’, Journal of
Studies in Education, 5(4), pp. 100–113.
McPeck, J. E. (2016) Critical thinking and education. ,.
London: Routledge.
Mertler, C. A. (2001) ‘Designing scoring rubrics for your
classroom’, Practical Assessment, Research &
Evaluation, 7(25), pp. 1–10.
Mullet, D. R. et al. (2016) ‘Examining teacher perceptions
of creativity: A systematic review of the literature’,
Thinking Skills and Creativity, 21(6), pp. 9–30.
Paul, R. and Linda, E. (2006) Critical thinking competency
standards. Dillon Beach, CA: Foundation for Critical
Thinking.
Sanjaya, W. (2006) Strategi pembelajaran berorientasi
standar proses pendidikan. Jakarta: Kencana.
Silver, E. A. and Cai, J. (1996) ‘An analysis of arithmetic
problem posing by middle school students’, Journal
for research in mathematics education, 27(5), pp.
521–539.
Suastika, I. K. and Wahyuningtyas, D. T. (2017)
‘Mathematics Learning Syntax Model Using Open-
Ended Problem Solving To Develop Students’
Creativity’, Pancaran Pendidikan, 6(4), pp. 105–112.
Torrance, E. P. (1972) ‘Predictive validity of the Torrance
tests of creative thinking’, The Journal of creative
behavior, 6(4), pp. 236–262.
ICRI 2018 - International Conference Recent Innovation
704

Wessels, H. M. (2014) ‘Levels of mathematical creativity
in model-eliciting activities’, Journal of Mathematical
Modelling and Application, 1(9), pp. 22–40.
Widyatiningtyas, R. et al. (2015) ‘The Impact of Problem-
Based Learning Approach to Senior High School
Students’ Mathematics Critical Thinking Ability’,
ndonesian Mathematical Society Journal on
Mathematics Education, 6(2), pp. 30–38.
Yen, T. S. and Halili, S. H. (2015) ‘Effective teaching of
higher order thinking (HOT) in education’, The Online
Journal of Distance Education and e-Learning, 3(2),
pp. 41–47.
Where Exactly for Enhance Critical and Creative Thinking: The Use of Problem Posing or Contextual Learning
705
