
Super Encryption Concepts using Vigenere Cipher Modification to
Produce Color Imaginary as Ciphertext
Moch. Hari Purwidiantoro
1
and Dany Fajar Kristanto Saputro Wibowo
1
1
STMIK Cipta Darma Surakarta, Veteran Street, Notosuman, Singopuran, Kartasura, Sukoharjo, Indonesia
Keywords: Super Encryption, Cryptography, Vigenere Cipher, Color, Image.
Abstract: For various reason data security and confidentially are needed. One way to improve data confidentiality in
data communications by modifying the classic cryptographic algorithm into a difficult algorithm to solve.
Vigenere Cipher is one of the most complicated classical cryptography algorithms to be solved, because it
uses substitution techniques and keywords. Although so Vigenere Cipher still have weaknesses and the
length of the keyword can be solved by using the kasiki’s method. This paper discussed about modification
of Vigenere Cipher, that is changing the contents of Vigenere square to decimal numbers 1…26, which then
the decimal symbol of the encryption result are coded RGB color, so the final encryption result of the
modification of Vigenere Cipher in this paper is a color image, so it becomes very difficult to solve.
Because a cryptanalyst does not necessarily think the color image is an encryption that should be solved.
1 INTRODUCTION
Cryptography is a science and art to keep the
message safe when message are sent, Cryptography
comes from greek, namely crypto which means
secret and graphia meaning writing (Stallings,
2014). The art word of the above definition comes
from historical facts, that in the early days of the
history of cryptography everyone has a unique way
of keeping messages secret, so each way of writing a
secret message has its own aesthetic value (Ariyus,
2007). In its development, cryptography developed
into a discipline of its own because cryptographic
techniques can be formulated mathematically to
become a method.
For various reason data security and confidentially
are needed in data communications. There are
various ways to improve the security and
confidentially of data. One of them with by
modifying the classical cryptographic algorithm into
a algorithm that is difficult to solve.
Super encryption can be done by modifying a simple
classical cryptography method. Classical
cryptography is character-based cryptography
(Styaningsih, C. Iswahyudi and N. Widyastuti,
2011). Vigenere cipher is one of the classic
cryptographic algorithms that encrypt plaintext using
substitution techniques. Vigenere cipher is basically
quite complicated to solve. Although so vigenere
cipher still have weaknesses. One of which is can be
known the length of the keyword using Kasiki
method (Putu, 2012). This is because there are
repetitive phrases in the resulting ciphertext. This
paper will discuss about modification of Vigenere
Cipher to strengthen this algorithm so it is not easy
to solve.
2 LITERATURE REVIEW
Some studies have discussed about the modification
of vigenere cipher to overcome the weakness of the
classic vigenere cipher. (Prabowo and Hangga,
2015) In their research discuss about encryption
using vigenere cipher which keywords use
encryption from caesar cipher, so there will be no
repetition words in the final cipher text.
In research by (Styaningsih, C. Iswahyudi and N.
Widyastuti, 2011) discuss about encryption using
combination of vigenere cipher with playfair, to
improve the security then used keystream generator
method to randomize the sequence of keywords so
cryptanalis will find it difficult to get the keywords.
In a study conducted by (M. Hidayatulloh and E.
Insannudin, 2014) resulting in a modification of
vigenere cipher which cipher text is ASCII symbol.
Purwidiantoro, M. and Saputro Wibowo, D.
Super Encryption Concepts using Vigenere Cipher Modification to Produce Color Imaginary as Ciphertext.
DOI: 10.5220/0009946230293035
In Proceedings of the 1st International Conference on Recent Innovations (ICRI 2018), pages 3029-3035
ISBN: 978-989-758-458-9
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
3029

Different to the classical vigenere cipher which
based on the alphabet, In the study was modified
vigenere cipher based on ascii table where there are
256 character. So the encryption result is safer
3 PROPOSE METHOD
3.1 Super Encryption
Super encryption is one of character based
cryptography that uses modification or combining
two ciphers. It aim to get a stronger cipher.In this
study used vigenere cipher modified to produces
ciphers in the form of color images.
3.2 Vigenere Cipher
Vigenere cipher is a method of encoding alphabetic
text by using a caesarean code sequence based on
the letters on the keyword. Vigenere cipher
technique can be done in two ways by numbers and
letters. Method to perform encryption and
decryption process on vigenere cipher that is using
recta table or also called vigenere square.
ABCDEFGHI J KLMNOPQRSTUVWXYZ
A ABCDEFGH I J KLMNOPQRSTUVWXYZ
B BCDEFGH I J KLMNOPQRS TUVWXY ZA
C CDE FGH I J K LMNOPQRS TUVWXY ZAB
D DEFGH I J KLMNOPQRSTUVWXYZABC
E EFGHI JKLMNOPQRSTUVWXYZABCD
F FGH I J KLMNOPQRS TUVWXY ZABCDE
G GH I J K LMNOPQR S TUVWX Y ZA B CDE F
H HIJKLMNOPQRSTUVWXYZABCDEFG
I IJKLMNOPQRSTUVWXYZABCDEFGH
J JKLMNOPQRSTUVWXYZABCDEFGHI
K KLMNOPQRSTUVWXYZABCDEFGHI J
L LMNOPQR S T UVWX Y Z A B CD E F GH I J K
M MN O P Q R S T U VW X Y Z A B C D E F G H I J K L
N NOPQRSTUVWXY ZA BCDEFGHI J K LM
O OPQRS TUVWXY ZA B CDE FGH I J K LMN
P PQRSTUVWXYZABCDEFGH I J KLMNO
Q QRS TUVWXY Z A BCD E F GH I J K LMNOP
R RS TUVWXYZABCDEFGH I J K LMNOPQ
S STUVWXYZABCDEFGHI J KLMNOPQR
T TUVWXY ZABCDEFGHI J K LMNOPQRS
U UVWX Y Z A BCDE F GH I J K LMNOPQR S T
V VWXYZABCDEFGHI J K LMNOPQRSTU
W WX Y Z A B C D E F GH I J K LMNO P Q R S T UV
X XY ZABCDEFGHI J KLMNOPQRS TUVW
Y YZABCDEFGH I J KLMNOPQRS TUVWX
Z ZABCDEFGH I J K LMNOPQRSTUVWXY
Figure 1 : Vigenere Square
The leftmost column of the square represents the
keyword letters, while the top line represents the
plaintext letters. Vigenere square is used to get
ciphertext by using predefined keywords. If the
length of the keywords is shorter than the length of
the plaintext, then the keyword is repeated use
(periodic system). For an example if the plaintext is
THIS IS THE PLAINTEXT and the keyword is
DANY, then the use of keys periodically is as
follows.
TH I S I STHEP LA I NTEX
T
DANYDANYDANYDANYD
A
Plain text
Kunci
To get the ciphertext from the plaintext and the
keyword above, for the first plaintext letter T, drawn
vertical line of the letter T, and drawn a horizontal
line from column D, the intersection would be the
first letter of ciphertext W. The same way is done on
the plaintext letters and letters of the next keyword.
ABCDEFGHI J KLMNOPQRSTUVWXYZ
A ABCDEFGH I J KLMNOPQRSTUVWXYZ
B BCDE FGH I J K LMNOPQRS TUVWXYZA
C CDE FGH I J K LMNOPQRS TUVWXY ZA B
D DEFGHI J K LMNOPQRS TUVWXY ZABC
E EFGHI J KLMNOPQRSTUVWXYZABCD
F FGH I J KLMNOPQRSTUVWXYZABCDE
G GH I J K LMNOPQR S TUVWX Y Z A B CD E F
H HI JKLMNOPQRSTUVWXYZABCDEFG
I IJKLMNOPQRSTUVWXYZABCDEFGH
J JKLMNOPQRSTUVWXYZABCDEFGHI
K KLMNOPQRSTUVWXYZABCDEFGHI J
L LMNOPQRS TUVWX Y Z A B CD E F GH I J K
M MN O P Q R S T UV W X Y Z A B C D E F G H I J K L
N NOPQR S T UVWXY ZA B CD E F GH I J K LM
O OPQRS TUVWXY ZA BCD E FGH I J K LMN
P PQRS TUVWXY ZA BCDE FGH I J K LMNO
Q QRS TUVWX Y ZA B CDE F GH I J K LMNOP
R RSTUVWXYZABCDEFGHI J K LMNOPQ
S STUVWXYZABCDEFGHI J KLMNOPQR
T TUVWXY ZABCDEFGHI J K LMNOPQRS
U UVWX Y Z A B CD E F GH I J K LMNOPQR S T
V VWX Y Z A B C D E F G H I J K LMNO P Q R S T U
W WX Y Z A B C D E F GH I J K LMN O P Q R S T UV
X XYZABCDEFGH I J K LMNOPQRSTUVW
Y YZABCDEFGHI JKLMNOPQRSTUVWX
Z ZABCDEFGH I J KLMNOPQRSTUVWXY
Figure 2 : How to use vigenere square
The result of its encryption is as follows :
TH I S I STHEP LA I NTEX
T
DANYDANYDANYDANYD
A
WHVQLSGFHPY Y LNGCAT
Plain text
Kunci
Cipher
The decryption process is done by searching the
cipher text letter on the plaintext line of the keyword
letter. From the example above, then it can be
concluded mathematical formula of encryption and
decryption vigenere cipher is (1):
Encryption :
Ci = (Pi + Ki) mod 26 (1)
Decryption :
Pi = (Ci – Ki) mod 26 ; for Ci >= Ki
Pi = (Ci + 26 – Ki) mod 26 ; for Ci <= Ki
Explanation :
Ci = Cipher text ; Pi = Plaintext ; Ki = Keyword
4 VIGENERE CIPHER
MODIFICATION
Vigenere cipher has a weakness that makes it can be
solve. One of them is to know the key length using
kasiki method. The keyword length can be more
ICRI 2018 - International Conference Recent Innovation
3030
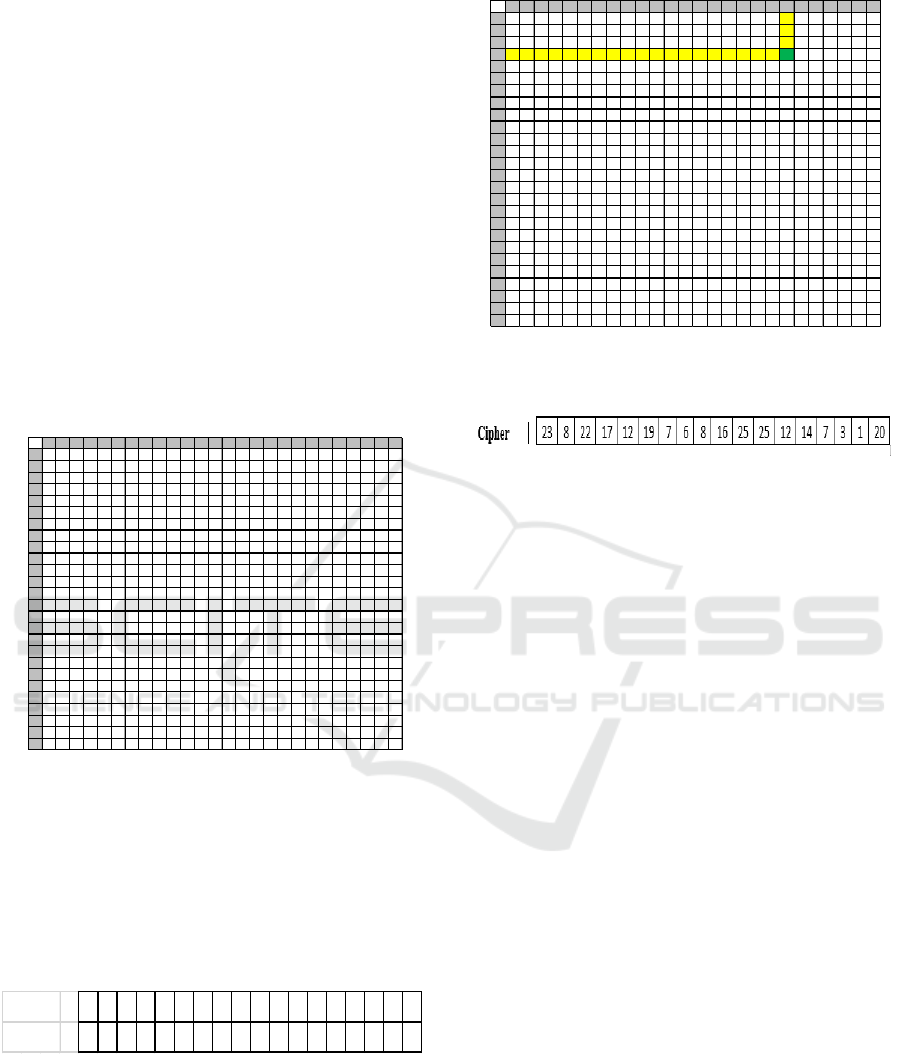
easily known, because if the key length is shorter
than plaintext then the next keyword is a repetition
of the keyword (Setyaningsih, 2011).
To overcome the weakness of vigenere cipher in this
paper will discuss the modification of vigenere
cipher which the encryption result is a colour image
with RGB colour code. In previous research there
are make modifications for vigenere cipher
technique, but it mostly modify keywords to reduce
the occurrence of phrase repetition (Hidayatulloh,
2014). While in this paper will modify the contents
of vigenere square. Previously there is also a modify
the contents of vigenere square, which contents are
modified into ASCII symbol (Prabowo, 2015), in
this paper the contents of vigenere square are
modified into decimal symbols 1 through 26. The
result of the vigenere square modification becomes
as follows (P.W. Springer, 2014) :
ABCDEFGHI J K LMNOPQRSTUVWXYZ
A 1 2 3 4 5 6 7 8 9 1011121314151617181920212223242526
B 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1
C 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2
D 4 5 6 7 8 9 1011121314151617181920212223242526 1 2 3
E 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4
F 6 7 8 9 1011121314151617181920212223242526 1 2 3 4 5
G 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6
H 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7
I 9 1011121314151617181920212223242526 1 2 3 4 5 6 7 8
J 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9
K 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10
L 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11
M 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12
N 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13
O 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14
P 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Q 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
R 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
S 1920212223242526 1 2 3 4 5 6 7 8 9 101112131415161718
T 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
U 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
V 2223242526 1 2 3 4 5 6 7 8 9 101112131415161718192021
W 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
X 242526 1 2 3 4 5 6 7 8 9 1011121314151617181920212223
Y 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Z 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Figure 3: Vigenere square modification
The encryption process of this vigenere cipher
modification is still the same as the classical
vigenere cipher, by finding the intersection of the
plaintext letter with the keyword letter. For an
example if the plaintext is THIS IS THE
PLAINTEXT and the keyword is DANY, then the
use of keys periodically is as follows.
TH I S I STHEP LA I NTEX
T
DANYDANYDANYDANYD
A
Plain text
Kunci
To get the ciphertext from the plaintext and the
keyword above, for the first plaintext letter T, drawn
vertical line of the letter T, and drawn a horizontal
line from column D, the intersection would be the
first letter of ciphertext 23. The same way is done on
the plaintext letters and letters of the next keyword.
ABCDEFGHI J KLMNOPQRSTUVWXYZ
A 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
B 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1
C 3 4 5 6 7 8 9 1011121314151617181920212223242526 1 2
D 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3
E 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4
F 6 7 8 9 1011121314151617181920212223242526 1 2 3 4 5
G 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6
H 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7
I 9 1011121314151617181920212223242526 1 2 3 4 5 6 7 8
J 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9
K 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10
L 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11
M 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12
N 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13
O 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14
P 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Q 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
R 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
S 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
T 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
U 212223242526 1 2 3 4 5 6 7 8 9 1011121314151617181920
V 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
W 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
X 242526 1 2 3 4 5 6 7 8 9 1011121314151617181920212223
Y 25 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Z 26 1 2 3 4 5 6 7 8 9 10111213141516171819202122232425
Figure 4 : How to use vigenere square modification
The result of its encryption is as follows :
The mathematical encryption formula of the
vigenere cipher modification is slightly different
from the classic vigenere cipher formula, on the
classical vigenere cipher the mathematical formula
uses the decimal value of the character of 0….25,
that is :
A = 0 B = 1 C = 2 D = 3
E = 4 F = 5 G = 6 H = 7
I = 8 J = 9 K = 10 L = 11
M = 12 N = 13 O = 14 P = 15
Q = 16 R = 17 S = 18 T = 19
U = 20 V = 21 W = 22 X = 23
Y= 24 Z = 25
While in vigenere cipher modification in this paper
the mathematical formula uses decimal character
from 1…26, that is :
A = 1 B = 2 C = 3 D = 4
E = 5 F = 6 G = 7 H = 8
I = 9 J = 10 K = 11 L = 12
M = 13 N = 14 O = 15 P = 16
Q = 17 R = 18 S = 19 T = 20
U = 21 V = 22 W = 23 X = 24
Y= 25 Z = 26
So that will be obtained mathematical formula
vigenere cipher slightly different modification, the
formula is (2):
Encryption : Ci = ((Pi + Ki) mod 26) – 1 (2)
Super Encryption Concepts using Vigenere Cipher Modification to Produce Color Imaginary as Ciphertext
3031

Decryption :
Pi = ((Ci – Ki) mod 26) + 1 ; for Ci >= Ki
Pi = ((Ci + 26 – Ki) mod 26) + 1 ; for Ci <= Ki
Explanation :
Ci = Ciphertext ; Pi = Plaintext ; Ki = Kunci
Using plaintext example THIS IS THE
PLAINTEXT and the keyword is DANY, then the
calculation of encryption using vigenere cipher
modification technique is, like this:
From the above example, the plaintext of the first
letter T which has the value Pi = 20 will be
calculated by the key letter D which has Ki = 4, then
the encryption process is as follows (3):
Ci = ((Pi + Ki) mod 26) – 1 (3)
Ci = ((20 + 4) mod 26) -1
Ci = (24 mod 26) -1
Ci = 24 -1 = 23
Ci = 23
Chipertext results from calculation of vigenere
cipher modification formula on the first letter is 23.
Once done the calculation of the formula vigenere
cipher modification according to the keyword on
each letter until all the plaintext has been encrypted.
Setelah semua huruf terenkripsi into ciphertext, then
the results of cipher text is as follows :
After obtaining all ciphertext numbers result from
the encryption process vigenere cipher modification,
then the numbers from the encryption process are
converted into RGB color codes , each sequence of
three numbers into one color code then that color
codes are converted into color images, the color
images that appears is the final result of modified
vigenere cipher. If the number of plaintext
characters is even numbered then at the end of the
plaintext is given an additional padding bit, which is
symbolized by the number 27. Based on the example
above, then the method to get the ultimate
encryption result is :
From the cipher text above there are six RGB color
codes, that is :
Code 1. R = 23
G = 8
B = 22
Color image :
Code 2. R = 17
G = 12
B = 19
Color image :
Code 3. R = 7
G = 6
B = 8
Color image :
Code 4. R = 16
G = 25
B = 25
Color image :
Code 5. R = 12
G = 14
B = 7
Color image :
Code 6. R = 3
G = 1
B = 20
Color image :
With the color image as a final result of encryption,
The secret messages will be more difficult to solve
and the secret message security level will be higher.
This vigenere cipher modification technique can be a
solution to cover the weakness of the classical
vigenere cipher. A Color image as the final result of
cipher text can be applied to an image, so that other
people see it as just an ordinary picture and will not
realize that there is a secret message in the picture,
so others who are not entitled to the secret message
will not attempt to solve it, because they think its
ICRI 2018 - International Conference Recent Innovation
3032

just as a regular picture. Technique of disguising
secret message in a picture is also called
steganography, not only images but also other media
such as video and audio.
5 DECRYPTION VIGENERE
CIPHER MODIFICATION
Decryption technique for this vigenere cipher
modification is the keyword must be known by the
recipient of the message, then the recipient can get
the color code from the color image that is sent, by
using image manipulation software like adobe
potoshop. From the example obtained the color code
as follows:
After getting the color codes and sorted in order of
color code sent, then for its decryption process can
use the mathematical formula (4):
Decryption :
Pi = ((Ci – Ki) mod 26) - 1 ; for Ci >= Ki (4)
Pi = ((Ci + 26 – Ki) mod 26) - 1 ; for Ci <= Ki
Ci = Ciphertext ; Pi = Plaintext ; Ki = Kunci
Ciphertext = 23
Pi = ((Ci – Ki) mod 26) + 1
Pi = ((23 – 4) mod 26) + 1
Pi = (19 mod 26) + 1
Pi = 20
Ciphertext = 8
Pi = ((Ci – Ki) mod 26) + 1
Pi = ((8 – 1) mod 26) + 1
Pi = (7 mod 26) + 1
Pi = 8
So that the overall calculation of Pi =
Pi 20 8 9 19 9 19 20 8 5 16
12 1 9 14 20 5 24 20
The Pi calculation result from decimal 1…26 to
character a…z
A = 1 B = 2 C = 3 D = 4
E = 5 F = 6 G = 7 H = 8
I = 9 J = 10 K = 11 L = 12
M = 13 N = 14 O = 15 P = 16
Q = 17 R = 18 S = 19 T = 20
U = 21 V = 22 W = 23 X = 24
Y= 25 Z = 26
So finally obtained its plaintext result :
THIS IS THE PLAINTEXT
6 IMPLEMENTATION
6.1 Vigenere Cipher Modification
Algorithm
The stages of the encryption algorithm with
modified vigenere cipher:
Stage 1:
a GetTextLen (plainteks)// Calculate the number
of arrays from the plaintext
Stage 2:
b GetTextlen (kunci)// Calculate the number of
arrays of keywords
Stage 3:
X 0// fill in the variable x with a value of 0
While x <= a
Begin
for j 1 to b do
begin
Stage 4:
P
Ord (plaintext [x]// Change char to ASCII code
Stage 5:
P p- 97// The ASCII code is changed (a to 0)
Tahap 6:
K ord (key[j])// key becomes ASCII
Tahap 7:
k k – 97 // The ASCII code is changed (a to 0) //
the operation of adding plaintext with its key.
Tahap 8:
Super Encryption Concepts using Vigenere Cipher Modification to Produce Color Imaginary as Ciphertext
3033

c (p + k) mod 26 // vigenere operation
Tahap 9:
Ciphertext Ciphertext + c // Write results in
Ciphertext inc (x) // x value
plus 1
end
end
6.2 Implementation of Modification of
Vigenere Cipher Algorithm in
Visual Basic
Super encryption implementation using visual basic
programming language functions that are used to
encrypt and decrypt plain text messages into text
ciphers using the modified vigenere cipher
algorithm:
FunctionVigenere_Cipher(ByValText
AsString,ByValkeyAsString,ByVal
EncryptAsBoolean)
DimResultAsString=""
DimtempAsString=""
DimjAsInteger=0
ForiAsInteger=0ToText.Length–
1
Ifj=key.Length
Thenj=0
EndIf
If
Char.IsLetter(key(j))Then
IfText(i)<>""And
Char.IsLetter(Text(i))Then
temp+=key(j)
j+=1
Else
temp+=Text(i)
EndIf
Else
j+=1
Ifj>=key.Length
Then
j=0
EndIf
i‐=1
EndIf
Next
ForiAsInteger=0To
Text.Length‐1
DimNAsInteger
DimNewAsciiAsInteger
IfChar.IsLetter(Text(i))Then
IfChar.IsLower(temp(i))Then
N=Asc(temp(i))‐Asc("a")
ElseIf
Char.IsUpper(temp(i))Then
N=
Asc(temp(i))‐Asc("A")
EndIf
IfEncryptThen
NewAscii=N+
Asc(Text(i))
Else
NewAscii=26‐
N+Asc(Text(i))
EndIf
If(NewAscii>
Asc("z")AndChar.IsLower(Text(i)))Or
(NewAscii>Asc("Z")And
Char.IsUpper(Text(i)))Then
NewAscii‐=26
EndIf
Else
NewAscii=
Asc(Text(i))
End
If
Result+=Chr(NewAscii)
Next
ReturnResult
EndFunction
6.3 Form Kriptografi
Cryptographic forms are used to change the plain
text of a secret message that will be sent into a text
cipher using a modified vigenere cipher algorithm.
The message is written in the text box that has been
provided, then write the agreed keyword into the text
box of the keyword and press the encryption key to
perform the modified vigenere cipher algorithm
function and get the cipher text result.
While the decryption button is used to return the
cipher text into plain text, the secret message is
encrypted.
ICRI 2018 - International Conference Recent Innovation
3034

Figure 5: Cryptography Form
7 ANALYSIS
There are some advantages gained by using super
encryption vigenere cipher modification compared
with classical vigenere cipher, that is the cipher text
of super encryption is more difficult to solve
because the encryption process is twice or more, so
that the cipher text result also experienced two or
more changes [10]. Besides changing the character
text to decimal also made a change from decimal to
color image, so the possibility of a solution to be
made to solve cipher text is also becoming more and
more difficult
8 CONCLUSIONS
Based on the analysis that has been done before, can
be drawn some conclusions related to the super
encryption concept using modification vigenere
cipher as described earlier, that is :
The use of decimal as the contents of
vigenere square, produces cipher text
decimal which makes it more difficult to
guess which keyword to use.
Color images cipher text as the final result
can be applied or inserted into an image so
that it can become steganography, which
causes others will not be aware of any
hidden messages during the process of
sending secret messages.
Color image as the cipher text causes
cryptanalysts difficult to guess what
cryptographic method is used, so the
possibility cipher text to solved is very
small
.
The
cryptographic algorithm in this paper
does not guarantee 100% unbreakable
The suggestion for using this algorithm is to apply it
the image using steganography technique and
implemented using the application so it is easier to
use.
REFERENCES
Aryus, D., 2007. Keamanan Multimedia. Yogyakarta:
Penerbit Andi.
Harini, R. T. & Utami, E., 2012. Aplikasi Enkripsi SMS
Dengan Modifikasi Vigenere Cipher Pada Ponsel
Android. JURNAL DASI, pp. 65-70.
Hidayatulloh, M. & Insannudin, E., 2014. Enkripsi dan
Dekripsi Menggunakan Vigenere Cipher ASCII JAVA,
Bandung: UIN Bandung.
Kester & Quist, A., 2013. Hybrid Cryptosystem Based On
Vigenere Cipher And Columnar Transposition Cipher.
IJATER.
Latifah, R., Ambo, S. N. & Kurnia, S. I., 2017. Modifikasi
Algoritma Caesar Cipher dan Rail Fence Untuk
Peningkatan Keamanan Teks Alfanumerik dan
Karakter Khusus. Seminar Nasional dan Teknologi
(SEMNASTEK).
P.W., Springer. & Allan, F., 2014. Cybersecurity And
Cyberwar. New York: Oxford University Press.
Painem & Rabbani, D., 2017. Pengamanan Pesan Email
Dengan Menggunakan Algoritma Caesar Cipher,
Vigenere Cipher dan QR Code Berbasis Web.
TELEMATIKA MKOM, pp. 42-46.
Prabowo, H. E. & Hangga, A., 2015. Enkripsi Data
Berupa Teks Menggunakan Metode Modifikasi
Vigenere Cipher. Seminar Nasional Aplikasi
Teknologi Informasi (SNATi), pp. D1-D4.
Putu H., A., Rahayu, T. P., Yakub & Hariyanto, 2012.
Implementasi Enkripsi Data Dengan Algoritma
Vigenere Cipher. Seminar Nasional Teknologi
Informasi dan Komunikasi (SENTIKA), pp. 164-169.
Stallings, W., 2014. Cryptography and Network Security.
New Jersey: Pearson Education.Inc.
Styaningsih, E., Iswahyudi, C. & Widyastuti, N., 2011.
Konsep Super Enkripsi Untuk Meningkatkan
Kemanan Data Citra. SNASTI, pp. 7-10.
Yoanes, M. & Jantan, A., 2008. Image Encryption Using
Block-Based Transformation Algorithm. International
Journal of Computer Science.
Super Encryption Concepts using Vigenere Cipher Modification to Produce Color Imaginary as Ciphertext
3035
