Size Optimization of Foil-shaped Center Bulb

on Catamaran Hull Form to Reduce Resistance

Eko Sasmito Hadi, Muhammad Iqbal and Gana Pranamya

Department of Naval Architecture, Universitas Diponegoro, Semarang, Indonesia

Keywords: Catamaran, Foil-shaped Center Bulb, Resistance.

Abstract: The interference of resistance between the two catamaran hulls is a very popular topic to discuss. Errors in

designing hull form and determining the distance between the hull will result in a large amount of interference

that causes the resistance of the catamaran increased. Some researchers try to reduce the resistance of

catamaran due to interference such as changing the shape of the demihull, giving a bulbous bow, and adding

a center bulb. The idea to use center bulb on catamarans is still relatively new and still requires a lot of studies.

Therefore, in this study the elliptical center bulb will be replaced with a foil-shaped center bulb. The purpose

of this study was to obtain the optimal length (𝑋1) and diameter (𝑋2) foil-shaped centrebulb on the NPL hull

catamaran scale model with Fr 0.7 using Response Surface Method (RSM). The optimal size of foil-shaped

center bulb is determined by the size that the most makes of ship wave resistance (Rw) to a minimum. The

results of the regression equation in Order 1 are 𝑅𝑤  0.168𝑋1  0.378𝑋2  14.862 and the results of

the regression equation in Order 2 are 𝑅𝑤  0.020239𝑋1  0.061318𝑋2  0.201557



𝑋1







0.261325



𝑋2





 0.015



𝑋1𝑋2



 13.34806. Optimal center bulb size is obtained at a length of 103.78 mm

and a diameter of 26.30 mm with a wave resistance value of 13.23 N. The center bulb size can reduce wave

resistance by 11.74% from the initial center bulb model and reduce 4.72% compared to not using a center

bulb.

1 INTRODUCTION

Catamarans are double hull ships, which have many

advantages over single-hull boats with the same

displacement. Among these advantages is the

catamaran has a broad deck so that designers are more

flexible in arranging the ship's accommodation space.

Besides, catamarans have excellent ship stability so

that catamarans are safer and more comfortable for

passengers (Seif & Amini, 2004; Zouridakis, 2005).

Because catamarans have two hulls, interference

between the two hulls is a prevalent topic to be

discussed on catamarans. Errors in designing the hull

shape and determining the distance between the hulls

will result in the amount of interference of the ship's

resistance, which makes the resistance of the

catamaran ship to increase by almost four times even

though the displacement has increased two times

compared to each demihull. (Samuel, et al., 2015).

Some researchers researched to reduce the

resistance of catamarans due to interference. Iqbal

and Samuel have researched to reduce the resistance

of catamaran fishing vessels by modifying the shape

of the ship's demihull hull using the Luckenby

method. The method changes the CSA form of the

boat to create a new hull. This method succeeded in

reducing the total resistance by 6.5% (Iqbal &

Samuel, 2017). The method has been successfully

used by Iqbal and Rindo to improve the quality of the

seakeeping of catamarans (Iqbal & Rindo, 2015).

Samuel et al. have also used the bulbous bow on

catamaran fishing vessels to reduce ship resistance.

Ship resistance can either be reduced or increase

depending on the type of bulbous bow used. In that

case, the kind used to overcome resistance is the nabla

type, where the resistance can reduce by 10%

(Samuel, et al., 2018).

Other research conducted to reduce the resistance

of catamaran vessels has been carried out using the

concept of the center bulb, which is bulbous that is

between the hulls of the catamaran (Saha, et al., 2005;

Danisman, 2014). The center bulb is bulbous between

the two hulls of the catamaran (in the middle). The

purpose of this center bulb installation is to provide

wave interference between two catamaran hulls.

When the waves were interfered, it expects that the

Hadi, E., Iqbal, M. and Pranamya, G.

Size Optimization of Foil-shaped Center Bulb on Catamaran Hull Form to Reduce Resistance.

DOI: 10.5220/0010055600670075

In Proceedings of the 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management (ISOCEEN 2019), pages 67-75

ISBN: 978-989-758-516-6

waves will break and reduce the wave resistance. In

addition to reducing ship resistance, the utilization of

center bulb can also improve the quality of

seakeeping of catamaran vessels (Bruzzone, et al.,

2008; Zotti, 2007; Aprjal, et al., 2018).

In Saha's research, the center bulb that used is

large and placed in the front and rear positions, as in

Figure 1. The results of the study provide

recommendations that the wave resistance on the

catamaran ship with the center bulb depends on size

and position of center bulb against catamaran hulls

and the interaction of the catamaran wave resistance

(Saha, et al., 2005).

Zotti gives fins at center bulb to examine its effect

on resistance and the motion of the ship (see Figure

2). The results of the study are center bulb with fin

reducing ship resistance at Fr> 0.3 and increasing

resistance at Fr <0.3. RAO curve peaks from heaving

and pithing center bulb with fins are lower than

catamarans without center bulb. This method

indicates center bulb with fins has a positive impact

on seakeeping ships (Zotti, 2007).

Figure 1: Concept of Center bulb on a catamaran (Saha, et

al., 2005).

Danisman optimizes the position and geometry of

the elliptical center bulb using Artificial Neural

Networks (ANN). The research has succeeded in

reducing wave resistance by 15% based on the results

of numerical calculations and 13% based on the

results of experimental tests in towing tanks

(Danisman, 2014). The elliptical bulb center from

Danisman has also been applied to catamaran fishing

vessels by Samuel and can reduce resistance by

25.76% (Samuel, et al., 2018).

The idea to use center bulb on catamarans is still

relatively new and still requires a lot of studies.

Therefore, in this study, the elliptical center bulb form

was replaced with a foil form. This form is expected

to reduce ship resistance further because the tapered

back shape of the foil will make the flow pattern

streamlined and will not cause vortex shading or

repetition as when flow passes through a circular or

ellipsoid shape.

Figure 2: Concept of Center bulb on a catamaran (Zotti,

2007).

To producing maximum performance from the

center bulb, the optimization method is used to get the

optimal center bulb length and diameter. In this study,

the optimization method used is Response Surface

Methods (RSM). RSM is one of the most practical

and economic optimization techniques that is widely

used to evaluate variables from experiments that

produce several responses (Bezerra, et al., 2008).

The advantage of this method is that Design of

Experiments (DoE) based on RSM does not require a

lot of trials/testing and does not require a lot of time

compared to actual experimental studies (Ma, et al.,

2015).

Some researchers have used this method to

optimize several research variables. In the field of

structure, Baroutaji optimizes the thickness, diameter,

and width of the hollow cylindrical tube to produce

the maximum capacity of Specific Energy-Absorbing

(SEA) and minimize the Collapse Load (F)

(Baroutaji, et al., 2015).

In the field of mechanical engineering, Awad et

al., Used the RSM method to maximize brake power

and thermal brake efficiency and minimize Brake

Specific Fuel Consumption (BSFC) and emissions

from NOx, HC, and CO by optimizing three

variables, which are fuel, engine speed, and throttle

valve (Awad, et al., 2017).

In the field of naval architecture, RSM is very

rarely used. Therefore, the research tries to apply the

method in the field of naval architecture to minimize

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

the resistance of catamarans by optimizing variable

length and diameter of the center bulb.

The purpose of this study was to obtain the

optimal length (𝑋1) and diameter (𝑋2) foil-shaped

centrebulb on the NPL hull catamaran scale model

with Fr 0.7 using Response Surface Methods (RSM).

The optimal size of foil-shaped center bulb is

determined by the size that the most makes of ship

wave resistance (Rw) to a minimum.

2 METHOD

In this study, the catamaran hull model used is the

standard 4a hull model of NPL (Bailey, 1976). The

principal dimension and experimental test results in

towing tanks both as demihull and as catamarans are

found in (Molland, et al., 2017). The shape of the

body plan and 3D are shown in Figure 3. The

principal dimension of the NPL ship model, when

tested in towing tanks, are in Table 1. The results of

the residual resistance in the experimental tests are

shown in Table. 2.

Figure 3. Body plan and 3D model of NPL hull.

Table 1: Principal Dimension of the NPL Hull Model.

Dimension Scale Model

Lwl 1.60 m

B demihull 0.15 m

T 0.10 m

Cb 0.395

WSA 0.346 m

Displacement 0.0102 ton

S/L 0.3

Table 2: Residual Resistance of NPL Hull.

In this study, the optimal size of elliptical center

bulb geometry in Danisman was adopted to

determining the initial size of the center bulb by

comparing its geometry to the ship's geometry

(Danisman, 2014). Table 3 shows the principal

dimensions of the Danisman ship model. The size and

calculation of the center bulb dimensions are listed in

Table 4. The comparison is used to determine the

geometry of the center of the foil-shaped bulb as

shown in Figure 4.

Table 3: Principal Dimension of Danisman’s Catmaran

(Danisman, 2014).

Lwl 2,525

B0,26

T0,14

Cb 0,41

Table 4: Comparison of Center bulb Dimension.

Elipsoidal

Center bulb

(Danisman,

2014)

Ratio Foil-Shaped

Center bulb

Length (a) =

0,141 m

Width (b) =

0,062 m

Height (c) =

0,034 m

0,141/2,525 =

0,0558

0,062/0,26 =

0,2384

0,034/0,14 =

0,2428

Length (a) =

0,089 m~ 0,090 m

Width (b) =

0,037 m;

Height (c) =

0,024 m

Diameter (d) =

(b+c)/2 =

0,0305 ~ 0,040

Size Optimization of Foil-shaped Center Bulb on Catamaran Hull Form to Reduce Resistance

(a)

(b)

Figure 4: Elipsoidal Center bulb Geometry (Danisman,

2014) (a) Foil-Shaped Center bulb Geometry in this

research (b).

The position of Center bulb is at 0.5 Lwl and 0.5

T. Ship resistance is simulated at Fr 0.7 (2.77 m/s).

Catamarans that use the center bulb at Fr 0.7 have

lower resistance than that do not use the center bulb

(Danisman, 2014) and (Samuel, et al., 2018).

Ship resistance calculation uses CFD Software

called Tdyn. This software can be downloaded and

used free of charge but with a limited amount of

meshing. To getting the full version, the password

was required. It can be downloaded by registering

first. The password is valid for a month since

registration. Like other CFD software, the Tdyn

analysis process is carried out in 3 stages: pre-

processor, solver, and post-processor.

Before simulating ship resistance in CFD, the

design of the experiment is determined by using the

Central Composite Design (CCD). The first stage is

Order I by making the minimum and maximum limits

of length (𝑋1) and diameter (𝑋2) center bulb

variations. Furthermore, the design of the second

phase of the experiment is Steepest Descent. This

stage is to find the minimum response value based on

the coefficients 𝑋1 and 𝑋2 of the linear equation

generated from Order I.

Next, the results of 𝑋1 and 𝑋2 from Steepest

Descent become the initial model in Order II. Like

Phase I, the minimum and maximum limits of

variation in length (𝑋1) and diameter (𝑋2) of the

center bulb of Steepest Descent are determined again

for later to be tested in CFD simulation.

3 RESULTS AND DISCUSSION

3.1 CFD Validation

The validation step is conducted to ensure that the

results of the CFD calculation have a small difference

to the experimental results. Validated results of the

CFD setup, such as mesh sizing (as shown in Table

5), number of steps, initial steps, and time increment,

are used to the condition of CFD simulation for other

models. These variables affect simulation results.

Table 5: Mesh Sizing.

Ship Surface 0.005

Free surface 0.05

Other Surface 0.1

Max Element 0.5

Transitional 0.5

Mesh size was obtained from several experiments

with consideration of the 3 Dimension shape of the

ship. The next stage is determining the CFD set up

like number of steps, time increments, and initial

steps. The final results are presented in Table 6 with

the total resistance results, RT of 19.11 N consisting

of wave resistance, RW of 13,855 N and viscous

resistance, RV of 6.0564 N.

Table 6: Tdyn Setup.

0.7

o. Of Steps 900

Time Incremen

0.08

Initial Steps 81

V (m/s) 2.77

RT (CFD) 19.11 N

RT (Molland) 18.89 N

Erro

0.12 %

3.2 Response Surface Methods

3.2.1 Order 1

There are various Designs of Experiment (DoE)

(Bezerra, et al., 2008). In this study, the DoE is used

using the Center of Composite Design (CCD) with

two factors/variables. The regression equation that

produced in Order 1 is linear. The variables used are

length of center bulb, L (X1) and diameter of center

bulb, D (X2). The difference given is ± 5%. The CFD

simulation conditions in Table 6 are used for the

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

calculation of wave resistance (RW) following the

DoE contained in Table 7.

Table 7: Design of Experiment based on Central Composite

Design and The Results of Wave Resistance, RW.

Model

Code Parameter

(N)

X1 X2

(mm)

1 0 0 90 40 14.99

2 -1 -1 85.5 38 14.529

3 -1 1 85.5 42 15.466

4 1 -1 94.5 38 14.375

5 1 1 94.5 42 14.95

Through the regression method, a linear equation

(found in Equation 1) is obtained from the

experiments conducted in Table 7. This equation has

the value R

= 0.908977, where the value can be

considered valid enough to be used.

𝑅𝑤  0.168𝑋1  0.378𝑋2  14.862

(1)

3.2.2 Steepest Descent

This process is carried out to determine the turning

point of the tendency of wave resistance (Rw), which

continues to fall and no longer matches the results of

Equation 1. Based on the coefficients of each variable

in the First Order model, the addition (∆) of each

coefficient for doing steepest descent was calculated

by using the coefficient X1 as the basis as shown in

Equations 2 and 3. Furthermore, the steepest descent

process is shown in Table 8 and Figure 5.

∆𝑋1 

0.168



1

(2)

∆𝑋2 

0.378



 2.26

(3)

Table 8: Steepest Descent.

Code Parameter

Rw -

CFD

(N)

Step X1 X2 L (mm) D (mm)

1 (Mod.1) 0 0 90 40 14.99

2 (Mod.6) 1.00 -2.26 94.50 35.49 14.19

3 (Mod.7) 2.00 -4.51 99.00 30.97 13.56

4 (Mod.8) 3.00 -6.77 103.50 26.46 13.35

5 (Mod.9) 4.00 -9.03 108.00 21.95 13.44

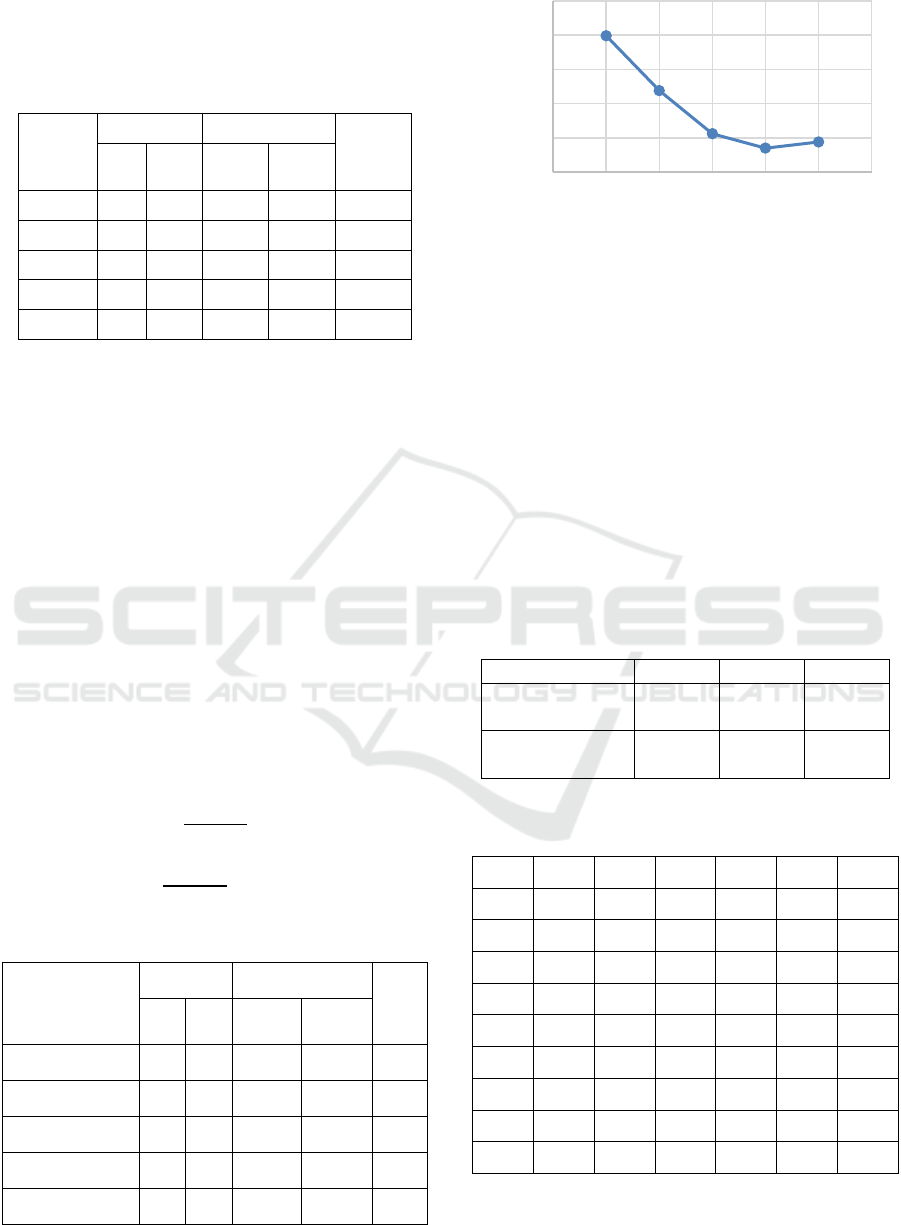
Figure 5: Steepest Descent.

Based on Figure 5, the lowest point is found in Step

4 or in Model 8. The wave resistance then increases in

Model 9 so that the variables in Model 8 are used as

the central point for experiments in Order 2.

3.2.3 Order 2

Experimental design in Order 2 produces non-linear

equations for quadratic functions. For this reason, the

number of experiments in DoE was added as in Table

9. The central points (X1 = 0 and X2 = 0) used were

Model 8. The code used for the Second Order was set

again as shown in Table 9. With reference to Table 9,

DoE for Order 2 is shown in Table 10.

Table 9: Code for Orde 2.

-1 0 1

𝑋1,

Len

th (mm)

98.33 103.50 108.68

𝑋1,

Diameter (mm)

26.46 26.46 27.78

Table 10: Design of Experiment in Order 2 and Wave

Resistance, Rw.

Mod X1 X2 X1

X1*X2 Rw (N)

8 0 0 0 0 0 13.35

10 -1 -1 1 1 1 13.92

11 -1 1 1 1 -1 13.95

12 1 -1 1 1 -1 13.55

13 1 1 1 1 1 13.64

14 -1.414 0 1.9994 0 0 13.62

15 1.414 0 1.9994 0 0 13.98

16 0 -1.414 0 1.9994 0 13.79

17 0 1.414 0 1.9994 0 14.05

The regression equation from the experiments

conducted in Table 10 is found in Equation 4. The

13,5

14,5

15,5

0123456

RW(N)

Step

Size Optimization of Foil-shaped Center Bulb on Catamaran Hull Form to Reduce Resistance

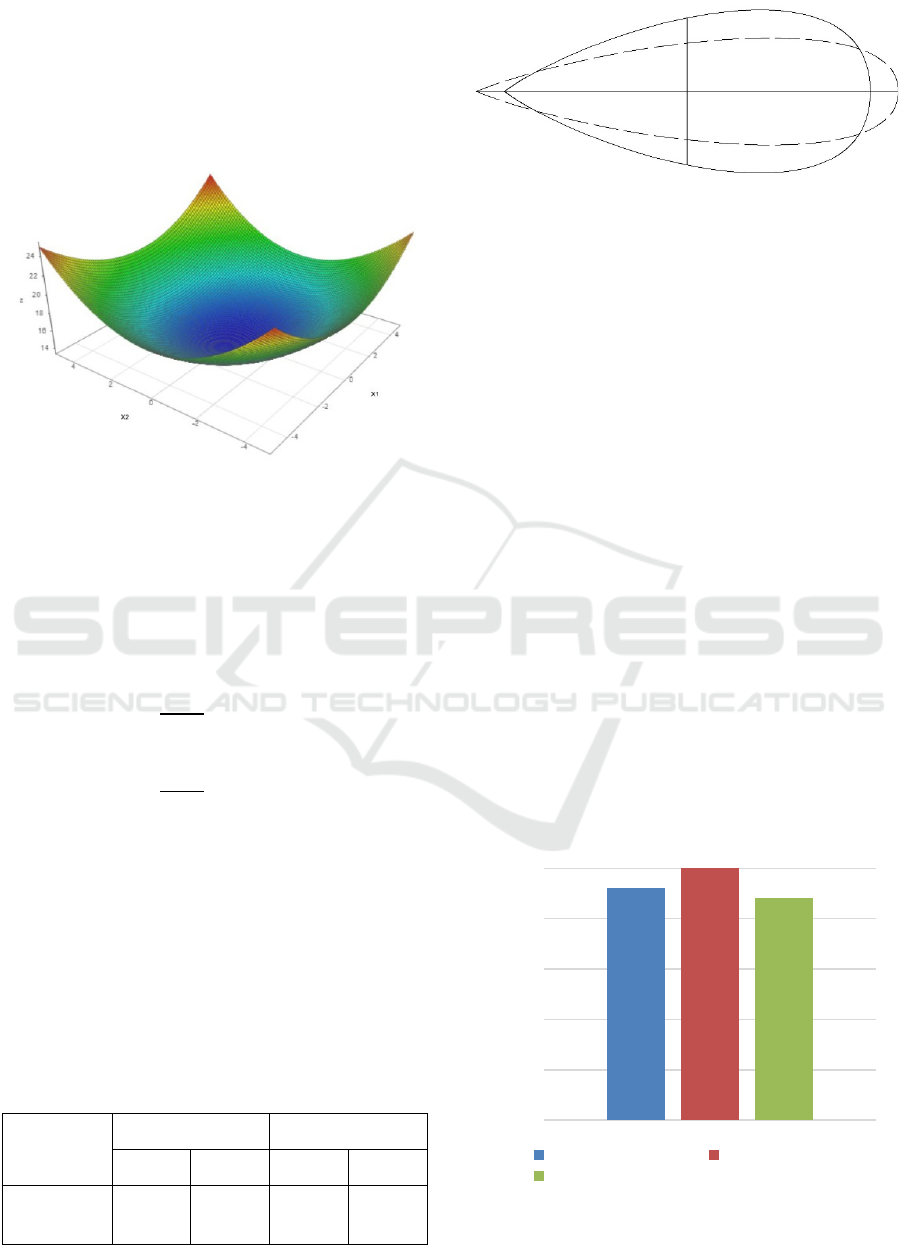
equation has the value R

= 0.540206. The 3D Surface

of Eq. 4 is shown in Figure 6.

𝑅𝑤  0.020239𝑋1  0.061318𝑋2

 0.201557



𝑋1





 0.261325



𝑋2





 0.015



𝑋1𝑋2



 13.34806

(4)

Figure 6: 3D Surface of Second Order Equation for wave

resistance, RW.

3.2.4 Optimum Point

To find the minimum value of the Order 2 regression

equation (Equation 4), then the first derivative of the

equation must have a zero value according to

Equations 5 and 6.

𝑑𝑅𝑊

𝑑𝑋1

0

(5)

𝑑𝑅𝑊

𝑑𝑋2

0

(6)

According to Equations 5 and 6, the optimum

point is located at X1 = 0.0546 and X2 = -0.1189 are

obtained. Based on the codification in Table 9, the

optimum length and diameter are shown in Table 11.

The center bulb length, which was 90 mm increased

by 15.31% to 103.78 mm. While the center bulb

diameter, which was 40 mm reduced by 34.25% to

26.30 mm. Visualization of the comparison of initial

center bulb size with optimum center bulb size is

shown in Figure 7.

Table 11: Optimum Size of Foil-Shaped Center bulb.

Model

Code Parameter

X1 X2 L (mm) D (mm)

(Optimum) 0.0546 -0.1189 103.78 26.30

Figure 7: Model 1 (initial model) with solid lines and Model

18 (optimal model) with dashed lines.

3.3 Hydrodynamic Comparisons

The value of the wave resistance, RW from the

optimum parameter based on CFD is 13.23 N, while

based on Equation 4 is 13.34 N. The difference

between the two is quite small at -0.83%.

The comparison of wave resistance between the

optimum model (Model 18) and the initial model

(Model 1) has been carried out. The optimum model

reduces the wave resistance by 11.74% from 14.99 N

to 13.23 N compared to the initial model, as presented

in Figure 8. This optimization method successfully

minimizes the wave resistance from initial center bulb

models.

The next discussion is about the comparison of

wave resistance using center bulb (initial and optimal

models) to models that do not use center bulb. The

value of wave resistance that does not use center bulb

as stated in the validation section is 13.855 N.

As can be seen in Figure 8, the use of the initial

center bulb model adds a wave resistance of 8.19%.

This reason is that model has not been optimized.

Center bulb configuration is also based only on center

bulb geometry, not varying the position of center bulb

placement. Besides, the determination of the

Figure 8: Comparison of Catamaran Without, Initial and

Optimum Center bulb.

RW(N)

NoCenterbulb InitialCenterbulb

OptimalCenterbulb

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

geometry of the initial model is obtained only by the

ratio. So for the initial center bulb model, it is still far

from the expectation to reduce wave resistance.

After the foil-shaped center bulb is optimized, the

wave resistance decreases by 4.72%. When compared

with the results of Danisman's research, this value is

not significant enough. The reason is due to the

optimization parameters still using two variables,

namely length and diameter, whereas in Danisman's

used 3 variables, namely height and width length of

center bulb. Besides, the configuration of center bulb

(a)

(b)

(c)

Figure 9: Comparison of Catamaran Pressure Contours that

do not use Center bulb (a), Initial Center bulb (b) and

Optimal Center bulb (c).

position was taken into account to produce a

significant reduction in wave resistance.

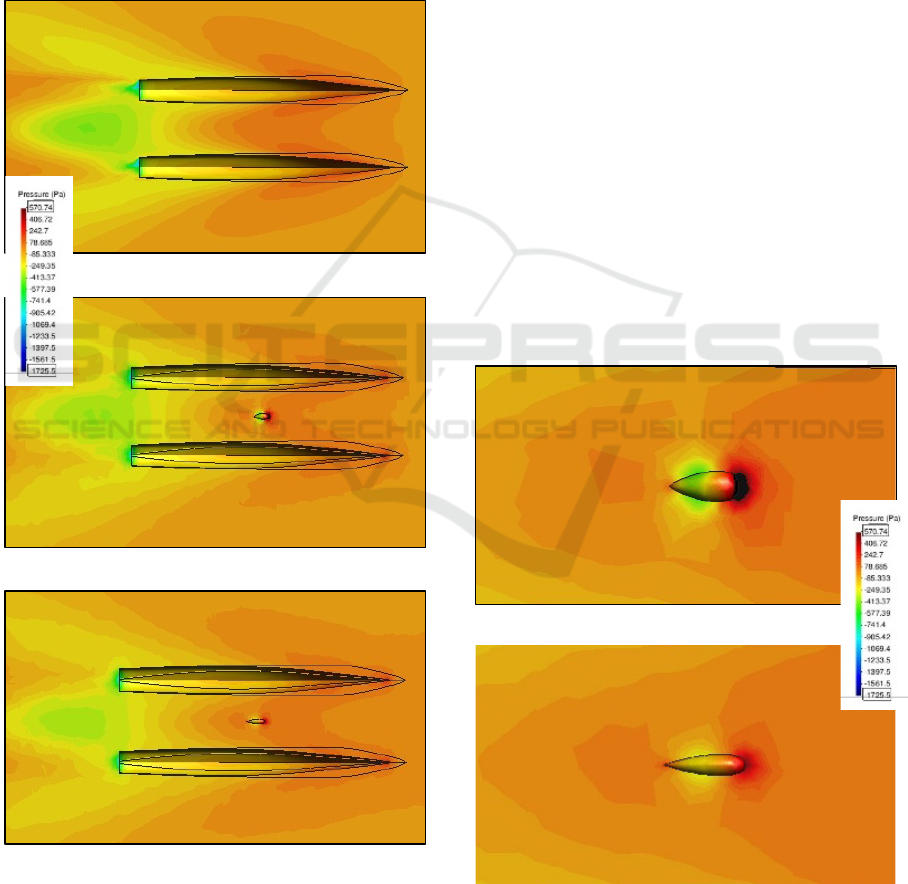
Figure 9 is an illustration of the pressure contour

between the two catamaran hulls seen based on the

intersection of the z-axis in the center of the center

bulb. It can be seen in Figure 9.a that overall, the

pressure between the two hull has a higher pressure

than that using center bulb (b and c). This

phenomenon indicates that center bulb reduces

pressure between the hull.

However, in Figure 9.b the pressure contour

increases significantly only in front of the center bulb.

The initial center bulb has wide shape making the

water flow hit the center bulb. The flow speed will

stop for a moment causing the pressure increases. In

Figure 9.c. the optimal center bulb shape is slender

than the initial model. When the flow hit the center

bulb, the pressure did not increase significantly. For

more details, see Figure 10.

The results of this study prove that the Response

Surface Method (RSM) can be used in field Naval

Architecture and successfully implemented as an

optimization tool to find the lowest wave resistance

based on the size of the center bulb. Overall, the

Response Surface Method (RSM) makes it easy to

find the optimal value of the shape size of the center

bulb.

(a)

(b)

Figure 10: Comparison of Catamaran Pressure Contours

Around Foil-Shaped Center bulb. (a) Initial model (b)

Optimum model.

Size Optimization of Foil-shaped Center Bulb on Catamaran Hull Form to Reduce Resistance

4 CONCLUSIONS

The optimal center bulb length is 103.78 mm or has

15.31% increase from the initial length of 90 mm. The

optimal diameter size is obtained at 26.30 mm or

reduced by 34.25% from the initial diameter of 40

mm. The optimal model reduces the wave resistance

by 11.74% from the initial center bulb model and

reduces by 4.72% compared to not using a center

bulb. Overall, the Response Surface Method is

another approach to determine the optimal size of

foil-shaped center bulb in order to reduce wave

resistance.

ACKNOWLEDGEMENTS

The authors would like to express their gratitude to

Faculty of Engineering, Diponegoro University for

the financial support of this research with contract

number: 167/UN7.5.3/HK/2019.

REFERENCES

Aprjal, R. P., Samuel, S. & Iqbal, M., 2018. Minimisasi

Hambatan Dan Gerak Vertikal Kapal Multihull

Catamaran Dengan Center bulbs. Teknik, 39(1).

Awad, O. I. et al., 2017. Response surface methodology

(RSM) based multi-objective optimization of fusel oil -

gasoline blends at different water content in SI engine.

Energy Conversion and Management, Volume 150, pp.

222-241.

Bailey, D., 1976. The NPL high speed round bilge

displacement hull series: resistance, propulsion,

manoeuvering and seakeeping data. s.l.:Royal

Institution of Naval Architects.

Baroutaji, A., Gilchrist , M. D., Smyth , D. & Olabi, A.,

2015. Crush analysis and multi-objective optimization

design for circular tube under quasi-static lateral

loading. Thin-Walled Structures, Volume 86, pp. 121-

131.

Bezerra, M. A. et al., 2008. Response surface methodology

(RSM) as a tool for optimization in analytical

chemistry. Talanta, Volume 76, pp. 965-977.

Bruzzone, D., Grasso, A. & Zotti, I., 2008. Nonlinear

Seakeeping Analysis of Catamarans with Central Bulb.

Naples, Proceedings of the 6th International

Conference on High-Performance Marine Vehicles.

Danisman, D. B., 2014. Reduction of Demi-Hull Wave

Interference Reistance in Fast Displacement

Catamarans Utilizing an Optimized Center bulb

Concept. Ocean Engineering, Volume 91, pp. 227-234.

Hadi, E. S., Manik, P. & Iqbal, M., 2018. Influence of hull

entrance angle "perintis 750 DWT", toward ship

resistance : the case study for design development

“Perintis 750 DWT. MATEC Web of Conferences,

Volume 159.

Harvald, S. A., 1983. Resistance and Propulsion of Ships.

New York : Wiley.

Insel, M. & Molland, A. F., 1992. An Investigation into the

Resistance Components of High Displacement

Catamarans. Transaction Royal Institutions of Naval

Architevture, Volume 134.

Iqbal, M. & Rindo, G., 2015. Optimasi Bentuk Demihull

Kapal Katamaran Untuk Meningkatkan Kualitas

Seakeeping. KAPAL, 12(1), pp. 19-24.

Iqbal, M. & Samuel, 2017. Traditional Catamaran Hull

Form Configurations That Reduce Total Resistance.

International Journal of Technology, 8(1), pp. 989-997.

Iqbal, M. & Utama, I., 2014. An Investigation into the Effect

of Water Depth on the Resistance Components of

Trimaran Configuration. Surabaya, Proceedings of the

9 th International Conference on Marine Technology.

Jamaluddin, A., Utama, I. K. A. P., Widodo, B. & Molland,

A. F., 2012. Experimental and Numerical Study of the

Resistance Component Interactions of Catamarans.

Proceedings of the Institution of Mechanical Engineers,

Part M: Journal of Engineering for the Maritime

Environment , 227(1), pp. 51-60.

Ma, L. et al., 2015. Optimization of acidified oil

esterification catalyzed by sulfonated cation exchange

resin using response surface methodology.. Energy

Convers Manage, Volume 98, p. 46–53.

Molland, A. F., 2008. A Guide to Ship Design, Construction

and Operation, The Maritime Engineering Reference

Book. s.l.:Butterworth- Heinemann, Elsevier.

Molland, A. F., Turnock, S. R. & Hudson, D. A., 2017. Ship

resistance and propulsion. s.l.:Cambridge university

press.

Saha, G. K., Suzuki, K. & Kai, H., 2005. Hydrodynamic

Optimization of a Catamaran Hull With Large Bow and

Stern Bulbs Installed on the Center Plane of the

Catamaran. Journal of Marine Science and Technology,

Volume 10, pp. 32-40.

Samuel, Iqbal, M. & Utama, I. K. A. P., 2015. An

Investigation Into The Resistance Components Of

Converting A Traditional Monohull Fishing Vessel Into

Catamaran Form. International Journal of Technology,

6(3), pp. 432-441.

Samuel, S. et al., 2018. Bulbous bow applications on a

catamaran fishing vessel for improving performance.

MATEC Web of Conferences, Volume 159.

Samuel, S. et al., 2018. Modification of traditional

catamaran to reduce total resistance: configuration of

Center bulb. Lisbon, International Maritime

Association of the Mediteranean (IMAM) Conference.

Seif, M. S. & Amini, E., 2004. Performance Comparison

Between Planing Monohull and Catamaran at High

Froude Numbers. Iranian Journal of Science &

Technology, 28(B4).

Zotti, I., 2007. Medium Speed Catamaran with Large

Centralbulbs: Experimental Investigation on

Resistance and Vertical Motions. Naples, Proceedings

of ICMRT'07.

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

Zouridakis, F., 2005. A Preliminary Design Tool for

Resistance and Powering Prediction of Catamaran

Vessels, s.l.: Master Thesis Massachusetts Institute of

Technology. Dept. of Ocean Engineering.

Size Optimization of Foil-shaped Center Bulb on Catamaran Hull Form to Reduce Resistance