
Risk Analysis on Offshore Pipeline Installation Delay:
A Case Study for Mahakam Block, Indonesia
Yohana Selliabreint
1
, Silvianita
1
, Daniel M. Rosyid
1
, Wahyudi Citrosiswoyo
1
and Cheng Yee Ng
2
1
Department of Ocean Engineering, Institut Teknologi Sepuluh Nopember, Surabaya, Indonesia
2
Department of Civil and Environmental Engineering, Universiti Teknologi Petronas, 32610 Seri Iskandar, Perak,
Malaysia
Keywords: Fuzzy Fault Tree Analysis, Fuzzy Event Tree Analysis, Bowtie Analysis, Project Delay, Offshore Pipeline
Installation.
Abstract: Pipeline has an important role in oil and gas industry to transfer oil or gas that have been discovered to
production station, one of which is pipeline system belong to one of the companies located in Mahakam
Block, East Borneo, Indonesia. Considering its important role, pipeline installation in not allowed for any
delay and needs to operate as planned. However, the said offshore pipeline installation has experienced 21
days of delay, whereby this project started on December 5
th
2018 and finished at February 3
rd
2019. To
analyse the delay of this project, this research uses two methods, namely fuzzy trapezoidal and bowtie
analysis. The fuzzy fault tree analysis (FTA) diagram will generate the probability value of top event project
delay of offshore pipeline installation. The fuzzy event tree analysis (ETA) diagram will generate how much
fine that the contractor has to pay and the risk level from every factor that causes the delay. The results from
bowtie analysis will determine preventive value which will be used as precaution and mitigation which will
be used as reduction due to delays.
1 INTRODUCTION
In this modern era, oil and gas demands continue to
rise, to meet consumer demands oil and gas
companies have to increase their production
performance. In this industry, pipeline has an
important role to transfer crude oil that has been
discovered from well to production station.
This research discuss the project of offshore
pipeline installation belongs to one of the oil and gas
company in Mahakam. This pipeline located in
Mahakam Block, East Borneo, Indonesia. This
pipeline is connecting two wells at a distance of
0.8km.which the installation shall be commenced
from 5th December 2018 to 13th January 2019.
during the execution, this project delayed for 21
days causing the project to be completed on 3rd
February 2019 instead.
Delays on projects can cause losses to both the
owner and the contractor. From ownerpoint of view,
the construction delay eventually will impact on the
progress of the production, in a way affecting the
profit. From contractor point of view, extra cost will
incurred e.g. on equipment rent and fines
(Muhamad, 2016).
To reduce the possibility of delays on offshore
pipeline installation in the future, risk analysis can
be used.Project delay for jacket structure and HRSG
have been reviewed by (Silvianita et al 2017a,
2017b) and another project delay using Fault Tree
Analysis (Silvianita et al 2014). This paper will
examine the most dominant factor causing the delay
on offshore pipeline installation project at the
company. Pipeline specification data can be seen in
Table 1.
Table 1: Pipeline Specification Data.
Description Specification
Pipe Material API 5L X 65
Outside Diameter 8.625 in
Line Pipe
Pipeline Wall Thickness
Pipe Length
12 m
20.6 mm
800m
106
Selliabreint, Y., Silvianita, ., Rosyid, D., Citrosiswoyo, W. and Ng, C.
Risk Analysis on Offshore Pipeline Installation Delay: A Case Study for Mahakam Block, Indonesia.
DOI: 10.5220/0010057601060112
In Proceedings of the 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management (ISOCEEN 2019), pages 106-112
ISBN: 978-989-758-516-6
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 LITERATURE STUDIES
Fault tree analysis (FTA) is a logic and graphical
representation that explores the interrelationships
between a potential critical events in a system and
the reason for event (Mokhtari et al, 2011). FTA
diagram consists of top event and basic events.
Commonly, FTA method is used to find the
probability of top event.
Meanwhile, Event tree analysis (ETA) is a
method to detect and analyze the different events of
pragmatic accidents possibilities with safety features
following an initiating event (Raiyan et al, 2017).
ETA diagram consists of initiating event and pivotal
events, which normally used to analyzeconsequence
that arise from failure or unwanted event.
To covers the loss event scenario uses a Bowtie
diagram that consists of fault tree (FT) and Event
Tree (ET) to identify the causes of top events or loss
events and shows the consequences of unwanted
events.The weakness of bowtie analysis is that the
opinions used in the analysis have uncertainties and
vaguenesses.
FTA and ETA considered probability value to
determine cost of delaying fortop event of FTA and
initiating event of ETA respectively. But in the
execusion, these methods will produce unrealistic
outcome as the probability values are solely depend
on assumptions and lead to erroneous conclusion.
Fuzzy logic was introduced to overcome the
ambiguity of human judgement as it can change the
probability value to possibility number within the
scale of 0-1. According to Aqlan et al (2014), fuzzy
logic is used to find aggregates or the value of the
word variable (linguistics) of the respondent, which
are converted into a collection of numbers. The scale
used in fuzzy logic is more flexible, making it easier
to assess linguistic variables according to condition
Table 2: Fuzzy Likelihood of an Event (Zarei et al, 2019).
Grade Likelihood
Membership
Function
1 Very High (VH) (0.8,1,1,1)
2
High-Very High
(HVH)
(0.7,0.9,1,1)
3 High (H) (0.6,0.8,0.8,1)
4 Fairly High (FH) (0.5,0.65,0.65,0.8)
5 Medium (M) (0.3,0.5,0.5,0.7)
6 Fairly Low (FL) (0.2,0.35,0.35,0.5)
7 Low (L) (0,0.2,0.2,0.4)
8 Low-Very Low (LVL) (0,0,0.1,0.3)
9 Very Low (VL) (0,0,0,0.2)
in the field (Shahriar, 2012). In this research, the use
of linguistic variables and fuzzy numbers are as
follow (Zarei et al, 2019).
This research using the trapezoidal fuzzy number
to determine the possibility value from respondents
assumptions based on interview. Trapezoidal fuzzy
number can be defined as:
(1)
The formula can be defined as follows :
𝑋
∗
=
𝑥𝑑𝑥 +
𝑥𝑑𝑥+
𝑥𝑑𝑥
𝑑𝑥+
𝑑𝑥 +
𝑑𝑥
𝑋
∗
=
1
3
×
(
𝑎
+𝑎
)
−𝑎
𝑎
−
(
𝑎
+𝑎
)
+𝑎
𝑎
(
𝑎
+𝑎
−𝑎
−𝑎
)
(2)
According to Clemen et al (1999) to change the
linguistic variable to fuzzy number and combine the
value of experts assumption to one fuzzy number,
the formula can be defined as follows:
𝑀
=𝑊
𝐴
,𝑗=1,2,…,𝑛
(3)
Where :
Aij = Linguistic expression of basic event by j
M = Number of basic events
n = Number of experts
W = Weighting factor of j and M
Representing the combined Fuzzy number of basic
event i.
According to Lavasani et al (2012) the value of
experts assumption can be determined by this
following formula :
Experts value = PP + ET + EL + A (4)
Wj=
value o
f
expert
∑
value o
f
expert
(5)
Where:
PP = Professional Position
ET = Education Level
EL = Experience Time (year)
A = Age (year)
Wj = weighting factor of experts
Risk Analysis on Offshore Pipeline Installation Delay: A Case Study for Mahakam Block, Indonesia
107
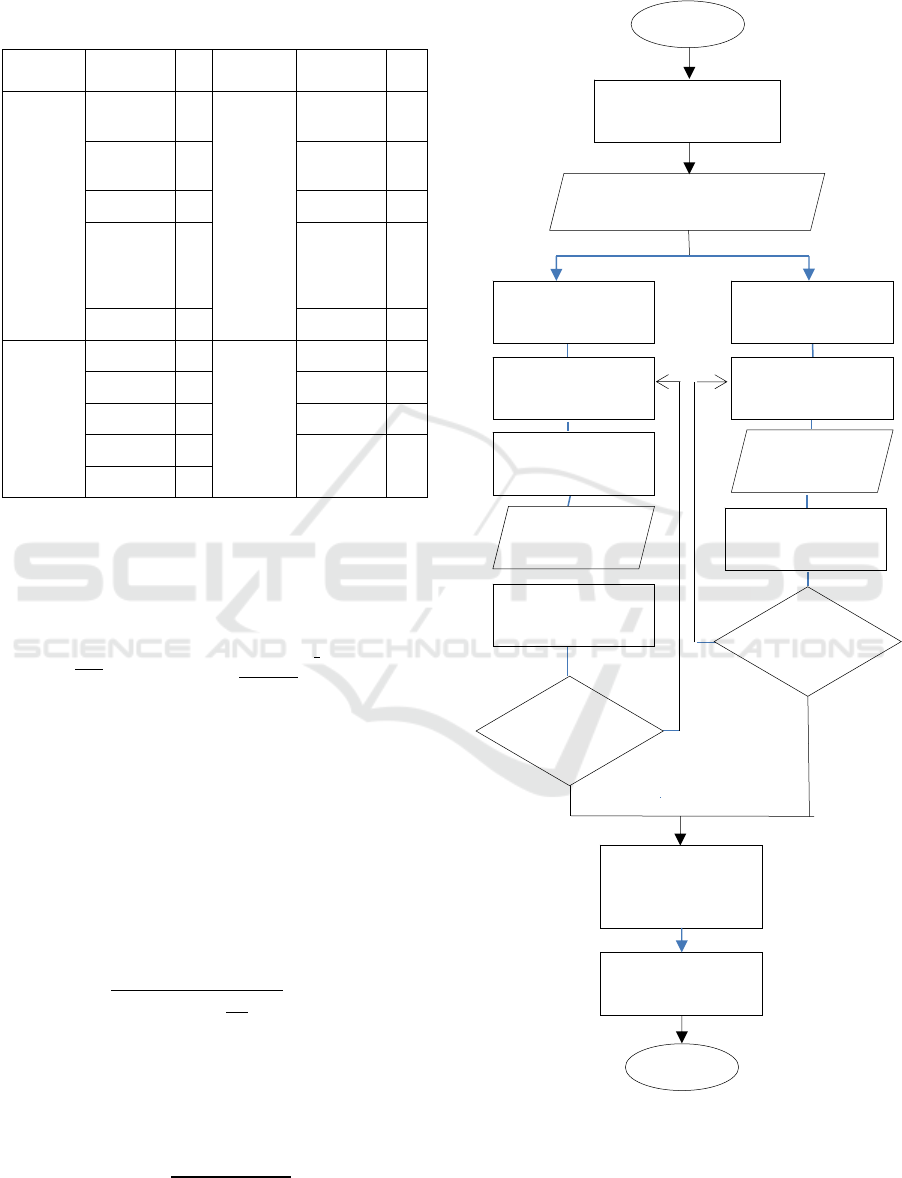
Table 3 shows the value of experts (Ramzali et al,
2015).
Table 3: Value for Experts.
Constitution Classification Score Constitution Classification Score
Professional
Position
Senior
academic
5
Education
Level
PhD 5
Junior
academic
4 Master 4
Engineer 3 Bachelor 3
Technician 2
Higher
National
Diploma
(HND)
2
Worker 1 School Level 1
Experience
Time (year)
≥30 5
Age (year)
≥50 4
20-29 4 40-49 3
10-19 3 30-39 2
6-9 2
<30 1
≤5 1
According to Onisawa (1998) to change the
fuzzy possibility score (FPs) by summing the three
fuzzy number parameters and the dividing by three.
For the last step, change the FPS to fuzzy probability
score (FPr) using the following formula:
FPr=
1
10
if FPs ≠0
0 if FPs =0
K
=
1−FPs
FPs
× 2.301
(6)
Where :
FPr = Fuzzy Probability Score
FPs = Fuzzy Posibilatas Score
K = Constant Numbers
The probability will be used to calculate the
possibility on ETA fuzzy diagrams. To change the
probability to possibility by using the following
formula (Onisawa, 1988):
FPs=f
(
FPr
)
FPs=
1
1 + k × log
,FPr≠0
0, FPr=0
(7)
Where :
FPr = Fuzzy Probability Score
FPs = Fuzzy Posibilatas Score
k =
(/(×
))
3 METHODOLOGY
Figure 1: Flowchart.
Start
data collection
Problem definition
and literaturestudies
Determine Risk
Value and Risk
Matrix
Generate Bow-Tie
Analysis
Finish
YES
YES
NO
Determine
Initiating Event
Determine Top
Event
Determine Pivotal
Event
Determine Basic
Event
CalculateFPs
InputFPs
InputFPs
ChangeFPsintoFPr
ChangeFPs
intoFPr
FTA
acceptable
ETA
acceptable
NO
ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management
108

The procedures of the research are as follow:
1. Formulations of Problems
The formulations of the problems are decided
as the purpose or the goal of the research.
2. Literature Studies
3. Data Collection
The data used in this research are:
a. Pipeline installation project master schedule
data
b. Actual pipeline installation project data
schedule
c. Contract data
d. General data about the pipeline installation
project
e. Make a questionnaire to look for the
probability
of basic FTA events, pivotal ETA events,
determination of risk matrices, barriers and
escalation factors in a bow-tie diagram.
4. Data Analysis and Discussion
a. Analysis of the results of the interview to
determine the work items that are
experiencing problems, thefactors that
cause delays in the project and
theconsequences caused by delays. At this
stage a weighting is carried out for each
respondent withequations 4 and 5
b. Fuzzy FTA stage
c. Fuzzy ETA stage
d. Determine the Risk Matrix
e. Bowtie Analysis
5. Conclusions and Suggestions
After all the results are obtained, conclusions
are then drawn up containing the answers to the
formulation of the existing problems and
suggestions for further research, especially in
the field of Risk Assessment.
4 RESULT AND DISCUSSION
4.1 Data Management Factors
Delaying Offshore Pipeline
Installation using Fault Tree
Analysis and Fuzzy Logic
Fault tree analysis (FTA) is a method used to find
therootcauses of a top event or peak failure
event.Thisresearch explained the factors that cause
the delay in the offshore pipeline installation project.
The basic causes of delays and the probability of
each basic event were illustrated through a fault tree
diagram. The basic events can be seen in Table 4.
Table 4: Basic Event of FTA Diagram.
No. Code Name of Event
1 A111
Equipment / machinery not
available
2 A112
Equipment / machinery is being
used in another location
3 A121
Poor equipment / machinery
maintenance
.....
25 B11
Miscommunication between
owner supervisor and contractor
26 B12
Workers do not understand the
work items to do
27 B2
The process is not according to
the initial plan
Meanwhile, the respondent's personal data can be
seen in Table 5, and the respondents involved in the
offshore pipeline installation were selected:
Table 5: Respondent Profile.
Expert
Category
Age Experiences Postion Education
1 34 12
Site
Planner
S2
2 29 11 Engineer S1
3 40 17 Supervior S1
4 26 5 Engineer S1
5 29 6 Engineer S1
6 32 8
Site
Manager
S1
7 26 5 Engineer S1
8 39 12 Supervisor S2
9 28 5 Engineer S1
Probability of each basic FTA was obtained
throughinterviewing the respondents. the frequency
of basic fuzzy FTA events was referred to the scale
proposed by Zarei, et al. (2019), as listed in Table 6.
Risk Analysis on Offshore Pipeline Installation Delay: A Case Study for Mahakam Block, Indonesia
109

Table 6: Scale Fuzzy Likelihood of an Event.
Linguistic
Variabel
Defenition
Membership
Function
Very High
(VH)
It happened every
pipeline installation
(0.8,1,1,1)
High-Very
High
(HVH)
It happened in a
span of 3 times the
pipeline installation
(0.7,0.9,1,1)
High (H)
It happened in a
span of 5 times the
pipeline installation
(0.6,0.8,0.8,1)
Fairly High
(FH)
It happened in a
span of 15 times the
pipeline installation
(0.5,0.65,0.65,0.8)
Medium
(M)
It happened in a
span of 25 times the
pipeline installation
(0.3,0.5,0.5,0.7)
Fairly Low
(FL)
It happened in a
span of 50 times the
pipeline installation
(0.2,0.35,0.35,0.5)
Low (L)
It happened in a
span of 75 times the
pipeline installation
(0,0.2,0.2,0.4)
Low-Very
Low (LVL)
It happened in a
span of 90 times the
pipeline installation
(0,0,0.1,0.3)
Very Low
(VL)
It happened in a
span of 100 times
the pipeline
installation
(0,0,0,0.2)
4.1.1 Calculating Fuzzy Possibility (FPs)
From the results of interviews and questionnaires, a
recapitulation of data for linguistic variable scales
were compiled in Table 7.
Table 7: Questionnaire Results from Experts.
Activity
Category
1 2 3 4 5 6 7 8 9
A111
VL VL H LVL LVL VL L M L
A112
L VL HVH L FL M L M M
A121
L LVL VH LVL FL L LVL M LVL
.....
B11
LVL LVL FL LVL M VL LVL H FL
B12
LVL FH FL VL L L VL M LVL
B2
LVL FH L M M L VL M FL
To determine the possibility of each basic event,
the first step to identify the weight for each
respondent adopting equations 4 and 5, while the
scores for respondents based on Table 3.
The example of value calculating of aexpert:
Value of expert = PP + ET + EL + A
= 3 + 3 + 4 + 2
=12
Wj =
∑
ί
Wj =
Wj =
Wj = 0,13
From the calculations above, we get the value of
each respondentas written in Table 8.
Table 8: Value of Each Experts.
Respondent Final Score
1 0.13
2 0.11
3 0.13
4 0.09
5 0.11
6 0.12
7 0.09
8 0.13
9 0.09
After knowing the weight of each respondent,
then determined possibilities (FPs) of each basic
event using equation 2 and 3.
We used Basic Event code A111 from the
questionnaire results as an example to calculate the
possibility (FPS).
Table 9: Questionnaire Results A111.
Experts
1 2 3 4 5 6 7 8 9
VL VL H LVL LVL VL L M L
Table 9 shows the outcome of questionnaire
survey. Then fuzzy numbers as in table 6 were
converted to calculate the possibility (FPs). The
results can be seen as below:
Expert 1 = (0, 0, 0, 0.2)
Expert 2 = (0, 0, 0, 0.2)
Expert 3 = (0.6, 0.8, 0.8, 1)
Expert 4 = (0, 0, 0.1, 0.3)
Expert 5 = (0, 0, 0.1, 0.3)
Expert 6 = (0,0, 0, 0.2)
Expert 7 = (0, 0.2, 0.2, 0.4)
Expert 8 = (0.3, 0.5, 0.5, 0.7)
Expert 9 = (0, 0.2, 0.2, 0.4)
ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management
110

using equation 3, by multiplying the following fuzzy
number with the weight of each respondent defined
in Table 8.The following results were derived:
Expert 1 = (0, 0, 0, 0.2) x 0.13
= (0, 0, 0, 0.026)
Expert 2 = (0, 0, 0, 0.2) x 0.11
= (0, 0, 0, 0.022)
Expert 3 = (0.6, 0.8, 0.8, 1) x 0.13
= (0.078, 0.104, 0.104, 0.13)
Expert 4 = (0, 0, 0.1, 0.3) x 0.09
= (0, 0, 0.009, 0.027)
Expert 5 = (0, 0, 0.1, 0.3) x 0.11
= (0, 0, 0.011, 0.033)
Expert 6 = (0,0, 0, 0.2) x 0.12
= (0, 0, 0, 0.024)
Expert 7 = (0, 0.2, 0.2, 0.4) x 0.09
= (0, 0.018, 0.018, 0.036)
Expert 8 = (0.3, 0.5, 0.5, 0.7) x 0.13
= (0.039, 0.065, 0.065, 0.091)
Expert 9 = (0, 0.2, 0.2, 0.4) x 0.09
= (0, 0.018, 0.018, 0.036)
The fuzzy numbers isthen summed, to obtain the
ultimate fuzzy number, as follows:
M = R1 + R2 + R3 + R4 + R5 + R6 +
R7 + R8 + R9
= (0 + 0+ 0.078 + 0 + 0 + 0 + 0 + 0.039 + 0 ;
0 + 0 + 0.104 + 0 + 0 + 0 + 0.018 + 0.065
+ 0.018 ; 0 + 0 + 0.104 + 0.009 + 0.011 + 0
+ 0.018+ 0.065 + 0.018 ; 0.026 + 0.022 +
0.130 + 0.027 + 0.033 + 0.024 +0.036 +
0.091 + 0.036)
= (0.12 ; 0.21 ; 0.23 ; 0.43)
Considering Eq (2), the Fuzzy Probability Score for
event A111 can beobtained as follows:
FPs =
×
(..)
(.×.)
(
..
)
(.×.)
(....)
=
×
.
.
= 0.25
Similar procedure was repeated for the rest of the
events and the results are as shown in Table 10.
Table 10: Calculation Results of Fuzzy Possibility (FPs).
No Code
Fuzzy Number
FPs
a b c d
1 A111 0.12 0.21 0.23 0.43 0.25
2 A112 0.22 0.39 0.40 0.57 0.39
3 A121 0.17 0.29 0.32 0.49 0.32
.... ... .... .... .... .... ....
25 B11 0.16 0.24 0.28 0.47 0.29
26 B12 0.12 0.23 0.25 0.44 0.27
27 B2 0.17 0.32 0.33 0.52 0.34
After finding the FPs of each basic event from
the Fuzzy FTA Diagram, were thenconverted the
possibility (FPs) to probability (FPr) using equation
6. The results of FPr are shown in Table 11.
Table 11: Calculation Results of Fuzzy Probability (FPr).
No. Code FPs K FPr
1 A111 0.25 3.30 0.0005
2 A112 0.39 2.66 0.0022
3 A121 0.32 2.,95 0.0011
.... ... .... .... ....
25 B11 0.29 3.09 0.0008
26 B12 027 3.23 0.0006
27 B2 0.,34 2.88 0.0013
The next step is calculating the minimum cut set
by input the Fuzzy probability from each basic event
to Top Event FTA software.
Calculations using the software will produce the
Top Event Probability and Intermediate Event
Probability values shown in Figure2.
Figure 2: Minimum cut set results from Fuzzy FTA.
Figure 2 showed the minimum cut sets of fuzzy
fault tree analysis (FFTA). The minimum cut set for
project delay of offshore pipeline installation are due
to disruption of pipeline installation process with a
probability 0.04135065 and inefficient management
project has a probability of 0.00130048. So the
minimum total cut set for the top event is 0.0426069.
Risk Analysis on Offshore Pipeline Installation Delay: A Case Study for Mahakam Block, Indonesia
111

5 CONCLUSION
Based on discussion in the previous chapter, it can
be conclude that the most dominant factor causing
delays in offshore pipeline installation projects is
Disruption of Pipeline Installation Process with a
probability of 0.0413 and Inefficient Management
Projectwith a probability of 0.0013.
REFERENCES
Aqlan, F., and Ali, E. 2014. Integrating lean principles
and fuzzy bowtie analysis for risk assessment in
chemical industry. Jurnalinternasional: www.elsevier.
com/locate/jlp.
Clemen, R.T., Winkler, R.L. 1999. Combine Probability
Distribution from Experts in Risk Analysis. Risk
Analysis. Vol 19, 187–203.
Lavasani, S.M.M., Wang, J., Yang, Z., and Finlay, J.
2012. Application of MADM in a Fuzzy Environment
for Selecting the Best Barrier for Offshore Wells.
Expert Syst. Appl. 39, 2466–2478.
Mokhtari, K., Ren, J., Roberts, C., and Wang, J. 2011.
Application of a Generic Bow-tie Based Risk
Analysis Framework on Risk Management of Sea
Ports and Offshore Terminals. Jurnalinternasional:
www.elsevier.com/locate/jhazmat.k
Muhamad, P. 2016. Analisa Faktor Penyebab
Keterlambatan Proyek Topside Platform ONE OF
THE COMPANYYZ. Surabaya: TugasAkhir.
Departement Teknik Kelautan Institut Teknologi
Sepuluh Nopember.
Onisawa, T. 1988. An Approach to Human Reliability in
Man-Machine Systems Using Error Possibility. Fuzzy
sets Syst. Vol. 27, 87–103.
Ramzali, N., Lavasani, M.R.M., Ghodousi, J. 2015. Safety
Barriers Analysis of Offshore Drilling System by
Employing Fuzzy Event Tree Analysis. Saf. Sci. Vol.
78, 49–59.
Raiyan, A., Das, S., Islam, M. R. 2011. Event
Tree Analysis of Marine Accidents in
Bangladesh. Jurnalinternasional: www.elsevier.com/
locate/ procedia.k
Shahriar, A., Sadiq, R., and Tesfamariam, S. 2012. Risk
analysis for oil & gas pipelines: A sustainability
assessment approach fuzzy based bowtie analysis.
Journal of Loss Prevention in the Process Industries.
Vol 25, 505-523.
Silvianita., Daniel M Rosyid, Dirta M Chamelia, Firza
Redana. 2017. “Project Delay Analysis on Jacket
Structure Construction.” Applied Mechanics and
Materials 862: 315–20.
Silvianita., Daniel M Rosyid, Anantya Novega S. 2017.
“Project Delay Analysis of HRSG.” In 79:12036. IOP
Conference Series: Earth and Environmental Science.
Silvianita., Daniel M Rosyid, Dirgha S Mahandeka. 2014.
“Fault Tree Analysis for Investigation on The Causes
of Project Problems.” Second International Seminar
on Ocean and Coastal Engineering Environment and
Natural Disaster Management 2014. Surabaya.
Zarei, E., Khakzad, N., Cozzani, V., Reniers, G. 2019.
Safety Analysis of Process Systems Using Fuzzy
Bayesian Network (FBN). Jurnalinternasional:
www.elsevier.com/locate/jlp. K
ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management
112
