Hydrostatic Stiffness as Displacement Boundary Condition of

Floating Cylindrical Structural Analysis in Waves

Raditya Danu Riyanto and Shade Rahmawati

Department of Ocean Engineering, Institut Teknologi Sepuluh Nopember, Surabaya, Indonesia

Keywords: Hydrostatic Stiffness, Displacement Boundary Condition, Structural Analysis, Natural Period.

Abstract: Motion analysis is one of the mandatory aspects to predict the performance of a floating structure, as well as

how its structural strength under certain wave load. However, in majority of floating body performance

prediction, the calculation of motion and strength performance is done separately. Practically, engineers

calculate the motion and hydrodynamics forces that work on the structure, then do separate calculations on

the structure to predict structure’s strength. These separate calculations often use assumptions that tend to be

unrealistic, either over-constrained or under-constrained. This paper provides an alternative to the constraint

problem by introducing hydrodynamic stiffness as boundary conditions, instead of using fixed or simply

supported boundary conditions, spring boundary conditions are applied with hydrodynamic stiffness of

floating body properties. It is expected that this model provides a more realistic constraint to the future

analyses. The results achieved are very promising, where the boundary condition resulting a close natural

frequency approximation compared with the analytical calculation. This configuration is hoped to be the

baseline of more complex structure to be carried out in future research, in order to represent a more realistic

structural displacement boundary condition.

1 BACKGROUND

Motion analysis is one of the mandatory aspects to

predict the performance of a floating structure, as well

as how its structural strength under certain wave load.

However, in majority of floating body performance

prediction, the calculation of motion and strength

performance is done separately.

Practical engineering software package tends to

disintegrate calculation of motion and

hydrodynamics forces that work on the structure for

used to assess the strength of particular floating body.

Traditionally, engineers consider the ship

structure as fixed ends beam (Okumoto, et al., 2009)

or simple beam (Molland, 2008).

Several researches on analytical level proposed

the methods to incorporate ‘sea springiness’ of

floating body during strength analysis. There are

researches conducted to integrate Computational

Fluid Dynamics (CFD) and Finite Element Analysis

(FEA) via Fluid Structure Interaction (FSI) software

packages. ANSYS, for instances, is one of the

established software packages that used for this

intention. In maritime application, various vessel

forms has been used as object. For example,

composite ship structures (Ma & Mahfuz, 2012),

horizontal cylinder (Raja, 2012) and ocean energy

harvesting device (Agamloh, et al., 2008). Several

open source software such as OpenFoam has also

been used for the same intention. Wave-structure

interaction method has been developed using

OpenFoam (Chen, et al., 2014).

Still, the performed researches are still focused on

the fluid interaction and tend to disregard the

displacement boundary condition aspects. Majority of

the those only consider the displacement boundary

condition as buoyancy versus gravity only.

Recent studies provide the hydrostatic stiffness

for linear hydroelasticity. The explicit formulation for

the complete hydrostatic stiffness for flexible floating

structures at rest in calm water is derived based on a

consistent linearization of the external hydrostatic

pressure and the internal structural stresses (Huang &

Riggs, 2000). It is also found that the hydroelasticity

formula deals with more terms, and, that under some

assumptions, it is reduced to the known complete

restoring stiffness (Senjanović, et al., 2011).

This paper introduces the practical hydrostatic

stiffness to be used directly as displacement boundary

condition of rigid floating body. Analytical

Riyanto, R. and Rahmawati, S.

Hydrostatic Stiffness as Displacement Boundary Condition of Floating Cylindrical Structural Analysis in Waves.

DOI: 10.5220/0010058501310137

In Proceedings of the 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management (ISOCEEN 2019), pages 131-137

ISBN: 978-989-758-516-6

131

calculation is introduced as an approach to assess the

application of ground spring to a floating cylinder.

This method is hoped to be an applied practical guide

to model a better and more realistic displacement

boundary conditions for those who cannot afford the

luxury of FSI study.

The proposed method has been initially

developed by American Bureau of Shipping, depicted

at ABS Floating Production Installation (ABS, 2014),

only for ship shaped structures. Authors inspired by

related theory explained at ABS FPI Part 5A, Chapter

3, Appendix 4, Point 17, to be used as basis of so-

called analytical-practical approach of cylindrical

floating structure’s displacement boundary condition.

2 UNCOUPLED

HYDRODYNAMIC MOTION

Based on classical theory as commonly known, the

free-floating body has six degree of freedom in

hydrodynamics motion, namely (Bhattacharya,

1978):

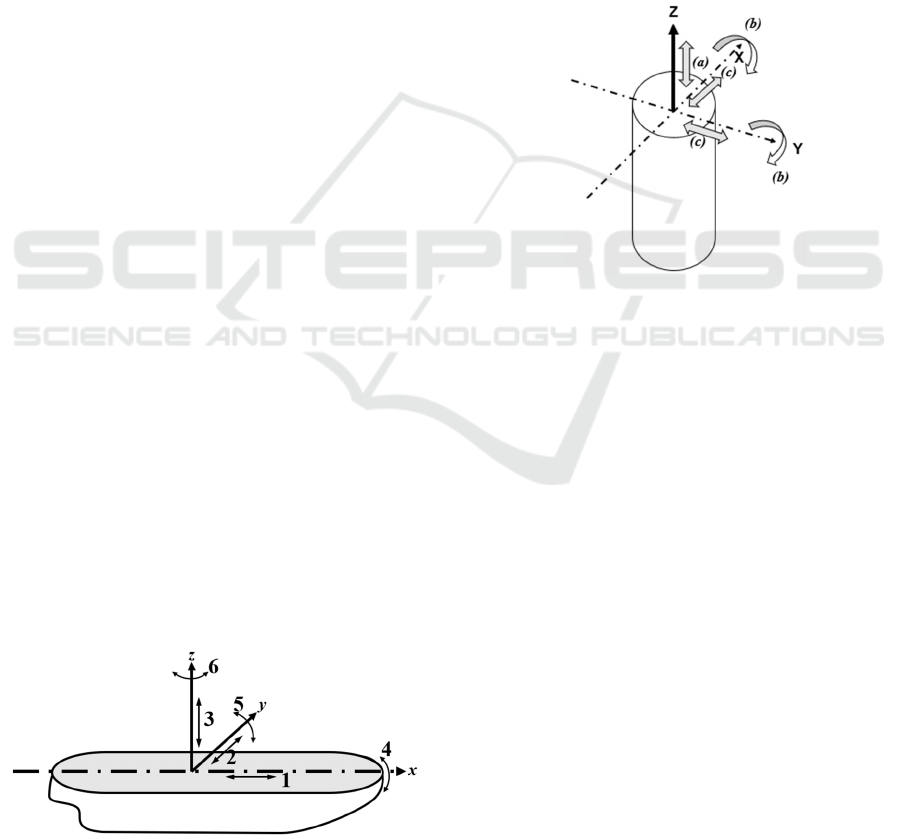
1 Surging = motion backward and forward

in the direction of ship travels

2 Swaying = athwartship motion of ship

3 Heaving = motion vertically up and down

4 Rolling = angular motion about

longitudinal axis (X axis).

Traditionally, the angular

motion alternating from

portside to starboard and vice

versa

5 Pitching = angular motion about the

transverse axis (Y axis).

Traditionally, the angular

motion alternating from bow to

stern and vice versa

6 Yawing = angular motion about the

vertical axis (Z axis)

Above list of motion is illustrated by Figure 1

below

Figure 1: Six Degree of Freedom Hydrodynamic Motion.

2.1 Uncoupled Hydrodynamic Motion

of Floating Cylinder

In this paper we limit the discussion only for

cylindrical structure, which is a bi-symmetrical

structure. Hence, the aforementioned hydrodynamic

motion can be reduced due to similarities, into

following motions:

1. Surging = swaying, with similar X and Y

translation motion.

2. Pitching = rolling, with similar X and Y

rotation motion.

3. Yawing, due to the bi-symmetrical structure,

the Z rotation is considered negligible.

Figure 2: Floating Cylinder Motion.

Figure 2 above explains the considered motions

of floating cylinder. As it can be seen, letter (a) coded

the heaving motion, while (b) coded the rolling

motion, and finally we have (c) coded for swaying

motion. (a) and (c) are the translational motions of the

cylinder, with equation described below:

𝑚𝑢+𝑐𝑢+𝑘𝑢= 𝐹



𝑡

(1)

Where:

𝑚𝑢 = translational inertial force

𝑐𝑢 = translational damping force

ku = translational restoring force

𝐹



𝑡 = translational excitation force

Inertial force for translational motion, is present

when the cylinder is in oscillatory motion, consist of

m (cylinder mass plus hydrodynamic added mass)

multiplied by 𝑢, the motion acceleration for

translational.

Damping force, is the force to resist the motion.

This force consists of damping coefficient c and

translational velocity, 𝑢.

Restoring force is the spring force that brings

back the cylinder into its equilibrium position.

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

132

Restoring force is composed of k, the hydrostatic

stiffness of the motion, multiplied by u for

translational motion, which is the translation of

cylinder’s Centre of Gravity (CoG)

Furthermore, (b) is the rotational motion of the

cylinder, with equation described below:

𝑚𝜃



+𝑐𝜃



+ 𝑘𝜃= 𝐹



𝑡

(2)

Where:

𝑚𝜃



= rotational inertial moment

𝑐𝜃



= rotational damping moment

k𝜃 = rotational restoring moment

𝐹



𝑡 = rotational excitation moment

Inertial moment for translational motion, is

present when the cylinder is in oscillatory motion,

consist of m (cylinder mass plus hydrodynamic added

mass) multiplied by 𝜃



, the motion angular

acceleration for rotation.

Damping moment, is the moment to resist the

motion. This moment consists of damping coefficient

c and rotational motion angular velocity, 𝜃



Restoring moment is the spring moment that

brings back the cylinder into its equilibrium position.

Restoring moment is composed of k, the hydrostatic

stiffness of the motion, multiplied by 𝜃 for

translational motion, which is the rotation of

cylinder’s Centre of Gravity (CoG)

This stiffness properties, both for translational

and rotational motion, are used for the ground spring

stiffness, to represent the actual condition when we

perform the structural analysis of the cylinder.

2.2 Hydrostatic Stiffness of Heaving

Motion

As stated at equation 1 above, the hydrostatic stiffness

of heaving is used for vertical translational spring

stiffness. The heaving stiffness is the waterplane area

of cylinder multiplied by the water specific weight

(Patel & Witz, 1991), consequently, the hydrostatic

stiffness of cylinder heaving motion is as follows:

𝑘=𝛾𝜋𝑟



(3)

Where:

k = heave stiffness

𝛾 = water specific weight

𝜋𝑟



= waterplane area of cylinder

The spring stiffness is attached at the bottom of

the cylinder, to represent the restoring motion of

heaving.

2.3 Hydrostatic Stiffness of Rolling

Motion

At the same time, for rotational motion, the

hydrostatic rolling stiffness is used. Rolling stiffness

is the righting moment of the cylinder. The righting

moment at any particular angle of inclination is

expressed as:

𝑘𝜃=∆𝐺𝑍



(4)

For small angle of inclination (in radians):

𝑘𝜃≅∆𝐺𝑀





𝜃

(5)

Hence the hydrostatic stiffness of rolling motion:

𝑘=𝛾∇GM





(6)

Where:

k = rolling motion stiffness

𝛾 = water specific gravity

∇ = water displacement





= metacentre height of cylinder

3 GROUND SPRING ELEMENT

The ground spring method has very long tradition to

be included in dynamic analysis of structures. It is

commonly used in seismic analysis to model the

damping and stiffness of soil-pile interaction (Datta,

2010). Unlike in hydrodynamic analysis, there are a

lot of established coefficient that model the spring

and dashpot for a variety of foundation types and soil

conditions (Gazetas, 1991). Figure 3 below shows the

example of ground spring applied to a building

(Datta, 2010).

Figure 3: Example of Spring-Dashpot Equivalent Method

to a Building (Datta, 2010).

Hydrostatic Stiffness as Displacement Boundary Condition of Floating Cylindrical Structural Analysis in Waves

133

The same concept applied to a floating cylinder

with the spring stiffness from the hydrostatic

properties of the body. In this paper, we only consider

the stiffness properties of spring.

4 CASE STUDY:

DISPLACEMENT BOUNDARY

CONDITION OF A FLOATING

CYLINDER

A simple cylindrical structure is presented to examine

the usability of the ground spring applied to

hydrodynamic case. Figure 4 below shows the

proposed ground spring placement to create

equivalent spring arrangement of hydrostatic

stiffness.

Figure 4: Equivalent Spring Arrangement.

4.1 Problem Setting

The proposed configurations above is treated as

structural system with precalculated heave and roll

spring as mentioned before at Chapter 2.2 and 2.3.

The heave and roll spring are placed at the bottom

of the cylinder, assumed that the support is located at

the bottom of the cylinder. This configuration is then

compared with traditionally ‘fixed’ boundary

condition at the bottom of the cylinder. In this paper,

we only compare the 1

order natural period of

heaving and rolling for:

1. Analytical hydrodynamic model

2. Rigid body-equivalent spring arrangement

model

3. Rigid body-traditional fixed boundary

condition arrangement model.

In analytical hydrodynamic model, the mass is

calculated as addition of water displacement and

added mass (Sarpkaya, 2010). Whereas the mass for

rigid body arrangement, both for spring and boundary

condition model, are modelled as its real mass,

instead of displacement and added mass. It is

important to calculate the mass with aforementioned

method, to check whether the ‘dry’ models, which

represented by rigid body model, can imitate the

natural frequency of ‘wet’ model, which represented

by hydrodynamics model.

Heave and roll spring stiffness are calculated as

mentioned in Chapter 2.2 and Chapter 2.3

respectively, and then placed at subsequent

arrangement as depicted in Figure 4.

4.2 Cylinder Diameter, Height and

Draught

The cylinder diameter (D) and height (T) are varied

with value 0.1≤D/T≤1.0. while the draught (T) is set

as 0.8H.

4.3 Natural Period

The natural period of heaving and rolling will be

calculated for the three configuration variations. The

natural period for ‘wet’ arrangement is calculated as

below for heaving motion:



=2π



m+m





(s)

(7)

Where:

m = real mass

maz = added mass for heaving motion

kz = heaving motion stiffness

And for rolling motion:



=2π



I+I





(s)

(8)

Where:

I = real inertial rolling motion

Iar = added inertial rolling motion

kr = rolling motion stiffness

The natural period for heaving motion for ‘dry’

arrangement is calculated as below:



=2π





(s)

(9)

Where:

m = real mass

kz = spring stiffness for heaving motion

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

134

The natural period for rolling motion for ‘dry;

arrangement is calculated as below:



=2π





(s)

(10)

Where:

I = real inertial rolling motion

kr = rolling motion stiffness

5 RESULT AND DISCUSSION

5.1 Hydrostatic Stiffness

Hydrostatic stiffness is calculated and used as spring

stiffness and adequately inputted as spring stiffness at

each motion. The natural period of each motion is

then calculated and discussed as below.

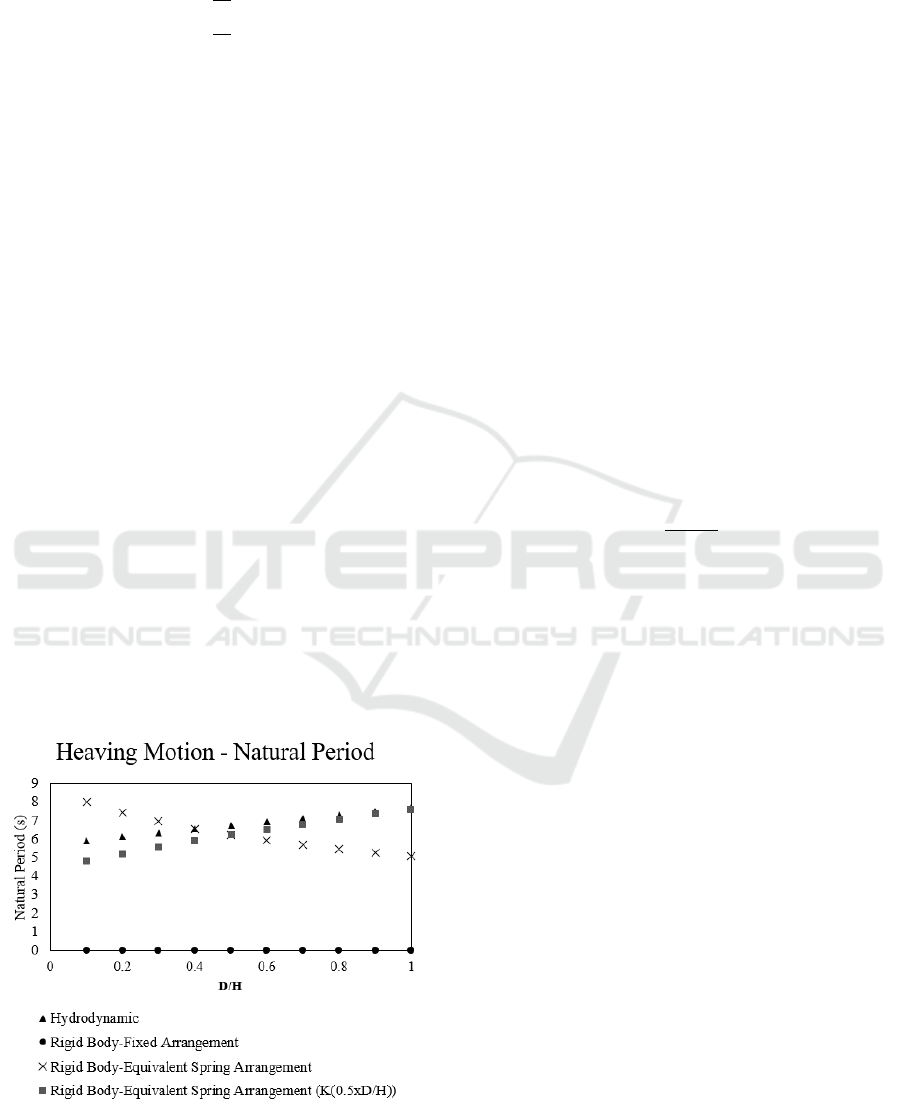
5.2 Heaving Motion Natural Period

Figure 5 below shows the natural period

characteristics for each boundary condition

arrangement. First of all, the hydrodynamic natural

period is calculated for each D/H, represented by

triangle dots. The natural period increases with the

increase of the D/H. Then the rigid body motion is

calculated. Fixed boundary condition gives very low

natural period, which is near to zero, and considered

as unrealistic boundary condition due to the very wide

gap between the hydrodynamic and this boundary

condition.

Figure 5: Heaving Motion Natural Period for Each

Arrangement.

Equivalent spring motion natural period is

calculated and presented at Figure 5 by the cross dots.

The pattern of the equivalent spring natural period is

rather different with the hydrodynamic one, but still

in the same region. Maximum natural period for

equivalent spring is at D/H=0.1, where the value is

8.034 s. Where the maximum natural period for

hydrodynamics is D/H=1.0, the value is 7.683 s.

Adjustments is made to equivalent spring

stiffness. In order to imitate the hydrodynamics

properties, the spring stiffness is calculated by adding

hydrostatic stiffness with the multiplication of the

half ratio between diameter and height.

The value of the equivalent spring natural period

is then matched with the hydrodynamics natural

period, as explained by square dots at Figure 5. It

turns out that by multiplying the hydrostatic stiffness

with 0.5xD/T, the natural character of spring

arrangement is similar to the hydrodynamic

characteristic.

Similar natural period can be achieved by

arranging the spring as shown at Figure 4 for the

heaving motion of cylinder, by applying below

equation for the spring stiffness:

𝐾



2𝛾𝜋𝑟



2𝐻

(11)

Where:

= heave equivalent spring stiffness

𝛾 = water specific weight

𝑟 = cylinder diameter

H = cylinder height

5.3 Rolling Motion Natural Period

Figure 6 below explains the natural period

characteristics for every boundary condition

arrangement. In the beginning, the hydrodynamic

natural period is analysed for each D/H, symbolized

by the triangular dots. Similar with heaving motion,

the natural period increases with the increase of the

D/H. The following result, which is rigid body

motion, is calculated. Again, identical with heaving

motion, fixed boundary condition gives very low

natural period, which is near to zero. This boundary

condition is considered as unrealistic due to the very

wide gap between the hydrodynamic and fixed

arrangement.

Equivalent spring motion natural period for

rolling motion is calculated and presented at Figure 6

by the cross dots. The pattern of the equivalent spring

natural period is similar with hydrodynamics motion

but resulting rather higher period.

Hydrostatic Stiffness as Displacement Boundary Condition of Floating Cylindrical Structural Analysis in Waves

135

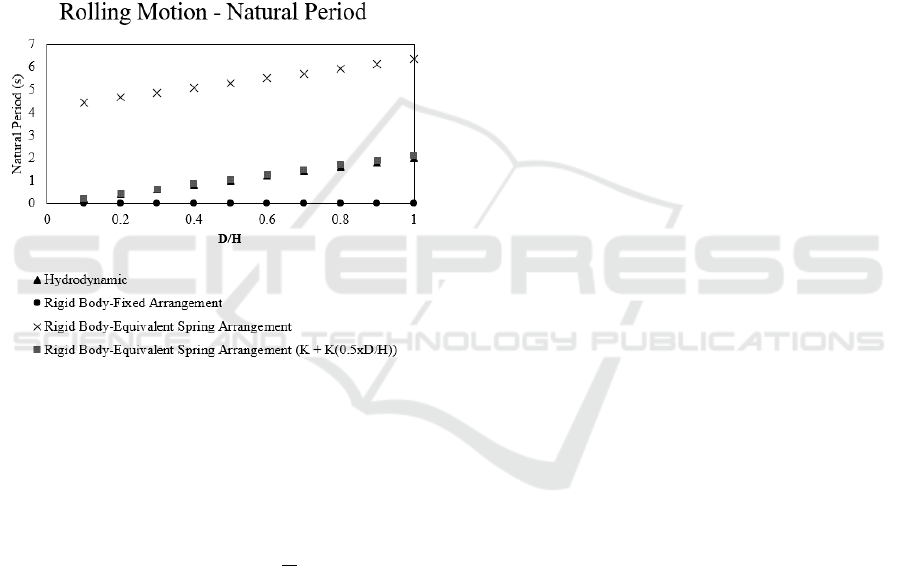
Maximum natural period for equivalent spring is

at D/H=1.0, where the value is 6.344 s. Where the

maximum natural period for hydrodynamics is

D/H=1.0, the value is 2.006 s. It turns out that the

difference between equivalent spring and

hydrodynamic natural characteristic can be

normalized by dividing the rolling natural period by

the ratio between the diameter and the height.

The value of the equivalent spring natural period

is then matched with the hydrodynamics natural

period, as explained by square dots at Figure 6. It

turns out that by dividing the rolling hydrostatic

stiffness by D/T, the natural character of spring

arrangement is similar to the hydrodynamic

characteristic for rolling motion.

Figure 6: Rolling Motion Natural Period for Each

Arrangement.

Similar natural period can be achieved by

arranging the spring as shown at Figure 4 for the

rolling motion of cylinder, by applying below

equation for the spring stiffness:

𝐾



=𝛾∇GM





(1 +

𝑟

𝐻

)

(12)

Where:

= roll equivalent spring stiffness

𝛾 = water specific gravity

∇ = water displacement





= metacenter height of cylinder

r = cylinder radius

H = cylinder height

6 CONCLUSION

After going with the explained procedures to create

equivalent spring arrangement for heaving and rolling

motion, especially to singular cylinder, we can draw

conclusions as follow:

1. The value of the equivalent spring natural

period matches with the hydrodynamics

natural period by dividing the rolling

hydrostatic stiffness by D/T the hydrodynamic

characteristic for rolling motion.

2. For heaving motion, in order to imitate the

hydrodynamics properties, the spring stiffness

is calculated by adding hydrostatic stiffness

with the multiplication of the half ratio

between diameter and height.

7 FURTHER WORKS

The future works should refine the hydrostatic

stiffness modelling by considering the ground spring

height.

Further works also should develop more

hydrostatic equivalent spring stiffness for more

complex structure, e.g.: boxes, multiple cylinders,

and ship shaped structures.

ACKNOWLEDGEMENT

This work is part of the research funded by DRPM

(Direktorat Riset dan Pengabdian Masyarakat) Insitut

Teknologi Sepuluh Nopember Surabaya, Indonesia.

Contract number 1233/PKS/ITS/2019. Author’s

gratitude to the funding department is acknowledged.

REFERENCES

ABS, 2014. Rules for Building and Classing Floating

Production Installation. Houston: American Bureau of

Shipping.

Agamloh, E., Wallace, A. & Jouanne, A., 2008. Application

of fluid–structure interaction simulation of an ocean

wave energy extraction device. Renewable Energy,

33(4), pp. 748-757.

Bhattacharya, R., 1978. Dynamics of Marine Vehicle. New

York: John Wiley & Sons.

Chen, L. et al., 2014. Numerical investigation of wave–

structure interaction using OpenFOAM. Ocean

Engineering, Volume 88, pp. 91-109.

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

136

Datta, T., 2010. Seismic Analysis of Structures. Singapore:

John Wiley & Sons (Asia).

Gazetas, G., 1991. Foundation Vibration, Chapter 15. In:

Foundation Engineering Handbook. New York: Van

Nostrand Reinhold, pp. 553-593.

Huang, L. & Riggs, H., 2000. The hydrostatic stiffness of

flexible floating structures for linear hydroelasticity.

Marine Structures, 13(2), pp. 91-106.

Ma, S. & Mahfuz, H., 2012. Finite element simulation of

composite ship structures with fluid structure

interaction. Ocean Engineering, Volume 52, pp. 52-59.

Molland, A., ed., 2008. The Maritime Engineering

Reference Book: A Guide to Ship Design,

Constructuion and Operation. Oxford: Butterworth-

Heinemann.

Okumoto, Y., Takeda, Y., Mano, M. & Okada, T., 2009.

Design of Ship Hull Structures: A Practical Guide for

Engineers. Berlin: Springer-Verlag Berlin Heidelberg.

Patel, M. & Witz, J., 1991. Compliant Offshore Structures.

Oxford: Butterworth-Heinemann Ltd.

Raja, R., 2012. Coupled fluid structure interaction analysis

on a cylinder exposed to ocean wave loading (Master's

Thesis). Gothenburg: Chalmers University of

Technology.

Sarpkaya, T., 2010. Wave Forces on Offshore Structures.

Cambridge: Cambridge University Press.

Senjanović, I., Hadžić, N. & i Vladimir, N., 2011. Restoring

Stiffness in the Hydroelastic Analysis of Marine

Structures.. Brodogradnja, 62 (3), pp. 265-279.

Hydrostatic Stiffness as Displacement Boundary Condition of Floating Cylindrical Structural Analysis in Waves

137