Experimental Study of the Effect of Waves on SPAR Responses with

and without Heave Plate in Intact and Damaged Mooring Systems

Murdjito

, Gilrandi Adi Negoro

, Eko Budi Djatmiko

and Baharuddin Ali

Department of Ocean Engineering, Institut Teknologi Sepuluh Nopember, Surabaya, Indonesia

Balai Teknologi Hidrodinamika (BTH) – BPPT, Surabaya, Indonesia

Keywords: SPAR, Heave Plate, Irregular Waves, Dynamic Responses.

Abstract: This research discusses the effects of heave plate utilization against dynamic responses of SPAR due to

random waves. The analysis has been done by numerical and experimental methods. The experimental method

was held in Maneuvering Ocean Engineering Basin of Balai Teknologi Hidrodinamika (BTH) – BPPT. The

model scale of SPAR was constructed based on the classic SPAR prototype with taut mooring systems using

four identical moorings in a 1:125 scale factor. Both experimental and numerical studies were conducted in

time domain analysis with heave plate utilization in the keel of SPAR as the main variable. The diameter of

the heave plate has a 1.5 ratio to the outer diameter of SPAR. Each analysis was conducted in intact and

damaged mooring systems. The analyzed variables of dynamic responses are the surge, heave, pitch, and

maximum offset of the SPAR. Results of both the experimental and numerical studies were then be compared,

showing that the heave plate does not affect surge and pitch responses significantly. On the other hand, it

significantly and consistently reduces the SPAR heave responses in every condition of analysis in both the

numerical and experimental methods. The most significant reduction of SPAR heave response occurred when

the mooring systems were in damaged condition, i.e., 33.29% and 27.84% heave reduction in the experimental

and numerical method, respectively. The study also shows that the heave plate reduces SPAR maximum offset

up to 31.69% in experimental analysis and 11.22% in numerical analysis.

1 INTRODUCTION

The necessity of hydrocarbon fuel which keep

growing each year, demands hydrocarbon exploration

in deep water to fulfil the hydrocarbon shortage.

Therefore, the needs of structural and technology

advancement for deep-water exploration cannot be

neglected any further (Soeb et al, 2017). Between all

development in deep-water exploration technology,

SPAR floating platform has been the most optimal,

efficient, and economic solution to be used as deep-

water drilling and production facility (Glanville et al,

1991) (Horton and Halkyard, 1992).

SPAR floating platform has also been developed

even further as a floater of floating offshore wind

turbine (FOWT), which economically efficient

choice in water depth above 50 meters (Jonkman and

Matha, 2011).

The motion responses of SPAR is relatively low

due to its very deep draught. This advantage,

enhances the security of rigid risers below SPAR in

deep-water production facility (Tao, Lim and

Thiagarajan, 2004). SPAR is also easier to be moved

to another location, and also does not affected by

water depth or earthquake (Soeb et al, 2017). Some of

SPAR excellences are:

- Can be operated in deep-water up to 3000 m water

depth, as drilling or production facility.

- It has absolute stability because of its center of

buoyancy, which always above the center of

gravity.

- Can be utilized as mobile drilling rig.

- It has better sea keeping characteristics compared

to the other mobile drilling unit.

- Simplify the installation and operation of mooring

and cable systems.

- Risers or other drilling units are protected inside

its hull.

These advantages, makes SPAR more likely to be

chose and more superior than the other alternative in

utilization as drilling or production facility in deep-

water (Jain and Agarwal, 2003).

The cylindrical hull of SPAR, which has a

massive draft, provides wave load reduction to the

Murdjito, ., Negoro, G., Djatmiko, E. and Ali, B.

Experimental Study of the Effect of Waves on SPAR Responses with and without Heave Plate in Intact and Damaged Mooring Systems.

DOI: 10.5220/0010060101810190

In Proceedings of the 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management (ISOCEEN 2019), pages 181-190

ISBN: 978-989-758-516-6

181

SPAR system due to its massive displacement which

produces damping effect (Jain and Agarwal, 2003).

SPAR also requires mooring systems to ensure its

position still and stable (station – keeping). The

dynamic responses of SPAR significantly affects the

mooring lines tension. Yet, the type and

characteristics of the mooring systems also govern the

dynamic responses of SPAR (Seebai and

Sundaravadivelu, 2009). Between all of dynamic

loads experienced by SPAR, wave load has the most

impact to SPAR dynamic responses. It is because the

more closer the natural period of the structure to the

wave period, the bigger dynamic responses produced

(Djatmiko, 2012). Therefore, it is important to inspect

the correlation of natural period of the structure and

its environment in design consideration.

A collision between dynamic loads of waves and

SPAR will produces dynamic responses in six degree

of freedom. Those are surge, sway, heave, roll, pitch,

and yaw. These dynamic responses, which hazardous

to risers integrity, need to be minimalized (Tao, Lim

and Thiagarajan, 2004). Heave response also has been

found harmful in small SPAR platform (Fischer and

Gopalkhrisnan, 1998). Some solutions to reduce the

heave responses of SPAR has been offered by

previous studies, which are: increase the damping of

the system, dissociate the natural period of the

structure further from the wave period, and reduce the

wave excitation forces acting on the structure

(Haslum and Faltinsen, 1999). The utilization of

heave plate at the SPAR keel will provide a

significant increase in the damping of the system,

which will also reduce the heave response of the

structure (Tao, Lim and Thiagarajan, 2004). Further

research results shows that the diameter of the heave

plate, affects the increase of added mass, which will

affects the damping of the system and the motion

responses of the structure (Sudhakar and Nallayarasu,

2014). The utilization of double heave plates in the

keel and the hull of classic SPAR also significantly

affects the heave response of the SPAR. The diameter

of the heave plates, and the distance between the

heave plates, are the main variable, which contributes

to the change in SPAR viscous damping

(Subbulakshmi et al, 2015).

This research, discusses about the effects of the

heave plate utilization in the keel of SPAR to its

dynamic responses against irregular waves in intact

and damaged mooring systems. The research has

been done in numerical and experimental method,

using classic SPAR model, which has been studied by

Ivandito Herdayanditya in his research and has 1:125

scale factor, with heave plate utilization as the main

modification. The numerical study has been done

using Orcaflex 9.2a, and the experimental study was

held in Maneuvering and Ocean Engineering Basin

(MOB) of Balai Teknologi Hidrodinamika (BTH) –

Badan Pengkajian dan Penerapan Teknologi (BPPT).

2 LITERATURE REVIEW

The research about non-linear response of SPAR

platform due to wave, and current load in ultra-deep

water and how water depth affects its responses has

been studied in detail (Soeb et al, 2017). Chitrapu, et

al. had also researched about non-linear responses of

SPAR in varies of environment using time domain

simulation (Chitrapu, Saha and Salpekar, 1998). Jain

and Agarwal also accomplished a dynamic analysis

of SPAR using time domain simulation, which

concludes that the responses of SPAR due to waves

and currents need to be restricted, since SPAR

platform usually used as production and drilling

facility (Jain and Agarwal, 2003). Tao, et al. also

studied the correlation between heave response in

classic SPAR and its viscous damping (Tao, Lim and

Thiagarajan, 2004). Fischer and Gopalkrishman

numerically and experimentally analyzed the

characteristics of SPAR heave response, and

represented the importance of heave response

consideration in SPAR (Fischer and Gopalkhrisnan,

1998). Halsum and Faltinsen offered some solutions

to reduce the heave responses of SPAR (Haslum and

Faltinsen, 1999), which are:

- Increase the total damping of the system.

- Dissociate the natural period of the structure

further from the wave period.

- And significantly reduce the wave load excitation

forces.

Tao, et al. research, shows that the heave response

of SPAR platform may be reduced by heave plate

utilization around its hull, which will dramatically

increase the damping of the structure (Tao, Lim and

Thiagarajan, 2004). Yet, Halsum and Faltinsen

mentioned that after using heave plate, the heave

response of SPAR still in a critical state (Haslum and

Faltinsen, 1999). Aside from heave plate utilization,

an additional damping system of a SPAR may be

achieved by installing helical strakes around its hull

or increasing its draught. Sudhakar and Nallayarasu

studied even further about the effects of heave plate

utilization and its diameter to the SPAR responses,

and found the optimal heave-plate diameter ratio to

SPAR diameter (Sudhakar and Nallayarasu, 2014).

Subbulakshmi, et al. also studied the effects of double

heave plates utilization to the heave response

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

182

reduction of SPAR, and found the optimal diameter

ratio of the heave plates and the optimal distance

between them to reduce the heave response

(Subbulakshmi et al, 2015).

3 OBJECTIVES AND SCOPE OF

STUDY

The objective of this research is to comprehend how

far the heave plate utilization in the SPAR keel affects

the stochastic parameter of its dynamic responses.

The dynamic responses which to be analysed are

surge, heave, pitch, and maximum offset. The scope

of study and boundaries of this research are as

follows.

- Experimental and numerical study only

considered one wave characteristic with 0º wave

heading.

- The type of mooring systems is taut mooring

system, with four identical mooring lines.

- The experimental and numerical study was

conducted in the condition of intact and damaged

mooring system.

- The influence of low frequency wave was not

included in the consideration of the analysis.

- The only mooring line tension considered in this

study is the pre-tension of mooring lines, which is

similar for each mooring lines.

- Numerical study was conducted in Orcaflex 9.2a

as a comparison of the experimental study.

4 METHODOLOGY

The flow and procedure of this research was

conducted in stages as follows.

- The literature reviews was performed by referring

to the previous study. The data collection of the

laboratory, scale model, and any other

experimental and numerical aspects was also

conducted in this step.

- The determination of design criteria like scale

factor, acceptance criteria, and so on.

- Modeling of the scale model, which comprised:

the design aspects of the scale model, instrument

preparation, trials, processing and analyzing the

experimental data result.

- Numerical modeling of the structure, which

consists: modeling stage in the software,

numerical model validation, and numerical trials.

- Analyzing and comparing the results of the

experimental and numerical study followed by

conclusions.

Figure 1: Scale model the SPAR with heave plate.

5 RESULTS AND DISCUSSION

5.1 Experimental Modeling

The experimental modeling consists two main

section, which are scale model modeling, and

mooring system modeling. The scale model of the

SPAR hull was made of PVC pipe with 14 cm

diameter. The heave plate was made of acrylic, while

the topside was made of plywood as can be seen in

Figure 1. The ballasting system of the SPAR was

installed inside of the hull, which was made of six

cylindrical steel with a shaft in the middle piercing

each cylindrical steel. These cylindrical steel’s

position can be optimized inside the hull to achieve

the desired stability equilibrium in water, its weight

distribution parameter like keel to gravity (KG) and

radius of gyration was obtained by a series of

calibration. The ballasting system of the scale model

was divided into two blocks of cylindrical steel. The

first block consists four cylindrical steel which

located in the keel of the SPAR, and the other blocks

consists two cylindrical steel which located at 91.5

cm above the keel. The mooring system model was

made of two section. The first section was rubber, and

the second section was steel wire sling. The stiffness

of the mooring lines, which need to be considered,

was obtained by a series of calibration and calculation

using Hooke’s law equation. The data results from

experimental modeling can be seen at table 1. The

mooring system of the SPAR model was installed in

Experimental Study of the Effect of Waves on SPAR Responses with and without Heave Plate in Intact and Damaged Mooring Systems

183

a configuration like Figure 2, 5.5, and 5.6. While the

ballast of the SPAR and its configuration can be seen

in figure 5.1.

Figure 2: Cylindrical steel as ballast (left) and its

configuration inside the SPAR hull (right).

Figure 3: Side view of mooring system configuration.

Table 1: SPAR data and properties.

SPAR PROPERTIES (SCALE 1:125)

Parameters

Scale

Model

Dim.

Scale

Factor

Full Scale

Dim.

Hull diameter (m) 0.140 λ 17.500

Keel diameter (m) 0.150 λ 18.750

Draft

without

heave

plate (m)

Free

floating

1.029 λ 128.681

Moored 1.111 λ 138.896

Draft with

heave

plate (m)

Free

floating

1.034 λ 129.305

Moored 1.116 λ 139.520

Hull height (m) 1.245 λ 155.625

Keel cylinder height

(m)

0.053 λ 6.625

Fairlead height of

SPAR without from

keel (m)

1.165 λ 145.625

Fairlead height with

heave plate from keel

(m)

1.170 λ 146.250

Mass of SPAR

without heave plate

(ton)

0.016 λ

31949.219

Mass of SPAR with

heave plate (ton)

0.017 λ

32295.918

Keel to Gravity of

SPAR without heave

plate, KG (m)

0.457 λ 57.125

Keel to Gravity of

SPAR with heave

plate, KG (m)

0.452 λ 56.508

Roll radius of

gyration, Rxx (m)

0.550 λ 68.750

Pitch radius of

gyration, Ryy (m)

0.550 λ 68.750

HEAVE PLATE PROPERTIES (SCALE 1:125)

Parameters

Scale

Model

Dim.

Scale

Factor

Full Scale

Dim.

Heave plate diameter

(m)

0.210 λ 26.250

Heave plate thickness

(m)

0.005 λ 0.625

Mass of heave plate

(ton)

0.000

283.203

SELECTED MOORING LINES PROPERTIES

(SCALE 1:125)

Parameters

Scale

Model

Dim.

Scale

Factor

Full Scale

Dim.

Pre-tension (KN) 0.003 λ

ε 6835.771

Rubber

Axial stiffness, EA

(MN)

0.000

0196

ε 39.278

Length (m) 0.2 λ 25.000

Steel wire sling

Axial stiffness, EA

(MN)

0.003

ε 7075.487

Length (m) 2.040 λ 255.000

5.2 Numerical Modeling

The numerical model was built based on experimental

data structure in full scale. The numerical modeling

also consists two main modeling section, which are

structural modeling and mooring system modeling.

First of all, numerical model of the SPAR was built

using 3D diffraction theory in MOSES at its operation

draught. The structure was modelled while using

heave plate and not. Modeling in MOSES was

intended to obtain the hydrodynamic and hydrostatic

parameter of SPAR in a particular draught, such as

damping matrix, added mass matrix, wave load RAO,

and so on. After the validation of the numerical

model, the numerical model of SPAR has also been

analysed in Orcaflex 9.2a to simulate the random

waves while SPAR in moored condition, using the

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

184

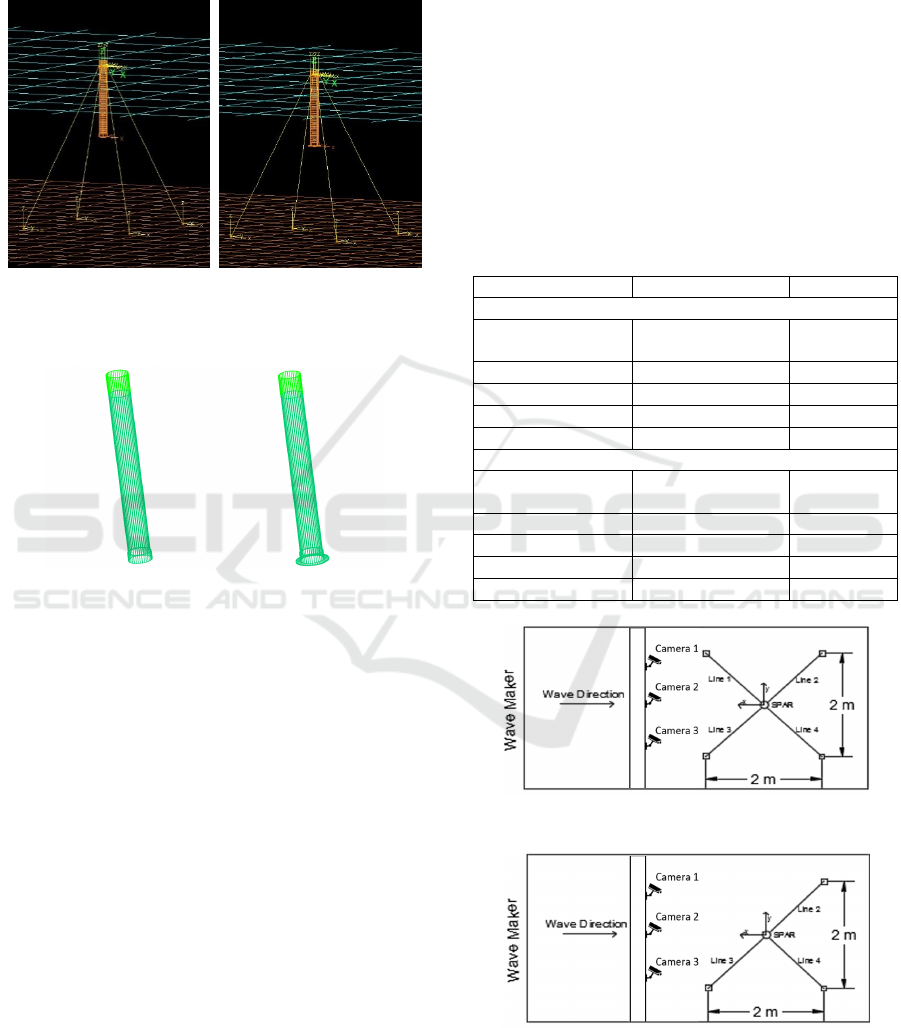
hydrodynamic and hydrostatic data obtained from

MOSES as an input in Orcaflex 9.2a. The result of

numerical modeling stages can be seen in Figure 4

and Figure 5.

Figure 4: Numerical moored model of SPAR in Orcaflex

9.2a (Full scale) without heave plate (left), and with heave

plate (right).

Figure 5: Numerical model of SPAR in MOSES (Full scale)

wihout heave plate (left), and with heave plate (right).

5.3 Experimental Analysis

The experimental analysis was conducted in

Maneuvering and Ocean Engineering Basin (MOB)

of Balai Teknologi Hidrodinamika (BTH) – BPPT.

SPAR and its mooring systems was attached together

in the MOB based on the planned configuration. The

experiment was conducted in four trial conditions,

which are:

1. SPAR without heave plate in intact mooring

system.

2. SPAR with heave plate in intact mooring system.

3. SPAR without heave plate in damaged mooring

systems.

4. SPAR with heave plate in damaged mooring

systems.

Each trial was conducted in time domain method

with 6 minutes duration, which equivalent as 67

minutes in full scale referring to Froude’s model

scaling law. Qualysis motion capture camera, which

placed under the moving bridge above the MOB, was

used to record the translational and rotational

responses of SPAR. During the simulation, Qualysis

recorded the whole SPAR’s movement based on the

coordinate of passive marker position shift, which

located on the topside of the SPAR. The output from

Qualysis was time history responses in six degree of

freedom. Whereas the elevation of the trial’s waves

was measured using wave probe, which placed under

the moving bridge, in front of the SPAR. The trial’s

wave characteristics can be seen in Table 2. The

configuration of intact and damaged mooring systems

used in the trials can be seen in Figure 6 and Figure

7. While the documentation of the moored model in

MOB can be seen in Figure 8.

Table 2: Trial's wave characteristics.

Parameters Values Units

Full Scale

Wave spectrum

theory

JONSWAP -

Hs 6.35 m

Tp 14.5 s

3.3 -

Wave heading 0 Degree

Model (Scale 1:125)

Wave spectrum

theory

JONSWAP -

Hs 0.0508 m

Tp 1.297 s

3.3 -

Wave heading 0 Degree

Figure 6: Intact mooring system configuration.

Figure 7: Damaged mooring system configuration.

Experimental Study of the Effect of Waves on SPAR Responses with and without Heave Plate in Intact and Damaged Mooring Systems

185

Figure 8: Moored scale model in MOB.

5.4 Numerical Analysis

Firstly, the numerical analysis was conducted in

MOSES in frequency domain while SPAR in free-

floating state using the operation draught. This

analysis was intended to obtain the hydrostatic and

hydrodynamic data of SPAR while in operation

draught. Then, these data obtained by MOSES such

as damping matrix, added mass matrix, and wave load

RAO, will be used in Orcaflex 9.2a as an input, then

further analyzed in moored condition. All trial set

conducted in MOSES can be seen in Table 3.

Table 3: Trial set conducted in MOSES.

Condition

Analysis

code

Operation draught

Without heave

plate

1 Intact, 138.896 m

Damaged, 136.845 m

(based on static

analysis in Orcaflex

9.2a)

With heave

plate

3 Intact, 138.896 m

Damaged, 137.473 m

(based on static

analysis in Orcaflex

9.2a)

In Orcaflex 9.2a, analysis was conducted using

time domain simulation, in intact and damaged

mooring system. Every aspects of simulation such as

the duration of the simulation, wave heading, wave

characteristics, was based on experimental data in full

scale and adjusted as similar as possible. The water

depth data in numerical analysis also based on the

depth of MOB that scaled into full scale, which is

312.5 meters. The intact and damaged mooring

system configuration in Orcaflex 9.2a is the same as

experimental configurations.

5.5 Data Results Processing and

Discussion

There are several steps conducted to obtain the

stochastic parameter of the SPAR responses. The

time history responses both from numerical and

experimental analysis need to be converted into

spectral density response in full scale condition for

each dynamic responses. Then further analysis had

been done in surge, heave, and pitch responses to

obtain their stochastic parameters. Whilst the

maximum offset can be obtained directly by plotting

the surge and sway responses together, then measure

the furthest movement of SPAR during simulation

from the initial coordinate. The time history

responses obtained from experimental analysis was

scaled into full scale using Froude’s law. The

example of time history responses in full scale can be

seen in Figure 9.

Figure 9: Time history responses output example.

Random waves and responses time history have

similar characteristics, so both of them can be

processed with the same method. First, the time

history data need to be prepared by dividing each

wave record into some segment. Every segment has a

same point of measurement with the same interval

length, which can be the point of zero-up crossing

period, zero-down crossing period, or peak period.

After that, incremental frequency or usually called

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

186

Nyquist frequency can be determined. The Nyquist

frequency was used as the interval of the frequency in

the converted time history responses, which was

converted into a frequency domain record graphic.

When the time history data ready, the conversion

process was conducted in MATLAB using its Fast

Fourier Transform (FFT) feature. The results, which

was a record of amplitude of waves or responses in

each frequency, further converted into an ordinate of

spectral density curve using equation (1) (Djatmiko,

2012). The example of converted time history

responses in time domain into frequency domain can

be seen in Figure 10. And the example of the

conversion results into the spectral density curves can

be seen in Figure 11 until Figure 13.



















2



(1)

Where,











= Spectral density ordinate

/(rad/s))

 = Nyquist frequency (rad/s)





= Wave or responses amplitude (m)

Figure 10: Example of time history FFT output (full scale).

After every component of amplitude in each

recorded frequency has been converted into an

ordinate of spectral density curve, each set of it was

plotted into a diagram with Nyquist frequency as the

abscissa. Then, the stochastic value of each diagram

can be calculated based on the variants of the wave or

responses elevations, which is equivalent with the

area under the spectral density curve. The second, and

fourth moment of spectral area can also be calculated

using equation (2).

























(2)

Where m

is the variant of wave elevations or

response amplitudes. m

, m

, and m

are the first,

second, and fourth moment of spectral area. By

knowing the value of these parameters, the stochastic

values of each responses can be calculated. In

accordance with the scope and boundaries stated

before, the contribution of the low frequency

components are neglected. Therefore, the stochastic

value calculations are started from the wave

frequency of 0.26 rad/s, which is the lower limit

frequency in wave energy spectrum density.

The stochastic responses calculated in this

research are: significant responses, mean of 1/10

highest responses, mean responses, the most probable

extreme responses, and the most probable extreme

responses with a probability of 99% confidence not

exceeded. Those stochastic responses can be

calculated using equations as follows.







2







(3)









2.5









(4)





/



5.08









(5)



⌢













2





2













(6)





⌢













2





2













(7)

Where,







= Significant responses (m)







= Mean responses (m)





/

= Mean of 1/10 highest responses (m)



⌢

= The most probable extreme

responses (m)





⌢

= The most probable extreme

responses with a probability of 99%

confidence not exceeded (m)

 = Duration of waves-making (s)

 = confidence number, 0.01 for 99%

confidence not exceeded (m)

According to the results, the response changes

between before and after heave plate utilization in

each type of stochastic responses are all the same in

percentage. Therefore, to simplify the analysis in

seeing the changes that occurs, the significant

responses was chosen as a representation of the SPAR

responses in each motion, which was compared

between each condition.

Experimental Study of the Effect of Waves on SPAR Responses with and without Heave Plate in Intact and Damaged Mooring Systems

187

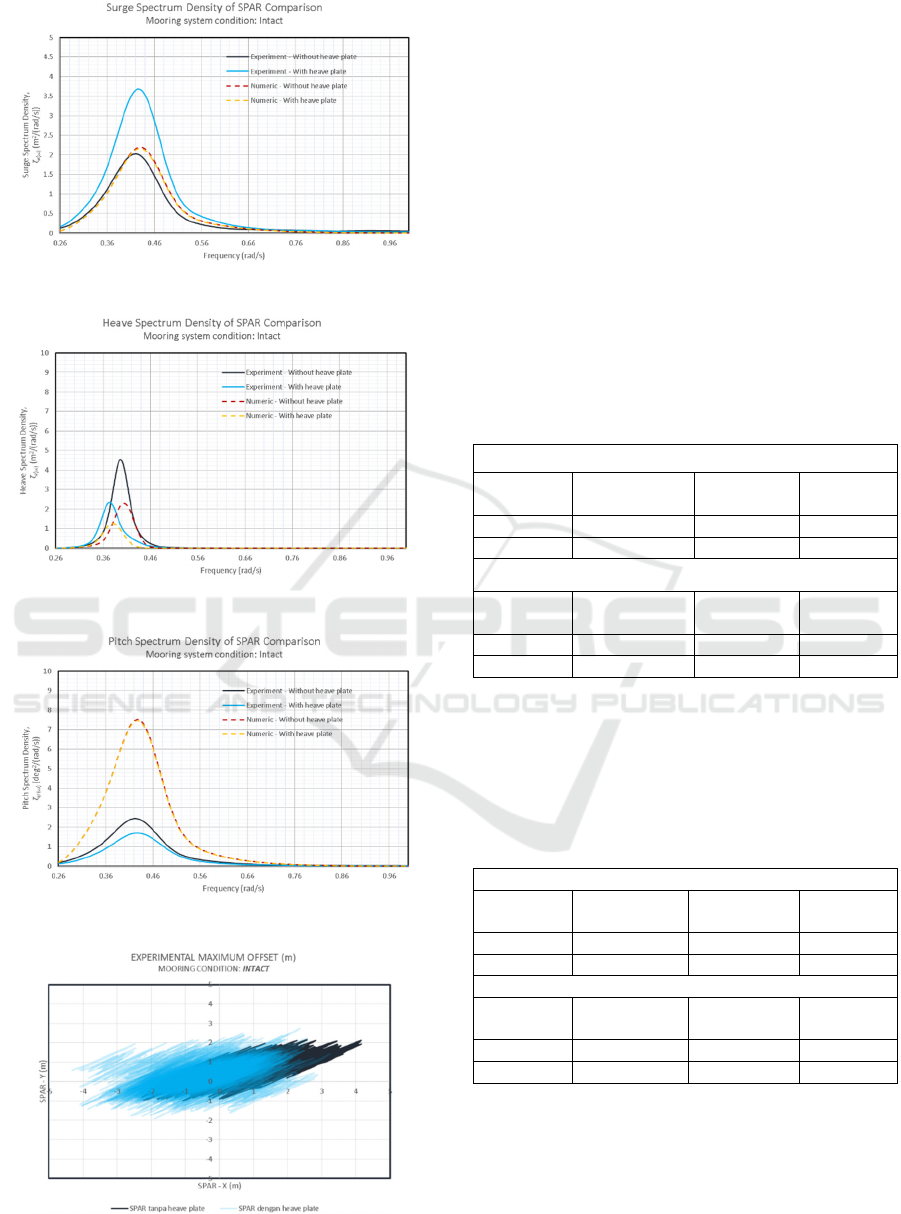
Figure 11: Example of surge responses spectrum density.

Figure 12: Example of heave responses spectrum density.

Figure 13: Example of pitch responses spectrum density.

Figure 14: Offset of SPAR graphic example.

All responses assessed from experiment and

numeric method was plotted together in both intact

and damaged condition to observe the responses

reduction due to heave plate utilization more clearly.

As discussed above, the area below the spectral

density graph is the response’s energy which equals

to the response’s value. Thus, from those comparative

graphics, it can be concluded that there are some

cases of response amplifications and reductions after

heave plate utilizations. All the results are presented

in Table 4 to Table 7 below.

5.5.1 Surge Responses

All of the calculation’s results of surge significant

response’s changes in each conditions are presented

in Table 4 below.

Table 4: Significant surge of SPAR.

Significant surge responses (m) – Experimental

Condition

Without

heave plate

With heave

plate

Reduction

Intact 1.64 1.74 -6.15%

Damaged 1.83 1.82 0.60%

Significant surge responses (m) – Numerical

Condition

Without

heave plate

With heave

plate

Reduction

Intact 1.16 1.15 0.84%

Damaged 1.06 1.05 0.86%

5.5.2 Heave Responses

All of the calculation’s results of heave significant

response’s changes in each conditions are presented

in Table 5 below.

Table 5: Significant heave of SPAR.

Significant heave responses (m) – Experimental

Condition

Without

heave plate

With heave

plate

Reduction

Intact 0.97 0.73 24.16%

Damaged 1.06 0.71 33.29%

Significant heave responses (m) – Numerical

Condition

Without

heave plate

With heave

plate

Reduction

Intact 0.73 0.54 26.39%

Damaged 1.12 0.71 27.84%

5.5.3 Pitch Responses

All of the calculation’s results of pitch significant

response’s changes in each conditions are presented

in Table 6 below.

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

188

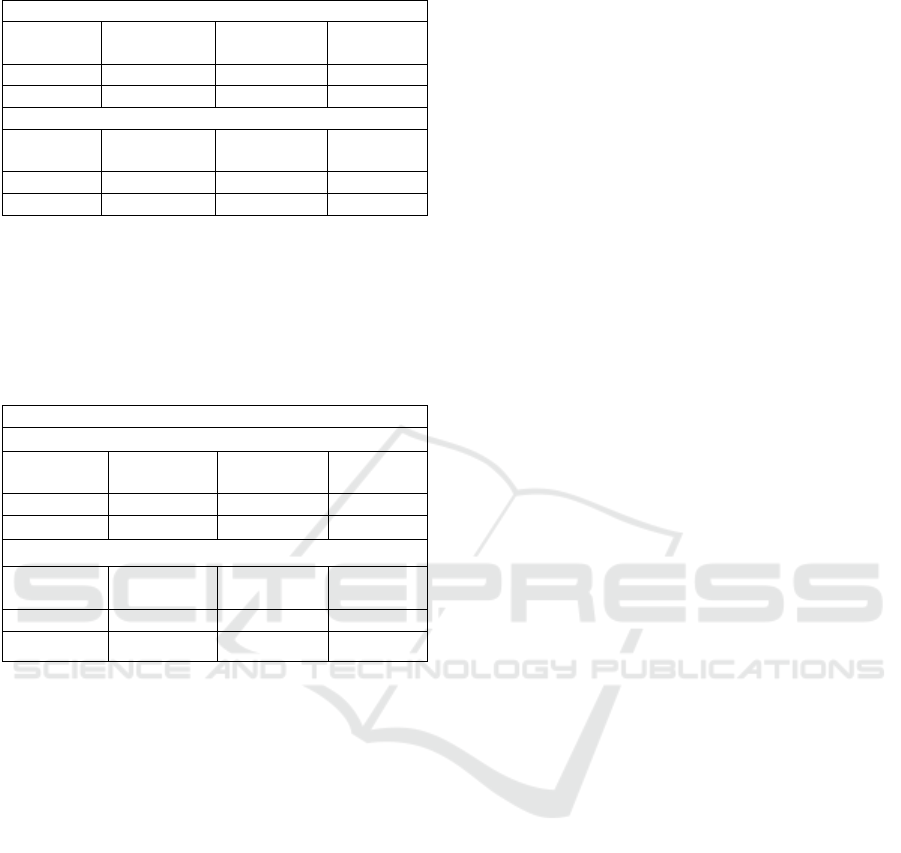
Table 6: Significant pitch of SPAR.

Significant pitch responses (m) – Experimental

Condition

Without

heave plate

With heave

plate

Reduction

Intact 1.46 1.20 17.65%

Damaged 1.34 1.40 -4.56%

Significant pitch responses (m) – Numerical

Condition

Without

heave plate

With heave

plate

Reduction

Intact 2.14 2.13 0.44%

Damaged 2.00 1.99 0.44%

5.5.4 Maximum Offsets

All of the calculation’s results of maximum offsets

changes in each conditions are presented in Table 7

below.

Table 7: Maximum offsets of SPAR.

Maximum offsets of SPAR (m)

Intact mooring system

Method

Without

heave plate

With heave

plate

Reduction

Experiment 4.65 4.36 6.22%

Numeric 2.46 2.23 9.61%

Damaged mooring system

Method

Without

heave plate

With heave

plate

Reduction

Experiment 5.02 3.43 31.69%

Numeric 2.37 2.11 11.22%

As stated before, the maximum offsets value was

obtained by plotting the surge and sway responses in

each condition during simulation together, then the

furthest SPAR movement from the initial condition

was calculated as the maximum offset. The plotted

graphic example can be seen in Figure 14.

6 CONCLUSIONS

The findings of the study could be revealed as

follows:

 Heave plate utilization does not constantly and

significantly reduce surge responses. It is

indicated by the biggest reduction of surge

responses that occurs during simulation was only

0.86%, which happened in numerical analysis.

There were some inconsistency happened in

experimental method, which the surge responses

was amplified by 6.15% in intact mooring system.

This inconsistency potentially caused by the

couple response between surge and pitch. On the

contrary, the heave plate utilization does reduce

the heave responses of SPAR, consistently and

significantly. It is indicated by the significant

reduction that occurs in every condition of

experimental and numerical study. The biggest

reduction happened in damaged mooring system

during experimental study, which was 33.29%. As

for pitch, the heave plate utilization numerically

does not affects the responses significantly, it is

indicated by the reduction are only 0.44% in each

condition. Yet, in the experimental study the pitch

responses inconsistently changes. Where in intact

mooring system it was reduced up to 17.65%, and

while in damaged mooring system it was

amplified by 4.56%. In some conditions, SPAR

model satisfies the requirements of Matthieau

instability to occurs, this phenomenon potentially

become the cause of the inconsistency in pitch

responses.

 Heave plate utilization does reduce SPAR

maximum offsets consistently in every

conditions. The biggest reduction happened in

damaged mooring system of experimental

analysis, which was 31.69%.

 The comparison between two methods has found

that in surge responses, inconsistency happened

while in intact mooring system. In the numerical

analysis, the surge responses are slightly reduced,

yet in experiment it was amplified. In heave

responses the results of the two method shows a

convenient agreement, where it has been reduced

consistently and significantly in both methods. As

for pitch, inconsistency happened while in

damaged mooring system, where experimentally

it was a bit amplified, but numerically it was

slightly reduced.

REFERENCES

Soeb, M. R., Islam, A. B. M. S., Jumaat, M. Z., Huda, N.,

dan Arzu, F., 2017. Response of Non-linear Offshore

SPAR Platform under Wave and Current. Ocean Eng.

144, 296-304.

Glanville, R., Paulling, J., Halkyard, J., Lehtinen, T., 1991.

Analysis of the SPAR Floating Drilling Production and

Storage Structure. In: Proceedings of the Offshore

Technology Conference, 6–9 May, Houston, Texas.

Offshore Technology Conference.

Horton, E., Halkyard, J., 1992. A SPAR Platform for

Developing Deep Water Oil Fields. MTS 998–1005.

Jonkman, J. M. and Matha, D. (2011), "Dynamics of

Offshore Floating Wind Turbines-analysis of Three

Concepts", Wind Energy, vol. 14, no. 4, pp. 557-569.

Experimental Study of the Effect of Waves on SPAR Responses with and without Heave Plate in Intact and Damaged Mooring Systems

189

Tao, Longbin, Lim, K. Y., and Thiagarajan K., 2004. Heave

Response of Classic SPAR with Variable Geometry.

Journal of Offshore Mechanics and Arctic Engineering.

Jain, A. K., and Agarwal A. K., 2003. Dynamic Analysis of

Offshore SPAR Platforms. Defence Science Journal,

Vol. 53, No. 2, 211-219. Indian Institute of Technology

Delhi, New Delhi – 110 016.

Seebai, T, and R Sundaravadivelu. 2009. “Effect of Taut

and Catenary Mooring on Spar Platform with 5MW

Wind Turbine.” Proceedings of the Eighth (2009)

ISOPE Ocean Mining Symposium. Chennai: ISOPE.

52-58.

Djatmiko, Eko Budi. 2012. Perilaku dan Operabilitas

Bangunan Laut di Atas Gelombang Acak. Surabaya:

ITS Press.

Fischer, F.J., Gopalkrishnan, R., 1998. Some observations

on the heave behaviour of spar platforms. Journal of

Offshore Mechanics and Arctic Engineering, 120, pp.

221—225.

Haslum, H. A. and Faltinsen, O. M., 1999. Alternative

Shape of Spar Platforms for Use in Hostile Areas.

Offshore Technology Conference, OTC 10953,

Houston, Texas.

Sudhakar, S. Dan Nallayarasu, S. “Hydrodynamic

Responses of a SPAR Hull with Single and Double

Heave Plates in Random Waves”. Internasional

Journal of Ocean System Engineering. Chennai, India

(2014).

Subbulakshmi, A., Jose, J., Sundaravadivelu, R., and

Selvam, R. P., 2015. Effect of Viscous Damping on

Hydrodynamics Response of SPAR with Heave Plate.

International Conference on Water Resources, Coastal

and Ocean Engineering (ICWRCOE 2015).

Department of Ocean Engineering, Indian Institute of

Technology Mardras, Chennai – 600 036, India.

Herdayanditya, I. 2017. Studi Analitis, Numeris, dan

Eksperimen Olah Gerak dan Dinamika Tegangan Tali

Tambat SPAR dengan Variasi Heading Gelombang.

Surabaya: Tugas Akhir Akhir Jurusan Teknik Kelautan,

ITS.

Chitrapu, A.S., Saha, S., Salpekar, V.Y. 1998. Time domain

simulation of spar platform response in random waves

and current. In: 17th International Conference on

Offshore Mechanics and Arctic Engineering,

(OMAE98-0380), pp. 1-8.

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

190