Dynamic Behavior Analysis of Porous Saw Floating Breakwater

under Regular Waves

Sujantoko, E. B. Djatmiko, W. Wardhana, H. D. Armono and Wahyudi

Department of Ocean Engineering, Institut Teknologi Sepuluh Nopember, Surabaya, Indonesia

Keywords: Floating Breakwater, Porous, Motion, RAO.

Abstract: Porous saw floating breakwaters are floated and tethered breakwaters for coastal protectors with typical steep,

deep, and relatively large choppy contours, designed with saw porous, to be able to absorb waves efficiently

and effectively. A proposed numerical model was developed for the porous saw type, while the model for the

pontoon and the saw type will be used as a comparative study. All types of the structure breakwaters were

physically placed inside the flume tank in which the direction of waves was perpendicular (to the structure)

with 3 cm height and 1.1 seconds of period conducted in 41 cm depth of water. The numerical model shows

that the Response Amplitude Operators (RAO) only affect the sway, heave, and roll motions. The porous saw

floating breakwater demonstrates the smallest RAO value among other types i.e. sway 0.66 cm/cm, heave 2.1

cm/cm, and roll 0.86 deg/cm. It means the porous saw type more advantages since the ability to absorb the

wave. Moreover, some of the wave energy will be reduced when the wave passes through the structure.

Therefore, the wave energy received by the structure and the mooring rope becomes smaller.

1 INTRODUCTION

In recent years, many sectors attempt to manage and

utilize the Indonesian coastal region. Such as

industry, trade, transportation, housing, and the

tourism sector. As population growth and increasing

socio-economic development activities, the "value"

of the coastal region continues to grow. Coastal areas,

despite their high economic value, are vulnerable to

many threats. One serious threat encountered is

abrasion, causes a reduction in coastal areas. It may

happen because of the large amount of wave energy

comes directly to the coast without any absorption

beforehand.

Preventing the negative effects caused by

abrasion, it is very important to build and install the

coastal protection structures to reduce wave energy

towards the coastal area. One of the coastal protection

structures that protect from abrasion and erosion is a

breakwater, a structure was built to protect the area

behind it from the wave attacks. There are two types

of breakwaters, namely fixed breakwater and floating

breakwater, both are built depending on the normal

water level elevation and tidal conditions in which

the structure is placed. Floating breakwater offers the

level of protection needed when working in deeper

waters with exposure to natural resources that are

stronger than conventional types of the breakwater.

Floating breakwater applying the concepts of

reflection, dissipation, and transformation to reduce

wave energy so that it can weaken the up-coming

wave to an acceptable level (Morey, 1998). This

breakwater is a floating structure on a limited draft

and depends on the interaction of building structures

at the top of the water column. Moreover, another

advantage of floating breakwater against the fixed

breakwater, the efficiency does almost not depend on

the tides and sea-level rise, then the impact to the

environment is low, the cost of structure

construction, installation and removal are low, short

time for installation, and ability to reset the layout if

there are changes in the future (Ruol et al. , 2012).

However, as a floated structure, then a mooring

system placed on the seabed (Fousert, 2006).

In general, floating breakwaters reduce the

surface waves through the mechanism of reflection,

destroying the movement of water particles and

attenuation of viscosity. When the waves hit the

structure, energy will be reflected, scattered, and

partially muted by the structure. The greater the wave

energy absorbed, the higher the intensity of the

following structure's motion. Since most of the wave

energy will be converted into motion energy. The

212

Sujantoko, ., Djatmiko, E., Wardhana, W., Armono, H. and Wahyudi, .

Dynamic Behavior Analysis of Porous Saw Floating Breakwater under Regular Waves.

DOI: 10.5220/0010119102120217

In Proceedings of the 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management (ISOCEEN 2019), pages 212-217

ISBN: 978-989-758-516-6

amount of energy absorbed is largely determined by

the magnitude of the cross-sectional area of the

structure relative to the perpendicular direction of the

incident wave. Therefore, a floating breakwater

design with minimum cross-section and interaction

effect is an important reference for producing designs

with minimum responsiveness. Such conditions can

be achieved with porous surface conditions.

Based on the concept of maximum energy

dissipation due to reflections and minimum energy

trajectories that pass through the structure, the

floating breakwater research continues to develop to

find better performance. The number of researchers

has conducted a study on the floating breakwater with

porous types, namely porous pontoon (Lee & Ker,

1997; Williams & Li, 1998; Wang & Sun, 2010),

porous boxes (Stainissie & Drimer, 2003; Koutandos

& Prinos, 2011; Zeng et al., 2018), porous plates

(Chwang & Dong, 1984; Wang & Ren, 1993; Cho,

2016; Fang at al., 2018), porous cylinder (William et

al., 2000; Zhao et al., 2010; Shih, 2012).

This research will study the porous floating

breakwater. This type of structure also reduces

extreme wave loads which can affect the performance

of floating structures. In an impermeable form, the

structure will receive the maximum wave force so

that it will transfer the wave energy to the mooring

rope. This undesirable condition since mooring ropes

will receive large loads so that the structure remains

stable receiving wave force. The response of

structural motions as a result of wave loads will affect

the performance of the structure, i.e. reflection and

transmission of waves. Therefore, during the design

stage, it is necessary to predict the structure's motion

to produce a small wave attenuation. Numerical

simulations will be carried out to determine the

characteristics of the 6 degrees of freedom structure

motions using the Ansys Aqwa Module.

2 METHOD OF RESEARCH

2.1 Floating Breakwater Design

The material used in the floating breakwater model is

High-Density Polyethylene (HDPE) with a density of

960 kg/m

. Figure 1 shows the pontoon, porous saw,

and saw type floating breakwater have the same

dimensions (length 20 cm, height 6 cm and width 6

cm). The types are slightly different, the porous saw

type has a pore, which is penetrated the structure

from the front to the back and there is also a triangle

shape lined up in the front of the structure.

In the porous saw type, the pipes are used so that

the front and rear sides of the breakwater are

perforated. The pipe used has an outside diameter of

0.4 cm. These three breakwater types above are floats

with a 4 cm draft. The pore in the porous saw type

floating breakwater is take up to 5% area of the

overall area in the side of the structure. The

difference between these three models requires the

thickness of the porous saw type floating breakwater

to be 0.36 cm to keep drafts are the same. The

reduction was caused by the loss of buoyant force due

to a hole in the floating breakwater.

Figure 1: Floating breakwater (a) type pontoon, (b) saw and

2.2 Hydrostatic Parameters

A series of floating breakwater models arranged in 3

directions longitudinal to the width of the flume tank.

The hydrostatic parameters in this numerical

simulation are used as a basis for measuring the

model validation. Based on the dimensions of the

floating breakwater model, it can be determined the

volume of the types of a pontoon, saw, and porous

saw respectively 2266.58 cm

, 2487.5 cm

, and 2274

. The mass of the floating breakwater can be

determined by multiplying the volume by the density

of HDPE so that the mass of the floating breakwater

type of pontoon, saw, and porous saw is 1457 gr,

1592 gr, and 1535 gr respectively. The third

dimension of this structure is designed to have a draft

of 4 cm.

The initial step before developing a numerical

model is calculating the center of gravity for each

structure. The value of the gravity center in the

floating structure is very important to determine the

stability of the floating breakwater. The center of

gravity calculation is done by dividing floating

(

)

(

)

(

)

Dynamic Behavior Analysis of Porous Saw Floating Breakwater under Regular Waves

213

breakwater into several parts. Then, determining the

value of inertia and the radius of structure gyration.

Complete data on hydrostatic parameters are shown

in Table 1.

Table 1: Hydrostatic data floating breakwater.

Hydrostatic

Parameters

Pontoon Saw

Porous

Saw

Vol. Dis

(

)

2266.6 2487.5 2274

Massa

)

1457 1592 1535

Ixx 3822 4498.9 4387.6

Iyy 40812 44553.75 44546.85

Izz 43197 47276.3 47253.4

Kxx 1.62 1.68 1.64

5.29 5.29 5.29

Kzz 5.45 5.45 5.45

WPA (cm

) 360 372 372

2.3 Validation of the Hydrostatic Model

Numerical simulations to determine the response of

floating breakwater motion are performed by

computational fluid dynamics with the ANSYS/

AQWA hydrodynamic simulation software. Figure 2

shows the layout of the model scenario with the

direction of the incident wave perpendicular to the

structure.

Figure 2: Degree of freedom of floating structures (Das &

Das, 2005).

Before conducting the structural motion analysis,

the floating breakwater model must be validated to

find out the floating breakwater by the conditions in

the analytical calculation. Important hydrostatic

parameters that will be used for the validation of this

model are the volume displacement and water plane

area. Based on The American Bereau of Shipping

(1998), the validation is a maximum of 2% and for

other provisions a maximum value of 1%. The

calibration results of the model are shown in Table 2

and 3.

Table 2: Validation of numerical models: volume

displacement.

Floating

Breakwater

Hydrostatic Parameters

Volume Displacement (cm

)

Analytic Numeric Error %

1 Pontoon 1457 1457 0

2 Saw 1657 1657 0

3 Porous Saw 1663.79 1658.28 0.303

Table 3: Validation of numerical models: water plane area.

Floating

Breakwater

Hydrostatic Parameters

Water Plane Area (cm

)

Anal

tic Numeric Error %

1 Pontoon 360 360.01 0.0001

2 Saw 372 371.8 0.002

3 Porous Saw 372 371.8 0.002

3 RESULTS AND DISCUSSION

Numerical simulations of floating breakwater motion

have been done at a depth of 41 cm, a wave period of

1.1 s and a wave height of 3 cm with the direction of

the wave perpendicular to the structure. The results

of numerical simulations are shown in figures 3-8.

The characteristic of surge motion in pontoons,

saw and porous saw floating breakwater in the

direction of waves perpendicular to the structure is

very small and almost close to 0 (Figure 3). Saw type

RAO is the biggest among other types because there

is additional displacement in front of the structure.

Generally in the surge motion, waves to the side do

not have an effect on the occurrence of surge

motions.

Figure 3: RAO Surge numerical prediction of various types

of the floating breakwater.

Sway motion characteristics are almost the same

as the surge motion where the maximum RAO value

is at low frequencies (Figure 4). The highest RAO on

the pontoon is 0.79 cm/cm. At the same frequency,

the maximum RAO for saw-type floating breakwater

is 0.98 cm/cm and porous saw-type RAO is 0.6

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

214

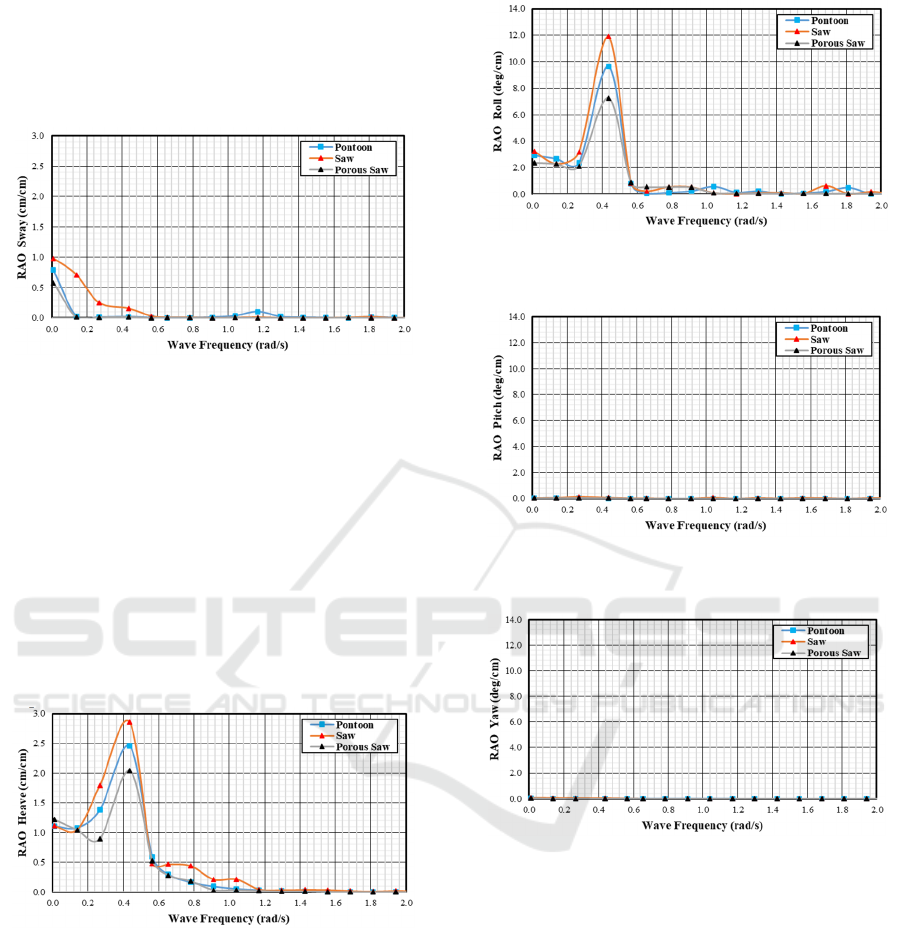
cm/cm. After that, the third RAO floating breakwater

decreases gradually. Sway motion has a higher

maximum value when compared to surge for side

waves because side wave propagation has a great

influence on sway motion.

Figure 4: RAO Sway numerical prediction of various types

of the floating breakwater.

Figure 5 shows the RAO heave motion is an

example to explain dynamic systems that experience

wave excitation. At low frequencies, the three RAO

types of floating breakwater are 1.11 cm/cm, 1.08

cm/cm, and 1.13 cm/cm and gradually increase

towards the resonant region at the natural frequency

of 0.436 rad/s. the largest maximum RAO heave

occurs in the saw type followed by porous pontoon

and gergagi types respectively 2.85 cm / cm, 2.45

cm/cm, and 2.1 cm/cm. After crossing the peak, the

RAO heave will decrease dramatically at high

frequencies.

Figure 5: RAO Heave numerical prediction of various

types of the floating breakwater.

Roll motion is almost the same as the

characteristics of the heave motion (Figure 6). In the

sub-critical region, the motion response represents

the same condition in all types of the floating

breakwater, then increases sharply in the resonant

region and decreases significantly in the supercritical

region. The natural frequency of the roll motion is

0.43 rad/s. The value of the highest response of roll

motion on a saw is 11.86 deg/cm, followed by the

pontoon type of 9.64 deg/cm, and the porous saw is

6.8 deg/cm.

Figure 6: RAO Roll numerical prediction of various types

of the floating breakwater.

Figure 7: RAO Pitch numerical prediction of various types

of the floating breakwater.

Figure 8: RAO Yaw numerical prediction of various types

of the floating breakwater.

In pitch and yaw motions (Figure 7-8), it is not

the same as roll motions which are both rotational

mode motions. However, pitch and yaw motion

intensity is not affected by side and bow waves, so

that the value is 0 or close to 0 so there is almost no

motions response.

Based on numerical simulations obtained floating

breakwaters motion behavior. The condition of a

free-floating structure without a mooring system will

produce a vertical motion mode (heave, roll, and

sway) which is more dominant than the horizontal

motion mode (surge, pitch, yaw). This happens

because all three modes of motion (vertical motion

modes) have a stiffness factor due to harmonic wave

excitation, the presence of this stiffness factor causes

Dynamic Behavior Analysis of Porous Saw Floating Breakwater under Regular Waves

215

the damping factor value to be small so that when the

motion reaches its resonant frequency, the change in

motion characteristics will have a sharply increased

part. Whereas the horizontal motion mode which

does not have a stiffness factor during free-floating

conditions will produce a relatively large damping

factor so that the motion will be damped by the

presence of the damping factor and the horizontal

motion mode does not experience a sharp increase. If

there is an increase in certain parts, then the increase

in the curve is influenced by the coupling effect of

other motions.

6 CONCLUSIONS

This paper compares the dynamic behavior of a

porous saw type floating breakwater with another

types. Numerical studies were carried out with

computation fluid dynamics on models of these

structures at a water depth of 41 cm, wave height of

3 cm, and a wave period of 1.1 seconds. some

findings may be explained as follows:

 The surge, pitch, and yaw motion modes are not

affected by side waves so the RAO value is very

small and almost close to 0.

 The floating breakwater motion in the direction of

incoming waves perpendicular to the structure

only affects the motion sway, heave, and roll.

 Sway motion has a higher maximum value when

compared to surge for side waves because side

wave propagation has a great influence on sway

motion. At the same frequency, the maximum

RAO for saw-type floating breakwater is 0.98

cm/cm, tipe pontoon is 0.79 cm/cm and porous

saw-type RAO is 0.6 cm/cm. After that, the third

RAO floating breakwater decreases gradually.

 The largest RAO maximum heave motion occurs

in the saw type followed by the type of pontoon

and porous saw by 2.85 cm/cm, 2.45 cm/cm, and

2.1 cm/cm respectively. After going through the

peak, the RAO heave will decrease dramatically

at high frequencies.

 The highest peak value of RAO roll occurs at

natural frequency 0.43 rad / s, in floating

breakwater type of saw, pontoon, and porous saw

of 11.86 deg/cm, 9.64 deg/cm, and 8.6 deg/cm

respectively.

ACKNOWLEDGEMENTS

This work was financially supported by The

Directorate of Research and Community Service,

Sepuluh November Institute of Technology (ITS),

Surabaya in research grand scema: "Basic Research

for Higher Education" dan Author thank the

Department Mechanical Engineering ITS for

providing the facilities of Ansys/Aqwa software.

REFERENCES

Cho, Il-Hyoung, 2016. Transmission coefficients of a

floating rectangular breakwater with porous side plates.

International Journal of naval Architecture and Ocean

Engineering 8, pp. 53-65

Chwang, A.T. and Dong, Z.N., 1984. Wave-trapping due

to a porous plate. Proceedings Fifteenth ONR

Symposium of Naval Hydrodynamics, pp. 407-414.

Das, S.N and Das, S.K.,2005. Mathematical model for

coupled roll and yaw motions of a floating body in

regular waves under resonant and non-resonant

conditions. Applied Mathematical Modelling 29. Pp.

19–34.

Fang, Z., Xiao, L., Kou, Y. and Li, J., 2018. Experimental

study of the wave-dissipating performance of a four-

layer horizontal porous-plate breakwater. Ocean

Engineering, vol. 151, pp. 222-233.

Fousert, M. W., (2006). Floating Breakwater: a Theoritical

Study of a Dnamic Wave Attenuating System. Thesis.

Section of Hydrolic Engineering. Faculty of Civil

Engineering and Geosciences. Delft University of

Technology. Netherland.

Koutandos, E.V. and Prinos, P.E., 2011. Hydrodynamic

characteristics of semi-immersed breakwater with an

attached porous plate. Ocean. Engineering 38, pp. 34-

48.

Lee, C.P. and Ker, W.K., 1997. Interaction of waves and a

porous tension leg platform with an impermeable top

layer. Proceedings Seventh International Offshore and

Polar Engineering Conference, Honolulu, USA, pp.

207-214.

Morey, Bradley J., 1998. Floating Breakwaters Predicting

Their Performance. Thesis. Faculty of Engineering and

Applied Science, Memorial University of

Newfoundland, Canada

Ruol, P., Martinelli, L., and Pezutto, P., (2012).

Experimental and Numerical Investigation of the Effect

of Mooring Stiffness on the Behaviour of π-Type

Floating Breakwaters. Proceedings of The Twenty-

second International Offshore and Polar Engineering

Conference. Greece : 17-22 June.

Shih, Ruey-Syan, 2012. Experimental study on the

performance characteristics of porous perpendicular

pipe breakwaters. Ocean Engineering 50, pp. 53-62.

Stainissie, M. and Drimer, N., 2003. On a freely floating

porous box in shallow water waves. Applied Ocean

Research 25, pp. 263-268.

The American Bereau of Shipping , 1998. Abs Rules for

Building and Classing Mobile Offshore Drilling Units

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

216

and The 1989 Imo Modu Code. United State Coase

guarrd Alternate Compliant Program.

Wang, K.H. and Ren, X., 1993. Water waves on flexible

and porous breakwaters. Journal of Engineering

Mechanics, ASCE 119, pp.1025-1047

Wang, H.Y. and Sun, Z.C., 2010. Experimental study on

the influence of geometrical configuration of porous

floating breakwater on performance. Journal of Marine

Science and Technology. 18 (4), pp. 574-579.

Williams, A.N. and Li, W., 1998. Wave interaction with a

semi-porous cylindrical breakwater mounted on a

storage tank. Ocean Engineering 25, pp.195-219

Williams, A.N, Li, W and Wang, K.H., 2000. Wang Water

wave interaction with a floating porous Cylinder.

Ocean Engineering 27, pp. 1-28

Zhao, F., Bao,W., Kinoshita,T. and Itakura, H., 2010.

Interaction of waves and a porous cylinder with an

inner horizontal porous plate. Applied Ocean Research,

vol. 32, pp. 252-259

Zheng, Y.N., Liu, X.M., Chen, C.P., Jiang, Y.P. and Zhang,

C.W., 2018. Experimental study on the wave

dissipation performance and mooring force of porous

floating breakwater. International Conference on Civil

and Hydraulic Engineering (IConCHE), IOP Conf.

Series: Earth and Environmental Science 189, 022058

Dynamic Behavior Analysis of Porous Saw Floating Breakwater under Regular Waves

217