Analysis Number Sense of Students in Different Level

using Decision Theory

Tulus

, R. I. Marpaung

and T. J. Marpaung

Department of Mathematics, Universitas Sumatera Utara, Medan, Indonesia

Department of Mathematics, Universitas Negeri Medan, Medan, Indonesia

Keywords: Number Sense

Abstract: In mathematics learning, numbers are often regarded as objects without meaning. When looking at numbers,

students often direct their thoughts directly to calculation operations. Students will immediately decide to

carry out the calculation process using opaque paper or calculators. In fact, the calculation process is a

diverse art, where students can develop their sensitivity to the calculation process in different ways. This

research aims to describe the number sense of fifth grade, sixth grade elementary school students and

seventh grade of junior high school in Noble School Medan. From this research we can take the conclusion

using decision theory, where the students’ number sense obtained is still low. A deeper assessment must be

made of the results of this test, so that students' number sense is expected to increase and students are more

creative in the process of learning mathematics.

1 INTRODUCTION

Mathematics is consist of facts, there are different

level of facts that will be more difficult when the

students go to the next level of class. Memorizing

the facts still possible for the students even they are

not fluent with the facts. However, teachers have to

know how to measure the students’ fluency ability in

mathematics facts. Susan Jo Russell there are three

criteria of fluency:

1. Efficiency

Efficiency means students must find the answer

quickly.

2. Accuracy

Not just finding the answer quickly, students

also must find the correct answer.

3. Flexibility

When the students cannot find the answer,

students must find another way or another

approach to find the answer

(Mohamed and

Johnny (2010)

Then, after knowing the meaning of “FLUENT”

in mathematics facts, students must be efficient,

accurate and flexible to solve the mathematics

problem.

Researcher found, in Noble School grade three,

there are some students memorizing the facts of

mathematics problem, she/he memorized the

calculation operation that they needed for solving

the problems, but they just can do it in short time,

because they memorized it. Researcher saw in the

class, students need to be flexible to find another

way to solve the problems, students should

RECALL their previous mathematics facts to solve

it. Students must fluent to use all mathematics facts

to solve the problems.

As an example 5 + 6 equal to 11. Most of the

students is great in that case, but they did not realize,

it was same with 6 + 6 then subtract 1. They also did

not realize it same wit 5 + 5 then add 1. Students just

know 5 + 6 equal to 11, without realized there are

many ways to find it. Students thought they already

good in mathematics, but then the researcher gave

them two digits addition, all they can do is

algorithm. They added those two numbers using line

up way. The researcher gave 35 + 26, then students

did not have another way, just line it up. They also

confused when the researcher gave the word

problems. Students is good in algorithm, but they

had weak number sense. That is also the reason, why

mostly students hated word problems, because

counting using algorithm is the students’ favorite to

do in Mathematics Class.

Tulus, ., Marpaung, R. and Marpaung, T.

Analysis Number Sense of Students in Different Level using Decision Theory.

DOI: 10.5220/0010163100002775

In Proceedings of the 1st International MIPAnet Conference on Science and Mathematics (IMC-SciMath 2019), pages 297-301

ISBN: 978-989-758-556-2

297

Those students who had good number sense, they

had good sensitivity or intuition about numbers and

operations. Those students who had good number

sense, they will fluent in mathematics facts. They

can use their sense to approach and make plans for

the next step to solve the problems. Number sense is

an important skills that all students should be

mastered to solve mathematics problems, including

the numerical problems in their daily life (

Maab et al.

(2018).

Number sense is an ability that students must be

mastered since they started school, because all

students have learnt mathematics since they were

kindergarten, the researcher want to see the students

grade five, six and seven number sense ability. The

researcher chose grade five, six and seven, because

they have learnt mathematics at least 4 years, so they

should be mastered number sense. That is the

objective of this research to describe the number

sense of fifth grade, sixth grade elementary school

students and seventh grade of Junior High School in

Noble School Medan.

2 BACKGROUND OF THE

STUDY

There are many students did not like mathematics,

because for them mathematics is a special lesson for

smart kids. There are some students who get extra

lesson outside school, they would be more confident

because they can count faster. How to make all

students who did not get tuition to have same ability

with all the students who get tuition, which was the

first question that the researcher want to solve ?

Those ability, count faster than other students that is

an ability that we can say as number sense.

Number sense is an ability for the kids to be

flexible to solve the problems. Basically, number

sense is consisted of two words, number and sense.

All people, every time we heard the word of number,

we’ll remember 1, 2, 3, … . But, actually those

numbers can be deeper than just a number. Joseph

Marie de Maistre said a crying can be a song

because of number, noise can be a rhythm because

of number, the spring can transformed to a dance,

then force can be dynamic and outlines figures

(Chapra and Steven, 2004.

Number is more than a number, then sense is a

feeling. So, the students can feel the number, they

can be friendly with those numbers. They can be

fluent to “communicate” with numbers, they can be

flexible to be with those numbers, integers,

fractions, decimals or any kind of numbers, they can

be flexible.

Students will always face mathematics problems

in their daily life. Those problems can be solved

with their number sense, as example if they went

grocery, then they wanted make sure whether their

money enough or not, then they can estimated.

Estimation as one of the number sense part. Then,

the students will not be fooled when they want to

buy or sell anything. If the students can

“communicate” with the numbers, they can solve

this problem.

Besides that, mental computation becomes a

favorite way to count faster. Mental computation

growing as one of flexible way, with flexible rules

and flexible steps to solve. Mental computation as

one part of number sense, as a way to

“communicate” with the numbers.

Number sense has not known widely, especially

in Indonesia. There are many teachers, who still

teach algorithm to students, they did not teach them

the flexibility for solving the problems. Number

sense can be taught as a hierarchical way, when the

students knew 5 + 5 equal to 10, teacher can used

that basic to explain 6 + 6, 7 + 7, 6 + 7, … . 5 + 5

will be drawn like below.

So, there are 5 blue coins and 5 red coins, will

make 10 coins altogether. It means 5 + 5 equal to 10

will be the students basic knowledge, then, when the

teacher asked them 6 + 6, it means the students will

add 1 blue coin and 1 red coin, just same with 10

coins that the students already had before add with

2 new coins equal to 12 coins. For 6 + 7, the

students just add 1 more red coin, it means 12 coins

that they had before add with 1 more new coin, it

will be 13 coins.

Students will know how to RECALL their basic

knowledge as a basic information to build their new

knowledge. Students will learn how to be flexible

with numbers and will improve the students’ number

sense. Here, can be seen how to taught number

sense, should be started from lower classes. The

students must improve their number sense, using

recall their basic knowledge and hierarchically

improve to the next knowledge. Number sense, will

be like coastline, when the students know how to be

IMC-SciMath 2019 - The International MIPAnet Conference on Science and Mathematics (IMC-SciMath)

298

flexible with the numbers, they will have deeper

understanding to solve their problems.

There are some research that conducted before

this research by other researchers about number

sense. The research that conducted by Mohini

Mohamed and Jacinta Johnny in 32 Primary Four

students in Malaysia, showed that students rarely

face problem with algorithms, then many students

still have low ability in number sense. Besides that,

there is other research conducted by Rahmah Johar

and Arhamni about the number sense ability of the

teachers in Aceh, then the result of the teachers’

number sense still low.

These all were the reasons, why the researcher

interested to conduct the research in the school,

where one of the researcher teach. The researcher

conducted the research for grade five to seven,

because at least they had learnt mathematics for four

years. The researcher want to know the students’

number sense ability.



3 METHODS

This research conducted in 3 different levels, grade

5, grade 6 and grade 7. The researcher chose ten

students randomly from each level. The researcher

chose 3 students who got Mathematics score more

than 90 in their progress report, 4 students who got

Mathematics score between 65 to 70, and 3 students

who got Mathematics score lower than 60.

Then, the researcher used decision theory for

choosing the materials, then after doing interview,

the students 90% said that fractions and decimals,

especially the word problems are the most difficult

materials. From the interviewed, according to

decision theory, using all of the information, then

which materials were told frequently, will be chosen

for being the materials (Fosnot and Dolk (2001).

Then, the researcher made 5 questions,

Note :

Without doing any counting operations, addition,

subtraction, multiplication and division, answer

these questions and give the reason.

1. How many decimals numbers between 3.

56 and 3. 57?

2. Which one is greater,

3. Which one is greater

4. Put the point in the right position for the

result of 217. 5  0. 485 = 1 0 5 4 8 7 5 .

5. Does



greater or less than 0. 5?

All of the answers collected and analyzed in

descriptive way became :

CNS, means correct and using number sense.

C-NS/C-R, means correct and did not use number

sense or without reason.

F+R, means false with reason.

F-R, means false without reason.

4 ANALYSIS AND DISCUSSION

4.1 Disease Free Equilibrium Point

After the researcher did the research, there are some

result that the researcher got. For the first question,

“How many decimals numbers between 3. 56 and 3.

57?”

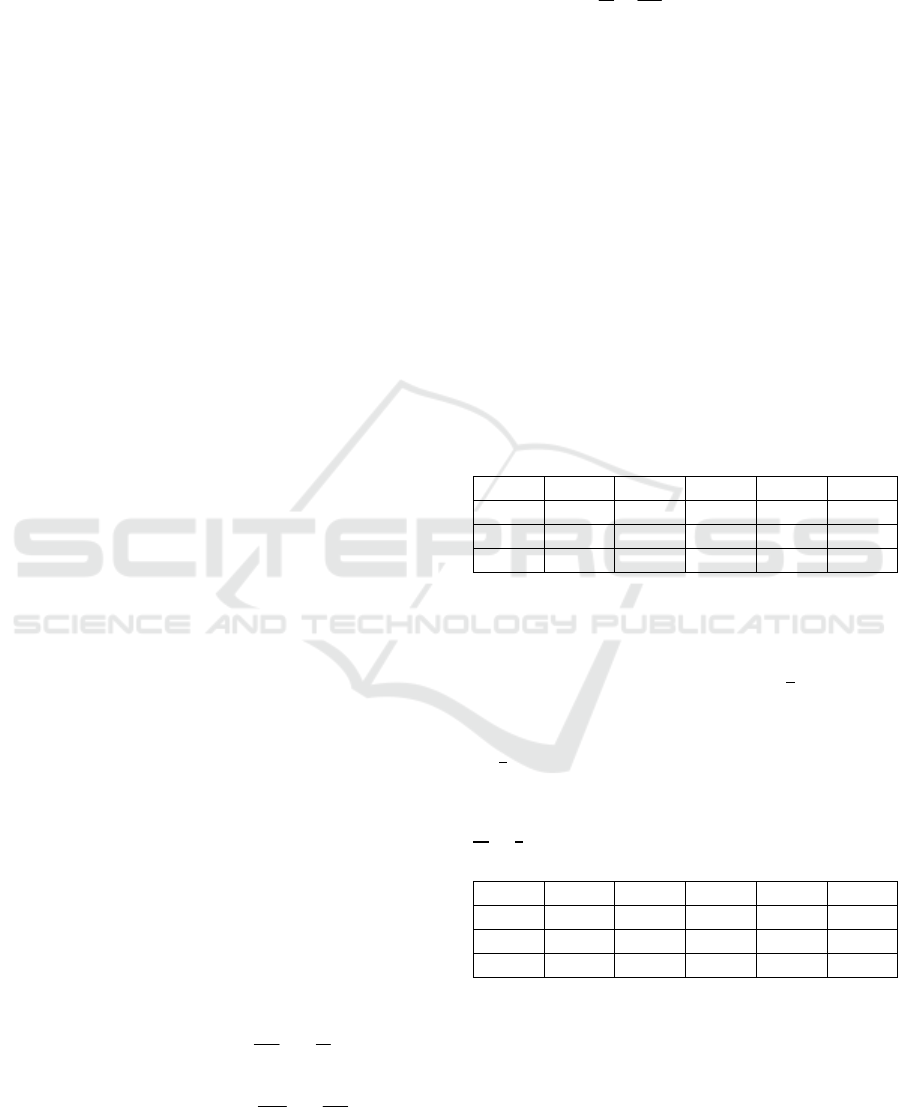
Grade CNS C-NS C-R F+R F-R

0% 0% 0% 55% 45%

2% 0% 0% 35% 63%

2% 0% 0% 45% 53%

From the result above, it can be seen so clear,

number sense of the students still so low. The

percentage of the students who can answered correct

using number sense there are just 1





% from the

total number of students. There are 0% from grade 5,

2% from grade 6 and 2% from grade 7. There are





% who still wrong for answering the first

question.

For the second question, “Which one is greater,









?”

Grade CNS C-NS C-R F+R F-R

5th 30% 50% 20% 0% 0%

6th 45% 50% 5% 0% 0%

7th 60% 35% 5% 0% 0%

From the result above, it can be seen that all students

from grade fifth to grade seventh can answer the

question correctly, none of them wrong, but, when

the researcher separate their answer according to the

way they answered it, the researcher can see that the

percentage of the students who used number sense

for solving the problems, there are 40% from grade

Analysis Number Sense of Students in Different Level using Decision Theory

299

fifth, 45% from grade sixth and 60% from grade

seventh. The conclusion, there are 45% of the whole

students, who used number sense as their way to

solve the problem and 55% of the whole students

who answered correctly without using number sense

and none of them are wrong.

For the third question, “Which one is greater









?”

Grade CNS C-NS C-R F+R F-R

5th 30% 50% 0% 0% 20%

6th 40% 45% 0% 0% 15%

7th 55% 35% 0% 0% 10%

From the result above, there was happened a little bit

different. There are some students who answered it

wrong. There are, 20% students who answered it

wrong and without reason in grade fifth, 15% in

grade sixth and 10% in grade seventh, the

conclusion there are 15% students who answered it

wrong. There are 30% students who answered it

correctly using number sense in grade fifth, 40 % in

grade sixth and 55% in grade seventh. The

conclusion, there are 41





% who answered it

correctly using number sense and 43





% who

answered it correctly without using number sense.

For the fourth question, “Put the point in the right

position for the result of 115. 4  0. 325=37505.”

Grade CNS C-NS C-R F+R F-R

5th 0% 57% 0% 43% 0%

6th 0% 79% 0% 21% 0%

7th 0% 100% 0% 0% 0%

From the result above, there were none students who

were answered it correctly using number sense, but

there are 78





% who answered correctly without

number sense. The students who answered it wrong

are 21





%. The conclusion, there are 100% students

who cannot answer the question using number sense.

For the fifth question, “Does











greater or less

than 0. 5?”

Grade CNS C-NS C-R F+R F-R

5th 0% 57% 0% 43% 0%

6th 0% 79% 0% 21% 0%

7th 0% 100% 0% 0% 0%

From the result, it was seen that the percentage was

same with the fourth condition. There was none

students who answered the question correctly using

number sense, they answered it correctly without

number sense, they used the algorithm there are





% students who answered it correctly and the

rest answered it wrongly, 21





%. The conclusion,

there are 100% students who cannot answered the

question correctly using number sense.

After the researcher look at all of the answers of

all students, the researcher took the conclusion, that

there are many students who still weak in number

sense. They used algorithm for solving the problems,

while actually they can used their number sense and

solve the problems without counting much on the

scrape paper. Students wasted their time for

counting, while they can use their number sense.

According to decision theory, the materials that

the researcher took were, fraction and decimals, the

researcher can took the conclusion that, the number

sense ability of the students in grade five, six and

seven in Noble School still low.

5 CONCLUSIONS

From the research, generally the students are weak

about the concepts of number and the operations,

they still weak in understanding the relationship

between the number and the operations. Besides, the

students had focus to get high score, then they did

many similar questions, until they can memorize the

algorithm, without understanding about the

algorithm and just do it because it is became

routinely.

Based on table 1, from the first question, it can

be seen that the percentage of the students there are





% who wrong and the students who can

answered correct using number sense there are just





% from the total number of students.

Based on table 2, from the second question, it

can be seen there are 45% students, who used

number sense as their way to solve the problem.

Then, based on table 3 there are 41





% who

answered it correctly using number sense. Based on

table 4 and 5 there are 100% students who cannot

answer the question using number sense.

Based on the research, it can be seen that the

students still have low understanding about fraction

and decimal, specially using number sense, then in

the future the researcher hope the students can

IMC-SciMath 2019 - The International MIPAnet Conference on Science and Mathematics (IMC-SciMath)

300

improve their understanding in fraction and decimal

using number sense.

REFERENCES

Chapra, Steven C. 2004. Applied Numerical Methods with

MATLAB for Engineers and Scientists. Medford: The

McGraw-Hill Companies.

Fosnot, C. T., Dolk, M. 2001. Young Mathematicians At

Work Constructing Number Sense, Addition, And

Subtraction. Portsmouth: Heinemann.

Maab, J., O’ Meara, N., Johnson, P., O’ Donoghue, J.

2018. Mathematical Modelling for Teachers A

Practical Guide to Applicable Mathematics Education.

Switzerland : Springer Texts in Education.

Mohamed, M., Johnny, J. 2010. Investigating Number

Sense Among Students. Procedia Social and

Behavioral Sciences 8 (2010) 317–324.

Tondevold, C. 2015. 4 Relationships That Will Increase

Your Students’ Number Sense. Orofino:

Mathematically Minded LLC.

Analysis Number Sense of Students in Different Level using Decision Theory

301