An Overview Graphs Theory and Its Application in Various Scientific

Field

Zahedi

, Suparni

, Yenni Suzana

and Fachrur Razi

Department of Mathematics, Universitas Sumatera Utara, Medan, Indonesia

State Institute for Islamic Studies Padangsidimpuan, Timbangan, Indonesia

State Institute for Islamic Studies Langsa, Langsa, Indonesia

Keywords: Graph Theory, Scheduling, Switching Theory, Physics, Graph Chemistry.

Abstract: As part of mathematics, the use of graphic theory at the present time in various other scientific fields such as

chemistry, physics, engineering and social science, is very widespread. This paper is trying to reveal some

of the uses of graph theory in several fields of science. It is realized that at this time, graph theory has

become one of the topics that attract attention because the models contained in graph theory can be applied

to problems such as transportation, electrical circuit networks, computer science, and many other fields.

Briefly stated that the graph is a representation of a picture of a system that uses two basic elements, namely

points and edges. A point represents a circle and an edge is represented by a line connecting two points.

This paper highlights various views on the application of graphs in the fields of chemistry and physics,

research operations and some general descriptions are presented.

1 INTRODUCTION

As one of the branches of science that is quite old,

graph theory has many applications in various fields

of science. Graph is useful for representing objects

and relationships contained in these objects. Visual

representation of a graph is to declare an object as a

point, circle or dot and the relationship that occurs

between these points is described as a line. An easy

example that can be found in everyday life is a map

of the highway network in a city. As a graph, cities

on the map are expressed by points while lines

connecting the points are edges. In this paper, we

review the notions of graph theory and its use in

several fields by referring to some of the materials

mentioned in the references.

2 GRAPH THEORY

Diagrams that consist of a set of points and lines

connecting certain pairs of points are widely used in

real-world situations. The focus here is about the

two points connected by one line, the way the two

points are connected is not important. It is this

mathematical abstraction that gave rise to the

concept of graphics.

Graph G is sequential triple [V(G), E(G), ∅



]

consisting of non-empty vertices V(G), set E(G),

disjoint from V(G), edges, and ∅



functions events

related to each edge G of the unordered pair of

vertices (not necessarily different) from G. If 𝑒 is the

edge and 𝑢 and 𝑣 are vertices such that PG(e) = 𝑢𝑣,

then 𝑒 is said to join 𝑢 and 𝑣; vertices 𝑢 and 𝑣 are

called ends 𝑒. The following are two examples of

graphs that serve to clarify the situation.

Example 1,

𝐺𝑉



𝐺



,𝐸



𝐺



,∅



, where 𝑉



𝐺





𝑣



,𝑣



,𝑣



,𝑣



,𝑣



 and 𝐸



𝐺





𝑒



,𝑒



,𝑒



,𝑒



,𝑒



,𝑒



,𝑒



,𝑒



, and ∅



defined by

∅





𝑒





𝑣



𝑣



, ∅





𝑒





𝑣



𝑣



, ∅





𝑒





𝑣



𝑣



, ∅





𝑒





𝑣



𝑣



∅





𝑒





𝑣



𝑣



, ∅





𝑒





𝑣



𝑣



, ∅





𝑒





𝑣



𝑣



, ∅





𝑒





𝑣



𝑣



Example 2,

𝐻𝑉



𝐻



,𝐸



𝐻



,∅



, where 𝑉



𝐻





𝑢,𝑣,𝑤,𝑥,𝑦, and 𝐸



𝐻



 𝑎,𝑏,𝑐,𝑑,𝑒,𝑓,𝑔,ℎ, and

∅



defined by

∅





𝑎



𝑢𝑣, ∅





𝑏



𝑢𝑢, ∅





𝑐



𝑣𝑤, ∅





𝑑



𝑤𝑥

∅





𝑒



𝑣𝑥, ∅





𝑓



𝑤𝑥, ∅





𝑔



𝑢𝑥, ∅





ℎ



𝑥𝑦

326

Zahedi, ., Suparni, ., Suzana, Y. and Razi, F.

An Overview Graphs Theory and Its Application in Various Scientiﬁc Field.

DOI: 10.5220/0010181200002775

In Proceedings of the 1st International MIPAnet Conference on Science and Mathematics (IMC-SciMath 2019), pages 326-330

ISBN: 978-989-758-556-2

Figure 1: Diagrams of graphs G and H.

Graphs represented graphically help to

understand the properties of the graphs. Each vertex

is represented by a point, and each edge by a line

connecting the points represent the edges. In Figure

1, diagrams G and H are shown in Figure 1. Another

G diagram, is given in Figure 2. The graph diagram

illustrates the relationship between the vertices and

their edges. Note that the two sides in the diagram of

the graph can intersect at points that are not vertices

(for example 𝑒



and 𝑒



of graph G in figure 1).

Figure 2: Another diagrams of G.

Graphs that have diagrams whose edges only

intersect at the edges are called planar, because such

graphs can be represented in simple fields. The

graphic image (3.i) is planar, and the graphic image

(3.ii), on the other hand, is nonplanar. Most of the

definitions and concepts in graph theory are given

by graphical representations. The edges are called

incident with edges, and vice versa. Two vertices

that are adjacent to the same edge are adjacent, as

are the two edges that intersect the common node.

Edges with identical ends are called loops, and edges

with different ends are links. For example, the 𝑒



edge of G (figure 2) is a loop; all other G edges are

links.

Figure 3: Planar and nonplanar graphs.

The graph is limited if the set of vertices and set of

edges is also limited. A graph is called simple if it

does not have a loop and no two links join the same

node pair. Graphic figure 1 is not simple, while the

graphic in figure 3 is simple.

2.1 Graphs in Chemistry and Physics

Graph Theory in Chemistry Graphs are used in

chemistry to model chemical compounds and their

structures. In computational biochemistry, the same

sequence of cell samples must be issued to resolve

conflicts between two sequences. This is modeled in

a graphical form where vertices represent sequences

in the sample. An edge will be drawn between two

vertices if and only if there is a conflict between the

corresponding order. The goal is to remove the

possibility of a node to eliminate all conflicts.

In physics, graphs are used in condensed matter

physics. Usually describes solid state and molecular

systems as a strict binding model. Graph theory is

also widely used in the field of statistical physics.

Statistical physics in the branch of science that deals

with methods of using probability and statistical

theories, and especially mathematical tools for

dealing with large populations and forecasts, in

solving physical problems. The main areas of

statistical physics that use graph theory are statistical

mechanics, particle physics, and statistical analysis

problems and thermodynamic results.

2.2 Graphs in Switching Theory

Ehrenfest (1910), presented a paper on switching

theory where he stated that Boolean algebra could be

applied to automatic telephone exchange. Next

Shannon (1938) introduced a mathematical

formulation of contact network behavior (a

particular type of switching network). Since then,

switching theory has developed very rapidly.

Initially, this was intended for engineers of

communication tools to analyze and synthesize large

scale relay switching networks, such as telephone

exchanges. And, in recent years, the rapid growth of

switching theory was motivated because of its use in

digital computer design. Unlike a signal in a

classical network (say, in a radio receiver), a

switching network signal has only two values -

defined as 0 and 1. A switching network is designed

to process and store the binary signal.

Switching networks can be classified as

combinational networks and / or sequential

networks. Combinational switching networks are

networks that output at a certain time only depend

An Overview Graphs Theory and Its Application in Various Scientiﬁc Field

327

on the input at that time. Sequential switching

networks, on the other hand, are those that output at

a particular time are a function of the inputs at that

time and during the entire past history. In other

words, sequential networks have memory, whereas

combinational networks do not. All digital systems,

are built from these two basic types of circuits -

combinations and sequences.

Combinational switching networks can then be

classified as (1) contact networks, or (2) gateway

networks. Here we limit ourselves to the contact

network only.

2.2.1

Contact Networks

Relay contacts (or contacts, for short) can be likened

to ordinary household switches that are used to

control light. This is a two-terminal device that has

two statuses; in the open state where there is no

conductive path between the terminals; and in a

closed state where there is a path that will allow

electric current to flow in both directions. So contact

is a bilateral device. Usually, a contact is represented

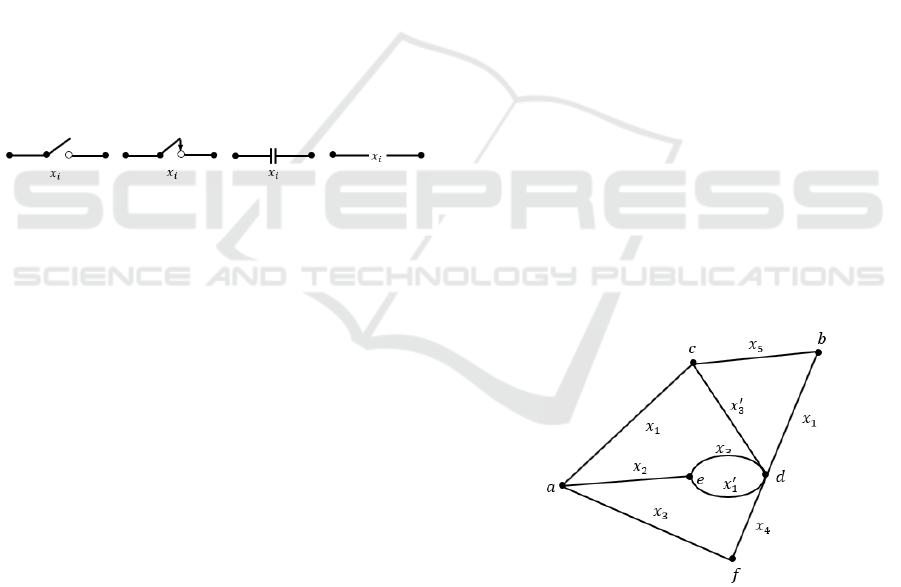
by one of the symbols shown in Figure 4 below.

Figure 4: Symbol used to represent a switch or contact.

Contact networks are interconnected networks

where each contact network can be represented by a

graph, where the ends are contacts and the node is

the terminal. For the purpose of writing, a definition

of contact network is given, namely: the contact

network is a directed, connected graph (without its

own loop) where each side has a binary variable 𝑥



associated with it, which can be assumed to have

only two values, 1 or 0 The binary variable 𝑥



specified for a contact is 1 when the contact is

closed and 0 when the contact is open.

The input-ouput behavior of the contact network

is usually expressed in terms of functions,

𝑓



𝑥



,𝑥



,…,𝑥



,

from binary variables. The 𝑓



function is called the

switching function (or Boolean) and is assumed to

have a value of 0 or 1, and where the Boolean

algebra consists of a limited set of 𝑥



,𝑥



,…,𝑥



and

two binary + operations (called Boolean addition)

and . (called Boolean duplication) that meets the

following postulates:

1. Either 𝑥



1 or 𝑥



0

2. For each 𝑥



there is another variable 𝑥





, called

the complementary 𝑥



, so that if 𝑥



0, 𝑥





1,

and if 𝑥



1, 𝑥





0.

3. (a). Sum 𝑥



𝑥





0, 𝑖𝑓 𝑥



𝑥



0,

1, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒

(b). Product 𝑥



𝑥





1, 𝑖𝑓 𝑥



𝑥



1,

0, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒

with this postulate a number of results can be

derived, which is useful in simplifying the

expression of switching. For example, it can be

easily shown that 𝑥



𝑥



𝑥



𝑥



In the contact network, two types of problems

will be found, namely the problem of analysis and

synthesis. Here we will discuss only the problem of

analysis only, where in the analysis given the G

contact network and how to find conditions where

there is an electrical conduction path between a pair

of vertices (𝑣



,𝑣



) in G.

Consider two nodes in the G contact network,

because G is connected, there is one or more paths

between these two nodes. Each path can be

identified by a Boolean product from variables

related to edges in the path. For example, in figure 5,

eight different paths between vertices 𝑎 and 𝑏 are

(𝑥



𝑥



,



𝑥



𝑥





𝑥







𝑥



𝑥



𝑥







𝑥



𝑥



𝑥





𝑥





(𝑥



𝑥





𝑥



,



𝑥



𝑥





𝑥





𝑥







𝑥



𝑥



𝑥







𝑥



𝑥



𝑥





𝑥





(*)

each of these products is called the path product

between nodes 𝑎 and 𝑏 in the contact network of G.

Obviously, the value of the path product is 1 if and

only if each variable in the path product has a value

of 1; if not, it is 0. The value 1 of the product line

implies the existence of an electric conduction path

between 𝑎 and 𝑏 through the appropriate contacts in

the network.

Figure 5: Contact network with six vertices and nine

contacts.

For electrical conduction between two vertices, it

is necessary and sufficient that at least one of the

path products be 1. In other words, the Boolean

number of path products between certain node pairs

(𝑣



,𝑣



) is 1 if and only if terminals 𝑣



and 𝑣



are

electrically connected in the contact network.

Therefore, the number of Boolean line products is

IMC-SciMath 2019 - The International MIPAnet Conference on Science and Mathematics (IMC-SciMath)

328

referred to as the contact network transmission

between two nodes that are determined. For

example, the transmission between vertices 𝑎 and 𝑏

in Figure 5 is

𝐹



𝑥



𝑥



𝑥



𝑥





𝑥



𝑥



𝑥



𝑥



𝑥



𝑥





𝑥





𝑥



𝑥



𝑥





𝑥



𝑥



𝑥





𝑥





𝑥



𝑥



𝑥



𝑥



𝑥



𝑥



𝑥





𝑥



Finding the transmission between the nodes

specified in the given contact network consists of

counting all the paths between the two nodes, and

finding the Boolean number of product lines.

Furthermore, the possibility of simplification based

on Boolean algebraic postulates was also carried out.

For example, in the product lines listed in (*), the

following identities are clear:

𝑥



𝑥





𝑥



𝑥



𝑥





𝑥



𝑥





𝑥





𝑥



0,

𝑥



𝑥





𝑥



0,

and

𝑥



𝑥



𝑥





𝑥



0.

Therefore, the switching function between

vertices 𝑎 and 𝑏 in Figure 5 is

𝐹



𝑥



𝑥



𝑥



𝑥





𝑥



𝑥



𝑥



𝑥





𝑥



𝑥





𝑥



𝑥



𝑥



𝑥



Obviously, 𝐹



provides all different conditions

where there is a conductive path between 𝑎 and 𝑏.

2.3 Graphs in Operation

Research - Activity Networks in

Project Planning

One of the most popular network applications in

operations research is the planning and scheduling of

complex projects. A project is divided into many

jobs called activities. Due to technical limitations,

work must be completed before the others start, each

activity also requires the duration or time of the

activity. Several lists of activities in a project,

including a list of direct prerequisites, and duration,

a weighted digraph can be made to describe the

project, as follows: each edge represents the activity,

and the weight represents the duration of the

activity, while the node represents the beginning and

end of the activity. Activity 𝑖,𝑗 cannot start before

all activities 𝑖 have finished. Every event in the

project is a well-defined event in time. Like a

weight, connected graphs describe activities in a

project called the activity network.

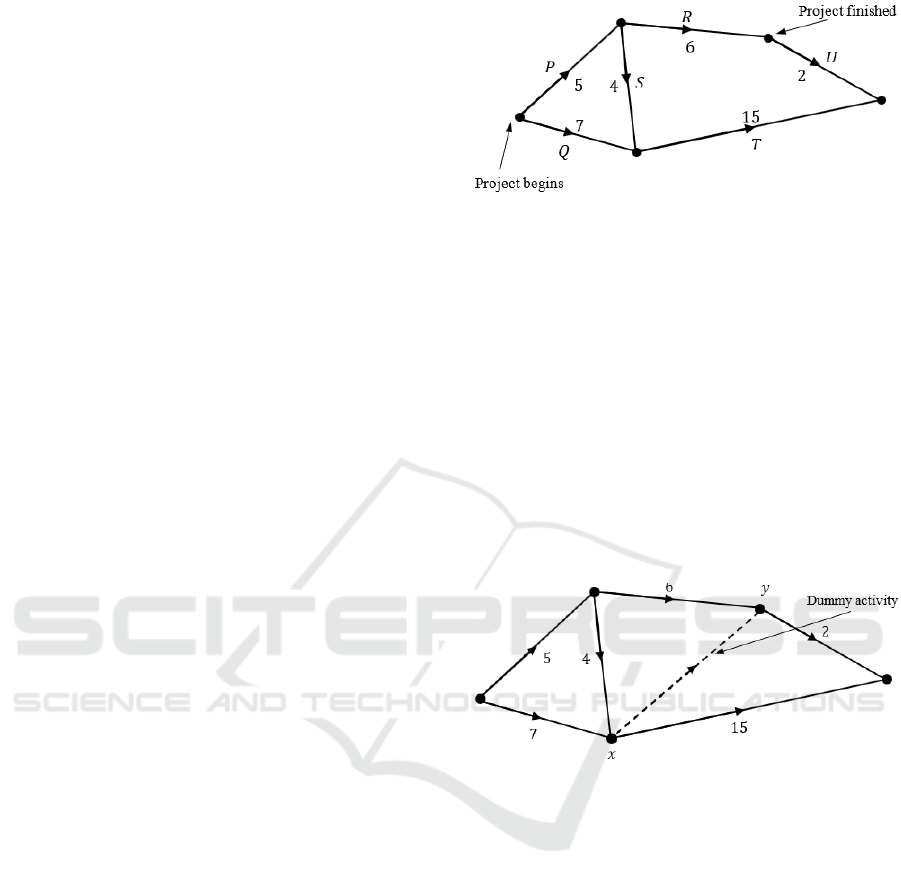
Suppose a project consists of six activities P, Q,

R, S, T, and U, with the limitation that P must

precede R and S; Q and S must precede T; and R

must precede U. The duration for activities P, Q, R,

S, T, and U are 5, 7, 6, 4, 15, and 2 days

respectively. This network of project activities is

shown in Figure 6.

Figure 6: Activity network.

Note that network activity must be acyclic; if

not, then there will be an impossible situation where

no activity on the directed circuit can be started.

Also note that the point indicating where the project

starts must have a zero degree, because there are no

activities that precede this point. Likewise, the point

indicating where the project ends must have zero

degrees, because there are no activities after this.

Dummy Activity; in the network activity

example in Figure 6, suppose there is an additional

limitation that activity U cannot begin before Q and

S are completed. This main relationship can be

described as an edge by connecting point 𝑥 to 𝑦

(Fig. 7). This is what is called a dummy activitiy.

Figure 7: Dummy activity in a network.

Dummy activities are important when there are

not enough activities to describe all the relationships

that are prioritized accurately. All puppet activity

has zero duration and is usually displayed in a dotted

line. Two parallel edges (e.g., activities that have the

same direct predecessor and the same direct

successor) can be replaced by one edge, combining

the two activities into one [Fig. 8 (a)]. However, if

activities must be tracked separately, then dummy

activities and dummy events must be created [Fig. 8

(b)]. And, because there is no self-loop in the

activity network, we only have a simple digraph for

the activity network.

An Overview Graphs Theory and Its Application in Various Scientiﬁc Field

329

Figure 8: Replacement of parallel edges.

A network of activities can be assumed to have

exactly one node with zero in degrees and exactly

one node with zero outside degrees. If there is more

than one node having zero degrees, someone

arbitrarily chooses one of these for the initial event

and draws the puppet activity from this to the other

node. Vertices with zero degrees are handled

equally.

In short, the activity network is a representation

of two aspects of the project: (1) the priority

relationship between activities, and (2) the time

period. These are connected, weighted, simple,

acyclic digraphs with exactly one zero point in

degrees and exactly one zero point outside the

degree.

3 CONCLUSION

In this paper the author has provided a basic

understanding of graph theory. Understanding is

quite easy to understand and provides a description

of several types of graphs. This paper also explains

where different graphs of graph theory can be used

in various fields of science. In other words, an idea

is given about the use of graphic theory terminology

in its use in various fields of science. Furthermore,

one can understand about this terminology and get

other ideas related to their use in the real world.

REFERENCES

Ehrenfest, P. (1910). Review of L. Coutrat, Algebra of

Logic. J. Russ. Phys. Chem. Soc. Phys. Sec., 42(10),

382–387.

Shannon, C. E. (1938). A Symbolic Analysis of Relay and

Switching Circuits. American Institute of Electrical

Engineers Transactions, 57, 713–723.

IMC-SciMath 2019 - The International MIPAnet Conference on Science and Mathematics (IMC-SciMath)

330