Forecasting the Amount of Foreign Tourists of Asean Country Origin

in North Sumatera using Monte Carlo Simulation

Suyanto and Andri Saputra Sk

Department of Mathematics, Faculty of Mathematics and Natural Sciences,

Universitas Sumatera Utara, Medan, Indonesia

Keywords: Forecasting, Monte Carlo Simulation.

Abstract: Forecasting is an important tool in effective and efficient planning to predict future events. The

characteristic of forecasting about future values of a variable for planning or decision making of a situation

to estimate future values. Monte Carlo simulation is a simulation model that includes a random series and

sampling with a probability distribution that can be known and determined, so this simulation can be used.

In this study, data was taken from the amount of foreign tourists from ASEAN member countries who

visited North Sumatra from 2009 to 2018 which indicated a trend data pattern over time. Then, data

processed and analyzed using Monte Carlo Simulation to determine the forecast results for 5 years after that.

As a result the amount of foreign tourists who visited North Sumatra from Malaysia, the Philippines,

Singapore and Thailand as a whole have increased respectively by 2.61%, 1.14%, 3.10% and 5.66%. The

number of foreign tourists who visited North Sumatra origin Brunei, Vietnam and Myanmar as a whole

decreased respectively by 3.56%, 4.90% and 28.11%.

1 INTRODUCTION

Tourism is an important economic sector in

Indonesia. Tourism placed is third in terms of state

foreign exchange earnings after oil and commodities

natural gas and palm oil in 2009. One indicator of

development tourism can be seen from the growth of

foreign tourists, apart from domestic tourist visits

and growth revenue from the trade and hotel sector.

Indonesia is a member of the ASEAN

(Association of Southeast Asian Nations) with

Malaysia, Thailand, Singapore, the Philippines,

Laos, Brunei Darussalam, Vietnam, Cambodia and

Myanmar where ASEAN leaders agreed to form a

single market in the Southeast Asia region at the end

of 2015 termed the ASEAN Economic Community

(AEC). Foreign tourists in this region much needed

to increase foreign exchange reserves in the region

of ASEAN member countries.

One of the provinces frequented by foreign

tourists, especially the country ASEAN is North

Sumatra. In the data of foreign tourists who came to

North Sumatra in

2016 were 233,668 people who experienced

increase 1.91% from 2015 and in 2017 were 270,792

people experienced increase of 15.96% from 2016

([BPS] Badan Pusat Statistik Provinsi Sumatera

Utara, 2019).

In the framework of the development of

international tourism, steps need to be taken steps to

increase the flow of foreign tourists by increasing

marketing needed to be able to predict the flow of

foreign tourists in North Sumatra, with information

quantitative and qualitative information about

tourism in the past in order to improve tourism

promotion in North Sumatra. One forecasting

technique used is by using Monte Carlo Simulation.

Monte Carlo simulation using data which is already

there to estimate important things in the future such

as sales, requests, and so on as an overview of past

data. From the existing model created a model so

that a random number can be generated based on a

model made.

Tüzüntürk et al. in his research on forecasting

drinking water demand using Monte Carlo

simulation, produces estimated values that are close

to the actual data, so that the Monte Carlo

Simulation can predict requests drinking water in the

next 12 months (Tüzüntürk et al., 2015). Research

by Alrabadi and Aljarayesh regarding the

comparison of simple moving average (SMA)

forecasting methods, exponential moving average

340

Suyanto, . and Sk, A.

Forecasting the Amount of Foreign Tourists of Asean Country Origin in North Sumatera using Monte Car lo Simulation.

DOI: 10.5220/0010182200002775

In Proceedings of the 1st International MIPAnet Conference on Science and Mathematics (IMC-SciMath 2019), pages 340-345

ISBN: 978-989-758-556-2

 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

(EMA) and Monte Carlo simulation in forecasting

stocks market returns on Amman shares which

results in the estimated value with Monte Carlo

Simulation is closer to the actual data so that the

Monte Carlo simulation can predict stock market

return (Alrabadi et al., 2015). Research by Sugiharto

regarding the application of Simulation in

forecasting demand and management Top Paint

brand paint produces an estimated volume of each

order and interval the time of arrival of the order for

the next 12 months (Sugiharto, 2007).

2 LITERATURE REVIEW

2.1 Forecasting

Forecasting is an important tool in effective and

efficient planning for predicting future events

(Makridakis et al., 1999). Forecasting has the

following objectives (Heizer & Render, 2011):

1. To review company policies that are in force

today and in the past and see the extent of

influence in the future

2. Forecasting is needed because of the time lag or

delay between when a policyoccurs company

policy is determined by the time of

implementation

3. Forecasting is the basis for preparing a business

in a company so that can increase the

effectiveness of a business plan.

Scientifically, the forecasting method can be

classified in two groups there are qualitative

methods and quantitative methods. Quantitative

methods can be divided into two, there are:

1. Forecasting methods based on the use of the

analysis of the relationship patterns between

variables to be estimated with time variables

(Time Series). The methods included in this type

are Smoothing Methods, Methods Box Jenkins,

Trend Projection Method with Regression and

Monte Carlo Method.

2. Forecasting methods based on the use of the

analysis of the relationship patterns between

variables to be estimated with no time variables

(correlation method or cause and effect).

Forecasting methods included in this type are

Regression and Correlation Methods,

Econometric Methods and Input Output

Methods.

2.2 Monte Carlo Simulation

Simulation is one way to solve various problems in

real life that is full of uncertainty by not using or

using models or certain methods and more emphasis

on using computers to get the solution (Kakiay,

2004). One method that plays a role in computer

simulations is the Monte Carlo method. The Monte

Carlo method is a withdrawal involves a series of

random numbers namely variations of U(0,1), which

are used for solving stochastic or deterministic

problems where the role of time is not requires

substantive rules, so the Monte Carlo method is

generally static rather than dynamic (Law & Kelton,

2000).

The Monte Carlo method illustrates the

possibility of using sample data already exists and

can be known or estimated distribution. With words

it is different if the simulation model includes a

random series and sampling with a probability

distribution that can be known and determined, then

this simulation can be used (Kakiay, 2004). In

operation, Monte Carlo involves a direct election

randomly repeating each other’s output so that a

solution is obtained certain approach. The increasing

number of experiments carried out then the error rate

for the results obtained will be smaller

(Rubiensten,

1981).

2.3 Random Number Generator

In the Monte Carlo technique, artificial data is

generated through random number generator and

cumulative distribution. Random numbers generated

actually not really random, so it is called a random

number generator means that what can actually be

produced is not random and makes has criteria that

must be met, namely:

1. Uniform distribution and does not correlate

between numbers

2. Generating quickly, storage is not large

3. Can be produced repeatedly

4. A large period, because random numbers may be

generated repeatedly.

The random number is symbolized by U, its

value from 0 to 1 which is expressed in U(0,1). The

method for random numbers is usually the Linear

Congruential Generator (LCG), and Multiplicative

Congruential Generator (MCG). LCG and MCG

have formula:

𝑋







𝑎𝑍



𝑐



𝑚𝑜𝑑 𝑚

(1)

𝑋







𝑎𝑍





𝑚𝑜𝑑 𝑚 (2)

with:

𝑋



 random number 𝑛-series

Forecasting the Amount of Foreign Tourists of Asean Country Origin in North Sumatera using Monte Carlo Simulation

341

𝑋



 previous random number

𝑎  multiplier factor

𝑐  constant number

𝑚  modulo number

From the LCG and MCG formulas a random

number (U

) is desired (for 𝑖  1,2,3, …) in [0,1],

then the formula is (Law & Kelton, 2000):

𝑈





𝑍



𝑚

(3)

2.4 Generate Random Variate

In generating random numbers through a computer is

very dependent on function or distribution of the

data being investigated. Then from the distribution

functions this can be found or derived random

variate from the distribution function

(Kakiay, 2004).

On this study discussed random distribution of

normal distribution. Algorithm generate random

numbers from the normal distribution, i.e.

1. Generate U

and U

, where U

and U

are

independent random numbers U(0,1)

2. Calculate X

and X

, using the formula:

𝑋







2ln 𝑈



cos2𝜋 𝑈



(4)

𝑋







2ln 𝑈



cos2𝜋 𝑈



(5)

3. Placed X

= µ + X

4. Then X

is random data from N(µ,σ

3 METHODOLOGY

The data used in this study are secondary data,

namely the amount foreign tourists who came to

North Sumatra from ASEAN member countries in

2007-2018 obtained from the Central Statistics

Agency (BPS) of North Sumatra. The calculation is

done by numerical calculations and simulated using

Monte Carlo simulation so that optimal forecasting

results are obtained. As for who carried out with

data that has been collected are as follows:

a Test the normality of data on the number of

foreign tourists from member countries ASEAN

with Liliefors Normal Test.

b Determine the parameters that are useful for

generating random numbers in terms of normal

contribution.

c Perform a simulation of 10 times.

d Test the average similarity of the two related

variables to find out whether there is a difference

between the simulation data and the actual data.

e Perform simulations to determine the results of

forecasting.

f Formulating conclusions.

4 RESULTS AND DISCUSSION

4.1 Data Collection

The data to be analyzed in this study is the number

of foreign tourists from the country ASEAN

members who visited North Sumatra in 2007-2018

were obtained from the Central Statistics Agency of

North Sumatra Province. The data can be seen in

Table 1 follows.

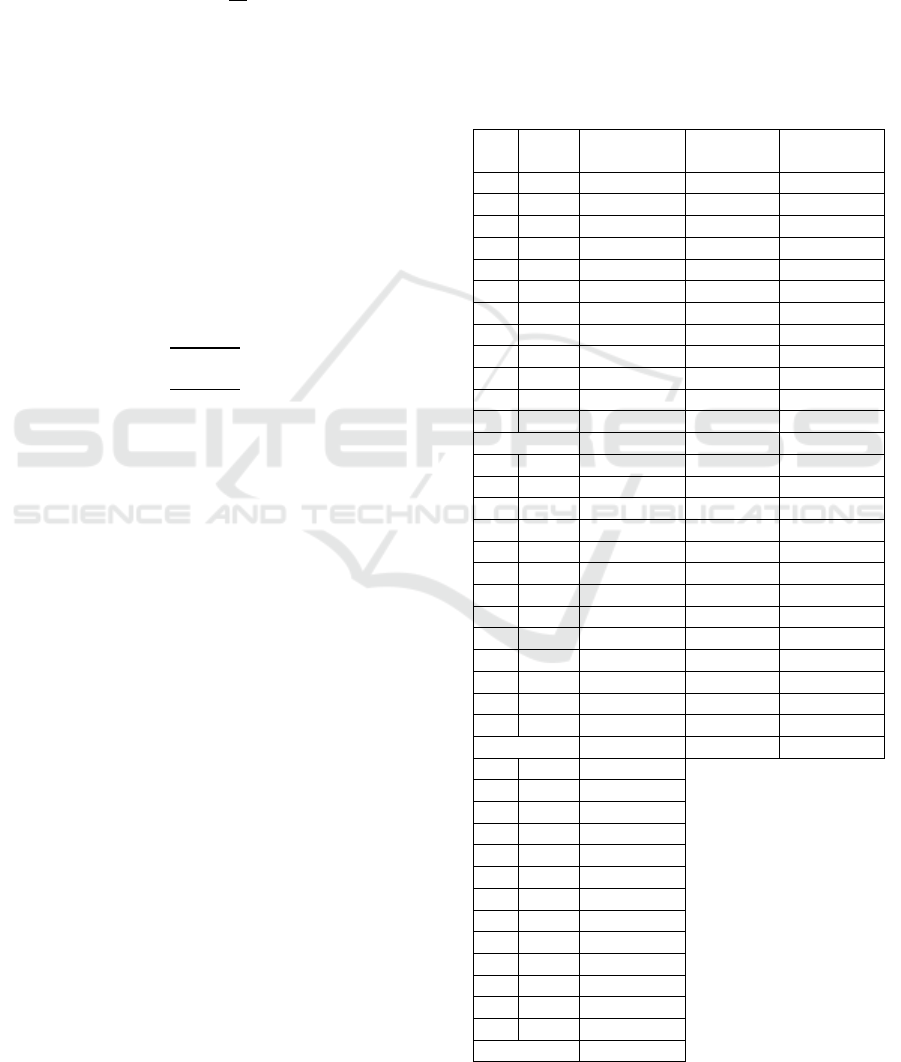
Table 1: Data of Foreign Tourists from ASEAN member

countries in North Sumatra in 2007-2018.

No Year

Brunei

Darussala

Malaysia Philippines

1 2007 133 81.347 899

2 2008 79 84.387 991

3 2009 94 102.685 986

4 2010 79 109.320 970

5 2011 103 132.037 942

6 2012 140 143.644 1.041

7 2013 248 148.465 1.341

8 2014 124 152.389 1.279

9 2015 218 129.203 1.551

10 2016 91 115.007 1.094

11 2017 172 128.761 1.541

12 2018 221 139.878 1.612

Total 1.702 1.467.033 14.247

No Yea

Singapore Thailan

Vietna

1 2007 7.622 988 147

2 2008 9.946 1.460 124

3 2009 10.361 1.677 102

4 2010 11.187 2.686 167

5 2011 11.592 2.180 250

6 2012 13.579 2.757 237

7 2013 18.276 3.906 337

8 2014 18.066 4.844 369

9 2015 12.516 3.087 405

10 2016 14.322 3.027 311

11 2017 17.312 3.688 1.356

12 2018 18.620 3.605 752

Total 1.702 163.399 33.905

No Yea

anma

1 2007 59

2 2008 120

3 2009 149

4 2010 1.014

5 2011 127

6 2012 157

7 2013 158

8 2014 182

9 2015 202

10 2016 147

11 2017 259

12 2018 317

Total 2.891

IMC-SciMath 2019 - The International MIPAnet Conference on Science and Mathematics (IMC-SciMath)

342

Source: Central Statistics Agency of North Sumatra

Province

4.2 Solution using Monte Carlo

Simulation

In doing simulations, the first thing to do is

determine the distribution that become a benchmark

in generating the number of foreign tourists in step

next. Data in the simulation generated depend on the

distribution known for such distribution. The

distribution used in this study is a Normal

distribution. After the distribution is known, the

simulation is carried out as much as you want. In

this study the simulation was carried out 10 times so

that the simulation results are expected to represent

actual data. This simulation works from each

country, as follows:

4.2.1 Data Simulation of Tourists from

Brunei Darussalam, Malaysia,

Philippines and Singapore

In the data of tourists from Brunei Darussalam, the

average (µ) and standard deviation (σ) are 141,8333

and 59,4869. For tourists from Malaysia, the values

µ and σ are 122.252,7500 and 23.859,4190. For

tourists from the Philippines, the values µ and σ are

1.187,2500 dan 264,4817. For tourists from the

Singapore, the values µ and σ are 13.616,5833 and

3.766,2653. First the values of U

and U

are raised

using the RAND function in Microsoft Excel. Then

taken as example to determine the value of X using

the formula (4), i.e:

𝑋 



2ln 𝑈



cos



2𝜋𝑈





 2 ln 0,6327

cos



2𝜋  0,2634



 0,0803.

Then the random number obtained is converted to

the amount of arrivals foreign tourists:

𝑋



𝜇𝜎𝑋

 141,8333  59,4869 



0,0803





 137,0545

 137.

So on up to 10 times the simulation. Table 2

explains the summary simulation data on the number

of foreign tourists from Brunei Darussalam,

Malaysia, the Philippines, and Singapore.

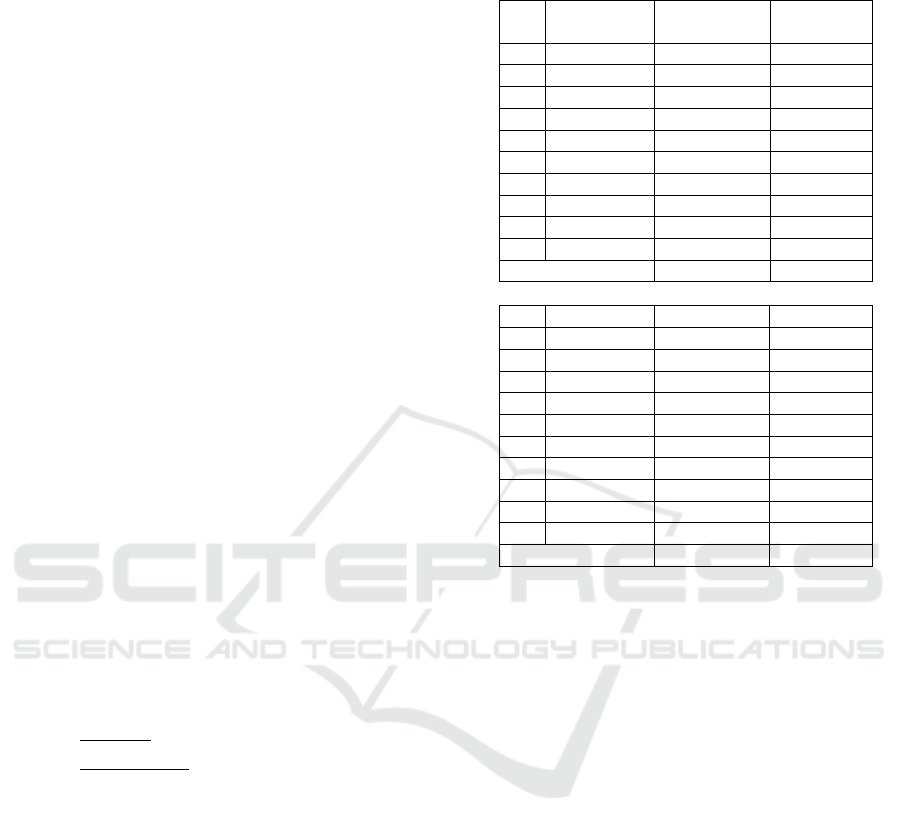
Table 2: Simulation of foreign tourists from Brunei

Darussalam, Malaysia, Philippines and Singapure.

No Simulation

Brunei

Darussala

Malaysia

1 I 1.924 1.455.333

2 II 1.410 1.521.579

3 III 1.645 1.465.864

4 IV 1.285 1.537.491

5 V 1.761 1.457.245

6 VI 1.993 1.691.073

7 VII 1.826 1.405.846

8 VIII 1.747 1.501.732

9 IX 1.806 1.311.412

10 X 1.655 1.540.604

Avera

e 1.705 1.488.818

No Simulation Phili

ines Sin

ore

1 I 16.247 158.282

2 II 13.019 165.122

3 III 15.062 156.121

4 IV 12.655 170.356

5 V 14.998 199.850

6 VI 13.942 164.224

7 VII 15.142 143.236

8 VIII 15.283 164.490

9 IX 14.205 178.277

10 X 12.560 157.354

Avera

e 14.311 165.731

In Table 2, the average of Brunei Darussalam

tourists from the simulation results is equal to 1.705

people, compared to the actual data which is 1.702

people. The average of Malaysian tourists from the

simulation result is equal to 1.488.818 people,

compared to actual data that is equal to 1.467.033

people. The average of Filipinos tourists from the

simulation results is equal to 14.311 people

compared to the actual data which is 14.247 person.

Meanwhile, the average of Singapore tourists from

the simulation results is equal to 165.731 people

compared to the actual data that is equal to 163.399

people.

4.2.2 Data Simulation of Tourists from

Thailand, Vietnam and Myanmar

In the data of tourists from Thailand, the average (µ)

and standar deviation (σ) is 2.825,4167 and

1.116,1298. In the data of tourists from Vietnam, the

values µ and σ are 379,7500 and 353,9571. In the

data of tourists from Myanmar, the values µ and σ

are 240,9167 and 252,3772. Generate U

and U

values using the RAND function on Microsoft

Excel. Then taken as an example to determine the

value of X with using the formula (4), i.e:

Forecasting the Amount of Foreign Tourists of Asean Country Origin in North Sumatera using Monte Carlo Simulation

343

𝑋 



2ln 𝑈



cos



2𝜋𝑈





 2 ln 0,9118

cos



2𝜋  0,2187



 0,0840.

Then the random number obtained is converted to

the amount of arrivals foreign tourists:

𝑋



𝜇𝜎𝑋

 2.825,4167 



1.116,1298  0,0840



 2.919,1861

 2.919.

So on up to 10 times the simulation. Table 3

describes the summary simulation data on the

number of tourists from Thailand, Vietnam and

Myanmar.

Table 3: Simulation of foreign tourists from Thailand,

Vietnam dan Myanmar.

No Simulation

Thailand Vietnam Myanmar

1 I

35.431 4.765 4.149

2 II

37.089 4.958 3.397

3 III

29.186 5.657 3.214

4 IV

26.867 5.045 3.844

5 V

32.284 4.861 5.652

6 VI

32.192 5.595 4.051

7 VII

34.966 4.202 3.173

8 VIII

33.858 4.965 3.375

9 IX

38.344 5.317 2.867

10 X

35.940 4.275 3.569

Average

1.705

33.615 4.964

In Table 3, the average of Thai tourists from

simulation results is 33.615 people compared to the

actual data of 33.905 person. The average of

Vietnamese tourists from simulation results is 4.964

people compared to the actual data of 4,557 people.

Meanwhile, the average of Myanmar tourists from

simulation results is 3.729 people compared to the

actual data of 2.891 people.

4.3 Forecasting Results

The data simulated again to make predictions about

the number of foreign tourists. The data has reached

optimal results because it has been simulated by

using use existing parameters. The following

forecasting results will be displayed Monte Carlo

Simulation of 2019-2023 in Table 4.

Table 4: Forecasting Results the tourists using Monte

Carlo Simulation.

No Year

Brunei

Darussala

Malaysia Philippines

1 2019 163 121.087 1.269

2 2020 180 123.351 1.287

3 2021 195 124.615 1.294

4 2022 171 125.752 1.304

5 2023 200 134.688 1.333

No Yea

Sin

ore Thailan

Vietna

1 2019 14.068 3.303 300

2 2020 14.614 3.375 435

3 2021 15.044 3.524 323

4 2022 15.112 3.558 528

5 2023 15.898 3.800 512

No Yea

anma

1 2019 338

2 2020 340

3 2021 374

4 2022 406

5 2023 416

In Table 4, the amount of foreign tourists who

visited North Sumatra from Malaysia, Philippines,

Singapore and Thailand as a whole have increased

respectively 2,61%, 1,14%, 3,10%, and 5,66%

compared to the number of foreign tourists who

visited from Brunei Darussalam, Vietnam and

Myanmar which as a whole have decreased

respectively 3,56%, 4,90% dan 28,11%.

5 CONCLUSION

5.1 Conclusion

Based on the analysis and discussion that has been

done, conclusions can be taken that the forecast

results of the number of foreign tourists coming to

North Sumatra from ASEAN member countries will

increase in the next five years. The amount of

foreign tourists visiting North Sumatra from

Malaysia, Philippines, Singapore and Thailand as a

whole have increased by 2,61%, 1,14%, 3,10%, and

5,66%. The amount of foreign tourists who visited

North Sumatra from Brunei Darussalam, Vietnam

and Myanmar as a whole have decreased by 3,56%,

4,90% and 28,11%. Therefore the number of foreign

tourists from Thailand is predicted to be more

significant compared to other countries.

IMC-SciMath 2019 - The International MIPAnet Conference on Science and Mathematics (IMC-SciMath)

344

5.2 Next Research

For next research of the same type it is

recommended to do the simulations with other

variables that influence the amount of tourists as

well, and simulate more than 10 times iteration so

that the results obtained can be more accurate.

REFERENCES

[BPS] Badan Pusat Statistik Provinsi Sumatera Utara.

(2019). Statistik Wisatawan Mancanegara Sumatera

Utara.

Alrabadi, Hanna, D. W., & Aljarayesh, N. I. A. (2015).

Forecasting Stock Market Returns Via Monte Carlo

Simulation: The Case of Amman Stock Exchange.

Jordan Journal of Business Administration, 11(3).

Heizer, J., & Render, B. (2011). Operations Management.

Pearson Education Inc.

Kakiay, T. J. (2004). Pengantar Sistem Simulasi. Andi.

Law, A. M., & Kelton, W. D. (2000). Simulation

Modeling and Analysis. McGraw-Hill.

Makridakis, S. G., Wheelwright, S. C., & McGee, V. E.

(1999). Metode dan aplikasi peramalan. Erlangga.

Rubiensten, R. Y. (1981). Simulation and The Monte

Carlo Method. John Wiley and Sons.

Sugiharto, B. (2007). Aplikasi Simulasi untuk Peramalan

Permintaan dan Pengeloaan Persediaan yang bersifat

Probabilistik. Industrial and Systems Engineering

Assessment Journal, 8(2).

Tüzüntürk, S., Sezen, K., & Şenaras, A. E. (2015).

Forecasting Water Demand by using Monte Carlo

Simulation. Akademik BakiŞ Dergisi.

Forecasting the Amount of Foreign Tourists of Asean Country Origin in North Sumatera using Monte Carlo Simulation

345