Analysis of Soil Retaining Wall from Geosynthetic for Sea

Reclamation to Become a New Land in the Beach

Liany Ayu Catherine

, Widi Agoes Pratikto

, Suntoyo

, Johnny Maruli Tua Simatupang

and Vivi Bachtiar

Garduate Student

Departement of Ocean Engineering, Sepuluh Nopember Institute of Technology, Surabaya, Indonesia

Department of Ocean Engineering, Sepuluh Nopember Institute of Technology, Surabaya, Indonesia

Department of Civil Engineering, Tanjungpura University, Pontianak, Indonesia

Keywords: Reclamation, Retaining Wall, Geosynthetic, Geobag.

Abstract: Reclamation is a business to get land that was covered by water into dry land and to be used as useful land in

accordance with its purpose. This reclamation can be carried out on lands that are on the coast, swamps, and

offshore. In this study, land reclamation is intended as a port development area so that land requirements are

in accordance with the port development plan on the coast. The location of this research is in the southern

area of Ketapang Regency, West Kalimantan, which is 18 km from the Ketapang City Center. This regency

does not yet have a coastal port, all of its ports are in the river, which certainly often occurs siltation due to

sedimentation. Land reclamation is carried out to pursue the depth of the waters in accordance with the

berthing of ships to be anchored so that no trestle construction is needed but by reclaiming it, it can save the

cost of building the structure. The research method used in this study, by analyzing wind data as a reference

for wave generation and calculating the wave deformation that occurs, bathymetry data as a reference for

water depth, tidal data is intended as one in the design of the retaining wall height, estimated loading above

the reclamation structure land, and the external forces that occur on the retaining wall. The design of the

retaining wall uses geobags in a stacked manner, has a total height of 6.3 m buildups from sea level to the

deepest seabed and forms a trapezoidal structure with a trapezoid peak width of 5.09 m (3 geobag lines) and

a trapezoid base width 26.47 m (11 lines/stack). The size of Geobag 2 x 1.5 x 0.6 m. Geobag size is obtained

from the calculation of the effect of waves on the geobag structure. So that the weight is determined by the

required volume size and then the size is further reviewed by the effect of soil pressure due to the embankment

for reclamation held by the geobag structure by analysis of overturning, sliding, and bearing capacity

permitted exceeded.

1 INTRODUCTION

1.1 Background

Ketapang Regency is one area that has abundant

natural resource potential, as a support in the

distribution of goods, this area needs a port for goods

and passengers loading and unloading facilities. This

Regency actually has a port on the Pawan River, but

as time goes by, the shipping lanes to and from the

port experience siltation due to sedimentation. This

area needs a new port that is no longer in a river but

on the coast.

Ketapang Regency itself in general has a fairly

long coastline, but to be used as a port with a specific

ship weight needs to be modified beach conditions.

Based on the results of a feasibility study in 2012 with

3 port locations, the selected ones were located in the

southern area of Ketapang Regency (KRTD, 2012)

but in those areas they have shallow water depths, to

obtain appropriate water depths, about ± 1 km from

the shoreline. So in this study, to solve the problem

we use the option to reclamation the portland because

the cost is more economical and materials will be

taken from nearby locations.

In this reclamation, geosynthetic is used as one of

the structural planning materials. Geosynthetic used

is the type of geobag. Geobag is used as a retaining

wall of land reclamation. The geobag material used is

from NAUE Germany whose geobag output material

is SECUTEX®H or SECUTEX® SOFT ROCK

Catherine, L., Pratikto, W., Suntoyo, ., Tua Simatupang, J. and Bachtiar, V.

Analysis of Soil Retaining Wall from Geosynthetic for Sea Reclamation to Become a New Land in the Beach.

DOI: 10.5220/0010287602710280

In Proceedings of the 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management (ISOCEEN 2019), pages 271-280

ISBN: 978-989-758-516-6

271

which is a special fiber nonwoven geotextile for

hydraulic engineering.

1.2 Formulatiom of the Problem

1. How to determine the dimension of retaining

wall?

2. How to determine the dimension of geobag?

3. How does the influence of the stability of the

external forces of the geobag as a retaining wall

of land reclamation?

1.3 Restricting the Problem

1. Land area for land reclamation plan is 372.417,5 m

x 389.011 m

2. Land reclamation location in in the southern area

of Ketapang Regency, West Kalimantan, which is

18 km from the Ketapang City Center

3. Planning a retaining wall in the form of

geosynthetic geobag types using data:

a. Wind data was obtained from BMKG Ketapang

in the years 2004 - 2013

b. Bathymetry data of land reclamation area with

the direct survey to the field as a reference for

water depth

c. Tidal data was obtained from a 15-day field

survey as a reference for the reclamation land

retaining wall height

d. Soil type data were obtained from field samples

and examination tests at the Soil Mechanics

Laboratory, Faculty of Engineering,

Tanjungpura University, as a reference to soil

types in filling geobags

4. Does not calculate the strength of the external

geobag material used

2 THEORY

2.1 Reclamation

Reclamation is a job/business utilizing areas or land

that are relatively useless or still empty and watery

into useful land by draining. For example in coastal

areas, swampy areas, offshore / in the sea, in the

middle of a wide river, or in a lake. Reclamation is

carried out following the procedures since the

planning stages (pre), implementation and

development (process), and its use (post) both above

and or below the reclaimed land (PWD, 2008).

The reclamation of large amounts of land in the

future may be needed to meet the food and adequate

space requirements of the developing population.

Land reclamation for housing, industry, or recreation

requires ecological, hydrological, and geological data

in addition to technical analysis. Geologists can

contribute to the planning of reclamation of

floodplains, wetlands, landmines, and geologically

dangerous areas. Geological data can be used to

predict the environmental impacts deposited by a

reclamation project (McComas, 1972). From a

commercial perspective, reclamations have been used

for airport expansions and new airports as well as port

expansions and new ports. Residential and

recreational developments along waterfronts have

been successfully constructed on reclaimed land

(Duan et al, 2016).

2.2 Retaining Wall

Retaining walls are structures used to provide

stability for earth or other materials at their natural

slopes. In general, they are used to hold back or

support soil banks and water or to maintain a

difference in the elevation of the ground surface on

each of the wall sides. Also, retaining walls are often

used; in the construction of buildings having

basements, roads, or bridges when it is necessary to

retain embankments or earth in a relatively vertical

position. Retaining walls are commonly supported by

soil (or rock) underlying the base slab, or supported

on piles; as in case of bridge abutments and where

water may erode or undercut the base soil as in

waterfront structures.

The conventional retaining walls can be divided

into four types, gravity, semi-gravity, cantilever, and

counterfort retaining walls. Stability analysis of

retaining wall is influenced by loads which burden the

structures. This load in the mechanic analysis can be

known as force. This force mainly can be divided into

two kind, lateral pressure and vertical pressure.

Lateral pressure itself comprises of soil and water

pressure. There are two types of lateral soil pressure,

namely active and passive pressure. The active

pressure commonly located behind the retaining wall

as the slope which wants to retain. On the other hand,

the passive pressure in front of the retaining wall is an

additional force on the retaining wall to maintain the

slope from collapse. If there is no soil in front of the

retaining wall, there will not any passive pressure.

Moreover, the lateral pressure also includes water

pressure if there is water existence in slope.

Furthermore, the vertical pressure of retaining wall

structure is influenced by the load above the slope

(Sari et al, 2020). Design Considerations of Gravity

as follows ; Scope, Limit State Design, Partial

Loading and Material Factors, Load Combinations

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

272

and Factors for Stability, Load Combinations and

Factors for Strength of Components, Live Loads,

Earthquake Loads, Wind Loads, Hydraulic Loads,

Drained v Undrained Parameters, Capacity Reduction

Factors, Soil Analysis Model, Active Pressure,

Pressure at Rest, Passive Pressure, Bearing Failure,

Sliding Failure, Overturning, Global slip, Foundation

Material, Lean Back (CMAA, 2013)

2.3 Geosynthetic

Geosynthetics can be defined as planar products

manufactured from polymeric material, which

areused with soil, rock, or other geotechnical

engineering-related material as an integral part of a

manmade project, structure, or system. Geosynthetics

are widely used in many geotechnical, environmental,

and hydraulic applications related to groundwater

quality and control. Geosynthetic types include ;

Geotextiles, Geomembranes, Geogirds, Geosynthetic

Clay Liners, Geocomposite Sheet Drains,

Geocomposite Strip (Wick) Drains, Geocells.

(Zornberg and Christopher, 2007).

NAUE geosynthetic is geosynthetic materials

from Germany (NAUE, 1967). The innovations of

NAUE are leading the geosynthetic industry into the

future. We offer project-specific product

development, geotechnical engineering support, and

provide solutions to complicated challenges,

simplifying your project. Geosynthetic types, among

others:

- Geosynthetic Clay Liner Bentofix® – the

“Bentonite liner”

- Secutex® multifunctional geotextile

- Geomembrane CARBOFOL® the HDPE liner

- Secugrid® geogrids for soil stabilisation and

reinforcement

- Combigrid® geogrids with integrated nonwoven

geotextile component

- Secumat® erosion control mat

- SECUDRAIN® WD

- SECUTEX® SOFT ROCK

2.4 Geobag

Geotextile bag or geobag, a geosynthetic product

made of polyester; polypropylene or polyethylene has

been used world wide for protecting riverbanks and

hydraulic structures from severe scouring and

erosion. The use of sand filled geobags underwater in

erosion protection work is being popular due to its

cost-effectiveness, availability, and easier

implementation. Some recent studies support that its

technical efficiency is similar or sometimes better

than the use of hard material (Wahed et. al, 2011).

A durable and effective alternative is a scour

protection system with sand-filled geotextile

containers Secutex® Soft Rock. The dynamic

interaction between waves and waterfront soils and

structures complicates hydraulic engineering.

Beachfront requires longterm protection, and the

solutions must be flexible, durable, and minimize the

impact on marine environments. Lightweight, robust

nonwoven geotextiles enable these engineered

installations to encapsulate sand (including local fill)

for the creation of long-term performing bags,

containers, and tubes. The impact of a sand container

solution made of Secutex® Soft Rock with respect to

the lifecycle consideration is only a fraction of the

impact of a conventional solution in an offshore

scours protection system. Secutex® nonwovens are

filter-stable and extremely robust. A special two-

layered nonwoven composite is available, which

features an integrated surface protection layer made

from rough fibers for exposed or covered designs.

The available sizes and mass per unit area of

Secutex® nonwoven geotextile containers enable

flexibility in infill selection and installation methods.

Bag size and arrangement depending on the

application and expected hydrodynamic conditions.

Secutex® Soft Rock standard design approaches are

available. Secutex® Soft Rock Applications:

- Sea walls, beach and dune revetments

- Groynes

- Submerged breakwaters and jetties

- Scour protection for waterfront structures, walls,

bridge piles andoffshore wind turbines

- Offshore cable protection

- Erosion control in flowing waters

- Filling of washed out material in dams

- Soil stabilisation in dams (NAUE, 1967)

3 METHOD

1. Analyze wind data on land from BMKG of

Ketapang Regency Airport:

a. Calculate wind speed at 10 m elevation



 U











/

(1)

b. Calculate the wind factor

c. Calculates the percentage of wind direction

and is made into windrose

d. Calculating Wind Tension Factor

Analysis of Soil Retaining Wall from Geosynthetic for Sea Reclamation to Become a New Land in the Beach

273

The wind tension produces a wave

generator at sea with a comparative

approach to existing wind data on land

(converting wind on land to wind at sea):



 0,71U

,

(2)

e. Calculating Effective Fetch (Feff)





∑



∑



(3)

where :

eff

= Fetch average effective

= the length of the fetch segment

measured from the wave observation

point to the final of the fetch

α = deviation on both sides of the wind

direction, using an increase of 6

to an

angle of 42

on both sides of the wind

direction

f. Calculate the wind reset period

g. Calculate periods and wave heights in the

deep sea

2. Analyze Wave Deformation

a. Calculate the value of H

Determine H

based on Hs obtained from

previous calculations.

b. Calculate wave period (T)

Determine the Period (T) also based on

previous calculations that have been

carried out a repeat period with the

approximating method

c. Calculate the length of a wave in the deep

sea (L

)



1,56T



(4)

d. Calculate the value of the coefficient of

refraction (Kr)













(5)

e. Calculate the value of the Shoaling

coefficient (Ks)









.







(6)

f. Calculate wave height (H’

)





 K







(7)

The concept of sea wave height in this

equivalent is used in the analysis of

breaking waves which include the height

and depth of the breaking waves

g. Calculate the slope of the seafloor (m)

m





(8)

where :

s = distance from deep shoreline

d = deep sea

h. Calculate the breaking wave height and

depth on formula and graphs









,

(9)

3. Analyze the average high and low tide for 15 days

and plot it into the elongated figure, according to

the area of land and the depth of the waters from

the bathymetry survey results.

4. Analyzing load on land reclamation

5. Analyzing the dimensions of the geobag

a. The weight of the geobag content, using the

calculation of the stability of the protective

stone with the Hudson formula

b. The geobag dimension uses the volume

weight formula with a trial and error

process

Wall height is known from the depth of

the waters to be reclaimed to the height of the

original land. The slope of the retaining wall is

adjusted to the determination of the contents

of the geobag grains against waves. Geobag

heaps from the bottom of the waters to the

height of the plan. Can be the width of the top

(a) and bottom width (B), the retaining wall of

the soil. Apply to AutoCAD to make it easier

to adjust the installation/stacking of geobags.

6. Analyzing Soil Pressure around the site

a. Calculate the coefficient of active soil

pressure (Ka)

(Bachtiar, 2010) :



 tan





45 





(10)

b. Calculate soil pressure due to load on the

structure

σq.K



(11)

c. Calculate soil pressure without ground

water level

σγ



.H.K



(12)

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

274

d. Calculate soil pressure for ground water

level

σγ



.H.K



(13)

e. The active forces on retaining walls:

1. Due to the load on the structure

(distributed load)



 H.σ (14)

2. Due to the presence and absence of

ground water level









H.σ (15)

f. The force center point:

1. Due to the load on the structure

(distributed load)





(17)

2. Due to the to the presence and absence

of ground water level





(18)

g. Calculate the height and distance at each

midpoint of each geobag layer from the

base to the top and determine the number

of geobags of each layer.

h. Calculate each force in each layer, in each

plane due to soil pressure. The force due to

the load on the structure (distributed load)

FP



(19)

7. Analyze the stability of external forces (Bachtiar,

2010) :

a. Overturning





∑





∑





 2 (20)

b. Sliding





∑







∑





1,5 (21)

c. Bearing Capacity Failure













3 (22)

4 RESULT AND DISCUSSION

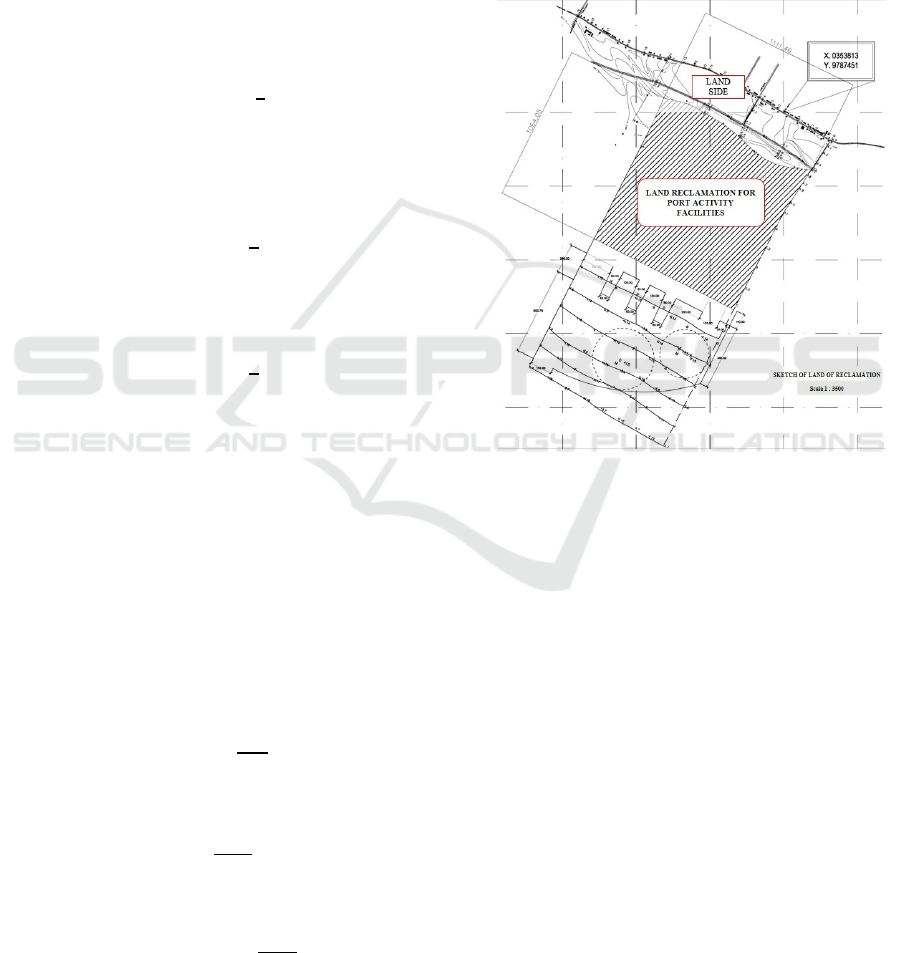
The results of the image as an area that will be

reclamation in the form of breadth and depth of water.

The area to be reclamation is adjusted to the land plan

for multipurpose buildings, warehouses, offices and

container land, which is 37,241, 75 m x 38,885 m. The

depth of the waters at the far end of the land area is

approximately 6 m below the highway elevation.

(Figure 1)

Figure 1: Land Reclamation Plan.

4.1 Wind Data

Analysis of wind data on land from BMKG Ketapang

Airport with a height of 9 m above sea level. In

planning structures at sea must use wind data above

the sea. Therefore, the data is reprocessed to get the

largest wind speed direction in the percentage scale,

effective fetch, period, and wave height from the deep

sea (Figure 2).

Analysis of Soil Retaining Wall from Geosynthetic for Sea Reclamation to Become a New Land in the Beach

275

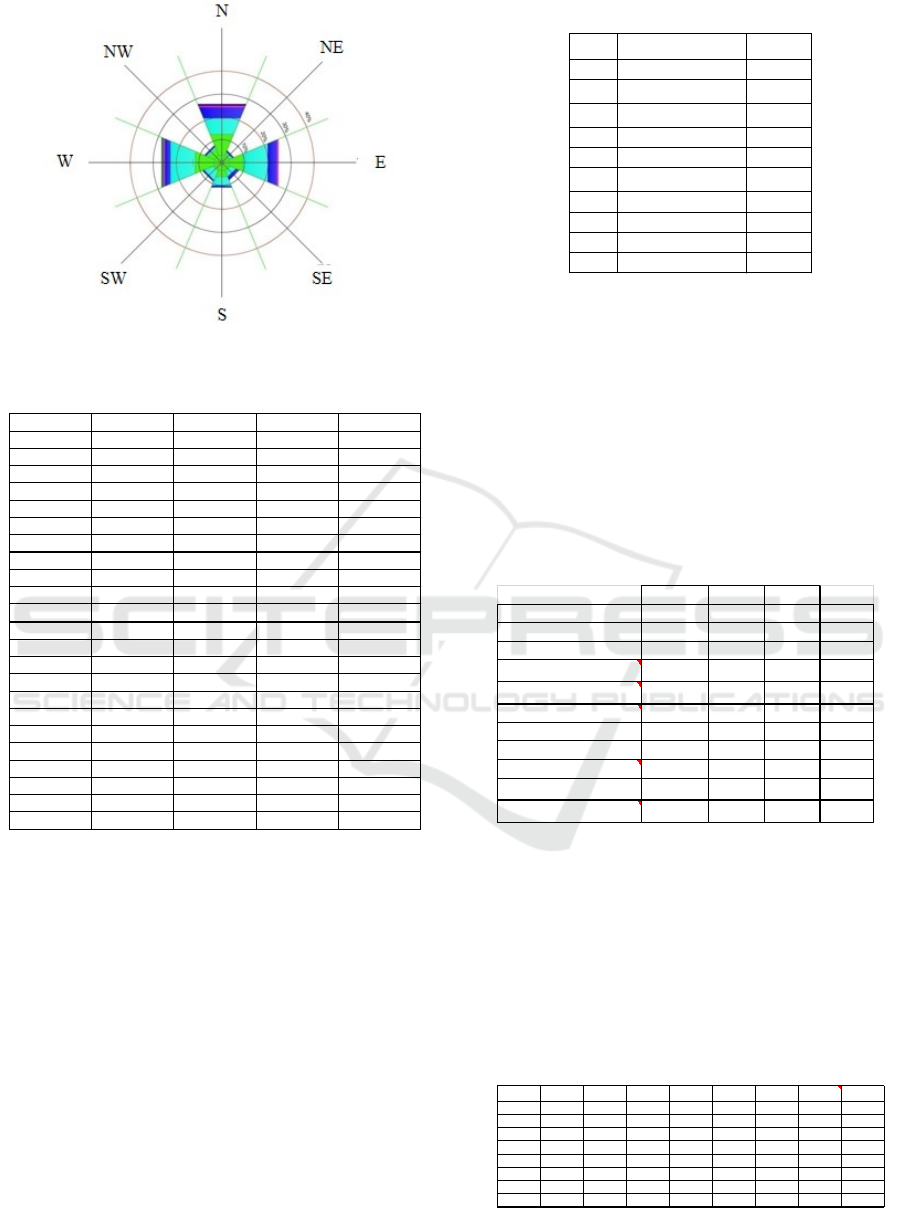
Figure 2: Windrose.

Table 1: Percentage of Speed and Direction of Wind.

So, the biggest wind direction comes from the West

by 25%, after that from the north and east by 24.17%

as given in Table 1 and Figure 2).

Measurement of wind data is carried out on land

at the airport. The measurement of the wind is not yet

suitable for wave forecasting, then the wind data

needs to be corrected. After that, it is converted into a

wind stress factor every year as given in Table 2.

Table 2: Wind Tension Factor Average (knots).

The determination of waves with certain return

periods requires wave data in a long enough

measurement period. Representative data for several

years of wind observation can be used to estimate the

expected wave is equaled or exceeded once in T years

and the wave is known as the return wave period, T

or annual wave period , T (Pratikto et al., 2014). There

are 3 methods used to calculate the wave return

period, namely Normal, Gumbell and Log Person

distribution as given in Table 3.

Table 3: Wave Return Period.

4.2 Wave Deformation

Calculation of wave deformation is done to get the

wave breaking from the deep waters towards to the

shoreline, the calculation results is given in Table 4,

Table 5 and Table 6 for the 2 years, 5 years and 10

years return periode prediction, respectively.

Table 4: Wave deformation calculation results for the 2

years wave return period.

Direction North North East East South East

0 - 10 0,00% 0,00% 0,00% 0,00%

10 - 20 10,00% 0,83% 6,67% 0,83%

20 - 30 7,50% 0,83% 11,67% 2,50%

30 - 40 5,00% 0,83% 4,17% 1,67%

40 - 50 0,83% 0,00% 0,83% 0,00%

50 - 60 0,00% 0,00% 0,00% 0,00%

60 - 70 0,00% 0,00% 0,00% 0,00%

70 - 80 0,00% 0,00% 0,00% 0,00%

80 - 90 0,00% 0,00% 0,00% 0,00%

90 - 100 0,83% 0,00% 0,83% 0,00%

Σ 24,17% 2,50% 24,17% 5,00%

South South West West North West Σ

0,00% 0,00% 0,00% 0,00% 0,00%

3,33% 0,83% 9,17% 3,33% 35,00%

4,17% 4,17% 11,67% 0,83% 43,33%

0,83% 0,83% 2,50% 0,83% 16,67%

0,00% 0,00% 0,83% 0,00% 2,50%

0,00% 0,00% 0,00% 0,00% 0,00%

0,00% 0,00% 0,83% 0,00% 0,83%

0,00% 0,00% 0,00% 0,00% 0,00%

0,00% 0,00% 0,00% 0,00% 1,67%

8,33% 5,83% 25,00% 5,00% 100,00%

No Year X (U

)

1 2004 25,02

2 2005 23,32

3 2006 35,92

4 2007 20,32

5 2008 19,91

6 2009 23,87

7 2010 27,83

8 2011 22,00

9 2012 30,65

10 2013 27,28

2 year 5 year 10 year

Normal 25,61 29,78 31,96 Knots

Gumbell 4,27 9,99 13,78 Knots

Log Person Type III 16,04 3,04 1,72 Knots

Average (U

) 15,31 14,27 15,82 Knots

Average (U

) 7,87 7,33 8,13 m/d

Duration 4 4 4 jam

Wave Height (Hs) 0,65 0,59 0,68 m

Wave Period (T) 3,75 3,55 3,75 s

Fetch 27 26 27 km

Wave Length (L

) 21,97 19,69 21,97 m

d/L

0,8194 0,9143 0,8194 m

d(m) H

(m) T(s) L

(m) Kr Ks H

'(m) m(slope)

'/gT

20 0.65 3.75 21.98 1.00 1.00 1.54 0.001 0.011

18 0.65 3.75 21.95 1.00 1.00 0.65 0.093 0.005

16 0.65 3.75 21.91 1.00 1.00 0.65 0.074 0.005

14 0.65 3.75 21.86 1.00 1.00 0.65 0.056 0.005

12 0.65 3.75 21.78 1.00 0.99 0.65 0.186 0.005

10 0.64 3.75 21.61 1.00 0.98 0.65 0.048 0.005

8 0.62 3.75 21.24 0.99 0.95 0.65 0.053 0.005

6 0.59 3.75 20.39 0.98 0.90 0.65 0.085 0.005

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

276

Table 5: Wave deformation calculation results for the 5

years wave return period.

Table 6: Wave deformation calculation results for the 10

years wave return period.

The wave deformation analysis involved the shoaling,

the refraction and the breaking waves. Then, the

relationship among the deep-sea wave height (H'

the incident angle of the wave (α), and the wave

height in the deep sea (H = 0.78d) is used to determine

the breaking wave.

Figure 3: The relationship among the deep-sea wave height

(H'0), the incident angle of the wave (α), and the wave

height in the deep sea (H = 0.78d) for the 2 years of wave

return period.

Figure 3 showed the results of the conditions in which

waves propagate from the deep sea and break with

wave height approaching the coastline, producing a

value; sea depth (d) = 0,7 m, wave height (H

') = 0,5

m and angle of the incident wave (α) = 42

for the 2

years of wave return period.

For the 5 years of wave return period prediction

condition, waves propagate from the deep sea and

break with wave height approaching the coastline

within the water depth (d) = 0,2 m, wave height (H

') = 0,2 m and angle of the incident wave (α) = 46

while within the water depth (d) = 0,9 m, wave height

') = 0,6 m and angle of the incident wave (α) =

42,5

, for the 5 years of wave return period prediction

condition as given in Figure 4 and Figure 5,

respectively.

Figure 4: The relationship among the deep-sea wave height

(H'0), the incident angle of the wave (α), and the wave

height in the deep sea (H = 0.78d) for the 5 years of wave

return period.

Figure 5: The relationship among the deep-sea wave height

(H'0), the incident angle of the wave (α), and the wave

height in the deep sea (H = 0.78d) for the 10 years of wave

return period.

Table 7: The calculation results of the structural load on the

reclamation area.

Source of Value : (ILRB, 1983)

d(m) H

(m) T(s) L

(m) Kr Ks H

'(m) m(slope)

'/gT

20 0.59 3.55 20.00 1.01 1.01 1.71 0.001 0.014

18 0.60 3.55 20.00 1.00 1.00 0.60 0.093 0.005

16 0.60 3.55 20.00 1.00 1.00 0.60 0.074 0.005

14 0.60 3.55 19.99 1.00 1.00 0.60 0.056 0.005

12 0.60 3.55 19.98 1.00 1.00 0.60 0.186 0.005

10 0.60 3.55 19.93 1.00 0.99 0.60 0.048 0.005

8 0.59 3.55 19.76 1.00 0.97 0.61 0.053 0.005

6 0.57 3.55 19.22 0.99 0.92 0.62 0.085 0.005

d(m) H

(m) T(s) L

(m) Kr Ks H

'(m) m(slope)

'/gT

20 0.68 3.75 21.98 1.00 1.00 0.68 0.001 0.005

18 0.68 3.75 21.95 1.00 1.00 0.68 0.093 0.005

16 0.68 3.75 21.91 1.00 1.00 0.68 0.074 0.005

14 0.67 3.75 21.86 1.00 0.99 0.68 0.056 0.005

12 0.67 3.75 21.78 1.00 0.98 0.68 0.186 0.005

10 0.65 3.75 21.61 1.00 0.96 0.68 0.048 0.005

8 0.63 3.75 21.24 0.99 0.93 0.67 0.053 0.005

6 0.58 3.75 20.39 0.98 0.88 0.66 0.085 0.005

=6,58 kg/m2

2,70 kg/m

33,44 m2

W = 30,48 kg

Wide = 2,44 m

2 = 1.818,2 kg/m2 = 661,16 kg/m

A = 24,75 m2

W= 45.000 kg

Wide = 2,75 m

3 = 2.376 kg/m2 = 410,35 kg/m

A = 33,52 m2

W= 79.650 kg

Wide = 5,79 m

4 = 3.050 kg/m2 = 3.050 kg/m

Live Load of Office Floor

(@3 tingkat)

250

kg/m2

=750 kg/m2

Live Load of Floor and

Meeting Room

400 kg/m2

Live Load of Ladder = 300 kg/m2

Live Load Parking Floor

Building Lower

800 kg/m2

Live Load Parking Floor

Building Level Other

400 kg/m2

5 = 167,80 kg/m2 = 1.598,10 kg/m

A = 0,02 m2

W = 3,70 kg

Wide = 0,11 m

6 = 91,06 kg/m2 = 0,09 kg/m

γsand = 1.517,72 kg/m3

Thick of Heap = 0,06 m

Wide of Land Heap = 1.061,00 m

= 8.259,53 kg/m2 = 5.722,39 kg/m

TOTAL

Live Load of Container Truck 45 ( W=45000kg, A = 2,75 x 9,0 m2)

Live Load of Container 6 @30,480 kg (uk.13,716 x 2,438 m2)

Live Load off Mobile Crane (W=79560 kg, A=5,79 x 5,79 m2)

Live Load of Building S tructure

Dead Load of Paving Block (Rectangle 10x10,5x21, W =3,7kg)

Dead Load for Heap Sand Paving Block

Live Load of Warehouse,

Tools Room and Archive

=400 kg/m3

Analysis of Soil Retaining Wall from Geosynthetic for Sea Reclamation to Become a New Land in the Beach

277

4.3 Tidal

Based on the tidal observations data, it can be

obtained the characteristics of water level in the form

of a formzal value related to the highest tides and

lowest tides that occur. The elevation of the original

land in the form of a highway is used as a benchmark

for an elevation of 0.00 meters. From the tide

analysis, it is obtained that the higest water level is -

1.00 m and the lowest water level is -3.20 m. So that

the height of the reclamation pole can be planned to

be parallel to or higher than the elevation of the

highway because the highest tidal elevation is still 1

meter below the road elevation.

4.4 Load

This reclaimed land will be used as land for the

construction of containers, offices, warehouses and

passenger waiting rooms. In planning for the

construction of the structure, a total load on the soil is

required so that the structure does not collapse. The

structural load planning to be built on the reclamation

area is given in Table 7.

4.5 Geobag

The geobag material used is the German NAUE type

Secutex® Soft Rock (NAUE, 1967). To determine

the dimensions of the geobag, the type of soil used to

fill into the geobag should be known in advance. In

this paper, the type of soil is given in Table 8 obtained

from the laboratory analysis of Soil mechanics

laboratory belong to Engineering Faculty,

Tanjungpura University. After that, the grain weight

of the geobag is calculated using the stability of the

protective stone.

Table 8: Type of soil.

A classic formula for the stability of rocks/stones

under breaking waves at a sloping surface is given by

the Hudson formula. The weight of geobag grain

content calculation steps are given, as follows:

1. γ

, obtained from the density of geobag fillers,

namely the type of soil (sand) on the seabed. The

data was obtained from the laboratory, which is

1,517.72 kg / m

2. γ

, obtained from the specific gravity of seawater

1.025 kg/m

3. H, is the wave height of the plan

4. K

, is the Stability Coefficient depending on the

shape of the protective stone. Obtained from the

table and used the number is 1.1

5. S

















1.517,72

1025

1,48

6. θ, is the angle of slope of the retaining wall. Enter

data according to the desired angle or with the

"trial and error" technique

7. cotθ





cotθ 











3,223

8. W





.







.









(

Pratikto, et.a., 2014)

W

1.517,72 x 0,6

1,1.1,48  1



cot





 2.674,5 kg

According to the results of the data above, the weight

of the contents of one geobag uses (W) = 2.674,5 kg

as given in Table 9 and the geobag dimension size is

shown in Figure 6.

Table 9: Weight of Geobag grain content.



Figure 6: Geobag dimension size.

The height, width and length of the geobag size are

determined from the height requirements of the

retaining wall that are planned for the geobag

(t/m

)(kg/m

)(t/m

)(kg/m

)

3 3 - 3,5 11,31 1,23 1.116 1,673 1.517,72

sat

Subsoil Depth (m)

(vol.kering)

W(kg) γ

(kg/m3) γ

(kg/m3) H (m)

-2683,01 1.517,72 1.025 0,6

-2678,62 1.517,72 1.025 0,6

-415,50 1.517,72 1.025 0,6

-35,62 1.517,72 1.025 0,6

2605,36 1.517,72 1.025 0,6

2674,50 1.517,72 1.025 0,6

-1915,39 1.517,72 1.025 0,6

-1564,88 1.517,72 1.025 0,6

1473,76 1.517,72 1.025 0,6

Sr θ cot θ (1/tan θ)

1,1 1,48 25 -7,489

1,1 1,48 28 -3,553

1,1 1,48 30 -0,156

1,1 1,48 33 -0,013

1,1 1,48 35 2,111

1,1 1,48 38 3,223

1,1 1,48 40 -0,895

1,1 1,48 43 -0,667

1,1 1,48 45 0,617

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

278

stacking or stacking place. Therefore, the size of this

geobag is determined using the "Volume Weight

Formula" with the "trial and error" technique until the

volume weight above is in accordance with or slightly

larger than the volume weight plan.

4.6 The Earth Pressure and Gravity

Retaining Walls

To obtain structural resistance, the active earth (soil)

pressure coefficient and the forces acting on each

layer of geobag that will be stacked can be obtained

so that the height and width of the structure are in

accordance with the dimensions planned. The

calculation results of the soil pressure and is given in

Table 10, while the working force on the geobag layer

is given in is given in Table 11. The diagram of soil

pressure and the cross-section of retaining wall are

given in Figure 7 and Figure 8, respectively. The top

view of geobag formation used to construct the

retaining wall is given in Figure 9.

Table 10: Soil pressure calculation results.

Table 11: The working force on the geobag layer.

Figure 7: Diagram of Soil Pressure.

Figure 8: Retaining Walls.

Figure 9: Top View of Geobag Formation.

The height of the retaining wall is determined by the

deepest point from the coastline to the length of the

reclaimed land and the width of the retaining wall

depending on the geobag stacking pattern adjusted to

the ground level.

4.7 Stability of External Forces

a. Overturning

Moment of prisoner due to own heavy

construction

∑





 2.423.370 kg.m

Overturning moment due to active force

∑





 589.210 kg.m.

𝐅𝐒

𝐨𝐯𝐞𝐫𝐭𝐮𝐫𝐧𝐢𝐧𝐠

𝟒,𝟏𝟏  𝟐 OK !

Retaining Wall Design is safe against collapse due

to overturning.

b. Sliding Failure

where :

ΣF

= 240,33

ΣF

= 128,825

𝐅𝐒

𝐬𝐥𝐢𝐝𝐢𝐧𝐠

 𝟏,𝟖𝟕 𝟏,𝟓 OK !

Retaining Wall Design is safe against collapse due

to sliding.

No H (m) Ka

Pressure σ

(Kg/m2)

Pa (Kg/m)

Point of

Force (m)

1 6.3 0.67 3845.88 24229.07 3.15

2 6.3 0.67 4724.55 14882.33 2.10

3 5 0.67 5100.12 12750.31 1.67

Height (m) Distance (m) Total

0.3 0.3 13 15626.45 13564.16

0.9 0.6 12 17362.72 15549.16

1.5 0.6 11 19533.06 18214.73

2.1 0.6 10 22323.50 4207.60

2.7 0.6 9 10630.24 6502.66

3.3 0.6 8 12756.28 8797.71

3.9 0.6 7 14882.33 11092.77

4.5 0.6 6 17008.38 13387.83

5.1 0.6 5 19134.43 15682.88

5.7 0.6 4 21260.47 17977.94

6.3 0.3 3

24229.07 170517.86 124977.43

Geobag Layer

Total

The wor king

force of each

geobag layer due

to load is evenly

distributed (kg/m)

The wor king

force of each dry

soi l geobag layer

(kg/m)

The working force

of each wet soil

geobag layer

(kg/m)

24229.07

Analysis of Soil Retaining Wall from Geosynthetic for Sea Reclamation to Become a New Land in the Beach

279

c. Bearing Capacity Failure

Where :

ult

= 34.774 kg

e = 5,61 < 4,4

maks

= 9.084 kg

𝐅𝐒

𝐛𝐞𝐚𝐫𝐢𝐧𝐠𝐜𝐚𝐩𝐚𝐜𝐢𝐭𝐲

𝟒,𝟒𝟏𝟑 OK !

Retaining Wall Design is safe against collapse due

to bearing capacity failure.

5 CONCLUSION

The dimensions of the retaining wall are determined

based on the water depth from the results of the

bathymetry and tide surveys. Meanwhile, the material

of filled geobag can be obtained from the results of

the type of soil that will be filled as geobag filling

material dan dimension use trial and error technique

until the volume weight above corresponds to or is

slightly greater than the volume weight plan. From

the results of the calculation of the strength of the

geobag retaining wall, the following points can be

concluded:

1. The height of the retaining wall is taken from the

deepest point of bathymetry, which is 6.3 m and

the break wave height per 10 year return period is

0.6 m. It’s width is adjusted by the geobag

stacking to the height of the retaining wall until it

forms a trapezoidal shape of 26.47 m. This

retaining wall has 11 geobag layers with the most

bottom layer are 13 geobags and the top layer are

3 geobags. The slope of the angles on the left and

right sides are different, on the left side which

attaches to the land which is 27

and the right side

on the seafront is 38

2. Geobag dimensions are 2 x 1.5 x 0.6 m using trial

and error until the weight is in accordance with the

grain weight of the protective stone.

3. Geobag retaining walls are strong against external

force stability due to overturning, sliding, and

bearing capacity. The result exceeds the standard

threshold value.

REFERENCES

Bachtiar, V., 2010. Foundation Engineering 1. Pontianak,

Tanjungpura University

CMAA (Concrete Mansory Association of Australia).

(2003) Concrete Masonry Gravity Retaining Walls.-

edn. Australia: Adbri Masonry

Duan, H., Zhang, H., Huang, Q., Zhang, Y., Hu, M., Niu,

Y., Zhu, J. 2016. ‘Charateristic and Enviromental

Impact Analysis of Sea Land Reclamation Activites in

China’, Journal of Ocean and Coastal Management 130,

p128-137

ILRB (Indonesian Loading Regulations for Buildings),

1983. Bandung. Directorate of Inquiry into Building

Problems.

Ketapang Regency Transportation Department (KRTD).

2012. Regional Port Feasibility Study in Ketapang

Regency, West Kalimantan Province. Ketapang.

McComas, M.R. 1972. ‘Geology and Land Reclamation’,

The Ohio Jurnal of Science, 72(2), p65-75.

Sarfaraz, M.D., Wahed, M.D., Sadik, S., Muhit, S.M.,

2011. ‘Enviromental Impacts of using Sand Filled Geo-

bag Technology Under Water in River Erosion

Protection of Major Rivers in Bangladesh’, Proceeding

of International Conference on Enviromental

Technology Construction Engineering for Sustainable

Development, ISBN: 978-984-33-3054-3

NAUE Germany. 1967. NAUE Geosynthetic [Online].

Available at: https://www.naue.com/naue-

geosynthetics/ (Accessed: 10 Juni 2020)

Public Works Department (PWD). 2008. Minister of Public

Works Regulation No.40 / PRT / M / 2007 concerning

the Applied Modules for Spatial Planning Guidelines

for Coastal Reclamation Areas. Jakarta.

Pratikto, W.A., Suntoyo, Solihin, Sambodho, K., 2014.

Struktur Pelindung Pantai, PT. Mediatama Saptakarya

(PT. Medisa), Yayasan Badan Penerbit Pekerjaan

Umum, Jakarta.

Sari, U.C., Sholeh, M.N., Hermanto, I., 2020. Stability

Analyisis Study of Conventional Retaining Walls

Variation Design in Vertical Slope’, Journal of Phyiscs

: Conference Series, 1444 (2020) 012053.

Zornberg, J.G. and Christopher, B.R. 2007 ‘Geosynthetic’

in Deller, Jacques W. (2nd ed.) The Handbook of

Groundwater Engineering.2nd edn. Florida : CRS

Press, Taylor & Francis Group, pp. 1-34.

ISOCEEN 2019 - The 7th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

280