Stress Concentration Analysis on Ship Plate with Hole using

Numerical Approach

Mohammad Nurul Misbah

1,a

, Dony Setyawan, Totok Yulianto, Rizky Chandra Ariesta,

andWing Hendroprasetyo Akbar Putra

Department of Naval Architecture, Institut Teknologi Sepuluh Nopember, Indonesia

Keywords: Numerical, Plate, Ship, Stress Concentration.

Abstract: The selection of construction firms affects the stress that occurs on the ship. Stress concentration on the

construction of the vessel is caused by the load when the ship is operating. A tensile test used to verify the

material strength and obtain the maximum stress range that could work on the ship material. In this study,

the analysis is conducted to determine the stress concentration of perforated plate stress on the ship. This

analysis uses numerical calculation methods and validates with analytical. Based on these results, the

approach might use to validate and applied for other shapes.

1 INTRODUCTION

Stress is a factor needed to calculate details when

designing ship construction. In its operation, the ship

is subject to stress due to a load of ocean waves. Stress

work on ship occurs at some point. Stress gradients

that have a small area with a dominant red colour

called a stress concentration. The stress concentration

carries out in the hotspot area. The effect of stress on

the hotspot may result in fatigue. Fatigue occurs due

to the influence of size, shape, and location rather

than damage. Stress distribution around the hole is

shown in Figure 1.

Figure 1: Distribution of stress concentration.

Simple construction of a ship was studied to

observe the occurrence of failures with crack

applications. This research aims to obtain the

difference between the numerical and analytical

methods. Thus, these results can be applied as a

reference in applying the size, shape, and location of

the damage to avoid stress concentration.

2 LITERATURE REVIEW

In general, the stress concentration occurs due to

tensile load and other factors that fail ship

construction. Damage is assumed to be holes that

cause stress concentration concentrations (Belamri,

2009). Stress concentration area could create to

reduce the stress concentration of the critical area

(Vable, 2010). Cracks were observed during

operation to predict construction life. From the

observations, the stress concentration increases in

proportion to the magnitude of the damage (Ogeman

and Mao, 2014). Previous research analyses plates

applicated with axial load conditions. Investigations

of the load carry out to prevent failure. Axial load

failure occurs in the stress concentration area. The

development of damage measurement was an early

stage to measure the magnitude of the stress. The

stress that occurs is measure in a certain period. This

study aims to prevent the stress concentration that

occurring on the plate with a hole. (Gokul, Kuriakose

and Kurian, 2016). Some cases of failure occur in

detailed construction so a simple form of construction

is required taking into account strength requirements

Misbah, M., Setyawan, D., Yulianto, T., Ariesta, R. and Putra, W.

Stress Concentration Analysis on Ship Plate with Hole using Numerical Approach.

DOI: 10.5220/0010855200003261

In Proceedings of the 4th International Conference on Marine Technology (senta 2019) - Transforming Mar itime Technology for Fair and Sustainable Development in the Era of Industrial

Revolution 4.0, pages 117-121

ISBN: 978-989-758-557-9; ISSN: 2795-4579

117

(Sujiatanti et al., 2018). Most of the cracked damage

to structural fatigue occurs under repeated loads. A

Crack has appeared on a plate that has a large stress

intensity. Stress concentration calculation is required

to evaluate crack on ship construction (Takaki and

Gotoh 2020). Based on several variations in this

study, an evaluation of the stress concentration was

carried out to obtain the stress concentration factor in

each variation of the holes on the plate. This hole

represents a detailed form of construction on a ship,

for example, dry holes, scallops, and manholes. The

construction details are an important part that serves

to reduce stress.

2.1 Working Load

In this research, the tensile load applies to determine

the stress distribution that occurs. This condition is

following where the plates on the ship experience

tensile and compressive stresses. The load is applied

on the model. The load condition is placed at the end

of the plate and clamped at the other end.

2.2 Stress Concentration

The stress concentration factor (K) is a

nondimensional value applied to measure the

concentration of stress that occurs in the material.

Stress concentration can also be mentioned as a stress

riser. The maximum nominal stress occurs on section

a-a, which is taken through the bar’s smallest cross-

sectional area shown in Figure 2.

Analytically, stress concentration calculation on

the perforated plate has been approached using

several variations and resulted in value for the stress

concentration factor on the perforated plate. The

stress concentration factor is influence by the ratio of

the plate width and the hole diameter. Where the large

hole gives different behaviour to the K value is all

created the table scheme shown in Figure 3.

Influence value of K by the radius and width

where the closer the ratio value to 0, the greater the

stress concentration.

3 METHODOLOGY

The method in this research is numerical and

validated with analytical solutions. The numerical

method is developing to obtain the interaction of the

load conditions, shape, and size of the hole so that the

stress concentration factor. Furthermore, compare the

results of the stress concentration factor to know the

difference in error between the two methods is seen.

The model analysed is a plate with a length of 300

mm and a width of 50 mm. The variation of the holes

in the centre of the plate is determined according to

the reference ratio (Hibbeler 2011). Some of the

variations are shown in Table 1.

Table 1: Variations of radius.

o w(mm) r(mm) r/w

0.1

50 10 0.2

50 15 0.3

50 20 0.4

50 25 0.5

Based on these variations, the stress concentration

is calculated using the equation below. The stress

concentration factor is determined as the ratio of the

maximum stress (σ

max

) is divided by nominal stress

(σ

nom

), which can obtain follows Equation (1).

𝐾

𝜎



𝜎



(1)

Figure 2: Tensile force working principle.

ure 3: Ratio of stress concentration.

senta 2019 - The International Conference on Marine Technology (SENTA)

118

The nominal stress is made from the total load by

neglecting the concentration areas such as the hole.

The approximate stress in the centre of the plate width

is solved by equation (1). The nominal stress value is

obtaining from the force (F) divided by the cross-

sectional area (A) as in Equation (2):

𝜎





𝐹

𝐴

(2)

Area (A) obtained from the cross-sectional width of

the plate. Then the value of K can be determined by

Equation (3) by (Young and Budynas, 2002).

𝐾



 3.003.13

2𝑟

𝐷

3.66

2𝑟

𝐷





1.53

2𝑟

𝐷





(3)

The approach used the above equation to get the

stress concentration. Where the stress concentration

depending on the ratio of the width and diameter of

the hole. The results of the large stress concentration

factor on the plates were then analysed by numerical

methods. The development of the numerical method

is carried out in several stages. Numerical modelling

is develops using the finite element method (Misbah,

et al. 2018). In the analysis, obtaining a good

accuracy required the convergence of studies by

changing the element size to obtain great result. The

relationship between the number of elements and the

accuracy of the results presented in Figure 4

Figure 4: Convergency study.

The results will begin to stabilize and not be

affected by the change of elements in range size and

amount of element (Logan, 2011). The initial stage is

modelling each variation of the model to determine

the amount of stress that occurs. This modelling aim

is to simplify the experimental process. Then, the

numerical results are validated by analytic

calculations. A model made of steel with material

properties such as properties used as density (ρ),

Young’s modulus (E), and Poisson’s ratio presented

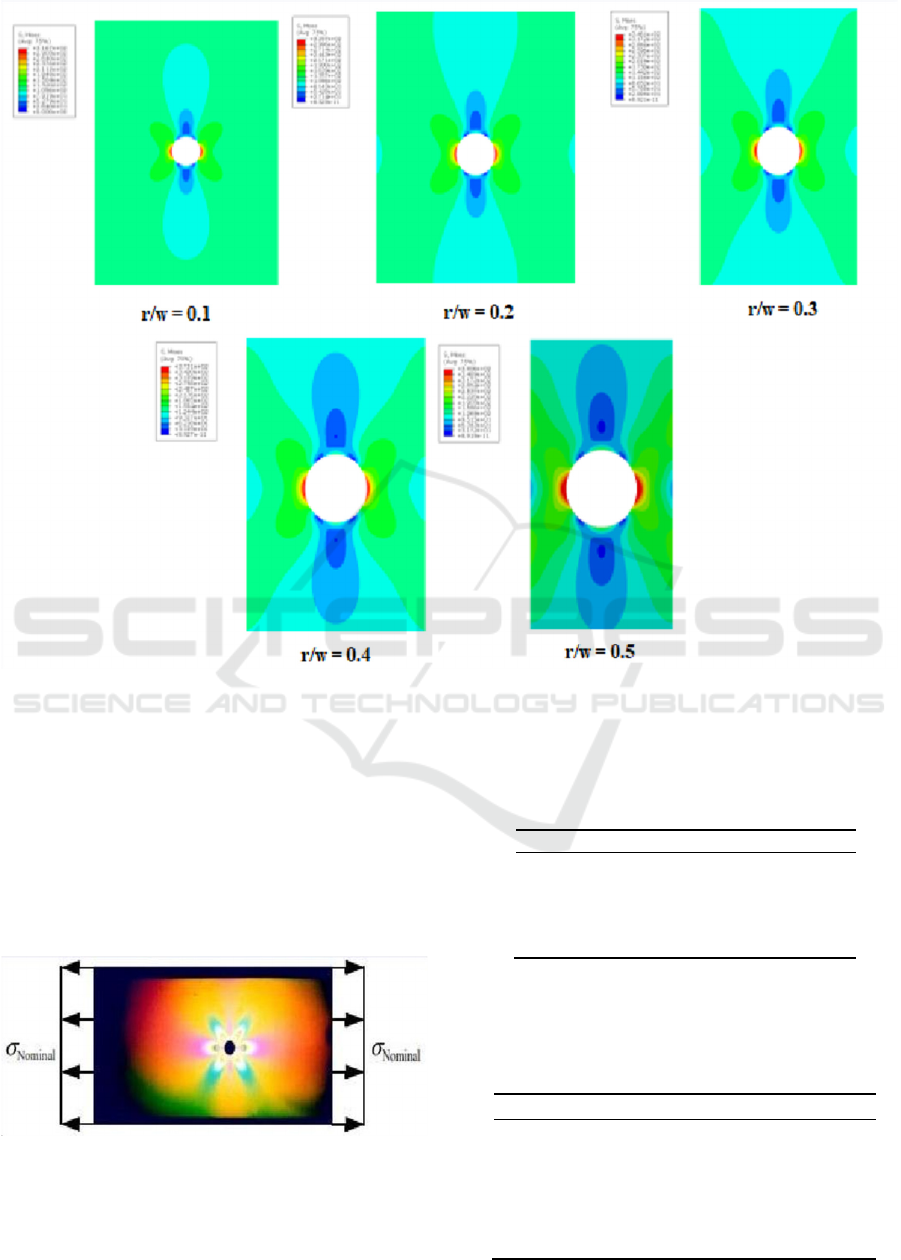
in Table 2. Model is defined in Figure 5 (a) left and is

the boundary condition (b) right.

Figure 5: (a) Model and (b) Boundary condition.

Furthermore, meshing was carried out to obtain

convergent results and continued in the analysis of the

results.

4 RESULTS AND DISCUSSION

The calculation design of variation hole radius and

the length ratio determine using equation (3) to obtain

the stress concentration factor (SCF). Theoretically,

the stress concentration factor is proof. That is a show

from the big will decrease the value of the stress

concentration. The results of the analysis of analytical

calculations are presented in Table 3.

Table 3: Stress concentration factor (K1) analytical.

(

)

r/w

0 0 3

0.1 2.595

10 0.2 2.375

15 0.3 2.25

20 0.4 2.15

25 0.5 2.08

Table 2: Material properties of steel.

Materials

/m3) E (MPa)

Steel 7850 2.06 x 10

0.3

Stress Concentration Analysis on Ship Plate with Hole using Numerical Approach

119

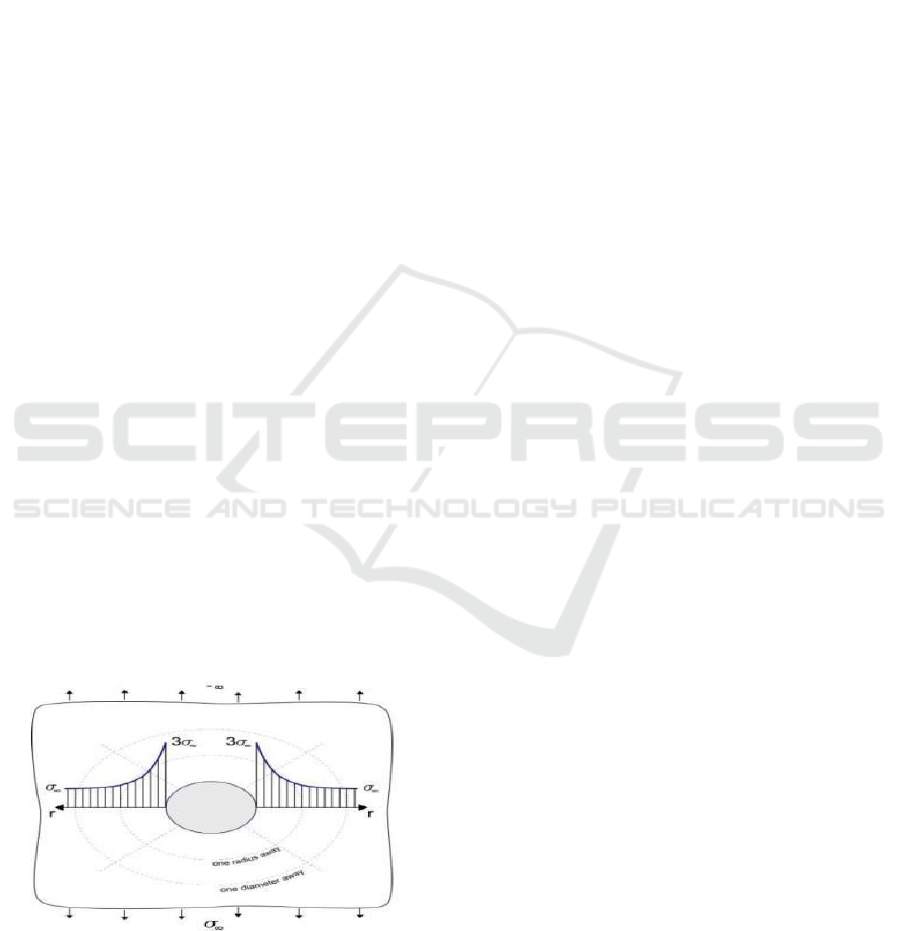
Based on this result, a numerical simulation is

performing to ensure that these results be good.

Obtained stress contours from the simulation results

are then processed to obtain the stress concentration

factor. The results of the simulated stress distribution

are shown in Figure 6. The stress concentration is

centre on the left and right sides of the hole due to the

working tensile load. The resulting contours in

numerical analysis are the same as in Figure 7.

Figure 7: Contour of the stress concentration (Vable, 2010).

Values of stress in Table 4 are using to input in the

equation for calculations. That calculation produces

the value of the stress concentration factor using

Equation (1).

Table 4: Maximum stress value.

Type Max Stress (MPa)

Variation 316

Variation 326

Variation 346

Variation 373

Variation 380

The stress distribution on the side of the plate

is shown in Figure 8. The resulting stress distribution

Figure 6: Stress concentration in numerical simulation.

Table 5: Stress concentration factor (K1) numeric.

r(mm)

𝑟

𝑤

⁄

0 0 3

8.4 0.16 2.57

10.3 0.205 2.49

13.9 0.278 2.38

17.5 0.35 2.28

25 0.5 2.16

senta 2019 - The International Conference on Marine Technology (SENTA)

120

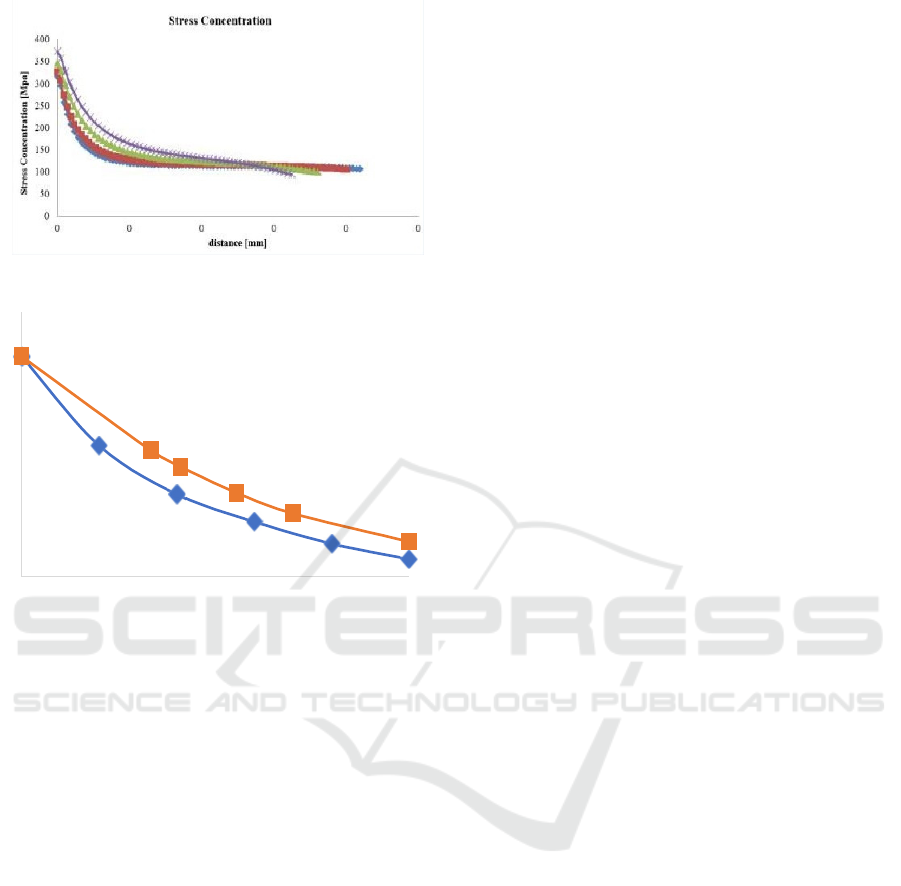
is numerically high in the vicinity of the hole and

decreases toward the edge of the plate. That same

with Figure 1 above. Finally, from the resulting stress,

SCF calculations are carried out so that the values

presented in Table 5 are obtained. That comparison of

results from the analytical and numerical formula

references is present in Figure 9. If attention to the

results of the numerical approach, the graph tends to

be the same. So that result can be said to be valid with

a difference of error below 2%.

5 CONCLUSIONS

Based on the analysis of the analytical and numerical

methods approach with the finite element method.

This technique allows it to use in other structural

forms with the addition of various load conditions.

The SCF value resulted in an error below 2% for all

variations. In the future, additional experiments need

to make sure the results correct.

REFERENCES

Belamri, S., Tamine, T., Nemdili, A. 2009. “Experimental

and Numerical Determenation of Stress Intensity

Factors of Crack in Plate with a Multiple Holes.”

Damaged and Fracture Mechanics: Failure Analysis of

Engineering Materials and Structures 285 – 295.

Gokul, P.V., Bennet Kuriakose, and Salini Theres N

Kurian. 2016. “Numerical Analysis of Thin Plates with

Holes.” Applied Mechanics and Materials 154-158

Hibbeler, R. 2011. Mechanics of Materials Eight Edition.

United Stated: Pearson Prentice Hall.

Logan, Daryl L. 2011. A First Course in the Finite Element

Method. 5th. Kanada: Cengage Learning.

Misbah, Muhammad Nurul, Septia Hardy Sujiatanti, Dony

Setyawan, Rizky Chandra Ariesta, and Satriyo

Rahmadianto. 2018. “Structural Analysis on the Block

Lifting in Shipbuilding Construction Process.”

MATEC Web of Conference. Surabaya: EDP Sciences.

1 - 6.

Ogeman, Viktor, and Wengang Mao. 2014. “Uncertainty in

Stress Concentration Factor Computation for Ship

Fatigue Design.” Proceedings of the ASME 2014 33rd

International Conference on Ocean, Offshore and

Arctic Engineering (OMAE). San Fransisco, USA:

ASME.

Sujiatanti, Septia Hardy, Totok Yulianto, Wing Prasetyo

Akbar Putra, and Rizky Chandra Ariesta. 2018.

“Influence of the Cut-out Shape on the Fatigue Ship

Structural Detail.” 6th International h International

Seminar on Ocean and Coastal Engineering,

Environmental and Natural Disaster Management.

Surabaya: SCITEPRESS. 111 -115.

Takaki, Yoshifumi, and Koji Gotoh. 2020. “Approximate

weight functions of stressintensity factor for a wide

range shapes of surface and an embedded elliptical

crack.” Marine Structures 70: 1 -22.

Vable, Madhukar. 2010. Mechanics of Materials second

Edition. Michigan: Michigan Technological University

Young, W.C., and R. G. Budynas. 2002. Roark's Formula

for Stress and Strain 7th Edition. United States:

McGraw -Hill.

Figure 9: SCF Analytical vs Numerical.

Figure 8: Stress distribution along path.

Stress Concentration Analysis on Ship Plate with Hole using Numerical Approach

121