Executable State Machines Derived from Structured Textual

Requirements - Connecting Requirements and Formal System Design

Benedikt Walter

, Jan Martin

, Jonathan Schmidt

, Hanna Dettki

and Stephan Rudolph

Research & Development MB Passenger Cars, Daimler AG, Kolumbusstraße 19 + 21, 71059 Sindelfingen, Germany

University of Stuttgart, IFB, Pfaffenwaldring 31, 70569 Stuttgart, Germany

Keywords: Requirements Engineering, Formalization, Executable Finite State Machines, System Design.

Abstract: There exists a gap between (textual) requirements specification and systems created in the system design

process. System design, particular in automotive, is a tremendously complex process. The sheer number of

requirements for a system is too high to be considered at once. In industrial contexts, complex systems are

commonly created through many design iterations with numerous hardware samples and software versions

build. System experts include many experience-based design decisions in the process. This approach

eventually leads to a somewhat consistent system without formal consideration of requirements or a traceable

design decision process. The process leaves a de facto gap between specification and system design. Ideally,

requirements constrain the initial solution space and system design can choose between the design variants

consistent with that reduced solution space. In reality, the true solution space is unknown and the effect of

particular requirements on that solution space is a guessing game. Therefore, we want to propose a process

chain that formally includes requirements in the system design process and generates an executable system

model. Requirements documented as structured text are mapped into the logic space. Temporal logic allows

generation of consistent static state machines. Extracting and modelling input/output signals of that state

machine enables us to generate an executable system model, fully derived from its requirements. This bridges

the existing gap between requirements specification and system design. The correctness and usefulness of this

approach is shown in a case study on automotive systems at Daimler AG.

1 INTRODUCTION

A common automotive system contains well above

1000 functional requirements. It is not possible to

manually consider such a number of requirements at

any moment during the system design process. The

informal textual representation prevents machine-

based support. The result is a system design process

(mostly detached from the given requirements) where

variants are created by system experts without a clear

design decision process. Once a design variant is (or

is perceived as) more or less consistent with the

requirements, this variant is accepted as sufficient.

Most design variants are never considered since the

true solution space, constraint through the

requirements, is unknown. We observe a gap between

specification and formal system design. In our

opinion, the core purpose of system design is to

consider, evaluate and choose from all variants, rather

than struggling with merely finding one variant. To

achieve that, requirements must become part of a

formal and decision based system design process. We

propose a formal process chain starting with

requirements and ending with an executable model in

form of a state machine. Representation of

requirements can be drastically improved with

specification patterns like Master (Sophist, 2016) and

EARS (Mavin and Wilkinson, 2009). Useful for our

formalization are specification pattern systems (SPS)

(Dwyer et al. 1998). It contains an empirical mapping

to linear temporal logic (LTL). LTL can be mapped

into various forms of state machines (FSMs) (Gastin

and Oddoux, 1980; Lu and Luo, 2012). In (Walter et

al., 2018) a process chain with these exact steps (SPS

to LTL to FSMs) is shown. Our process builds on this

approach and extends it towards executable state

machines. It can serve as input for requirements

validation, product design variants and digital

verification. In addition it seems useful since it

maintains traceability for all design objects and

design decisions made. We discuss and answer three

research questions in this paper:

Walter, B., Martin, J., Schmidt, J., Dettki, H. and Rudolph, S.

Executable State Machines Derived from Structured Textual Requirements - Connecting Requirements and Formal System Design.

DOI: 10.5220/0007236601930200

In Proceedings of the 7th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2019), pages 193-200

ISBN: 978-989-758-358-2

193

RQ1: What steps are necessary to automatically

derive an executable state machine from structured

textual requirements?

RQ2: Does an industrial case study show the

correctness and practicality of the derived executable

machine?

RQ3: What are the limitations to the approach of

automatically derived executable stat machines?

The paper is structured in the following way: Section

2 explains the underlying data structure, logic and

state machines. Section 3 provides existing work on

requirements formalization as well as our own

approach which explains the derived execution layer

for state machines. In addition, section 3 shows a

qualitative analysis for one requirement example.

Section 4 explains the dynamic execution, while

section 5 contains a quantitative analysis (scaled

industrial systems). Limitations are discussed in

Section 6 followed by related work in Section 7 and a

brief conclusion in Section 8.

2 DATA STRUCTURE

This section provides the data structure in regards to

the used patterns (specification pattern system), the

used (linear temporal) logic and the state machines.

2.1 Specification Pattern Systems (SPS)

Natural language requirements are problematic for

various reasons like consistency, unambiguity and

redundancy. One solution are specification patterns,

which maintain readability but still provide formal

structure. (Dwyer et al., 1998) derived a template

called specification pattern systems (SPS). It was

initially designed for model checking with SPIN. To

allow that, SPS contains an empirically researched,

case based mapping between each pattern and a linear

temporal logic (LTL) expression.

2.2 Linear Temporal Logic (LTL)

Logical expressions allow formal conversion and

processing (of requirements data). First order logic

(FOL) is capable of connecting (AND), alternating

(OR) and negating (NOT). Further operators are

required to perform temporal ordering. (Prior, 1967)

defined linear temporal logic (LTL) to describe

temporal relations including operators like Global

(G), Next (N) and Future (F). (Kamp, 1968) extended

LTL with the Until (U) operator. (Walter et al., 2017)

described such operators as 'selected’ FOL and LTL.

We use definitions provided in this work. Further

operators are allowed if it can be transformed to the

given set of operators.

2.3 Finite State Machines (FSM)

Complex systems can be formally represented

through automata. One class of automata are finite

state machines. (Walter et al. 2017) showed and

discussed that deterministic finite state machines are

suitable to represent the given LTL input. Thus, we

use definitions from (Kam et al., 2013).

Def. 1 – Moore DFSM: Moore DFSM is a 6-tuple

M={S,I,O,δ,λ,r}. S represents the finite stat space, I

represents the finite input space and O represents the

finite output space. δ is the next state function

(transition logic). λ is the output function (output

logic), r represents reset to start. (Kam et al. 2013).

Combining SPS, LTL and state machines, allows us

to represent and transform requirements from

(structured) text to finite state machines.

3 STATIC MODEL

This section shows how to derive static models from

structured textual requirements, towards executable

state machines. We explain process, core principals

and key process steps. With that, we answer RQ1.

3.1 Overall Process

The overall process separates three core steps.

Deriving LTL expressions from natural language

requirements, creating state machines (FSM) from

representation and connecting the FSM to generate

one system state machine (system FSM). All steps,

except first transformation NL to SPS is automated.

Figure 1: Static model generation (Walter et al., 2018).

In addition all steps are based on correct

mathematical transformations, thus derived system

FSMs are always stepwise provable and thus correct.

We discuss the three core steps more in detail.

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

194

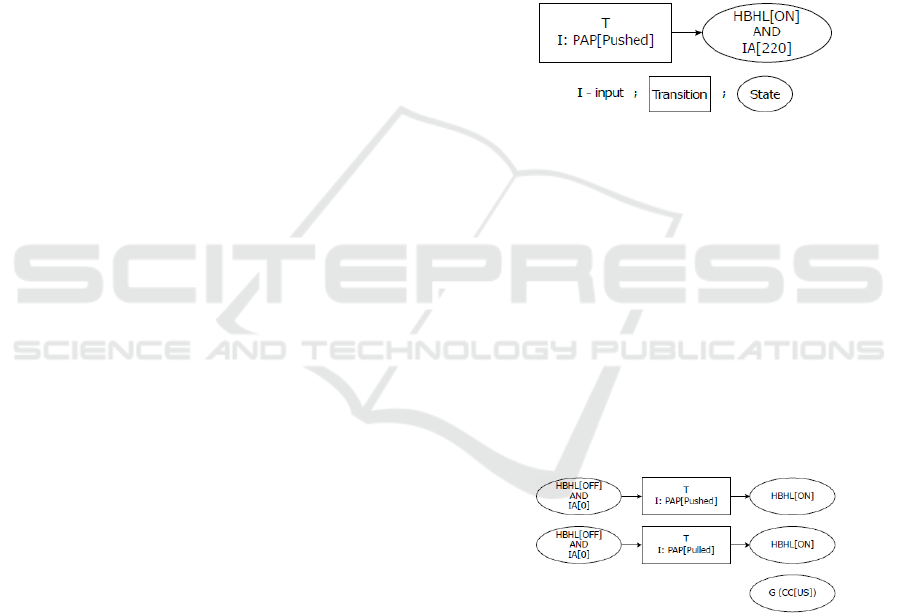
3.2 Specification Patterns to Logic

Requirements in industrial contexts exists mostly as

unstructured text. There exists no formal process to

convert free text into formal representation form.

Thus, the first process step 'NL to SPS' is manual. SPS

maintains readability while providing enough formal

structure to allow machine based processing.

Conversion from textual to logic representation can

be performed with Dwyer’s ‘SPS to LTL' mapping.

NL: Pulling the pitman arm causes the activation of

the high beam headlight with a fixed illumination

range of 220 m.

SPS: (HBHeadlights[ON] AND IlumRange[220]) is

true after PitmanArmPosition[Pushed]

LTL: G PitmanArmPosition[Pushed] I G

(HBHeadlights[ON] AND IlumRange[220])

I = Implies; G - Global

LTL representation is minimal (compact) but it

describes requirements in relation to each other. It

lacks the ability to describe requirements in isolation.

Information is nested and depending on each other.

To remove this problem, LTL is converted into a

state-wise time discrete FOL form.

3.3 Temp. Logic to State Machines

Mapping of LTL onto forward chains in FOL form

was shown in (Walter et al., 2017). Finite state

machines are not simple forward chains but complex

structures consisting of arbitrary arrangements of

states and transitions. It is called diverging structures

for now. (Walter et al., 2018) showed a solution for

'LTL to FOL' mapping for diverging structures. All

variants of forward chains in diverging structure are

extracted. Limitations are: 1. 'A forward chain must

be free of cycles (each existing state can only occur

once per chain)'; 2. 'Start (reset) state must be the

begin of a chain'; 3. 'End state must be the end of a

chain'. This removes repetitions, ring closures and

methodically incorrect chains. Extracted chains are

processed separately. It shows whether all information

for a state or transition are consistent. Inconsistencies

indicate contradicting requirements. Next ‘requirement

FSMs’ are merged into ‘system FSM’.

3.4 System Synthesis

The process to derive static state machines was shown

in Figure 1. It contains processing of requirements

from text (NL) to normal form (CNF). In addition,

different forms of finite state machines are shown.

Each state machine type shall be defined:

Def. 2 – Req. State Machine: A requirement FSM

represents exactly one textual described requirement

in form of a state machine.

Def. 3 – Atomic Req. State Machine: An atomic

requirement FSM represents one atomic requirement

as a state machine.

Def. 4 – System State Machine: System FSM

represents unity of all requirements for the system.

CC – Country Code; IA – Illuminated Range

PAP – PitArmPosition; HBHL – HighBeamHeadlights

Figure 2: Requirement FSM.

One requirement generates one requirement state

machine. Multiple information (e.g. ‘left’ & ‘right’)

can be combined in one requirement in SPS. To

aggregate the system FSM, a synthesis of the

generated atomic requirement FSMs is necessary.

(Walter et al. 2018) splits system synthesis into three

steps:

I - Atomization: Separation of requirement FSMs

into atomic requirement FSMs

Figure 3: Atomization - Atomic Requirement FSMs.

II - Minimization: Connection and minimization of

system FSM with three rules. 'Merge Transitions',

'Merge States' and 'Add Links’. Identical transitions

and identical states are merged. Links that can be

retrieved through logic dependencies are added.

III - Generalization: Generalization of local

requirements with global requirements

Executable State Machines Derived from Structured Textual Requirements - Connecting Requirements and Formal System Design

195

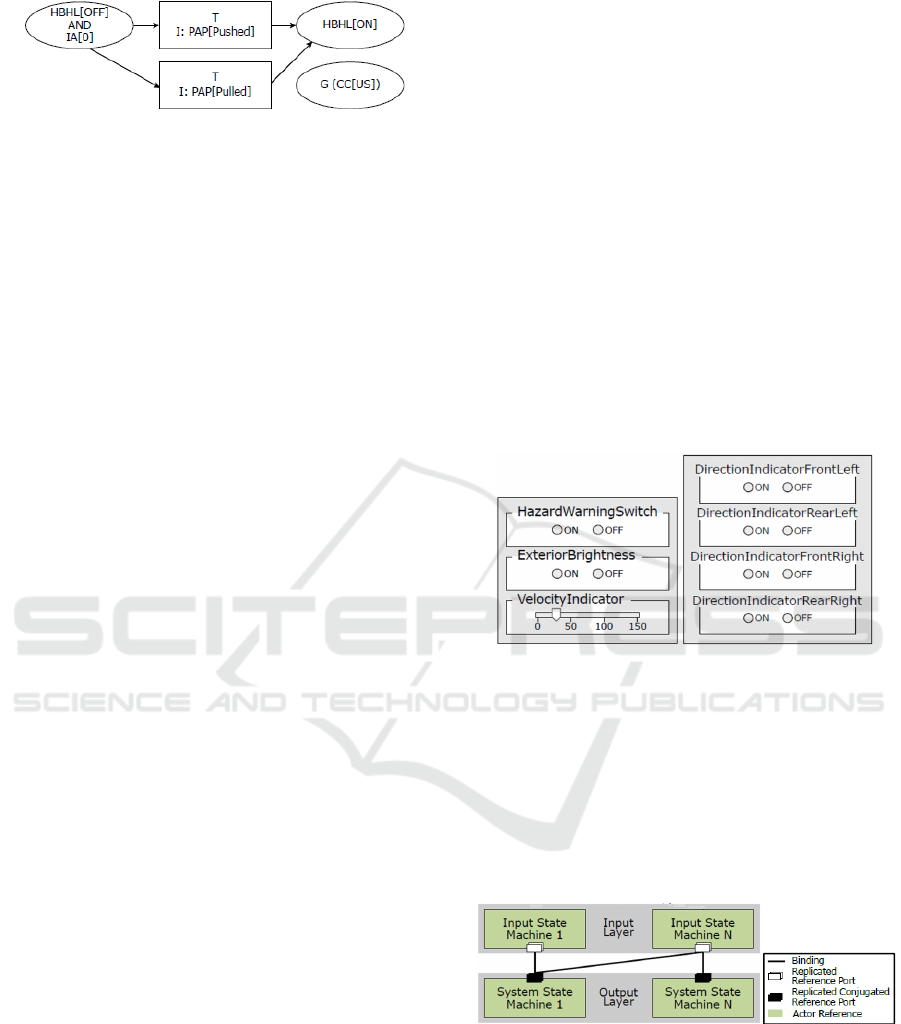
Figure 4: Minimization – System FSM.

Step II and Step III are applied in a loop until the

model is stable. Step III is performed with the same

approach described in Subsection 3.3. Each unique

path through the state machine is extracted and

checked against all global conditions. If the condition

is not yet included, the states and transitions of that

particular path are revised. The updated model is

checked for potential minimization in step II. This

loop eventually converges to a stable model. The

retrieved model is called system FSM. It is a static

representation of the system specified as structured

textual requirements in form of states and transitions.

Systems are generally dynamic. To replicate dynamic

behaviour of the actual system accurately, an

execution layer is included. Such layer enables the

model to show and simulate the dynamic operations.

In this section, we will discuss the implementation of

such an execution layer. This includes the model

structure, GUI for external data input, internal

processing and output.

4 DYNAMIC STATE MACHINE

A static system FSM represents the system specified

by the requirements. To makes such a model

executable, it requires two layers. An external

interaction layer with a GUI and output console as

well as an internal processing layer. This layer

contains the underlying logic and internal signal

transfers. The FSM is exported to ‘eTrice’ and both

layers are added to the existing ‘system FSM’.

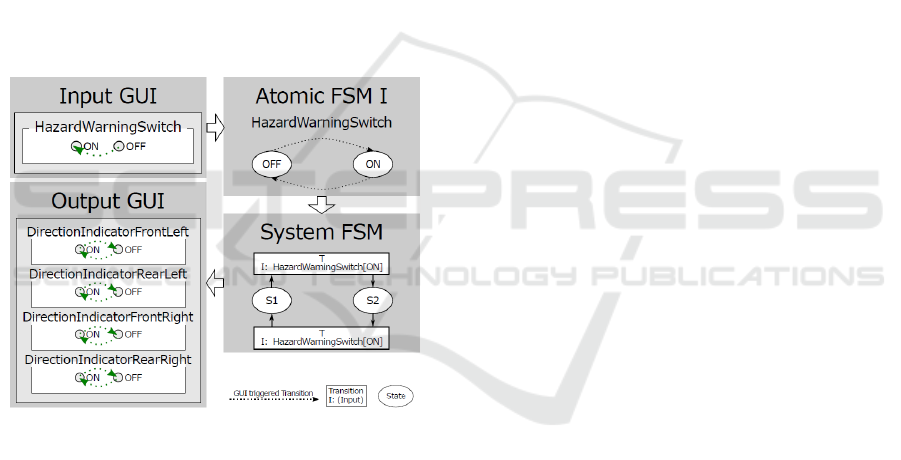
4.1 External Interaction Layer

The external layer serves the purpose to control the

user inputs into the system FSM. The user (tester,

specification engineer, system designer) can change

parameters through a GUI as shown in Figure 5. This

triggers the internal processing layer. The parameters

displayed at the GUI, are all parameters that affect the

system to transition between states. The complete list

of GUI entries is created by crawling all transition

inputs for unique Parameter[StateValue]

combinations. Parameters are methodically split into

two classes. First, parameters for user interactions

(e.g. buttons). Second, parameters that observe the

environment (e.g. sensors). Buttons are intended for

user interaction. Sensors are used for passive

controlling.

Through internal logic, current state is

transitioned to a new current state and a signal with

an output message is sent. This output has to be

represented alongside the new current state.

Therefore, beside input control, the second purpose

of the external layer is displaying output messages.

In its simplest form, this can be performed through

console outputs shown in Figure 5. Next state and

output message are variables of the finite state

machine. In Moore DFSM next state is a function of

current state and transition logic. The internal

processing layer executes this function and returns

the next state to the console. In addition, output logic

which is a function of current state only, generates

the output message and returns that message to the

console.

Figure 5: External Interaction Layer (Input / Output).

4.2 Internal Interaction Layer

To make a FSM truly executable, user interaction

must be possible. It includes user input, processing

and system reaction as feedback. Parameters at

the input layer are parameters that occur in

transitions while parameters at the output layer

occur in states.

Figure 6: Communication Layer.

Def. 5 – Atomic FSM: An atomic FSM represents a

FSM for one parameter with all possible values (one

state per value) and all possible transitions. All other

FSMs (requirement, atomic requirement and system)

consist of combinations of atomic FSMs.

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

196

Implementation occurs in the way that each atomic

FSM is extended with its personal communication

layer. This makes the atomic FSM executable. Once

input changes a particular atomic FSM, atomic FSM

receives a message with new parameter[value] and

current state for the atomic FSM is changed. System

FSM cannot actively request current atomic FSM

states but receives push messages from the particular

atomic FSM once a change occurs. Start state,

therefore current state of system FSM is reset state.

Communicated input is compared with a transition

condition from current state to all connected states. If

fulfilled, system FSM changes its current state and

generates output (see: Figure. 6).

4.3 Execution Example

Overall, section 4 discussed all steps to answer RQ1

with qualitative examples. This is consolidated now

in one overall example. All graphical visualizations

of GUIs and FSM are represented in Figure 7.

Figure 7: Execution Example.

Initially input shows

HazardWarningSwitch[OFF]. Output shows all

DirectionIndicators as initially [OFF]. The current

state for the Atomic FSM and System FSM are in

accordance (Atomic FSM I is in state [OFF] and

System FSM is in state S

). User input changes

HazardWarningSwitch[ON]. The communication

layer broadcasts this change to the Atomic FSM

where current state is changed to [ON]. Further,

Atomic FSMs communicate changes to system FSM.

Here, the transition condition at current state is

checked. Since it is now fulfilled, current state is

adjusted from S

to S

. The corresponding output is

generated in the form that all DirectionIndicators turn

to [ON]. Again, the transition condition at the new

current state (S

) is checked. It is fulfilled, thus

current state changes back to S

with its

corresponding output of all DirectionIndicators equal

to [OFF]. Obviously, as long as the Atomic FSM is

in state [ON], the System FSM changes between S

and S

periodically. Transition condition of S

and S

are not fulfilled as soon as input changes

HazardWarningSwitch[OFF]. This change is broad-

casted to the Atomic FSM, which communicates this

change to System FSM. In this case all

DirectionIndicators remain [OFF].

5 APPLICATION

In this section, RQ2 is addressed. We show the

derived executable model in an industrial case study.

With the Adaptive Outside Light Control (AOLC)

a Mercedes-Benz Car Systems is investigated.

We show correctness of our executable model by

applying a set of test cases for functional

system tests against the model and comparing the

generated output messages to the expected results

for the test cases. Subsection 5.1 provides a brief

overview of the assumptions and requirements for

data and tool chain. Subsection 5.2 explains case

study and detailed approach. It is evaluated in

Subsection 5.3.

5.1 Assumptions

The AOLC system has to fulfil a set of conditions and

constraints: Requirements are represented in a

structured specification while test cases exist in a

structured test specification. All requirements and test

cases are tagged for the attribute 'object type' with

either 'requirement' or 'test case'. Linking between

requirements and test cases exists. Requirements,

tests cases and links are stored in a requirements

management tool with ReqIF file export (e.g. IBM

Rational Doors). The systems is initially represented

in natural language expressions. Requirements are

converted from text to SPS. Tests remain in natural

language. Textual representation prevents machine-

based processing, which is not needed in our case.

The static model is derived in Design Cockpit 43

(DC43), which is based on an Eclipse framework.

The executable model therefore is represented in the

Eclipse extension ‘eTrice’.

5.2 Setup and Approach

This section explains the data set of the AOLC

system, setup and approach used to generate the

Executable State Machines Derived from Structured Textual Requirements - Connecting Requirements and Formal System Design

197

results for the evaluation. We choose this system

based on availability. AOLC is a publicly available

set of requirements and tests of the original system. It

was investigated (Föcker et al., 2015 and Walter et

al., 2018) and is therefore already formalized in SPS.

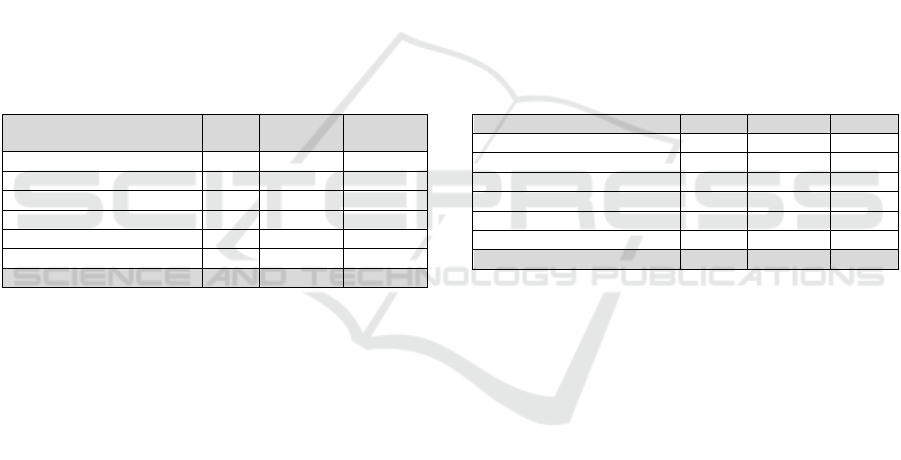
Table 1 shows the system in quantitative form. From

the full set of 50 requirements we only choose 38

functional requirements for the investigation. Data is

structured by functions. Each function contains

requirements and test cases that are linked to each

other. Overall, we consider 38 requirements and 38

test cases. Our approach for the given data set is to

derive the executable model and to apply the

specified test cases. The static model is based on the

functional requirements. The process generated a

system FSM with 47 system states and 256

transitions. Test cases are compared against output

generated for a specific system state. A test case

contains a set of steps (TS), where each step has a

precondition, action and pass condition. All tests are

represented in natural language.

Table 1: System metrics AOLC.

Function

Total

Req.

Func.

Req.

Test

Cases

Turn and Warning Sig. 21 15 20

Low Beam Headlight 9 6 7

Adapt. HB Headlights 9 9 2

Man. HB Headlights 2 2 2

Fault Detection 6 3 6

Headlight Technology 3 3 1

Total System 50 38 38

Linking between tests and requirement in addition

to the traceability between requirement and system

states, allows locating the system states related to a

particular test case. (Walter et al., 2018) showed

correctness and practicality of the generated static

system FSMs. We intend to verify the executable

machine by execution of the related buttons at the

GUI and comparing output to specified tests in a

black box test. The assumption is that requirements

and test cases are correct. We do not intend to test the

system specification but we show that the executable

machine represents the specification.

5.3 Evaluation

In this subsection we evaluate the case study. We

discuss our findings, comment on the results and

overall answer RQ2. Table 2 shows the quantitative

evaluation of the test steps. The results of test steps

are divided into three branches: Passed test steps,

blocked TS and failed TS. Passed test steps generate

the specified output. Starting with the precondition,

performing the given action and checking the pass

conditions. Passed tests are in alignment with the

approach and need no further discussion. Blocked

tests sequence of precondition, action and pass

condition which are not executable. A closer look at

these test steps and the reason for the blocking has

to be considered. Failed test steps are characterized

with incorrect output generation (pass condition)

after performing the specified action starting from

the specified precondition. Occurrences of failed TS

are critical and have to be reviewed to assure that

such a test does not challenge the overall

approach. Generally, 63 out of 80 test steps are

classified as passed test steps and therefore need no

further discussion. Eight test steps turned out to be

blocked. All eight of them, located in the vehicle

function ‘Turn and Warning Signalling', are blocked

due to a not yet fully developed interface to 'eTrice'.

The 'Bounded existence' pattern requires encoding

of a counter, which caused implementation

problems.

Table 2: Evaluation AOLC with test steps (TS).

Function Passed Blocked Failed

Turn and Warning Sig. 36 8 2

Low Beam Headlight 17 0 2

Adapt. HB Headlights 4 0 2

Man. HB Headlights 4 0 0

Fault Detection 2 0 3

Headlight Technology 0 0 0

Total System 63 8 9

A fully developed interface should change these

test steps to passed test steps. The failed test steps are

distributed among nearly all vehicle functions. A

case-wise review and analysis is required. Two failed

tests were caused by imprecise structuring of

requirements text at the manual transformation from

NL to SPS. The remaining seven test steps can be

traced back to incomplete specifications in the initial

text form. In conclusion, neither blocked nor failed

test steps are caused by our developed formalization

process. Our findings for the selected AOLC system

validate correctness of the generated system FSM. All

states and transitions are plausible. All blocked and

failed tests were caused by pre-processing errors or

‘eTrice’ limitations. Thus, our approach to derive

state machines from structured text with the provided

process seems valid.

6 LIMITATIONS

In this section we discuss limitations to our approach

and with this we answer RQ3. First we have to

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

198

address the general scope of the described approach.

The specification patterns we used are designed for

functional requirements. It is possible to include

certain non-functional requirements, but the majority

cannot be formalized in SPS. Informal knowledge is

a problem that exceeds the scope of this paper. We

therefore limit the overall approach to functional

requirements with the possibility to process selected

non-functional requirements. Regarding scale, we

observe multiple points to discuss: We see run time

for scaled systems as uncritical. Tasks like importing

scaled ReqIF data sets and generating industry sized

graphs were performed and did not cause extended

run times. More critical is readability for particular

states and its descriptions in scaled systems. The

shown application contained up to ten parameters for

a state description. In scaled systems this will

dramatically increase and might reduce human

readability drastically. One solution is to use this

approach mostly for machine based analysis. Second,

it is possible to investigate only reduced systems for

particular analysis by filtering the overall system for

particular parameters. This option maintains the

complexity and correctness of the represented system

FSM while focusing the analysis on the particular

parameters relevant. Last, we want to discuss scope.

We applied this approach only to the automotive light

domain, yet we strongly believe that other domains

can use this approach without adaptations. Once a

specification pattern can express a requirement, it can

be used for modelling. SPS were developed domain

independent. We showed work in the field of

automotive. Yet, we emphasize other fields to use this

approach. We see no hindrance to express

requirements of various domains in SPS and to derive

system FSMs. Pre-processing of requirements in SPS

and representation as system FSM should still be

reviewed by domain experts.

7 RELATED WORK

This work included previous work in various fields.

In the introduction, we discussed the structured

representation of requirements in form of

specification patterns. Common patterns are Master

(Sophist, 2018) EARS (Mavin and Wilkinson, 2009),

Volere (Robertson and Robertson, 2009) and

Specification Pattern Systems (SPS) (Dwyer et al.,

1998). SPS are tightly connected with linear temporal

logic. Linear temporal logic was initially described by

(Prior, 1967, and Kamp, 1968). Representation of

complex systems is often performed in form of state

machines. We used the work of (Kam et al., 2013) as

the foundation for finite state machines. The

connection between linear temporal logic and state

machines occurs through mapping. We based our

own mapping efforts on (Gastin and Oddoux, 2001,

Lu and Luo 2012 and Walter et al., 2018). To

represent derived state machines we use Design

Cockpit 43 as a software. Design Cockpit 43 is based

on design grammars. (Rudolph, 2006, Rudolph et al.,

2013, Alber et al., 2002) described the underlying

methodology of vocabularies, rule set, production

system and compiler. The Graph-based design

methodology paired with the described processing

chain, allows us to derive a consistent model from

textual requirements. The general idea for model

generation from structured text was provided by

(Walter et al., 2017) and extend here towards

executable models.

8 CONCLUSIONS AND

OUTLOOK

This paper showed an approach to formally process

structured textual requirements into executable finite

state machines. The process chain from textual requi-

rement representation to system creation is often not

continuous and contains gaps. This leads to informal

decision making throughout the process and signify-

cantly limits the exploration of the solution space

during system design. Our approach bridges that gap

by providing a systematic transformation chain that

generates a formally correct executable representation

of the system specified through its requirements. We

see this as a valuable support for specification and

system design. The approach limits manual decision

making in steps where decisions can be formally

derived. It allows specification engineers and system

design engineers to evaluate what consequences and

design constraints arise from creation or adjustment of

a particular requirement. Execution of the derived state

machine enables engineers to expose missing states

and transitions, non-deterministic behaviours and

inconsistencies in their specification or design. In this

setup, an executable FSM serves as a model in the loop

(MIL). Specifications can be adjusted and changes in

the system can be evaluated instantly. We provide a

qualitative example and a quantitative case study to

show applicability in industrial setups. This work

provides the basis for further applications. We would

like to show scalability and intend to add further

system design steps towards a requirement driven

digital design process for complex (automotive)

systems.

Executable State Machines Derived from Structured Textual Requirements - Connecting Requirements and Formal System Design

199

ACKNOWLEDGEMENTS

We want to thank our collaborators at Daimler AG:

Frank Houdek, Marco Piechotta and Jakob Hammes

in the testing department for their input, help with

data set and system knowledge for the case study.

REFERENCES

Alber, R., Rudolph S., Kröplin, B. "On Formal Languages

in Design Generation and Evolution." 5th World

Congress on Comp. Mechanics, 2002.

Alber, R., Rudolph, S.”43 - A Generic Approach for

Engineering Design Grammars.” AAAI Spring Symposium

Computational Synthesis, 2003.

Alber, R, Rudolph, S. "On a Grammar-Based Design

Language that Supports Automated Design Generation

and Creativity." In Knowledge Intensive Design

Technology, Springer, 2004.

Artale, A, Franconi, E. "A Temporal Description Logic for

Reasoning about Actions and Pans." Journal of

Artificial Intelligence Research, 1998.

Artale, A.. ”Linear Temporal Logic.” LectureNotes:

Formal Methods Lecture III, 2010.

Bühler, D., Minker, W. “Domain-Level Reasoning for

Spoken Dialogue Systems. Springer Science, 2011.

Clarke, E., Emerson, A., Sistla, P.”Automatic Verification

of Finite-State Concurrent Systems Using Temporal

Logic Specifications.” ACM, Transactions on

Programming Languages & Systems (TOPLAS), 1986.

Czerwinski, R, Kania, D.”Finite State Machine Logic

Synthesis for Complex Programmable Logic Devices”.

Springer Science, 2013.

Dwyer, M., Avrunin, G., Corbett, J.”Property Specification

Patterns for Finite-State Verification.” In Proceedings

of the Second Workshop on Formal Methods in

Software Practice, ACM, 1998.

Dwyer, M., Avrunin, G., Corbett, J. "Patterns in Property

Specifications for Finite-State Verification." Software

Engineering, 1999.

Föcker, F., Houdek, F., Daun, M., Weyer. T., ”Model-

Based Engineering of an Automotive Adaptive Exterior

Lighting System: Realistic Example Specifications of

Behavioural Requirements and Functional Design.”,

2015.

Gabbay, D., Pnueli, A., Shelah, S., Stav, J. ”On the

Temporal Analysis of Fairness.” In Proceedings of the

7th ACM SIGPLAN-SIGACT Symposium on Principles

of Programming Languages, ACM, 1980.

Gastin, P., Oddoux, D.”Fast LTL to Büchi Automata

Translation.” In International Conference on Computer

Aided Verification, Springer, 2001.

Glinz, M.. ”On Non-Functional Requirements.” In

Requirements Engineering Conference, 2007.

IILS mbH, "Design Cockpit 43" http://iils.de (05/ 2018).

IILS mbH,”Total Engineering Automation Vision and

Realization with Graph-based Design Languages and

the Design Cockpit 43.” http://iils.de, (05/2018).

ISO/IEC/IEEE 29148: 2011(E): ISO/IEC/IEEE Int.

Standard, Systems & Software Engineering Life Cycle

Processes Requirements Engineering. IEEE, 2011.

Etrice, Eclipse Plugin. https://www.eclipse.org/etrice/,

(02/2018).

Kamp, H. ”Tense Logic and the Theory of Linear Order.”,

1968.

Kam, T., Villa, T., Brayton, R., Sangiovanni-Vincentelli, A.

"Synthesis of Finite State Machines: Functional

Optimization." Springer Science, 2013.

Lu, X., Luo, G. ”Direct Translation of LTL Formulas to

Büchi Automata.” In Cognitive Informatics &

Cognitive Computing, 2012.

Maalej, W. Thurimella, A. “Managing Requirements

Knowledge, 2013.

Mavin, Alistair, Wilkinson, P. "Big Ears (The Return of

"Easy Approach to Requirements Engineering")." In

Requirements Engineering Conference, 2010.

Mavin, A., Wilkinson, P., Harwood, A., Novak, M. ”Easy

Approach to Requirements Syntax (EARS).” In

Requirements Engineering Conference IEEE, 2009.

Pahl, G, Beitz, W. ”Engineering Design: A Systematic

Approach.” Springer Science, 2013.

Prior, A. ”Past, Present and Future.” Oxford: Clarendon

Press, 1967.

Robertson, J., Robertson, S. ”Volere Requirements

Specification Template.”, 2009.

Rudolph, S.”A Semantic Validation Scheme for Graph-

Based Engineering Design Grammars.” In Design

Computing and Cognition06, Springer, 2006.

Rudolph, S., Beichter, J., Eheim M., Hess, S., Motzer, M.,

Weil, R. "On Multi-Disciplinary Architectural

Synthesis and Analysis of Complex Systems with

Graph-Based Design Languages." DGLR, 2013.

Sophist GmbH:”MASTeR Schablonen für alle Fälle” 2016

Spillner, A., Linz, T., ”Basiswissen Softwaretest”,

dpunkt.Verlag GmbH, 2005.

Villa, T., Kam, T., Brayton, R., Sangiovanni-Vincentelli, A.

”Synthesis of Finite State Machines: Logic

Optimization.” Springer Science, 2012.

Walter, B., Hammes, J., Piechotta, M., Rudolph, S.”A

Formalization Method to Process Structured Natural

Language to Logic Expressions to Detect Redundant

Specification and Test Statements.” In Requirements

Engineering Conference (RE), IEEE, 2017.

Walter, B., Schilling M., Piechotta, M., Rudolph, S.

”Improving Test Execution Efficiency through

Clustering and Reordering of Independent Test Steps.

„Software Testing, Verification & Validation, 2018.

Walter, B., Martin, J., Rudolph, S. ”A Method to

Automatically Derive the System State Machine from

Structured Natural Language Requirements through

Requirements Formalization.” INCOSE, 2018.

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

200