A Fast and Efﬁcient Method for Solving the Multiple Closed Curve

Detection Problem

Una Radoji

, Rudolf Scitovski

and Kristian Sabo

Department of Mathematics, University of Osijek, Trg Ljudevita Gaja 6, 31 000 Osijek, Croatia

Keywords:

Multiple Closed Curve Detection Problem, k-means Algorithm, Globally Optimal Partition, DIRECT.

Abstract:

The paper deals with the multiple closed curve detection problem, i.e. the multiple circle and the multiple

ellipse detection problem are especially considered. Based on data coming from a number of closed curves not

known in advance, it is necessary to recognize these curves. The approach we propose is based on center-based

clustering, which means that the problem is reduced to searching for an optimal partition whose cluster-centers

are the closed curves we searched for. By using a modiﬁed well-known k-means algorithm with carefully

chosen initial approximation we shall look for these curves. For detecting the most appropriate number of

clusters (closed curves), we have also proposed a new, specialized index that was signiﬁcantly better than

other well-known indexes.

1 INTRODUCTION

Let A = {a

= (x

)

∈R

: i = 1,...,m}, A ⊂∆ :=

[α

,β

] ×[α

,β

] be a set of data points coming from

a number of multiple closed curves in the plane not

known in advance that should be reconstructed or de-

tected. Suppose that data coming from a curve are ho-

mogeneously distributed around that curve such that

random errors from normal distribution with expecta-

tion 0 are added to uniformly distributed points on the

curve in the direction of a normal.

The paper is organized as follows. In Section 3

the multiple closed curve detection problem is de-

ﬁned, a modiﬁcation of the well-known k-means al-

gorithm for such problems is given and two new al-

gorithms are proposed, in which a new index for de-

tecting the most appropriate number of clusters is ap-

plied. In Section 4, we analyze some special cases

and give corresponding illustrative and numerical ex-

amples. Finally, some conclusions are given in Sec-

tion 5.

2 PRELIMINARIES

The method for solving the multiple closed curve de-

tection problem proposed in this paper is based on

https://orcid.org/0000-0003-0329-0595

https://orcid.org/0000-0002-7386-5991

https://orcid.org/0000-0002-1787-3161

center-based clustering; hence we shall outline the

main facts. In addition to using some distance-like

function d : R

×R

→ R

, R

= [0,+∞⟩ (see e.g.

(Kogan, 2007; Sabo et al., 2013)), the set A can be

partitioned into k clusters π

,...,π

with centers

:= argmin

x ∈conv(A)

∑

∈π

d(x, a

), (1)

by solving an appropriate global optimization prob-

lem (

GOP

)

argmin

c∈conv(A)

F(c), F(c) =

∑

i=1

min

1≤j≤k

d(c

), (2)

where F : R

→ R

is a Lipschitz continuous sym-

metric, but nondifferentiable and nonconvex function.

Problem (2) is well known under the name center-

based clustering problem.

The problem of recognizing some closed curve

and the problem of detecting a partition with the most

appropriate number of clusters with curve-centers can

be observed separately, but these two problems are es-

sentially closely related. The new index, proposed in

our paper, is specialized in such situations and shows

very good results.

Radoji

c, U., Scitovski, R. and Sabo, K.

A Fast and Efﬁcient Method for Solving the Multiple Closed Curve Detection Problem.

DOI: 10.5220/0007238902690276

In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 269-276

ISBN: 978-989-758-351-3

269

3 THE MULTIPLE CLOSED

CURVE DETECTION

PROBLEM

In our paper, we consider the multiple closed curve

detection problem as a special center-based cluster-

ing problem, where cluster-centers are closed curves

), j = 1,...,k, where p

∈ R

is a vector of pa-

rameters. This means that the set A will be partitioned

into k ≥ 1 nonempty mutually disjoint clusters whose

centers will be curves C

. In what follows, they will

be called C -cluster-centers.

For example, we can consider the multiple cir-

cle detection problem (Akinlar and Topal, 2013; Sc-

itovski and Maro

sevi

c, 2014), the multiple ellipse

detection problem (Akinlar and Topal, 2013; Grbi

et al., 2016; Maro

sevi

c and Scitovski, 2015; Mosh-

taghi et al., 2011), the multiple generalized circle de-

tection problem (Thomas, 2011), etc. For each of

these types of curves, specialized methods have been

developed, which can be seen in the aforementioned

references.

Such problems occur in a number of applica-

tions like pattern recognition, computer vision and

robotics (Akinlar and Topal, 2013; Prasad et al.,

2013), anomaly detection in wireless sensor networks

(Moshtaghi et al., 2011), medical diagnosis (Grbi

et al., 2016), agriculture etc.

According to (2), the problem of searching for an

optimal k-partition will be deﬁned as the following

GOP

argmin

p∈R

F(p), F(p) =

∑

i=1

min

1≤j≤k

D(C

),a

), (3)

where p = (p

,..., p

) and D(C

),a

) is the dis-

tance from the point a

∈ A to the curve C

. This dis-

tance can be determined numerically (see e.g. (Ute-

shev and Goncharova, 2018)), but for the most com-

monly used curves there are explicit formulas.

Since with an increase in the number of clusters

k in the partition the value of the corresponding ob-

jective function F

decreases monotonically (Kogan,

2007; Scitovski and Scitovski, 2013) and since the

number of clusters (the number of curves) k is not

known in advance, we shall search for optimal k-

partitions for k = 1, 2, . . . until the following condi-

tion is met for some small ε

> 0 (say .005) (Bagirov,

2008):

k−1

−F

< ε

. (4)

Among the obtained optimal partition we should

choose the one with the most appropriate number of

clusters. Some modiﬁcation of standard indexes such

as Davies-Bouldin, Calinski-Harabasz, etc. (see e.g.

(Morales-Esteban et al., 2014)), can be used for this

purpose. By using a special structure of the problem

in Subsection 3.4 we deﬁne a new index that is signif-

icantly better. This index will enable us to stop the

procedure of searching for new optimal partitions be-

fore meeting criterion (4).

For solving

GOP

(3) we can use a derivative-

free, deterministic sampling method for global opti-

mization of a Lipschitz continuous function g: D →

R deﬁned on a bound-constrained region D ⊂ R

named Dividing Rectangles (

DIRECT

) was proposed

by (Jones et al., 1993). The function g is ﬁrst trans-

formed into f : [0,1]

→ R, and after that, by means

of a standard strategy (see, e.g. (Grbi

c et al., 2013;

Gablonsky, 2001; Jones et al., 1993; Jones, 2001;

Paulavi

cius and

Zilinskas, 2014)), the unit hypercube

[0,1]

is divided into smaller hyperrectangles, among

which the so-called potentially optimal ones are ﬁrst

searched for and then further divided. It should be

noted that this procedure does not assume knowing

the Lipschitz constant L > 0. However, although the

objective function F from (3) is Lipschitz-continuous,

solving

GOP

(3) directly by applying the algorithm

DIRECT

is not acceptable since F is a symmetric func-

tion with n ×k variables in k parameters p

,... , p

∈

, which, due to these reasons, has at least k! dif-

ferent points in which it reaches the global minimum.

The

DIRECT

algorithm would search for all of these

points and because of that its efﬁciency would be very

low.

Therefore for solving

GOP

(3) we propose the

method which can be shortly described in two steps.

First, ﬁnd a good initial approximation by applying

the

DIRECT

algorithm and after that ﬁnd an optimal

solution by applying the k-means algorithm modiﬁed

for the case of C -cluster-centers.

3.1 Searching for an Initial

Approximation for GOP (3)

An initial approximation for

GOP

(3) will be searched

for such that we consider the problem of search-

ing for an optimal partition whose cluster-centers

are some simple geometrical objects resembling our

closed curves and possibly with a small number of pa-

rameters. By applying a smaller number of iterations

of the

DIRECT

algorithm we can obtain an acceptable

initial approximation for

GOP

(3). In this way, we

will try to at least position well the closed curves we

search for.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

270

3.2 Modiﬁcation of the k-means

Algorithm for C -cluster-centers

In order to ﬁnd an optimal k-partition, we shall use the

well-known k-means algorithm modiﬁed for the case

of C -cluster-centers. The algorithm can be described

in two steps repeated successively.

Algorithm 1: Modiﬁcation of the k-means algorithm for C -

cluster-centers (

KMCC

Modiﬁcation of the k-means algorithm for C -cluster-

centers (

KMCC

A: For each set of mutually different curves

),. . . , C

), the data set A should be parti-

tioned into k disjoint nonempty clusters by using

the minimum distance principle

= {D(C

),a) ≤ D(C

),a), ∀s ̸= j} (5)

B: For the given partition Π = {π

,... ,π

} of the

set A, we should determine the corresponding C -

cluster-centers

( ˆp

), j = 1,. . . , k by solving the

following

GOPs

( ˆp

) ∈ argmin

p∈R

∑

a∈π

D(C

(p),a). (6)

GOP

(6) could be solved by applying the

DIRECT

algo-

rithm, but if we are able to ﬁnd a good initial approxi-

mation for the curve C

as a representant of the cluster

, then we can apply some local optimization method

(i.e. Nelder-Mead or some Quasi-Newton method).

3.3 A New Algorithm for Searching for

an Optimal k-partition

As already mentioned in Subsection 3.1, a new algo-

rithm for solving

GOP

(3) refers to ﬁnding a good ini-

tial approximation, which will be used in the

KMCC

algorithm in order to search for an optimal solution.

Algorithm 2: Searching for an optimal k-partition.

Input: A ⊂ ∆ ⊂ R

{Set of data points}; k ≥ 1;

1: Choose a family of some simple curves

and

ﬁnd an approximation of

GOP

(3) for them by ap-

plying a few iterations of the

DIRECT

algorithm;

2: Apply the

KMCC

algorithm with the initial approx-

imation from Step 1;

Output: {k,Π

⋆

, {C

⋆

,... ,C

⋆

}, F

⋆

3.4 A New Index for Detecting the Most

Appropriate Number of Clusters

Let A ⊂ R

be a given set of data points coming

from a number of closed curves not known in ad-

vance. Assume that data coming from a curve are ho-

mogeneously distributed in the neighborhood of that

curve such that random errors from normal distribu-

tion with expectation 0 are added to uniformly dis-

tributed points on the curve in the direction of a nor-

mal. By uniformly distributed points on the curve we

mean points randomly chosen in such a way that the

probability of choosing a point on a particular arc is

proportional to its length. By using the concept from

the DBSCAN algorithm (see e.g. (Ester et al., 1996;

Viswanath and Babu, 2009)), we will try to estimate

the density of points in the neighborhood of the curve.

For the given MinPts > 2 (according to (Ester

et al., 1996) we take MinPts = 3) and for every a ∈A

we deﬁne the radius ε

> 0 of the circle in which

there are MinPts elements of the set A. For the set

R = {ε

: a ∈ A} of all these radii, we determine the

mean and the variance, and we deﬁne the parameter ε

as:

ε := µ + 3σ,

µ = Mean(R ), σ

|R |−1

∑

a∈B

(ε

−µ)

. (7)

Figure 1: Determination of the parameter ε.

Example 1. Let us consider the set of data A coming

from 4 ellipses (see Fig. 1a). A sequence (ε

) and the

options for choosing the parameter ε are shown in

A Fast and Efﬁcient Method for Solving the Multiple Closed Curve Detection Problem

271

Fig. 1b. We have opted for ε = µ + 3σ because in this

case, for almost all points a ∈ A, the circle C(a,ε)

contains at least MinPts points from A.

Let Π = {π

,... ,π

} be an optimal k-partition of

the set A, whose cluster-centers are closed curves

,... ,C

and let ε > 0 be the parameter value esti-

mated by (7). For each cluster π

, j = 1, . . . , k we

deﬁne a set V

= {D

,a): a ∈ π

} of orthogonal

distances from the points of the cluster π

to the curve

. Due to the character of the set A, the elements of

the set V

come from the folded normal distribution

with the location parameter 0 (see, e.g. (Tsagris et al.,

2014)).

Because of the assumption of homogeneity of data

around the curves searched for if the curve C

is well

detected, the absolute deviation of the majority of

points from π

to the curve C

(i.e. Quantile Abso-

lute Deviation (

QAD

)),

QAD

( j) = µ

+ 2σ

, (8)

= Mean(V

), σ

|−1

∑

∈V

−µ

)

should be less than ε.

The new index should depict this property for ev-

ery curve C

; thus the new Density Based Clustering

index (

DBC

) is deﬁned by:

DBC

(k) = max

j=1,...,k

QAD

( j). (9)

Note that the

DBC

-index deﬁned in this way describes

a k-partition such that it detects the cluster whose

representant deviates most (in terms of the 95th per-

centile) from data associated to that cluster.

3.5 A New Algorithm for Searching for

an Optimal Partition With the Most

Appropriate Number of Clusters

The concept of the algorithm is as follows. First,

according to (7), for the given set A we deﬁne the

parameter ε. After that, in accordance with Algo-

rithm 2, we determine optimal k-partitions and the

corresponding values of the

DBC

-index in line with

(8)-(9) for k = 1,... until the

DBC

(k) value becomes

less than ε or until criterion (4) is met.

If among these k partitions we do not ﬁnd a glob-

ally optimal one, the

DBC

-index will not be less than

ε, and the algorithm will stop running based upon cri-

terion (4) in the k-th step.

Algorithm 3 : Searching for an optimal partition with the

most appropriate number of clusters.

Input: A ⊂ ∆ ⊂ R

{Set of data points }; ε

> 0

{According to (Bagirov, 2008)};

1: Determine parameter ε > 0 according to (7);

2: Set k = 1 and call Algorithm 2; Determine Π

, F

QAD

, and

DBC

;

3: if

DBC

< ε, then

4: GO TO Output;

5: end if

6: while

Set k = k +1 and call Algorithm 2; Determine Π

,... ,C

, F

QAD

, and

DBC

;

DBC

> ε & (F

−F

)/F

> ε

7: Set F

= F

;

8: end while

9: if

DBC

< ε, then

10: k curves C

,... ,C

detected;

11: else

12: Investigate especially cases when

QAD

( j) <

ε;

13: end if

Output: {k,Closed curves detected}.

Remark 1. If DBC > ε occurs at the end of

Algorithm 3, then all components of the vector

(QAD(1),. . . , QAD(k)) should be checked up. For ev-

ery s ∈{1,...,k}, for which QAD(s) < ε, there is hope

that the s-th curve has been detected, which can be

additionally checked up based upon the density of

data by curves ρ

|π

, s = 1,...,k.

4 SOME SPECIAL CURVES

Some closed curves will be analyzed that most fre-

quently occur in the literature and that have signiﬁcant

applications in different areas.

4.1 Multiple Circle Detection Problem

Let A ⊂ ∆ ⊂R

be a set of data points coming from a

number of multiple circles in the plane not known in

advance.

When searching for an optimal k-partition (see

Subsection 3.3) we will use the algebraic distance

D(C (S, r),a) from the point a ∈A to the circle C with

the center S and the radius r, and when deﬁning the set

by the

DBC

-index (see Subsection 3.4) we will use

the Least Absolute Distance (LAD) D

(C (S, r),a):

(C (S, r),a) = |∥S −a∥−r| (10)

D(C (S, r),a) = (∥S −a∥

−r

)

(11)

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

272

Now

GOP

(3) can be written in the following way:

argmin

S∈∆

,r∈[0,R]

∑

i=1

min

1≤j≤k

D(C

),a

). (12)

Example 2. Let A be the set of data points coming

from k circles C

,... ,C

homogeneously distributed

in the neighborhood of the circles. Four selected ex-

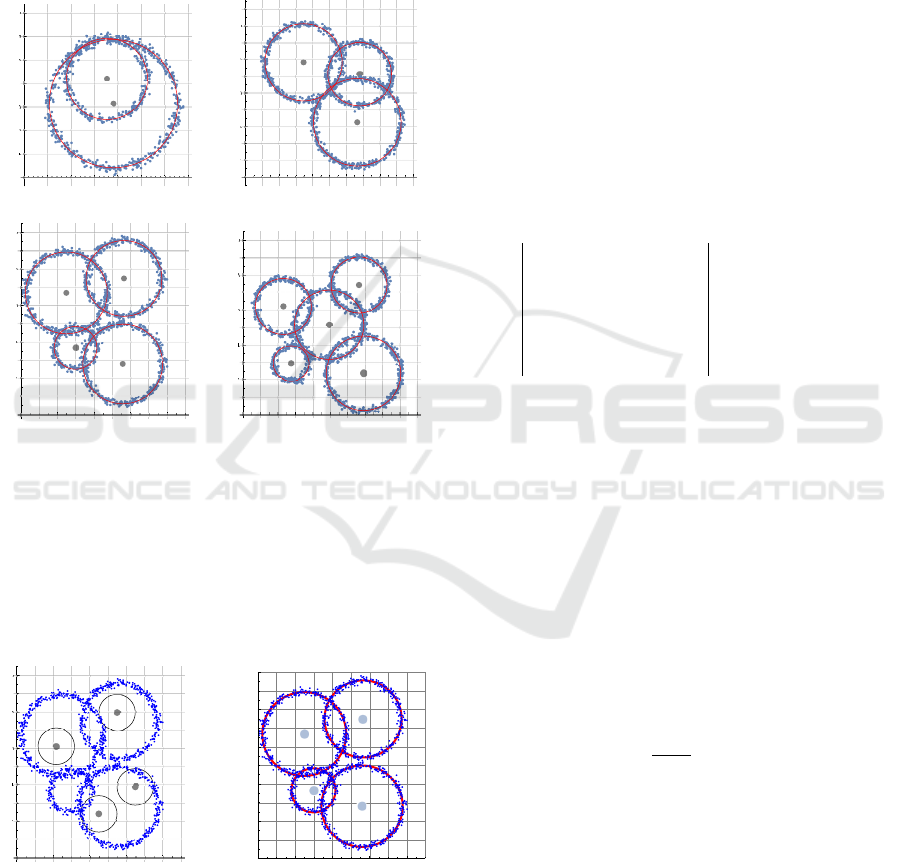
amples with k = 2,3,4,5 circles are shown in Fig. 2.

3 4 5 6 7 8 9

(a) k = 2

2 4 6 8 10

(b) k = 3

4 6 8 10

2 4 6 8 10

(d) k = 5

Figure 2: Four selected examples with k = 2,3,4,5 cir-

cles.

Let us consider a data point set A shown in

Fig. 2c. According to Algorithm 2, by using the

DIRECT

algorithm, we ﬁrst determine an initial ap-

proximation (unit circles shown in Fig. 3a), and after

that, by using the KMCC algorithm, we obtain the so-

lution (Fig. 3b)).

4 6 8 10

(a) Initial approximation

2 4 6 8 10

(b) Solution

Figure 3: Implementation of Algorithm 2 for circles.

Searching for an optimal partition with the most

appropriate number of clusters will be illustrated by

using the same example. Algorithm 3 terminates when

the value of the DBC-index drops below the estimated

value of the parameter ε = 0.227 deﬁned by (7).

We obtained DBC(1) = 1.93, DBC(2) = 1.07,

DBC(3) = 0.47, and DBC(4) = 0.17. This means that

the 4-partition is an optimal partition and all circles

have been recognized.

Example 3. The method for solving the multiple

circle detection problem given in Algorithm 3 will

be tested on 100 sets of data points generated as

in Example 2. Whether some circle is recognized

among calculated circles will be established by QAD-

index or by the Hausdorff distance between these

circles. As can be seen in Table 1, Algorithm 3

recognizes very well circles the set of data points

A was generated from and necessary

CPU

-time is

reasonably low. All evaluations were done on the

basis of our own Mathematica-modules, and were per-

formed on the computer with a 2.90 GHz Intel(R)

Core(TM)i7-75000 CPU with 16GB of RAM.

Table 1: Result analysis for circles.

No. Circles detected

CPU

-time

circ.

2 3 4 5 6

DIRECT

k-means Total

2 19 0 0 0 0 0.147 1.175 1.322

3 0 20 2 0 0 2.339 4.858 7.197

4 0 0 31 0 0 2.563 7.967 10.53

5 1 0 0 26 1 28.60 18.25 46.85

4.2 Multiple Ellipse Detection Problem

Let A ⊂ ∆ ⊂ R

be a set of data points coming from

a number of multiple ellipses in the plane not known

in advance.

An ellipse E can be interpreted as a Mahalanobis

circle (M-circle) M(S,r; Σ) with the center at the

point S ∈ R

, the radius r and the covariance matrix

Σ,

M(S,r;Σ) = {u ∈ R

: d

(S,u; Σ) = r

}, (13)

where d

: R

× R

→ R

is the Mahalanobis

distance-like function given by

(S,u; Σ) =

√

detΣ(S −u)

−1

(S −u)

= ∥u −v∥

. (14)

When searching for an optimal k-partition (see

Subsection 3.3) we will use the algebraic distance

D(M(S,r,Σ),a) from the point a ∈ A to the M-circle

M, and when deﬁning the set V

by the

DBC

-index

(see Subsection 3.4) we will use the LAD-distance

(M(S,r,Σ),a) (see e.g. (Grbi

c et al., 2016)):

(M(S,r,Σ),a) = |∥S −a∥

−r| (15)

D(M(S,r,Σ),a) = (∥S −a∥

−r

)

(16)

A Fast and Efﬁcient Method for Solving the Multiple Closed Curve Detection Problem

273

Now

GOP

(3) can be written as:

argmin

S∈∆

,r∈[0,R]

Σ∈M

∑

i=1

min

1≤j≤k

D(M

,Σ

),a

) (17)

where M

is the set of positive deﬁnite symmetric ma-

trices of order two.

Example 4. Let A be the set of data points coming

from k ellipses E

,... ,E

homogeneously distributed

in the neighborhood of the ellipses. Four selected ex-

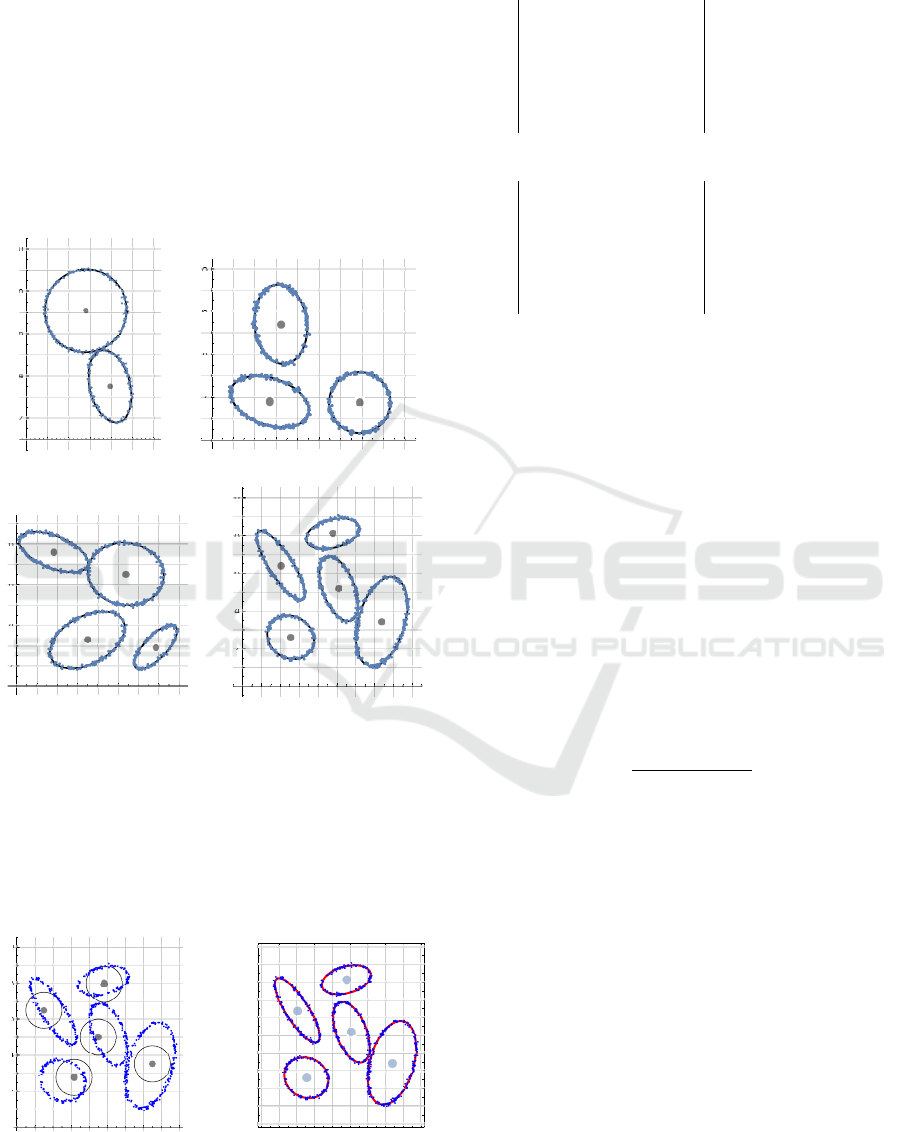
amples with k = 2,3,4,5 circles are shown in Fig. 4.

1 2 3 4 5 6

(a) k = 2

2 4 6 8 10

(b) k = 3

2 4 6 8

2 4 6 8 10

(d) k = 5

Figure 4: Four selected examples with k = 2, 3, 4, 5 el-

lipses.

Let us consider a data point set A shown in

Fig. 4d. According to Algorithm 2, by using the

DIRECT

algorithm, we ﬁrst determine an initial ap-

proximation (unit circles shown in Fig. 5a), and after

that, by using the KMCC algorithm, we obtain the so-

lution (Fig. 5b).

2 4 6 8 10

(a) Initial approximation

2 4 6 8 10

(b) Solution

Figure 5: Implementation of Algorithm 2 for ellipses.

Table 2: Result analysis for ellipses that mostly do not

intersect.

No. Ellipses detected

CPU

-time

ell

1 2 3 4 5

DIRECT

k-means Total

2 0 20 0 0 0 0.093 1.258 1.351

3 0 0 25 0 0 0.262 3.319 3.580

4 2 0 0 23 2 1.141 8.776 9.917

5 0 1 0 0 27 4.916 19.11 24.03

Table 3: Result analysis for intersecting ellipses.

No. Ellipses detected

CPU

-time

ell. 1 2 3 4 5

DIRECT

k-means Total

2 0 20 0 0 0 0.093 2.270 2.363

3 0 1 24 0 0 0.319 4.766 5.086

4 1 3 0 22 1 3.337 15.55 18.89

5 0 2 5 1 20 15.36 31.24 46.60

Searching for an optimal partition with the most

appropriate number of clusters will be illustrated

by using the same example (see Fig. 4d). The esti-

mated value of parameter (7) is ε = .235, and Algo-

rithm 3 terminates when the value of the DBC-index

drops below that value. We obtained DBC(1) = 2.72,

DBC(2) = 1.70, DBC(3) = 1.46, DBC(4) = 1.22, and

DBC(5) = 0.19. This means that the 5-partition is

an optimal partition and all ellipses have been rec-

ognized.

Example 5. The method for solving the multiple el-

lipse detection problem given in Algorithm 3 will be

tested on 100 sets of data points generated as in Ex-

ample 4. Whether some ellipse, interpreted as an M-

circle M(S,r,Σ), is recognized among calculated M-

circles as an M-circle N(

S, ˆr,

Σ) will be established

by QAD-index or by calculating the distance (Grbi

et al., 2016):

D(N,M) =

√

(

S,S,

Σ +Σ) + |ˆr −r|. (18)

As can be seen in Table 2, Algorithm 3 recognizes very

well ellipses the set of data points A was generated

from as in Example 4 and necessary

CPU

-time is very

low.

Example 6. Similarly to Example 5, Algorithm 3 will

be tested on 100 sets of data points generated from

2,3,4 or 5 intersected ellipses. Four different exam-

ples can be seen in Fig. 6

As can be seen in Table 3, Algorithm 3 still recognizes

well ellipses and

CPU

-time increases a little bit in the

case of many ellipses.

Example 7. Another advantage of the DBC-index will

be illustrated by an example in which a globally op-

timal partition has not been found (see Fig. 7a). The

estimated value of the parameter ε is ε = 0.217, and

the algorithm terminates when condition (4) is met,

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

274

4 5 6 7 8

(a) k = 2

1 2 3 4 5 6 7

(b) k = 3

0 2 4 6 8

2 4 6 8 10

(d) k = 5

Figure 6: Four selected examples with k = 2, 3, 4, 5 in-

tersected ellipses.

with ε

= 0.005. The 5-partition that was found is

not globally optimal, and characteristics of its clus-

ters are given in Table 4: centers of ellipse-centers,

values of the parameter QAD and densities of points

around ellipses according to Remark 1.

0 2 4 6 8 10

(a) 5-optimal partition

4 6 8 10

(b) Set A \(π

∪π

)

4 6 8 10

0 2 4 6 8 10

(d) Final Solution

Figure 7: An example of data for which Algorithm 3

has not found any globally optimal partition.

Table 4: Characteristics of calculated ellipses.

j S

QAD

( j) ρ

(2.12,7.23) 0.134 20.6

2 (7.57,6.24) 0.198 17.5

(

)

0.618 24.9

4 (4.78,3.14) 0.133 19.9

5 (4.11,6.48) 0.471 30.2

It can be stated that ellipses E

have been rec-

ognized among original ellipses since the correspond-

ing values of the parameter QAD are less than 0.217,

where we should carefully take into account ellipse

since the density of points ρ

signiﬁcantly deviates

from the average density

ρ = |A|/

∑

j=1

| = 21.5 .

On the basis of this brief analysis, we can leave

out clusters π

,π

from the set A and reconsider a

simple multiple ellipse detection problem for the set

A \(π

∪π

) (see Fig. 7b). We obtain the remaining

three ellipses (see Fig. 7c). By applying the KMCC

algorithm to the whole set A, the initial approxima-

tion obtained in this way yields the Final Solution (see

Fig. 7d).

4.3 Some Other Possibilities

Some other similar problems can be treated in the

same way. For example, we can observe a mul-

tiple generalized circle detection problem, where a

generalized circle implies a set C (O(p),r) = {u ∈

: D(O(p),u) = r, r > 0, p ∈ R

}, where O(p) is

some simple geometrical object.

For example, O(p) can be a line segment seg(µ,ν)

ending in points µ,ν ∈ ∆ (see Fig. 8a), or an arc

arc(C,t

) of a circle, where C is the center of a cir-

cle, and t

∈ [0,2π], t

< t

(see Fig. 8b).

1 2 3 4 5 6 7 8

(a)

0 2 4 6 8 10

(b)

Figure 8: Generalized circles.

After deﬁning the distance from the point a ∈ A

to the generalized circle C ,

D(C (O(p),r),a) = (D(O(p),a)

−r

)

, (19)

where D is the distance from the point a ∈ A to geo-

metrical objects O(p), then

GOP

(3) becomes

argmin

p∈R

,r∈[0,R]

∑

i=1

min

1≤j≤k

D(C

),r

),a

). (20)

5 CONCLUSIONS

The proposed method for solving the multiple closed

curve detection problem has been shown to be very

efﬁcient in special cases of multiple circle and multi-

ple ellipse detection problems.

A Fast and Efﬁcient Method for Solving the Multiple Closed Curve Detection Problem

275

Let us also mention that in the literature there are

some other possibilites such as path-based clustering

approach (see (Fischer and Buhmann, 2003)) that can

also be used for solving multiple closed curve detec-

tion problem.

The proposed

DBC

-index for detecting the most ap-

propriate number of clusters (closed curves) enables

this procedure to be carried out as fast as possible.

In more complex cases of intersecting closed curves,

i.e. when Algorithm 3 does not give a globally opti-

mal partition, construction of the

DBC

-index enables

the detection of some closed curves and the algorithm

to be run on a constrained data set.

The proposed DBC-index should be further inves-

tigated and corrected. We will try to apply the pro-

posed method to other curves. In the meantime, we

successfully applied the method to multiple gener-

alised circle detection problem with application in Es-

cherichia Coli and Enterobacter-cloaca recognizing.

The proposed algorithm could also be applied to

real-world images.

ACKNOWLEDGEMENTS

The author would like to thank Mrs. Katarina Mor

zan

for signiﬁcantly improving the use of English in

the paper. This work was supported by the Croa-

tian Science Foundation through research grants

IP-2016-06-6545

and

IP-2016-06-8350

REFERENCES

Akinlar, C. and Topal, C. (2013). Edcircles: A real-time

circle detector with a false detection control. Pattern

Recognition, 46:725–740.

Bagirov, A. M. (2008). Modiﬁed global k-means algo-

rithm for minimum sum-of-squares clustering prob-

lems. Pattern Recognition, 41:3192–3199.

Ester, M., Kriegel, H., and Sander, J. (1996). A density-

based algorithm for discovering clusters in large spa-

tial databases with noise. In 2nd International Con-

ference on Knowledge Discovery and Data Mining

(KDD-96), pages 226–231, Portland.

Fischer, B. and Buhmann, J. M. (2003). Path-based clus-

tering for grouping of smooth curves and texture seg-

mentation. IEEE Transaction on Pattern Analysis and

Machine Intelligence, 25:1–6.

Gablonsky, J. M. (2001). Direct version 2.0. Technical

report, Center for Research in Scientiﬁc Computation.

North Carolina State University.

Grbi

c, R., Grahovac, D., and Scitovski, R. (2016). A

method for solving the multiple ellipses detection

problem. Pattern Recognition, 60:824–834.

Grbi

c, R., Nyarko, E. K., and Scitovski, R. (2013). A modi-

ﬁcation of the DIRECT method for Lipschitz global

optimization for a symmetric function. Journal of

Global Optimization, 57:1193–1212.

Jones, D. R. (2001). The direct global optimization algo-

rithm. In Floudas, C. A. and Pardalos, P. M., edi-

tors, The Encyclopedia of Optimization, pages 431–

440. Kluwer Academic Publishers, Dordrect.

Jones, D. R., Perttunen, C. D., and Stuckman, B. E. (1993).

Lipschitzian optimization without the Lipschitz con-

stant. Journal of Optimization Theory and Applica-

tions, 79:157–181.

Kogan, J. (2007). Introduction to Clustering Large and

High-dimensional Data. Cambridge University Press,

New York.

Maro

sevi

c, T. and Scitovski, R. (2015). Multiple ellipse ﬁt-

ting by center-based clustering. Croatian Operational

Research Review, 6:43–53.

Morales-Esteban, A., Mart

ınez-

Alvarez, F., Scitovski, S.,

and Scitovski, R. (2014). A fast partitioning algorithm

using adaptive Mahalanobis clustering with applica-

tion to seismic zoning. Computers & Geosciences,

73:132–141.

Moshtaghi, M., Havens, T. C., Bezdek, J. C., Park,

L., Leckie, C., Rajasegarar, S., Keller, J. M., and

Palaniswami, M. (2011). Clustering ellipses for

anomaly detection. Pattern Recognition, 44:55–69.

Paulavi

cius, R. and

Zilinskas, J. (2014). Simplicial Global

Optimization. Springer.

Prasad, D. K., Leung, M. K. H., and Quek, C. (2013). Elliﬁt:

An unconstrained, non-iterative, least squares based

geometric ellipse ﬁtting method. Pattern Recognition,

46:1449–1465.

Sabo, K., Scitovski, R., and Vazler, I. (2013). One-

dimensional center-based l

-clustering method. Op-

timization Letters, 7:5–22.

Scitovski, R. and Maro

sevi

c, T. (2014). Multiple circle

detection based on center-based clustering. Pattern

Recognition Letters, 52:9–16.

Scitovski, R. and Scitovski, S. (2013). A fast partitioning

algorithm and its application to earthquake investiga-

tion.

Computers & Geosciences

, 59:124–131.

Thomas, J. C. R. (2011). A new clustering algorithm based

on k-means using a line segment as prototype. In Mar-

tin, C. S. and Kim, S.-W., editors, Progress in Pattern

Recognition, Image Analysis, Computer Vision, and

Applications, pages 638–645. Springer Berlin Heidel-

berg.

Tsagris, M., Beneki, C., and Hassani, H. (2014). On the

folded normal distribution. Mathematics, 2:12–28.

Uteshev, A. Y. and Goncharova, M. V. (2018). Point-to-

ellipse and point-to-ellipsoid distance equation analy-

sis. Journal of Computational and Applied Mathemat-

ics, 328:232–251.

Viswanath, P. and Babu, V. S. (2009). Rough-DBSCAN: a

fast hybrid density based clustering method for large

data sets. Pattern Recognition Letters, 30:1477–1488.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

276