
Actual Impact of GAN Augmentation on CNN Classification
Performance
Thomas Pinetz, Johannes Ruisz and Daniel Soukup
Center for Vision, Automation & Control, AIT Austrian Institute of Technology GmbH, Giefinggasse 4, 1210 Vienna, Austria
Keywords:
Generative Adversarial Networks, Deep Learning, Classification, Data Augmentation.
Abstract:
In industrial inspection settings, it is common that data is either hard or expensive to acquire. Generative
modeling offers a way to reduce those costs by filling out scarce training data sets automatically. Generative
Adversarial Networks (GANs) have shown incredible results in the field of artificial image data generation,
but until recently were not ready for industrial applications, because of unclear performance metrics and
instabilities. However, with the introduction of Wasserstein GAN, which comprises an interpretable loss
metric and general stability, it is promising to try using those algorithms for industrial classification tasks.
Therefore, we present a case study on a single digit image classification task of banknote serial numbers, where
we simulate use cases with missing data. For those selected situations, different data generation algorithms
were implemented incorporating GANs in various ways to augment scarce training data sets. As a measure
of plausibility of those artificially generated data, we used the classification performance of a CNN trained
on them. We analyzed the gains in classification accuracy when augmenting the training samples with GAN
images and compare them to results with either more classically generated, rendered artificial data and near
perfect training data situations, respectively.
1 INTRODUCTION
Sufficient amounts of relevant training data for real
world machine learning tasks are hard to obtain. Es-
pecially, edge classes, such as certain error classes,
are often underrepresented. Machine learning algo-
rithms tend to have problems with correctly classi-
fying unbalanced datasets (More, 2016). In order to
overcome such deficiencies, usually training data are
augmented with plausible, artificially generated ex-
ample images to enrich the amount of variation in the
training data sets. This has advantageous regularizing
effects on the training procedure, e.g. mitigate over-
fitting. Although, there are a number of methods to
fight overfitting within the deep learning model (Sri-
vastava et al., 2014), carefully fostering ones train-
ing data should not be underestimated as a primary
requirement. Particularly in real world applications,
one wants to be sure that predictions are made on the
basis of as adequate as possible training data.
In the past, this was often accomplished by sim-
ply including randomly slightly shifted and/or rotated
versions of available training examples, which al-
ready provides a significant amount of classification
accuracy (He et al., 2016). For certain types of data,
it is also possible to generate yet more variations of ar-
tificial training data by means of 3D or text rendering
algorithms. However, a solution to such problems is
offered by generative modeling. In generative model-
ing, approximations of the actually underlying prob-
ability distributions of the available real data sets are
learned, which are used to generate realistically look-
ing new samples to fill out an underrepresented data
class (Goodfellow et al., 2014). Generative Adversar-
ial Networks (GANs) currently form the state-of-the-
art in generative modeling (Karras et al., 2017) and
have been applied with state-of-the-art results in do-
mains such as data generation (Arjovsky et al., 2017),
few shot learning (Antoniou et al., 2017), and data re-
finement (Pinetz et al., ).
GANs consist of two Neural Networks (NN),
which are trained adversarial. The first network (gen-
erator) learns to construct artificial images to fool the
second network (critic), while the critic tries to dis-
tinguish artificially generated from real data. Since
the original inception of GANs by Goodfellow et
al. (Goodfellow et al., 2014), GANs have been noto-
rious for being unstable and dependent on the weight
initialization of the networks (Salimans et al., 2016).
Substantial amounts of research have gone into mak-
Pinetz, T., Ruisz, J. and Soukup, D.
Actual Impact of GAN Augmentation on CNN Classification Performance.
DOI: 10.5220/0007244600150023
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 15-23
ISBN: 978-989-758-351-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
15

ing GANs more stable (Arjovsky and Bottou, 2017;
Arjovsky et al., 2017; Salimans et al., 2016; Gulrajani
et al., 2017; Yadav et al., 2017), produce higher res-
olution or better quality images (Karras et al., 2017),
or to better model the actual variations inherent in the
real data (Antoniou et al., 2017; Pinetz et al., ). GAN
algorithms learn to smartly interpolate/extrapolate in
high dimensional spaces (Karras et al., 2017). There-
fore, if only a subset of the clusters of a real data sam-
ple is available, even a GAN algorithm will not mag-
ically generate vastly different plausible data clusters
or completely missing classes of data.
An open research field is the quality evaluation of
GAN generated data, as it is still unclear which met-
ric to use (Theis et al., 2015). One metric in use is the
inception score, which has been shown to correlate
well with human perception (Salimans et al., 2016).
However, the inception score has also been shown
to be misleading (Barratt and Sharma, 2018). For
Wasserstein GANs, the estimated Wasserstein Dis-
tance is used as a quality metric. While there were
attempts to compare various GAN algorithms, the re-
sults were inconclusive and showed, that GANs are
strongly dependent on their hyper parameters and ran-
dom seeds (Lucic et al., 2017).
This work aims to investigate possible advantages
of data augmentation with GAN algorithms over a
classical augmentation approach such as digit ren-
dering, both w.r.t. perfect training data situations.
Therefore, a relatively simple industrial task is con-
sidered, namely 10-class single digit image classi-
fication of banknote serial numbers, where nearly
100% classification accuracy can be achieved given
enough training data (Fig. 1 column a.). The sim-
plicity of the selected task itself and the knowledge
that it is virtually perfectly solvable allows to iso-
late the actual influences of augmentation strategies.
The availability of sufficient data enables the simu-
lation of situations with different amounts of avail-
able training data from none up to a quasi perfect
training set. Certain use cases are simulated, such
that only {0, 1, 10, 20, 50, 100, 200} example images
of one selected underrepresented digit class existed.
Classical and GAN data augmentation strategies are
used to compensate those lacks of data and classifi-
cation CNNs were trained for all simulated training
set scenarios. The quality of augmented training sam-
ples was compared and evaluated by means of testing
those CNNs on a shared test set of real BN number
digits.
In this context our contributions are as follows:
• A showcase on how reliable GAN augmentation
in fact works for an actual realistic classification
task.
• In terms of applicability of augmentation algo-
rithms for image classification:
– Confrontation of image rendering algorithm
with GAN augmentation.
– Comparison of different GAN augmentation
strategies.
The remaining paper is organized as follows. In
Section 2, the augmentation algorithms - classical
rendering and GAN - are explained in detail. Sec-
tion 3 contains descriptions of used data, experiment
scenarios, and a presentation of results. Finally, a
summary and conclusions are presented in Section 4.
2 DESCRIPTION OF DATA
GENERATION ALGORITHMS
2.1 Digit Image Generation by Text
Rendering
The chosen use case of banknote serial number single
digit image classification offers the possibility of ren-
dering additional digit image data with a text renderer
in order to compensate for a lack of training data. We
used Matlab’s text renderer (MATLAB, 2016). The
rendering script generated a huge number of simu-
lated sample images for each digit class, whereas the
corresponding fonts were randomly drawn from all
fonts that were installed on the computer. Fonts used
on banknotes are special, such that the rendered fonts
do not exactly correspond to them. The large varia-
tion of fonts in the rendering procedure on the other
hand should avoid that the classification CNN focuses
too much on special font features.
The images were rendered on higher resolution
and down-sampled to the target resolution of 24 × 16
by interpolation, according to the resolution of the
real banknote serial number digit images. Font color
was black, background white. Banknotes in gen-
eral contain patterns of high frequency and high con-
trast drawings. Those also appear in the backgrounds
of serial numbers, which might cause the classifica-
tion CNN to cling to them, especially when only a
small sample of real images is at hand. Thus, we
blended a random salt-and-pepper noise pattern mul-
tiplicatively onto the synthetic images, which made
the background of simulated data noisy instead of
plain white. This measure added another regulariz-
ing effect, which obviates that the classification CNN
gets distracted by background features rather than an-
alyzing pure digit strokes.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
16

Figure 1: Example images for digit class ’6’ used for training the classification CNNs (3 examples per type): original real
banknote serial number digits (a.), Rendered blank (b.), Rendered noise (c.), RGAN blank (d.), RGAN noise (e.), DGAN (f.),
and DAGAN (g.).
For experiments (see Section 3), we randomly
sampled images from those synthetically generated
data in order to fill out small real data samples.
2.2 Data Augmentation using GAN
Methods
Generative Adversarial Networks (GANs) (Goodfel-
low et al., 2014) are the prevalent way to generate new
data points of a sample based dataset (Lucic et al.,
2017). The objective of GANs is to learn a probabil-
ity distribution P
r
. This is done by approximating said
distribution with a parametric distribution referred to
as P
θ
. Samples from P
θ
are used to augment an ex-
isting dataset with artificially generated yet plausible
new examples, and use those for training to improve
classification performance.
The GAN principle relies on two neural networks
(NN). The first NN, named generator, transforms a
noise distribution in a latent space, e.g. Gaussian
(z ∼ N (0, I)), into examples from a parametric dis-
tribution (g
θ
(z) ∼ P
θ
). The second NN, denoted as
critic (Arjovsky et al., 2017) is used to distinguish
generated data from real data. Using the classical log-
loss for the critic yields following saddle point prob-
lem:
min
θ
max
D
L(θ, D) = E
x∼P
r
[log(D(x))] +
E
z∼N (0,I)
[log(1 − D(g
θ
(z)))]
(1)
It is well known, that optimizing Eq. (1) min-
imizes the Jensen-Shannon Divergence between P
r
and P
θ
(Goodfellow et al., 2014). The solution to
such a problem is called a Nash equilibrium, where
the generator produces data, which follows the same
distribution as the real data, i.e. P
θ
= P
r
. The com-
mon procedure to achieve those saddle point solu-
tions is to alternatingly perform gradient ascent for
the critic parameters and gradient descent for the gen-
erator parameters (Yadav et al., 2017). Eventually,
trained generator NNs produce artificial new training
images, which are used to augment scarce real train-
ing samples in an actual deep learning task.
However, two distributions on low dimensional
manifolds in high dimensional spaces are unlikely
to comprise large enough overlap for the Jensen-
Shannon Divergence to be defined (Arjovsky and Bot-
tou, 2017). Using noise on the real data to smooth
out the distributions (Arjovsky and Bottou, 2017) re-
sulted in blurry generated images. A better solution
is to change the distance metric between the distri-
butions, namely using the Wasserstein distance (Ar-
jovsky et al., 2017), which yields following GAN for-
mulation:
L = min
θ
max
Lip( f )≤1
E
x∼P
r
[ f (x)] − E
z∼N (0,I)
[ f (g
θ
(z))].
(2)
Wasserstein distance is well defined even if there is no
overlap between two distributions. Moreover, using
this GAN formulation produces an interpretable critic
output, which alleviates balancing the Wasserstein
loss term with additional regularizing loss terms (An-
toniou et al., 2017). Such might be a required regu-
larizer penalizing deviations from the Lipschitz con-
straint (Lip( f ) ≤ 1). A number of them have been
proposed (Arjovsky et al., 2017; Gulrajani et al.,
2017; Wei et al., 2018). Due to consistent good per-
formance in comparison experiments, we chose Gra-
dient Penalty (Gulrajani et al., 2017). Therefore, loss
Actual Impact of GAN Augmentation on CNN Classification Performance
17

functions for generator and critic are modified as fol-
lows:
L
g
(θ
g
) = −E
z∼p
noise
[ f (g
θ
g
(z))] (3)
L
d
(θ
c
) = E
x∼p
data
[ f
θ
c
(x)] −
E
z∼p
noise
[ f
θ
c
(g(z))] +
E
¯x∼p
¯x
λ||∇
¯x
f
θ
c
( ¯x) − 1||
2
,
(4)
where p
¯x
is defined as a linearly interpolated distri-
bution between the generated distribution and the real
distribution. In all of our experiments, we set λ = 10,
which was reported to perform well across various
datasets and architectures (Gulrajani et al., 2017).
There are multiple ways the GAN principle can
be utilized for data augmentation based on real data
at hand. We investigated following methods:
• DGAN Direct GAN: Generating plausibly look-
ing, artificial images for an underrepresented ob-
ject class based on a few given real examples of
that class.
• RGAN Refinement GAN (Pinetz et al., ): On
the basis of rendered simulated images and real
images (not necessarily of the underrepresented
class) learn to transform the rendered images to
look more realistically in terms of image ap-
pearance rather than object structure, e.g. digit
strokes.
• DAGAN Data Augmentation GAN (Antoniou
et al., 2017): A realistic object distortion function
is learned from real images that mimics inherent
real distortions within real image distributions.
In all those GAN methods, the critic function
is modeled as a CNN, whereas they all utilize the
same CNN architecture, which is inspired by DC-
GAN (Radford et al., 2015). We use 3 strided convo-
lution layers with 3×3 filter kernels and {32, 64, 128}
feature maps, followed by leaky ReLU activation. A
fully connected layer with 1 output unit yields the
distribution distance measure. Gradient penalty was
added to the critic loss during GAN training. All
weights were initialized with Glorot’s initialization
scheme (Glorot and Bengio, 2010).
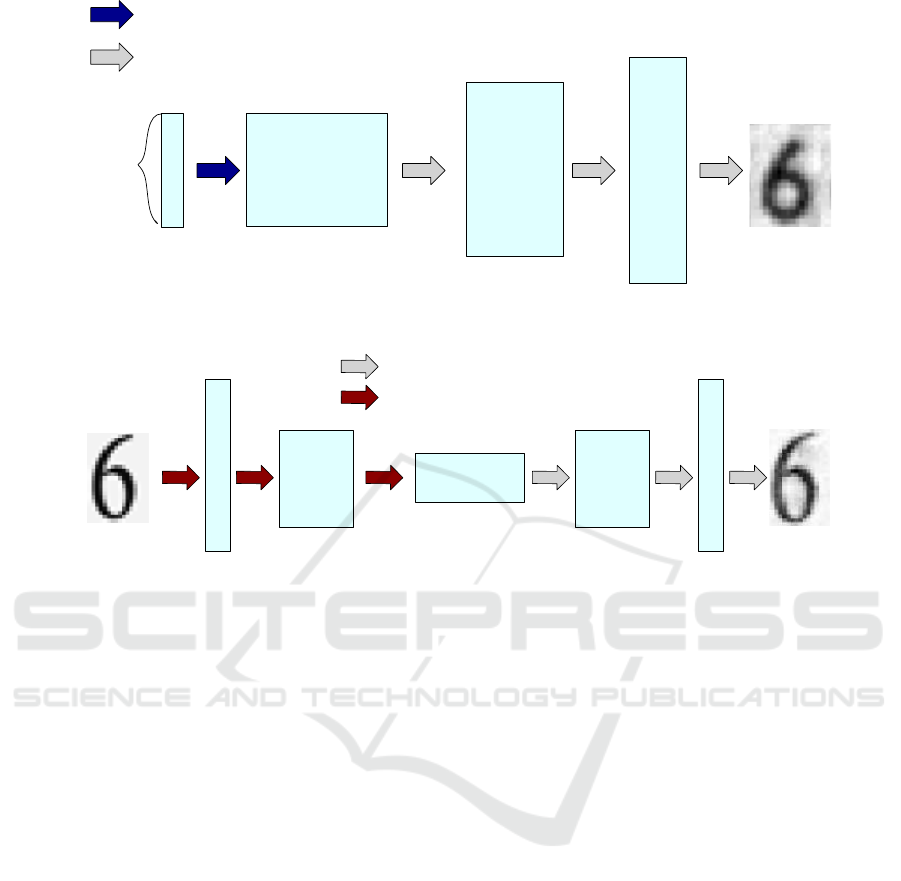
2.2.1 DGAN
In DGAN, only the actual available real images of an
underrepresented image class are used. In our simula-
tion experiments (Section 3), we decided to use digit
class ’6’ to play that role. Based on those images, dur-
ing the GAN training procedure, the generator eventu-
ally learns to generate artificial images mimicking the
corresponding appearances of those real examples of
the according class without simply reproducing them
exactly.
The generator is modeled as a NN, whose archi-
tecture is a DCGAN variant visualized in Fig. 2. 5×5
convolution kernels were implemented together with
ReLU activations. In the training procedure, the pro-
posed hyper parameter setting by Gulrajani et al (Gul-
rajani et al., 2017) was used.
2.2.2 RGAN
Unlike DGAN, RGAN not only requires real exam-
ples, but also synthetically generated data, e.g. by a
renderer. In RGAN, instead of learning to generate
plausibly looking images from an underlying real im-
age distribution P
r
, a refinement function is learned,
which transforms synthetic images into more realisti-
cally looking versions. In order that it mimics the typ-
ical statistics of the image acquisition systems of real
images without changing the depicted object struc-
tures. While one requires synthetic data to perform
the task, one is not restricted to a scarce sample of an
underrepresented object class during GAN training.
Those image appearance statistics can also be learned
from the other classes. Incorporating RGAN refined
images into training sets in different learning tasks
like fingerprint minutia detection or gaze estimation
showed notable performance improvements (Pinetz
et al., ; Shrivastava et al., 2016), respectively.
In order to ensure that the actual object struc-
tures in the synthetic input images are preserved by
the generator NN, an additional regularization term in
the generator loss L
g
is required, penalizing excessive
structural deviations of the output w.r.t. the input im-
ages:
L
g
= E
z∼p
synthetic
[( f (g
θ
(z))) + ω||g
θ
(z) − z||
2
] (5)
During training RGANs, the balance of loss terms
by the regularization parameter ω is critical in or-
der to achieve good results (Salimans et al., 2016).
As an RGAN generator produces images from other
(synthetic) images rather than from random vectors
in some latent space, a U-shaped CNN architec-
ture is utilized to model the corresponding gener-
ator NN (Ronneberger et al., 2015). Similarly to
an auto-encoder NN, a U-shaped CNN has a coder
and decoder part, connected by a bottleneck layer
(see Fig. 3). The generator’s input consists only of
an image and no additional noise component, why
the RGAN generator is fully deterministic. Conse-
quently, each input image results in one and only one
refined output image.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
18
128 z
Project and Reshape, ReLU
Feature Maps:
Image Shape:
256
2 × 3
4 × 6
128
64
8 × 12
5 × 5 Transposed Conv, ReLU
Figure 2: Generator used for the DGAN approach, inspired by the DCGAN architecture.
3 × 3 Transposed Conv, ReLU
3 × 3 Strided Conv, ReLU
Feature Maps:
Image Size:
32
8 × 12
64
4 × 6
2 × 3
4 × 6
8 × 12
128
64
32
Figure 3: Generator used for the RGAN approach, inspired by the U-Shaped NN architecture (Ronneberger et al., 2015).
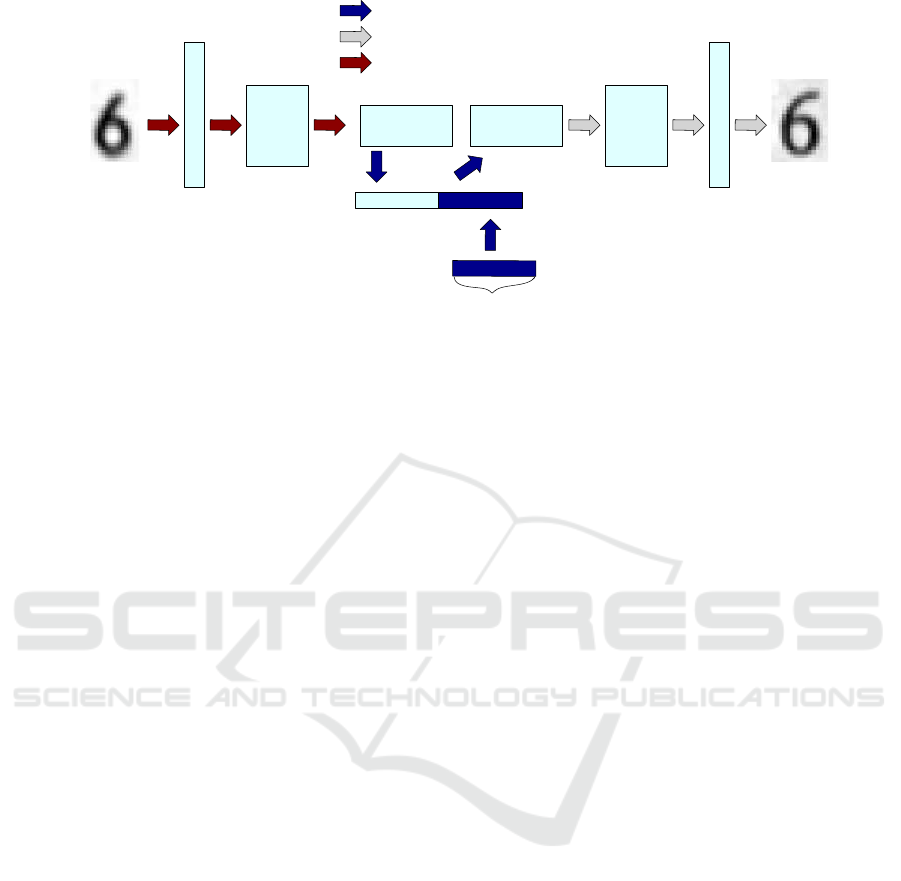
2.2.3 DAGAN
The aim of this GAN variation is to learn realistic
distribution manifolds of the real object classes along
which plausible inner-class distortions take place, i.e.
learn to realistically distort given real images rather
locally. The generator NN is trained to construct ran-
domly slightly and - w.r.t. the real image sample -
consistently distorted versions of real input images.
Randomness is introduced by adding a random vec-
tor in the latent space (NN bottleneck layer) of the
U-shaped generator NN (Fig. 4). Concurrently, the
critic NN learns to distinguish pairs of real/real im-
ages from pairs of real/generated images. The DA-
GAN training procedure is considered converged as
soon as the critic is unable to discern that generated
images are involved in those image pairs.
Similarly to the RGAN method, the generator in
DAGAN is trained to modify input images in such
a way that the output images comprise appearances
consistent with the real training data set. While in
RGAN the aim is to induce statistics of the real image
acquisition systems to synthetic images, in DAGAN,
the generator learns distortion models of real object
classes in order to increase variation of the available
real data sample appropriately. Moreover, the DA-
GAN method comprises a random component enabl-
ing the generation of arbitrarily many variations of
each input image. DAGAN can be trained on basis
of images of all object classes, so that one is not re-
stricted only to real examples of the certain underrep-
resented object class.
DAGAN only makes sense though, if the images
across different classes share similar distortion mod-
els (Antoniou et al., 2017). That assumption is com-
monly accepted for fine-grained classification tasks
such as the one covered in this work.
The generator NN’s architecture is similar to
RGAN’s, except for an additional injection of the al-
ready mentioned random noise vector, which is con-
catenated to the latent representation in the bottleneck
layer (Fig. 4). The input to the critic NN is a pair of
input images:
• an original real image AND the generator’s output
w.r.t. to that real image, OR
• an original real image AND another real image of
the same object class.
The critic measures deviations between distributions
of real/generated image pairs and real/real image
pairs. This is similar to comparing different distri-
butions of images, only that pairs of images are con-
sidered as twice as high dimensional images, e.g.
stacked along the color dimension.
Actual Impact of GAN Augmentation on CNN Classification Performance
19
Project and Reshape, ReLU
3 × 3 Transposed Conv, ReLU
3 × 3 Strided Conv, ReLU
Feature Maps:
Image Size:
32
8 × 12
64
4 × 6
2 × 3
4 × 6
8 × 12
128
64
50
1
128
128 z
50
1
256
2 × 3
Figure 4: Generator used for the DAGAN approach, inspired by the U-Shaped NN architecture (Ronneberger et al., 2015).
Notice the additional noise component added to the latent representation.
3 EXPERIMENTS
We chose a simple 10-class classification problem of
printed digits ’0’ to ’9’ for our experiments. Those
digit images were extracted from serial numbers of
banknote images with different background patterns,
fonts, and sizes. NN achieve near perfect performance
on this task, given enough training data. Therefore
this task allows to investigate the influences of various
situations of insufficient training data and according
methods to overcome them.
Digit class ’6’ was selected to play the role of
an underrepresented class, i.e. a class with too lit-
tle available training images to varying degrees, from
none to sufficiently many. To each of those situa-
tions, the augmentation methods mentioned in Sec-
tion 2 were applied to compensate the simulated miss-
ing data situations for digit class ’6’. The other classes
were represented with sufficient training images in all
setups, i.e. 300 digit images for each class ’0’, ’1’,
’2’, ’3’, ’4’, ’5’, ’7’, ’8’, and ’9’.
In order to solve the classification task, we trained
CNNs with six convolution layers, where three layers
were configured with stride 2 for pooling. The output
is a one-hot encoded layer of 10 values with a soft-
max applied to it. The network architecture was held
constant for all conducted experiments.
The outcome of those experiments shall show if
there is a preferred method of data generation for the
particular problem, in order to compensate lacks of
training data.
3.1 Missing Data Scenarios and
Corresponding Data Augmentation
For all classes except for digit class ’6’, we used the
same training data for each run, i.e. 300 example im-
ages per class consisting of 24 × 16 gray scale im-
ages depicting banknote serial number digits. A lack
of training data for digit class ’6’ was simulated by
only using 0, 1, 10, 20, 30, 40, 50, 100, 200 origi-
nal digit ’6’ images. In each of those 10 settings, we
added artificially generated class-6 data by means of
the data generation algorithms described in Section 2,
such that we always filled up the data lack and ob-
tained 300 training images for class ’6’ as well.
On each of those data configurations, a digit clas-
sification CNN was trained and its according perfor-
mance was measured on a shared test set of 350 origi-
nal digit ’6’ images that were never used for training.
Naturally, for each setting, we additionally trained
the CNN without using artificially generated images
for augmentation. Those performances were taken as
references from which to improve by augmentation.
In the worst case, where no images of digit ’6’ were
contained in the training set, neither original nor arti-
ficial, digit ’6’ test images were never classified cor-
rectly by a fully trained CNN.
3.1.1 Rendered Images
As described above, we utilized Matlab’s text ren-
derer (MATLAB, 2016) to generate synthetic digit
images comprising various fonts and variations (see
Fig. 1). We generated two versions of that data set:
• Rendered blank: digit image set with blank white
image background.
• Rendered noise: digit image set with a blended
random noise pattern in the image background.
As we argued earlier that the noise pattern might be
advantageous due to a regularizing effect, conducting
experiments on both versions allows to evaluate that
argumentation.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
20

3.1.2 Direct GAN (DGAN)
For DGAN training, only those images of class ’6’
considered to be at our disposal in each setting were
used. Since DGANs learn the underlying data dis-
tribution of given data, that procedure only makes
sense for more than 1 original image example, so that
DGANs were only applied to those situations suppos-
ing 10, 20, 30, 40, 50, 100, 200, 300 available real
examples.
3.1.3 Refinement GAN (RGAN)
The RGAN critic was trained with all the available
original data, i.e. real examples from all classes were
used, plus those few class-6 images considered to be
at our disposal in each setting. The input to the RGAN
generator consists of rendered synthetic digit images,
for which we utilized the already rendered data sets.
Due to the usage of synthetic data, the RGAN algo-
rithm is also suited for test cases, where not a single
real image was used for training. Based on the used
two rendered datasets, RGANs also yielded two dif-
ferent augmentation data sets (see Fig. 1 columns d.
and e.):
• RGAN blank: Refinement of rendered images
with blank background.
• RGAN noise: Refinement of rendered images with
random noise background.
3.1.4 Data Augmentation GAN (DAGAN)
In DAGAN, images of all digit classes are used to
train the DAGAN augmentation generator. However,
the classes have to be carefully balanced, so that for
DAGAN, only as many images per class can be used
as are available for the considered underrepresented
digit class ’6’.
From the real example images of digit ’6’ and ran-
dom vectors from the latent space, the fully trained
generator eventually generated the necessary amount
of random augmentation image variations of class ’6’,
such that the scarce training sets could be augmented
appropriately (see Fig. 1 columns g.).
3.2 Results
Fig. 5 shows the performance plots of 10-fold cross-
validated classification accuracies for each setting (0,
1, 10, 20, 30, 40, 50, 100, 200, and 300 original digit
’6’ images in training set) and the corresponding Ren-
dered blank, Rendered noise, RGAN blank, RGAN
noise, DGAN, and DAGAN generated training sets.
Naturally, for DGAN and DAGAN only settings with
more than 1 real digit ’6’ image were considered. For
each setting and algorithm, the corresponding classifi-
cation CNN was trained with 10-fold cross-validation
and the classification accuracies on a shared test set
of 350 original class ’6’ images were averaged. Note,
that we only present test performances for class ’6’
due to presentational reasons.
The following observations are apparent from the
performance plots:
• More original data improves classification in gen-
eral.
• If there are quasi no training images of digit
class ’6’ at hand, augmentation with rendered data
make training possible, whereas RGAN based on
those data already yields really good classification
results (Fig. 5 left).
• The introduced noise pattern in the background
of rendered images ensures better performance,
which also elevates performance of RGAN based
on those images.
• RGAN improves quality of rendered images w.r.t.
to achievable classification accuracies in both
cases, blank and noisy image background, respec-
tively. That is an indicator that RGAN drags the
rendered image distributions more towards the un-
derrepresented real image distributions.
• DGAN augmentation, which is the classical setup
in terms of GAN strategies, improves classifica-
tion, but lies behind performances with rendered
images with noisy background and significantly
behind RGAN based on those (Fig. 5 right).
• DAGAN augmentations contribute to classifica-
tion improvements, but not in a consistent man-
ner, which makes it difficult to make reliable pre-
dictions of their impact (Fig. 5 right).
4 CONCLUSION
The goal of the work was to investigate the actual im-
pact of image augmentation strategies on the CNN
classification performance in a real industrial sce-
nario. We utilized a relatively simple 10-class classi-
fication problem of digit images extracted from ban-
knote serial numbers. While the task is quasi per-
fectly solvable with the sufficient image sample at
hand, it allowed to simulate various scenarios of too
little training images for one certain digit class that we
considered to be underrepresented to varying degrees.
We augmented the supposedly underrepresented
training sample by means of different methods, clas-
sical digit rendering and various GAN oriented proce-
Actual Impact of GAN Augmentation on CNN Classification Performance
21
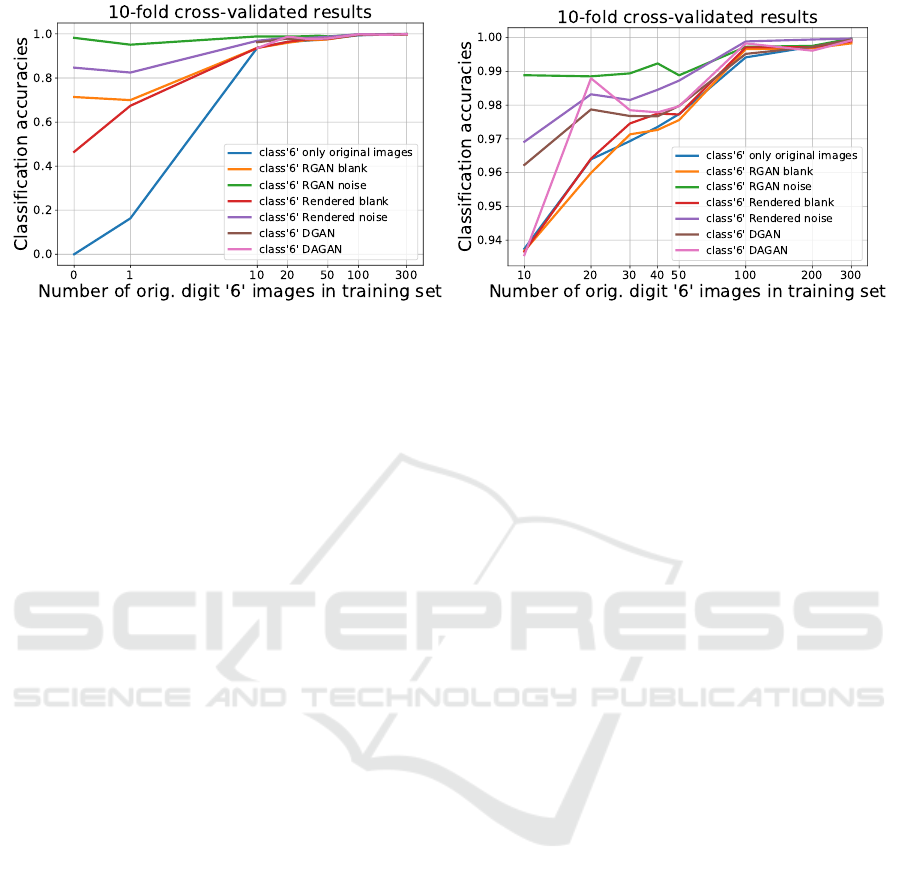
Figure 5: Left: 10-fold cross-validated CNN classification results for digit class ’6’ based on different original training data
sample sizes for digit ’6’ and augmented with various data generation strategies. Right: Zoom into left plot for class ’6’s
training data sample sizes 10 to 300 and corresponding classification accuracies ≥ 0.9. Note the scale of y-axes.
dures, respectively. The analysis of classification per-
formance of each scenario was carried out on a shared
real test sample of digit images. Results showed
that classical digit rendering contributes a lot to im-
provements already for very scarce training samples.
However, GAN refined versions of those data yet
still elevated performances significantly. Moreover,
it pays off investing into the rendering model, e.g. by
background modeling. GAN augmentation strategies
based only on available real training images do have a
positive impact on classification, but to a much lesser
extent and not necessarily reliably.
Finally, our results revealed the simple truth that
the more possibly realistic information is put into an
augmentation strategy the better will be the final clas-
sification outcome. While GANs are often reported
of yielding astonishing results, their performances
are only as good as the underlying data they operate
on. However, combined with image rendering, they
clearly showed the capability of overcoming signifi-
cant missing training data scenarios.
REFERENCES
Antoniou, A., Storkey, A., and Edwards, H. (2017). Data
augmentation generative adversarial networks. arXiv
preprint arXiv:1711.04340.
Arjovsky, M. and Bottou, L. (2017). Towards principled
methods for training generative adversarial networks.
arXiv preprint arXiv:1701.04862.
Arjovsky, M., Chintala, S., and Bottou, L. (2017). Wasser-
stein generative adversarial networks. In International
Conference on Machine Learning, pages 214–223.
Barratt, S. and Sharma, R. (2018). A note on the inception
score. arXiv preprint arXiv:1801.01973.
Glorot, X. and Bengio, Y. (2010). Understanding the diffi-
culty of training deep feedforward neural networks.
In Proceedings of the thirteenth international con-
ference on artificial intelligence and statistics, pages
249–256.
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,
Warde-Farley, D., Ozair, S., Courville, A., and Ben-
gio, Y. (2014). Generative adversarial nets. In
Advances in neural information processing systems,
pages 2672–2680.
Gulrajani, I., Ahmed, F., Arjovsky, M., Dumoulin, V., and
Courville, A. C. (2017). Improved training of wasser-
stein gans. In Advances in Neural Information Pro-
cessing Systems, pages 5769–5779.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-
ual learning for image recognition. In Proceedings of
the IEEE conference on computer vision and pattern
recognition, pages 770–778.
Karras, T., Aila, T., Laine, S., and Lehtinen, J. (2017). Pro-
gressive growing of gans for improved quality, stabil-
ity, and variation. arXiv preprint arXiv:1710.10196.
Lucic, M., Kurach, K., Michalski, M., Gelly, S., and Bous-
quet, O. (2017). Are gans created equal? a large-scale
study. arXiv preprint arXiv:1711.10337.
MATLAB (2016). version 9.1.0 (R2016b). The MathWorks
Inc., Natick, Massachusetts.
More, A. (2016). Survey of resampling techniques for
improving classification performance in unbalanced
datasets. arXiv preprint arXiv:1608.06048.
Pinetz, T., Soukup, D., Huber-M
¨
ork, R., and Sablatnig, R.
Using a u-shaped neural network for minutiae extrac-
tion trained from refined, synthetic fingerprints.
Radford, A., Metz, L., and Chintala, S. (2015). Unsu-
pervised representation learning with deep convolu-
tional generative adversarial networks. arXiv preprint
arXiv:1511.06434.
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:
Convolutional networks for biomedical image seg-
mentation. In International Conference on Medical
image computing and computer-assisted intervention,
pages 234–241. Springer.
Salimans, T., Goodfellow, I., Zaremba, W., Cheung, V.,
Radford, A., and Chen, X. (2016). Improved tech-
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
22

niques for training gans. In Advances in Neural Infor-
mation Processing Systems, pages 2234–2242.
Shrivastava, A., Pfister, T., Tuzel, O., Susskind, J., Wang,
W., and Webb, R. (2016). Learning from simulated
and unsupervised images through adversarial training.
CoRR, abs/1612.07828.
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,
and Salakhutdinov, R. (2014). Dropout: A simple way
to prevent neural networks from overfitting. The Jour-
nal of Machine Learning Research, 15(1):1929–1958.
Theis, L., Oord, A. v. d., and Bethge, M. (2015). A note on
the evaluation of generative models. arXiv preprint
arXiv:1511.01844.
Wei, X., Gong, B., Liu, Z., Lu, W., and Wang, L. (2018).
Improving the improved training of wasserstein gans:
A consistency term and its dual effect. arXiv preprint
arXiv:1803.01541.
Yadav, A., Shah, S., Xu, Z., Jacobs, D., and Goldstein, T.
(2017). Stabilizing adversarial nets with prediction
methods. arXiv preprint arXiv:1705.07364.
Actual Impact of GAN Augmentation on CNN Classification Performance
23
