
Real-Time Encoding/Decoding for Pairwise Communication Over an
Unreliable Sensor Network
Daniel Graham
1
, Arnold Yim
2
, Gang Zhou
3
and Weizhen Mao
3
1
Department of Computer Science, University of Virginia, Charlottesville, VA, U.S.A.
2
Department of Mathematics and Computer Science, Bridgewater College, Bridgewater, VA, U.S.A.
3
College of William And Mary, Williamsburg, VA, U.S.A.
Keywords:
Compression Algorithm, Energy Efficient Sensing, Wireless Sensor Networks.
Abstract:
The length of time that a wireless sensor can be deployed is limited by its internal power supply. To increase
the deployment lifetime of these sensors we must find ways to conserve power. In this paper, we propose an
algorithm that reduces the amount of energy the transceiver consumes by compressing the bytes that are sent
and received over the network. The algorithm compresses a data stream by exploiting its temporal locality
and is designed to function efficiently on an unreliable network in real-time. A stream is compressed by using
fewer bits to represent elements that frequently recur. We evaluate the proposed compression algorithm using
a collection of independently collected traces from the crawdad database. We calculated the compression ratio
for each trace and found that we were able to reduce the number of bytes transmitted by an average of 60%,
resulting in a 30% increase in energy savings.
1 INTRODUCTION
Wireless sensors have been used in a variety of data
collection and monitoring applications. These sensors
are often deployed in locations where they do not have
access to the energy grid and often rely on their in-
ternal energy supply. These locations vary from bat-
tlefields (Keally et al., 2010) and remote geological
locations (Kenney et al., 2009) to deployment within
the human body (Gao et al., 2005). In many cases, re-
placing the batteries in these sensory devices is incon-
venient and costly. Addressing the problem of energy
consumption in wireless sensor nodes will make the
application of sensor nodes more practical.
Real-time compression algorithms have been pro-
posed as a method for improving the energy efficiency
of wireless sensors. A real-time compression algo-
rithm reduces the amount of energy the transceiver
consumes by reducing the number of bytes that are
sent over the network.
Though numerous compression algorithms have
been proposed, most of them are not suitable for real-
time use and do not function efficiently over an unre-
liable network. The S-LZW (Sadler and Martonosi,
2006) and LEC (Marcelloni and Vecchio, 2008) com-
pression algorithms are currently the state of the art
real-time compression algorithms. Both algorithms
are dictionary compression algorithms, which com-
press data by storing the compressed values and un-
compressed values as key value pairs in a dictionary.
The S-LZW algorithm tailors the original LZW algo-
rithm (Nelson, 1989) to real-time embedded systems.
In particular, the S-LZW algorithm trades the com-
pression ratio of the LZW algorithm for a more effi-
cient use of memory and the ability to tolerate packet
losses. The S-LZW algorithm uses the LZW algo-
rithm to compress the data stream in blocks. This
restricts the size of the dictionary and limits packet
losses to only corrupting sections of the stream. The
LEC algorithm further improves on the compression
ratio of the S-LZW algorithm. Unlike the state of the
art algorithms, the algorithm that we propose in this
paper performs efficiently over an unreliable network
without delaying the stream.
The intuition behind the proposed algorithm is
that the sender and receiver will automatically agree
upon a set of codes that they will use to communicate.
Instead of a lengthy message, the sender will trans-
mit a shorter code that conveys the same meaning.
For example, instead of transmitting the 8-bit value
00010100 for the integer 20, the sender instead sends
a 2-bit value 01. The receiver then interprets the value
01 as 00010100. Communicating using a set of codes
reduces the amount of energy the sensor consumes by
Graham, D., Yim, A., Zhou, G. and Mao, W.
Real-Time Encoding/Decoding for Pairwise Communication Over an Unreliable Sensor Network.
DOI: 10.5220/0007247000690076
In Proceedings of the 8th International Conference on Sensor Networks (SENSORNETS 2019), pages 69-76
ISBN: 978-989-758-355-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
69

reducing the number of bytes a node’s transceiver has
to send and receive.
We evaluate the proposed algorithm by using it
to compress traces from Columbia University’s En-
HANTS dataset (Gorlatova et al., 2011a). The En-
HANTS dataset contains irradiance (light) readings
collected using TAOS TSL230rd photometric sensors.
The photometric sensors were placed in different lo-
cations and readings were collected at 30 second in-
tervals for 392 days. We compress the traces using
both the proposed algorithm and the LZW algorithm.
We compare the performance of the algorithms us-
ing four metrics: compression ratio, energy efficiency,
memory usage, and the delay the algorithm induces
on each packet. We evaluate the energy efficiency of
the algorithms using the energy model for the cc2420
transceiver proposed by D Schmidt et.al (Schmidt
et al., 2007).
The proposed algorithm improves on the state
of the art algorithms by efficiently tolerating packet
losses and reducing the delay induced on the data
stream. This paper makes three contributions:
• Presents a distributed real-time compression algo-
rithm that compresses a data stream by exploiting
its temporal locality.
• Extends the algorithm to ensure that it operates on
an unreliable network.
• Evaluates the compression performance and en-
ergy efficiency of the algorithm using traces col-
lected by independent researchers.
The remainder of the paper is structured as fol-
lows: Section 2 presents the compression and decom-
pression algorithm. Section 3 discusses the algorithm
and proves its correctness. Section 4 evaluates the al-
gorithm. Section 5 surveys the related work. Section
6 concludes the paper.
2 THE TEMPORAL
COMPRESSION ALGORITHM
(TCA)
Designing a real-time lossless compression algorithm
presents three unique challenges. The first challenge
is designing an algorithm that is able to compress data
without having access to the entire data stream.
The second challenge is ensuring that the algo-
rithm works on an unreliable network. This means
that the algorithm should still be able to decompress
subsequent elements if an element in the series is lost.
The third challenge is maintaining the consistency
of the distributed encoding table on the sender and re-
ceiver. An encoding table is the data structure that
is used to compress and decompress the stream. In
a non real-time application the encoding table is con-
structed and sent along with the compressed data so
that the compressed data can be decompressed later.
However, in a real-time scenario it is not feasible to
wait to send a decompression table since the receiver
must decompress the values in real-time. This means
that both the sender and receiver must either agree on
the decoding table beforehand or independently gen-
erate the same decoding table in real-time.
Encoding tables provide a mapping from the origi-
nal bytes to their compressed representations. For ex-
ample, an encoding table would map the original bits
1111 to the encoding 01. Table 1 shows an example
of an encoding table with 3 entries. An encoding table
Table 1: Example of an encoding table.
00 1001
01 1111
10 1000
can also be used to map a series of uncompressed val-
ues to a series of compressed values. For example the
values {1111, 1001, 1000, 1111} are mapped to the
values {01, 00, 10, 01}. The same encoding table can
also be used to decompress a series of values since
it is a one-to-one mapping. For example, the series
{01, 00, 10,01} can be decompressed using the same
encoding table, thus resulting in the reverse mapping:
{01, 00, 10,01} → {1111, 1001, 1000, 1111}.
Formally, we can think of an encoding table as a
one-to-one function f that maps the original value v to
its compressed form c. Written more briefly, f : v 7→ c.
Values are encoded by using the function f to find the
corresponding encoding.
Values are decoded using the inverse of f . The
inverse function f
−1
maps the compressed value c to
its original value v. The decoding function can be
written more briefly as: f
−1
: c 7→ v.
Encoding tables are usually implemented using
associative arrays or hashmaps. The keys of the
hashmap represent the compressed values and the en-
tries represent the original values. We can think of
each entry in the hashmap as an evaluation of the f
−1
for a specific compressed value v.
Encoding tables are normally used by a class of
compression algorithms called dictionary encoders.
Dictionary encoding algorithms compress data by
reading all the data and constructing an encoding ta-
ble which is then packaged along with the compressed
data, so that it can be decompressed later.
Creating an encoding table for all the data is not
feasible in a real-time scenario, since the algorithm
will not have access to all the data beforehand. This
means that the algorithm on the sender must dynam-
SENSORNETS 2019 - 8th International Conference on Sensor Networks
70
ically create the encoding table and communicate it
without affecting the real-time constraints of the ap-
plication.
Algorithms 1 and 2 show how the sender and re-
ceiver dynamically create the encoding table without
any communication overhead. The algorithms dy-
namically create an encoding table by caching the last
N values. A value’s encoding corresponds to its index
in the encoding table. If a value reoccurs, the algo-
rithm compresses it by reporting its index in the en-
coding table. If a value is added to an encoding table
for the first time the algorithm reports the value in-
stead of the index. Reporting the value instead of the
index allows the receiver to update its encoding table
so that it is consistent with the sender.
During the remainder of this section, we discuss a
detailed example. We use this example to explain how
algorithms I and II are used to establish the distributed
encoding tables dynamically.
Algorithm 1: Algorithm For Compressing
Packets.
Input: Packet To Encode (PTE) ,
N-bitCounter, Encoding Table
Output: Encoded Packet (EP)
if PTE is an entry in the Encoding Table then
EP←Index of the [Entry] return EP
else
Increment N-bitCounter
Encoding← N-bitCounter Add Entry
[PTE] at Index [Encoding] return PTE
end
Algorithm 2: Algorithm For Decompressing
Packets.
Input: Packet To Decode (PTD) ,
N-bitCounter, Encoding Table
Output: Decoded Packet (DP)
if length(PTD)≤ log
2
(N) then
DP←Entry in Encoding Table at Index
PTD return DP
else
Increment N-bitCounter
Encoding← N-bitCounter Add Entry
[PTD] at Index [Encoding] return PTD
end
Figure 1 shows an example of how the datastream
{1111, 1010, 1111,0000} is compressed and decom-
pressed in real-time. As the first value 1111 arrives,
it is inserted at the first index in the encoding table.
In this example, we consider an encoding table that
holds a maximum of two encoding pairs. Each value
is encoded using the index of the value in the table.
Ϭ ϭϭϭϭ
ϭ
Ϭ ϭϭϭϭ
ϭ
Ϭ ϭϭϭϭ
ϭ ϭϬϭϬ
Ϭ ϭϭϭϭ
ϭ ϭϬϭϬ
Ϭ ϭϭϭϭ
ϭ ϭϬϭϬ
Ϭ ϭϭϭϭ
ϭ ϭϬϭϬ
Ϭ ϬϬϬϬ
ϭ ϭϬϭϬ
Ϭ ϬϬϬϬ
ϭ ϭϬϭϬ
ϭϭϭϭ
ϭ
ϯ
Ϯ
ϰ
ϭϬϭϬ
ϭϭϭϭ
ϭϭϭϭ
ϭϬϭϬ
ϭϬϭϬ
ϭϭϭϭ
Ϭ
ϭϭϭϭ
ϬϬϬϬ
ϬϬϬϬ
ϬϬϬϬ
Figure 1: The diagram above shows an example of how the
algorithm compresses and decompresses a stream of infor-
mation in real-time.
Since the value 1111 is the first in the series it is in-
serted at the first index in the encoding table: 0. This
is because there are two positions in the table and each
position can be addressed using a single bit. The value
0 corresponds to the first position while value 1 cor-
responds to the second position in the table. We use
the 1-bit counter to track the next available position in
the decoding table. In this example the encoding table
is restricted to a maximum of two encoding pairs so
we use a 1-bit counter to represent the index values
{0, 1}.
Once the value 1111 is placed into position 0 the
following encoding pair {1111} → {0} is created.
The sender then sends the value 1111 to the receiver,
so that the receiver can establish the same encoding
pair for the value 1111. Upon receipt of the update
value 1111 the receiver inserts the value at the first in-
dex of its decoding table, thus creating the following
encoding pair {0} → {1111}. Now that the decoding
table on the receiver has been synced with the encod-
ing table on the sender, the next time the sender en-
counters the value 1111 it can simply send the com-
pressed value 0 and the receiver will be able to de-
compress the value and interpret it as the value 1111.
Both the sender and receiver maintain a 1-bit
counter. Upon encountering a new value both the
sender and receiver increment the 1-bit counter. If
both counters on the sender and receiver start with
the same index value, every entry will be assigned the
same encoding value on the sender and receiver since
both counters are incremented in sync.
The compression and decompression algorithms
follow the same procedure for the next value 1010.
Since the value is not contained in the encoding table
it will be added to the encoding table. So both al-
gorithms increment their 1-bit counters and insert the
value into the encoding table at position 1.
However, the third packet is treated differently be-
cause the packet is already contained in the encoding
table of the sender. This implies that the encoding
scheme has already been established for this packet.
Therefore, the sender sends the encoded value 0 in-
stead of the value of 1111. The Receiver checks the
Real-Time Encoding/Decoding for Pairwise Communication Over an Unreliable Sensor Network
71

length of the value and determines that it corresponds
to an encoding value. It then looks up in the encod-
ing table and returns the value at position 0 which is
1111.
Limiting the size of the encoding table helps
decrease the lookup time so that the compression
and decompression processes meet the real-time con-
straints of the application. An N-bit counter only al-
lows for 2
N
possible encoding keys. The 1-bit counter
in this example only allows for two encoding keys.
When the fourth value (0000) arrives, all the en-
tries in the encoding table have been filled. Therefore
one of the entries must be overridden, since the en-
coding table can only hold two unique entries. The
first value is overwritten, since the N-bit counter is
cyclic, so the fourth packet is placed at the first index.
This does not affect the consistency of the encoding
tables, since the counters are cyclic, both the sender
and receiver override the same value in the encoding
table.
3 DISCUSSION OF TEMPORAL
COMPRESSION ALGORITHM
3.1 Proof of Correctness
Let S be a stream of packets {p
1
, p
2
....p
n
}. Let f
x
(p
i
)
denote the compression function implemented using
a hashmap of size x. Recall that this hashmap rep-
resents the encoding table that was described earlier
in this section. We formally define the compression
function below in equation 1.
f
x
(p
i
) =
p
i
if H
x
(p
i
) =
/
0
H
x
(p
i
) otherwise
(1)
The function H
x
(p
i
) denotes the hash function that
is applied to the packets. We denote the length of a
packet as |p
i
|. We detect compressed packets by ex-
amining their length |p
i
| ≤ log
2
(x). The decompres-
sion function is formally denoted below.
d
x
(p
i
) =
p
i
if |p
i
| > log
2
(x)
H
−1
x
(p
i
) if |p
i
| ≤ log
2
(x)
(2)
Theorem 1 (Dictionary Consistency). The dictionary
on the sender s remains consistent with the dictionary
on the receiver r for any arbitrary data stream of or-
dered packets.
Proof. To prove the correctness of the algorithm we
must show that the following invariant holds.
Invariant:
d
x
( f
x
(p
i
)) = p
i
(3)
Maintenance of Invariant: We must prove that
the invariant holds in two cases. The first case is when
the packet is not in the hash table, while the second
case is when the packet is in the hash table.
In the first case the packet has not been com-
pressed and |p
i
| ≥ log
2
(x) and therefore the decom-
pression function correctly returns the value. The in-
variant holds in this first case.
In the second case, equation 4 must be true for the
invariant to hold.
H
−1
x
(H
x
(p
i
)) = p
i
(4)
Equation 4 is true by construction, since every key
value pair that is inserted into the hash table H
x
(p
i
)
is also inserted as an inverse key value pair in the
H
−1
x
(p
i
) in which the value is treated as the key and
the key is treated as the value.
Termination: The algorithm will terminate be-
cause the data stream is of finite length and the al-
gorithm only operates on each packet once. The al-
gorithm has a time complexity that is linear with the
number of packets.
3.2 Dealing with Packet Losses
In this section we demonstrate how the proposed al-
gorithm deals with packet losses. To aid our explana-
tion, we introduce three categories of packets: update
packets, compressed packets and locking/unlocking
packets. Update packets cause new key value pairs
to be inserted into the encoding table. compressed
packets contain the encoded values. Locking packets
are used to lock the encoding table, while unlocking
packets are used to unlock the encoding table. Lock-
ing the encoding table prevents new packets from be-
ing added to the encoding table.
The loss of a compressed packet is naturally tol-
erated by the algorithm, since compressed packets do
not affect the consistency of the encoding table. How-
ever, if an update packet is lost the encoding table on
the sender will become inconsistent with the encod-
ing table on the receiver. There are two methods for
ensuring the consistency of the encoding tables. The
first method uses acknowledgments to guarantee the
delivery of update packets, while the second method
prevents a lost update packet from updating the en-
coding tables by locking the encoding tables. Each
method has trade-offs. The first method is suited for
periods of high temporal locality, while the second
method is suited for periods of low temporal locality.
SENSORNETS 2019 - 8th International Conference on Sensor Networks
72
^ Z
^ Z
^ Z
y
W
͛
Ă Đ Ŭ
^ Z
^ Z
W
͛
Ă Đ Ŭ
y
Z Ğ Đ Ğ ŝǀ Ğ Ě
Z
Ğ
Đ
Ğ
ŝ
ǀ
Ğ
Ě
> Ž Ɛƚ
>
Ž
Ɛ
ƚ
ZĞ ũĞĐƚW ͛
Đ Đ Ğ Ɖ ƚ W ͛
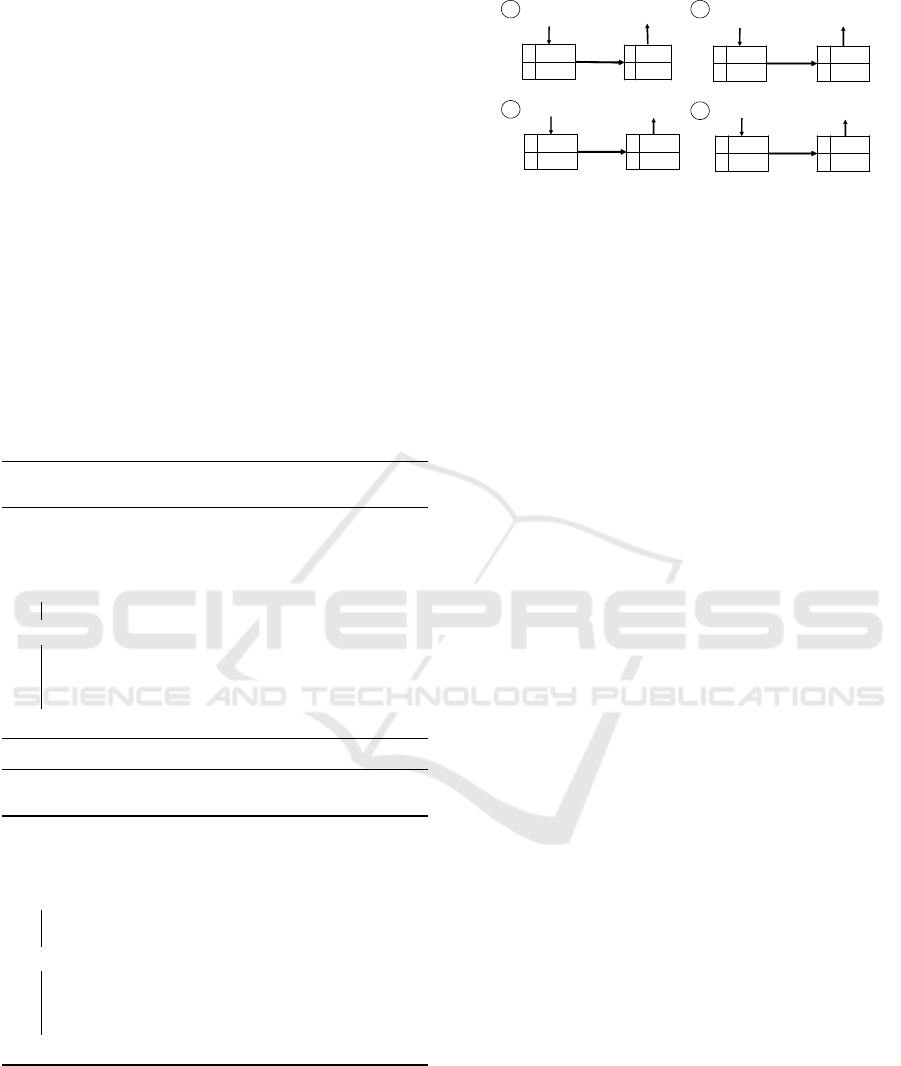
Figure 2: A Karnaugh map showing a visual proof that
the algorithm guarantees delivery of all update and control
packets under different loss conditions. P
0
represents the
duplicate packet while X represents a lost packet.
The proposed algorithm accommodates data streams
with sections of both high and low temporal locality
by using both methods. The first method is discussed
in subsection 3.3 And the second method is discussed
in subsection 3.4
3.3 Using Acknowledgments for Update
Packets
The sender and receiver use acknowledgments to
guarantee the delivery of update packets, locking
packets, and unlocking packets. The sender starts a
timer and waits for an acknowledgement from the re-
ceiver. Once the sender has sent an update packet
the sender does not update its encoding table or send
another packet until it receives an acknowledgement
from the receiver. If the sender does not receive an ac-
knowledgement within a given time period the sender
resends the packet. The receiver gets a duplicate up-
date packet and resends and acknowledgement. By
using acknowledgments both the sender and receiver
guarantee the consistency of their encoding tables. To
prove that this mechanism works in all scenarios we
use the Karnaugh map shown in figure 2 to construct
a visual proof.
The first cell in the Karnaugh map represents the
condition in which both the packet and the acknowl-
edgment are received. In this case the algorithm func-
tions normally.
The second cell represents the condition under
which the packet is lost but the acknowledgment is
received. This state is not possible since the receiver
will only acknowledge packets that it has received.
The third cell represents the condition under
which an update packet has been received but the ac-
knowledgment has been lost, in which case the sender
retransmits the packet. When the receiver receives the
re-transmitted packet it checks to see if it has already
received the packet by checking the last entry in the
decoding table. If the update packet is already con-
tained in the decoding table, the receiver knows that it
has already received the packet and can conclude that
the acknowledgment was lost. Once the receiver has
concluded that the acknowledgement has been lost it
retransmits the acknowledgement to notify the sender
that it has received the packet.
It may seem that this recovery strategy would
fail if the stream contains two consecutive and iden-
tical update packets since this strategy would drop
the second packet. However, update packets can-
not be duplicated in a sequence. By definition, if
the packet following an update packet is identical
to the update packet it will be encoded using the
update packet’s index, thus making it a compressed
packet. Consider the following example data stream:
{0001, 0010, 0010}. The second packet 0010 is a
compressed packet since the first packet would have
already been stored in the update table. So, instead of
sending the value 0010, the algorithm would transmit
the index, which is a compressed packet.
The fourth cell represents the condition under
which the update packet is lost. If an update packet
is lost, the algorithm will follow the same procedure
described above to ensure that the encoding tables
are kept consistent. It should be noted that using ac-
knowledgements would result in a slight delay since
sender and receiver would wait until the acknowledg-
ment is received.
The algorithm tolerates out-of-order arrivals for
compressed packets but does not tolerate out-of-order
arrivals for update packets. However, this is not a
problem because the algorithm ensures the in-order
arrival of all update packets by buffering the stream
until it has received an acknowledgment.
3.4 Locking the Encoding Table
Acknowledging packets introduces additional delay,
since the sender must wait for an acknowledgement
before allowing the stream to progress. Such delays
may outweigh the benefits of the compression algo-
rithm. This is tolerable, if update packets are rare then
acknowledgments are rarely sent. However, if update
packets are common then acknowledgments have to
be sent frequently. Frequent update packets imply low
temporal locality and the benefits of the compression
may not be worth the delay. To mitigate this we pro-
pose locking the encoding table. Locking the table
stops any additional packets from being added to the
encoding table; thus removing the need for acknowl-
edgments.
To ensure that the algorithm functions efficiently
we lock the table during periods of low temporal lo-
Real-Time Encoding/Decoding for Pairwise Communication Over an Unreliable Sensor Network
73
cality and unlock the table during periods of high tem-
poral locality. We propose using the number of unique
packets within a given time period as a measure of
temporal locality and propose locking the table when
the rate of unique packets rises above a fixed thresh-
old and unlocking the encoding table when the rate
of unique packets falls below a set threshold. This
threshold is determined empirically.
4 EVALUATION
We have evaluated the proposed Temporal Compres-
sion Algorithm using four metrics: 1) the compres-
sion ratio, 2) the energy used by the transceiver, 3)
the number of bytes required for compression. We
use these metrics to compare the temporal compres-
sion algorithm to the state of the art LZW algorithm.
The the temporal compression algorithm reduces the
amount of energy used by the transceiver by 30%
when compared with the uncompressed data stream.
The temporal compression algorithm does not delay
any packets, while the LZW algorithm delays an av-
erage of 80% of the packets.
We evaluate the performance of our algorithm by
examining four traces of irradiance readings obtained
from Columbia University’s EnHANTs dataset (Gor-
latova et al., 2011b). The readings were collected
at 30 second intervals using TAOS TSL230rd photo-
metric sensors installed on LabJack U3 DAQ devices.
Each trace was collected from a sensor placed in a
different location. The first trace (Setup A) was col-
lected from a sensor placed on the windowsill of a
south-facing window on the 6
th
floor of a building.
The second trace (Setup B) was collected from a sen-
sor placed on top of a bookshelf; this sensor only re-
ceived light for a short portion of the day. The third
trace (Setup C) was collected using a sensor placed on
the windowsill of a north-facing window in a confer-
ence room where the shades were frequently adjusted.
The forth trace was collected by holding a sensor and
walking around time square in New York City.
4.1 Compression Performance
We evaluate the compression performance of an algo-
rithm by calculating its compression ratio. The com-
pression ratio is calculated by dividing the size of the
compressed data by the size of the original data. A
compression ratio of 0.5 means that the compressed
data is half the size of the original data. We calculate
the compression ratio of the TCA algorithm and com-
pare it to the compression ratio of the LZW algorithm.
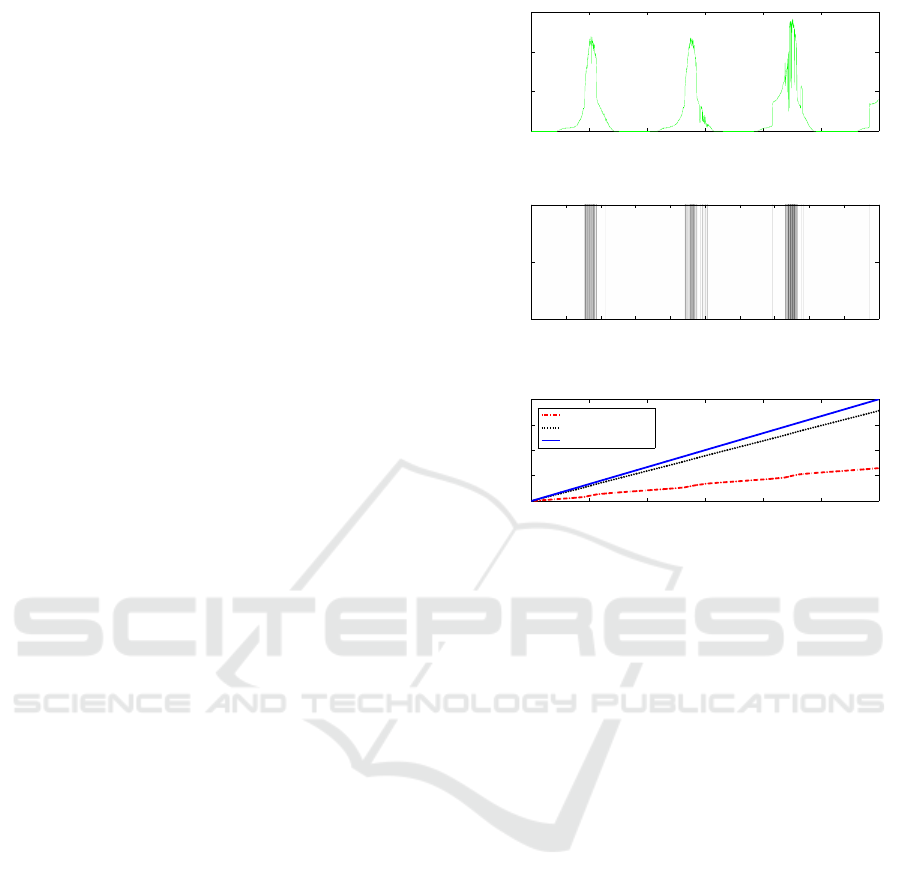
0 0.5 1 1.5 2 2.5 3
x 10
5
0
50
100
150
Time(Seconds)
Irradiance(/muJ)
(a) Irradiance Readings
Frozen/UnFrozen
Time(Seconds) x 10
5
0.3 0.6 0.9 1.2 1.5 1.8 2.1 2.4 2.7 3.0
(b) State of Encoding Table
0 0.5 1 1.5 2 2.5 3
x 10
5
0
2
4
6
8
x 10
4
Time(Seconds)
Total Bytes Transfered
TCA 2 bits
TCA 7 bits
uncompressed 8 bits
(c) Total Bytes Transferred
Figure 3: Figure (a) shows the irradiance reading vs time.
Figure (b) is a color map. This color map shows the state
of the encoding table. Dark regions represent a locked state
while light regions represent an unlocked state. Figure (c)
shows the total number of bytes transmitted.
Figure 3(a) shows 10,000 irradiance readings col-
lected over a period of 83.333 hours (3.5 days). These
readings were taken from the trace associated with
setup A. Notice the periodicity between the low ir-
radiance readings and high irradiance readings.
Figure 3(b) shows a colormap. The x-axis shows
the time, while the color of the map represents the
state of the encoding table. Dark regions indicate that
the encoding table is in a locked state, while light
regions indicate that the encoding table is in an un-
locked state. We ran the TCA algorithm using a table
size of four and a threshold of four update packets
every two minutes. As expected dark regions on the
map correspond to sections of low temporal locality
while light regions of the map correspond to sections
of high temporal locality. Therefore we conclude that
using a threshold to identify sections of high and low
temporal locality is an effective strategy for determin-
ing when to lock and unlock the encoding table.
Figure 3(c) shows the total number of bytes vs.
time. The solid blue line represents the total num-
ber of bytes that would be transferred if the stream
was uncompressed (8 bits). The dotted black line
represents the total number of bytes that would be
transferred if the data was compressed using the 7-
SENSORNETS 2019 - 8th International Conference on Sensor Networks
74
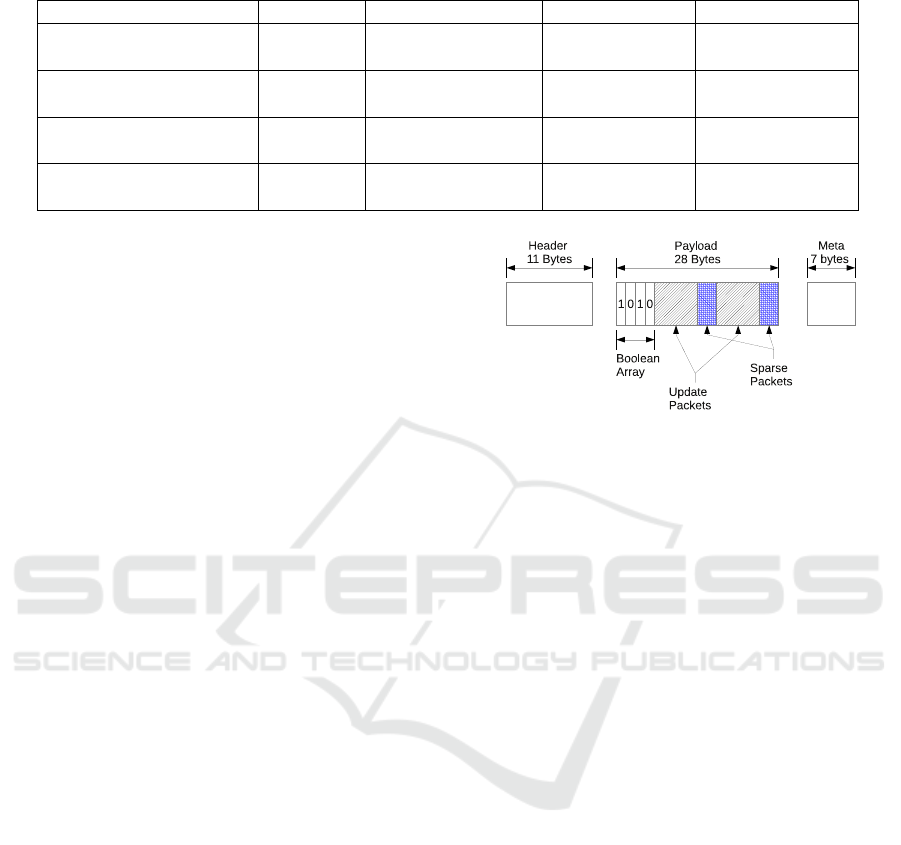
Table 2: (NC) No Compression, (TCA) Temporal Compression Algorithm, (LZW) Lempel Ziv Welch Algorithm.
Trace Algorithm Compression Ratio Memory (bytes) Energy Range (J)
Setup A EnHANTs TCA 0.3233 4 0.0144 → 0.0246
LZW 0.1605 930 0.0030 → 0.0055
Setup B EnHANTs TCA 0.2626 4 0.0139 → 0.0236
LZW 0.0546 401 0.0009 → 0.0018
Setup C EnHANTs TCA 0.2978 4 0.0142 → 0.0242
LZW 0.0791 523 0.0015 → 0.0026
Mobile Trace EnHANTs TCA 0.7261 4 0.0064 → 0.0113
LZW 0.5121 1050 0.0034 → 0.0062
bit encoding temporal compression algorithm. The
dashed red line represents the total number of bytes
that would be transferred if the data was compressed
using the 2-bit encoding temporal compression algo-
rithm.
Figure 3(c) shows how increasing the number of
encoding bits affects the compression ratio. Using
a 2-bit encoding scheme achieves a better compres-
sion ratio than using a 7-bit encoding scheme, because
the 2-bit encoding scheme allows for smaller encoded
packets, which makes up for its inability to capture the
diversity in the stream since it only encodes 4 values
(2
2
). Though a 7-bit encoding scheme encodes up to
128 values, the compressed packets are 7-bits, 5 bits
larger than the encoded packets used by the 2-bit en-
coding scheme. Since the sections of the data stream
that exhibit high temporal locality contain less than
4 unique values; the 2-bit encoding scheme is better
suited for this trace.
We found that the temporal compression algo-
rithm is able to achieve an average compression ra-
tio of 0.398. This means that the temporal compres-
sion algorithm allows the transceiver to transmit an
average of 60% fewer bytes than the uncompressed
stream.
4.2 Energy Efficiency
The energy model for the CC2420 transceiver pro-
posed in (Schmidt et al., 2007) is used to evaluate
the energy efficiency of the algorithms. The CC2420
transceiver is commonly found in sensor nodes like
micaz (Polastre et al., 2005).
It is not energy efficient to send a payload that is
only 8 bits long, since 18 bytes of additional informa-
tion must be transmitted along with it. Several sensing
applications solve this problem by packaging multiple
packets into the 28 byte payload. The receiver recov-
ers the packets by parsing the payload. When simulat-
ing the energy consumption of the LZW and tempo-
ral compression algorithm we place multiple packets
in the payload of each data frame. Each data frame
Figure 4: 802.15.4 frame layout.
is packed with 24 packets. Each packet may be an
update packet or a sparse packet. A 24 bit boolean ar-
ray is used to indicate the index of sparse packets and
update packets. A boolean value of 1 means that the
packet is an update packet while a boolean value of 0
means that it is a sparse packet. The boolean array is
stored at the beginning of the frame’s payload. The
receiver uses the boolean array to parse the frame’s
payload.
Figure 4 shows an example of a data frame. The
payload in this example is approximately 4 bytes long
and contains 2 update packets and 2 sparse packets.
Typical payloads will contain 24 packets, however for
the purpose of this example we only show 4 packets.
Since the payload only contains 4 packets, 4 bits of
payload are reserved for the boolean array {1, 0,1, 0}.
The receiver uses this boolean array to parse the pay-
load. A boolean value of 1 means that the receiver
should read the next 8 bits as the value for the up-
date packet, while a value of 0 means that the receiver
should read the next 2 bits as the value for the sparse
packet. In our experiments the payload was filled with
24 packets. This results in a boolean array that is only
3 bytes long.
5 RELATED WORK
Dictionary coding algorithms have been proposed as
an alternative to tree based encoding algorithms. Dic-
tionary coding algorithms encode values by storing
the compressed value and the original value as key
Real-Time Encoding/Decoding for Pairwise Communication Over an Unreliable Sensor Network
75

value pairs in a dictionary. This results in fast encod-
ing and decoding times but does not address the space
constraints of embedded devices, as the dictionaries
can become very large.
The LZ77 algorithm encodes data using a dictio-
nary and sliding window (Ziv and Lempel, 1977) .
The algorithm works by sliding an expanding window
across the bytes stream. If the bytes in the window are
in the dictionary the algorithm reports the index of the
bytes. If the bytes in the window are not in the dic-
tionary the algorithm adds the bytes to the dictionary.
However, the LZ77 algorithm does not meet real-time
constraints as the entire data stream is needed in ad-
vance to construct the dictionary.
The LZW algorithm (Nelson, 1989) attempts to
address some of the real-time constraints of the LZ77
algorithm. The LZW algorithm is also a dictionary
coding algorithm and is a modification of LZ78 (Ziv
and Lempel, 1978), which is based on the LZ77 com-
pression algorithm. The LZW algorithm starts by ini-
tializing the dictionaries on the sender and receiver
with 256 entries. As the sender gets values it encodes
the values using the dictionary. If the sender gets a
value that is not in the dictionary it adds the value to
the dictionary and sends the value to the receiver so
that it can also add the value to its dictionary. This
is how the algorithm ensures that both the dictionar-
ies on the sender and the receiver are consistent while
still meeting the real-time constraints. However, this
algorithm fails if a single packet is lost. The loss of a
single packet corrupts the dictionaries. The algorithm
does not impose a size constraint on the dictionaries.
This means that the dictionaries can grow to be very
large. It is difficult to store large dictionaries on sen-
sor devices with limited memory.
The S-LZW (Sadler and Martonosi, 2006) algo-
rithm was introduced to address the memory con-
straints and packet loss constraints of the LZW algo-
rithm. The S-LZW algorithm restricts the dictionary
to 512 entries and divides the data stream into inde-
pendent blocks. A new dictionary is created for each
block. If the dictionary is filled, it is frozen, and no
new entries are added.
6 CONCLUSION
In this paper we present a real-time compression and
decompression algorithm for unreliable networks.
The algorithm compresses a data stream by exploiting
the stream’s temporal locality. Fewer bits are used to
represent elements that frequently recur in a tempo-
ral sequence. The sender and receiver automatically
agree upon the bits that will be used to encode the el-
ements. These bits are then stored in encoding tables
which are used to compress and decompress the data
in real-time.
REFERENCES
Gao, T., Greenspan, D., Welsh, M., Juang, R., and Alm,
A. (2005). Vital signs monitoring and patient tracking
over a wireless network. In Engineering in Medicine
and Biology Society, 2005. IEEE-EMBS 2005. 27th
Annual International Conference of the, pages 102–
105.
Gorlatova, M., Wallwater, A., and Zussman, G. (2011a).
Networking low-power energy harvesting devices:
Measurements and algorithms. In INFOCOM, 2011
Proceedings IEEE, pages 1602–1610. IEEE.
Gorlatova, M., Zapas, M., Xu, E., Bahlke, M., Kymissis,
I. J., and Zussman, G. (2011b). CRAWDAD data set
columbia/enhants (v. 2011-04-07). Downloaded from
http://crawdad.cs.dartmouth.edu/columbia/enhants.
Keally, M., Zhou, G., and Xing, G. (2010). Watchdog: Con-
fident event detection in heterogeneous sensor net-
works. In Real-Time and Embedded Technology and
Applications Symposium (RTAS), 2010 16th IEEE,
pages 279–288.
Kenney, J., Poole, D., Willden, G., Abbott, B., Morris, A.,
McGinnis, R., and Ferrill, D. (2009). Precise position-
ing with wireless sensor nodes: Monitoring natural
hazards in all terrains. In Systems, Man and Cybernet-
ics, 2009. SMC 2009. IEEE International Conference
on, pages 722–727.
Marcelloni, F. and Vecchio, M. (2008). A simple algo-
rithm for data compression in wireless sensor net-
works. Communications Letters, IEEE, 12(6):411–
413.
Nelson, M. R. (1989). Lzw data compression. Dr. Dobb’s
Journal, 14(10):29–36.
Polastre, J., Szewczyk, R., and Culler, D. (2005). Telos: en-
abling ultra-low power wireless research. In Informa-
tion Processing in Sensor Networks, 2005. IPSN 2005.
Fourth International Symposium on, pages 364–369.
IEEE.
Sadler, C. M. and Martonosi, M. (2006). Data compres-
sion algorithms for energy-constrained devices in de-
lay tolerant networks. In Proceedings of the 4th inter-
national conference on Embedded networked sensor
systems, pages 265–278. ACM.
Schmidt, D., Krämer, M., Kuhn, T., and Wehn, N. (2007).
Energy modelling in sensor networks. Advances in
Radio Science, 5(12):347–351.
Ziv, J. and Lempel, A. (1977). A universal algorithm for se-
quential data compression. Information Theory, IEEE
Transactions on, 23(3):337–343.
Ziv, J. and Lempel, A. (1978). Compression of individual
sequences via variable-rate coding. Information The-
ory, IEEE Transactions on, 24(5):530–536.
SENSORNETS 2019 - 8th International Conference on Sensor Networks
76
