
Planar Motion Bundle Adjustment
Marcus Valtonen
¨
Ornhag
1
and M
˚
arten Wadenb
¨
ack
2
1
Centre for Mathematical Sciences, Lund University, Lund, Sweden
2
Department of Mathematical Sciences, Chalmers University of Technology and the University of Gothenburg,
Gothenburg, Sweden
Keywords:
Planar Motion, Bundle Adjustment.
Abstract:
In this paper we consider trajectory recovery for two cameras directed towards the floor, and which are
mounted rigidly on a mobile platform. Previous work for this specific problem geometry has focused on
locally minimising an algebraic error between inter-image homographies to estimate the relative pose. In or-
der to accurately track the platform globally it is necessary to refine the estimation of the camera poses and
3D locations of the feature points, which is commonly done by utilising bundle adjustment; however, existing
software packages providing such methods do not take the specific problem geometry into account, and the
result is a physically inconsistent solution. We develop a bundle adjustment algorithm which incorporates the
planar motion constraint, and devise a scheme that utilises the sparse structure of the problem. Experiments
are carried out on real data and the proposed algorithm shows an improvement compared to established generic
methods.
1 INTRODUCTION
Structure from Motion (SfM) is a classic problem in
computer vision, and concerns the simultaneous de-
termination of the scene geometry (the structure) and
the pose of the cameras (the motion) from a number
of images of a scene (Hartley and Zisserman, 2004;
Szeliski, 2011). Modern systems for SfM, such as the
ones famously used to “build Rome” (Agarwal et al.,
2011; Frahm et al., 2010) or the popular Bundler sys-
tem (Snavely et al., 2008), are able to generate im-
pressive reconstructions of increasingly large scenes
from large unordered and unlabelled collections of
images.
Among the key enabling technologies for these
successes in large scale SfM are algorithms for per-
forming Bundle Adjustment (BA), i.e. solving the
SfM problem as a large optimisation problem (Triggs
et al., 1999). In this optimisation problem, a cost
function—often chosen as the sum of squared geo-
metric reprojection errors—is to be minimised with
respect to a set of parameters describing the scene
geometry and the camera poses. Formulating SfM
as a BA problem has a number of benefits when it
comes to the problem modelling, e.g. (a) it can, in a
unified way, incorporate assumptions concerning the
camera calibration, (b) it allows the use of a suit-
able parametrisation and/or explicit constraints for the
purpose of enforcing a particular motion model, and
(c) the cost function can be chosen to be a physically
meaningful quantity, as opposed to a purely algebraic
error.
Due to its relatively high computational cost, BA
has traditionally been applied mainly in offline batch
processing systems such as the ones mentioned above.
During the last two decades, however, BA has started
to surface in online SfM systems used for cam-
era based Simultaneous Localisation and Mapping
(SLAM) and Visual Odometry (VO), where it can be
performed at regular intervals e.g. to reduce scale
drift or to improve consistency in general. This devel-
opment has been driven by improvements in the per-
formance of hardware as well as by advances in the al-
gorithms and their implementation, and we anticipate
that more and more application specific implementa-
tions of BA will move towards real-time systems.
In visual SLAM there is sometimes additional
information available compared to a general SfM
problem, and this can be exploited to improve the
performance of the system. For instance, the im-
ages are acquired in an ordered sequence, and this
avoids expensive “all-vs-all” matching of the images
when searching for correspondences. Another possi-
ble source of valuable information is a suitable mo-
tion model, which can be used e.g. for feature predic-
tion (Davison et al., 2007; Davison, 2003), to exploit
24
Örnhag, M. and Wadenbäck, M.
Planar Motion Bundle Adjustment.
DOI: 10.5220/0007247700240031
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 24-31
ISBN: 978-989-758-351-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

non-holonomic constraints (Zienkiewicz and Davi-
son, 2015; Scaramuzza, 2011a; Scaramuzza, 2011b),
or to constrain the camera motion to a plane (Hajj-
diab and Lagani
`
ere, 2004; Ort
´
ın and Montiel, 2001;
Wadenb
¨
ack and Heyden, 2014).
In this paper, we will consider BA in the con-
strained planar motion case for a pair of cameras—not
necessarily with overlapping fields of view—attached
to a mobile platform in such a way that each of the
two cameras are subject to a planar motion model, in
addition to the rigid body motion connecting them.
2 RELATED WORK
An early approach by Ort
´
ın and Montiel used a pla-
nar motion model to parametrise the essential matrix
between successive views in terms of two translation
parameters and one rotation angle, which allowed the
relative motion to be recovered from two point corre-
spondences using a non-linear solver (Ort
´
ın and Mon-
tiel, 2001). One limitation of this approach is that
it does not contain any way to determine the length
of the translation between the camera positions. An-
other limitation is that the camera must be mounted
in such a way that the optical axis is horizontal, to a
reasonably high precision, in order to allow the sim-
ple parametrisation employed. A similar approach
was considered for the stereo case in (Chen and Liu,
2006).
In the monocular case, the problems of scale am-
biguity and scale drift are connected to the use of the
fundamental matrix to solve the relative pose prob-
lem. An additional drawback of these methods is
that the fundamental matrix cannot be determined
from co-planar correspondences—see e.g. (Hartley
and Zisserman, 2004) for further discussion of this
degeneracy—which is a considerable issue in indoor
environments where planar structures are common.
These considerations, among others, have led re-
searchers to consider homography based methods in-
stead.
The homography based method by Liang and
Pears used correspondences in the ground plane, to-
gether with a planar motion model (Liang and Pears,
2002). They showed that the rotation angle about the
vertical axis can be found via the eigenvalues of the
homography matrix, regardless of how the camera is
mounted. A similar geometric situation, but allowing
only one tilt angle in the possible camera orientations,
was studied in (Hajjdiab and Lagani
`
ere, 2004). They
also devised an effective scheme for estimating the
full set of motion parameters.
More recent work by Wadenb
¨
ack and Heyden ex-
tended the homography based methods for planar mo-
tion and co-planar keypoints to the general 5-DoF sit-
uation (Wadenb
¨
ack and Heyden, 2013). Their method
used a decoupling of the underlying 2D rigid body
motion from the camera tilt, which was first esti-
mated iteratively. The same general geometric situ-
ation was also considered by Zienkiewicz and Davi-
son, who proposed a dense matching of the images
based on non-linear optimisation for determining the
correct motion parameters (Zienkiewicz and Davison,
2015).
The general 5-DoF situation was extended to a
binocular setup, with possibly non-overlapping fields
of view, in (Valtonen
¨
Ornhag and Heyden, 2018a;
Valtonen
¨
Ornhag and Heyden, 2018b). The cameras
were assumed to be connected by a rigid body mo-
tion, and it was shown that it is possible to recover the
relative pose between the cameras.
Bundle adjustment is a well-studied problem and
an excellent overview is that of (Triggs et al., 1999),
mentioned in the introduction. Since bundle ad-
justment often involves solving a large system of
equations it is necessary to account for the struc-
ture of the problem, e.g. by exploiting sparsity pat-
terns. One sparse bundle adjustment package avail-
able is SBA (Lourakis and Argyros, 2009), which
utilises the sparsity in the Jacobian matrix by using
Schur complementation in order to speed up the algo-
rithm. The SBA package has been successfully used
in e.g. (Snavely et al., 2008; Agarwal et al., 2011;
Frahm et al., 2010).
Among more recent implementations of sparse
bundle adjustment is Sparse Sparse Bundle Adjust-
ment (sSBA) (Konolige, 2010) and Simple Sparse
Bundle Adjustment (SSBA) (Zach, 2014), which uses
a similar approach as SBA in the sense that the aug-
mented normal equations are solved, but utilises pack-
ages that exploit the sparsity more efficiently. To
speed up convergence, and move into the domain
of real-time applications, Parallel Bundle Adjustment
was introduced in (Wu et al., 2011) which supports
GPU acceleration where a preconditioned Conjugate
Gradients (CG) system is solved. Another GPU im-
plementation by H
¨
ansch et al. shows that is is possi-
ble to efficiently parallelise the Levenberg-Marquardt
algorithm (LM) (H
¨
ansch et al., 2016). Recent papers
dealing with very large scale SfM problems have suc-
cesfully employed distributed methods, by employing
splitting methods (Eriksson et al., 2016; Zhang et al.,
2017).
Furthermore, choosing the cost function to be the
sum of squared geometric reprojection errors is not
the only viable option—for monocular visual odome-
try photometric bundle adjustment, where the photo-
Planar Motion Bundle Adjustment
25

metric consistency is maximised, has proven to be a
good competitor (Alismail et al., 2016).
3 THEORY
3.1 Problem Geometry
In this paper we consider a mobile platform with two
cameras directed towards the floor. The world coor-
dinate system is chosen such that the ground floor is
positioned at z = 0, whereas the cameras move in the
planes z = a and z = b, respectively. Furthermore,
the fields of view of the cameras are not assumed to
be overlapping, and both cameras are assumed to be
mounted rigidly onto the platform. Due to this setup,
the cameras are connected by a rigid body motion,
and, without loss of generality, we may assume that
the centre of rotation of the mobile platform is located
in the first camera centre, as is illustrated in Figure 1.
z = 0
z = b
z = a
Figure 1: The problem geometry considered in this paper.
The cameras are assumed to move in the planes z = a and
z = b, the relative orientation between them as well as the
tilt towards the floor normal is assumed to be constant as the
mobile platform moves freely.
3.2 Camera Parametrisation
A camera parametrisation well suited to the inter-
nally calibrated monocular case of this specific prob-
lem geometry was derived in Wadenb
¨
ack and Hey-
den (Wadenb
¨
ack and Heyden, 2013), and we adopt
this parametrisation here. The camera matrix associ-
ated with the image taken at position j is thus written
as
P
P
P
( j)
= R
R
R
ψθ
R
R
R
( j)
ϕ
[I
I
I | − t
t
t
( j)
], (1)
where R
R
R
ψθ
is a rotation θ about the y-axis followed
by a rotation of ψ about the x-axis. The movement
of the mobile platform is modelled by a rotation ϕ
( j)
about the z-axis, corresponding to R
R
R
( j)
ϕ
, and a trans-
lation vector t
t
t
( j)
. In (Valtonen
¨
Ornhag and Heyden,
2018a) the camera matrices for the second camera are
parametrised as
P
P
P
0( j)
= R
R
R
ψ
0
θ
0
R
R
R
η
T
T
T
τ
τ
τ
(b)R
R
R
( j)
ϕ
[I
I
I | −t
t
t
( j)
], (2)
where ψ
0
and θ
0
are the tilt angles, defined analo-
gously as for the first camera, τ
τ
τ is the relative transla-
tion between the camera centres and η is the constant
rotation about the z-axis relative to the first camera.
None of the constant parameters are assumed to be
known. The translation matrix T
T
T
τ
τ
τ
(b) is defined as
T
T
T
τ
τ
τ
(b) = I
I
I − τ
τ
τn
n
n
|
/b, where τ
τ
τ =
(τ
x
, τ
y
, 0)
|
, n
n
n is a floor
normal and b is the height above the ground floor. Due
to the global scale ambiguity we may assume a = 1.
4 PREREQUISITES
4.1 Geometric Reprojection Error
Consider the pose of the first camera at position j,
given by the camera matrix in (1), and let
ˆ
x
x
x
( j)
i
denote
the estimated measurement of the scene point X
X
X
i
in
homogeneous coordinates, i.e.
ˆ
x
x
x
( j)
i
∼ P
P
P
( j)
X
X
X
i
. Let x
x
x
( j)
i
denote the measured image point, and define the
residual r
r
r
i j
as r
r
r
i j
= x
x
x
( j)
i
−
ˆ
¯
x
x
x
( j)
i
, where
ˆ
¯
x
x
x
( j)
i
is the in-
homogeneous representation of
ˆ
x
x
x
( j)
i
. Analogously to
the first camera, define the residual r
r
r
0
i j
for the image
of X
X
X
i
in the second camera. Given N stereo camera
locations and M scene points, we seek to minimise
the geometric reprojection error E given by
E(β
β
β) =
N
∑
i=1
M
∑
j=1
kr
r
r
i j
k
2
2
+ kr
r
r
0
i j
k
2
2
, (3)
where β
β
β is the parameter vector consisting of the cam-
era parameters and the scene points.
4.2 The Levenberg-Marquardt
Algorithm
For bundle adjustment it is common to use the
Levenberg-Marquardt algorithm (LM) which solves
the augmented normal equations
J
J
J
|
J
J
J + µI
I
I
δ
δ
δ = J
J
J
|
ε
ε
ε, (4)
where J
J
J is the Jacobian of the cost function and ε
ε
ε
the residual vector. The reader is referred to (Triggs
et al., 1999; Lourakis and Argyros, 2009) for more
details regarding the LM algorithm and its application
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
26

to bundle adjustment. There are other options to the
LM algorithm, e.g. the dog-leg solver (Lourakis and
Argyros, 2005) and preconditioned CG (Byr
¨
od and
˚
Astr
¨
om, 2010); however, LM is one of the most com-
monly used algorithms today, and is used in modern
systems such as SBA (Lourakis and Argyros, 2009)
and sSBA (Konolige, 2010). Note, however, that SBA
assumes the camera parameters for each camera to be
decoupled, which is not the case for this specific prob-
lem geometry.
4.3 Initial Solution for Camera Poses
A good initial solution for the camera poses can be
generated using the method described in Wadenb
¨
ack
and Heyden (Wadenb
¨
ack and Heyden, 2014) for the
monocular case. The method takes as input the inter-
image homographies for the path. These can be es-
timated using Direct Linear Transform (DLT) (Hart-
ley and Zisserman, 2004) from point correspondences
established by automatic matching of features, e.g.
SIFT (Lowe, 2004) or SURF (Bay et al., 2006). Re-
gardless of how the homographies are obtained, the
method continues to estimate the overhead tilt R
R
R
ψθ
from one or several homographies, and then computes
the translation and orientation about the floor normal
by QR decomposition of R
R
R
|
ψθ
H
H
HR
R
R
ψθ
.
In order to initialise the stereo parameters the
method proposed in (Valtonen
¨
Ornhag and Heyden,
2018a) can be used. This method relies on the
the estimates from the monocular method described
above, by first treating the two trajectories individu-
ally. When the trajectories are known individually,
the relative pose between the two cameras may be ex-
tracted. Both methods benefit from using more than
one homography to estimate the motion of the mobile
platform.
4.4 Triangulation of 3D Points
Linear triangulation of 3D points can be posed as find-
ing the null-space of a matrix relating the scene points
and the camera matrices, see e.g. (Hartley and Zisser-
man, 2004); however, this may not result in a physi-
cally meaningful solution in the sense that all points
may not be on the plane z = 0. There is a homog-
raphy between the measured points and the ground
plane; namely, given an image point x
x
x and the corre-
sponding camera P
P
P and scene point X
X
X ∼
(X, Y, 0, 1)
|
it
holds that x
x
x ∼ P
P
PX
X
X = H
H
H
˜
X
X
X. Let P
P
P
i
denote the i:th col-
umn of P
P
P, then H
H
H =
[P
P
P
1
P
P
P
2
P
P
P
4
]
is the homography we
seek and
˜
X
X
X ∼
(X, Y, 1)
|
contains the unknown scene
point coordinates. It follows that the corresponding
scene point can be extracted from
˜
X
X
X ∼ H
H
H
−1
x
x
x.
Having more than one camera will generally re-
sult in different 3D points; however, all of them will
be on the plane z = 0. We use a simple heuristic to tri-
angulate the points by computing the centre of mass.
This is fast, but suffers from the presence of outliers,
which must be removed prior to triangulation in order
to achieve reasonable performance.
5 PLANAR MOTION BUNDLE
ADJUSTMENT
5.1 Block Structure
Consider the general case of N stereo camera po-
sitions, with M scene points. For convenience, let
γ
γ
γ =
(ψ, θ)
and γ
γ
γ
0
=
(ψ
0
, θ
0
, τ
x
, τ
y
, b, η)
denote the un-
known and constant parameters for each camera path
and ξ
ξ
ξ
j
=
(ϕ
( j)
, t
( j)
x
, t
( j)
y
)
be the nonconstant parameters
for position j. Then, the Jacobian J
J
J has the following
block structure:
J
J
J =
Γ
Γ
Γ
11
A
A
A
11
B
B
B
11
.
.
.
.
.
.
.
.
.
Γ
Γ
Γ
1N
A
A
A
1N
B
B
B
1N
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Γ
Γ
Γ
M1
A
A
A
M1
B
B
B
M1
.
.
.
.
.
.
.
.
.
Γ
Γ
Γ
MN
A
A
A
MN
B
B
B
MN
Γ
Γ
Γ
0
11
A
A
A
0
11
B
B
B
0
11
.
.
.
.
.
.
.
.
.
Γ
Γ
Γ
0
1N
A
A
A
0
1N
B
B
B
0
1N
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Γ
Γ
Γ
0
M1
A
A
A
0
M1
B
B
B
0
M1
.
.
.
.
.
.
.
.
.
Γ
Γ
Γ
0
MN
A
A
A
0
MN
B
B
B
0
MN
, (5)
where the derivative blocks are defined as
A
A
A
i j
=
∂r
r
r
i j
∂ξ
ξ
ξ
j
, B
B
B
i j
=
∂r
r
r
i j
∂
˜
X
X
X
i
, Γ
Γ
Γ
i j
=
∂r
r
r
i j
∂γ
γ
γ
,
A
A
A
0
i j
=
∂r
r
r
0
i j
∂ξ
ξ
ξ
j
, B
B
B
0
i j
=
∂r
r
r
0
i j
∂
˜
X
X
X
i
, Γ
Γ
Γ
0
i j
=
∂r
r
r
0
i j
∂γ
γ
γ
0
,
(6)
and where
˜
X
X
X
i
=
(X
i
, Y
i
)
are the unknown scene coor-
dinates. We write this compactly as
J
J
J =
Γ
Γ
Γ 0
0
0 A
A
A B
B
B
0
0
0 Γ
Γ
Γ
0
A
A
A
0
B
B
B
0
. (7)
5.2 Utilising the Sparse Structure
As in SBA (Lourakis and Argyros, 2009) and other
similar frameworks, we would like to use Schur com-
plementation; however, it is not directly applicable
Planar Motion Bundle Adjustment
27

due to the contributions from the constant parame-
ters. Consider, the approximate Hessian J
J
J
|
J
J
J in the
compact form
J
J
J
|
J
J
J =
C
C
C E
E
E
E
E
E
|
D
D
D
, (8)
where C
C
C contains the contribution from the constant
parameters, D
D
D contains the contribution from the non-
constant parameters and the scene points and E
E
E the
mixed contributions. The matrix D
D
D may further be
decomposed into
D
D
D =
U
U
U W
W
W
W
W
W
|
V
V
V
, (9)
with block diagonal matrices U
U
U = diag(U
U
U
1
,. .. ,U
U
U
N
)
and V
V
V = diag(V
V
V
1
,. .. ,V
V
V
M
), where
U
U
U
j
=
M
∑
i=1
A
A
A
|
i j
A
A
A
i j
+ A
A
A
0|
i j
A
A
A
0
i j
,
V
V
V
i
=
N
∑
j=1
B
B
B
|
i j
B
B
B
i j
+ B
B
B
0|
i j
B
B
B
0
i j
,
W
W
W
i j
= A
A
A
|
i j
B
B
B
i j
+ A
A
A
0|
i j
B
B
B
0
i j
.
(10)
The solution to a system on the form (D
D
D + µI
I
I)δ
δ
δ = ε
ε
ε,
where D
D
D is defined as in (9), is well-known, and is
solved efficiently, with minor modifications, using ex-
isting software packages by utilising Schur comple-
mentation.
The main idea of our method is to incorporate the
constant parameters and consider the decomposition
of (8) as nested Schur complements, which reduces
the problem to the form used in SBA and other well-
established software packages, which in turn can be
efficiently solved. To achieve this, consider the aug-
mented normal equations (4) in block form
C
C
C
∗
E
E
E
E
E
E
|
D
D
D
∗
δ
δ
δ
c
δ
δ
δ
d
=
ε
ε
ε
c
ε
ε
ε
d
, (11)
where C
C
C
∗
and D
D
D
∗
denote the augmented matrices,
with the µ term added on the main diagonals, as in (4).
Applying Schur complementation yields
C
C
C
∗
− E
E
ED
D
D
∗−1
E
E
E
|
0
0
0
E
E
E
|
D
D
D
∗
δ
δ
δ
c
δ
δ
δ
d
=
ε
ε
ε
c
− E
E
ED
D
D
∗−1
ε
ε
ε
d
ε
ε
ε
d
(12)
Some remarks are in order. First, note that D
D
D
∗−1
appears in (12) twice, and is infeasible to compute
explicitly, which is avoided using the following ob-
servations: introduce the auxiliary variable δ
δ
δ
aux
, such
that
D
D
D
∗
δ
δ
δ
aux
= ε
ε
ε
d
, (13)
which can be solved with e.g. SBA. In a similar man-
ner D
D
D
∗
∆
∆
∆
aux
= E
E
E
|
can be solved by iterating over the
columns of E
E
E
|
. This may at first seem like a time
consuming task, however, given that the number of
constant parameters is low—as in the problem geom-
etry considered in this paper—having already solved
for (13), the computation of the Schur complement,
as well as intermediate matrices not depending on the
right hand side, can be stored and reused.
When the auxiliary variables are solved for, it is
possible to compute δ
δ
δ
c
from
C
C
C
∗
− E
E
E∆
∆
∆
aux
δ
δ
δ
c
= ε
ε
ε
c
− E
E
Eδ
δ
δ
aux
, (14)
and, finally, for δ
δ
δ
d
by back-substitution
D
D
D
∗
δ
δ
δ
d
= ε
ε
ε
d
− E
E
E
|
δ
δ
δ
c
. (15)
Again, note the resemblance of (13) and (15), hence
the computation of the Schur complement and inter-
mediate matrices can be stored and reused.
6 EXPERIMENTS
6.1 Initial Solution
The inter-image homographies were estimated us-
ing the MSAC algorithm (Torr and Zisserman, 2000)
from four point correspondences by extracting SURF
keypoints and applying a KNN algorithm to establish
the matches.
Using all available homographies, the monocular
parameters were recovered by the method proposed
in (Wadenb
¨
ack and Heyden, 2014) and the binocu-
lar parameters using (Valtonen
¨
Ornhag and Heyden,
2018a). The output is given in terms of the relative
pose between the frames, and by aligning the first
camera position to the origin the absolute poses for
the remaining cameras can be computed. Knowing
the poses, the scene points were triangulated as dis-
cussed in Section 4.4.
6.2 Choice of Dataset
Due to the lack of a good and established planar mo-
tion evaluation dataset the KITTI Visual Odometry
/ SLAM benchmark (Geiger et al., 2012), was cho-
sen to demonstrate the proposed method. The dataset
contains several sequences and subsequences of pla-
nar or near planar motion, in which a significant por-
tion of the images depict the road. There are, how-
ever, sequences containing irregularities in the road
causing the camera to move up and down, which is
not a valid motion according to the planar motion
model. Such sequences were shortened to contain im-
ages where the assumption is a reasonable approxi-
mation. Furthermore, it is known a priori that parts
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
28

Figure 2: Images from the KITTI Visual Odometry / SLAM benchmark, Sequence 01 (left) and 03 (right). The input images
are cropped (thick border) in order for them to contain a large portion of a near planar surface. This assumption is only valid
in a subset of the sequences, e.g. the highway of Sequence 01 (left). In many cases occlusions, such as the car in Sequence 03
(right), or the non-planar background surface, is not approximated well by the planar motion model. These situations often
occur at road intersections and turns. Image credit: KITTI dataset (Geiger et al., 2012).
of the image is not approximated well by the planar
motion model, e.g. the sky and non-planar structures
often visible on the side of the road. Therefore these
parts are cropped out before estimating the homogra-
phy, see Figure 2.
6.3 Bundle Adjustment Comparison
From the initial trajectory a general 6-DoF model was
used and solved with SBA for both camera trajecto-
ries and compared to the proposed method. For a fair
comparison, no feature points were matched between
the stereo views, as to demonstrate that the overlap-
ping of fields of view are not necessary to achieve
better performance. The different BA algorithms used
the same settings for termination and control of the
damping parameter µ. The results are shown in Fig-
ure 3.
In all cases the performance of the proposed
method is better or as good as the ones obtained
with the general 6-DoF model and SBA. In the cases
where the initial trajectory is irregular SBA often
converges to a solution where these irregularities are
still present, and thus produces a physically improb-
able solution. This phenomenon is rarely seen in our
method, which converges to a smooth trajectory un-
der fairly general circumstances, regardless of the ini-
tial solution. This holds true even in cases where the
planar motion model is not valid, see e.g. Figure 3(b)
depicting Sequence 03, where the subsequence of the
turn in the road, cf. Figure 2, is non-planar—apart
from the degree of the turn being too sharp, the re-
maining characteristics of the ground truth trajectory
are present, which is not the case for the general 6-
DoF model.
7 CONCLUSION
In this paper we have devised a bundle adjustment
method taking the specific planar motion problem ge-
ometry into account. An implementation scheme that
utilises the sparse structure of the problem has been
proposed and the method has been tested on sub-
sequences of the KITTI Visual Odometry / SLAM
benchmark and compared to state-of-the-art methods
for sparse bundle adjustment. The results show that
the method performs well and gives a physically rea-
sonable solution, despite some of the model assump-
tions not being fulfilled.
ACKNOWLEDGEMENTS
This work has been funded by the Swedish Research
Council through grant no. 2015-05639 ‘Visual SLAM
based on Planar Homographies’.
REFERENCES
Agarwal, S., Furukawa, Y., Snavely, N., Simon, I., Cur-
less, B., Seitz, S. M., and Szeliski, R. (2011). Build-
ing Rome in a Day. Communications of the ACM,
54(10):105–112.
Alismail, H., Browning, B., and Lucey, S. (2016). Photo-
metric Bundle Adjustment for Vision-Based SLAM.
In Asian Conference on Computer Vision (ACCV),
pages 324–341, Taipei, Taiwan.
Bay, H., Tuytelaars, T., and Van Gool, L. (2006). SURF:
Speeded Up Robust Features. In European Confer-
ence on Computer Vision (ECCV), pages 404–417,
Graz, Austria.
Byr
¨
od, M. and
˚
Astr
¨
om, K. (2010). Conjugate gradient bun-
dle adjustment. In European Conference on Computer
Vision (ECCV), pages 114–127, Heraklion, Crete,
Greece.
Chen, T. and Liu, Y.-H. (2006). A robust approach for struc-
ture from planar motion by stereo image sequences.
Machine Vision and Applications (MVA), 17(3):197–
209.
Davison, A. J. (2003). Real-Time Simultaneous Localisa-
tion and Mapping with a Single Camera. In Interna-
tional Conference on Computer Vision (ICCV), pages
1403–1410, Nice, France.
Davison, A. J., Reid, I. D., Molton, N. D., and Stasse,
O. (2007). MonoSLAM: Real-Time Single Camera
Planar Motion Bundle Adjustment
29
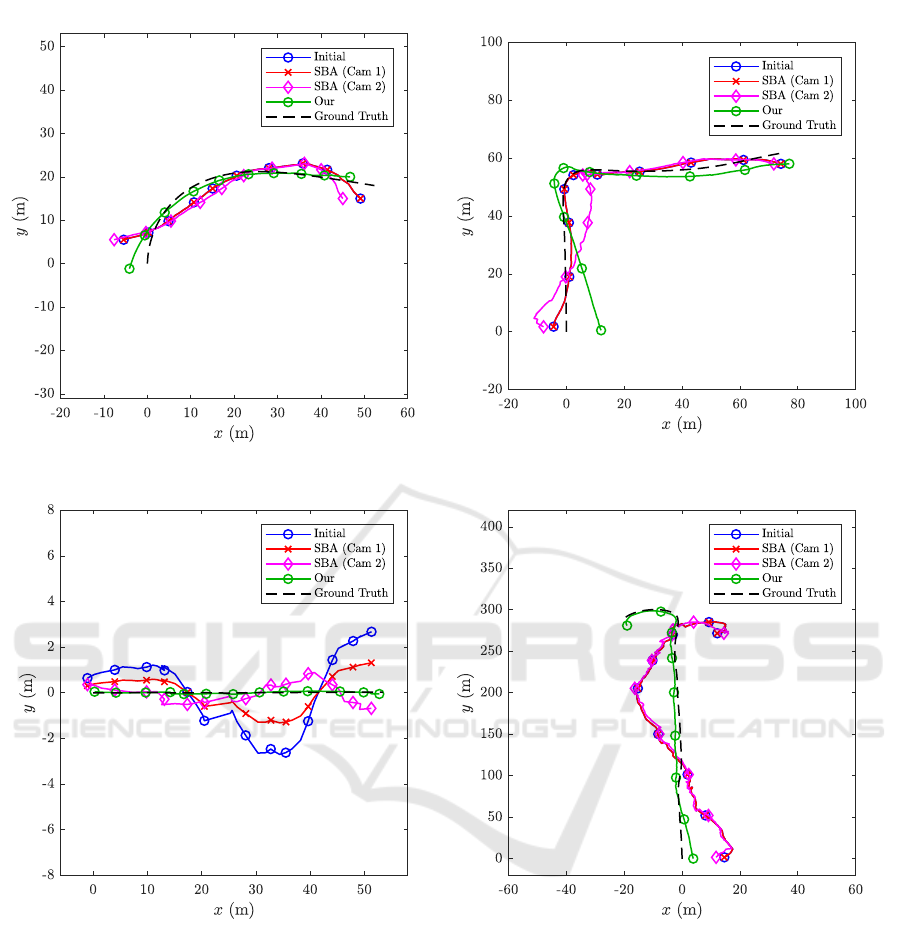
(a) Sequence 01 (60 images). (b) Sequence 03 (200 images).
(c) Sequence 04 (40 images). (d) Sequence 06 (330 images).
Figure 3: Estimated trajectories of subsequences of Sequence 01, 03, 04 and 06. Procrustes analysis has been carried out
to align the estimated paths with the ground truth. N.B. the axes do not have the same aspect ratio in (c) in order to clearly
visualise the difference.
SLAM. IEEE Transactions on Pattern Analysis and
Machine Intelligence (PAMI), 29(6):1052–1067.
Eriksson, A., Bastian, J., Chin, T., and Isaksson, M. (2016).
A consensus-based framework for distributed bundle
adjustment. In Conference on Computer Vision and
Pattern Recognition (CVPR), pages 1754–1762, Las
Vegas, NV, USA.
Frahm, J.-M., Fite-Georgel, P., Gallup, D., Johnson, T.,
Raguram, R., Wu, C., Jen, Y.-H., Dunn, E., Clipp,
B., Lazebnik, S., and Pollefeys, M. (2010). Building
Rome on a Cloudless Day. In European Conference
on Computer Vision (ECCV), pages 368–381, Herak-
lion, Crete, Greece.
Geiger, A., Lenz, P., and Urtasun, R. (2012). Are we ready
for Autonomous Driving? The KITTI Vision Bench-
mark Suite. In Conference on Computer Vision and
Pattern Recognition (CVPR), Providence, RI, USA.
Hajjdiab, H. and Lagani
`
ere, R. (2004). Vision-based Multi-
Robot Simultaneous Localization and Mapping. In
Canadian Conference on Computer and Robot Vision
(CRV), pages 155–162, London, ON, Canada.
H
¨
ansch, R., Drude, I., and Hellwich, O. (2016). Mod-
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
30

ern Methods of Bundle Adjustment on the GPU. In
ISPRS Annals of Photogrammetry, Remote Sensing
and Spatial Information Sciences (ISPRS Congress),
pages 43–50, Prague, Czech Republic.
Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-
ometry in Computer Vision. Cambridge University
Press, Cambridge, England, UK, second edition.
Konolige, K. (2010). Sparse Sparse Bundle Adjustment.
In British Machine Vision Conference (BMVC), pages
102.1–11, Aberystwyth, Wales, UK.
Liang, B. and Pears, N. (2002). Visual Navigation using
Planar Homographies. In International Conference
on Robotics and Automation (ICRA), pages 205–210,
Washington, DC, USA.
Lourakis, M. I. A. and Argyros, A. A. (2005). Is levenberg-
marquardt the most efficient optimization algorithm
for implementing bundle adjustment? In International
Conference on Computer Vision (ICCV), pages 1526–
1531, Beijing, China (PRC).
Lourakis, M. I. A. and Argyros, A. A. (2009). SBA: A
Software Package for Generic Sparse Bundle Adjust-
ment. ACM Transactions on Mathematical Software
(TOMS), 36(1):2:1–2:30.
Lowe, D. G. (2004). Distinctive Image Features from Scale-
Invariant Keypoints. International Journal of Com-
puter Vision (IJCV), 60(2):91–110.
Ort
´
ın, D. and Montiel, J. M. M. (2001). Indoor robot motion
based on monocular images. Robotica, 19(3):331–
342.
Scaramuzza, D. (2011a). 1-Point-RANSAC Structure from
Motion for Vehicle-Mounted Cameras by Exploiting
Non-holonomic Constraints. International Journal of
Computer Vision (IJCV), 95(1):74–85.
Scaramuzza, D. (2011b). Performance Evaluation of 1-
Point-RANSAC Visual Odometry. Journal of Field
Robotics (JFR), 28(5):792–811.
Snavely, N., Seitz, S. M., and Szeliski, R. (2008). Modeling
the World from Internet Photo Collections. Interna-
tional Journal of Computer Vision (IJCV), 80(2):189–
210.
Szeliski, R. (2011). Computer Vision: Applications and
Algorithms. Springer-Verlag, London, England, UK.
Torr, P. H. S. and Zisserman, A. (2000). MLESAC: A New
Robust Estimator with Application to Estimating Im-
age Geometry. Computer Vision and Image Under-
standing (CVIU), 78(1):138–156.
Triggs, B., McLauchlan, P. F., Hartley, R. I., and Fitzgib-
bon, A. W. (1999). Bundle Adjustment — A Modern
Synthesis. In International Workshop on Vision Al-
gorithms — Vision Algorithms: Theory and Practice,
pages 298–372, Corfu, Greece.
Valtonen
¨
Ornhag, M. and Heyden, A. (2018a). Generaliza-
tion of Parameter Recovery in Binocular Vision for a
Planar Scene. In International Conference on Pattern
Recognition and Artificial Intelligence, pages 37–42,
Montr
´
eal, Canada.
Valtonen
¨
Ornhag, M. and Heyden, A. (2018b). Rela-
tive Pose Estimation in Binocular Vision for a Pla-
nar Scene using Inter-Image Homographies. In Inter-
national Conference on Pattern Recognition Applica-
tions and Methods (ICPRAM), pages 568–575, Fun-
chal, Madeira, Portugal.
Wadenb
¨
ack, M. and Heyden, A. (2013). Planar Motion
and Hand-Eye Calibration Using Inter-Image Homo-
graphies from a Planar Scene. In International Con-
ference on Computer Vision Theory and Applications
(VISAPP), pages 164–168, Barcelona, Spain.
Wadenb
¨
ack, M. and Heyden, A. (2014). Ego-Motion Re-
covery and Robust Tilt Estimation for Planar Motion
Using Several Homographies. In International Con-
ference on Computer Vision Theory and Applications
(VISAPP), pages 635–639, Lisbon, Portugal.
Wu, C., Agarwal, S., Curless, B., and Seitz, S. M. (2011).
Multicore Bundle Adjustment. In Computer Vision
and Pattern Recognition (CVPR), pages 3057–3064,
Providence, RI, USA.
Zach, C. (2014). Robust Bundle Adjustment Revisited. In
European Conference on Computer Vision (ECCV),
pages 772–787, Zurich, Switzerland.
Zhang, R., Zhu, S., Fang, T., and Quan, L. (2017). Dis-
tributed very large scale bundle adjustment by global
camera consensus. In International Conference on
Computer Vision (ICCV), pages 29–38, Venice, Italy.
Zienkiewicz, J. and Davison, A. J. (2015). Extrinsics Auto-
calibration for Dense Planar Visual Odometry. Jour-
nal of Field Robotics (JFR), 32(5):803–825.
Planar Motion Bundle Adjustment
31
