
Detection of Primitives in Engineering Drawing using Genetic Algorithm
Salwan Alwan
1
, Jean-Marc Le Caillec
1
and Gerard Le Meur
2
1
Image and Information Processing, IMT Atlantique, Brest, France
2
Thales Group, Brest, France
Keywords:
Vectorization, Raster-to-vector Conversion, Engineering Drawings, Primitives Detection.
Abstract:
This paper presents a method for vectorizing paper drawings (raster). The method consists of skeletonizing
the input image, segmenting the skeleton based on junction detection and recognizing primitives using genetic
algorithm. The method is tested on different images and compared with previous works, results are promising
and show the high accuracy of our method.
1 INTRODUCTION
Nowadays, virtual reality (VR) and augmented reality
(AR) technologies are needed more than ever. Those
technologies are used in many environments for dif-
ferent purposes. For example, in the industrial field,
VR and AR can be used for marketing purpose to of-
fer to the client an interactive 3D model of the prod-
uct. In addition, they can be used for training pur-
poses to teach new employs to install and repair dif-
ferent parts safely.
Paper drawings are highly available, in particu-
lar when coming to old manufactured components.
Therefore, the need for a computer-aided system con-
verting paper drawings to 3D models is essential. The
conversion from paper drawings to 3D models can be
divided into two main problems. First, raster to vec-
tor conversion, known as vectorization, which mainly
contains two sub-problems: texts/graphics separation
and primitives detection. Second, 2D drawings to 3D
models conversion.
In this paper, unlike the approaches detailed in
section 2, we propose a vectorization algorithm com-
paring primitives and selecting the best one without
extracting (remove detected pixels) or fragmenting.
This system segment skeleton using junction detec-
tion algorithm and primitive recognition using a ge-
netic algorithm by maximizing the number of pixels
of the primitive. Currently, the algorithm detects only
straight lines, circles and arcs primitives nevertheless
it can be easily extended to detect other primitives.
The outline of the paper is given as follows: Sec-
tion 2 presents related previous work of the vectoriza-
tion problem. We present in Section 3 the proposed
method of raster to vector image conversion. Section
4 describes the experimental results obtained for the
image conversion. The conclusion and some perspec-
tives of this work are given in Section 5.
2 RELATED WORKS
Image representation is classified into two categories,
raster and vector. Raster images are based on pix-
els, however, vector images are based on geometrical
shapes. The main advantage of vector images is their
ability to be scaled without affecting the resolution.
To the best of our knowledge, 3D reconstruction
algorithms C¸ ıc¸ek and G
¨
ulesın (2004); Liu and Ye
(2005); Lee and Han (2005) have as input vector im-
ages. However, paper drawings are scanned and saved
as raster images. Thus, the aim of this paper is to pro-
pose a method to convert raster images into vectors.
Vectorization is a well-known issue in computer
vision. Several methods Dori (1997); Mandal et al.
(2010); Hilaire and Tombre (2006); De et al. (2016);
Chen et al. (1996); Song et al. (2002) have been pro-
posed to vectorize raster images for various objec-
tives. Yuan Chen et al. Chen et al. (1996) developed
RENDER which is a vectorization system showing
interesting results. However, this method is sensitive
to noise and variation of resolution. Additionally, the
inability to recreates all arcs is another weakness of
this approach. Orthogonal zig-zag Dori (1997) is a
method proposed by Dov Dori and inspired by a light
beam conducted by an optic fiber. This technique out-
performs the Hough transform method in terms of ex-
ecution time and vectorization results. Mandal et al.
Alwan, S., Caillec, J. and Meur, G.
Detection of Primitives in Engineering Drawing using Genetic Algorithm.
DOI: 10.5220/0007248802770282
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 277-282
ISBN: 978-989-758-351-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
277

Mandal et al. (2010) vectorize horizontal and verti-
cal line segments by using mathematical morpholog-
ical tools. Also, some digital geometric properties of
straightness are used to vectorize inclined and curve
line.
One of the most interesting and robust algorithms
was done by Hilaire et Tombre Hilaire and Tombre
(2006) who used 3-4 chamfer distance for extract-
ing skeleton and maintaining all geometrical features.
By using random sampling and fuzzy primitives, the
skeleton is segmented. This method is accurate, ro-
bust to noise and precise to junction points localiza-
tion. However, this method only detects arcs and
line segments and has a high computation complex-
ity. More recently, Parmita De et al. De et al. (2016)
proposed a method called ASKME which uses also
3-4 Chamfer distance skeletonization. Parmita De et
al. propose to segment primitives by label connected
components after deleting all junctions. An adaptive
sampling method is used to detect and classify prim-
itives based on mechanical domain knowledge. This
method has several interesting features but still, Hi-
laire et Tombre method is more accurate in terms of
circle detection.
These systems yield good results, but they can
fragment primitives and decrease the accuracy of cir-
cle detection by extracting detected lines before circle
detection or fail to correctly recognize some primi-
tives which is contrary to our goal. Despite the ex-
isting systems for vectorization, there is room for im-
provement in this domain.
3 PROPOSED METHOD
The proposed method (see figure 1) aims to vector-
ize raster drawings. The algorithm uses a binarization
and a filtering method to enhance the input image. It
uses (3,4) chamfer distance skeletonization algorithm
to generate the skeleton image. In addition, it uses
a junction detection algorithm to separate primitives
and a genetic algorithm to detect straight line and cir-
cles/arcs equations and endpoints. Those equations
and endpoints are used to produce vector drawings.
Figure 1: Overview of the proposed algorithm.
3.1 Preprocessing
The preprocessing step is divided into four stages: Bi-
narization, Noise Filtering, skeletonization and junc-
tion detection. The output of this algorithm is a clean
wellshaped skeleton with labeled junctions.
3.1.1 Binarization and Filtering
Due to the binary type of most source images used
to be analyzed, the binarization stage is considered
as optional. However, if the input image is not a bi-
nary image, then Otsu algorithm is used to binarize it.
Concerning the filtering process, most noises gener-
ated by scanners are salt and peeper noises. A bench
of effective filters can be used for this type of noise,
we choose the median filter, which mainly replaces
each pixel with the median of neighboring entries.
3.1.2 Skeletonization and Segmentation
Skeletonization algorithms are widely used for draw-
ings vectorization. Chamfer distance skeletonization
proposed by Di Bajadi Baja (1994) is used in our
method for different reasons. First, this skeletoniza-
tion method produces a wellshaped skeleton. Sec-
ond, 3,4 chamfer distance skeletonization is robust
to noise. Moreover, this algorithm is reversible so
we can predict the original thickness of line drawing.
Those features are discussed in detail in Hilaire and
Tombre 2006.
After generating the skeleton, a junction detection
algorithm detects and label junctions of the skeleton.
The junction detection algorithm counts the detected
pixels in 8-neighbors and classifies the selected pixel
based on the number of detected pixels. When the
number of detected pixels is less than two the selected
pixel is classified as an End-Point pixel. However, if
more than two pixels are detected the selected pixel is
classified as junction Arganda-Carreras et al. (2010).
A skeleton with labeled junction points is generated
and used as input for the genetic algorithm which is
explained in section 3.2.
3.2 Genetic Algorithm
A Genetic algorithm is a heuristic search method in-
spired by evolutionary biology and is widely used in
image processing and pattern recognition Lutton and
Martinez (1992); Zhang et al. (2003) fields. In this
paper, the Genetic algorithm is implemented to detect
primitives (circles/arcs and straight lines). The aim of
this method is to vectorize raster engineering draw-
ings.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
278

As mentioned before, the output of the previous
stages is a skeleton image whit labeled junctions. This
image is treated to generate two lists J and P where J
contains junction pixels coordinates and P contains
the rest of skeleton pixels coordinates. P is used to
generate a list CC of connected components sorted
based on their length. The longest connect compo-
nent LC is selected to be the input of the genetic al-
gorithm. An algorithm is implemented to optimize
connected components by calculating the distances
between endpoints and joining components when the
distance is smaller the threshold T HC (T H C is ob-
tained by computing the maximum length in longest
connected components in J). The genetic algorithm
generates individuals using coordinates belonging to
LC. Those individuals estimate the equation of LC
and calculate their fitness function. A selection,
crossover and mutation algorithm is used to generate
new individuals. The best individual is saved and pix-
els belonging to it are deleted (The fitness function
use a static copy of list P where pixels are not deleted
see section 3.2.2). In case LC is composed of several
primitives, the genetic algorithm loops until the num-
ber of pixels belonging to LC reach a certain thresh-
old T H. Each loop, the algorithm select a primitive
and update CC and LC. The algorithm loops until the
length of P reach a certain threshold T H. (see Algo-
rithm 1) The output of the algorithm is a set of solu-
tions structured as follows:
• Line solution: [m, n,c], [(x
EL1
, y
EL1
), (x
EL2
, y
EL2
)]
where (x
EL1
, y
EL1
)and((x
EL1
, y
EL1
) are the end-
points of the straight line and verifying mx +ny +
c = 0 .
• Arc solution: [(x
0
, y
0
), r], [(x
EL1
, y
EL1
), (x
EL2
, y
EL2
)]
where (x
EL1
, y
EL1
) and (x
EL1
, y
EL1
) are the end-
points of the arc and verifying (x
0
− x)
2
+ (y
0
−
y)
2
− r
2
= 0.
• Circle solution:
[(x
0
, y
0
), r], [(In f , In f ), (In f , In f )] where x
0
, y
0
, r
verifying (x
0
− x )
2
+ (y
0
− y)
2
− r
2
= 0.
3.2.1 Individuals Generation
In this stage, we select LC from CC and use its coor-
dinates to produce individuals. A random list LI of
two different categories of individual is generated:
• Individual 1 (I1) is created by selecting two dis-
tinct points belonging to LC . These points are
used to generate the coefficients of a straight
line equation. I1 is structured as follow:
{(x
1
, y
1
), (x
2
, y
2
), [m, n, c]} where (x
1
, y
1
), (x
2
, y
2
)
are the coordinates of chosen points.
Input: Raster Image
Output: Vector Output
Preprocessig;
Generating P and J list;
CC=Connected(P);
LC = CC[0];
while len(P) and len(LC) > T H do
Generate I;
Calculate F of each individual in I;
for i in range GenNb do
save Best Objective in Generation;
Generate the NewPopulation;
Calculate F of each individual in I;
Selection, Crossover, Mutation
end
Best Primitive Saved;
Update LC and P;
if len(LC) > T H then
CC
1
=Connected(LC);
LC=CC
1
[0];
if len(LC) < T H and len(P) > T H
then
CC=Connected(P);
LC=CC[0]
end
end
else
if len(P) > T H then
CC=Connected(P);
LC=CC[0]
end
end
end
Algorithm 1: Vectorization Algorithm.
• Individual 2 (I2) is created by selecting three
distinct points belonging to LC. These points
are used to generate the coefficients of a
circle equation. I2 is structured as fol-
low: {(x
1
, y
1
), (x
2
, y
2
), (x
3
, y
3
), [(x
0
, y
0
), r]} where
(x
1
, y
1
), (x
2
, y
2
), (x
3
, y
3
) are the coordinates of
chosen points.
the length of LI is equal to k
I
and k
I1
= k
I2
=
k
I
2
where
k
I1
and k
I2
are respectively the length of individuals
generated of type 1 and type 2.
To summarize, we generate 50% of individuals of
type 1 and 50% individuals of type 2. Those individ-
uals are considered as solutions (equation of LC) and
they are sorted based on their Fitness Function.
3.2.2 Fitness Function
The fitness or evaluation function appraises solutions
and sorts them according to the closeness to the opti-
Detection of Primitives in Engineering Drawing using Genetic Algorithm
279

Figure 2: VRI scores comparison.
mum solution of the problem. To calculate the fitness
function of each individual in I, we save all pixels in
P that belongs to the equation of each one (With tol-
erance ±1 pixel). The fitness function is used to rate
individuals based on the length of a longest connected
component of detected pixels LCS (taking into con-
sideration that LCS ∩ LC 6= 0). Several equations can
detect the same length of LCS due to this tolerance.
To be more precise, we sum and average the distance
between detected pixels in LCS and the solution equa-
tion, then we subtract it from the length of LCS. The
fitness function is expressed as following:
F = LLCS −
∑
i=LLCS
i=0
distance[i]
LLCS
where LLCS = length(LCS) and distance[i] is the dis-
tance between the primitive and pixel i in LCS
3.2.3 Selection, Crossover and Mutation
The selection, crossover, and mutation aim to find the
optimal solution by converging previous solutions.
The selection algorithm used is tournament selection.
Tournament selection chooses x random individual
and then choose the best one to be a parent for the next
generation. After selecting parents, a crossover pro-
cess generates a new population by combining a ran-
dom individual with the selected parent. In addition, a
mutation variable M is used to produce new individu-
als when M < R where R is a random value between 0
and 10. Those steps allow us to converge towards the
optimal solution by generating a new population. The
following example describes the crossover process:
• Selected Parent: (x
1
, y
1
), (x
2
, y
2
)
• Generated Individual (x
3
, y
3
), (x
4
, y
4
)
• New Individual {(x
1
, y
1
), (x
4
, y
4
), [m, n, c]}
4 EXPERIMENTAL RESULTS
In this section, we present the experimental results
of our algorithm. The numbers of individuals, gen-
erations, line width, and T H are fixed to 40, 50, 2
and 10 respectively. To evaluate the performance of
our method we use the Vector Recovery Index (VRI)
score Wenyin and Dori (1997) and GREC database
Liu (2003) GREC-Dataset (2003) which contains
twelve images (four original images with three dif-
ferent conditions). Figure 2 shows the VRI scores for
four previous works compared to ours. The red and
purple lines in figure 2 are the average VRI scores of
ten executions and the maximum VRI scores reached
in ten executions respectively (For more details see
table 1 in Appendix).
Figure 2 shows that our method outperforms other
methods for all images except four. However, re-
sults of those four images are promising and compet-
itive with other scores. Furthermore, maximum VRI
scores reached during ten executions outperform oth-
ers in all images except one. Moreover, our average
VRI score is the best comparing to other methods.
To the best of our knowledge, Hilaire-Tombre and
ASKME methods are producing the best results as
shown in table 1, those methods reconstruct junctions
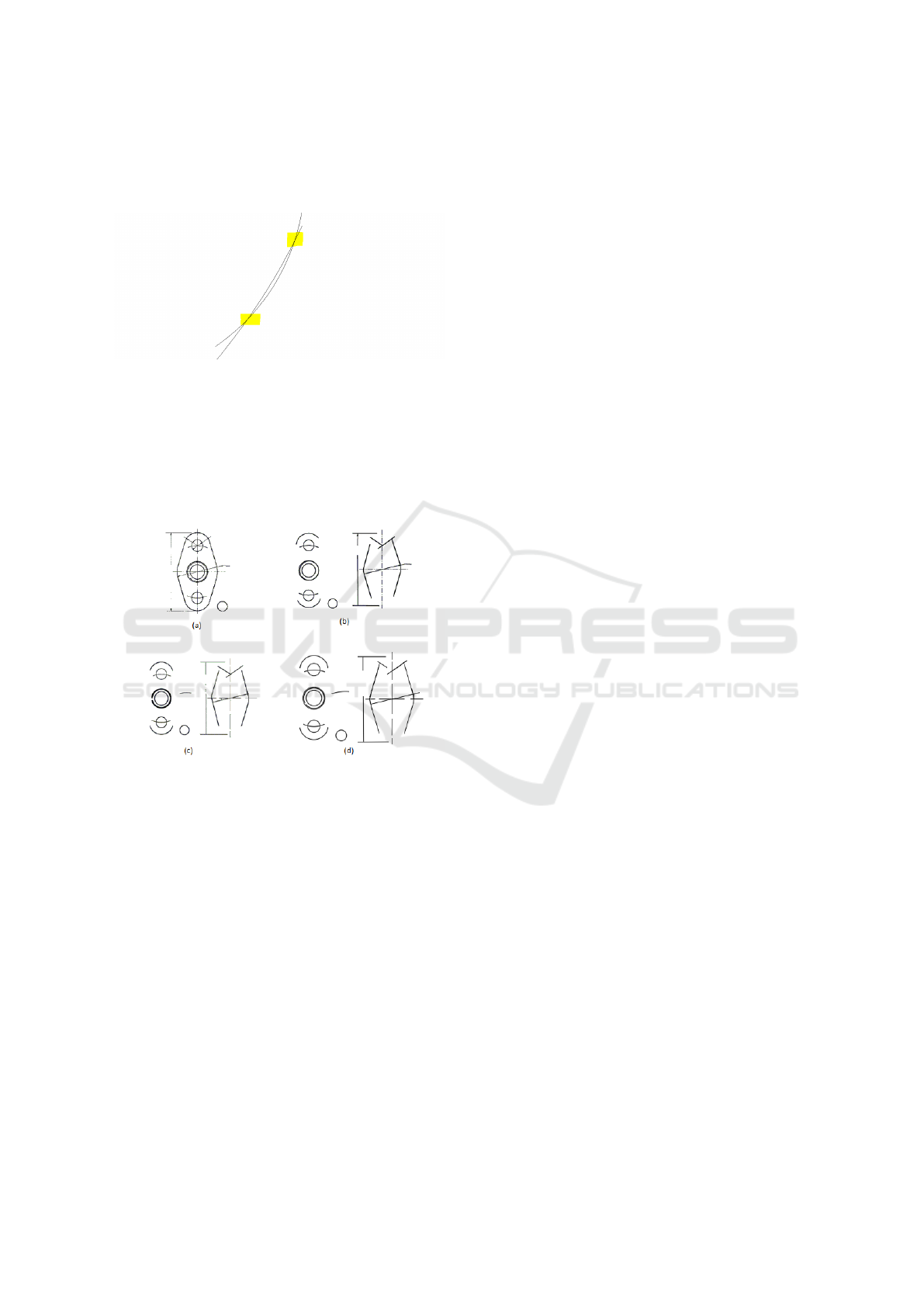
and estimates line width. As shown in figure 3, primi-
tives sometimes overlap which cause the error of end-
points detection. In addition, we fixed the line width
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
280
to 2 which affects VRI scores. Thus, by estimating
the line width and trimming primitives we expect to
improve our VRI scores.
Figure 3: Arcs intersection from vectorized image ”3”.
Based on the figure 4, we see that our algo-
rithm estimate the upper arc better than the ASKME
method and middle circles better than Hilaire-Tombre
method. To summarize, our algorithm outperforms
previous work and shows promising results. How-
ever, it needs an algorithm to unify primitives and es-
timate their width.
Figure 4: Visual comparision: (a) original image (b)
ASKME algorithm De et al. (2016) (c) Hilaire-Tombre Hi-
laire and Tombre (2006) (d) Our Method.
5 CONCLUSION AND
PERSPECTIVE
In this paper, we have presented a vectorization al-
gorithm to convert raster images into vectors. The
method is based on junction detection and genetic al-
gorithm. Our algorithm outperforms previous works
based on the VRI average score. Nevertheless, an al-
gorithm to estimate line width and solving primitives
overlapping is needed.
For the perspective of this work, we aim first to
implement an algorithm unifying detected primitives.
Furthermore, we are looking to classify primitives and
estimate their width. Moreover, we aim to separate
dimension tools from graphics.
REFERENCES
Arganda-Carreras, I., Fern
´
andez-Gonz
´
alez, R., Mu
˜
noz-
Barrutia, A., and Ortiz-De-Solorzano, C. (2010). 3d
reconstruction of histological sections: application to
mammary gland tissue. Microscopy research and
technique, 73(11):1019–1029.
Chen, Y., Langrana, N. A., and Das, A. K. (1996). Perfect-
ing vectorized mechanical drawings. Computer Vision
and Image Understanding, 63(2):273–286.
C¸ ıc¸ek, A. and G
¨
ulesın, M. (2004). Reconstruction of 3d
models from 2d orthographic views using solid extru-
sion and revolution. Journal of materials processing
technology, 152(3):291–298.
De, P., Mandal, S., Bhowmick, P., and Das, A. (2016).
Askme: adaptive sampling with knowledge-driven
vectorization of mechanical engineering drawings.
International Journal on Document Analysis and
Recognition (IJDAR), 19(1):11–29.
di Baja, G. S. (1994). Well-shaped, stable, and reversible
skeletons from the (3, 4)-distance transform. Jour-
nal of visual communication and image representa-
tion, 5(1):107–115.
Dori, D. (1997). Orthogonal zig-zag: an algorithm
for vectorizing engineering drawings compared with
hough transform. Advances in Engineering Software,
28(1):11–24.
ELLIMAN, D. (2002). Tif2vec, an algorithm for arc seg-
mentation in engineering drawings. Lecture notes in
computer science, pages 350–358.
GREC-Dataset (2003). Grec’03 dataset. http:
//www.cs.cityu.edu.hk/
∼
liuwy/ArcContest/
test-images-2003.zip. Accessed: 2018-07-16.
Hilaire, X. and Tombre, K. (2006). Robust and accu-
rate vectorization of line drawings. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
28(6):890–904.
Lee, H. and Han, S. (2005). Reconstruction of 3d interact-
ing solids of revolution from 2d orthographic views.
Computer-Aided Design, 37(13):1388–1398.
Liu, J. and Ye, B. (2005). New method of 3d reconstruction
from mechanical engineering drawings based on en-
gineering semantics understanding. In International
Conference GraphiCon’2005.
Liu, W. (2003). Report of the arc segmentation contest.
In International Workshop on Graphics Recognition,
pages 364–367. Springer.
Lutton, E. and Martinez, P. (1992). A genetic algorithm for
the detection of 2D geometric primitives in images.
PhD thesis, INRIA.
Mandal, S., Das, A. K., and Bhowmick, P. (2010). A fast
technique for vectorization of engineering drawings
using morphology and digital straightness. In Pro-
ceedings of the Seventh Indian Conference on Com-
puter Vision, Graphics and Image Processing, pages
490–497. ACM.
Song, J., Lyu, M. R., and Cai, S. (2004). Effective mul-
tiresolution arc segmentation: Algorithms and perfor-
mance evaluation. IEEE transactions on pattern anal-
ysis and machine intelligence, 26(11):1491–1506.
Detection of Primitives in Engineering Drawing using Genetic Algorithm
281

Song, J., Su, F., Li, H., and Cai, S. (2002). Raster to vec-
tor conversion of construction engineering drawings.
Automation in construction, 11(5):597–605.
Wenyin, L. and Dori, D. (1997). A protocol for performance
evaluation of line detection algorithms. Machine Vi-
sion and Applications, 9(5-6):240–250.
Zhang, L., Xu, W., and Chang, C. (2003). Genetic algorithm
for affine point pattern matching. Pattern Recognition
Letters, 24(1-3):9–19.
APPENDIX
Table 1: Comparision of experimental results based on VRI.
Image Previous Methods Our Method
TIF2VEC
ELLIMAN (2002)
Song J.
Song et al. (2004)
Hilaire
Hilaire and Tombre (2006)
ASKME
De et al. (2016)
Av. Max.
1 0.567 0.641 0.756 0.769 0.869 0.906
1 230 0.589 0.64 0.752 0.745 0.878 0.883
1 n4 0.664 0.509 0.762 0.714 0.801 0.819
2 0.439 0.753 0.653 0.654 0.708 0.794
2 100 0.513 0.786 0.707 0.613 0.730 0.826
2 n4 0.612 0.703 0.791 0.615 0.697 0.772
3 0.272 0.532 0.724 0.645 0.698 0.773
3 100 0.519 0.301 0.74 0.69 0.769 0.834
3 n4 0.451 0.224 0.697 0.635 0.72 0.781
4 0.5 0.735 0.663 0.747 0.834 0.893
4 230 0.323 0.79 0.795 0.739 0.847 0.868
4 n4 0.399 0.688 0.782 0.727 0.854 0.883
Average 0.487 0.609 0.735 0.691 0.784 0.836
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
282
