
Zero-sum Distinguishers for Round-reduced GIMLI Permutation
Jiahao Cai
1,2,3
, Zihao Wei
1,2,3
, Yingjie Zhang
1,2,3
, Siwei Sun
1,2,3
and Lei Hu
1,2,3
1
State Key Laboratory of Information Security, Institute of Information Engineering, Chinese Academy of Sciences, China
2
Data Assurance and Communication Security Research Center,
Chinese Academy of Sciences, China
3
School of Cyber Security, University of Chinese Academy of Sciences, China
Keywords:
GIMLI, Integral, Division Property, Zero-sum, Degree evaluation, MILP.
Abstract:
GIMLI is a 384-bit permutation proposed by Bernstein et al. at CHES 2017. It is designed with the goal of
achieving both high security and high performance across a wide range of hardware and software platforms.
Since GIMLI can be used as a building block for many cryptographic schemes, it is important to understand
its concrete security. To the best of our knowledge, third party cryptanalysis of GIMLI is limited. In this
paper, we identify some zero-sum distinguishers for 14-round GIMLI with the inside-out technique, which are
one-round longer than the integral distinguishers presented by the designers. Although we obtain improved
cryptanalysis results, these zero-sum distinguishers are far from threatening the full version of GIMLI.
1 INTRODUCTION
Permutations with large state sizes and desired cryp-
tographic properties facilitate the construction of
many cryptographic schemes, including high-security
(tweakable) block ciphers, stream ciphers, message
authentication codes, hash functions, etc. For ex-
ample, the winner of the SHA-3 competition, Kec-
cak hash function, uses a permutation operating on
a 1600-bit state known as the Keccak- f permuta-
tion (Bertoni et al., 2013). Also, we have message
authentication code (Chaskey (Mouha et al., 2014)),
and stream cipher (Salsa20 (Bernstein, 2008)) built on
ARX permutations. However, existing designs suffer
from the problem of showing significant performance
variation when implemented in different platforms,
severely limiting their range of applications. There-
fore, a single primitive that performs well (not neces-
sarily the best) on all common platforms will benefit
the designers and implementors a lot.
With this goal in mind, Bernstein et al. pre-
sented the GIMLI design at CHES 2017 (Bernstein
et al., 2017). What distinguishes GIMLI from pre-
vious designs is that its performance strikes the bal-
ance across a wide spectrum of platforms by skill-
fully avoiding those platform-specific hazards lead-
ing to poor performance for many primitives simulta-
neously. Therefore, cryptographic schemes designed
based on GIMLI are expected to be efficient when
implemented on 64-bit Intel/AMD server CPUs, 32-
bit ARM smartphone CPUs, 32-bit ARM microcon-
trollers, 8-bit AVR microcontrollers, FPGAs, and
ASICs with or without side-channel protections. We
refer the reader to http://gimli.cr.yp.to for sample im-
plementations and detailed benchmarks.
Given these merits of GIMLI, it has the potential
to be employed in many future designs. Therefore,
it is essential to have a thorough understanding of its
security. Besides the initial cryptanalysis provided by
the designers (Bernstein et al., 2017), we are aware of
only one third party cryptanalysis (Hamburg, 2017).
However, the claimed results of (Hamburg, 2017)
is largely irrelevant to the original design, since the
“attack” is against an artificial and ad-hoc mode (see
http://gimli.cr.yp.to/statement.html for the statement
from the GIMLI team). In this paper, we provide an-
other third party cryptanalysis concerning Zero-Sum
Distinguishers by using MILP, which has been used
to automate many cryptanalytic techniques (Mouha
et al., 2012; Sun et al., 2014; Xiang et al., 2016;
Sasaki and Todo, 2017; Cui et al., 2016; Shi et al.,
2018; Fu et al., 2016). We identify a set of zero-sum
distinguishers for 14-round GIMLI. To the best of
our knowledge, these are the best distinguishers for
GIMLI so far.
Organization. In Section 2, we give a brief de-
scription of the GIMLI permutation. We show how
38
Cai, J., Wei, Z., Zhang, Y., Sun, S. and Hu, L.
Zero-sum Distinguishers for Round-reduced GIMLI Permutation.
DOI: 10.5220/0007249000380043
In Proceedings of the 5th International Conference on Information Systems Security and Privacy (ICISSP 2019), pages 38-43
ISBN: 978-989-758-359-9
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved
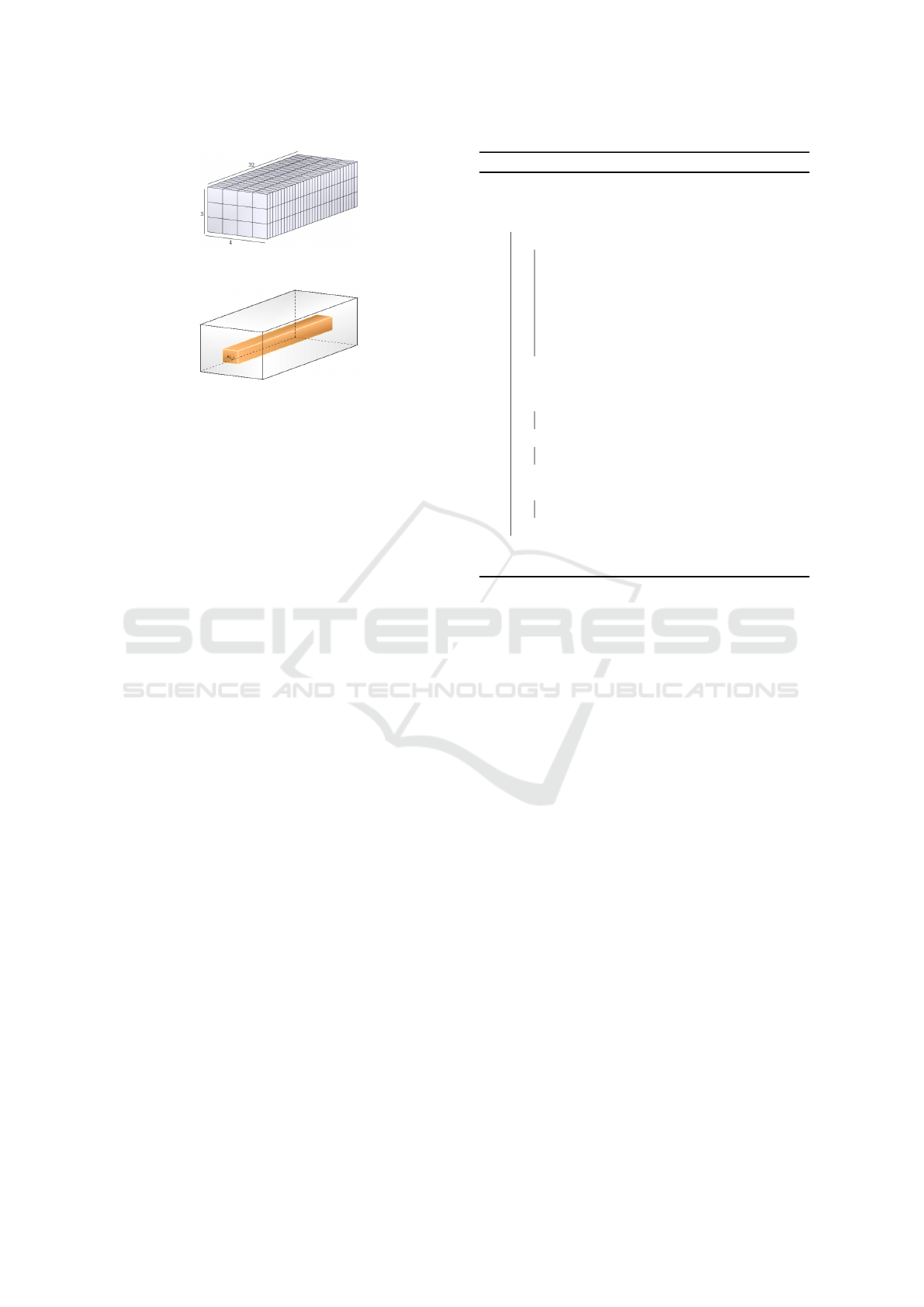
Fig 1: The state of GIMLI.
Fig 2: The 32-bit word s
i, j
in row i and column j.
to evaluate the algebraic degree of a boolean function
with division property in Section 3, which is the main
cryptanalytic tool employed in this work. The inside-
out technique for finding zero-sums is introduced in
Section 4. In Section 5, we identify many zero-sum
distinguishers of 14-round GIMLI with the methods
presented in Section 3 and Section 4. We conclude in
Section 6 and give some discussion of future work.
2 DESCRIPTION OF THE GIMLI
PERMUTATION
GIMLI is a 384-bit permutation. There are 24 rounds
in GIMLI, numbered 24,23, . . . , 1. The input 384-bit
data is arranged into a 3 × 4 matrix of 32-bit words as
shown in Fig. 1. Let s
i, j
∈ W denote the 32-bit word
in row i and column j for 0 ≤ i < 3 and 0 ≤ j < 4,
where W is the set of all 32-bit words (see Fig. 2).
The 384-bit state is then manipulated according to Al-
gorithm 2 to produce the output. The inverse of the
GIMLI permutation can be derived from Algorithm 1
and we put it into Appendix 6.
3 ALGEBRAIC DEGREE
EVALUATION WITH DIVISION
PROPERTY
The Division property, introduced by Todo at EU-
ROCRYPT 2015 (Todo, 2015), is a generalization
of the integral property, and its bit-based version
was applied in the cryptanalysis of SIMON at FSE
2016 (Todo and Morii, 2016).
Let F
2
denote the finite field of two elements, and
Z represent the set of integers. The Hamming weight
wt(v) of a vector v ∈ F
n
2
is defined as the number of
Algorithm 1: The GIMLI permutation.
Input: s = (s
i, j
) ∈ W
3×4
Output: GIMLI(s) = (s
i, j
) ∈ W
3×4
1 for r from 24 downto 1 inclusive do
2 for j ∈ {0, · · · , 3} do
3 x ← s
0, j
≪ 24
4 y ← s
1, j
≪ 9
5 z ← s
2, j
6 s
2, j
← x ⊕ (z 1) ⊕ ((y ∧ z) 2)
7 s
1, j
← y ⊕ x ⊕ ((x ∨ z) 1)
8 s
0, j
← z ⊕ y ⊕ ((x ∧ y) 3)
9 end
10
11 if r mod 4 = 0 then
12 s
0,0
,s
0,1
,s
0,2
,s
0,3
← s
0,1
,s
0,0
,s
0,3
,s
0,2
13 else if r mod 4 = 2 then
14 s
0,0
,s
0,1
,s
0,2
,s
0,3
← s
0,2
,s
0,3
,s
0,0
,s
0,1
15 end
16 if r mod 4 = 0 then
17 s
0,0
= s
0,0
⊕ 0x9e377900 ⊕ r
18 end
19 end
20 return (s
i, j
)
nonzero entries in v. For vectors k = (k
0
,k
1
,··· , k
n−1
)
and u = (u
0
,u
1
,··· , u
n−1
) in {0, 1}
n
⊆ Z, we say u <
k if u
i
≥ k
i
for any i ∈ {0, ··· , n − 1}.
Let f : F
n
2
→ F
2
be an n-variable boolean function
whose Algebraic Normal Form (ANF) is
f (x) =
M
v∈F
n
2
a
f
v
· x
v
where v = (v
0
,v
1
,··· , v
n−1
), x
v
=
∏
n−1
i=0
x
v
i
i
, and we
call a
f
v
∈ F
2
the ANF coefficient of f . The algebraic
degree of f is defined as deg( f ) = max{wt(v) : a
f
v
6=
0}. A vectorial boolean function G = (g
0
,··· , g
m−1
) :
F
n
2
→ F
m
2
is a sequence of m boolean functions g
i
:
F
n
2
→ F
2
with 0 ≤ i < m, and the algebraic degree
deg(G) of G is defined as max{deg(g
i
) : 0 ≤ i < m}.
Definition 1 (Bit-based Division Property (Todo and
Morii, 2016)). Let X be a multiset whose elements
belong to F
n
2
. When the multiset X has the division
property D
1
n
K
, where K denotes a subset of {0, 1}
n
⊆
Z
n
, it satisfies the following condition
M
x∈X
π
u
(x) =
(
unknown if there are k ∈ K, s.t. u < k
0 otherwise
where u = (u
0
,u
1
,··· , u
n−1
) ∈ {0, 1}
n
⊆ Z
n
, x =
(x
0
,x
1
,··· , x
n−1
) ∈ F
n
2
, and π
u
(x) =
∏
n−1
i=0
x
u
i
i
.
If a multiset X has division property D
1
n
K
, after the
application of a vectorial boolean function F : F
n
2
→
Zero-sum Distinguishers for Round-reduced GIMLI Permutation
39

F
m
2
, the division property of the output multiset Y be-
comes D
1
m
K
0
. We say D
1
n
K
propagates to D
1
m
K
0
, which is
denoted by D
1
n
K
F
−→ D
1
m
K
0
, or K
F
−→ K
0
.
Definition 2 (Division Trail (Xiang et al., 2016)). Let
F be the round function of an iterated block cipher.
Assume that the input multi-set to the block cipher has
initial division property D
1
n
K
0
with K
0
= {k}. This ini-
tial division property propagates through the round
function which forms a chain
D
1
n
K
0
F
−→ D
1
n
K
1
F
−→ D
1
n
K
2
F
−→ ·· ·
For any vector k
∗
i
∈ K
i
(i ≥ 1), there must exist a
vector k
∗
i−1
in K
i−1
such that k
∗
i−1
can propagate to
k
∗
i
according to the rules of division property prop-
agation. Furthermore, for (k
0
,k
1
,··· , k
r
) ∈ K
0
×
K
1
× · ·· × K
r
, if k
i−1
can propagate to k
i
for all
i ∈ {1,2,··· , r}, we call (k
0
,k
1
,··· , k
r
) an r-round
division trail.
Given k and k
0
, whether there is a division trail
k → k
0
for F can be determined by the resolution of
a Mixed-Integer Linear Programming (MILP) model
encoding the propagation rules of the division proper-
ties (Xiang et al., 2016). We refer the reader to (Xi-
ang et al., 2016) for more information on MILP-aided
analysis of division properties.
Besides its natural application in finding integral
distinguishers, it turns out that the division property
can be a very generic tool for probing the structure of
boolean functions whose explicit ANFs are not avail-
able due to resource limitation. In particular, the prop-
agation of division properties can be used to evaluate
the degree of a boolean function (Todo et al., 2017).
Lemma 1 (Todo, Isobe, Hao, and Meier (Todo et al.,
2017)). Let f : F
n
2
→ F
2
be a boolean function whose
ANF coefficients are denoted by a
f
v
(v ∈ F
n
2
), and k ∈
F
n
2
. Then a
f
v
= 0 for all v < k if there is no division
trail such that k
f
−→ 1.
Lemma 1 leads to the following two propositions
for evaluating the degrees of (vectorial) boolean func-
tions.
Proposition 1. Let f : F
n
2
→ F
2
be a boolean function.
Then the degree of f is upper bounded by d + 1 where
d = max
k∈F
n
2
{wt(k) : k
f
−→ 1 is a division trail}.
Proposition 2. Let F : F
n
2
→ F
n
2
be a vectorial
boolean function. Then the degree of F is upper
bounded by d + 1 where d = max
k∈F
n
2
{wt(k) : k
F
−→
e
j
is a division trail for some j ∈ {0, ·· · , n − 1}} and
e
j
is the jth unit vector.
x
G H
F(x)
Fig 3: F = H ◦ G.
4 THE INSIDE-OUT TECHNIQUE
FOR FINDING ZERO-SUM
DISTINGUISHERS
The so-called zero-sum distinguisher was proposed
by Aumasson and Meier in (Aumasson and Meier,
2009), which can be regarded as a generalization
of the integral property (a.k.a. saturation prop-
erty) (Daemen et al., 1997; Knudsen and Wagner,
2002).
Definition 3 (Zero-Sum Distinguisher (Aumasson
and Meier, 2009; Boura and Canteaut, 2010)). Let
F : F
n
2
→ F
n
2
be a permutation. A zero-sum is a set
X ⊆ F
n
2
of inputs such that
M
x∈X
x ≡ 0 and
M
x∈X
F(x) ≡ 0 .
Since it is expected that a randomly chosen permuta-
tion does not have many zero-sums, the existence of
many such sets of inputs can be seen as a distinguish-
ing property of F.
The zero-sum distinguishers are intimately related
to the integral distinguishers whose existence has a
close connection with the degree of the underlying
boolean functions.
Let I be a subset of {0,··· , n−1} with cardinality
|I |, and δ(I ) be the subspace spanned by {e
i
: i ∈ I }.
For a vector a ∈ F
n
2
, δ
a
(I ) is defined to be the set
{x + a : x ∈ δ(I )}. That is, δ
a
(I ) is the set of all
vectors whose values indexed by I traverse all pos-
sible values while the values at other positions are
fixed to constants according to a. It is easy to check
that for any a ∈ F
n
2
, and any I whose cardinality is
strictly greater than 1, ⊕
x∈δ
a
(I )
x ≡ 0. Moreover, if
deg(F) < n, and |I | > deg(F), then for any a ∈ F
n
2
,
M
x∈δ
a
(I )
F(x) ≡ 0.
Therefore, many zero-sums δ
a
(I ) for F with
deg(F) < n can be identified. Since F is a permu-
tation, we can construct zero-sums from the mid-
dle (the inside-out technique (Aumasson and Meier,
2009; Boura and Canteaut, 2010)) by exploiting the
knowledge of the degrees of both the forward and
backward directions of F as depicted in Fig. 3.
Firstly, F is decomposed into H ◦ G, where G and
H are n-bit permutations. Assuming that deg(G
−1
) <
n and deg(H) < n, then for any a ∈ F
n
2
and I with
ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy
40

0 1
. . .
4
δ
a
(I)
5 rounds
5 6
. . .
13
9 rounds
Fig 4: Apply the inside-out technique to 14-round GIMLI.
|I | = max{deg(G
−1
),deg(H)} + 1, δ
a
(I ) is a zero-
sum for both G
−1
and H. Consequently, we have
M
x∈G
−1
(δ
a
(I ))
x ≡ 0
and
M
x∈G
−1
(δ
a
(I ))
F(x) =
M
x∈G
−1
(δ
a
(I ))
H ◦ G(x)
=
M
y∈δ
a
(I )
H(y)
= 0
which indicates that G
−1
(δ
a
(I )) is a zero-sum for F.
5 ZERO-SUM DISTINGUISHERS
FOR ROUND-REDUCED GIMLI
To apply the inside-out technique, We split the 14-
round GIMLI into the first 5 rounds (denoted by G)
and the last 9 rounds (denoted by H) as depicted in
Fig. 4. Then the degrees of G
−1
and H are evaluated
with the method introduced in Sect. 3. Therefore, we
need to set up MILP models encoding the propagation
of division properties for round-reduced GIMLI and
its inverse. According to the specification of GIMLI
presented in Algorithm 1 (also see Appendix 6 for
its inverse), the MILP models can be constructed by
properly assembling the MILP models for the follow-
ing three operations.
Modeling S-box. We treat the non-linear operation
(x
0
,y
0
,z
0
) = (y ∧ z,x ∨ z, x ∧ y) in GIMLI as a 3 × 3 S-
box, and use the method presented in (Boura and Can-
teaut, 2016) to retrieve its propagation rules (see Ta-
ble 1) of the division property. Using the convex hull
computation approach (Sun et al., 2014), the propa-
gation rule shown in Table 1 can be transformed into
the following linear inequalities
x + z − 2x
0
− 3y
0
− 2z
0
+ 2 ≥ 0
− x +y
0
+ z
0
≥ 0
− z + x
0
+ y
0
≥ 0
− y + x
0
+ z
0
≥ 0
x + y + z − x
0
− y
0
− z
0
≥ 0
where all variables involved are binaries.
Table 1: Propagation rule of (x
0
,y
0
,z
0
) = (y ∧ z, x ∨z, x ∧ y).
Input Output
(0,0, 0) (0,0, 0)
(0,0, 1) (0,1, 0) (1, 0, 0)
(0,1, 0) (0,0, 1) (1, 0, 0)
(0,1, 1) (1,0, 0)
(1,0, 0) (0,0, 1) (0, 1, 0)
(1,0, 1) (0,1, 0) (1, 0, 1)
(1,1, 0) (0,0, 1)
(1,1, 1) (1,0, 1)
Modeling COPY. Let a
COPY
−−−→ (b
0
,··· , b
m−1
) be a
division trail of COPY. Then a = b
0
+ · ·· + b
m−1
,
where all variables involved are binaries.
Modeling XOR. Let (a
0
,··· , a
m−1
)
XOR
−−−→ b be a di-
vision trail of XOR. Then a
0
+ ··· + a
m−1
= b, where
all variables involved are binaries.
After assembling the above constraints for all op-
erations involved in the underlying permutation, we
can check whether d is an upper bound of the degree
of the permutation as follows. We impose additional
constraints dictating that
n−1
∑
i=0
u
i
≥ d and
n−1
∑
i=0
v
i
= 1, (1)
where u
i
’s and v
i
’s are the variables representing the
input and output division properties, respectively (n =
384 for GIMLI). If the resulting model is infeasible,
then the algebraic degree of the underlying permuta-
tion is upper bounded by d due to Proposition 2.
Firstly, we evaluate the degree of H. Note that the
degree evaluation of H has already been done by the
design team. However, we still perform this process
to verify our implementation against the results pro-
vided by the designers. The upper bounds of the de-
grees for round reduced versions of H (up to 9 rounds)
are summarized in Table 2, which match the results
provided in (Bernstein et al., 2017).
We then evaluate the degrees of round-reduced
G
−1
, and the results are listed in Table 3. Note that
the bounds we get are not necessarily tight. In our
experiment, we observed that when we set the d in
equation (1) to be a very small value, the resolution
time of the MILP model can be very long. Therefore,
we prefer to choose a d which may be much larger
than the degree of the analyzed permutation.
According to the above results and the discus-
sion of Sect. 4, We can conclude that G
−1
(δ
a
(I ))
with |I | > 350 is a zero-sum of 14-round GIMLI for
any a ∈ F
n
2
. Finally, we note that all models are
solved by the Gurobi optimizer (Gurobi Optimization,
2013) and all experiments are performed on a com-
Zero-sum Distinguishers for Round-reduced GIMLI Permutation
41

Table 2: The upper bounds of the degrees of round-reduced GIMLI.
# Rounds 1 2 3 4 5 6 7 8 9
Bounds 2 4 8 16 29 52 95 163 266
Table 3: The upper bounds of the degrees of round-reduced G
−1
.
# rounds 1 2 3 4 5
Bounds 32 63 141 170 350
puter running Ubuntu 16.04 TLS system with Intel(R)
Core(TM) i5-4590 CPU @ 3.30GHz.
6 CONCLUSION AND
DISCUSSION
In this work, by analyzing the degrees of round-
reduced versions of the GIMLI permutation and its
inverse, we obtained a set of 14-round zero-sum dis-
tinguishers, which achieves one-round improvement
compared with the results offered by the designers.
More specifically, the 14-round zero-sum distinguish-
ers are constructed with the knowledge of the alge-
braic degree of the vectorial boolean function repre-
senting the output of 9-round GIMLI permutation and
the upper bound of the degree of the inverse of 5-
round GIMLI permutation, where the evaluation of the
algebraic degrees is performed by solving MILP mod-
els encoding the propagation of the division proper-
ties. Note that we are only able to get the upper bound
of the algebraic degrees under our current computa-
tional resources. Therefore, it is interesting to investi-
gate whether tighter bounds can be obtained. We ex-
pect that a more accurate degree evaluation may help
to extend the zero-sum distinguisher one more round.
ACKNOWLEDGEMENTS
The authors thank the anonymous reviewers for many
helpful comments. The work is supported by the Chi-
nese Major Program of National Cryptography De-
velopment Foundation (Grant No. MMJJ20180102),
the National Natural Science Foundation of China
(61732021, 61802400, 61772519, 61802399), the
Youth Innovation Promotion Association of Chinese
Academy of Sciences, and the Institute of Informa-
tion Engineering, CAS (Grant No. Y7Z0251103).
REFERENCES
Aumasson, J.-P. and Meier, W. (2009). Zero-sum distin-
guishers for reduced Keccak-f and for the core func-
tions of Luffa and Hamsi. Available at http://131002.
net/data/papers/AM09.pdf.
Bernstein, D. J. (2008). The salsa20 family of stream
ciphers. In New Stream Cipher Designs - The
eSTREAM Finalists, pages 84–97. https://cr.yp.to/
snuffle/salsafamily-20071225.pdf.
Bernstein, D. J., K
¨
olbl, S., Lucks, S., Massolino, P. M. C.,
Mendel, F., Nawaz, K., Schneider, T., Schwabe, P.,
Standaert, F., Todo, Y., and Viguier, B. (2017). Gimli
: A cross-platform permutation. In Cryptographic
Hardware and Embedded Systems - CHES 2017 - 19th
International Conference, Taipei, Taiwan, September
25-28, 2017, Proceedings, pages 299–320.
Bertoni, G., Daemen, J., Peeters, M., and Assche, G. V.
(2013). Keccak. In Advances in Cryptology - EU-
ROCRYPT 2013, 32nd Annual International Confer-
ence on the Theory and Applications of Cryptographic
Techniques, Athens, Greece, May 26-30, 2013. Pro-
ceedings, pages 313–314. https://keccak.team/files/
Keccak-reference-3.0.pdf.
Boura, C. and Canteaut, A. (2010). A zero-sum property
for the Keccak-f permutation with 18 rounds. In IEEE
International Symposium on Information Theory, ISIT
2010, June 13-18, 2010, Austin, Texas, USA, Proceed-
ings, pages 2488–2492.
Boura, C. and Canteaut, A. (2016). Another view of the di-
vision property. In Advances in Cryptology - CRYPTO
2016 - 36th Annual International Cryptology Confer-
ence, Santa Barbara, CA, USA, August 14-18, 2016,
Proceedings, Part I, pages 654–682.
Cui, T., Jia, K., Fu, K., Chen, S., and Wang, M. (2016). New
automatic search tool for impossible differentials and
zero-correlation linear approximations. IACR Cryp-
tology ePrint Archive, 2016:689.
Daemen, J., Knudsen, L. R., and Rijmen, V. (1997). The
block cipher square. In Fast Software Encryption, 4th
International Workshop, FSE 1997, Haifa, Israel, Jan-
uary 20-22, 1997, Proceedings, pages 149–165.
Fu, K., Wang, M., Guo, Y., Sun, S., and Hu, L. (2016).
Milp-based automatic search algorithms for differen-
tial and linear trails for speck. In Fast Software En-
cryption - 23rd International Conference, FSE 2016,
Bochum, Germany, March 20-23, 2016, Revised Se-
lected Papers, pages 268–288.
ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy
42

Gurobi Optimization (2013). Gurobi optimizer reference
manual. http://www.gurobi.com.
Hamburg, M. (2017). Cryptanalysis of 22
1
2
rounds of
Gimli. Cryptology ePrint Archive, Report 2017/743.
https://eprint.iacr.org/2017/743.
Knudsen, L. R. and Wagner, D. A. (2002). Integral crypt-
analysis. In Fast Software Encryption, 9th Interna-
tional Workshop, FSE 2002, Leuven, Belgium, Febru-
ary 4-6, 2002, Revised Papers, pages 112–127.
Mouha, N., Mennink, B., Herrewege, A. V., Watanabe, D.,
Preneel, B., and Verbauwhede, I. (2014). Chaskey:
An efficient MAC algorithm for 32-bit microcon-
trollers. In Selected Areas in Cryptography - SAC
2014 - 21st International Conference, Montreal, QC,
Canada, August 14-15, 2014, Revised Selected Pa-
pers, pages 306–323.
Mouha, N., Wang, Q., Gu, D., and Preneel, B. (2012). Dif-
ferential and linear cryptanalysis using mixed-integer
linear programming. In Information Security and
Cryptology –ISC 2012, pages 57–76. Springer.
Sasaki, Y. and Todo, Y. (2017). New impossible differen-
tial search tool from design and cryptanalysis aspects
- revealing structural properties of several ciphers.
In Advances in Cryptology - EUROCRYPT 2017 -
36th Annual International Conference on the Theory
and Applications of Cryptographic Techniques, Paris,
France, April 30 - May 4, 2017, Proceedings, Part III,
pages 185–215.
Shi, D., Sun, S., Derbez, P., Todo, Y., Sun, B., and Hu, L.
(2018). Programming the demirci-selc¸uk meet-in-the-
middle attack with constraints. In Advances in Cryp-
tology - ASIACRYPT 2018 - 24th International Con-
ference on the Theory and Application of Cryptology
and Information Security, Brisbane, QLD, Australia,
December 2-6, 2018, Proceedings, Part II, pages 3–
34.
Sun, S., Hu, L., Wang, P., Qiao, K., Ma, X., and Song, L.
(2014). Automatic security evaluation and (related-
key) differential characteristic search: Application to
simon, present, lblock, DES(L) and other bit-oriented
block ciphers. In Advances in Cryptology - ASI-
ACRYPT 2014 - 20th International Conference on the
Theory and Application of Cryptology and Informa-
tion Security, Kaoshiung, Taiwan, R.O.C., December
7-11, 2014. Proceedings, Part I, pages 158–178.
Todo, Y. (2015). Structural evaluation by generalized in-
tegral property. In Advances in Cryptology - EU-
ROCRYPT 2015 - 34th Annual International Confer-
ence on the Theory and Applications of Cryptographic
Techniques, Sofia, Bulgaria, April 26-30, 2015, Pro-
ceedings, Part I, pages 287–314.
Todo, Y., Isobe, T., Hao, Y., and Meier, W. (2017). Cube
attacks on non-blackbox polynomials based on divi-
sion property. In Advances in Cryptology - CRYPTO
2017 - 37th Annual International Cryptology Confer-
ence, Santa Barbara, CA, USA, August 20-24, 2017,
Proceedings, Part III, pages 250–279.
Todo, Y. and Morii, M. (2016). Bit-based division prop-
erty and application to SIMON family. In Fast
Software Encryption - 23rd International Conference,
FSE 2016, Bochum, Germany, March 20-23, 2016,
Revised Selected Papers, pages 357–377.
Xiang, Z., Zhang, W., Bao, Z., and Lin, D. (2016). Apply-
ing MILP method to searching integral distinguishers
based on division property for 6 lightweight block ci-
phers. In Advances in Cryptology - ASIACRYPT 2016
- 22nd International Conference on the Theory and
Application of Cryptology and Information Security,
Hanoi, Vietnam, December 4-8, 2016, Proceedings,
Part I, pages 648–678.
APPENDIX
Algorithm 2: The reversed GIMLI permutation
Input: s = (s
i, j
) ∈ W
3×4
Output: GIMLI
−1
(s) = ( ˜s
i, j
) ∈ W
3×4
1 for r from 24 downto 1 inclusive do
2 if r mod 4 = 0 then
3 s
0,0
= s
0,0
⊕ 0x9e377900 ⊕ r
4 end
5 if r mod 4 = 0 then
6 s
0,0
,s
0,1
,s
0,2
,s
0,3
← s
0,1
,s
0,0
,s
0,3
,s
0,2
7 else if r mod 4 = 2 then
8 s
0,0
,s
0,1
,s
0,2
,s
0,3
← s
0,2
,s
0,3
,s
0,0
,s
0,1
9 end
10
11 for j ∈ {0, · · · , 3} do
12 ˜s
0, j,0
← s
2, j,0
13 ˜s
1, j,0
← s
1, j,0
⊕ ˜s
0, j,0
14 ˜s
2, j,0
← s
0, j,0
⊕ ˜s
1, j,0
15 ˜s
0, j,1
← s
2, j,1
⊕ ˜s
2, j,0
16 ˜s
1, j,1
← s
1, j,1
⊕ ˜s
0, j,1
⊕ (˜s
2, j,0
∨ ˜s
0, j,0
)
17 ˜s
2, j,1
← s
0, j,1
⊕ ˜s
1, j,1
18 ˜s
0, j,2
← s
2, j,2
⊕ ˜s
2, j,1
⊕ (˜s
1, j,0
∧ ˜s
2, j,0
)
19 ˜s
1, j,2
← s
1, j,2
⊕ ˜s
0, j,2
⊕ (˜s
2, j,1
∨ ˜s
0, j,1
)
20 ˜s
2, j,2
← s
0, j,2
⊕ ˜s
1, j,2
21
22 for k ∈ {3,··· , 31} do
23 ˜s
0, j,k
← s
2, j,k
⊕ ˜s
2, j,k−1
⊕ (˜s
1, j,k−2
∧
˜s
2, j,k−2
)
24 ˜s
1, j,k
←
s
1, j,k
⊕ ˜s
0, j,k
⊕ (˜s
2, j,k−1
∨ ˜s
0, j,k−1
)
25 ˜s
2, j,k
←
s
0, j,k
⊕ ˜s
1, j,k
⊕ (˜s
0, j,k−3
∧ ˜s
1, j,k−3
)
26 end
27
28 ˜s
0, j
← ˜s
0, j
≪ −24
29 ˜s
1, j
← ˜s
1, j
≪ −9
30 end
31 end
32 return (˜s
i, j
)
Zero-sum Distinguishers for Round-reduced GIMLI Permutation
43
