
Experimental Evaluation of a Method for Simulation based Learning for
a Multi-Agent System Acting in a Physical Environment
Kun Qian, Robert W. Brehm and Lars Duggen
SDU Mechatronics, Mads Clausen Institute, University of Southern Denmark, Denmark
Keywords:
Cooperative Multi-Agent Systems, Multi-Agent Reinforcement Learning, Multi-Agent Actor-Critic, Cooper-
ative Navigation, Simulation Based Learning.
Abstract:
A method for simulation based reinforcement learning (RL) for a multi-agent system acting in a physical
environment is introduced, which is based on Multi-Agent Actor-Critic (MAAC) reinforcement learning. In
the proposed method, avatar agents learn in a simulated model of the physical environment and the learned
experience is then used by agents in the actual physical environment. The proposed concept is verified using
a laboratory benchmark setup in which multiple agents, acting within the same environment, are required
to coordinate their movement actions to prevent collisions. Three state-of-the-art algorithms for multi-agent
reinforcement learning (MARL) are evaluated, with respect to their applicability for a predefined benchmark
scenario. Based on simulations it is shown that the MAAC method is most applicable for implementation as
it provides effective distributed learning and suits well to the concept of learning in simulated environments.
Our experimental results, which compare simulated learning and task execution in a simulated environment
with that of task execution in a physical environment demonstrate the feasibility of the proposed concept.
1 INTRODUCTION
Multi-agent systems (MASs) have been considered as
one of the most promising technologies for Industry
4.0 applications (Sycara et al., 1996; Xie and Liu,
2017). In a MAS, several agents act autonomously
in a shared environment, in order to follow and ful-
fill specific objectives (Wooldridge, 2009). RL, con-
cerned with how agents learn by trial-and-error inter-
action with an environment, is closely coupled to the
concept of an agent (Neto, 2005). The agent interacts
with the environment by executing specific actions,
which result in a state change of the environment.
The agent learns by accumulated rewards, which it
receives for a series of executed actions (Wooldridge,
2009; Neto, 2005; Sutton et al., 2018).
In many applications, agents act individually to
achieve a given objective. However, if several agents
are acting within the same environment, there is a
need to cooperate, coordinate, and negotiate with one
another to cope with shared resources, data, knowl-
edge or coordination of given tasks. Integrating RL
methods into a MAS has attracted increasing atten-
tion in recent years (Stone and Veloso, 2000; Bu-
soniu et al., 2008), since the complexity of some
tasks make it hard to coordinate between agents us-
ing pre-programmed agent behaviors. Applications
for MARL ranges from game playing to industrial ap-
plications. In (Wang and De Silva, 2006; Yang and
Gu, 2004), a multi-agent robot scenario is introduced,
in which learning is required to specify optimal ac-
tions for all states that each robot might encounter. A
set of MARL systems for traffic lights control is pre-
sented in (Wiering, 2000; Bakker et al., 2010), which
help to optimize driving policies. A method for opti-
mization of distributed energy resources using MARL
is introduced in (Raju et al., 2015).
Formation control is one of the most popular prob-
lems considered in MASs. The aim is to form a
prescribed geometrical shape in a given environment
while preventing collisions with obstacles and other
agents. In (Lowe et al., 2017), a cooperative navi-
gation problem is presented, in which agents are sit-
uated in an environment and are given the objective
to navigate to a set of locations. Agents must visit
all locations without colliding with each other. The
methods presented in (Matignon et al., 2007; Wang
and De Silva, 2006; Lowe et al., 2017; Li et al., 2008;
Foerster et al., 2017) can easily be applied to solve the
given cooperative navigation problem. However, the
validations of the proposed methods are based on sim-
ulations, a validation and evaluation of MARL and
the applicability in real environments is missing. In
this paper we present the evaluation and application of
MARL on the bases of a laboratory benchmark setup,
as shown in Figure 1.
Qian, K., Brehm, R. and Duggen, L.
Experimental Evaluation of a Method for Simulation based Learning for a Multi-Agent System Acting in a Physical Environment.
DOI: 10.5220/0007250301030109
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 103-109
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
103

Figure 1: Laboratory benchmark model for MARL evalu-
ation. The length of each axis is 400 pixels, which corre-
sponds to the physical length of 1 meter.
In the laboratory benchmark setup, spherical
robots are able to move within a predefined area. A
camera, mounted on the ceiling, monitors the move-
ment of the robots and continuously monitors the
robots positions. The robots manoeuvring range is
selected to be restricted to a specific area which is vis-
ible to the camera. There are two goal landmarks at
specific locations inside the area. Further the spher-
ical robots are originally positioned at two base sta-
tions inside the given area. The robots know the rel-
ative position of each other and also the positions of
the landmarks and the base stations. In the benchmark
scenario, the robots will be requested to simultane-
ously move to one of these goal landmarks without
colliding into each other, stay at that location for a
short period of time, and then move back to the base
station.
In the remaining of this paper, in Section 2, an
evaluation and comparison of three suitable MARL
algorithms based on a simulation of a self-defined en-
vironment is given. In Section 3 the detailed setup of
the laboratory benchmark setup and the design of the
final MAS is introduced. For validation of the pro-
posed simulation based learning method, in Section
4, the implementation of the MAS and the experimen-
tal results are presented. The experimental results are
compared to results from the simulated environment.
The paper ends with concluding remarks and sugges-
tions for future work.
2 MULTI-AGENT
REINFORCEMENT LEARNING
In RL, an agent that is situated in an environment
learns which action to take for a particular environ-
mental state in order to maximize its total received
reward. The agent discovers the best actions for an
environmental state, by trying them. Finite Markov
decision processes (MDP) are mathematically ideal-
ized forms of RL problems. The agent perceives its
environment, and after a decision, it takes an action,
which leads to an environment state transition and a
reward for the agent. The introduced MARL frame-
works are based on the MDP. However, the difference
to single-agent RL is that actions of other agents will
have an effect on the environment as well. This leads
to a non-deterministic interaction of an agent with the
environment it acts in. Following the assumptions for
MASs as stated in (Poole and Mackworth, 2017), the
exsiting approaches integrate developments in the ar-
eas of single agent RL, game theory, and direct policy
search techniques (Busoniu et al., 2008).
In (Matignon et al., 2007), a comparison of basic
Q-learning algorithms is presented. Centralized Q-
learning shows good performance but there is a high
information demand and a larger state-action space to
be maintained. In decentralized Q-learning the state-
action space is reduced. Noticeably, an agent can get
punished even if it takes a correct action. The reason
for this is that other agents may take wrong actions
and the joint action then leads to punishment. This
can be avoided by distributed Q-learning method,
which restricts Q-values to only increment. A key
issue with distributed Q-learning is that it does not
guarantee to convergence to the optimal joint policy
in difficult coordination scenarios. For this reason,
hysteretic Q-learning has been proposed (Matignon
et al., 2007). This learning method is decentralized
in the sense that each agent builds its own Q-table
whose size is independent of the number of agents in
the environment and a linear function of its own ac-
tions. According to (Matignon et al., 2007), the per-
formance of hysteretic Q-learning is similar to cen-
tralized algorithms while much smaller Q-value tables
are used.
Apart from adapting Q-learning to multi-agent
scenarios, policy gradient based methods have also
been applied, especially the actor-critic method
(Lowe et al., 2017; Li et al., 2008; Foerster et al.,
2017). To ease training, a framework based on cen-
tralized training with decentralized execution is ap-
plied. The critic is based on extra information, such
as the policies of other agents, while the actor only
uses the local observations to choose actions. In a
fully cooperative environment, there is only one critic
for all actors since all always have the same reward.
However, in a mixed cooperative-competitive envi-
ronment, there is one critic for each actor.
In the remainder of this section, centralized
Q-learning, hysteretic Q-learning and the MAAC
method with linear function approximation will be in-
troduced. Further, these three methods are evaluated
with respect to applicability in the introduced labora-
tory benchmark setup.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
104

2.1 Multi-Agent Task Description
Figure 2 shows the simulated environment used for
the evaluation of the MARL methods. Similar to the
laboratory benchmark setup, two robot agents are ini-
tially positioned at two base stations, which are lo-
cated in x/y-direction at (7, 7) and (7, 21). Further,
there are two goal locations at (14, 14) and (21, 14).
The maneuvering area of the two agents is restricted
to 30 × 30 units. The objective of the agents is to si-
multaneously move to one of the goal locations with-
out colliding with the other agent. The current posi-
tion of each agent represents the environments state.
When both agents are at the same location, the in-
teraction is terminated with a reward of r = −100.
If each agent is occupying one goal location or it is
in close proximity of less then two pixels, the inter-
action is terminated with a reward of r = 10. Apart
from the mentioned terminal states, the agents will
get a reward of r = −1 each time they interact with
the environment. The rewards are generally defined
as positive for desired actions while negative for poor
actions. The reward r = −100 indicates that the col-
lision is the most undesired situation for the agents.
The reward r = −1 means that the agents are consum-
ing time. The reward r = 10 encourages the agents to
reach the goal.
Figure 2: Benchmark MAS environment for MARL meth-
ods evaluation.
The set of possible agent actions is given by A =
{up, down, right, le f t}. These actions will take the
agent into the chosen direction, except if the chosen
heading will take the agent out of the restricted area,
in that case, the agents position will stay unchanged.
2.2 MARL Methods Evaluation
2.2.1 Centralized Q-learning
For the introduced scenario, in the environment state
s, an action consists of the two agent actions, a =
(a
1
, a
2
) with a
1
, a
2
∈ A. The extracted state fea-
tures are given by horizontal and vertical distances
φ
φ
φ(s) = (φ
1
, φ
2
, ..., φ
10
) summarized in Table 1.
Table 1: Summery of the features for a state. Here h
d
de-
noted the horizontal and v
d
the vertical distance, respec-
tively.
Feature Description
φ
1
h
d
from the 1
st
agent to the 1
st
goal
φ
2
v
d
from the 1
st
agent to the 1
st
goal
φ
3
h
d
from the 1
st
agent to the 2
nd
goal
φ
4
v
d
from the 1
st
agent to the 2
nd
goal
φ
5
h
d
from the 2
nd
agent to the 1
st
goal
φ
6
v
d
from the 2
nd
agent to the 1
st
goal
φ
7
h
d
from the 2
nd
agent to the 2
nd
goal
φ
8
v
d
from the 2
nd
agent to the 2
nd
goal
φ
9
h
d
from the 1
st
agent to the 2
nd
agent
φ
10
v
d
from the 1
st
agent to the 2
nd
agent
Similar to what is mentioned in (Geramifard et al.,
2013), the features for the state action pair can be re-
encoded in a manner such that the 10 features for each
possible a
1
, a
2
combination are indexed accordingly,
yielding a re-encoded state action set φ
φ
φ(s, a
1
, a
2
) =
(φ
1
(s), φ
2
(s), ..., φ
160
(s)) of size 160 (φ
φ
φ(s, a
1
, a
2
) ∈
A
16
× R
10
). From this, the action values can be ap-
proximated by:
q
ω
ω
ω
(s, a
1
, a
2
) =ω
0
+
160
∑
i=1
ω
i
φ
i
(s, a
1
, a
2
)
(1)
with ω
ω
ω being the parameter vector to be learned,
which is updated by:
ω
ω
ω
t+1
= ω
ω
ω
t
+
α
r + γmax
a
0
1
,a
0
2
q
ω
ω
ω
t
s
0
, a
0
1
, a
0
2
− q
ω
ω
ω
t
(s, a
1
, a
2
)
φ
φ
φ(s, a
1
, a
2
).
(2)
Here, s, a
1
, and a
2
denote the state and actions chosen
at time step t, while r, s
0
, a
0
1
, and a
0
2
are the reward,
state, and available actions at time step t + 1.
2.2.2 Hysteretic Q-learning
Hysteretic Q-learning provides decentralised RL in
deterministic multi-agent environments. In a certain
state of the above-defined environment, the action
space for an agent is only of size 4. For the defined en-
vironment this shrinks down the size of features rep-
resenting the state-action pair from 160 (feature size
of centralized Q-learning) to just 40. To approximate
the action values for two agents, two parameter vec-
tors ω
ω
ω
1
, ω
ω
ω
2
are required, which need to be learned.
Experimental Evaluation of a Method for Simulation based Learning for a Multi-Agent System Acting in a Physical Environment
105
The update rule for the parameter vectors is given by:
δ = r + γmax
a
0
q
i
(s
0
, a
0
) − q
i
(s, a
i
), (3)
ω
ω
ω
i,t+1
=
(
ω
ω
ω
i,t
+ αδ if δ ≥ 0
ω
ω
ω
i,t
+ βδ else
. (4)
Here, i denotes the index of the agent, with a
i
, a
0
∈ A
and α, β are the increase and decrease rate for the
parameter updates.
2.2.3 Multi-Agent Actor-Critic
In the MAAC method a centralized critic is learned to
critique the actors. The critic approximates the val-
ues for a state with a parameter vector ω
ω
ω based on
feature vector
e
φ
φ
φ(s) = (
e
φ
1
,
e
φ
2
,
e
φ
3
). With
e
φ
1
being the
Euclidean distance from the first agent to a goal,
e
φ
2
being the Euclidean distance from the second agent
to the other goal and
e
φ
3
being the Euclidean distance
from the first agent to the second agent. Thus, the
state value v(s) is approximated by:
v
ω
(s) = ω
0
· 1 + ω
1
e
φ
1
(s) + ω
2
e
φ
2
(s) + ω
3
e
φ
3
(s). (5)
To calculate the policy π
i
(a
i
| s) for each actor, pa-
rameterized numerical preferences h
i
(s, a
i
, θ
θ
θ
i
) need to
be formed for each state-action pair:
h
i
(s, a
i
, θ
θ
θ) = θ
θ
θ
>
i
φ
φ
φ(s, a
i
). (6)
Here, i denotes the index of the agent, with a
i
∈ A.
θ
θ
θ
i
is the parameter vector for parametrising the pol-
icy and φ
φ
φ(s, a
i
) is found based on the features listed
in Table 1. For the interaction between agents and
environment the parameter vectors are updated using:
δ
t
= r + γv
ω
ω
ω
t
s
0
− v
ω
ω
ω
t
(s), (7)
ω
ω
ω
t+1
= ω
ω
ω
t
+ α
ω
δ
t
e
φ
φ
φ(s), (8)
θ
θ
θ
i,t+1
= θ
θ
θ
i,t
+ α
θ
δ
t
∇
θ
θ
θ
i
lnπ(a
i
| s, θ
θ
θ
i
). (9)
Here, s and a
i
are the state and action chosen at time
step t, while r and s
0
are the reward and state at time
step t + 1.
2.2.4 Methods Evaluation
For a comparative evaluation of these three methods,
each is simulated for a 1000 episodes, consisting of
the steps from initial position to a terminal state, and
the sum of rewards for each episode is collected. The
hyperparameters used for the simulations are shown
in Table 2.
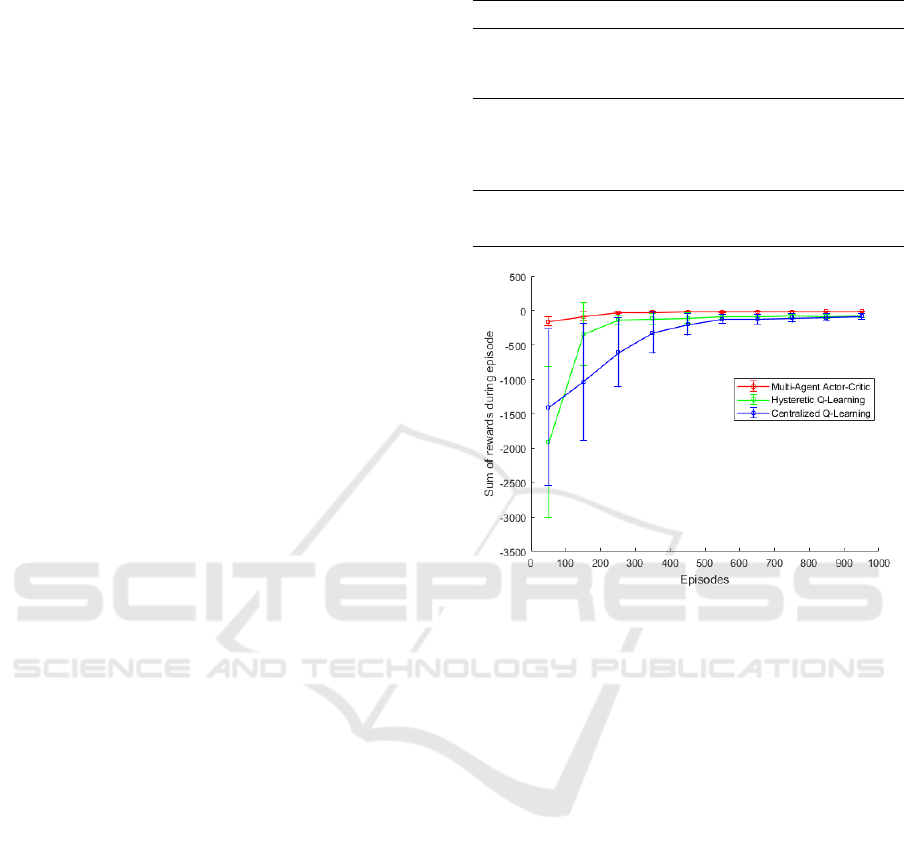
The mean value and standard deviation for ev-
ery 100 episodes is shown in Figure 3, with the er-
ror bar showing the standard deviations. It can be
Table 2: Hyperparameters for the above three methods.
Methods Hyperparameters
Centralized
Q-
learning
Learning rate α = 0.05, discount fac-
tor γ = 0.99, ε-soft policy with ε de-
creasing slowly from 0.8 to 0.1
Hysteretic
Q-
learning
Increasing rate α = 0.05, decreasing
rate β = 0.005, discount factor γ =
0.99, ε-soft policy with ε decreasing
slowly from 0.8 to 0.1
MAAC Learning rate α
ω
= 0.0025, α
θ
= 0.05,
discount factor γ = 0.99
Figure 3: Mean values and standard deviations of rewards.
observed that in centralized Q-learning, the param-
eters are learned more slowly, due to the larger ac-
tion space. Futher, Hysteretic Q-learning shows good
performance while MAAC can solve the task with
best performance. In centralized Q-learning the ac-
tion space grows exponentially with the number of
agents. In compliance with the concept of decentral-
ized decision making in a MAS, hysteretic Q-learning
and MAAC are more applicable. However, in MAAC
at least one centralized critic is needed, which means,
during the execution process, the parameters will not
be able to be updated. And this will only work if the
dynamics of the environment are stable. In the co-
ordinated multi-agent scenario as studied herein, the
dynamics will not change. Therefore, it is proposed
to use a concept in which avatar agents learn in a
simulated model of the given environment using the
MAAC method with a central critic. The learned pa-
rameters are then to be used by the real agents in a real
environment. The feasibility of this concept will be
proven based on the experimental benchmark setup,
which is described in the following section.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
106
3 EXPERIMENTAL
BENCHMARK SETUP
3.1 Multi-Agent System Architecture
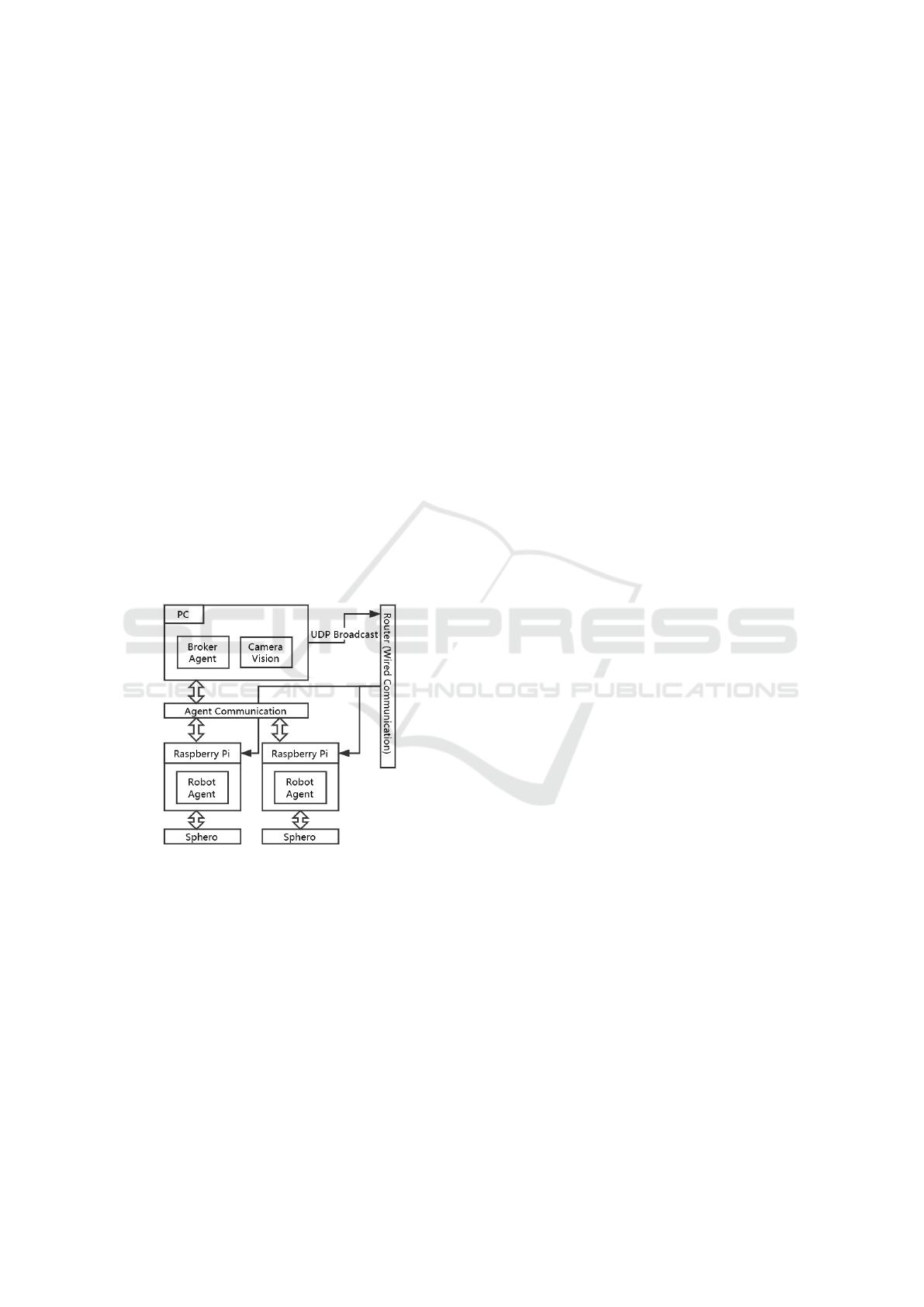
The JADE framework is used for the implementation
of the MAS in the benchmark setup. Agents com-
munication is based on FIPA compliant messaging.
There are two ways of designing the software archi-
tecture: coupled design and embedded design. The
coupled design is currently popular in automation sce-
narios, while the embedded design promotes the de-
coupling of agents logically and geographically, ef-
fectively enabling the creation of plug-and-produce
entities comprising the artifact being controlled, the
controller, and the agent (Leit
˜
ao and Karnouskos,
2015). In the implementation of the benchmark sce-
nario, an embedded design is used. Here, the agents
and the low-level control system are situated on the
same embedded platform. Each robot agent is de-
ployed on a single board computer (SBC), which con-
trols a spherical robot (Sphero) using a wireless Blue-
tooth link. A simplified architectural diagram for used
MAS is shown in Figure 4. The current position of the
Figure 4: Structural diagram.
Spheros is monitored using a camera mounted on the
ceiling. The video stream is send to a computer vision
program on a central server which detects the current
position of the individual Spheros. The server streams
(via UDP broadcasting) the individual positions to the
robot agents, which are executed on the SBC. Based
on the experimental evaluation, MAAC will be used
for the benchmark scenario. And as motivated in Sec-
tion 2.2.4, the goal is to demonstrate the concept of
learning in a simulated, and execution in a physical
environment.
3.2 Benchmark Scenario
The benchmark scenario consists of three agents, two
robot agents and a broker agent. The broker agent
is able to send FIPA compliant requests to the robot
agents. This requests the robot agents to move to a
goal location (e.g. to pick something up) and return
to the base station.
Two simplified models of the real environment
are used to train the agents. The first model is used
to train the agents to move from the base stations
to the goal location, while the second model is used
to train the agents to move from the goal locations
back to the base stations. In the model, as for the
physical environment as shown in Figure 1, the two
agents are restricted to move only within an area of
the size of 400 × 400 pixels. There are two base sta-
tions which are located in x/y-direction at (100, 100)
and (100, 300) while there are two landmarks located
at (200, 200) and (300, 200). Terminal states with a
reward of r = −1000 are defined around these loca-
tions if an agent is within a circle, of a radius of 10
pixels, around the other agent. A reward of r = 100
is returned, and the interaction is terminated, if each
agent occupies each target location with a distance of
less than 5 pixels. If an action takes the agent out of
the restricted area, the position will stay unchanged.
The parameter vectors for policies which are obtained
by the agent avatars during the training in the simu-
lated environment will be used for the real agents on
the SBC, which control the Sphero robots in the phys-
ical environment.
3.3 Experimental Results
Experiments to prove the concept of learning in a sim-
ulated environment and usage of the learned experi-
ence for tasks in a physical environment have been
carried out. The presented and discussed results are
based on four episodes in which, simultaneously, two
agents are requested to each move to one goal loca-
tion, as described in Section 3.2.
Shown in Figure 5 and 6 are the traces of the
two robots as they simultaneously move through the
benchmark environment. For each executed episode,
the traces of robots are identified by two different col-
ors as denoted in the legend of the figures.
Figure 5 shows the movement of the robots based
on learning in a simulated environment and also exe-
cution of the task in the simulated environment. In
contrast, shown in Figure 6, are four episodes for
the movement of the real robots in the real environ-
ment based on learning in the simulated environment.
Comparing the results shown in Figure 5 and 6, it can
Experimental Evaluation of a Method for Simulation based Learning for a Multi-Agent System Acting in a Physical Environment
107
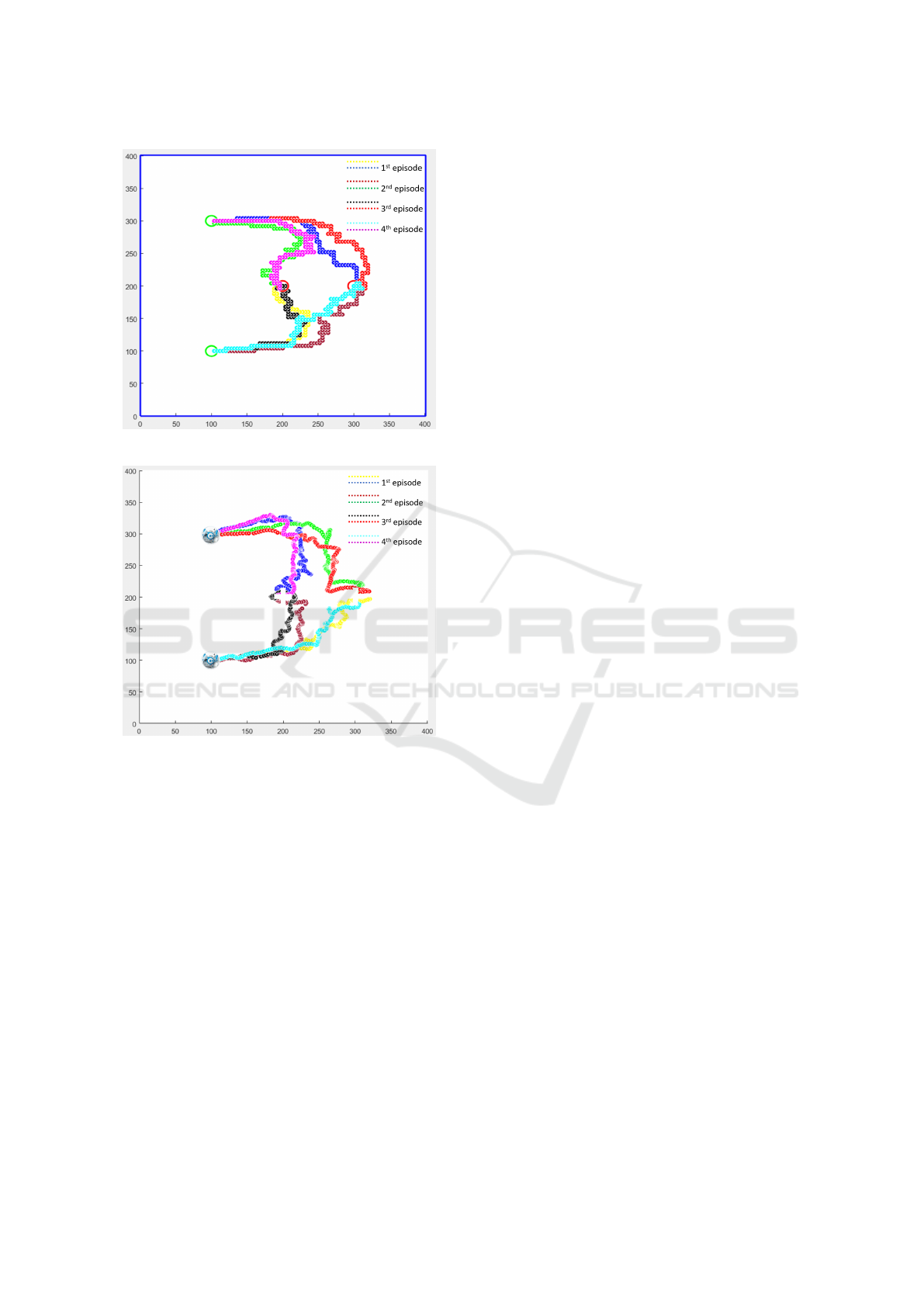
Figure 5: Simulation in MATLAB.
Figure 6: Experimental result.
be observed that for both cases agents coordinate with
each other and move to one goal landmark each, with-
out colliding with each other. The Figure is in fact
representative of approximately 20 episodes, in which
no collision has been observed. Though, it can also be
observed that the paths are not always optimal since
it is hard to perceive the real environment and control
the agents precisely. For clarity, only four episodes
are shown. From this results it is evidenced that us-
ing learned parameters from a simulated environment
in a real environment is applicable for the benchmark
setup. Further if agents reach their goal landmarks,
they are each able to move back to a base station with-
out collision, for clarity this return path is not shown
in the presented results.
4 DISCUSSION AND FUTURE
WORK
An introduction to applications for RL in MAS has
been given, with a focus on formation control and co-
ordinated movement of robots in a shared two dimen-
sional environment like a factory floor. A benchmark
scenario, in which two agents are requested to simul-
taneously pick up a virtual good at two goal land-
mark locations and deliver this to two base stations
has been introduced. In order to prevent collisions be-
tween agents, while simultaneously moving through
the environment, MARL has been used. Suitable al-
gorithms for MARL have been evaluated on the basis
of a predefined scenario. For effective and fast learn-
ing it has been proposed to use avatar agents which
learn in a simulated environment while the learned
parameters are then used by agents in the real environ-
ment. It has been shown, based on simulations of the
given benchmark scenario that, by using the MAAC
method agents learn effectively and that MAAC is ap-
plicable for the given benchmark scenario. The lab-
oratory benchmark setup to implement the given sce-
nario and the agent architecture has been introduced.
With the experiment conducted and on the basis of
the presented results, it is evidenced that the MAAC
method, in combination with learning in simulated
environment and usage of the learned parameters in
a real environment, is well applicable for the given
use case scenario.
Since real environments are not always static in
time, as in our example, further studies have to be
carried out in order to investigate the applicability
of avatar agents for learning. Nevertheless our re-
sults stipulate the feasibility of the MAAC method for
these general scenarios.
REFERENCES
Bakker, B., Whiteson, S., Kester, L., and Groen, F. C. a.
(2010). Traffic light control by multiagent reinforce-
ment learning systems. Interactive Collaborative In-
formation Systems, pages 475–510.
Busoniu, L., Babuska, R., De Schutter, B., and Schutter,
B. D. (2008). A comprehensive survey of multiagent
reinforcement learning. Systems, Man, and Cybernet-
ics, Part C: Applications and Reviews, 38(2):156–172.
Foerster, J., Farquhar, G., Afouras, T., Nardelli, N., and
Whiteson, S. (2017). Counterfactual Multi-Agent Pol-
icy Gradients. ArXiv e-prints.
Geramifard, A., Walsh, T. J., Tellex, S., Chowdhary, G.,
Roy, N., and How, J. P. (2013). A tutorial on lin-
ear function approximators for dynamic programming
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
108

and reinforcement learning. Foundations and Trends
in Machine Learning, 6(4):375–451.
Leit
˜
ao, P. and Karnouskos, S. (2015). Industrial Agents:
Emerging Applications of Software Agents in Industry.
Li, C.-G., Wang, M., and Yuan, Q.-N. (2008). A
Multi-agent Reinforcement Learning using Actor-
Critic methods. In 2008 International Conference on
Machine Learning and Cybernetics, volume 2, pages
878–882.
Lowe, R., Wu, Y., Tamar, A., Harb, J., Abbeel, P., and Mor-
datch, I. (2017). Multi-agent actor-critic for mixed
cooperative-competitive environments. Neural Infor-
mation Processing Systems (NIPS).
Matignon, L., Laurent, G. J., and Le Fort-Piat, N. (2007).
Hysteretic Q-Learning : An algorithm for decen-
tralized reinforcement learning in cooperative multi-
agent teams. In IEEE International Conference on In-
telligent Robots and Systems, pages 64–69.
Neto, G. (2005). From single-agent to multi-agent rein-
forcement learning: Foundational concepts and meth-
ods learning theory course.
Poole, D. L. and Mackworth, A. K. (2017). Artificial Intel-
ligence: Foundations of Computational Agents. Cam-
bridge University Press, New York, NY, USA, 2nd
edition.
Raju, L., Sankar, S., and Milton, R. S. (2015). Distributed
optimization of solar micro-grid using multi agent re-
inforcement learning. In Procedia Computer Science,
volume 46, pages 231–239.
Stone, P. and Veloso, M. (2000). Multiagent systems: a sur-
vey from a machine learning perspective. Autonomous
Robots, 8(3):345–383.
Sutton, R. S., Barto, A. G., and Klopf, H. (2018). Rein-
forcement Learning : An Introduction Second edition.
MIT Press, 2nd edition.
Sycara, K., Pannu, A., Williamson, M., Zeng, D., and
Decker, K. (1996). Distributed intelligent agents.
IEEE Expert-Intelligent Systems and their Applica-
tions, 11(6):36–46.
Wang, Y. and De Silva, C. W. (2006). Multi-robot
box-pushing: Single-agent Q-learning vs. team Q-
learning. In IEEE International Conference on Intel-
ligent Robots and Systems, pages 3694–3699.
Wiering, M. A. (2000). Multi-agent reinforcement learning
for traffic light control. In Machine Learning: Pro-
ceedings of the Seventeenth International Conference,
pages pp. 1151–1158.
Wooldridge, M. (2009). An Introduction to MultiAgent Sys-
tems [Paperback].
Xie, J. and Liu, C.-C. (2017). Multi-agent systems and
their applications. Journal of International Council
on Electrical Engineering, 7(1):188–197.
Yang, E. and Gu, D. (2004). Multiagent reinforcement
learning for multi-robot systems: A survey. Univer-
sity of Essex Technical Report CSM-404, . . . , pages
1–23.
Experimental Evaluation of a Method for Simulation based Learning for a Multi-Agent System Acting in a Physical Environment
109
