Effect of Dispersive Reflectivity on the Stability of Gap Solitons in
Dual-core Bragg Gratings with Cubic-quintic Nonlinearity
Afroja Akter
1
, Md. Jahedul Islam
2
and Javid Atai
1
1
School of Electrical and Information Engineering, The University of Sydney, NSW 2006, Australia
2
Department of Electrical and Electronic Engineering, Khulna University of Engineering and Technology,
Khulna 9203, Bangladesh
Keywords:
Fiber Bragg Gratings, Gap Solitons, Cubic-quintic Nonlinearity, Dispersive Reflectivity.
Abstract:
We consider dynamical stability of quiescent gap solitons in coupled Bragg gratings with dispersive reflectivity
in a cubic-quintic nonlinear medium. It is found that there exist two disjoint families of quiescent solitons
within the bandgap, namely Type 1 and Type 2 solitons. Also, in each family, there exist symmetric and
asymmetric solitons. It is found that dispersive reflectivity has a stabilizing effect on asymmetric solitons. In
addition, the symmetric Type 2 solitons are always unstable.
1 INTRODUCTION
The periodic variation of the refractive index in a fiber
Bragg grating (FBG) results in the formation of a
bandgap in the transmission spectrum of FBGs, where
linear waves cannot propagate. As a result of the cou-
pling between forward- and backward-propagating
waves, FBGs possess a strong effective dispersion
(Russell, 1991). At high intensities the induced dis-
persion and nonlinearity in FBGs may be balanced
and gives rise to gap solitons (GSs). GSs may have
any velocity in between zero and speed of light in a
medium (Christadoulides and Joseph, 1989; Aceves
and Wabnitz, 1989; Barashenkov et al., 1998).
GSs in Kerr media have been the subject of in-
tensive theoretical and experimental research due to
their potential applications in optical signal process-
ing such as optical delay lines, buffers and logic gates
(Sipe, 1992; Sipe and Winful, 1988; de Sterke and
Sipe, 1994; Sterke et al., 1997; Eggleton et al., 1997;
Krauss, 2008). They have also been investigated theo-
retically in other nonlinear systems such as quadratic
nonlinearity (Mak et al., 1998b), cubic-quintic non-
linearity (Atai and Malomed, 2001), coupled FBGs
(Mak et al., 1998a; Baratali and Atai, 2012), nonuni-
form gratings (Atai and Malomed, 2005), waveguide
arrays (Mandelik et al., 2004) and photonic crystals
(Xie and Zhang, 2003; Neill and Atai, 2007; Monat
et al., 2010).
It has previously been shown that propagation of
light in dual-core and birefringent fibers with Kerr
nonlinearity exhibits very rich dynamics (Atai and
Chen, 1992; Atai and Chen, 1993; Nistazakis et al.,
2002; Bertolotti et al., 1995; Chen and Atai, 1998;
Chen and Atai, 1995). Therefore, in this paper, we in-
vestigate the existence and stability of GSs in a dual-
core system with identical cores where each core con-
tains a Bragg grating with dispersive reflectivity writ-
ten in a cubic-quintic medium.
2 THE MODEL
-3 -2 -1 0 1 2 3
k
-2
0
2
ω
m = 0.0
m = 0.4
Figure 1: Examples of dispersion diagrams for λ = 0.1.
Propagation of light in two linearly coupled Bragg
gratings (FBGs) with dispersive reflectivity in a
Akter, A., Islam, M. and Atai, J.
Effect of Dispersive Reflectivity on the Stability of Gap Solitons in Dual-core Bragg Gratings with Cubic-quintic Nonlinearity.
DOI: 10.5220/0007251200190023
In Proceedings of the 7th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2019), pages 19-23
ISBN: 978-989-758-364-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
19

cubic-quintic nonlinear medium is described by fol-
lowing equations:
iu
1t
+ iu
1x
+

1
2
|u
1
|
2
+ |v
1
|
2

u
1
−
η

1
4
|u
1
|
4
+
3
2
|u
1
|
2
|v
1
|
2
+
3
4
|v
1
|
4

u
1
+
v
1
+ λu
2
+ mv
1
xx
= 0,
iv
1t
−iv
1x
+

1
2
|v
1
|
2
+ |u
1
|
2

v
1
−
η

1
4
|v
1
|
4
+
3
2
|v
1
|
2
|u
1
|
2
+
3
4
|u
1
|
4

v
1
+
u
1
+ λv
2
+ mu
1xx
= 0,
iu
2t
+ iu
2x
+

1
2
|u
2
|
2
+ |v
2
|
2

u
2
−
η

1
4
|u
2
|
4
+
3
2
|u
2
|
2
|v
2
|
2
+
3
4
|v
2
|
4

u
2
+
v
2
+ λu
1
+ mv
2xx
= 0,
iv
2t
−iv
2x
+

1
2
|v
2
|
2
+ |u
2
|
2

v
2
−
η

1
4
|v
2
|
4
+
3
2
|v
2
|
2
|u
2
|
2
+
3
4
|u
2
|
4

v
2
+
u
2
+ λv
1
+ mu
2xx
= 0.
(1)
In Eqs. (1), u
1,2
(x,t) and v
1,2
(x,t) are the am-
plitudes of the forward- and backward-propagating
waves in cores 1 and 2, respectively. η > 0 is a real pa-
rameter and denotes the strength of the quintic nonlin-
earity. λ is coefficient of linear coupling between two
cores and is real and positive. m > 0 is the strength
of the dispersive reflectivity. It should be noted that
equation (1) is normalized so that the group velocity
coefficient 1. It should be noted that in the absence of
dispersive reflectivity (i.e. m = 0), Eqs. (1) reduce to
the model of Ref. (Islam and Atai, 2015).
To obtain the spectrum bandgap within
which the GSs may exist, plane wave solutions
u
1,2
,v
1,2
∼ exp(ikx −iwt) are substituted into
linearized version of Eqs. (1) and after some straight-
forward algebraic manipulations the following
dispersion relation is obtained:
ω
2
=

1 −mk
2

2
+ λ
2
+ k
2
±2λ


1 −mk
2

2
+ k
2
(2)
Eq. (2) leads to the bandgap ω
2
< ω
2
0
= (1 −|λ|)
2
for m≤ 0.5 and ω
2
< ω
2
0
=

√
4m−1
2m
−|λ|

2
for m >
0.5. Examples of dispersion diagrams for various val-
ues of m are shown in Fig. 1. It should be noted that
since m > 0.5 may not be physically achievable, we
will limit our analysis to m ≤ 0.5.
3 SOLITON SOLUTIONS
To obtain the quiescent soliton solutions, we substi-
tute u(x,t) = U(x)e
−iωt
and v(x,t) = V (x)e
−iωt
into
Eqs. (1) which results in the following systems of
coupled equations:
−mU
1xx
= ωV
1
−iV
1x
+

1
2
|V
1
|
2
+ |U
1
|
2

V
1
−
η

1
4
|
V
1
|
4
+
3
2
|
V
1
|
2
|U
1
|
2
+
3
4
|
U
1
|
4

V
1
+
U
1
+ λV
2
,
−mV
1xx
= ωU
1
+ iU
1x
+

1
2
|U
1
|
2
+ |V
1
|
2

U
1
−
η

1
4
|U
1
|
4
+
3
2
|U
1
|
2
|V
1
|
2
+
3
4
|V
1
|
4

U
1
+
V
1
+ λU
2
,
−mU
2xx
= ωV
2
−iV
2x
+

1
2
|V
2
|
2
+ |U
2
|
2

V
2
−
η

1
4
|V
2
|
4
+
3
2
|V
2
|
2
|U
2
|
2
+
3
4
|U
2
|
4

V
2
+
U
2
+ λV
1
,
−mV
2xx
= ωU
2
+ iU
2x
+

1
2
|U
2
|
2
+ |V
2
|
2

U
2
−
η

1
4
|U
2
|
4
+
3
2
|U
2
|
2
|V
2
|
2
+
3
4
|V
2
|
4

U
2
+
V
2
+ λU
1
.
(3)
There is no analytical solution for Eqs. (3). These
equations can be solved numerically using the relax-
ation algorithm. We found that similar to the case of
a single core Bragg grating with cubic-quintic non-
linearity (i.e. model of Ref. (Atai and Malomed,
2001)), there exist two distinct and disjoint families
of solitons in the model of Eqs. (1) that are sep-
arated by a border. We refer to these soliton fami-
lies as Type 1 and Type 2. In each of these families,
there exist symmetric (u
1
= u
2
, v
1
= v
2
) and asym-
metric (u
1
̸= u
2
, v
1
̸= v
2
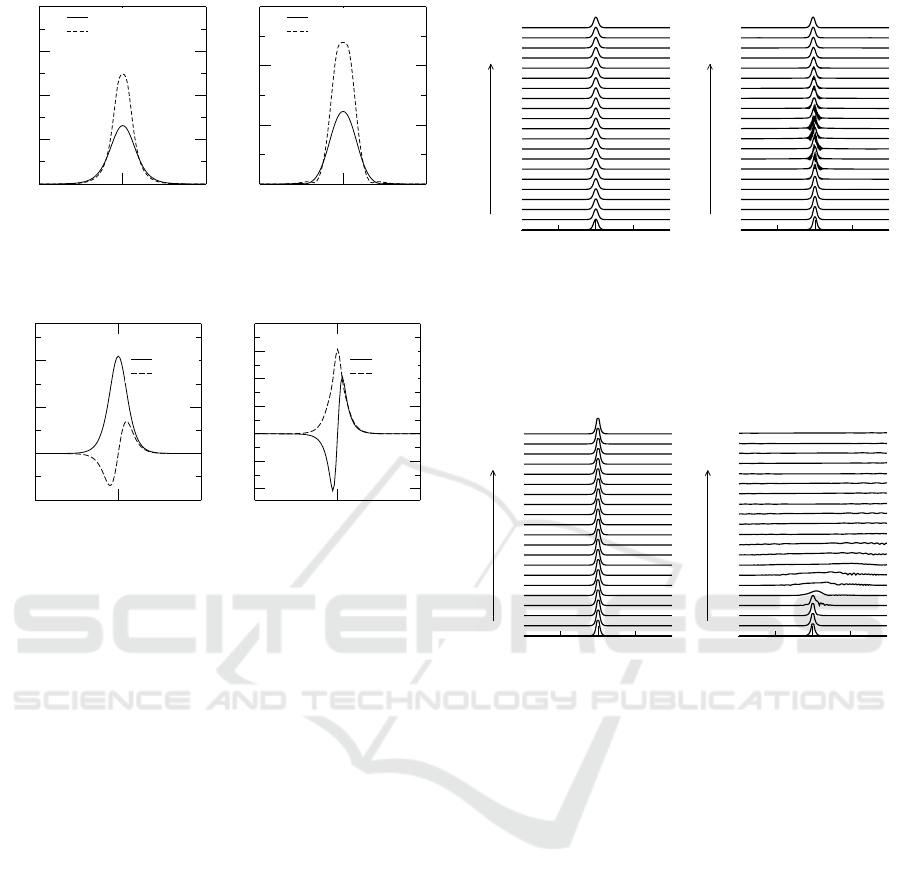
) solitons. Examples of sym-
metric Type 1 and Type 2 soliton profiles are shown
in Fig. 2. Soliton families differ in terms of their
amplitude, phase, and parities. More specifically, as
is shown in Fig. 3, Re(u(x)) and Re(v(x )) of Type 1
solitons are even and Im(u(x)) and Im(v(x)) are odd
functions of x. The opposite occurs in the case of Type
2 solitons.
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
20

0
x
0
0.5
1
1.5
2
|u|
ω = 0.60, η = 0.3
ω = −0.75, η = 0.6
(a)
0
x
0
0.5
1
1.5
|u|
ω = 0.60 , η = 0.3
ω = −0.75, η = 0.6
(b)
Figure 2: Symmetric Type 1 (solid line) and Type 2 (dashed
line) stationary solitons profiles for (a) λ = 0.1, m = 0.2 (b)
λ = 0.1, m = 0.4.
0
x
-0.5
0
0.5
1
Re (U )
Im (U )
(a)
1
1
0
x
-1
-0.5
0
0.5
1
1.5
2
Re (U )
Im (U )
(b)
1
1
Figure 3: Real and Imaginary part of asymmetric gap soli-
tons for λ = 0.1 and m = 0.2. (a) Type 1 at ω = 0.3,
η = 0.2,(b) Type 2 at ω = −0.2, η = 0.4.
4 STABILITY OF QUIESCENT
SOLITONS
To analyze the stability of the quiescent gap solitons,
we have employed symmetrized split-step Fourier
method to solve Eqs. (1) numerically. The numer-
ical stability analysis shows that stable and unstable
Type 1 and Type 2 solitons exist in the system. Exam-
ples of the evolution of asymmetric Type 1 and Type
2 solitons are shown in Fig. 4 and Fig. 5 respec-
tively. Examples of propagation of symmetric Type 1
and Type 2 solitons are shown in Fig. 6. As is shown
in Figs. 4 to 6 unstable solitons are either completly
destroyed or sheds some energy in the form of radi-
ation and evolves to another quiescent soliton in the
system. Another interesting finding is that symmetric
Type 2 solitons are always unstable.
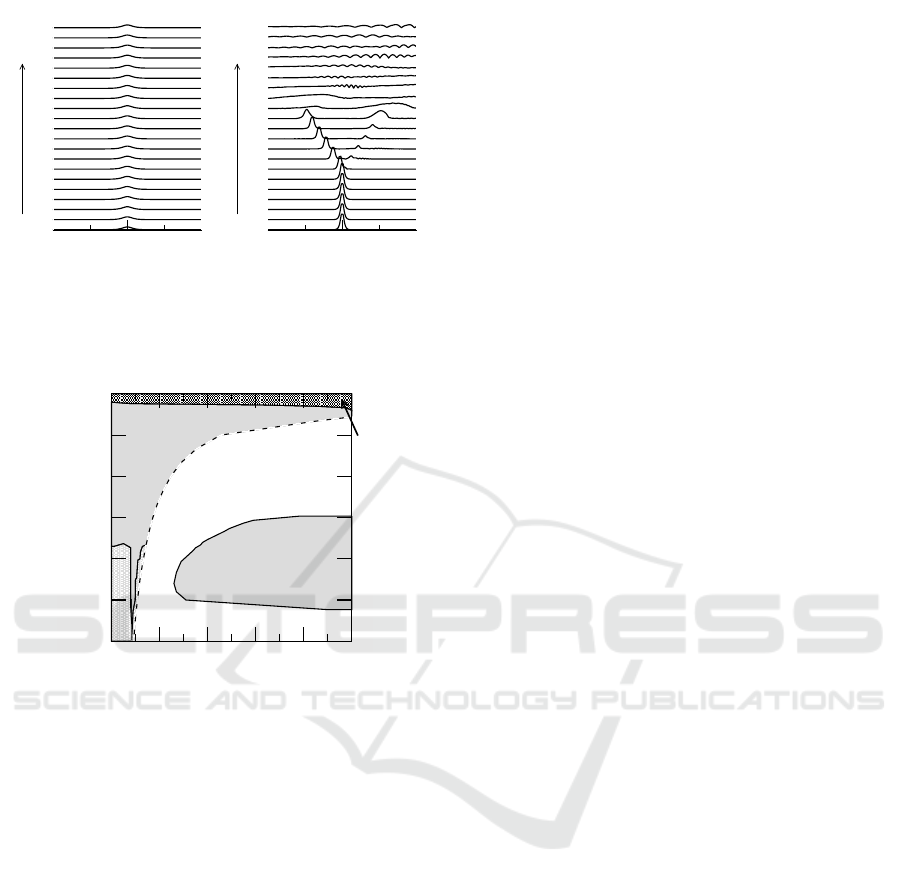
The stability diagram for asymmetric and sym-
metric quiescent solitons corresponding to m = 0.2
at λ = 0.1 is displayed in Fig. 7. The dashed curve
in Fig. 7 separates the Type 1 and Type 2 fami-
lies of asymmetric solitons. As is shown in Fig. 7,
there exist vast regions of stable solitons within the
bandgap. Compared with the case of m = 0 (i.e. the
model of Ref. (Islam and Atai, 2015)), it is found
-40 0 40
x
0
2000
t
(a)
-40 0 40
x
0
2000
t
(b)
Figure 4: Examples of propagation of asymmetric Type 1
solitons for λ = 0.1, m = 0.2. (a) Stable asymmetric soliton
for ω = 0.3, η = 0.20 and (b) unstable asymmetric soliton
for ω = −0.55, η = 0.01. In this figure and following fig-
ures only u
1
component is shown.
-40 0 40
x
0
2000
t
(a)(a)
-40 0 40
x
0
200
t
(b)(b)
Figure 5: Examples of propagation of asymmetric Type 2
solitons for λ = 0.1, m = 0.2. (a) Stable asymmetric Type
2 for ω = −0.20, η = 0.40, (b) unstable asymmetric Type 2
soliton for ω = 0.50, η = 1.0.
that the presence of dispersive reflectivity leads to the
expansion of stable regions. This finding is consis-
tent with that for the single core Bragg grating with
cubic-quintic nonlinearity and dispersive reflectivity
(i.e. Ref. (Dasanayaka and Atai, 2010)).
5 CONCLUSIONS
We have numerically investigated the effect of dis-
persive reflectivity on the stability of quiescent gap
solitons in coupled Bragg gratings with cubic-quintic
nonlinearity. There exists a genuine bandgap within
the linear spectrum of the system. Using the numer-
ical techniques, it is found that stationary quiescent
gap solitons exist throughout the bandgap. Further-
more, the model supports two disjoint families of qui-
escent solitons, namely Type 1 and Type 2 solitons.
Additionally, both symmetric and asymmetric soli-
Effect of Dispersive Reflectivity on the Stability of Gap Solitons in Dual-core Bragg Gratings with Cubic-quintic Nonlinearity
21

-40 0 40
x
0
2000
t
(a)(a)(a)
-40 0 40
x
0
200
t
(b)(b)
Figure 6: Example of evolution of symmetric solitons for
λ = 0.1, m = 0.2 (a) stable Type 1 symmetric soliton for ω =
0.84, η = 0.01 and (b) unstable Type 2 symmetric soliton
for ω = −0.30, η = 0.39.
0 0.2 0.4 0.6 0.8 1
η
-0.9
-0.6
-0.3
0
0.3
0.6
0.9
ω
Stable (T1)
Unstable (T1)
Stable (T2)
Unstable (T2)
Stable (T1) (Symmetric)
Figure 7: Stability diagram of asymmetric quiescent soli-
tons for m = 0.2, λ = 0.1. The dashed curve is the border
between Type 1 (T1) and Type 2 (T2) soliton families.
tons exist in each family.
We have conducted a numerical stability analy-
sis for symmetric and asymmetric Type 1 and Type
2 solitons. It is found that symmetric Type 2 solitons
are always unstable. For asymmetric solitons, the re-
sults of the stability analysis show that the presence
of dispersive reflectivity has a stabilizing effect.
REFERENCES
Aceves, A. and Wabnitz, S. (1989). Self-induced trans-
parency solitons in nonlinear refractive periodic me-
dia. Phys. Lett. A, 141(1):37 – 42.
Atai, J. and Chen, Y. (1992). Nonlinear couplers composed
of different nonlinear cores. J. Appl. Phys., 72:24–27.
Atai, J. and Chen, Y. (1993). Nonlinear mismatches be-
tween two cores of saturable nonlinear couplers. IEEE
J. Quant. Elec., 29:242–249.
Atai, J. and Malomed, B. A. (2001). Families of bragg-
grating solitons in a cubic-quintic medium. Phys. Lett.
A, 284(6):247 – 252.
Atai, J. and Malomed, B. A. (2005). Gap solitons in bragg
gratings with dispersive reflectivity. Physics Letters A,
342(5):404 – 412.
Barashenkov, I. V., Pelinovsky, D. E., and Zemlyanaya,
E. V. (1998). Vibrations and oscillatory instabilities
of gap solitons. Phys. Rev. Lett., 80:5117–5120.
Baratali, B. H. and Atai, J. (2012). Gap solitons in dual-core
Bragg gratings with dispersive reflectivity. J. Opt.,
14(6):065202.
Bertolotti, M., Monaco, M., and Sibilia, C. (1995). Role of
the asymmetry in a third-order nonlinear directional
coupler. Opt. Comm., 116:405–410.
Chen, Y. and Atai, J. (1995). Polarization instabilities in
birefringent fibers: A comparison between continuous
waves and solitons. Phys. Rev. E , 52:3102–3105.
Chen, Y. and Atai, J. (1998). Stability of fundamental soli-
tons of coupled nonlinear schrdinger equations. Opt.
Comm., 150:381 – 389.
Christadoulides, D. N. and Joseph, R. I. (1989). Slow Bragg
solitons in nonlinear periodic structures. Phys. Rev.
Lett., 62:1746–1749.
Dasanayaka, S. and Atai, J. (2010). Stability of Bragg grat-
ing solitons in a cubic-quintic nonlinear medium with
dispersive reflectivity. Phys. Lett. A, 375(2):225 – 229.
de Sterke, C. M. and Sipe, J. E. (1994). Gap Solitons. Prog.
Opt., 33:203–260.
Eggleton, B. J., de Sterke, C. M., and Slusher, R. E. (1997).
Nonlinear pulse propagation in bragg gratings. J. Opt.
Soc. Am. B, 14(11):2980–2993.
Islam, M. J. and Atai, J. (2015). Stability of gap solitons
in dual-core bragg gratings with cubic-quintic nonlin-
earity. Laser Phys. Lett., 12(1):015401.
Krauss, T. F. (2008). Why do we need slow light? Nature
Photon., 2:448–450.
Mak, W. C. K., Chu, P. L., and Malomed, B. A. (1998a).
Solitary waves in coupled nonlinear waveguides with
Bragg gratings. J. Opt. Soc. Am. B, 15(6):1685–1692.
Mak, W. C. K., Malomed, and Chu, P. L. (1998b).
Asymmetric solitons in coupled second-harmonic-
generating waveguides. Phys. Rev. E, 57:1092–1103.
Mandelik, D., Morandotti, R., Aitchison, J. S., and Silber-
berg, Y. (2004). Gap solitons in waveguide arrays.
Phys. Rev. Lett., 92:093904.
Monat, C., de Sterke, M., and Eggleton, B. J. (2010). Slow
light enhanced nonlinear optics in periodic structures.
J. Opt., 12:104003.
Neill, D. R. and Atai, J. (2007). Gap solitons in a hollow
optical fiber in the normal dispersion regime. Phys.
Lett. A, 367:73–82.
Nistazakis, H. E., Frantzeskakis, D. J., Atai, J., Malomed,
B. A., Efremidis, N., and Hizanidis, K. (2002). Mul-
tichannel pulse dynamics in a stabilized ginzburg-
landau system. Phys. Rev. E, 65:036605.
Russell, P. S. J. (1991). Bloch wave analysis of disper-
sion and pulse propagation in pure distributed feed-
back structures. J. Mod. Opt., 38(8):1599–1619.
Sipe, J. E. (1992). Gap Solitons, pages 305–318. Springer
Netherlands, Dordrecht.
Sipe, J. E. and Winful, H. G. (1988). Nonlinear schr
¨
odinger
solitons in a periodic structure. Opt. Lett., 13(2):132–
133.
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
22

Sterke, C. M. D., Eggleton, B. J., and Krug, P. A. (1997).
High-intensity pulse propagation in uniform gratings
and grating superstructures. J. Lightwave Technol.,
15(8):1494–1502.
Xie, P. and Zhang, Z.-Q. (2003). Multifrequency gap soli-
tons in nonlinear photonic crystals. Phys. Rev. Lett.,
91:213904.
Effect of Dispersive Reflectivity on the Stability of Gap Solitons in Dual-core Bragg Gratings with Cubic-quintic Nonlinearity
23