
Deep Learning for Radar Pulse Detection
Ha Q. Nguyen, Dat T. Ngo and Van Long Do
Viettel Research and Development Institute, Hoa Lac High-tech Park, Hanoi, Vietnam
Keywords:
Deep Neural Network, Radar Pulse Detection, Radar Pulse Parameter Estimation, Pulse Description Word,
Change Point Detection, Pruned Exact Linear Time.
Abstract:
In this paper, we introduce a deep learning based framework for sequential detection of rectangular radar
pulses with varying waveforms and pulse widths under a wide range of noise levels. The method is divided
into two stages. In the first stage, a convolutional neural network is trained to determine whether a pulse
or part of a pulse appears in a segment of the signal envelop. In the second stage, the change points in the
segment are found by solving an optimization problem and then combined with previously detected edges to
estimate the pulse locations. The proposed scheme is noise-blind as it does not require a noise floor estimation,
unlike the threshold-based edge detection (TED) method. Simulations also show that our method significantly
outperforms TED in highly noisy cases.
1 INTRODUCTION
The detection of radar pulses—or the estimation of
the times of arrival (TOAs) and the times of departure
(TODs)—plays a central role in passive location sys-
tems as it provides input for other algorithms to locate
the emitter (Torrieri, 1984; Poisel, 2005). This is a
challenging task since radar pulses are modulated and
coded with a variety of waveforms and most of the
time buried in noise. Existing methods for radar pulse
detection are usually threshold-based (Torrieri, 1974;
Iglesias et al., 2014) in which the thresholds are deter-
mined via an estimation of the noise statistics. These
methods work well with high or moderate Signal-to-
Noise-Ratios (SNRs) but perform poorly with low
SNRs. Furthermore, the noise floor estimation—a
prerequisite of these algorithms—is itself a hard prob-
lem, especially in highly varying environments.
In the past few years, Deep Learning (LeCun
et al., 2015; Goodfellow et al., 2016) has proved
a powerful tool for many tasks in computer vi-
sion and signal processing, notably, image classifica-
tion (Krizhevsky et al., 2012; Szegedy et al., 2015; He
et al., 2016) and object detection (Ren et al., 2017;
Redmon et al., 2016; Liu et al., 2016). Motivated
by these successes, we propose a novel method for
radar pulse detection in which edges are sequentially
estimated from segments of the received signal en-
velop via a deep-learning-based segment classi-
fication followed by a find-change-points algorithm
(Killick et al., 2012). The segment classification es-
sentially determines if a pulse is present, partially
present, or absent in a segment through a Convo-
lutional Neural Network (CNN). For a segment of
small-enough length, it can only fall into one of the
5 categories: ‘2 edges’, ‘TOA only’, ‘TOD only’, ‘All
pulse’, and ‘All noise’. Based on the output of the
CNN, the find-change-points routine seeks edges in
the segment by minimizing a cost function associated
to the number of edges, instead of a thresholding pro-
cedure. This approach is therefore able to get rid of
the unreliable noise floor estimation. The contribu-
tions of our paper are summarized as follows.
A novel CNN architecture for segment classifica-
tion.
An algorithm for adaptive segment classification
in which the CNN predicts the class of the current
segment based on the confidence of its previous
prediction.
An algorithm for sequential pulse localization
that combines the segment classification with
a find-change-points algorithm. This method
significantly surpasses the performance of the
Threshold-based Edge Detection (Iglesias et al.,
2014), especially in the low-SNR regimes.
The rest of the paper is outlined as follows: Sec. 2
formulates the problem. Sec. 3 constructs the CNN
and integrates it into an adaptive algorithm for seg-
ment classification. Sec. 4 presents the main algo-
32
Nguyen, H., Ngo, D. and Do, V.
Deep Learning for Radar Pulse Detection.
DOI: 10.5220/0007253000320039
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 32-39
ISBN: 978-989-758-351-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

rithm for sequential pulse localization. Sec. 5 reports
some numerical results. Finally, Sec. 6 provides con-
cluding remarks.
2 PROBLEM FORMULATION
In this paper, we are interested in the detection
of radar pulses in a narrow bandwidth of, say,
78.125 MHz, centered at frequency 0.
1
Assuming
Nyquist sampling, we acquire a discrete-time cor-
rupted signal
ˆx[n] = x[n] + w[n], n ∈ Z, (1)
where x is a complex-valued signal that contains a
train of rectangular pulses and w is an additive white
Gaussian noise (AWGN). Note that, each sample of
the discrete-time signal then corresponds to a period
of 12.8 ns. The pulses might have various wave-
forms and pulse widths. We consider in this pa-
per 7 types of pulse modulations that are commonly
used in modern radar systems (Levanon and Moze-
son, 2004; Richards, 2014; Pace, 2009), namely, Con-
tinuous Waveform (CW), Step Frequency Modulation
(SFM), Linear Frequency Modulation (LFM), Non-
Linear Frequency Modulation (NLFM), Costas code
(COSTAS), Barker code (BARKER), and Frank code
(FRANK). See Fig. 1 for an illustration of these mod-
ulations. The pulse widths vary in an extremely large
range from about 0.1 µs to about 400 µs, which corre-
sponds to a range from 8 samples to 31250 samples.
The location of each pulse is characterized by
the time of arrival (TOA)—the middle of the rising
edge—and the time of departure (TOD)—the middle
of the falling edge. Our task is to estimate the series
of TOAs and TODs in an sequential manner by look-
ing at one segment of the noisy signal ˆx at a time. To
reduce the effect of noise, we perform a preprocess-
ing step in which a lowpass filter h of bandwidth 20
MHz is applied to ˆx to get
ˆx
f
= h ∗ ˆx = h ∗ x + h ∗ w =: x
f
+ w
f
, (2)
where w
f
is now a color Gaussian noise. Our detec-
tion algorithm takes as input sequential segments of
the envelop (or magnitude) | ˆx
f
| and outputs a list of
pulse description words (PDWs), each of which con-
sists of a TOA and a TOD of the corresponding pulse.
This is done via a CNN-based adaptive classification
of the segments followed by a find-change-points al-
gorithm that will be described in the next sections.
1
In practice, the detection of radar pulses would involve
a frequency tuning from wide band to narrow band. This
crucial step is out of the scope of this paper and will be
discussed elsewhere.
0 5 10 15 20 25
Time (us)
0
0.2
0.4
0.6
0.8
1
(a) CW
0 5 10 15 20 25
Time (us)
0
0.2
0.4
0.6
0.8
1
(b) SFM
0 5 10 15 20 25
Time (us)
0
0.2
0.4
0.6
0.8
1
(c) LFM
0 5 10 15 20 25
Time (us)
0
0.2
0.4
0.6
0.8
1
(d) NLFM
0 5 10 15 20 25
Time (us)
0
0.2
0.4
0.6
0.8
1
(e) COSTAS
0 5 10 15 20 25
Time (us)
0
0.2
0.4
0.6
0.8
1
(f) BARKER
0 5 10 15 20 25
Time (us)
0
0.2
0.4
0.6
0.8
1
(g) FRANK
Figure 1: Envelops of 7 modulation types of rectangu-
lar pulses without noise. What shown here are the results
achieved after the 20-MHz-lowpass filtering.
3 CNN-BASED SEGMENT
CLASSIFICATION
From a practical point of view, we can reasonably as-
sume that the distance between consecutive pulses is
at least 30 µs, which is equivalent to about 2344 sam-
ples. Therefore, we choose to divide the envelop | ˆx
f
|
into segments of k = 2000 samples with 50% overlap-
ping.
2
This is to make sure that there will be at most
one pulse in a segment. Then, each segment can only
fall into one of the following 5 classes.
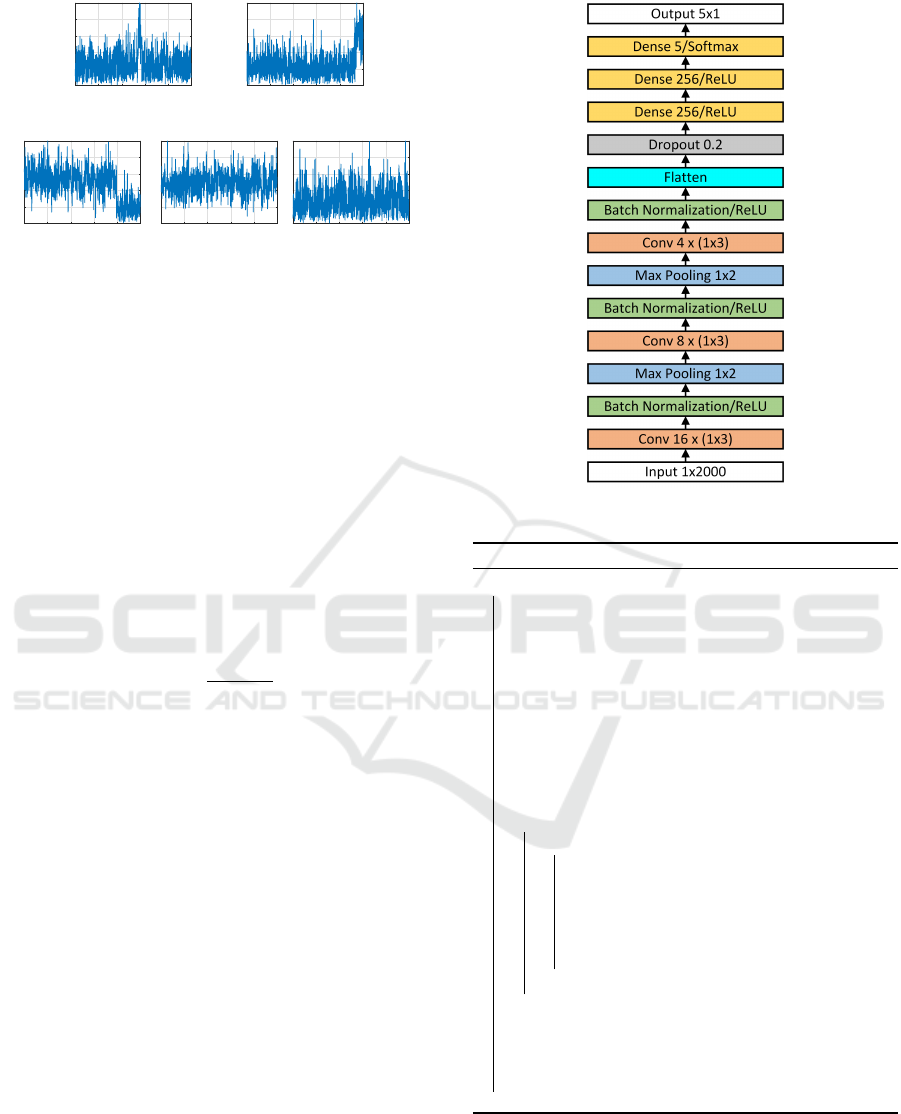
• Class 1 (‘2 edges’): a TOA and a TOD of a pulse
both appear in the segment.
• Class 2 (‘TOA only’): a TOA appears in the seg-
ment without TOD.
• Class 3 (‘TOD only’): a TOD appears in the seg-
ment without TOA.
• Class 4 (‘All pulse’): the whole segment is part of
a long pulse.
• Class 5 (‘All noise’): the segment contains only
background noise.
Fig. 2 depicts these classes under a relatively low
SNR. To perform the segment classification, we pro-
pose a Convolutional Neural Network (CNN) whose
architecture is shown in Fig. 3. This network consists
of 13 hidden layer, including 3 convolution layers and
3 dense layers. Each convolution layer is followed
2
In general, the segment length should be chosen to be
equal to the minimum distance between consecutive pulses.
Deep Learning for Radar Pulse Detection
33
0 5 10 15 20 25
Time (us)
0
0.2
0.4
0.6
0.8
1
(a) 2 edges
0 5 10 15 20 25
Time (us)
0
0.2
0.4
0.6
0.8
1
(b) TOA only
0 5 10 15 20 25
Time (us)
0
0.2
0.4
0.6
0.8
1
(c) TOD only
0 5 10 15 20 25
Time (us)
0
0.2
0.4
0.6
0.8
1
(d) All pulse
0 5 10 15 20 25
Time (us)
0
0.2
0.4
0.6
0.8
1
(e) All noise
Figure 2: The 5 classes of segments of the signal envelop
for SNR = 7dB at bandwidth 20 MHz.
by a batch normalization, which helps eliminate the
internal covariate shift problem (Ioffe and Szegedy,
2015). Two max pooling layers are also inserted to
reduce the number of features by a factor of 4 after
the first two convolutions. That results in a vector of
the same length as the input (2000) right after the flat-
ten layer. A dropout layer with dropping ratio 0.2 is
then added to avoid over-fitting. We use the Rectified
Linear Unit (ReLU) as the activation function in all
layers except for the last dense layer where the soft-
max function is applied to produce a score vector of
the 5 classes. Note that, before feeding a segment s to
the CNN, we normalize it according to
s
norm
[n] =
s[n]
max
i
s[i]
,∀n. (3)
It is remarkable that the classes of the segments
are not independent of each other. Specifically, the
following rules must hold:
• ‘2 edges’ cannot be followed by ‘All pulse’
• ‘TOA only’ cannot be followed by ‘All noise’
• ‘TOD only’ cannot be followed by ‘All pulse’
• ‘All pulse’ must be followed by ‘TOD only’ or
‘All pulse’
• ‘All noise’ cannot be followed by either ‘TOD
only’ or ‘All pulse’.
Putting these observations together, we devise an al-
gorithm for adaptive segment classification. In this
method, the current prediction and confidence are
computed from the CNN and the previous prediction
if the previous confidence is above some threshold
T ; otherwise, the CNN makes a prediction as nor-
mal. The confidence of a prediction is nothing but the
score of the predicted class. In experiments, we al-
ways choose the confidence threshold to be T = 0.7.
The pseudocode for this algorithm is provided in Al-
gorithm 1.
Figure 3: Architecture of the classification network.
Algorithm 1: Adaptive Classification.
function AdaptClass(s,net, clPr,c f Pr,T )
input : A segment s, classification model net,
previous class cl Pr, previous
confidence c f Pr, confidence threshold
T
output: A class cl and a confidence c f
// predict using pretrained net
score ← net.predict(s);
// check previous confidence
if c f Pr < T then I ← {1,2,3,4,5};
else // restrict the score vector
switch clPr do
case 1 I ← {1, 2, 3, 5};
case 2 I ← {1, 2, 3, 4};
case 3 I ← {1, 2, 3, 5};
case 4 I ← {3, 4};
case 5 I ← {1, 2, 5};
endsw
end
cl ← argmax
i∈I
(score[i]);
c f ← score[cl];
return cl,c f ;
end function
4 PULSE LOCALIZATION
Based on the outputs of the adaptive segment
classification, we sequentially perform the estima-
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
34

tion of TOAs and TODs via two find-change-
point functions denoted by FindChangePts(s, 1) and
FindChangePts(s,2). Specifically, for a segment s of
length k, the function FindChangePts(s, 1) returns a
single point p
∗
∈ {1,2,...,k − 1} that minimizes the
cost function
C (p) = p Var(s
1:p
) + (k − p)Var(s
p+1:k
), (4)
where Var(s
m:n
) denotes the variance of the se-
quence {s[i]}
m≤i≤n
. Similarly, the function
FindChangePts(s,2) returns two points p
∗
1
and
p
∗
2
that minimize the cost function
C (p
1
, p
2
) = p
1
Var(s
1:p
1
) + (p
2
− p
1
)Var(s
p
1
+1:p
2
)
+ (k − p
2
)Var(s
p
2
+1:k
). (5)
These optimization problems can be efficiently solved
by using the Pruned Exact Linear Time (PELT) (Kil-
lick et al., 2012), which is a speed-up version of the
optimal partition method (Jackson et al., 2005).
Once the TOAs and TODs are estimated, overlap-
ping or nearby pulses must be merged into a single
one. In particular, if the difference between the cur-
rent TOA and the previous TOD is less than some
minimum distance d, we update the previous TOD to
the current TOD and discard the current pulse. The
whole procedure for sequential pulse localization is
described in Algorithm 2.
5 SIMULATIONS
In this section, we provide some numerical results for
the detection of simulated radar pulses. We generated
all data and implemented Algorithms 1 and 2 in Mat-
lab 2018a running on PC with an Intel Core i7-7700
CPU @ 3.6 GHz. To realize the find-change-points
algorithm, we invoked the Matlab built-in function
findchangepts. The training of the classification
network was implemented in Python with Keras li-
brary and Tensorflow backend running on an Nvidia
Tesla P100 GPU. The trained Keras model was then
imported and run in Matlab via the Neural Network
Toolbox.
5.1 Training the Classification Net
We trained the classification net using 500,000 train-
ing examples, each of which is a segment of 2000
samples randomly truncated from a longer signal with
a single rectangular pulse. Each pulse is randomly
generated with one of the 7 modulation types in
Fig. 1, with a pulse width in the range from 0.1 µs to
400 µs, and with an SNR (at bandwith 20 MHz) in
the range from 0 dB to 30 dB. To guarantee that the
Algorithm 2: Sequential Pulse Localization.
input : An envelop env, segment length k, overlap
length m, classification model net,
confidence threshold T , minimum pulse
distance d
output: A list of PDWs with TOA and TOD
attributes
Initialize an empty list PDW;
idx ← 0; start ← 1; stop ← k;
c f = 0; cl = 1;
while stop ≤ Length(env) do
// extract a segment
s = env[start : stop] ;
// classify the segment
[cl, c f ] ← AdaptClass(s,net, cl, c f ,T );
// Find change points
switch class do
case 1
[toa,tod] ← FindChangePts(s,2);
case 2
toa ← FindChangePts(s, 1);
tod ← k;
case 3
toa ← 1;
tod ← FindChangePts(s, 1);
case 4
toa ← 1; tod ← k;
end
endsw
// convert to global coordinates
toa ← toa + start − 1;
tod ← tod + start − 1;
if idx = 0 then
idx ← idx + 1;
PDW (idx).TOA ← toa;
PDW (idx).TOD ← tod;
end
else
if toa − PDW(idx).T OD < d then
// Update TOD
PDW (idx).TOD ← tod;
end
else
idx ← idx + 1;
PDW (idx).TOA ← toa;
PDW (idx).TOD ← tod;
end
end
start ← stop − m + 1;
stop ← start + k − 1;
end
Deep Learning for Radar Pulse Detection
35
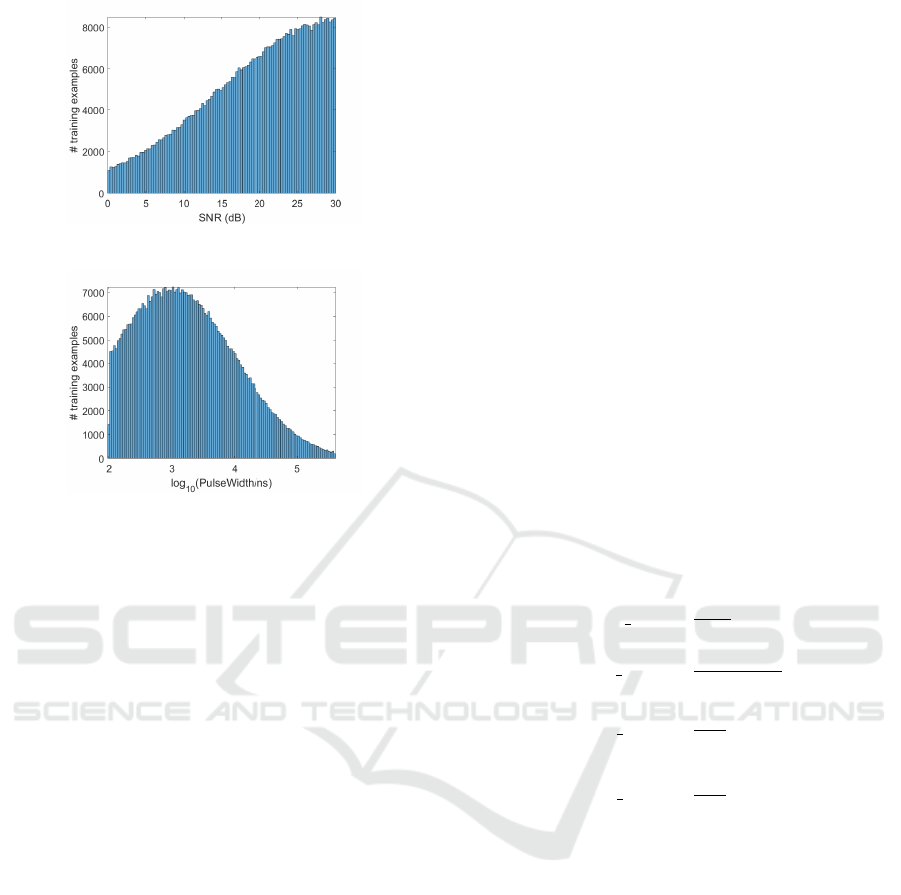
Figure 4: Distribution of the number of training examples
with respect to SNR level.
Figure 5: Distribution of the number of training examples
with respect to pulse width in logarithmic scale.
classification accuracy would increase with SNR, we
generated each noisy signal with an SNR drawn from
a truncated normal distribution rather than a uniform
distribution, as shown in Fig. 4. As the range of the
pulse widths is too large compared to the length of a
segment, we chose to draw each pulse width from a
truncated normal distribution in the logarithmic scale,
as shown in Fig. 5. Furthermore, to reduce the number
of false alarms in later detection, too-short pulses with
too-low SNRs were excluded from the training set.
More precisely, we restricted the range of the pulse
widths to [PW
min
,PW
max
] where PW
max
= 400µs and
PW
min
is dependent on SNR as
PW
min
(SNR) = max{2 × 10
−SNR/10
, 0.1} (µs).
For instance, PW
min
= 2µs for SNR = 0 dB, PW
min
≈
0.4µs for SNR = 7 dB, PW
min
= 0.1 µs for all SNR ≥
13 dB, and so on.
For the purpose of testing the classification net,
we also simulated a testing set of 125,000 examples
using the same procedure as that of the training set.
The classification net was trained via Adam optimizer
with a learning rate of 10
−4
for 100 epochs with a
batch size of 256. After being trained for about half
an hour, the classification net yields an accuracy of
99.47% on the training set and of 99.18% on the test-
ing set. The confusion matrices are plotted in Fig. 6.
5.2 Pulse Detection Results
To test the whole detection procedure, we run Algo-
rithm 2 on a sequence of N
true
= 10,000 randomly
generated pulses under different SNR levels. The
intervals between consecutive pulses are fixed to be
6,000 samples. It is noteworthy that, in contrast to
training the classification net, we generated the pulse
widths in the fixed range [0.1µs, 400 µs] regardless of
the SNR level.
Let us denote the list of ground-truth TOAs and
TODs by {(a
i
,d
i
)}
N
true
i=1
and the list of estimated TOAs
and TODs by {( ˆa
i
,
ˆ
d
i
)}
N
est
i=1
. A pulse (a
i
,d
i
) is called
detected if there exists j ∈ {1, 2, . . . , N
est
} such that
|a
i
− ˆa
j
| < 200 ns. (6)
By a renumbering, suppose the set of detected pulses
is {(a
i
,d
i
)}
N
det
i=1
, which is matched by the subset
{( ˆa
i
,
ˆ
d
i
)}
N
det
i=1
of estimated pulses. The remaining
pulses, {( ˆa
i
,
ˆ
d
i
)}
N
est
i=N
det
+1
, are considered false alarms.
The detection performance of the proposed algorithm
is then measured by 4 numbers: the detection rate,
the F1 score, the TOA mean absolute error (MAE),
and the TOD MAE. In particular, these parameters are
computed as
Detection Rate =
N
det
N
true
, (7)
F1 Score =
2N
det
N
true
+ N
est
, (8)
TOA MAE =
1
N
det
N
det
∑
i=1
|a
i
− ˆa
i
|, (9)
TOD MAE =
1
N
det
N
det
∑
i=1
|d
i
−
ˆ
d
i
|. (10)
Note that the detection rate measures the sensitivity
of the algorithm while the F1 score balances the true
detection rate and the false alarm rate.
As a baseline, we also implemented the
Threshold-based Edge Detection (TED) algo-
rithm (Iglesias et al., 2014) in Matlab with some
modifications to optimize the performance for the
data of interest. The variance of the noise was
estimated using the first 2000 samples of the signal,
which were known to be all of noise. The detection
performances of the two algorithms on the same set of
testing signals under various SNR levels are reported
in Table 1. It can be seen that the proposed method
significantly outperforms TED in all measures for
low SNR levels. For example, in the fairly noisy
case when SNR = 6 dB, the proposed scheme boosts
the F1 score from 46.87% to 85.03%. In high-SNR
regimes, we are on par with TED in terms of the
detection rate and the F1 score while surpass TED in
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
36

Table 1: Performance comparison between the proposed method and the Threshold-based Edge Detection (TED) for different
SNR levels at the bandwidth of 20 MHz.
Detection Rate F1 Score
TOA MAE
(ns)
TOD MAE
(ns)
SNR = 15 dB
TED 99.14% 99.51% 19 27
Ours 99.24% 99.43% 10 16
SNR = 12 dB
TED 98.37% 99.03% 22 35
Ours 97.99% 98.72% 16 19
SNR = 9 dB
TED 89.62% 92.52% 42 135
Ours 92.19% 95.14% 28 45
SNR = 6 dB
TED 52.81% 46.87% 75 2538
Ours 78.39% 85.03% 44 180
SNR = 3 dB
TED 9.99% 5.13% 92 13791
Ours 53.29% 62.66% 59 1331
SNR = 0 dB
TED 2.23% 1.84% 100 17404
Ours 24.79% 32.72% 75 3539
Accuracy: 99.47%
99.1%
168319
0.1%
128
0.1%
89
0.0%
0
0.8%
1384
0.1%
59
99.3%
41129
0.0%
0
0.0%
6
0.6%
244
0.2%
75
0.0%
0
99.2%
41609
0.0%
7
0.6%
260
0.1%
12
0.1%
22
0.1%
15
98.6%
17232
1.2%
202
0.0%
33
0.0%
47
0.0%
60
0.0%
0
99.9%
229068
2 edges TOA only TOD only All pulse All noise
True Label
2 edges
TOA only
TOD only
All pulse
All noise
Predicted Label
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
(a) Training
Accuracy: 99.18%
98.4%
41760
0.1%
44
0.1%
30
0.0%
1
1.4%
598
0.3%
31
98.8%
10166
0.0%
0
0.1%
7
0.8%
83
0.3%
33
0.0%
0
98.6%
10396
0.1%
6
1.0%
104
0.3%
13
0.1%
4
0.0%
2
99.1%
4528
0.5%
23
0.0%
17
0.0%
22
0.0%
9
0.0%
0
99.9%
57123
2 edges TOA only TOD only All pulse All noise
True Label
2 edges
TOA only
TOD only
All pulse
All noise
Predicted Label
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
(b) Testing
Figure 6: Confusion matrices of the classification net.
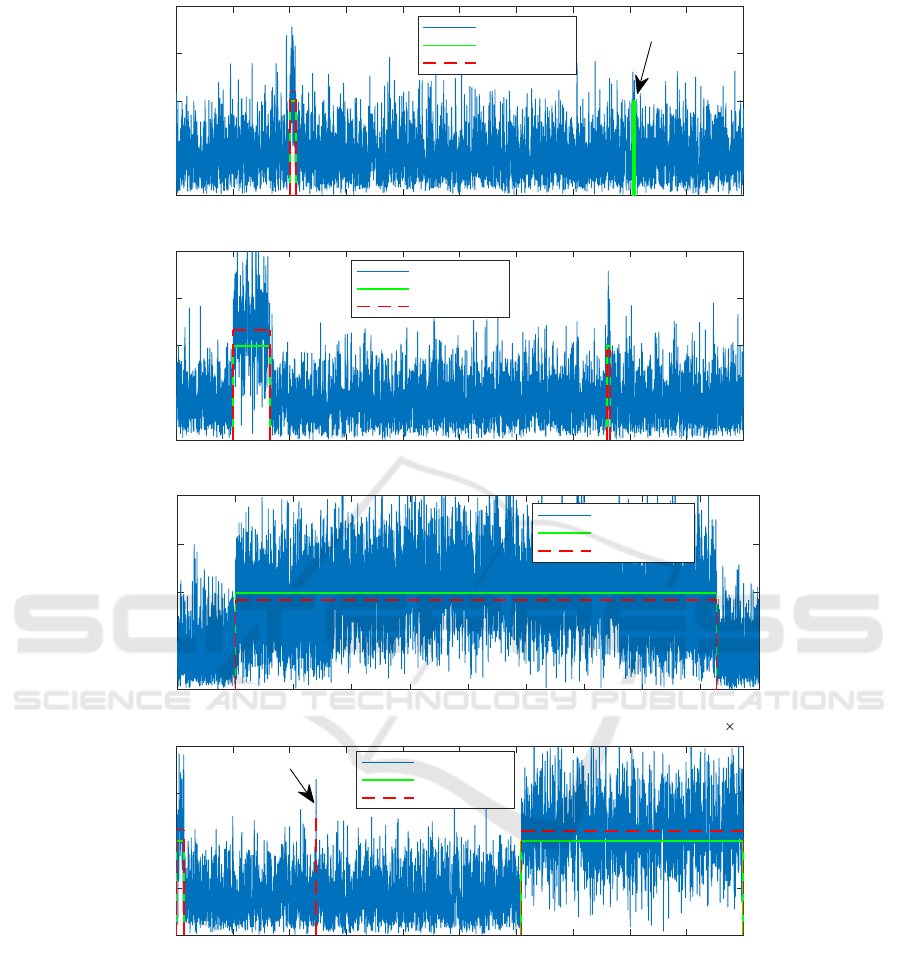
the other 2 measures. Fig. 7 visualizes the estimation
of TOAs and TODs in some parts of the testing signal
for SNR = 6 dB.
6 CONCLUSION
We have presented a deep-learning-based approach
to the detection of radar pulses with various wave-
forms over a wide range of SNRs. The proposed
scheme combines a classical find-change-points algo-
rithm with a convolutional neural network for seg-
ment classification. Informally speaking, the clas-
sification net plays a guiding role to facilitate the
find-change-points routine. Experiments on simu-
lated data suggest that our method strikingly outper-
forms the Threshold-based Edge Detection (TED) al-
gorithm, especially in low-SNR regimes. Another ad-
vantage of the proposed method is its noise-blindness,
as opposed to TED which heavily relies on a noise
floor estimation. The shortcoming of our method,
however, is its costly computations, while TED can be
implemented in FPGA for a real-time system. For the
moment, the running time of the algorithm is about
1 µs/sample, which is still far from the real-time tar-
get, 12.8 ns/sample. Future work would, therefore,
focus on reducing the computational cost of the algo-
rithm via a compression of the classification net like
what have been done in (Han et al., 2016), as well as
a more efficient implementation of the find-change-
points procedure. Another potential direction would
be replacing the find-change-points algorithm with a
deep neural network.
REFERENCES
Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep
Learning. MIT Press.
Han, S., Mao, H., and Dally, W. J. (May 02-04, 2016).
Deep compression: Compressing deep neural net-
works with pruning, trained quantization and huffman
Deep Learning for Radar Pulse Detection
37
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
Sample
0
0.5
1
1.5
2
Magnitude
Signal envelop
True Pulses
Detected Pulses
Missed
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
Sample
0
0.5
1
1.5
2
Magnitude
Signal envelop
True Pulses
Detected Pulses
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
Sample
10
4
0
0.5
1
1.5
2
Magnitude
Signal envelop
True Pulses
Detected Pulses
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
Sample
0
0.5
1
1.5
2
Magnitude
Signal envelop
True Pulses
Detected Pulses
False Alarm
Figure 7: Detection results in different parts of the noisy signal with SNR = 6 dB at bandwidth 20 MHz. For each detected
pulse, the pulse amplitude is estimated by averaging the signal magnitudes in between the estimated TOA and TOD. Misses
and false alarms are marked with arrows.
coding. In Proc. Int. Conf. Learning Representations
(ICLR), pages 1–14, Puerto Rico.
He, K., Zhang, X., Ren, S., and Sun, J. (Jun. 27-30, 2016).
Deep residual learning for image recognition. In Proc.
Conf. Comput. Vis. Pattern Recogn. (CVPR), pages
770–778, Las Vegas, NV, USA.
Iglesias, V., Grajal, J., Yeste-Ojeda, O., Garrido, M.,
S
´
anchez, M. A., and L
´
opez-Vallejo, M. (May 19-23,
2014). Real-time radar pulse parameter extractor. In
Proc. IEEE Radar Conf., pages 1–5.
Ioffe, S. and Szegedy, C. (Jul. 06-11, 2015). Batch nor-
malization: Accelerating deep network training by re-
ducing internal covariate shift. In Proc. Int. Conf.
Machine Learning (ICML), pages 1097–1105, Lille,
France.
Jackson, B., Scargle, J. D., Barnes, D., Arabhi, S., Alt, A.,
Gioumousis, P., Gwin, E., Sangtrakulcharoen, P., Tan,
L., and Tsai, T. T. (2005). An algorithm for optimal
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
38

partitioning of data on an interval. IEEE Signal Pro-
cess. Lett., 12(2):105 – 108.
Killick, R., Fearnhead, P., and Eckley, I. A. (2012). Optimal
detection of changepoints with linear computational
cost. J. Am. Stat. Assoc., 107(500):1590–1598.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (Dec. 03-
08, 2012). Imagenet classification with deep convo-
lutional neural networks. In Proc. Adv. Neural Inf.
Process. Syst. (NIPS), pages 1097–1105, Lake Tahoe,
NV, USA.
LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learn-
ing. Nature, 521:436–444.
Levanon, N. and Mozeson, E. (2004). Radar Signals.
Wiley-Interscience.
Liu, W., Anguelov, D., Erhan, D., Szegedy, C., Reed, S.,
Fu, C.-Y., and Berg, A. C. (Oct. 08-16, 2016). SSD:
Single shot multibox detector. In Proc. Eur. Conf.
Comput. Vis. (ECCV), pages 21–37, Amsterdam, The
Netherlands.
Pace, P. E. (2009). Detecting and Classifying Low Proba-
bility of Intercept Radar. Artech House, 2 edition.
Poisel, R. (2005). EW Target Location Methods. Artech
House.
Redmon, J., Divvala, S., Girshick, R., and Farhadi, A. (Jun.
27-30, 2016). You Only Look Once: Unified, real-
time object detection. In Proc. Conf. Comput. Vis. Pat-
tern Recogn. (CVPR), pages 779–788, Las Vegas, NV,
USA.
Ren, S., He, K., Girshick, R., and Sun, J. (2017). Faster
R-CNN: Towards real-time object detection with re-
gion proposal networks. IEEE Trans. Pattern Anal.
Machine Intell., 39(6):1137–1149.
Richards, M. A. (2014). Fundamental of Radar Signal Pro-
cessing. McGraw-Hill Education, 2 edition.
Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S.,
Anguelov, D., Erhan, D., Vanhoucke, V., and Rabi-
novich, A. (Jun. 07-12, 2015). Going deeper with
convolutions. In Proc. Conf. Comput. Vis. Pattern
Recogn. (CVPR), pages 1–9, Boston, MA, USA.
Torrieri, D. J. (1974). Arrival time estimation by adaptive
thresholding. IEEE Trans. Aerospace Electro. Sys-
tems, AES-10(2):178–184.
Torrieri, D. J. (1984). Statistical theory of passive location
systems. IEEE Trans. Aerospace Electro. Systems,
AES-20(2):183–198.
Deep Learning for Radar Pulse Detection
39
