Deep Learning for Pulse Repetition Interval Classiﬁcation

Ha P. K. Nguyen, Ha Q. Nguyen and Dat T. Ngo

Viettel Research and Development Institute, Hoa Lac High-tech Park, Hanoi, Vietnam

Keywords:

Pulse Repetition Intervals, PRI Modulation Classiﬁcation, Convolutional Neural Network, Deep Learning.

Abstract:

Pulse Repetition Intervals (PRI)—the distances between consecutive times of arrival of radar pulses—is an

important characteristic of the radar emitting source. The recognition of various PRI modulation types is

therefore a key task of an Electronic Support Measure (ESM) system for accurate identiﬁcation of threat

emitters. This problem is challenging due to the missing and spurious pulses. In this paper, we introduce

a deep-learning-based method for the classiﬁcation of 7 popular PRI modulation types. In this approach, a

convolutional neural network (CNN) is proposed as the classiﬁer. Our method works well with raw input

PRI sequences and, thus, gets rid of all preprocessing steps such as noise mitigation, feature extraction, and

threshold setting, as required in previous approaches. Extensive simulations demonstrate that the proposed

scheme outperforms existing methods by a signiﬁcant margin over a variety of PRI parameters, especially in

severely noisy conditions.

1 INTRODUCTION

An Electronic Support Measures (ESM) system cap-

tures radar signals from multiple sources and identi-

ﬁes the radars based on several characteristics of the

received signals. One of the most important features

of a radar signal is the sequence of pulse repetition

intervals (PRI) that consists of distances between the

times of arrival (TOAs) of consecutive radar pulses.

In modern radar technology, various types of com-

plicated PRI modulation are used rather than just a

simple constant pattern. Therefore, the recognition of

PRI modulations will greatly help identify the emit-

ting sources. This is, however, far from a trivial prob-

lem due to the unavoidable miss-detections and false

alarms of the TOAs, which might result in very noisy

PRI sequences. In addition, the diversity of parame-

ters in each type of PRI modulation makes the recog-

nition task much more challenging.

To solve the PRI modulation classiﬁcation is-

sue, extensive research has been conducted. Existing

methods can generally be divided into 3 categories:

statistics-based, decision-tree-based, and learning-

based. In the classical statistics-based methods (Mar-

dia, 1989; Milojevic and Popovic, 1992), histogram

techniques are used to recognize PRI modulation

types. Since these methods are simple, they work only

with a limited number of PRI modulation types and

their performances are drastically degraded in noisy

situations. Decision-tree based methods (Kauppi and

Martikainen, 2007; Hu and Liu, 2010; Song et al.,

2010) usually consist of three steps: ﬁrst, a noise mit-

igation technique is applied to compensate the impact

of missing and spurious pulses on the PRI sequence;

second, discriminative features are extracted from the

denoised PRI sequence; and, ﬁnally, a decision-tree is

carried out to differentiate PRI modulation types. The

main shortcoming of decision-tree-based approaches

is the requirement of heavily-handcrafted thresholds,

which are not only time-consuming but also very sen-

sitive to the level of noise and the change of PRI pa-

rameters. Existing learning-based methods for PRI

modulation classiﬁcation often rely on shallow neu-

ral networks. Noone proposed in (Noone, 1999) a

neural-network classiﬁer with a single hidden layer

that is trained on a set of the second differences of

the TOAs. More recently, Liu and Zhang introduced

in (Liu and Zhang, 2017) a feed-forward neural net-

work consisting of an input layer with 3 features de-

rived from (Noone, 1999) and a single hidden layer

of only 8 neurons. This method can only classify 4

types of PRI modulations. It is noteworthy that all

the aforementioned learning-based methods require a

careful design of features and a feature extraction pro-

cess before the neural network can be applied. This

drawback prevents these methods from quick adapta-

tion to changes in the PRI modulations.

Recently, deep learning (LeCun et al., 2015;

Goodfellow et al., 2016) has emerged as a power-

ful tool for many classiﬁcation tasks. In this paper,

Nguyen, H., Nguyen, H. and Ngo, D.

Deep Learning for Pulse Repetition Interval Classiﬁcation.

DOI: 10.5220/0007253203130319

In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 313-319

ISBN: 978-989-758-351-3

313

we introduce a novel deep-learning-based scheme in

which a deep Convolutional Neural Network (CNN)

is trained to classify 7 types of PRI modulations.

To the best of our knowledge, we are the ﬁrst to

adopt a deep learning approach to solve this prob-

lem. The main advantage of the proposed method

is that the CNN takes raw PRI sequences as input

and, therefore, bypasses the feature extraction proce-

dures as in previous approaches. Furthermore, as will

be demonstrated in simulations, our approach is very

noise-robust and effective for classifying PRI modu-

lations compared to existing methods. In particular,

for a wide range of missing and spurious pulse frac-

tions, the proposed method noticeably outperforms

the other competitors with an accuracy gap of at least

2%. This gap even increases quickly with the noise

level.

The rest of this paper is organized as follows: Sec-

tion 2 presents some preliminaries about PRI mod-

ulations; Section 3 describes the architecture of the

CNN; Section 4 evaluates the performance of the pro-

posed method on simulated data against state-of-the-

art classiﬁers; and, ﬁnally, Section 5 concludes the

paper.

2 PRI MODULATIONS

An ESM system receives radar signals and estimates

the parameters associated with each of the detected

pulses. Given a sequence of TOAs of the radar signal

{t[n]}

n=0

, where t[n] is the estimated arrival time of

the nth radar pulse and N is the number of detected

pulses, the PRI sequence is deﬁned as

p[n] = t[n +1] − t[n], n = 0,... ,N − 1. (1)

The pattern of a PRI sequence is dictated by a speciﬁc

PRI modulation type. In this paper, we consider the

following 7 PRI modulation types that are frequently

used in modern radar systems:

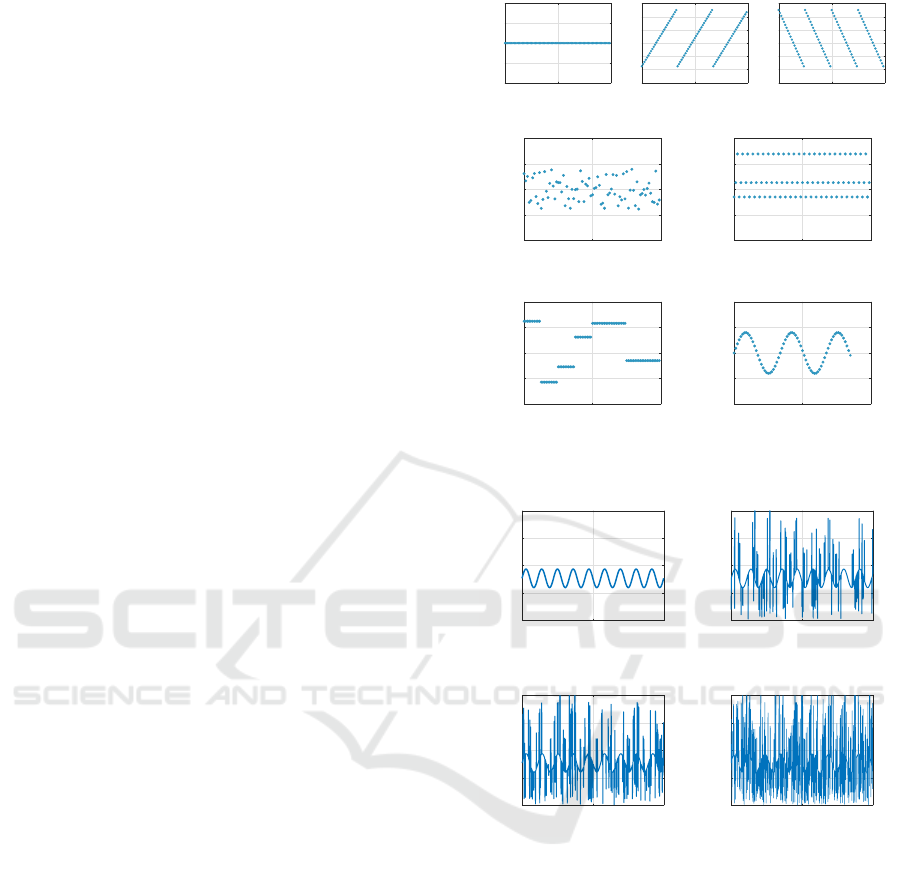
1. Constant (CST): the simplest PRI modulation in

which the pulses are equally spaced.

2. Sliding Up (SLU): the PRIs periodically linearly

increase with respect to some slope.

3. Sliding Down (SLD): the PRIs periodically lin-

early decrease with respect to some slope.

4. Jittered (JIT): the PRIs are randomized according

to a Gaussian distribution.

5. Staggered (STG): the PRIs periodically jump

through a ﬁxed number of levels.

6. Dwell & Switch (DS): piecewise-constant PRIs,

where each piece is called a burst.

0 0.05 0.1

Time (sec)

700

750

800

850

900

PRI (usec)

(a) CST

0 0.05 0.1

Time (sec)

300

400

500

600

700

800

900

PRI (usec)

(b) SLU

0 0.05 0.1

Time (sec)

300

400

500

600

700

800

900

PRI (usec)

0 0.05 0.1

Time (sec)

700

750

800

850

900

PRI (usec)

(d) JIT

0 0.05 0.1

Time (sec)

700

750

800

850

900

PRI (usec)

(e) STG

0 0.05 0.1

Time (sec)

700

750

800

850

900

PRI (usec)

(f) DS

0 0.05 0.1

Time (sec)

700

750

800

850

900

PRI (usec)

(g) WOB

Figure 1: Ideal examples of the 7 PRI modulations.

0 0.05 0.1

Time (sec)

1000

2000

3000

4000

PRI (usec)

(a) ideal

0 0.05 0.1

Time (sec)

1000

2000

3000

4000

PRI (usec)

(b) 5%

0 0.05 0.1

Time (sec)

1000

2000

3000

4000

PRI (usec)

0 0.05 0.1

Time (sec)

1000

2000

3000

4000

PRI (usec)

(d) 30%

Figure 2: A Wobulated PRI sequence with different frac-

tions of missing and spurious pulses. Each subplot from

(b) to (d) is captioned with the rate of missing and spurious

pulses.

7. Wobulated (WOB): sinusoidal PRIs.

Fig. 1 illustrates ideal examples of these PRI mod-

ulations. In practice, however, PRIs are subject to per-

turbations, miss-detections (missing pulses) and false

alarms (spurious pulses) due to the imperfection of

the TOA estimation process. The combined effect

of these errors may signiﬁcantly distort the original

form of a PRI sequence, as showed in Fig. 2, posing a

great challenge for the classiﬁcation task. A common

method for suppressing the speckle noise on PRI se-

quences is to apply median ﬁlters as a preprocessing

step. However, the choice of the ﬁlter length, which

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

314

is critical, is very sensitive to the noise level. Fur-

thermore, the median ﬁltering might destroy the pat-

tern of the PRIs, making the classiﬁcation even harder

in some cases. Also, note that existing classiﬁcation

methods rely on handcrafted features and/or thresh-

olds are that are not robust to a wide range of noise

imposed on PRI sequences. The above shortcomings

can be overcome with a deep Convolutional Neural

Network (CNN) as will be described next.

3 CNN ARCHITECTURE

We propose in this section a CNN, whose architecture

is depicted in Fig. 3, for the PRI classiﬁcation. As op-

posed to the previous neural-network schemes, the in-

put to the proposed CNN is the raw PRI sequence of

ﬁxed size 1 × 1000, supposedly obtained from a TOA

estimation algorithm. That is, both the denoising and

the feature extraction are handled by the network it-

self. This is done via a concatenation of 8 convolution

layers and 2 fully connected (dense) layers. Roughly

speaking, the convolution layers play the role of a fea-

ture extraction that is robust to noise, while the dense

layers take care of the classiﬁcation based on the out-

put of the ﬁnal convolution layer. The whole network

is trained end-to-end on a dataset of PRI sequences

labeled with ground-truth modulation types indexed

from 0 to 6. Note that before feeding a PRI sequence

p[n] to the network, we normalize it as

norm

[n] =

p[n]

max

p[i]

, ∀n. (2)

Following the design philosophy of the VGG-

net (Simonyan and Zisserman, 2015), all ﬁlters used

in the 8 convolution layers are of ﬁxed size 1 × 3,

resulting in a receptive ﬁeld of 8 × 2 + 1 = 17 sam-

ples. The number of ﬁlters is decreased from 32 to 4

along the convolution layers. Note that, in each con-

volution layer, a batch normalization is used to com-

bat the internal covariate shift as suggested in (Ioffe

and Szegedy, 2015). Moreover, the Rectiﬁed Linear

Unit (ReLU) is used as the activation function for all

convolution layers. The result of the ﬁnal convolu-

tion layer is 4 feature maps, each of size 1 × 1000,

which are then ﬂattened into a single feature vector

of length 4000. This vector is fully connected to a

layer of 256 neurons with ReLU activation. To pre-

vent over-ﬁtting, a dropout layer (Srivastava et al.,

2014) with dropping ratio of 0.7 is inserted in be-

tween these layers. Finally, the output of the Dense-

256 layer is transformed to a score vector of length

7 via the last fully connected layer with the softmax

activation function. The score vector can be thought

of as a probability distribution of the 7 classes.

The network weights are trained by minimizing

a loss function deﬁned as the cross-entropy between

the output vector of the network and the one-hot vec-

tor associated with the ground-truth label of the input

PRI sequence. This optimization procedure can be re-

alized by a stochastic gradient descent algorithm. In

the testing phase, the class of an input PRI sequence

is simply determined by taking the index of the output

vector that yields the maximum score.

4 PERFORMANCE EVALUATION

In order to evaluate the performance of our CNN-

based PRI classiﬁcation, a set of 140,000 randomly

generated PRI sequences (20,000 for each modulation

type) was used for training and another set of 35,000

(5,000 for each class) was used for testing. Both train-

ing and testing data were generated randomly accord-

ing to a variety of parameters given in Table 1. It

should be noted that the training set and the testing set

are separated and different from each other. There-

fore, the testing set can be fairly used to verify the

accuracy and generalization of the proposed model.

The data generation was performed in Matlab, while

the training was implemented in Python with Keras li-

brary and TensorFlow backend, running on an Nvidia

Tesla P100 GPU. The ﬁnal CNN model was obtained

after being trained for 100 epochs with Adam opti-

mizer and with a learning rate of 10

−4

We compare CNN with 3 state-of-the-art competi-

tors including both decision-tree-based and learning-

based methods as follows:

• The proposed scheme in (Song et al., 2010): This

method is able to classify only 5 PRI modula-

tion types (DS, SLD, SLU, JIT, and WOB) by ap-

plying a decision tree on features extracted from

the symbolizations of PRI and differential PRI

sequences. Hence, we refer to this method as

Symbolization-based Decision Tree (SDT). The

thresholds used in this algorithm were carefully

chosen to optimize the classiﬁcation accuracy.

• The proposed scheme in (Noone, 1999), which

we call Transform-based Neural Network (TNN):

This learning-based method uses the second dif-

ferences of TOAs feature as the input of a feed-

forward neural-network.

• The proposed scheme in (Liu and Zhang, 2017):

This method uses a feed forward neural network

consisting of an input layer with 3 extracted fea-

tures based on the second differences of TOAs to

classify 4 PRI modulation types (WOB, JIT, DS,

and Sliding). It should be noted that in that pa-

Deep Learning for Pulse Repetition Interval Classiﬁcation

315

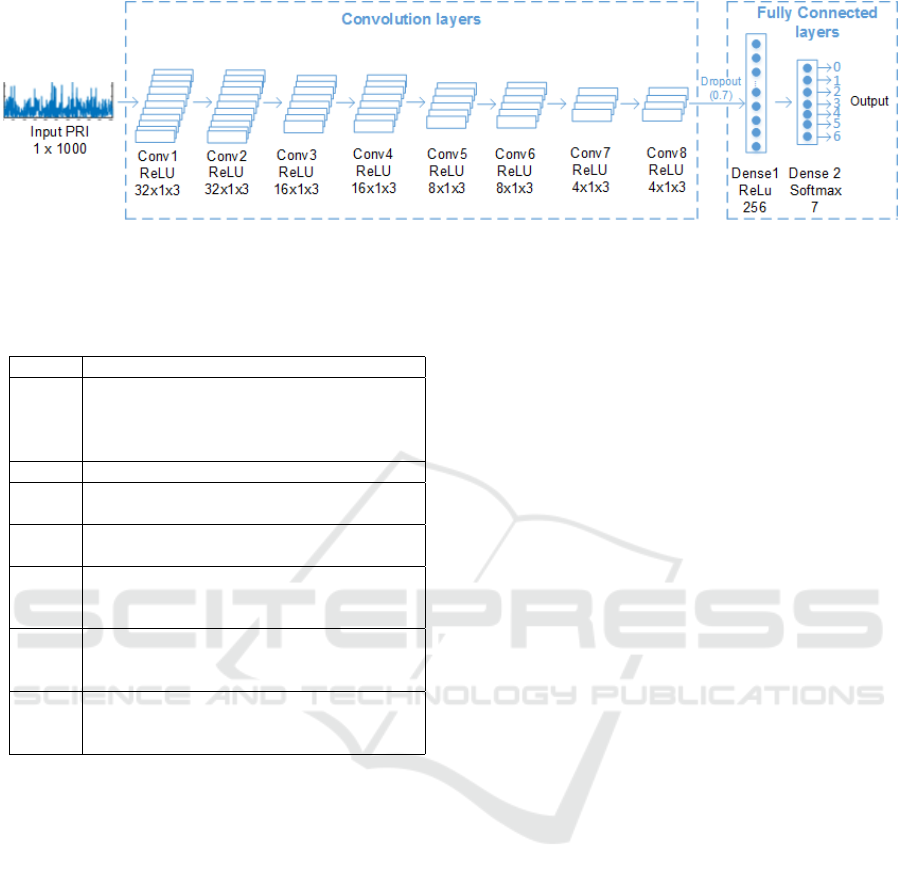
Figure 3: Architecture of the proposed CNN for PRI classiﬁcation.

Table 1: PRI parameters used in simulations. Each PRI

sequence is generated by a combination of parameters ran-

domly selected from the given ranges.

Type Parameters

All

Number of TOAs = 1001

PRI pertubation = ±(0.5 ÷ 2.0)µs

Rate of Missing pulses = (0 ÷ 30)%

Rate of Spurious pulses = (0 ÷ 30)%

CST PRI value = (50 ÷ 4000)µs

STG

PRI value = (50 ÷ 4000)µs

Number of PRI levels = (2 ÷ 10)

JIT

PRI value = (50 ÷ 4000)µs

PRI deviation = (5 ÷ 20)% of PRI value

PRI value = (50 ÷ 4000)µs

Number of bursts = (2 ÷ 10)

Burst length = (30 ÷ 120) pulses

Sliding

PRI

max

/PRI

min

ratio = (2 ÷ 6)

PRI

max

∈

{

200,600,1000, 1500,2000, 4000

}

Number of slides = (2 ÷ 10)

WOB

PRI mean value = (50 ÷ 2000)µs

PRI

max

/PRI

mean

ratio = (1.02 ÷ 1.5)

Number of periods = (2 ÷ 10)

per, the authors combined two PRI modulations,

SLU and SLD, into a single type called Slid-

ing (SL). We name this scheme Improved Feed-

forward Neural Network (IFNN).

Since TNN and IFNN are also learning-based, for

a fair comparison, they were trained on the same train-

ing dataset of CNN. The training of these two net-

works was done in Matlab with Neural Network Tool-

box. After training all the models, we used the same

testing dataset to verify the PRI classiﬁcation accu-

racy of CNN, TNN, IFNN, and SDT. The comparison

of the 4 methods was performed on a mixed dataset

of all noise levels, as well as on several datasets of

speciﬁc noise levels.

4.1 Overall Accuracy

Figs. 4, 5, and 6 show the training and testing confu-

sion matrices of CNN, TNN, and IFNN, respectively.

Since SDT is a decision-based method without any

training, we only report the confusion matrix of the

testing dataset for this scheme in Fig. 7. It can be seen

from Fig. 4 that the proposed CNN achieves a classiﬁ-

cation accuracy of 99.40% and 98.42% on the training

dataset and testing dataset, respectively. It means that

the recognition correctness of CNN is 24.42% higher

than that of a typical decision-tree-based scheme,

SDT. CNN also yields a superior performance com-

pared to TNN, which only reaches a classiﬁcation ac-

curacy of 63.35% on the testing dataset. Additionally,

comparing to a recent learning-based method, IFNN,

CNN also improves the classiﬁcation performance by

about 2%. It is worth noting that our proposed scheme

outperforms SDT and IFNN, although it should clas-

sify for many more PRI modulation classes. More-

over, by using only the raw noisy PRI sequences as

input, our method can get rid of the threshold setting

process of SDT and the preprocessing steps, such as

noise compensation and feature extraction, of TNN

and IFNN.

4.2 Accuracy with Varying Noise

In this subsection, we further investigate the effect of

missing pulse rate and spurious pulse rate on the clas-

siﬁcation performance. We tested our CNN method

against the other competitors under various noisy con-

ditions by using different datasets with varying ranges

of missing pulse rate and spurious pulse rate as fol-

lows:

• Dataset 1: Rates of missing and spurious pulses

are randomly varied from 0% to 5%;

• Dataset 2: Rates of missing and spurious pulses

are randomly varied from 5% to 10%;

• Dataset 3: Rates of missing and spurious pulses

are randomly varied from 10% to 15%;

• Dataset 4: Rates of missing and spurious pulses

are randomly varied from 15% to 20%;

• Dataset 5: Rates of missing and spurious pulses

are randomly varied from 20% to 25%;

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

316

(a) Training

(b) Testing

Figure 4: Confusion matrices of CNN on the whole testing

dataset with the rates of missing and spurious pulses ranging

from 0% to 30%.

• Dataset 6: Rates of missing and spurious pulses

are randomly varied from 25% to 30%.

Each of the above dataset contains 3000 samples for

each PRI modulation type and is generated randomly

with parameters presented in Table 1. Fig. 8 com-

pares the classiﬁcation accuracies of the 4 methods

with varying ranges of missing and spurious pulse

rate. It can be observed that TNN achieves the worst

performance. The reason is that the second differ-

ence of PRI sequence is not adequate to discrimi-

nate many complex PRI modulation types. This fea-

ture is also very sensitive with missing and spurious

pulses. In less noisy conditions, SDT performs quite

well with an accuracy greater than 90%. However, its

quality is seriously degraded when the missing and

spurious pulse rates increase. Speciﬁcally, the accu-

racy of SDT is reduced by more than 40% when the

fractions of missing and spurious pulse exceed 20%.

(a) Training

(b) Testing

Figure 5: Confusion matrices of TNN on the whole testing

dataset with the rates of missing and spurious pulses ranging

from 0% to 30%.

This observation proves that the ﬁxed thresholding

of decision-tree-based methods is very vulnerable to

noise and, thus, fails to classify the PRI modulations

over a large range of miss-detections and false alarms.

It is remarkable that CNN and IFNN signiﬁcantly

outperform SDT and TNN. When the missing and

spurious pulse rates are less than 20%, the classiﬁ-

cation accuracy of CNN and IFNN are 99.1% and

97.5% on average, respectively. Nevertheless, the

performance gap between CNN and IFNN increases

considerably with the rates of missing and spurious

pulses. For instance, CNN attains an improvement of

6% compared to IFNN when the missing and spuri-

ous pulse rates are in the range from 25% to 30%.

Again, we recall that CNN outperforms IFNN with

many more classiﬁed PRI modulation types (7 of

CNN against 4 of IFNN).

Deep Learning for Pulse Repetition Interval Classiﬁcation

317

(a) Training

(b) Testing

Figure 6: Confusion matrices of IFNN on the whole testing

dataset with the rates of missing and spurious pulses ranging

from 0% to 30%.

From the above analysis, we can conclude that our

CNN classiﬁer is able to recognize different PRI mod-

ulation types with high accuracy and is resilient to

heavily missing and spurious pulses.

5 CONCLUSION

In this paper, we have proposed a deep-learning-

based method to solve the PRI modulation classiﬁ-

cation for the ﬁrst time. We have trained a convo-

lution neural network that can efﬁciently recognize

7 PRI modulation types. The major advantage of

the proposed method is twofold. First, the input of

our classiﬁer is raw PRI sequences; thus, it can by-

pass the noise ﬁltering and the tedious calibration of

many thresholds in decision-tree-based methods, as

well as the feature extraction in previous learning-

Figure 7: Confusion matrices of SDT on the whole testing

dataset with the rates of missing and spurious pulses ranging

from 0% to 30%. Training is not needed for this method.

Figure 8: Classiﬁcation accuracies of the 4 different meth-

ods are plotted against the range of missing and spurious

rate.

based approaches. Second, in severely noisy environ-

ments with high missing and spurious pulse rates, our

scheme still achieves an impressive classiﬁcation ac-

curacy, in contrast to other methods. The simulation

results have demonstrated that our proposed method

strikingly surpasses the state-of-the-art PRI classiﬁers

on a wide range of simulation parameters. For fu-

ture research, it is worth investigating deep neural

networks for estimating the parameters associated to

each type of PRI modulation after the classiﬁcation.

REFERENCES

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep

Learning. MIT Press.

Hu, G. and Liu, Y. (2010). An efﬁcient method of pulse rep-

etition interval modulation recognition. In Proc. IEEE

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

318

Int. Conf. Commun. Mobile Comput., pages 287–295,

Shenzhen, China.

Ioffe, S. and Szegedy, C. (Jul. 06-11, 2015). Batch nor-

malization: Accelerating deep network training by re-

ducing internal covariate shift. In Proc. Int. Conf.

Machine Learning (ICML), pages 1097–1105, Lille,

France.

Kauppi, J.-P. and Martikainen, K. S. (2007). An efﬁcient

set of features for pulse repetition interval modulation

recognition. In Proc. IET Int. Conf. Radar Syst., pages

1–5, Edinburgh, UK.

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learn-

ing. Nature, 521:436–444.

Liu, Y. and Zhang, Q. (2017). An improved algorithm for

PRI modulation recognition. In Proc. IEEE Int. Conf.

Signal Process. Commun. Comput., pages 1–5, Xia-

men, China.

Mardia, H. K. (1989). New techniques for the deinterleav-

ing of repetitive sequences. IEE Proc. F Commun.

Radar & Signal Process., 136(4):149–154.

Milojevic, D. J. and Popovic, B. M. (1992). Improved algo-

rithm for the deinterleaving of radar pulses. IEE Proc.

F Commun. Radar & Signal Process., 139(1):98–104.

Noone, G. P. (1999). A neural approach to automatic pulse

repetition interval modulation recognition. In Proc.

IEEE Information, Decision and Control (IDC), pages

213–218, Phoenix, AZ, USA.

Simonyan, K. and Zisserman, A. (2015). Very deep con-

volutional networks for large-scale image recognition.

In Proc. Int. Conf. Learning Representations (ICLR),

pages 1–14, San Diego, USA.

Song, K. H., Lee, D. W., Han, J. W., and Park, B. K. (2010).

Pulse repetition interval modulation recognition using

symbolization. In Proc. IEEE Int. Conf. Digit. Im-

age Comput.: Techniques and Applications (DICTA),

pages 540–545, Sydney, NSW, Australia.

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,

and Salakhutdinov, R. (2014). Dropout: A simple

way to prevent neural networks from overﬁtting. J.

Machine Learning Research, 15(1):1929–1958.

Deep Learning for Pulse Repetition Interval Classiﬁcation

319