Cost Partitioning for Multi-agent Planning
Michal
ˇ
Stolba, Michaela Urbanovsk
´
a, Daniel Fi
ˇ
ser and Anton
´
ın Komenda
Department of Computer Science, Czech Technical University in Prague,
Karlovo n
´
am
ˇ
est
´
ı 13, 121 35, Prague, Czech Republic
Keywords:
Multi-agent Planning, Distributed Search, Distributed Heuristic Computation.
Abstract:
Similarly to classical planning, heuristics play a crucial role in Multi-Agent Planning (MAP). Especially,
the question of how to compute a distributed heuristic so that the information is shared effectively has been
studied widely. This question becomes even more intriguing if we aim to preserve some degree of privacy, or
admissibility of the heuristic. The works published so far aimed mostly at providing an ad-hoc distribution
protocol for a particular heuristic. In this work, we propose a general framework for distributing heuristic
computation based on the technique of cost partitioning. This allows the agents to compute their heuristic
values separately and the global heuristic value as an admissible sum. We evaluate the presented techniques in
comparison to the baseline of locally computed heuristics and show that the approach based on cost partitioning
improves the heuristic quality over the baseline.
1 INTRODUCTION
Modern real-world large-scale personal, corporate or
military applications often consist of multiple inde-
pendent entities. Such entities may need to cooperate
in the plan synthesis, while still wanting to protect
the privacy of their input data and internal proces-
ses. Multi-agent and privacy-preserving multi-agent
planning allow the definition of factors of the global
planning problem private to the respective entities (i.e.,
agents) in order to improve the efficiency of planning
and/or to maintain the privacy of the information.
In such privacy-preserving planning sys-
tems (Torre
˜
no et al., 2014; Nissim and Brafman, 2014;
Maliah et al., 2016; To
ˇ
zi
ˇ
cka et al., 2014), each agent
has access only to its part of the global problem, thus
can plan only using its operators. The agent can
compute a heuristic estimate from its view of the
global problem, i.e., its projection. Such projection
also contains a view of other agents’ public operators,
which allows for a heuristic estimate of the entire
problem, but such estimate may be significantly
misguided as shown in (
ˇ
Stolba et al., 2015). The
reason is that the projection does not take into account
the parts of the problem private to other agents.
Moreover in some problems, the optimal heuristic
estimate may be arbitrarily lower for the projection
than for the global problem.
To obtain a better guidance, a global heuristic es-
timate can be computed using a distributed process
while, in some cases, still preserving privacy. The ad-
missible distributed LM-Cut heuristic was proposed
in (
ˇ
Stolba et al., 2015) and in (Maliah et al., 2015),
the authors present a distributed admissible pattern
database heuristic. Recently, a distributed variant of
the class of potential heuristics has been proposed
in (
ˇ
Stolba et al., 2016a).
MAD-A* (Nissim and Brafman, 2012) and its se-
cure variant secure-MAFS (Brafman, 2015) are the
only optimal privacy-preserving multi-agent planners.
There is a number of optimal multi-agent planners not
concerning privacy (Dimopoulos et al., 2012; Jezequel
and Fabre, 2012).
All distributed heuristics published up-to-date pre-
sent ad-hoc techniques to distribute each particular
heuristic. Typically, the distributed computation of
heuristic estimate requires the cooperation of all (or
at least most of) the agents and incurs a substantial
amount of communication. In many scenarios, the
communication may be very costly (multi-robot sys-
tems) or prohibited (military) and even on high-speed
networks, communication takes significant time com-
pared to local computation. In such cases, it may pay
off to use the projected heuristic instead of its better-
informed counterpart. Most of the referenced heuris-
tics are also missing any formal treatment of privacy,
which is a nontrivial undertaking for such complex
algorithms indeed.
40
Štolba, M., Urbanovská, M., Fišer, D. and Komenda, A.
Cost Partitioning for Multi-agent Planning.
DOI: 10.5220/0007256600400049
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 40-49
ISBN: 978-989-758-350-6
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

In (Nissim and Brafman, 2014), the authors men-
tion an idea of an additive heuristic such that projected
estimates of two agents could be added together and
still maintain admissibility. In this paper, we apply
the results of research of additive heuristics, namely
the approach of cost partitioning, to the case of dis-
tribution of heuristics for multi-agent planning. This
way we obtain a fully general approach allowing us
to compute any heuristic additively in a distributed
way. Also, it allows us to combine different heuristics,
which adheres to the idea of independent agents (that
is, each agent can use the heuristic it sees most fit).
Last but not least, the presented approach allows us to
compute an admissible sum of admissible heuristics.
In classical planning, the cost partitioning is ty-
pically computed for each state evaluated during the
planning process. In privacy-preserving MAP, such
approach does not make much sense as we want to
keep the computation as local as possible. Thus, the
envisioned use of such cost partitioning is to compute
it once at the beginning of the planning process, use
the cost partitioned problems to evaluate heuristics lo-
cally and sum the local heuristics to obtain a global
estimate.
2 FORMALISM
In this section, we present the formalism used throug-
hout the paper. First of all, we define a general (that
is single-agent) planning task in the form of Multi-
Valued Planning Task (MPT) (Helmert, 2006). The
MPT is a tuple
Π =

V , O, s
I
, s

, cost

where V is a finite set of finite-domain variables, O is
a finite set of operators, s
I
is the initial state, s

is the
goal condition and cost : O 7→ R
+
0
is a cost function.
Each V in the finite set of variables V has a finite
domain of values dom(V ) . A fact
h
V, v
i
is a pair of a
variable V and one of the values v from its domain (i.e.
an assignment). Let p be a partial variable assignment
over some set of variables V . We use vars(p) ⊆ V to
denote a subset of V on which p is defined and p[V ]
to denote the value of V assigned by p . Alternatively,
p can be seen as a set of facts
{h
V, p[V ]
i
|V ∈ vars(p)
}
corresponding to that partial variable assignment. A
complete assignment over V is a state over V . A
(partial) assignment p is consistent with an assignment
p
0
iff p[V ] = p
0
[V ] for all V ∈ vars(p).
An operator o from the finite set O has a precon-
dition pre(o) and effect eff(o) which are both partial
variable assignments. An operator o is applicable in
a state s if pre(o) is consistent with s . Application of
operator o in a state s results in a state s
0
such that
all variables in eff(o) are assigned to the values in
eff(o) and all other variables retain the values from s ,
formally s
0
= o ◦ s.
A solution to MPT Π is a sequence π = (o
1
, ..., o
k
)
of operators from O (a plan), such that o
1
is applica-
ble in s
I
= s
0
, for each 1 ≤ l ≤ k , o
l
is applicable in
s
l−1
and s
l
= o
l
◦ s
l−1
and s
k
is a goal state (i.e., s

is
consistent with s
k
).
Similarly as MA-STRIPS (Brafman and Domshlak,
2008) is an extension of STRIPS (Fikes and Nilsson,
1971) towards privacy and multi-agent planning, MA-
MPT is a multi-agent extension of the Multi-Valued
Planning Task. For n agents, the MA-MPT problem
M = {Π
i
}
n
i=1
consists of a set of n MPTs. Each MPT
for an agent α
i
∈ A is a tuple
Π
i
=
D
V
i
= V
pub
∪ V
priv
i
, O
i
= O
pub
i
∪ O
priv
i
, s
Bi
I
, s
Bi

, cost
i
E
where V
priv
i
is a set of private variables, V
pub
is a set
of public variables shared among all agents V
pub
∩
V
priv
i
=
/
0 and for each i 6= j , V
priv
i
∩ V
priv
j
=
/
0 and
O
i
∩ O
j
=
/
0.
All variables in V
pub
and all values in their re-
spective domain are public, that is known to all agents.
All variables in V
priv
i
and all values in their respective
domains are private to agent α
i
which is the only agent
aware of such V and allowed to modify its value.
A global state is a state over V
G
=
S
i∈1..n
V
i
. A
global state represents the true state of the world, but
no agent may be able to observe it as a whole. Instead,
each agent works with an i -projected state which is
a state over V
i
such that all variables in V
G
∩ V
i
are equal in both assignments (the assignments are
consistent).
The set O
i
of operators of agent α
i
consists of pri-
vate and public operators such that O
pub
i
∩ O
priv
i
=
/
0 . The precondition pre(o) and effect eff(o) of pri-
vate operators o ∈ O
priv
i
, are partial assignments over
V
priv
i
, whereas in the case of public operators o ∈
O
pub
i
the assignment is over V
i
and either pre(o) or
eff(o) assigns a value to at least one public variable
from V
pub
. Because V
pub
is shared, public operators
can influence (or be influenced by) other agents. The
function cost
i
: O
i
7→ R
+
0
assigns a cost to each opera-
tor of agent α
i
. The initial state s
I
and the partial goal
state s

(partial variable assignment over V
G
) are in
each agent’s problem represented only as i -projected
(partial) states.
We define a global problem (MPT) as a union of
the agent problems, that is
Π
G
=
*
[
i∈1..n
V
i
,
[
i∈1..n
O
i
, s
I
, s

, cost
G
+
Cost Partitioning for Multi-agent Planning
41

where cost
G
is a union of the cost functions cost
i
. The
global problem is the actual problem the agents are
solving.
An i -projected problem is a complete view of agent
α
i
on the global problem Π
G
. The i -projected problem
of agent α
i
contains i -projections of all operators of all
agents. Formally, an i -projection o
i
of o ∈ O
i
is o . For
a public operator o
0
∈ O
pub
j
of some agent α
j
s.t. j 6= i ,
an i -projected operator o
0i
is o
0
with precondition and
effect restricted to the variables of V
i
, that is pre(o
0i
)
is a partial variable assignment over V
i
consistent with
pre(o
0
) ( eff(o
0
) treated analogously). An i -projection
of a private operator o
00
∈ O
priv
j
s.t. j 6= i is o
00i
= ε ,
that is a no-op action with cost
i
(o
00i
) = cost
i
(ε) = 0 .
The cost of i -projection of o
00
∈ O
pub
j
is preserved,
formally cost
i
(o
i
) = cost
j
(o).
The set of i-projected operators is
O
i
= {o
i
|o ∈
[
j∈1...n
O
j
}
and an i-projected problem is
Π
i
=

V
i
, O
i
, s
Bi
I
, s
Bi

, cost
i

The set of all i -projected problems is then M

=
{Π
i
}
n
i=1
.
2.1 Example
Here we present a small running example with two
agents α
1
and α
2
. The problems Π
1
and Π
2
of agents
α
1
and α
2
are:
agent: α
1
α
2
V
pub
= {V
3
∈ {u, g}}
V
priv
i
= {V
1
∈ {i
1
, p
1
}} {V
2
∈ {i
2
, p
2
}}
O
pub
i
= {b
1
} {b
2
}
O
priv
i
= {a
1
} {a
2
}
s
Bi
I
=
h
V
1
, i
1
i
,
h
V
3
, u
i h
V
2
, i
2
i
,
h
V
3
, u
i
s
Bi

=
h
V
3
, g
i h
V
3
, g
i
where the actions a
1
, b
1
and a
2
, b
2
are:
a pre(a) eff(a) cost
1
(a)
a
1
h
V
1
, i
1
i h
V
1
, p
1
i
cost
1
(a
1
) = 1
b
1
h
V
1
, p
1
i h
V
1
, i
1
i
,
h
V
3
, g
i
cost
1
(b
1
) = 2
a
2
h
V
2
, i
2
i h
V
2
, p
2
i
cost
2
(a
2
) = 1
b
2
h
V
2
, p
2
i h
V
2
, i
2
i
,
h
V
3
, g
i
cost
2
(b
2
) = 2
In addition, the actions of projected problem Π
1
are
O
1
= {a
1
1
, b
1
1
, b
1
2
} , where a
1
1
, b
1
1
are unchanged
and b
1
2
:
a pre(a) eff(a) cost
1
(a)
b
1
2
/
0
h
V
3
, g
i
cost
1
(b
1
2
) = 2
Π
G
: Π
1
:
Figure 1: a) Transition system of the global problem Π
G
respective to the example. b) Example transition system,
1-projection (abstraction).
Analogously, the actions of projected problem Π
2
are O
2
= {a
2
2
, b
2
2
, b
2
1
} , where a
2
2
, b
2
2
are unchan-
ged and b
2
1
:
a pre(a) eff(a) cost
2
(a)
b
2
1
/
0
h
V
3
, g
i
cost
2
(b
2
1
) = 2
Obviously, a global solution to the problem is
either (a
1
, b
1
) or (a
2
, b
2
) , both of cost 3 . The optimal
solution of Π
1
is (b
1
2
) with the cost of 2 and symme-
trically for Π
2
. Thus if we take the baseline approach
and maximize the two optimal costs we obtain 2 which
is a bound on the value any two admissible heuristics
can give as a maximum of projected heuristics.
2.2 Transition Systems
The set M

of all i -projected problems can be seen
as a set of abstractions of the global problem Π
G
. To
do so, we first define the transition system of an MPT
problem Π.
Definition 1. (Transition system) A transition system
of a planning task Π is a tuple T (Π) =
h
S, L, T, s
I
, S

i
,
where S =
∏
V ∈V
dom(V ) is a set of states, L is a
set of transition labels corresponding to the actions
in O and T ⊆ S × L × S is a transition relation of Π
s.t.
h
s, a, s
0
i
∈ T if a ∈ O s.t. a is applicable in s and
s
0
= a ◦ s . A state-changing transition is
h
s, a, s
0
i
∈ T
such that s 6= s
0
. The state s
I
∈ S is the initial state
and S

is the set of all goal states (that is all states s
s.t. s

is consistent with s ). The cost of a transition
h
s, a, s
0
i
∈ T is cost(a).
Next, we proceed with the definition of an ab-
straction.
Definition 2. (Abstraction) Let T =
h
S, L, T, s
I
, S

i
and T
0
=
h
S
0
, L
0
, T
0
, s
0
I
, S
0

i
be transition systems with
the same label set L = L
0
and let σ : S, S
0
. We say
that T
0
is an abstraction of T with abstraction function
(mapping) σ if
• s
0
I
= σ(s
I
),
• for all s ∈ S

also σ(s) ∈ S
0

, and
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
42

• for all
h
s, a, s
0
i
∈ T ,
h
σ(s), a, σ(s
0
)
i
∈ T
0
.
To conclude this section, we show that an i -
projection is an abstraction.
Theorem 3. (Projection is an abstraction) Let
T (Π
G
) =

S
G
,
S
i∈1..n
O
i
, T
G
, s
I
, S


be the transition
system of the global problem Π
G
and T (Π
i
) =

S
i
, O
i
, T
i
, s
i
I
, S
i


the transition system of the i -
projected problem Π
i
. Then T (Π
i
) is an abstraction
of T (Π
G
) with respect to the state-changing transiti-
ons.
Proof. We define an abstraction mapping σ
i
: S
G
, S
i
such that for a state s ∈ S
G
we define σ
i
(s) as a re-
striction of s to the variables in V
i
. Then from defi-
nition, σ
i
(s) = s
i
. From definition also s
i
I
= σ
i
(s
I
) .
If s ∈ S

then s

is compatible with s , if both are re-
stricted to V
i
, the compatibility is not violated and
thus σ
i
(s) ∈ S
i

.
For each action a ∈ O
i
and each transition
h
s, a, s
0
i
∈ T
G
there is a transition

s
i
, a
i
, s
0i

∈ T
i
as a
i
= a . For j 6= i and for each action a
0
∈ O
pub
j
and each transition
h
t, a
0
,t
0
i
∈ T
G
, there is a tran-
sition

t
i
, a
0i
,t
0i

∈ T
i
as pre(a
0i
) is pre(a
0
) re-
stricted to V
i
and t
i
is t restricted to V
i
(the same
goes for eff(a
i
) . For each action a
00
∈ O
priv
j
and
each transition
h
u, a
0
, u
0
i
∈ T
G
, there is no transition

u
i
, a
00i
, u
0i

∈ T
i
, but as both pre(a
00
) and eff(a
00
)
are defined only over V
priv
j
, u
i
= u
0i
and thus the
missing transition

u
i
, a
00i
, u
0i

∈ T
i
is a loop.
The missing loops never influence the shortest path
and thus can be ignored (or added at will).
3 COST PARTITIONING
In this section, we describe the idea of cost partitio-
ning (Katz and Domshlak, 2010) as used in classical
planning and define a novel notion of multi-agent cost
partitioning. We restrict ourselves to the non-negative
cost partitioning, where the costs of actions are not
allowed to be less than 0, but all notions and techni-
ques generalize to the case of general cost partitioning
without such restriction.
Definition 4. (Cost partitioning). Let Π be a planning
task with operators O and cost function cost . A cost
partitioning for Π is a tuple cp =
h
cp
1
, ..., cp
k
i
where
cp
l
: O → R
+
0
for 1 ≤ l ≤ k and
∑
k
l=1
cp
l
(o) ≤ cost(o)
for all o ∈ O .
As shown in (Katz and Domshlak, 2010), a sum of
admissible heuristics computed on the cost partitioned
problem is also admissible, formally
Proposition 5. (Katz and Domshlak 2010). Let Π be a
planning task, let h
1
, ..., h
k
be admissible heuristics for
Π , and let cp =
h
cp
1
, ..., cp
k
i
be a cost partitioning for
Π . Then h
cp
=
∑
k
l=1
h
l
(s) where each h
l
is computed
with cp
l
is an admissible heuristic estimate for a state
s.
Based on the particular cost partitioning cp , the
heuristic estimate can have varying quality. By opti-
mal cost partitioning (OCP) we mean a cost partitio-
ning which maximizes h
cp
. Now we proceed with the
definition of a multi-agent variant of cost partitioning,
which differs in that the partitions are defined apriori
by the set of the i-projected problems.
Definition 6. (Multi-agent cost partitioning). Let
M

= {Π
i
}
n
i=1
be the set of all i -projected problems
with respective cost functions cost
i
. A multi-agent
cost partitioning for M

is a tuple of functions cp =
h
cp
1
, ..., cp
n
i
where cp
i
: O
i
→ R
+
0
. For 1 ≤ i ≤ n and
for each o ∈ O
G
holds
∑
n
i=1
cp
i
(o
i
) ≤ cost
j
(o) where
α
j
is the owner of o, that is o ∈ O
j
.
Theorem 7. Let M

= {Π
i
}
n
i=1
be the set of all i -
projected problems, Π
G
the global problem respective
to M and cp a multi-agent cost partitioning for M

.
Then cp is a cost partitioning for Π
G
.
Proof. The theorem follows from Definition 4, Defini-
tion 6 for all public actions and from setting o
i
= ε for
all o ∈ O
priv
j
s.t. j 6= i . As cost
i
(o
i
) = cost
i
(ε) = 0
and cost
 j
(o
 j
) = cost
j
(o) , the cost partitioning pro-
perty
∑
n
i=1
cp
i
(o
i
) ≤ cost
j
(o) holds also for private
operators.
Thanks to Theorem 7 we can apply the Proposi-
tion 5 also in the multi-agent setting using a multi-
agent cost partitioning. Thus, each agent α
i
can com-
pute its part of the heuristic locally on Π
i
using cp
i
instead of cost
i
as the cost function. To obtain the
global heuristic, the individual parts can be simply
summed
h
cp
(s) =
n
∑
i=1
h
i
cp
i
(s
i
) (1)
where h
i
cp
i
is an i -projected heuristic computed on Π
i
using cp
i
. We contrast this approach to a baseline
solution which is the current state of the art. The
baseline combines individual projected heuristics by
taking the maximum, formally
h
max
(s) = max
1≤i≤n
h
i
(s
i
) (2)
where h
i
is any (admissible) heuristic computed on
Π
i
using the original cost
i
.
Cost Partitioning for Multi-agent Planning
43

4 COMPUTING MULTI-AGENT
COST PARTITIONING
To compute the optimal cost partitioning (OCP) for
i -projections, based on Theorems 3 and 7 we can re-
adily apply the results from classical planning. We
adopt the computation of optimal cost partitioning for
abstractions (Pommerening et al., 2014b) and intro-
duce a novel cost partitioning based on the potential
heuristic linear program formulation (Pommerening
et al., 2015) which we later show to be well suited to
the problem at hand.
Note that in all cost partitionings private actions are
partitioned implicitly as only their respective owners
are aware of them, formally:
cp
j
(a
 j
) =
(
cost
i
(a
i
) ifi = j
0 else
The very baseline is the uniform cost partitioning,
where
cp
j
(a
 j
) =
cost
i
(a
i
)
n
(3)
for each action a ∈ O
pub
i
and each agent α
j
∈ A .
Example. On the running example, the uniform CP
results in cp
1
(b
1
1
) = 1, cp
1
(b
1
2
) = 1 and cp
2
(b
2
1
) =
1, cp
2
(b
2
2
) = 1 . The sum of optimal costs computed
on such cost partitioning is 2.
4.1 Optimal Cost Partitioning on
Abstractions
The idea behind the following linear program (LP) is
to encode the abstract transition systems and possible
shortest paths in it. The LP variables used for each
α
i
∈ A are
¯
h
i
encoding the i -projected heuristic value
(given the cost partitioning), ¯s
0i
representing the cost
of shortest path from a state s (or actually s
i
) to s
0i
in the i -projected problem given the cost partitioning
and ¯a
i
representing the cost partitioned cost of action
a
i
∈ O
i
. The LP is formulated as follows:
Maximize
∑
n
i=1
¯
h
i
subject to
¯s
0i
= 0 foralls
0i
= s
i
¯s
00i
≤ ¯s
0i
+ ¯a
i
forall

s
0i
, a
i
, s
00i

∈ T
i
¯
h
i
≤ ¯s
0i
forall ¯s
0i
∈ s
i

∑
n
j=1
¯a
 j
≤ cost
i
(a) foralla ∈ O
pub
i
¯a
i
≤ cost
i
(a) foralla ∈ O
priv
i
(4)
where the first set of constraints sets all states equal (in
the i -projection) with the current state s to have zero
cost of shortest path. The second set of constraints en-
code the actual (abstracted) transitions and their costs
(transitions where s
0i
= s
00i
can be ignored), the third
set of constraints places an upper bound on the actual
heuristic estimate to keep it admissible. The fourth and
fifth sets of constraints represent the cost partitioning
of public and private actions respectively. As already
mentioned, private actions of agent α
i
always occur
only as i -projections and are not partitioned (i.e. any
other projection of such action has the cost of 0).
Example. Let us show how the optimal cost parti-
tioning is computed on the running example. The
global transition system is shown in Figure 1 a) and
the transition system projected to agent α
1
in Figure 1
b) (transition system projected to α
2
is symmetrical).
The LP is constructed according to Equation 4 and
the solution gives h
1
+ h
2
= 3 as the value of the ob-
jective function and
¯
b
1
1
= 1,
¯
b
2
1
= 1,
¯
b
1
2
= 2,
¯
b
2
2
= 0
as the values of (relevant) LP variables. The values
directly give the cost partitioning. When applied, the
optimal solutions of Π
1
and Π
2
has the cost of 1 and
2 respectively, which is the maximal value so that the
sum does not violate admissibility.
In contrast to the use in classical planning, we
intend to compute the cost partitioning LP only once
at the beginning of the planning process. Obviously,
this results in a possibly sub-optimal cost partitioning
for other states than the initial one.
Unfortunately, even computing such OCP once
may be intractable in general, as the i -projected pro-
blems may be as large and as hard as the global pro-
blem, e.g., in a scenario where all (or most of) actions
and variables are public. The optimal cost partitioning
can be approximated by first constructing smaller ab-
stractions out of the i -projections using some standard
technique such as Merge & Shrink (Helmert et al.,
2007).
4.2 Cost Partitioning based on Potential
Heuristic
Potential heuristics are a family of admissible heu-
ristics introduced in (Pommerening et al., 2015). As
shown in (
ˇ
Stolba et al., 2016a), the potential heuristics
are very well suited for distributed heuristic computa-
tion. In this work, we apply the LP used to compute
the potentials to derive a multi-agent cost partitioning.
We first briefly describe the original centralized ver-
sion of the potential heuristic (denoted as h
pot
) and the
LP used to compute it. A potential heuristic associates
a numerical potential with each fact. The potential
heuristic for a state s is simply a sum of potentials
of the facts in s . The potentials can be determined
as a solution to a linear program, a detailed formu-
lation is described in (Pommerening et al., 2014a).
The objective function of the LP is simply the sum of
potentials for a state (or average for a set of states).
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
44

The simplest variant is to use the initial state s
I
as the
optimization target.
For a partial variable assignment p , let
maxpot(V, p) denote the maximal potential that
a state consistent with p can have for variable V ,
formally:
maxpot(V, p) =
(
pot(
h
V, p[V ]
i
)
max
v∈dom(V )
pot(
h
V, v
i
)
ifV ∈ vars(p)
otherwise
The LP will have a potential LP-variable
pot(
h
V, v
i
) for each fact (that is each possible assign-
ment to each variable) and a maximum potential LP-
variable maxpot
V
for each variable in V . The con-
straints ensuring the maximum potential property are
simply
pot(
h
V, v
i
) ≤ maxpot
V
(5)
for all variables V and their values v ∈ dom(V ) . To
ensure goal-awareness of the heuristic, i.e., h
pot
(s) ≤ 0
for all goal states s, we add the following constraint
∑
V ∈V
maxpot(V, s

) ≤ 0 (6)
restricting the heuristic of any goal state to be less
or equal to 0 . The final set of constraints ensures
consistency. A consistent heuristic is such h that for
every two states s, s
0
and all operators s.t. s
0
= s ◦ o
holds h(s) ≤ h(s
0
) + cost(o) . Consistency together
with the goal-awareness implies admissibility. For
each operator o in a set of operators O we add the
following constraint
∑
V ∈vars(eff(o))
(maxpot(V, pre(o)) − pot(
h
V, eff(o)[V ]
i
))
(7)
≤ cost(o)
The optimization function of the LP can be set to
the sum of potentials in the initial state. A solution of
the LP yields the values for potentials which are then
used in the heuristic computation.
Example. Let us consider the running example. The
consistency constraint of the potential heuristic LP
constructed for the public action b
2
is
pot(
h
V
2
, p
2
i
) − pot(
h
V
2
, i
2
i
) + maxpot
V
3
− pot(
h
V
3
, g
i
)
≤ cost
2
(b
2
)
where cost
2
(b
2
) = 2 . For the variable V
2
we use the
potential for the precondition and the effect and for V
3
we use the maxpot
V
3
variable for the precondition as
V
3
has no value in the precondition of b
2
.
We can simply obtain a cost partitioning LP by
replacing the action costs with variables, concatenating
the respective LPs for each of the agent problems and
adding the cost partitioning constraints. There are
separate LP variables even for the potentials of public
variables for each of the agents. Let o ∈ O
pub
i
be a
public operator of α
i
, the consistency constraints from
Equation 7 for operator o are formulated as
∑
V ∈vars(eff(o))
(maxpot(V, pre(o))
Bi
−
pot(
h
V, eff(o)[V ]
i
)
Bi
) ≤ ¯o
Bi
(8)
∑
V ∈vars(eff(o
B j
))
(maxpot(V, pre(o
B j
))
B j
−
pot(
D
V, eff(o
B j
)[V ]
E
)
B j
) ≤ ¯o
B j
∀ j 6= i (9)
n
∑
k=1
¯o
Bk
≤ cost
i
(o)
(10)
where maxpot(V, v)
Bk
and pot(
h
V, v
i
)
Bi
represent the
LP variables respective to agent α
k
. Note that in the
case of projected operators o
B j
, the set vars(eff(o
B j
))
contains only public variables. The cost partitioning
LP can also be seen as a set of n individual potential
heuristic LPs which are interconnected only by the
cost partitioning variables ¯o
Bk
and the respective CP
constraint. Also, the optimization function can be con-
structed simply as a sum of the individual optimization
functions.
A significant advantage of the potential-based CP
over the abstraction-based OCP is that it is computa-
tionally tractable as the whole transition system does
not have to be constructed. Moreover, the distributed
LP computation techniques from (
ˇ
Stolba et al., 2016a)
can be used in the case of the potential-based CP as
well.
Example. The action b
2
will then be represented by
two consistency constraints, one for b
2
in the context
of Π
1
and one for b
B2
2
in the context of Π
B2
. The
constraints for b
2
(including the cost partitioning con-
straint) are as follows.
pot(
h
V
2
, p
2
i
)
2
− pot(
h
V
2
, i
2
i
)
2
+
maxpot
2
V
3
− pot(
h
V
3
, g
i
)
2
≤
¯
b
2
2
maxpot
1
V
3
− pot(
h
V
3
, g
i
)
1
≤
¯
b
1
2
¯
b
1
2
+
¯
b
2
2
≤ cost
2
(b
2
)
where cost
2
(b
2
) = 2 . Other constraints are formu-
lated analogously. There are multiple possibilities for
the optimization function, if we base the function on
the initial state, we obtain the following one:
Cost Partitioning for Multi-agent Planning
45

Maximize :
pot(
h
V
1
, i
1
i
)
1
+ pot(
h
V
2
, i
2
i
)
2
+
pot(
h
V
3
, u
i
)
1
+ pot(
h
V
3
, u
i
)
2
The resulting cost partitioning is
¯
b
1
1
= 1,
¯
b
2
1
=
1,
¯
b
1
2
= 2,
¯
b
2
2
= 0 which gives h
1
+ h
2
= 3 , that is,
the same value as the optimal cost partitioning based
on abstractions.
5 SEARCH WITH
AGENT-ADDITIVE
HEURISTICS
In this work, we aim to provide a general technique for
additive heuristic computation in multi-agent planning.
By additive we mean that each part of the heuristic can
be computed by each respective agent separately an
then added together.
Definition 8. (Agent-additive heuristic) A global
heuristic h estimating the global problem Π
G
is
agent-additive iff for any agent α
i
∈ A it can be
represented as
h(s) = h
pub
(s
B
) +
∑
α
j
∈A
h
j
(s
B j
)
where h
pub
is a heuristic computed on the public pro-
jection problem Π
B
and h
j
is a heuristic computed on
the j-projected problem Π
B j
.
A heuristic is agent-additive even without the pu-
blic part, that is, if h
pub
(s
B
) = 0 for all states, which
is the case of the heuristic computed on multi-agent
cost partitioning defined in Equation 1.
Theorem 9. Let M

= {Π
i
}
n
i=1
be the set of all i -
projected problems, Π
G
the global problem respective
to M and cp a multi-agent cost partitioning for M

.
Then the heuristic h
cp
(s) (Equation 1) is agent-additive
(Definition 8).
Proof. Follows trivially from Definition 8 by having
the public part equal to zero, that is, h
pub
(s
B
) for all i
and all states.
In the rest of this section, we show how the agent-
additive property can be utilized in the search. The
principle of the multi-agent heuristic search presented
here is based on the MAD-A* algorithm (Multi-Agent
Distributed A*) (Nissim and Brafman, 2012). We first
briefly summarize the main principles. The MAD-
A* algorithm is a simple extension of classical A*.
The agents search in parallel, possibly in a distributed
setting (i.e., communicating over a network). Each
agent α
i
∈ A searches using its operators from O
i
and if a state s is expanded using a public operator
o ∈ O
pub
i
, the resulting state s
0
is sent to other agents
(the agents may be filtered in order to send the state
only to the relevant ones). When some other agent
α
j
receives the state s
0
, s
0
is added to the OPEN list
of α
j
and expanded normally when due. The origi-
nal MAD-A* uses only projected heuristics computed
on Π
Bi
. Each state sent by α
i
is also accompanied
with its i -projected heuristic estimate and when recei-
ved, the receiving agent α
j
computes the j -projected
heuristic estimate of the received state s
0
and takes
h(s) = max(h
Bi
(s
Bi
), h
B j
(s
B j
)).
Let us now consider how can the agent-additive
heuristic be utilized in the search to reduce heuristic
computation and communication. In order to do so,
we first state the following two propositions.
Proposition 10. Let M = {Π
i
}
n
i=1
be a multi-agent
problem and let h(s) = h
pub
(s
B
) +
∑
α
i
∈A
h
i
(s
Bi
) be
an agent-additive heuristic. Let s and s
0
be two states
where s
0
is created from s by the application of a pri-
vate operator o ∈ O
priv
j
of some agent j . Then for all
h
j
such that j 6= i holds h
j
(s
B j
) = h
j
(s
0B j
) and
h(s
0
) = h(s)− h
pub
(s
B
)−h
i
(s
Bi
)+h
pub
(s
0B
)+h
i
(s
0Bi
) (11)
Proof. As o ∈ O
priv
i
the states s, s
0
differ only in va-
riables private to agent i and thus s
B j
= s
0B j
and
consequently h
j
(s
B j
) = h
j
(s
0B j
) for all j 6= i . Equa-
tion 11 follows directly from the fact that from the
point of view of the agent i , the value of the pri-
vate parts of the agent-additive heuristic of all ot-
her agents can be expressed as
∑
α
j
∈A\{α
i
}
h
j
(s
B j
) =
h(s) − h
pub
(s
B
) − h
i
(s
Bi
).
This means, that the heuristic estimate of a state s
0
can be easily determined from the heuristic estimate
of its predecessor s if s
0
was obtained from s by the ap-
plication of a private action. When a state is received
from some other agent j , it is accompanied with its
global heuristic estimate computed by agent j . When a
state s is expanded by agent i with a private action, the
heuristic estimate of its successor s
0
can be computed
using Equation 11. In order to avoid excessive heuris-
tic computations, the values of h
pub
(s
B
) and h
i
(s
Bi
)
can be cached when first computed.
Proposition 11. Let M = {Π
i
}
n
i=1
be a multi-agent
problem and let h(s) = h
pub
(s
B
) +
∑
α
i
∈A
h
i
(s
Bi
) be
an agent-additive heuristic. Let s and s
0
be two states
such that for some agent j holds s
B j
= s
0B j
. Then
h
j
(s
B j
) = h
j
(s
0B j
).
Proof. Holds trivially.
Proposition 11 means that from the perspective of
agent i , the states s, s
0
differ only in the private parts
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
46

of other agents. This information can be again used to
reduce the heuristic computation by caching the values
of h
i
(s
Bi
) . If the computation of h
i
(s
0Bi
) is requested
for some state s
0
such that s
B j
= s
0B j
, the cached value
can be returned directly.
6 EVALUATION
We have evaluated the proposed approach on the ben-
chmark set of the CoDMAP’15 (Komenda et al., 2016)
competition. In the evaluation we focus on three key
metrics: i) the heuristic value in the initial state, ii)
the number of expanded states, and iii) the number of
problems solved in time limit of 30 minutes (coverage).
The proposed methods were implemented in the MA-
Plan planner (Fi
ˇ
ser et al., 2015) and evaluated on the
LM-Cut heuristic (Helmert and Domshlak, 2009). The
configurations we have evaluated are the following:
max is the baseline solution where the heuristic is
computed on the projected problems without any
cost partitioning. The resulting heuristic is com-
puted using maximum (Equation 1). We have also
evaluated proj which is the classical projection
heuristic computed by a single agent only.
uni is the uniform baseline cost partitioning (Equa-
tion 3).
abs-N is the abstraction-based optimal cost partitio-
ning computed using the LP in Equation 4 where N
denotes the number of states of the abstraction of
each agent. The abstractions are computed using
the Merge&Shrink heuristic (Helmert et al., 2007)
implemented in Fast-Downward (Helmert, 2006).
pot is the potential-based cost partitioning computed
using the LP in Equation 10. The implementation
is based on the distributed potential heuristic LP
computation (
ˇ
Stolba et al., 2016a).
6.1 Heuristic Quality
In this section, we focus on the quality of the heuristic
computed using the cost partitioning (CP) and compu-
ted as a maximum of projections. First, we compare
the heuristic values computed for the initial state by
each of the configuration. Note that the CPs are op-
timized for the initial state and thus may give worse
heuristic estimates for further states during the search.
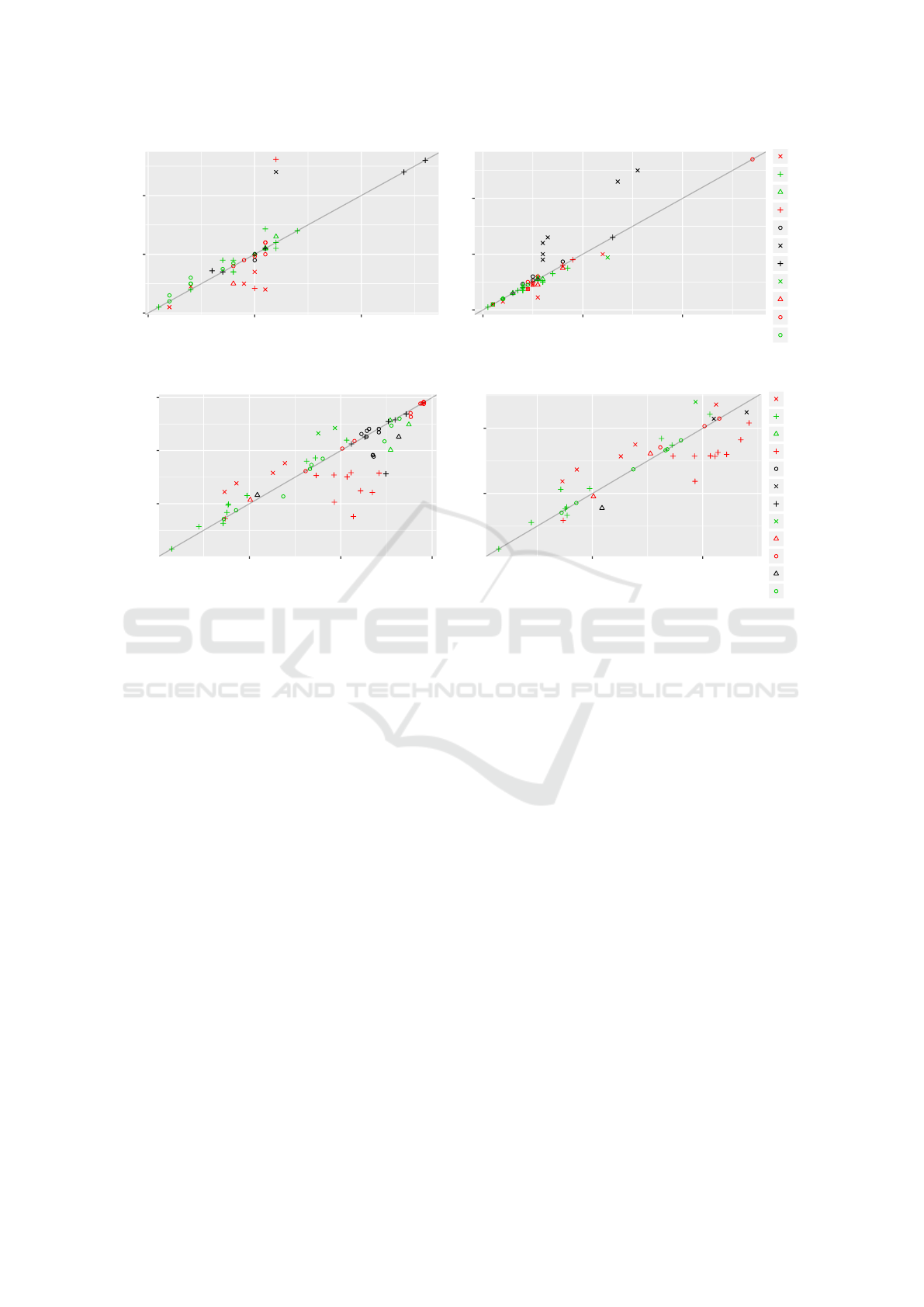
Figure 2 shows the comparison of heuristic values
for the best performing configurations. In both cases,
we can see that there are some problems where the CP
gives lower estimates and some cases where it gives
higher. The most prominent example is the elevators
domain where both CPs outperform the baseline.
Table 1: Numbers of problems solved (coverage).
domain
abs abs proj max uni pot
1000 10k
blocksworld 2 2 0 3 2 3
depot 1 3 3 0 1 1
driverlog 11 11 14 12 14 12
elevators 2 1 5 5 6 9
logistics 4 6 5 8 8 7
rovers 5 2 2 4 4 5
satellites 6 2 1 3 5 7
sokoban 6 5 13 10 8 8
taxi 3 1 3 3 1 3
wireless 0 0 1 1 0 0
woodwork. 1 1 1 0 1 0
zenotravel 7 6 6 9 8 9
∑
48 40 54 58 58 64
Let us now focus on the actual heuristic guidance
during the search, that is, the number of expanded sta-
tes shown in Figure 3. The figure shows, that in many
smaller problems, the abstraction-based CP provides
worse guidance. In the taxi domain and a couple of
other larger problems, the performance is improved.
The potential-based CP exhibits a similar pattern.
6.2 Coverage
In this section, we focus on the actual performance
of the MAD-A* algorithm together with the proposed
heuristics and the search improvements described in
this work. In order to perform this evaluation, we have
replicated the configuration of the distributed track of
the CoDMAP’15 (Komenda et al., 2016) competition,
where each agent runs on a dedicated machine with 4
cores on 3.2GHz and 8GB
1
RAM. The agents commu-
nicated over TCP-IP on a local area network. The main
difference between our setting and the competition is
a different network topology, in our case, there were
multiple switches between some nodes which could
have negatively influenced the performance.
The results in Table 1 show a number of interest-
ing points. First, the classical projection (proj) and
the maximum of projections (max) are on par overall
but perform differently on some domains, e.g., logis-
tics, where the max heuristic benefits from the ad-
ditional information. Second, the abstraction-based
CPs (abs) perform badly. This is because of the time
and especially memory requirements of the abstrac-
tion computation. This may possibly be improved by
a future work on the CP computation. Finally, the
best performance is obtained by the potential-based
1
Note, that the Fast-Downward planner used to compute
the abstractions was limited to 3GB due to the 32-bit archi-
tecture (1GB is restricted for the kernel).
Cost Partitioning for Multi-agent Planning
47

drive
rover
taxi
block
eleva
satel
wirel
depot
logis
sokob
zenot
0
10
20
0 10 20
max of projections
abstraction−1000
0
20
40
0 20 40
max of projections
potential
Figure 2: Initial state heuristics of the abstraction-based and potential-based cost partitionings compared with the maximum of
projections.
1e+03
1e+05
1e+03 1e+05
max of projections
potential
drive
rover
taxi
block
eleva
satel
wirel
depot
logis
sokob
zenot
1e+03
1e+05
1e+07
1e+03 1e+05 1e+07
max of projections
abstraction−1000
woodw
Figure 3: Expanded states on solved problems of the abstraction-based and potential-based cost partitionings compared with
the maximum of projections (log scale).
CP (pot) which is relatively fast to compute and im-
proves heuristic guidance on a significant number of
problems.
7 DISCUSSION OF PRIVACY
Privacy is a crucial issue in multi-agent planning, here
we discuss a number of issues concerning privacy in
the context of multi-agent cost partitioning.
Let us first focus on the heuristic computation it-
self, assuming we already have a cost-partitioning.
The authors in (To
ˇ
zi
ˇ
cka et al., 2017) have shown that
a search-based algorithm such as MAFS or MAD-A*
can never preserve privacy fully. Moreover, the aut-
hors in (
ˇ
Stolba et al., 2016b) have proposed a method
for measuring the amount of leaked private informa-
tion. We argue that the heuristic h
cp
based on the cost-
partitioning does not leak more information than the
baseline h
max
, the classical projection-based heuristic,
or any distributed heuristic (with respect to the heu-
ristic values) as the sum of the individual h
cp
i
can be
computed using a secure sum algorithm, e.g., (Sheikh
et al., 2010) (causing additional computation).
Naturally, the computation of the cost partitioning
may leak some private information as well, except for
the most simple variants such as the uniform CP. The
potential-based CP is computed using an LP very si-
milar to the original potential heuristic LP. A secure
variant of the potential LP computation was proposed
in (
ˇ
Stolba et al., 2016a), the same technique can be
used in our case, thus avoiding the information leakage.
We assume that a similar technique would be applica-
ble to the abstraction-based CP LP computation.
The last source of private information leakage is
the cost partitioning itself, that is, the new costs of the
public action which somehow reflect the structure of
the private parts of the problem. We leave the analysis
of how much and what information can be learned
from the cost partitioning for future work.
8 CONCLUSION AND FUTURE
WORK
In this work, we have presented a novel general tech-
nique to compute distributed admissible heuristics for
multi-agent planning based on the principle of cost par-
titioning. We have shown that this approach is promis-
ing and improves over the baseline projected heuristics.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
48

A promising future work is the development of a cost
partitioning more specific to the multi-agent planning.
ACKNOWLEDGEMENTS
This research was supported by the Czech Science
Foundation (grant no. 18-24965Y). The authors ackno-
wledge the support of the OP VVV MEYS funded pro-
ject CZ.02.1.01/0.0/0.0/16 019/0000765 ”Research
Center for Informatics”.
REFERENCES
Brafman, R. I. (2015). A privacy preserving algorithm for
multi-agent planning and search. In Proceedings of
the Twenty-Fourth International Joint Conference on
Artificial Intelligence, IJCAI, pages 1530–1536.
Brafman, R. I. and Domshlak, C. (2008). From one to many:
Planning for loosely coupled multi-agent systems. In
Proceedings of the 18th International Conference on
Automated Planning and Scheduling (ICAPS’08), pa-
ges 28–35.
Dimopoulos, Y., Hashmi, M. A., and Moraitis, P. (2012).
µ -satplan: Multi-agent planning as satisfiability.
Knowledge-Based Systems, 29:54–62.
Fikes, R. and Nilsson, N. (1971). STRIPS: A new appro-
ach to the application of theorem proving to problem
solving. In Proceedings of the 2nd International Joint
Conference on Artificial Intelligence (IJCAI’71), pages
608–620.
Fi
ˇ
ser, D.,
ˇ
Stolba, M., and Komenda, A. (2015). MAPlan.
In Proceedings of the Competition of Distributed and
Multi-Agent Planners (CoDMAP-15), pages 8–10.
Helmert, M. (2006). The Fast Downward planning system.
Journal of Artificial Intelligence Research, 26:191–
246.
Helmert, M. and Domshlak, C. (2009). Landmarks, critical
paths and abstractions: What’s the difference anyway?
In Proceedings of the 19th International Conference on
Automated Planning and Scheduling (ICAPS), pages
162–169.
Helmert, M., Haslum, P., and Hoffmann, J. (2007). Flexible
abstraction heuristics for optimal sequential planning.
In Proceedings of the 17th International Conference
on Automated Planning and Scheduling (ICAPS’07),
pages 176–183.
Jezequel, L. and Fabre, E. (2012). A#: A distributed version
of A* for factored planning. In Proceedings of the 51th
IEEE Conference on Decision and Control, (CDC’12),
pages 7377–7382.
Katz, M. and Domshlak, C. (2010). Implicit abstraction
heuristics. Journal of Artificial Intelligence Research,
pages 51–126.
Komenda, A., Stolba, M., and Kovacs, D. L. (2016). The
international competition of distributed and multiagent
planners (CoDMAP). AI Magazine, 37(3):109–115.
Maliah, S., Brafman, R. I., and Shani, G. (2016). Privacy
preserving LAMA. In Proceedings of the 4th Works-
hop on Distributed and Multi-Agent Planning, DMAP–
ICAPS’16, pages 1–5.
Maliah, S., Shani, G., and Stern, R. (2015). Privacy pre-
serving pattern databases. In Proceedings of the 3rd
Distributed and Multiagent Planning (DMAP) Works-
hop of ICAPS’15, pages 9–17.
Nissim, R. and Brafman, R. I. (2012). Multi-agent A*
for parallel and distributed systems. In Proceedings
of the 11th International Conference on Autonomous
Agents and Multiagent Systems (AAMAS’12), pages
1265–1266.
Nissim, R. and Brafman, R. I. (2014). Distributed heuristic
forward search for multi-agent planning. Journal of
Artificial Intelligence Research, 51:293–332.
Pommerening, F., Helmert, M., R
¨
oger, G., and Seipp, J.
(2014a). From non-negative to general operator cost
partitioning: Proof details. Technical Report CS-2014-
005, University of Basel, Department of Mathematics
and Computer Science.
Pommerening, F., Helmert, M., R
¨
oger, G., and Seipp, J.
(2015). From non-negative to general operator cost
partitioning. In Proceedings of the 29th AAAI Confe-
rence on Artificial Intelligence, pages 3335–3341.
Pommerening, F., R
¨
oger, G., Helmert, M., and Bonet, B.
(2014b). LP-Based heuristics for cost-optimal planning.
In Proceedings of the 24th International Conference on
Automated Planning and Scheduling (ICAPS), pages
226–234.
Sheikh, R., Kumar, B., and Mishra, D. K. (2010). A dis-
tributed k-secure sum protocol for secure multi-party
computations. arXiv preprint arXiv:1003.4071.
ˇ
Stolba, M., Fi
ˇ
ser, D., and Komenda, A. (2015). Admissi-
ble landmark heuristic for multi-agent planning. In
Proceedings of the 25th International Conference on
Automated Planning and Scheduling (ICAPS), pages
211–219.
ˇ
Stolba, M., Fi
ˇ
ser, D., and Komenda, A. (2016a). Potential
heuristics for multi-agent planning. In Proceedings
of the 26th International Conference on Automated
Planning and Scheduling, ICAPS’16, pages 308–316.
ˇ
Stolba, M., To
ˇ
zi
ˇ
cka, J., and Komenda, A. (2016b). Secure
multi-agent planning. In Proceedings of the 1st In-
ternational Workshop on AI for Privacy and Security,
pages 11:1–11:8. ACM.
Torre
˜
no, A., Onaindia, E., and Sapena, O. (2014). FMAP:
Distributed cooperative multi-agent planning. Applied
Intelligence, 41(2):606–626.
To
ˇ
zi
ˇ
cka, J., Jakubuv, J., and Komenda, A. (2014). Gene-
rating multi-agent plans by distributed intersection of
Finite State Machines. In Proceedings of the 21st Euro-
pean Conference on Artificial Intelligence (ECAI’14),
pages 1111–1112.
To
ˇ
zi
ˇ
cka, J.,
ˇ
Stolba, M., and Komenda, A. (2017). The limits
of strong privacy preserving multi-agent planning. In
Proceedings of the 27th International Conference on
Automated Planning and Scheduling, ICAPS’17.
Cost Partitioning for Multi-agent Planning
49