
On Enumerating All the Minimal Models for Particular
CNF Formula Classes
Yakoub Salhi
CRIL-CNRS, Universit
´
e d’Artois, F-62307 Lens Cedex, France
Keywords:
Minimal Models, SAT, Enumeration Problem, Computational Complexity.
Abstract:
In this work, we propose approaches for enumerating all the minimal models for two particular classes of CNF
formulæ. The first class is that of PN formulæ which are defined as CNF formulæ where each clause is either
positive or negative, whereas the second class is that of PH formulæ in which each clause is either positive
or a Horn clause. We first provide an approach for enumerating all the minimal models in the case of PN
formulæ that is based on the use of an algorithm for generating the minimal transversals of a hypergraph. We
also propose a SAT-based encoding for solving the same problem. Then, we provide a characterization of the
minimal models in the case of PH formulæ, which allows us to use our approaches in the case of PN formulæ
for solving the problem of minimal model enumeration for PH formulæ. Finally, we describe an application
in datamining of the problem of enumerating the minimal models in the case of PN formulæ.
1 INTRODUCTION
The problem of minimal model enumeration is based
on preferring models that assign false to the proposi-
tional variables (see, e.g., (Ben-Eliyahu and Dechter,
1996; Niemel
¨
a, 1996)). This problem has impor-
tant applications in AI, such as propositional circum-
scription (McCarthy, 1980), minimal diagnosis (Re-
iter, 1987) and logic programming (Bidoit and Froide-
vaux, 1987; Gelfond and Lifschitz, 1988).
It is noteworthy that the problem of checking
whether a model is minimal in the general case
is coNP-complete (Cadoli, 1992b). Different algo-
rithms have been proposed in the literature for com-
puting minimal models. The algorithms that have
been proposed in (Ben-Eliyahu and Dechter, 1996)
exploit tractable classes. For instance, knowing that
any Horn formula admits a single minimal model,
which can be found in linear time using the procedure
of unit propagation, the main idea consists in instan-
tiating as few variables as possible so that the remain-
ing formula is a Horn formula. In addition, an in-
cremental algorithm for enumerating all the minimal
models has been proposed in (Ben-Eliyahu-Zohary,
2005). Other algorithms and approaches for the prob-
lem of enumerating minimal models and some re-
lated problems are proposed in (Reiter, 1987; Avin
and Ben-Eliyahu-Zohary, 2001; Angiulli et al., 2014;
Ben-Eliyahu-Zohary et al., 2017).
In this work, we mainly propose approaches to
enumerate all the minimal models for two particular
classes of CNF formulæ. The first class corresponds
to CNF formulæ where each clause is either positive
or negative, called PN formulæ. The second class is
that of CNF formulæ where each clause is either pos-
itive or a Horn clause, called PH formulæ. Clearly,
the class of PH formulæ is a generalization of that
of PN formulæ. From the computational complexity
point of view, we show that the problem of checking
whether a model is minimal is tractable in the case
of PN formulæ, while it is coNP-complete in the case
of PH formulæ. To the best of our knowledge, the
formula classes of PN formulæ and PH formulæ have
not been studied in the case of the problem of minimal
model enumeration.
We provide two methods to enumerate the min-
imal models in the case of PN formulæ. The first
one consists in using the problem of enumerating the
minimal transversals of a hypergraph to obtain all the
minimal models that are contained in a model. Note
that we provide an interesting property that allows us
to reduce the search space in solving the latter prob-
lem. Indeed, we provide in this property the part
shared between all the minimal models that are con-
tained in a given model. Our second method consists
in a SAT-based encoding. The main idea consists in
using a formula expressing the fact that the truth value
true is assigned to a variable if and only if there is a
Salhi, Y.
On Enumerating All the Minimal Models for Particular CNF Formula Classes.
DOI: 10.5220/0007257104030410
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 403-410
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
403

positive clause which is satisfied only by this assign-
ment. Since checking whether a Boolean interpreta-
tion is a model of a CNF formula or not is a linear
time task, our encoding can be seen as a proof that the
problem of checking whether a model is minimal or
not is tractable in the case of PN formulæ.
Our approach in the case of PH formulæ is based
on enumerating the minimal models of its greatest PN
subformula (the subset of all the positive and negative
clauses). In fact, we provide a simple characterization
of the minimal models in the case of PH formulæ that
uses the procedure of unit propagation and the mini-
mal models of the greatest PN subformulæ. Using this
characterization, we propose an algorithm that uses
our SAT-based encoding in the case of PN formulæ.
2 PRELIMINARIES
2.1 Propositional Satisfiability and
Minimal Models
A CNF formula is a conjunction of clauses where a
clause is a disjunction of literals. A literal is a propo-
sitional variable (positive literal) or its negation (neg-
ative literal). A positive clause (resp. negative clause)
is a clause that contains only positive (resp. negative)
literals. In addition, a Horn clause is a clause that
contains at most one positive literal. We denote by
Var(φ) (resp. Lit(φ)) the set of propositional vari-
ables (resp. literals) occurring in the formula φ. A
CNF formula is binary if each clause contains at most
two literals. Propositional variables are denoted by
the lowercase letters p, q, r, and CNF formulæ by the
Greek letters φ, ψ, χ.
A CNF formula can also be seen as a set of clauses
and a clause as a set of literals. Thus, a CNF formula
of the form (l
1
1
∨ · ·· ∨ l
1
k
1
) ∧ ··· ∧ (l
n
1
∨ · ·· ∨ l
n
k
n
) can
be also represented in this work by the set of clauses
{(l
1
1
∨ ·· · ∨ l
1
k
1
),. .. ,(l
n
1
∨ ·· · ∨ l
n
k
n
)} and the set of sets
of literals {{l
1
1
,. ..,l
1
k
1
},. ..,{l
n
1
,. ..,l
n
k
n
}}.
A Boolean interpretation of a formula φ is an as-
signment that associates truth values in {0,1} to the
propositional variables in Var(φ), where 0 stands for
false and 1 stands for true. It is extended to formulæ
as usual. A model of a formula is a Boolean inter-
pretation satisfying this formula, i.e., an interpreta-
tion making this formula true. We use Models(φ) to
denote the set of models of φ. The problem of de-
termining if there exists a model that satisfies a given
propositional formula (|Models(φ)| ≥ 1), abbreviated
as SAT, is one of the most studied NP-complete prob-
lems.
Given a set of literals L, we use φ
|L
to denote the
formula obtained from φ by removing every clauses
containing a literal in L and by removing all the
complement literals of those in L. More precisely,
φ
|L
= {c ∈ φ | ∀l ∈ L,l /∈ c & l /∈ c} ∪ {c \ {l} | c ∈
φ & l ∈ L & l ∈ c}.
For convenience purposes, we represent the
Boolean interpretations as sets of variables. More pre-
cisely, the set m represents the Boolean interpretation
that associates 1 to the variables in m and 0 to the
variables in Var(φ) \ m. Further, we use (m)
−
to de-
note the set of negative literals that are true by m, i.e.,
(m)
−
= {¬p | p ∈ Var(φ) \ m}.
Definition 2.1 (Minimal Model). Let φ be a CNF for-
mula and m a model of φ. Then, m is a minimal model
of φ iff there is no model m
0
of φ such that m
0
is a
proper subset of m (m
0
⊂ m).
The problem of checking whether a model of a
CNF formula is minimal is coNP-complete (Cadoli,
1992a).
We use MinModels(φ) to denote the set of min-
imal models of φ. Moreover, given a model m of
φ, we use MinMS(φ,m) to denote the set of minimal
models that are contained in m, i.e., MinMS(φ,m) =
MinModels(φ) ∩ {m
0
∈ Models(φ) | m
0
⊆ m}.
2.2 PN and PH formulæ
We here describe two classes of CNF formulæ,
namely PN (for Positive and Negative) and PH (for
Positive and Horn) formulæ. In this work, we de-
fine different methods for enumerating all the mini-
mal models in the case of these classes.
Definition 2.2 (PN formula). A PN formula φ is a
CNF formula where each clause is either positive or
negative.
We use Pos(φ) (resp. Neg(φ)) to denote the set of
positive (resp. negative) clauses of φ.
One can easily show that each CNF formula can
be linearly transformed into an equisatisfiable PN for-
mula. Indeed, we only have to use fresh proposi-
tional variables for renaming negative literals in the
mixed clauses. As a consequence, the problem of
checking the satisfiability of a PN formula is also NP-
complete. Note that this property has been pointed
out in (Boumarafi et al., 2017).
Definition 2.3 (PH formula). A PH formula φ is a
CNF formula where each clause is either positive or
Horn.
We use Pos(φ) (resp. Horn(φ)) to denote the set
of positive (resp. Horn) clauses of φ.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
404
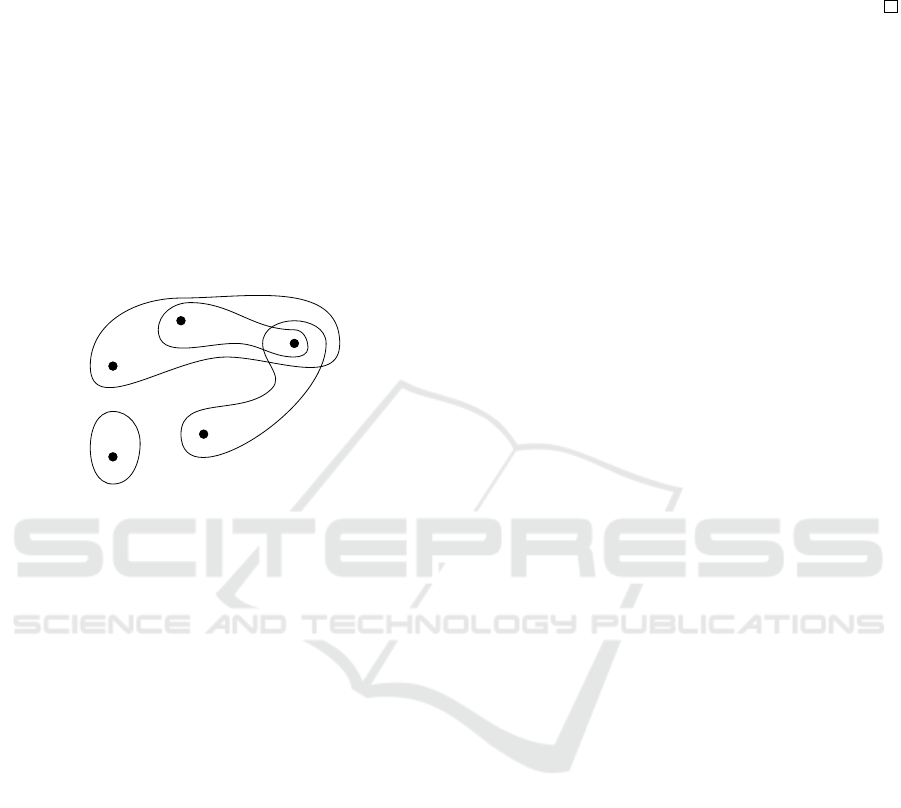
2.3 Hypergraphs and Minimal
Transversals
A hypergraph H is an ordered pair (V,E) where V is a
non empty set of vertices and E ⊆ P (V ) \
/
0 is a set of
hyperedges, where P(V ) denotes the power set of V ,
i.e., its set of subsets. In other words, the hypergraph
notion is a generalization of that of undirected graph.
Further, a transversal of H is a set of vertices s ⊆ V
that intersects every hyperedge of H, i.e., e ∩ s 6=
/
0
for every e ∈ E. A transversal of H is minimal if it
is not a proper superset of any other transversal of
H, i.e., s
0
6⊂ s for every transversal s
0
of H. Given a
hypergraph H, we use MT (H) to denote the set of all
the minimal transversals of H.
1
2
3
4
5
Figure 1: A Hypergraph.
Consider, for instance, the hypergraph described
in Figure 1, the set s = {3,5} is a minimal transversal
since it intersects every hyperedge. The set {2, 4,5}
is the only other minimal transversal.
In the literature, there are several methods for gen-
erating the minimal transversals of a hypergraph (see
eg (Fredman and Khachiyan, 1996; Khachiyan et al.,
2005; Khachiyan et al., 2007; H
´
ebert et al., 2007)).
In particular, the authors of (H
´
ebert et al., 2007) have
shown how efficient datamining techniques, such as
the levelwise framework, can be used for generating
the minimal transversals. In this work, we use an al-
gorithm for generating the minimal transversals as a
black box in our methods for generating the minimal
models.
3 COMPUTATIONAL
COMPLEXITY
In this section, we provide computational complexity
results for the problem of checking whether a model is
minimal in the case of PN formulæ and PH formulæ.
Theorem 3.1. The problem of checking whether a
model of a PN formula is minimal or not is in P.
Proof. Using the SAT-based encoding defined in Sec-
tion 5, we know that the problem of checking whether
a model of a PN formula is minimal or not is in P. In-
deed, it is well known that the problem of checking
whether a Boolean interpretation is a model of a for-
mulæ can be solved in linear time.
Let G = (V, E) be an undirected graph such that V
is the set of its vertices and E is the set of its edges.
A 3-coloring of G corresponds to a partition of V into
3 subsets P = {V
c
1
,V
c
2
,V
c
3
} so that no two vertices in
a same subset are adjacent, and V
c
1
, V
c
2
and V
c
3
re-
fer to three different colors c
1
, c
2
and c
3
respectively.
It is well known that deciding whether an undirected
graph admits a 3-coloring is an NP-complete prob-
lem. In the following theorem, we show that the com-
plement of the 3-coloring problem can be transformed
into the problem of checking whether a model of PH
formula is minimal.
Theorem 3.2. The problem of checking whether a
model of PH formula is minimal is coNP-complete.
Proof. Using the fact that the same problem in the
general case is coNP-complete, we know that it is
also in coNP in the case of PH formulæ. In order
to show the coNP-completeness, we reduce the com-
plement of the 3-coloring problem to the problem of
checking whether a model of a PH formula is mini-
mal. Let G = (V, E) be an undirected graph such that
V = {1, ... ,n}. We associate to each vertex i ∈ V
and each color c ∈ {r,g,b} a propositional variable
denoted p
c
i
. We also use an additional fresh variable
denoted s. Then, the encoding is defined as the con-
junction of the following formulæ:
^
i∈1..n
(p
r
i
∨ p
g
i
∨ p
b
i
) (1)
^
i∈1..n
[(p
r
i
∨ ¬p
g
i
∨ ¬p
b
i
)∧
(¬p
r
i
∨ p
g
i
∨ ¬p
b
i
) ∧ (¬p
r
i
∨ ¬p
g
i
∨ p
b
i
)]
(2)
^
i∈1..n−1
[¬p
r
i
∨ ¬p
g
i
∨ ¬p
b
i
∨ (p
r
i+1
∧ p
g
i+1
∧ p
b
i+1
)]
∧[¬p
r
n
∨ ¬p
g
n
∨ ¬p
b
n
∨ (p
r
1
∧ p
g
1
∧ p
b
1
)]
(3)
^
i< j,{i, j}∈E,c∈{r,g,b}
(¬p
c
i
∨ ¬p
c
j
∨ s) (4)
(¬s ∨ p
r
1
) ∧ (¬s ∨ p
g
1
) ∧ (¬s ∨ p
b
1
) (5)
(1) is used to express that each vertex has at least
one color, and (2) expresses that if a vertex has more
than one color, then it has the three considered col-
ors. (3) is used to add the fact that if there is a vertex
that has three colors, then every other vertex has also
three colors. (4) means that s is true if there are two
adjacent vertices that have the same color. Finally, (5)
On Enumerating All the Minimal Models for Particular CNF Formula Classes
405

expresses that the fact that s is true implies that the
vertex 1 has three colors. In fact, we show that our
encoding captures the complement of the 3-coloring
problem by showing that there is no 3-coloring iff the
model that associates three colors to every vertex is a
minimal model.
Using the fact that each formula of the form ¬p
1
∨
·· · ∨¬p
k
∨(q
1
∧· ·· ∧q
l
) is equivalent to the conjunc-
tion of Horn clauses (¬p
1
∨ ·· · ∨ ¬p
k
∨ q
1
) ∧ ·· · ∧
(¬p
1
∨ ·· · ∨ ¬p
k
∨ q
l
), we know that the encoding
φ
G
= (1) ∧ (2) ∧ (3) ∧ (4) ∧ (5) corresponds to a PH
formula.
Knowing that each clause in our encoding con-
tains at least one positive literal, we have m =
{s, p
r
1
, p
g
1
, p
b
1
,. .., p
r
n
, p
g
n
, p
b
b
} is a model of this encod-
ing. In this context, the proof of coNP-completeness
comes from the fact that m is a minimal model of our
encoding iff G does not admit a 3-coloring. Using
(1) ∧ (2), we know that each model of φ
G
satisfies
either a unique positive literal or the three literals in
{p
r
i
, p
g
i
, p
b
i
} for every i ∈ 1..n. In addition, using (3),
we know that if a model of φ
G
satisfies the three pos-
itive literals {p
r
i
, p
g
i
, p
b
i
} for some i ∈ 1..n, then this
model satisfies all the positive literals in {p
r
j
, p
g
j
, p
b
j
}
for every j ∈ 1..n. In other words, every model of φ
G
different from m associates a single color to each ver-
tex of G. (4) ∧ (5) is used to force every model of
φ
G
to satisfy all the literals in {s, p
r
1
, p
g
1
, p
b
1
} if it asso-
ciates the same color to two adjacent vertices. Thus,
every model of φ
G
which is different from m (and con-
sequently contained in m) corresponds to a 3-coloring
of G. Conversely, every 3-coloring of G can be eas-
ily used for defining a model of φ
G
different from m.
Thus, m is not a minimal model of φ
G
if and only if G
admits a 3-coloring.
4 PN FORMULÆ AND MINIMAL
MODELS
We here provide interesting properties that allow us to
reduce the search space for solving in the case of PN
formulæthe problem of enumerating all the minimal
models that are contained in a given model. We also
show how the problem of listing the minimal transver-
sals can be directly used for enumerating these mini-
mal models. Then, we use this result for defining an
algorithm for enumerating all the minimal models of
a PN formula.
Definition 4.1. Let φ be a PN formula, m a model
of φ and n ∈ N. Then, we define π(φ,m) and ν(φ, m)
as follows: π(φ,m) = {p ∈ Var(φ) | p ∈ φ
|(m)
−
} and
ν(φ,m) = {¬p | p ∈Var(φ) and ∀c ∈ ψ w. p ∈ c, ∃c
0
∈
ψ : c
0
⊆ c \ {p}}, where ψ = φ
|(m)
−
∪π(φ,m)
.
Note that φ
|(m)
−
∪π(φ,m)
contains only positive
clauses, since φ is a PN formula and all the negative
clauses are satisfied by satisfying the literals in (m)
−
.
Proposition 4.1. Given a PN formula φ and a model
m of φ, (m)
−
⊆ ν(φ,m) holds.
Proof. This property is a direct consequence of the
fact that there is no clause in φ
|(m)
−
∪π(φ,m)
that con-
tains a variable occurring in (m)
−
.
One can easily see that π(φ, m) is included in ev-
ery model which is contained in m, since this set cor-
responds to unit clauses occurring in φ after assign-
ing the truth value 0 to the variables in Var(φ) \ m.
Moreover, from the definition of ν(φ,m), the for-
mula obtained by assigning 0 to the variables in S =
{p ∈ Var(φ) | ¬p ∈ ν(φ,m)} is equisatisfiable to ψ =
φ
|(m)
−
∪π(φ,m)
. As a consequence, we get m
0
∩S =
/
0 for
every minimal model m
0
⊆ m.
Let us recall that a positive monotone formula is
defined as a CNF formula that contains only positive
clauses.
Proposition 4.2. Let φ be a positive monotone for-
mula s.t., for every clause c ∈ φ, c contains at least
two literals. Then, for every positive literal p ∈
Lit(φ), if ∃c ∈ φ s.t. p ∈ c and c
0
6⊆ c for every c
0
∈ φ,
then there exists a minimal model m of φ s.t. p ∈ m
0
.
Proof. Let p a literal in Lit(φ) and c ∈ φ s.t. p ∈ c and
c
0
6⊆ c for every c
0
∈ φ. Let us consider the formula
ψ = φ
|{¬q|q∈c\{p}}
. Clearly, ψ does not contain the
empty clause since there is no clause c
0
∈ φ s.t. c
0
⊆
c \ {p}. Knowing that all the models of ψ contain the
literal p since it is a unit clause in ψ, we deduce that
there exists a minimal model of φ that contains p.
The following theorem allows us to reduce the
search space for solving the problem of enumerating
all the minimal models in the case of PN formulæ.
Theorem 4.1. Let φ be a PN formula and m
a model of φ. Then, the following properties
are satisfied: (i)
T
m
0
∈MinMS(φ,m)
m
0
= π(φ,m) and
(ii)
T
m
0
∈MinMS(φ,m)
(m
0
)
−
= ν(φ,m).
Proof. We here use S (resp. S
0
) to denote the set
T
m
0
∈MinMS(φ,m)
m
0
(resp.
T
m
0
∈MinMS(φ,m)
(m
0
)
−
). We
only consider the part ⊇, the other being similar. For
this part, it suffices to show the two following proper-
ties: (i) π(φ,m) ⊆ S and (ii) ν(φ,m) ⊆ S
0
. Clearly,
all the minimal models in MinMS(φ, m) satisfy the
literals in (m)
−
. Moreover, all the models of φ
|(m)
−
includes all the unit clause occurring in φ
|(m)
−
. As
a consequence, π(φ,m) ⊆ S holds. Further, let p
be a propositional variable s.t. ∀c ∈ Pos(φ
|(m)
−
∪π(φ,m)
)
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
406

Algorithm 1: An algorithm for computing the minimal mod-
els of a PN formula.
1: procedure MINMODSPN(φ)
2: r ←
/
0
3: ψ ← φ
4: while SAT(ψ) do
5: tmp ← MinMS(φ,m) m is a model of ψ
6: ψ ← ψ ∧
V
m
0
∈tmp
m
0
7: r ← r ∪ tmp
8: return r
with p ∈ c, ∃c
0
∈ Pos(φ
|(m)
−
∪π(φ,m)
) s.t. c
0
⊆ c \ {p}.
Then, for every model m
0
of φ
|(m)
−
∪π(φ,m)
, m
0
\ {p}
satisfies also φ
|(m)
−
∪π(φ,m)
. Thus, ν(φ,m) ⊆ S
0
holds.
Given a positive monotone formula φ, we use H
φ
to denote a hypergraph associated to φ and defined as
the ordered pair (Lit(φ), φ). Clearly, using the defini-
tion of H
φ
and the notion of minimal transversal, we
get the following property.
Proposition 4.3. Let φ be a positive monotone CNF
formula. Then, we have MinModels(φ) = MT (H
φ
).
Thus, using Theorem 4.1, we obtain a simple char-
acterization of the minimal models that are contained
in a given model in the case of PN formulæ. Indeed,
the following property shows that enumerating these
minimal models is reduced to enumerating the mini-
mal transversals of a hypergraph.
Proposition 4.4. Let φ be a PN formula and m a
model of φ. Then, we have MinMS(φ,m) = {s ∪
π(φ,m) | s ∈ MT (H
ψ
)} where ψ = φ
|π(φ,m)∪ν(φ,m)
.
Algorithm 1 shows how the method described in
Proposition 4.4 can be simply used for enumerat-
ing all the minimal models of a PN formula. In-
deed, given a PN formula φ, MINMODSPN(φ) uses
MinMS(φ,m) to get all the minimal models that are
contained in m in every step of the while loop (see
Line 5). The soundness of Algorithm 1 is a direct
consequence of Proposition 4.4. It is worth mention-
ing that we add in Line 6 the negations of the found
minimal models to avoid finding the same minimal
model more than once.
As a side note, connections between minimal
transversals and minimal models have already been
made in the literature (e.g. (Reiter, 1987)). More-
over, the graph structure has already been used for
computing minimal models through the notion of de-
pendency graph (Ben-Eliyahu-Zohary, 2000; Ben-
Eliyahu-Zohary, 2005; Angiulli et al., 2014).
Algorithm 2: An algorithm for computing a minimal models
of a PN formula contained in a given model.
1: procedure SOLVEMMP(φ, m)
2: r ← m
3: for p ∈ m do
4: if MOD(r \ {p},φ) then
5: r ← r \ {p}
6: return r
5 A SAT-BASED APPROACH FOR
ENUMERATING MINIMAL
MODELS
In this section, we provide a SAT-based encoding for
enumerating all the minimal models of a PN formula.
the main idea consists in using a formula expressing
the fact that the truth value 1 is assigned to a proposi-
tional variable if and only if there is a positive clause
which is satisfied only by this assignment.
The following proposition provides a characteri-
zation of the minimal models in the case of PN for-
mulæ.
Proposition 5.1. Given a PN formula φ and a model
m of φ, m is a minimal model of φ iff for all p ∈ m,
there exists a clause c ∈ Pos(φ) s.t. p ∈ c and
c \ {p} ⊆ Var(φ)\ m.
Proof.
Part ⇒. Let m be a minimal model of φ. Assume that
there exists p ∈ m s.t. for every clause c in Pos(φ)
containing p, we have c \ {p} 6⊆ Var(φ) \ m. Thus,
m \ {p} satisfies all the clauses containing p, and con-
sequently, it satisfies φ. Therefore, we get a contra-
diction since m is a minimal model of φ.
Part ⇐. Let m be a model of φ s.t., for all p ∈ m,
there exists a clause c ∈ Pos(φ) s.t. p ∈ c and c\{p} ⊆
Var(φ)\m. Then, for all p ∈ m, φ∧(
V
q∈Var(φ)\m
¬q)∧
¬p is unsatisfiable. As a consequence, m is a minimal
model of φ.
Now, using the characterization provided in
Proposition 5.1, we propose a SAT-based encoding
for enumerating all the minimal models of a PN for-
mula. Given a PN formula φ, we use E
PN
(φ) to de-
note the following SAT encoding: φ ∧ (
V
p∈Var(φ)
p →
W
c∈Pos(φ),q∈c
¬(c \ {q})).
Let us recall that any propositional formula can
be translated to CNF using Tseitin’s linear encod-
ing (Tseitin, 1968). To translate our encoding to
CNF, one can associate to each subformula of the
form c \ {p} a fresh propositional variable r with the
clauses (¬r ∨ c \ {p}) ∧
V
q∈c\{p}
(r ∨ ¬q) that repre-
sent the equivalence r ↔ c \ {p}.
On Enumerating All the Minimal Models for Particular CNF Formula Classes
407

Theorem 5.1 (Soundness). Let φ be a PN formula.
Then, Models(E
PN
(φ)) = MinModels(φ) holds.
Proof. The soundness of the SAT encoding E
PN
(φ)
is a consequence of Porposition 5.1. Indeed, the
subformula (
V
p∈Var(φ)
p →
W
c∈Pos(φ),p∈c
c \ {p}) al-
lows us to get the property that for all p ∈ m,
there exists a clause c ∈ Pos(φ) s.t. p ∈ c and
{¬q | q ∈ c \ {p}} ⊆ m.
As mentioned in our proof of Theorem 3.1, this
encoding shows that the problem of checking whether
a model is minimal (called minimal model checking
problem) in the case of PN formulæ is tractable, since
checking whether a Boolean interpretation is a model
of a CNF formula or not can be performed in linear
time.
Let us now consider a problem related to minimal
model computation, called model minimization prob-
lem (Angiulli et al., 2014).
Definition 5.1 (Model Minimization Problem).
Given a propositional formula φ and a model m of
φ, compute a minimal model m
0
for φ contained in the
model m.
The model minimization problem is P
NP[O(log(n))]
-
hard in the general case where n is the number of
variables (Angiulli et al., 2014). This means that this
problem is as hard as a problem that can be solved us-
ing a polynomial deterministic algorithm which uses
O(log(n)) calls of an NP oracle.
Theorem 5.2. The model minimization problem is
tractable in the case of PN formulæ.
Proof. We here show that Algorithm 2 is sound.
In this algorithm the procedure MOD(r \ {p},φ) in
Line 4 is used for checking whether r \{p} is a model
of φ or not. Clearly, the returned Boolean interpreta-
tion r is a model of φ and contained in m. Assume
now that this returned interpretation is not a minimal
model of φ. Then using Proposition 5.1, there exists
p ∈ r s.t. c \ {p} ∩ r 6=
/
0 for every clause c contain-
ing the literal p. Thus, for all m
0
with r ⊆ m
0
, we get
c\{p}∩m 6=
/
0 for every clause c containing the literal
p. As a consequence, for all m
0
with r ⊆ m
0
, m
0
\ {p}
is a model of φ. Therefore, p /∈ r holds and we get a
contradiction.
6 MINIMAL MODEL
ENUMERATION FOR PH
FORMULÆ
In this section, we propose an approach for enumerat-
ing all the minimal models in the case of PH formulæ.
Algorithm 3: An algorithm for computing the minimal mod-
els of a PH formula.
1: procedure MINMODSPH(φ)
2: r ←
/
0
3: ψ ← E
PN
(Pos(φ) ∪ Neg(φ))
4: while SAT(ψ) do m is a minimal model of
Pos(φ) ∪ Neg(φ)
5: m
0
← m ∪ pup(M(φ)
|m
)
6: if (∀c ∈ Neg(φ), {p | ¬p ∈ c} 6⊆ m
0
) then
7: r ← r ∪ {m
0
}
8: ψ ← ψ ∧ m
0
9: return r
This approach is based on enumerating the minimal
models of its greatest PN subformula (the subformula
consisting of all the positive and negative clauses),
which means that our methods for enumerating the
minimal models in the case of PN formulæ can be
used in the case of PH formulæ.
Unit propagation is a procedure consisting in ap-
plying the following two rules for every unit clause l
occurring in the CNF formula: (i) every clause con-
taining the literal l, except the unit clause l, is re-
moved; and (ii) all the occurrences of l are removed.
For instance, applying unit propagation to the for-
mula {¬p ∨ ¬q, p, p ∨ r,q ∨ r} produce the formula
{¬q, p,r}. Indeed, using the two rules with the lit-
eral p produces the unit clause ¬q and removes p ∨ r,
and then, we get the literal r from the clause q ∨ r by
propagating ¬q. It is worth noting that an efficient im-
plementation of unit propagation in linear time is pro-
vided in (Crawford and Auton, 1993). In this work,
we use pup(φ) to denote the set of positive literals
that are propagated in the procedure of unit propaga-
tion. Considering again the previous example, we get
pup({¬p ∨ ¬q, p, p ∨ r, q ∨ r}) = {p,r}.
Given a PH formula φ, we use M(φ) to denote the
set of clauses φ \ (Pos(φ) ∪ Neg(φ)). Note that each
clause in M(φ) contains at least one negative literal
and exactly one positive literal.
Theorem 6.1. Let φ be a PH formula. Then,
MinModels(φ) = {m ∪ pup(M(φ)
|m
) | m ∈
MinModels(Pos(φ) ∪ Neg(φ)) & ∀c ∈ Neg(φ),{p |
¬p ∈ c} 6⊆ m ∪ pup(M(φ)
|m
)} holds.
Proof. We use in this proof S to denote the
set {m ∪ pup(M(φ)
|m
) | m ∈ MinModels(Pos(φ) ∪
Neg(φ)) & ∀c ∈ Neg(φ),{p | ¬p ∈ c} 6⊆ m ∪
pup(M(φ)
|m
)}.
Part ⊆. Let m be a minimal model in MinModels(φ).
Then, we know that there exists a minimal model
m
0
of Pos(φ) ∪ Neg(φ) s.t. m
0
⊆ m since Pos(φ) ∪
Neg(φ) is a subformula of φ. Clearly, we have
pup(M(φ)
|m
0
)) ⊆ m \ m
0
. Moreover, knowing that
∀c ∈ Neg(φ),{p | ¬p ∈ c} 6⊆ m since m satisfies φ,
{p | ¬p ∈ c} 6⊆ m
0
∪ pup(M(φ)
|m
0
) holds for every
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
408

c ∈ Neg(φ). As a consequence, using the fact that m
is a minimal model of φ, we get m = m
0
∪ pup(φ
|m
0
).
Thus, m belongs to the set S.
Part ⊇. Let m = m
0
∪ pup(M(φ)
|m
0
) an element of
S. Then, using the property ∀c ∈ Neg(φ),{p | ¬p ∈
c} 6⊆ m and the fact that m
0
satisfies ψ = Pos(φ) ∪
Neg(φ), we know that m is a model of φ. Further,
for all p ∈ m
0
, φ ∧
V
q/∈m
¬q ∧ ¬p is unsatisfiable since
m
0
∈ MinModels(ψ). We know also that for all p ∈
pup(M(φ)
|m
), φ∧
V
q/∈m
¬q ∧¬p is unsatisfiable since
all the elements of pup(M(φ)
|m
) are logical conse-
quences of φ
|m
0
. Thus, m is a minimal model of φ.
Theorem 6.1 shows how a method for enumerat-
ing the minimal models of a PN formula can be used
to define a method in the case of PH formulæ. For
instance, Algorithm 3, shows how our SAT-based en-
coding proposed in Section 5 can be used for gener-
ating all the minimal models of a PH formula. In-
deed, given a PH formula φ, MINMODSPH(φ) uses
the SAT-based encoding E
PN
(Pos(φ) ∪ Neg(φ)) for
generating the minimal models of Pos(φ)∪ Neg(φ).
It is noteworthy that, using the fact that each bi-
nary CNF formula is also a PH formula, we get the
following property.
Corollary 6.1. Let φ be a binary CNF for-
mula. MinModels(φ) = {m ∪ pup(M(φ)
|m
) | m ∈
MinModels(Pos(φ) ∪ Neg(φ)) & ∀c ∈ Neg(φ),{p |
¬p ∈ c} 6⊆ m ∪ pup(M(φ)
|m
)} holds.
7 A MODELING EXAMPLE
We here describe a modeling example showing that
the problem of enumerating the minimal models in
the case of PN formulæ can be used for solving the
datamining problem of enumerating the minimal gen-
erators (Zaki, 2004).
Let T be a set of items. From now on, we as-
sume T fixed. A transaction over T is an ordered
pair (tid,I) where tid ∈ N is its identifier and I ⊆ T
is an itemset. A transaction database is a finite set of
transactions where each identifier refers to only one
transaction. Given an itemset J, we say that (tid,I)
supports J if we have J ⊆ I. Further, the cover of an
itemset J in a database D, denoted C(J, D), is defined
as follows: C(J,D) = {tid | (tid,I) ∈ D & J ⊆ I}.
Definition 7.1 (Closed Itemset). Let D be a transac-
tion database and I an itemset. Then, I is closed if, for
every itemset J with I ⊂ J, C (J,D) ⊂ C (I,D) holds.
Definition 7.2 (Minimal Generator). Let D be a
transaction database and I an itemset. Then, I is a
minimal generator if, for every itemset J with J ⊂ I,
C(I,D) ⊂ C (J,D) holds.
Table 1: Transaction database D.
tid itemset
1 a,b,c, d,e
2 a,b,c, f
3 a,b, c, m
4 a,c,d, f , j
5 j,l
6 e, f
Note that for every minimal generator I, there
exists a single closed itemset J such that C(I,D) =
C(J, D), and we say that I generates J.
Consider the transaction database D described in
Table 1. In this database, {a,b,c} and {a, c} are
closed itemsets and {a,b} and {a} are minimal gen-
erators that generate {a,b, c} and {a,c} respectively.
To define the encoding of the problem of gen-
erating all the minimal generators, we associate to
each item a a variable denoted p
a
which is used to
represent the fact that a is in the minimal genera-
tor. Further, for all i ∈ 1..n, the variable q
i
is used
to represent the fact that the itemset appears in the
transaction t
i
. The encoding M G(D) is
V
n
i=1
(¬q
i
↔
W
a/∈T \t
i
p
a
). Clearly, each subformula of the form
¬q
i
↔
W
a/∈t
i
¬p
a
is equivalent to the following PN
formula: (q
i
∨
W
a/∈T \t
i
p
a
) ∧
V
a/∈T \t
i
(¬p
a
∨ ¬q
i
).
It is important to note that the encoding M G(D)
is similar to that proposed in (Jabbour et al., 2017) for
generating the frequent itemsets. Furthermore, a SAT-
based encoding for generating the minimal generators
has been proposed in (Boudane et al., 2017).
Proposition 7.1. Let D = {(1,t
1
),. .. ,(n,t
n
)} be a
transaction database over the set of items T . Then, m
is a minimal model of M G(D) iff I
m
= {a | p
a
∈ m}
is a minimal generator in D such that C (I
m
,D) = {i ∈
1..n | q
i
∈ m}.
Proof. We only consider the only if part, the other
part being similar. Let m be a minimal model of
M G(D). Then, C (I
m
,D) = {i ∈ 1..n | m(q
i
) = 1}
holds. Assume that I
m
is not a minimal generator.
Then there exists a ∈ I
m
such that C(I
m
,D) = C (I
m
\
{a},D). Then, m\{p
a
} is a model of M G(D). Thus,
we get a contradiction since m is a minimal model of
M G(D). Therefore, I
m
is a minimal generator in the
transaction database D.
8 CONCLUSION AND
PERSPECTIVES
We proposed approaches for generating all the mini-
mal models in two particular classes of CNF formulæ.
The first class is that of PN formulæ which are defined
as CNF formulæ where each clause is either positive
On Enumerating All the Minimal Models for Particular CNF Formula Classes
409

or negative, whereas the second class is that of PH for-
mulæ in which each clause is either positive or a Horn
clause. The first contribution consists in showing that
the problem of determining whether a model is mini-
mal is tractable in the case of PN formulæ, whereas it
is coNP-complete in the case of PH formulæ. Then,
we introduced our first approach for enumerating all
the minimal models of a PN formula, which is based
on the use of an algorithm for generating the minimal
transversals. We also proposed a SAT-based encoding
for enumerating all the minimal models of a PN for-
mula. Next, we provided an interesting characteriza-
tion of the minimal models in the case of PH formulæ
that allows us to use our approaches in the case of PN
formulæ for enumerating the minimal models for the
PH formulæ. Finally, we described a simple modeling
example in datamining.
As a future work, we intend to implement and
evaluate the proposed methods for generating the
minimal models. We also plan to use similar ap-
proaches for other formula classes.
REFERENCES
Angiulli, F., Ben-Eliyahu-Zohary, R., Fassetti, F., and
Palopoli, L. (2014). On the tractability of minimal
model computation for some CNF theories. Artificial
Intelligence, 210:56–77.
Avin, C. and Ben-Eliyahu-Zohary, R. (2001). Algorithms
for computing x-minimal models. In Logic Program-
ming and Nonmonotonic Reasoning, 6th International
Conference, LPNMR 2001, Vienna, Austria, Proceed-
ings, pages 322–335.
Ben-Eliyahu, R. and Dechter, R. (1996). On computing
minimal models. Annals of Mathematics and Artifi-
cial Intelligence, 18(1):3–27.
Ben-Eliyahu-Zohary, R. (2000). A demand-driven algo-
rithm for generating minimal models. In Proceedings
of the 17th National Conference on Artificial Intelli-
gence and 12th Conference on on Innovative Applica-
tions of Artificial Intelligence, USA, pages 267–272.
Ben-Eliyahu-Zohary, R. (2005). An incremental algorithm
for generating all minimal models. Artificial Intelli-
gence, 169(1):1–22.
Ben-Eliyahu-Zohary, R., Angiulli, F., Fassetti, F., and
Palopoli, L. (2017). Modular construction of minimal
models. In Logic Programming and Nonmonotonic
Reasoning - 14th International Conference, LPNMR
2017, Finland, Proceedings, pages 43–48.
Bidoit, N. and Froidevaux, C. (1987). Minimalism sub-
sumes default logic and circumscription in stratified
logic programming. In Proceedings of the Symposium
on Logic in Computer Science (LICS ’87), USA, pages
89–97.
Boudane, A., Jabbour, S., Sais, L., and Salhi, Y. (2017).
Enumerating non-redundant association rules using
satisfiability. In Advances in Knowledge Discov-
ery and Data Mining - 21st Pacific-Asia Conference,
PAKDD 2017, South Korea, Proceedings, Part I,
pages 824–836.
Boumarafi, Y., Sais, L., and Salhi, Y. (2017). From SAT to
maximum independent set: A new approach to char-
acterize tractable classes. In LPAR-21, 21st Inter-
national Conference on Logic for Programming, Ar-
tificial Intelligence and Reasoning, Botswana, pages
286–299.
Cadoli, M. (1992a). The complexity of model checking
for circumscriptive formulae. Information Processing
Letters, 44(3):113–118.
Cadoli, M. (1992b). On the complexity of model finding
for nonmonotonic propositional logics. In 4th Ital-
ian conference on theoretical computer science, pages
125–139.
Crawford, J. M. and Auton, L. D. (1993). Experimental re-
sults on the crossover point in satisfiability problems.
In Proceedings of the 11th National Conference on Ar-
tificial Intelligence (AAAI-93), USA., pages 21–27.
Fredman, M. L. and Khachiyan, L. (1996). On the com-
plexity of dualization of monotone disjunctive normal
forms. Journal of Algorithms, 21(3):618–628.
Gelfond, M. and Lifschitz, V. (1988). The stable model
semantics for logic programming. In Logic Program-
ming, Proceedings of the Fifth International Confer-
ence and Symposium, Seattle, Washington, (2 Vol-
umes), pages 1070–1080.
H
´
ebert, C., Bretto, A., and Cr
´
emilleux, B. (2007). A data
mining formalization to improve hypergraph minimal
transversal computation. Fundamenta Informaticae,
80(4):415–433.
Jabbour, S., Sais, L., and Salhi, Y. (2017). Mining top-k
motifs with a sat-based framework. Artificial Intelli-
gence, 244:30–47.
Khachiyan, L., Boros, E., Elbassioni, K. M., and Gur-
vich, V. (2005). A new algorithm for the hyper-
graph transversal problem. In Computing and Combi-
natorics, 11th Annual International Conference, CO-
COON 2005, China, Proceedings, pages 767–776.
Khachiyan, L., Boros, E., Elbassioni, K. M., and Gurvich,
V. (2007). A global parallel algorithm for the hyper-
graph transversal problem. Information Processing
Letters, 101(4):148–155.
McCarthy, J. (1980). Circumscription - a form of non-
monotonic reasoning. Artificial Intelligence, 13(1-
2):27–39.
Niemel
¨
a, I. (1996). A tableau calculus for minimal
model reasoning. In Theorem Proving with Ana-
lytic Tableaux and Related Methods, 5th International
Workshop, TABLEAUX’96, Italy, 1996, Proceedings,
pages 278–294.
Reiter, R. (1987). A theory of diagnosis from first princi-
ples. Artificial Intelligence, 32(1):57–95.
Tseitin, G. (1968). On the complexity of derivations in the
propositional calculus. In Slesenko, H., editor, Struc-
tures in Constructives Mathematics and Mathematical
Logic, Part II, pages 115–125.
Zaki, M. J. (2004). Mining non-redundant association rules.
Data Mining and Knowledge Discovery, 9(3):223–
248.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
410
