
“Coherent Transitions” and Rabi-type Oscillations between Spatial
Modes of Classical Light
A. V. Bogatskaya
1,2,3
, N. V. Klenov
1,3,4,5
,
A. M. Popov
1,2,4
and A. T. Rakhimov
1,4
1
Skobeltsyn Institute of Nuclear Physics, Moscow State University, 119991, Moscow, Russia
2
Lebedev Physical Institute, RAS, Moscow, 119991, Russia
3
Moscow Technical University of Communication and Informatics, 111024, Moscow, Russia
4
Department of Physics, Moscow State University, 119991, Moscow, Russia
5
MIREA – Russian Technological University, 119454, Moscow, Russia
Keywords: Optical Mechanical Analogy, Slow-varying Amplitude Approximation, Schroedinger Equation, Rabi
Oscillations, Light Beam Propagation in Inhomogeneous Media.
Abstract: In this paper we apply approaches and concepts from quantum mechanics to analyze the propagation of
classical electromagnetic waves in the elements of integrated optical circuits. We consider here regions of
transparent materials as potential wells between barriers of complex shape formed by opaque media. This
allows us to build an analogy between coherent oscillations in a quantum system and the redistribution of
the field strength of a classical wave in space in the framework of the slow-varying amplitude
approximation for the wave equation. We also demonstrate the possibility of controlling the mode
composition of a classical light in a spatially inhomogeneous waveguide structure. The proposed description
is based on the analogy with Rabi-type oscillations in quantum mechanics.
1 INTRODUCTION
Photons (electromagnetic wave-packets) interact
only weakly with an optically transparent medium
but not with each other; they have several degrees of
freedom for encoding of information (including
quantum information) and provide fast propagation
speed. So they are an attractive choice for creating
information processing networks (Shvartsburg,
2007; Knill et al, 2001; Bogdanov et al, 2016;
Kovalyuk et al, 2013; Khasminskaya et al, 2016;
Crespi et al, 2013; Tillmann et al, 2013). Nowadays
the implementation of several computational
protocols with photons is possible in free space, but
the requirement for a large number of optical
components and their precise configuration push for
new solutions. Integrated optical circuits seems to be
the most promising due to their scalability, stability,
no need for optical alignment as well as low power
consumption and compatibility with traditional
electronic circuits.
For the realization of such circuits silicon
gallium arsenide and diamond platforms have been
suggested. Each idea has its own advantages and
disadvantages and is currently in different stages of
development (Bogdanov et al, 2016). Nevertheless,
all of these platforms rely on combining single
photon sources (e.g. carbon nanotube), detectors
(e.g. superconducting nanowire single-photon
detectors) and linear optical elements (e.g. silicon-
nitride waveguides). Some proof-of-principle
concepts have already been implemented on a single
chip (Khasminskaya et al, 2016). And in this article
we propose a new approach to the analysis of
nontrivial processes of light pulse propagation in
structures along linear waveguides, interconnects
and splitters.
We have already accomplished the analysis of
tunneling processes for electromagnetic waves in
opaque media regions on the basis of the well-
known optical-mechanical analogy to solve the
urgent communication blackout problem
(Bogatskaya, et al, 2018a) as well as for increasing
of the efficiency of bolometric photodetectors
(Bogatskaya, et al, 2018b).
Bogatskaya, A., Klenov, N., Popov, A. and Rakhimov, A.
“Coherent Transitions” and Rabi-type Oscillations between Spatial Modes of Classical Light.
DOI: 10.5220/0007257500970101
In Proceedings of the 7th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2019), pages 97-101
ISBN: 978-989-758-364-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
97

2 NONSTATIONARY
SCHROEDINGER EQUATION
IN OPTICS
Let us consider spatially inhomogeneous
nonmagnetic medium characterized by the
susceptibility
)(r
, or permittivity
)(41)( rr
. Let us also suppose that these
functions are slowly varying functions in space
k
(here
2k
is the wave vector and
is the wave length) Then for the linearly
polarized electromagnetic wave with slowly varying
amplitude propagating in z - direction
))(exp()(),(
0
tkzirEtrE
, (
00
kEE
,
/2 с
is the radiation frequency) we can use
the well-known slow-varying amplitude
approximation that results in the equation
(Akhmanov and Nikitin, 1997)
EzrE
z
E
ik ),(
2
1
0
2
0
.
(1)
Here
yxr ,
are coordinates perpendicular to the
propagation direction,
2
is the Laplace operator
over these coordinates and
),(2),(
2
zrkzr
. The equation (1) is
mathematically similar to the nonstationary
Schroedinger equation for the particle motion in two
-dimensional space
yxr ,
:
),(),(),(
2
2
2
trtrVtr
mt
i
.
(2)
The mathematical identity of equations (1) and (2) is
the basis of so-called optical-mechanical analogy
(Bohm, 1952) being widely used nowadays for
analyzing of different problems both in quantum
theory and wave optics. The time evolution of wave
function of a one(two)-dimensional quantum system
turns out to be analogous to the problem of
calculating of electric field strength amplitude in a
light beam propagating in an inhomogeneous
medium. The coordinate z along which the light
beam propagates is analogous to the time t in
quantum theory, and the function
),( zr
determined by the susceptibility of the medium has
the meaning of a potential
),( trV
. In particular, if
),( zr
=0 (vacuum) then the problem (1) is
equivalent to the study of free particle motion.
We will start our study from the situation when
the media susceptibility depends on only
perpendicular coordinate (
)(
r
). Such
situation is similar to the stationary (time
independent) potential in quantum theory
(
)(
rVV
). Then general solution of eq.(2) can be
found as a superposition of initially populated
stationary states with amplitudes
n
C
:
n
nnn
tiErCtr )/exp()(),(
.
(3)
Here wave functions and energies of stationary
states should be found from the stationary
Schroedinger equation
)()()(
2
2
2
rErrV
m
nnn
.
(4)
By analogy with quantum mechanics we can find the
solution of problem (1) in a form
n
n
nn
z
k
irRCtrE
2
exp)(),(
2
0
.
(5)
where
)(
rR
n
and
n
obey the eigenvalue problem
similar to (4):
0)()(4
222
rRrk
nn
.
(6)
The solution of (6) gives rise to a number of
transverse modes in the beam propagating in z -
direction. We use the following normalization
condition for eigenfunctions
)(
rR
n
:
2
0
2
0
2
8
)( LrdrR
n
.
(7)
Here
0
is the normalization field constant (this
value can be chosen arbitrary),
2
0
L
- normalization
volume.
The solution of eigenvalue problem (6) gives
rise to a number of transverse modes of light beam
propagating in our structure.
Now we will study the possibility to control the
"population" of transverse modes. Let us suppose
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
98
that dielectric layer parameters (its thickness or
permittivity) are slightly modulated along z -
direction. In this case we can write the "potential"
function
),( zr
in a form
),()(),(
10
zrrzr
.
(8)
where the first term in the right part determines the
parameters of the layer discussed above while the
second one provides the spatial modulation of the
layer. We will suppose that
)cos()(),(
1
Kzrzr
.
(9)
with
)()(
0
rr
. Here
K
is the wave vector
of the longitudinal structure. Then the additional
term in (8) can be taken into account as small
perturbation to the "potential"
)(
0
r
. The
additional perturbation will cause the coherent
transitions between transverse modes of the beam
similar to the transitions between atomic states
caused by the external perturbation, for example,
laser field action. The transitions are governed by
the set of equations
Kzz
k
i
MzC
dz
dC
ik
nf
n
fin
f
cos)(
2
exp)(
22
.
(10)
which are similar to those obtained in quantum
mechanical theory of light-atom interaction. Here
rdrRrrR
L
M
nffi
)()()(
8
*
2
0
2
0
.
(11)
If we restrict ourselves by the first order of
perturbation theory the expression for the probability
of transition between different modes reads
.)2(
2
exp
2
)(
22
zKk
k
i
M
k
i
dz
zdС
iffi
f
(12)
where
i
R
stands for the initially excited mode. We
see that if
02
22
Kk
if
the coherent
transitions between the transverse modes are
possible.
3 COHERENT CONTROL OF
CLASSICAL LIGHT BEAM
To be more specific let us consider a light beam
propagating along the one-dimensional uniform
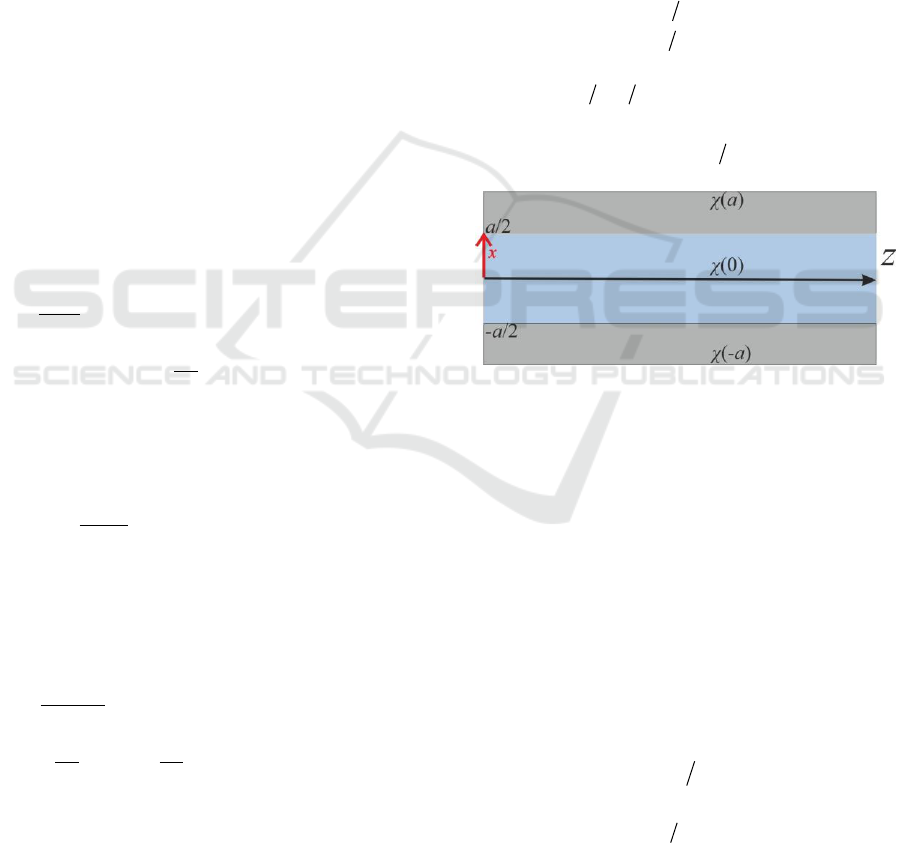
dielectric layer of thickness a and permittivity
1
0
covered by dielectric substrate with
permittivity
)(a
close to unity (see Fig.1). Such a
structure is similar to the one-dimensional potential
well that contains a number of discrete levels. Under
the assumption that this "well" is deep the problem
(5), (6) has approximate solution
,...6,4,2),sin(
,...5,3,1),cos(
~)(
naxn
naxn
xR
n
(13)
where
)2,2( aax
and
2
0
22
4 ank
n
.
(14)
Figure 1: The three-layer planar structure. The central
layer is characterized by the susceptibility greater than the
covering layers. Such a structure represents the "potential
well" for the propagation beam and can prevent it from the
diffraction divergence.
These modes are stable against the diffraction
divergence along the beam propagation. Any
superposition of these modes is also stable against
the divergence. Nevertheless, superposition of
different transverse modes results in specific spatial
beam oscillations and reconstruction during its
propagation along the structure. For example, if only
two lowest transverse modes are populated the
spatial period of these oscillations will be given by
the expression
34
2
kaL
.
(15)
For example, if
4
102
k
cm and
3
10
a
cm one obtains
027.0L
cm. For the above
mentioned parameters transverse mode oscillations
are presented at. Fig.2.
“Coherent Transitions” and Rabi-type Oscillations between Spatial Modes of Classical Light
99
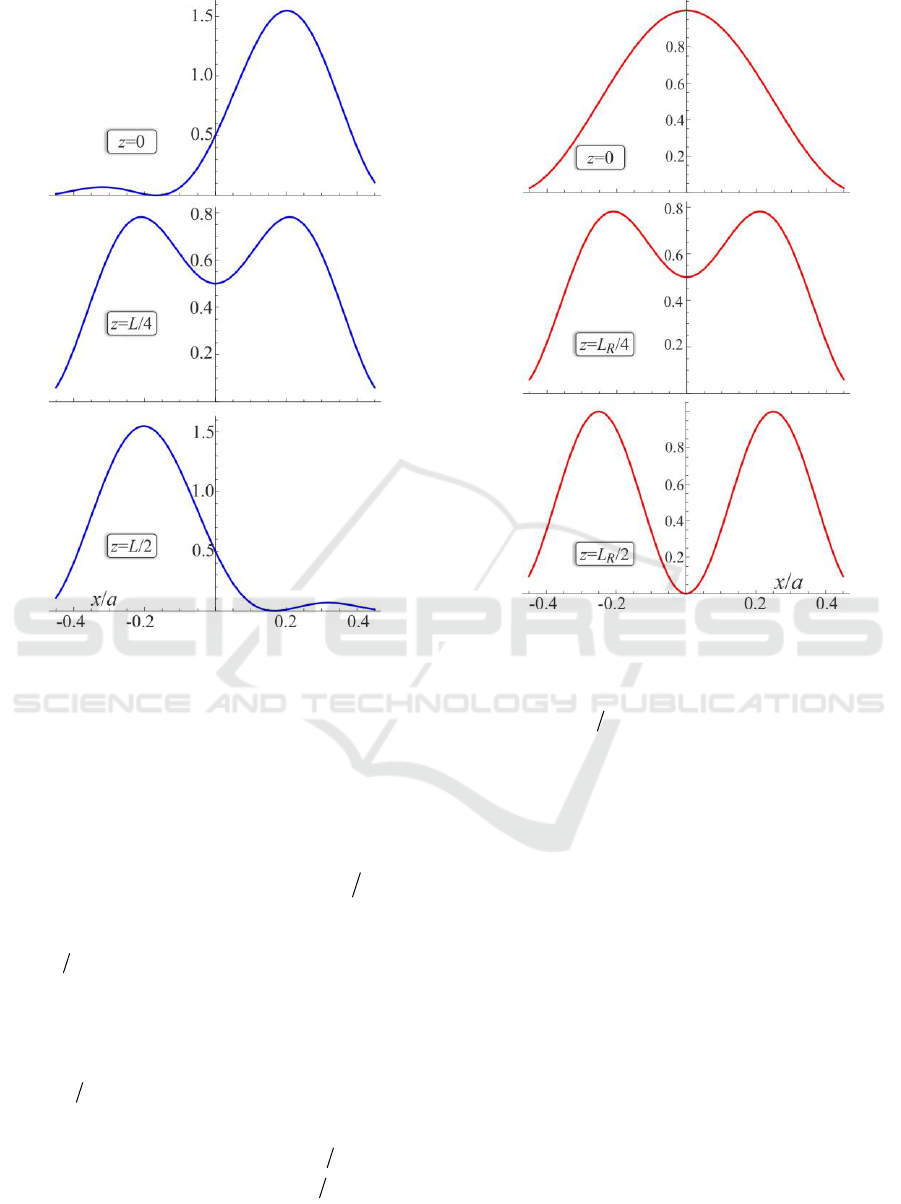
Figure 2: Illustration to the spatial beam oscillations and
reconstruction during its propagation along the fiber-like
structure for the case of initially excited two lowest
transverse modes.
More interesting situation is the possibility of Rabi -
type oscillations. Here we mean the energy transfer
from one mode to another and back in a spatially
inhomogeneous waveguide. For example, for two
lowest modes (
)2,1 fi
such Rabi - type
oscillations are possible if
kK 2)(
2
1
2
2
. For
our simple one-dimensional structure discussed
above this relation is satisfied for the period
K
2
of the longitudinal structure given by
(15). The length of the structure
R
L
(Rabi length)
for the total conversion of the energy from the one
transverse mode to another and back depends on the
matrix element (11) and is given by the expression:
21
4 MkL
R
. If we suppose that
)(2)(
2
xkx
with
)(x
given by the step-
like structure
),2,0(,1
),0,2(,1
)(
0
ax
ax
x
it is
easy to obtain
0
2
21
kM
. For
001.0
0
one
Figure 3: Rabi - type oscillations between two lowest
transverse modes in a spatially inhomogeneous
waveguide.
obtains
01.0~~
0
R
L
cm. Typical distribution
of electromagnetic energy in the regime of Rabi-type
oscillation between two lowest spatial modes is
presented at fig.2.
4 CONCLUSIONS
Thus, the discussed coherent oscillations of the
spatial structure of the light beam as well as the
Rabi-type oscillation can be observed in experiments
with photonic circuits designed for bosonic sampling
simulations (Spring, et al, 2013; Lund, et al, 2014;
Motes, et al, 2015). Even in the simplest Y-splitter
in order to demonstrate the idea we can launch light
with different weights of only two modes to the
single input. This test will lead to the radiation
intensities at two outputs, governed by the geometric
dimensions of the structure according to the
formulas given above. In the future, the use of
superposition of various classical light modes in
such networks together with the proposed spatial
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
100

methods of control, can be useful in solving of a
number of practical problems of analog modeling.
ACKNOWLEDGMENTS
This work was supported by the Russian Foundation
for Basic Research (projects 16-29-09515-ofi_m,
18-02-00730).
REFERENCES
Akhmanov, S. A., Nikitin, S. Yu. 1997. Physical Optics
Clarendon Press.
Bogatskaya, A. V., Klenov, N. V., Tereshonok, M. V.,
Adjemov, S. S., Popov, A. M. 2018a. J. Phys. D: Appl.
Phys., 51, 185602.
Bogatskaya, A. V., Klenov, N. V., Tereshonok, M. V.,
Popov, A. M. 2018b. Tech. Phys. Lett., 44, № 15, 29.
Bogdanov, S., Shalaginov, M. Y., Boltasseva, A., Shalaev,
V. M. 2016. Opt. Mater. Express, 7, 111.
Bohm, D. 1952. Quantum theory N.Y., Prentice-Hall, Inc.
Crespi, A., Osellame, R., Ramponi, R., Brod, D. J.,
Galvao, E. F., Spagnolo, N., Sciarrino, F. 2013. Nature
Photonics, 7(7), 54.
Knill, E., Laflamme, R. and Milburn, G. J. 2001. Nature
409, 46.
Khasminskaya, S., Pyatkov, P., Słowik, K., Ferrari, S.,
Kahl, O., Kovalyuk, V., Rath, P., Vetter, A.,
Hennrich, F., Kappes, M. M., Gol’tsman, G.,
Korneev, A., Rockstuhl, C., Krupke, R., and Pernice,
W. H. P. 2016. Nat. Photonics, 10, 727 .
Kovalyuk, V., Hartmann, W., Kahl, O., Kaurova, N.,
Korneev, A., Goltsman, G., and Pernice, W. H. P.
2013. Opt. Express, 21, 22683.
Lund, A. P., Laing, A., Rahimi-Keshari, S., Rudolph, T.,
O’Brien, J. L., and Ralph, T. C. 2014. Phys. Rev.
Lett., 113, 100502.
Motes, K. R., Olson, J. P., Rabeaux, E. J., Dowling, J. P.,
Olson, S. J., and Rohde, P. P. 2015. Phys. Rev. Lett.,
114, 170802
Shvartsburg, A. B. 2007. Phys. Usp., 50, 37.
Spring, J. B., Metcalf, B. J., Humphreys, P. C.,
Kolthammer, W. S., Jin, X. M., Barbieri, M., & Gates,
J. C. 2013. Science, 339(6121), 798.
Tillmann, M., Dakić, B., Heilmann, R., Nolte, S., Szameit,
A., Walther, P. 2013. Nature Photonics, 7(7), 540.
“Coherent Transitions” and Rabi-type Oscillations between Spatial Modes of Classical Light
101
