
Implementation of Trajectory Planning for Automated Driving Systems
using Constraint Logic Programming
Christian Wriedt
1
and Christoph Beierle
2
1
Audi Electronics Venture GmbH, Sachsstr. 20, 85080 Gaimersheim, Germany
2
Department of Computer Science, FernUniversit
¨
at in Hagen, 58084 Hagen, Germany
Keywords:
Constraint Logic Programming, Trajectory Planning, Automated Driving Systems, ADAS, Autonomous
Driving, Explainable AI.
Abstract:
Automated driving systems are a maturing technology that is considered to have a significant impact on
mobility. Trajectory Planning is a safety-critical task that plays an important role in automated driving
systems. In this paper, we present the implementation of a trajectory planning module called CLPTP
(CLPTRAJECTORYPLANNER) using constraint logic programming (CLP) and evaluate it in simulated traf-
fic situations. CLP allows us to express the constraints of the problem of trajectory planning in a declarative
way. The approach makes the code less complex and more readable for domain experts compared to code
using an imperative programming language. Compared to approaches making use of neural networks to man-
age the complexity of the problem of trajectory planning, the results of CLPTP are more comprehensible and
easier to verify. Thus CLPTP can be seen as a step towards solving the problem of trajectory planning with
explainable artificial intelligence. An evaluation of the execution time performance of our implementation
shows that further research is needed to apply the approach in real world vehicles.
1 INTRODUCTION
In the past few decades, the level of automation in
road vehicles has been steadily increasing, result-
ing in a significant decrease of traffic accidents (ITF,
2017). Not only safety, but also accessibility, con-
venience and efficiency of automotive mobility are
expected to be enhanced by automated driving sys-
tems (Paden et al., 2016; Arbib and Seba, 2017).
Although many different automated driving sys-
tems are known to exist in research and development
projects, most of them share a similar functional ar-
chitecture in which the driving task is split in three
parts: Perception, decision and control, vehicle plat-
form manipulation (Behere and T
¨
orngren, 2015). De-
cision and control is typically divided into three lev-
els: route planning, behavioural decision making and
trajectory planning (Paden et al., 2016).
It is the responsibility of the trajectory planning
level to find a safe, comfortable and dynamically fea-
sible trajectory for the vehicle in its dynamic envi-
ronment. Due to space limitations, this paper focuses
on trajectory planning. Other related problems such
as object movement prediction or trajectory execution
are not discussed in this paper. The problem of trajec-
tory planning can be formulated as an optimization
problem with constraints imposed by traffic rules, the
dynamic environment, vehicle dynamics etc. Many
algorithms have already been developed for solving
this problem. Some of them represent vehicle states
in the form of a graph and use search algorithms like
A* (Hart et al., 1968) for finding a minimum cost path
on the graph (Ziegler and Stiller, 2009; Gu and Dolan,
2012). Other solutions describe trajectories as poly-
nomials that are optimized under consideration of a
cost functional (Werling, 2011; McNaughton, 2011;
Kelly and Nagy, 2016; Rathgeber, 2016). Aside from
that, there are other implementations e.g. based on
neural networks and reinforcement learning (Dubey
et al., 2013; Zuo et al., 2014; Grigorescu et al., 2017).
Refer to (Paden et al., 2016) for a detailed presenta-
tion of the trajectory planning problem and an exten-
sive survey of motion planning techniques for self-
driving vehicles.
Translating the aforementioned constraints of the
problem of trajectory planning into software code can
be a challenging task when using imperative program-
ming languages because the specification of the con-
straints are often present as declaratively written re-
quirements in natural language or in formal or semi-
Wriedt, C. and Beierle, C.
Implementation of Trajectory Planning for Automated Driving Systems using Constraint Logic Programming.
DOI: 10.5220/0007257904110418
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 411-418
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
411
formal notations. Moreover, operational details in im-
perative code make it hard to read for domain experts
and more difficult to verify, which is an important as-
pect for safety-critical software. Approaches using
neural networks overcome the challenging program-
ming task by learning desired planning behaviour
implicitly. However, verifying neural networks for
safety-critical systems, where international standards
such as ISO 26262 (ISO, 2011) must be applied, is
still an open problem (Grigorescu et al., 2017).
In this paper, we present the design and implemen-
tation of a trajectory planning module called CLPTP
(CLPTRAJECTORYPLANNER). CLPTP uses con-
straint logic programming (CLP), a programming
paradigm enhancing the declarative paradigm of logic
programming by mechanisms for specifying and solv-
ing constraints. By using this programming paradigm
with its high level of abstraction, program code is ex-
pected to be easier to understand and more concise
than its imperative counterpart. The planning results
are expected to be more comprehensible and easier
to verify than the output of a neural network, thus
supporting the trend for explainable artificial intelli-
gence (Biran and Cotton, 2017) with a different ap-
proach than e.g. (Bojarski et al., 2017).
Logic programming has already been used in (Pi-
aggio and Sgorbissa, 2000) for the symbolic compo-
nent of an autonomous robot navigator. CLP has been
successfully used to implement programs for solving
general planning and optimization problems (Lever
and Richards, 1994; Apt and Wallace, 2006). How-
ever, no attempt to apply CLP to the specific problem
of trajectory planning seems to exist yet.
In Section 2, we present the background of trajec-
tory planning as far as needed here. In Section 3, the
design and implementation of CLPTP is described,
Section 4 contains an evaluation of the system, and
Section 5 concludes and points out further work.
2 TRAJECTORY PLANNING
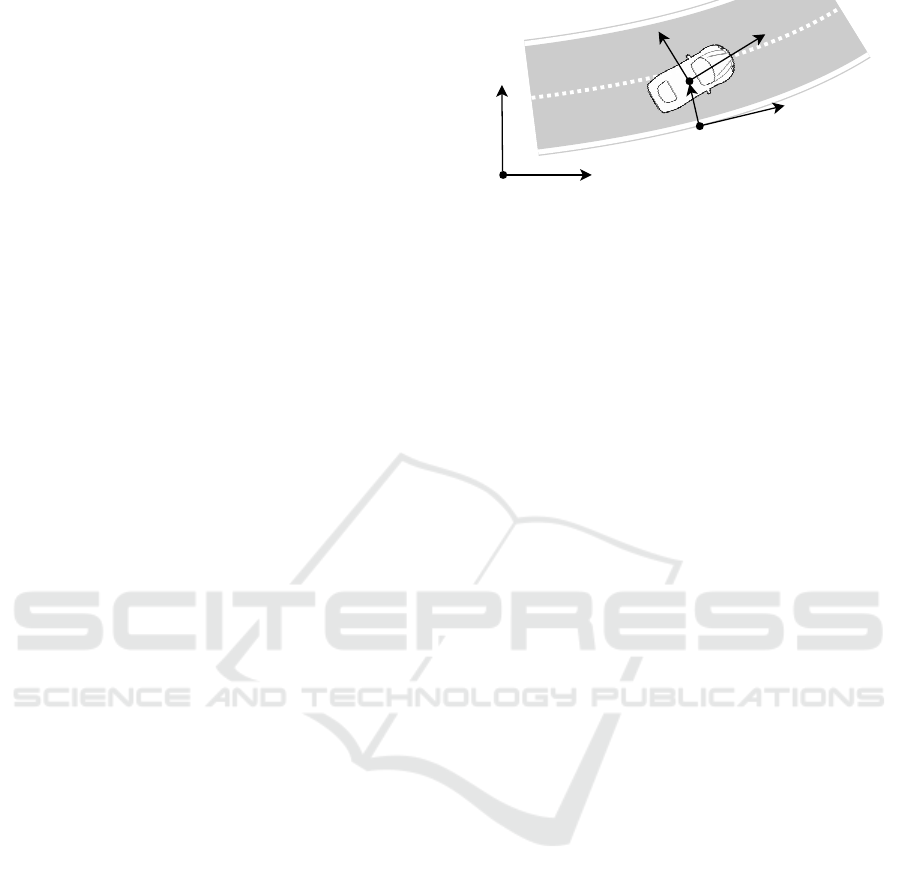
Modeling Mobility of a Vehicle. Mobility of a ve-
hicle can be modeled beginning with the notion of a
vehicle configuration, representing its position in the
world (Paden et al., 2016). In this paper, configura-
tion is expressed as the planar coordinate of the vehi-
cle center. Rather than directly using cartesian coor-
dinates in some world coordinate system with a fixed
base or the body frame of the vehicle, we use the dy-
namic Frenet frame (Bauchau, 2011) as the coordi-
nate system for the vehicle configuration space. The
Frenet frame is commonly used for trajectory plan-
ning implementations. As depicted in Figure 1, it is
0
y
w
x
w
s
r
d
r
P
v
x
v
y
v
P
r
Figure 1: Coordinate systems used for automated driving
systems: world coordinate system F
w
= {0, x
w
, y
w
}, vehicle
coordinate system F
v
= {P
v
, x
v
, y
v
} (body frame), road co-
ordinate system F
r
= {P
r
, x
r
, y
r
} (Frenet frame, commonly
used in implementations of trajectory planning) (Rathgeber,
2016).
given by the tangential and normal vector at a certain
point of some curve referred to as the centerline in
the following (Werling et al., 2010). The centerline
either represents an ideal path along a free lane or the
result of a path planning algorithm for unstructured
environments (Werling et al., 2010). Hence a position
in the configuration space of the vehicle is expressed
as a longitudinal offset s
r
along the straightened cen-
terline and a perpendicular lateral offset d
r
.
The Problem of Trajectory Planning. Trajectories
prescribe the evolution of the configuration of a vehi-
cle in time. So in theory, a trajectory is a continuous
time-parameterized function π(t) : [0, T ] → X , where
T is the planning horizon and X is the configuration
space of the vehicle (Paden et al., 2016). The trajec-
tory planning problem is to find a trajectory that starts
at the initial vehicle configuration x
init
∈ X and satis-
fies given requirements or constraints.
Trajectory planning for automated vehicles has a
high computational cost for most real world scenar-
ios because of their complexity resulting from the
number of dynamic and static objects. One possi-
bility to reduce the computational cost is to split the
planning into a general planning and a detailed plan-
ning (Rathgeber, 2016). In general planning, the
whole available space is considered (e.g. multiple
lanes on a highway) and a reduced target space is de-
termined for the trajectory. In detailed planning, only
this reduced space has to be considered for the opti-
mization of the exact trajectory shape.
Because of space limitations and the goal of this
paper to rather demonstrate the application of CLP to
the problem of trajectory planning instead of develop-
ing a new algorithm, we only present the implemen-
tation of a general trajectory planning module. The
presented approach is also applicable to detailed tra-
jectory planning, but rather demanding on resources
(cf. Section 4).
Our implementation strongly discretizes the con-
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
412

Table 1: Quantization of the 4-dimensional configuration
space of the vehicle.
Coordinate Quantization step
size
s (longitudinal offset) 1 cm
d (lateral offset) 1 centerline
v (longitudinal velocity) 1 cm
2
s
−1
a (longitudinal acceleration) 20 cm
3
s
−1
figuration space of the vehicle in lateral direction so
that only the centerline or lines parallel to the cen-
terline (e.g. on a multi-lane road) are considered as
valid configurations. This approximation is sufficient
for general trajectory planning and increases execu-
tion performance. Time is discretized in a way that
vehicle configurations can be planned at arbitrary dis-
crete time instances t
k
= k ·∆t with ∆t = 1s and k ∈ N.
As planned vehicle configurations are supposed to
be eventually passed to a vehicle controller for execu-
tion, they do not only contain position coordinates in
our implementation, but also values for velocity and
acceleration in longitudinal direction. This means that
the configuration space is 4-dimensional. As a simpli-
fication for ease of demonstration, we assume center-
line changes to be completed within one configura-
tion transition, so lateral velocity, steering etc. must
not be considered. Furthermore, both centerlines are
assumed to be blocked on the occasion of a (lane)
change.
For efficiency reasons, the implementation pre-
sented here uses CLP over finite domains (CLP(FD))
instead of e.g. CLP over reals (CLP(R)). Thus con-
straint variables can only be bound to integer values,
so the vehicle configuration space must be quantized
considering the conflicting goals of high accuracy and
small configuration space. Table 1 summarizes our
choice of configuration space quantization.
3 DESIGN AND
IMPLEMENTATION OF CLPTP
System Overview. With logic programming, elegant
programs solving complex problems can be imple-
mented by applying the generate-and-test technique.
Such a program consists of one (often very sim-
ple) predicate generating possible solutions and an-
other predicate checking the solution for correctness.
Thereby the search for a solution is accomplished by
the interpreter’s backtracking mechanism rather than
by an explicitly stated (and often difficult to find) al-
gorithm. It is easy to realize that this approach is
infeasible for problems with big solution spaces in
practice. With CLP, the generate-and-test technique
can be improved to a constrain-and-generate pattern,
where the solution space is narrowed down by con-
straints, thereby increasing the efficiency of solution
search or optimization, but still separating concerns
very well. Therefore, the general structure of our im-
plementation is based on this programming technique.
All code presented in this paper has been devel-
oped using SICStus Prolog (Carlsson and Mildner,
2012). SICStus Prolog supports CLP(FD). When-
ever we mention predefined predicates or interpreter-
specific details, we refer to SICStus Prolog. With
respect to our approach, other Prolog variants sup-
porting CLP(FD) like SWI-Prolog (Wielemaker et al.,
2012) or GNU-Prolog (Diaz, 2001; Diaz et al., 2012)
are very similar in most aspects.
Before starting to actually define predicates that
describe the problem of trajectory planning, we need
to define how to represent trajectories, vehicle config-
urations and environmental elements such as objects.
A trajectory is represented by a list of vehicle con-
figurations at discrete time instances. Vehicle config-
urations are represented by program terms conf(T,D
,S,V,A), where T denotes the discrete time instance
this configuration belongs to and D, S, V and A are the
four dimensions of the quantized configuration space
as outlined in Table 1. General vehicle parameters,
quantization factors etc. are expected to be supplied
by the predicate param/2 that implements some kind
of key-value-store. Parameters could also be time- or
position-parameterized in principle. Lateral bound-
aries of the configuration space (i.e. road boundaries
in a particular planning situation) are modeled by
two predicates left_boundary/2 and right_boundary
/2 dependent on the longitudinal offset s. Recognized
objects are modeled in the clause database as facts
object(ID,T,D,SR,SF,V), where ID uniquely identi-
fies an object, T is the time the recognition is valid
for, D denotes the lateral coordinate (i.e. the center-
line) of the object, SR/SF are the longitudinal offsets
of the rear/front object boundaries, respectively, and
V denotes the longitudinal velocity of the recognized
object. Speed limits are modeled similar to objects by
a predicate speed_limit(S,V). S is the longitudinal
offset from where on the limit with value V is valid.
Now we can describe the two main predicates
our implementation consists of. They are given in
Listing 1. optimal_trajectory/3 is the high-level
predicate expected to be called by the user. It re-
lates an initial vehicle configuration and a list of dis-
crete time instances to an optimized trajectory. It
is based on the constrain-and-generate technique ex-
plained above. Two helper predicates trajectory/4
and variable_order/2 are used to, firstly, prescribe a
feasible trajectory and its costs for optimization and,
Implementation of Trajectory Planning for Automated Driving Systems using Constraint Logic Programming
413

secondly, order the constraint variables of a list of
vehicle configurations (i.e. a trajectory) in a spe-
cific way that can be optimized for an efficient la-
beling strategy.
1
These helper predicates can be im-
plemented with fairly simple Prolog code and are
therefore not outlined in detail here. transition/3
constrains the variables of the second of two con-
secutive vehicle configurations and relates costs to
this transition in the configuration space. It makes
use of four helper predicates vehicle_motion/2,
collision_avoidance/3, speed_limit_compliance/3
and costs/3 that encapsulate the implementation of
various requirements or constraints of trajectory plan-
ning. The implementation of these predicates is ex-
plained in detail hereafter.
Listing 1: Predicates implementing general trajectory plan-
ning using CLP(FD). The predicates findall/3, setof/3,
minimize/2 and labeling/2 are part of the modules
aggregate and clpfd provided by SICStus Prolog.
op t i ma l _ tr a j ec t o ry ( InitialConf ,
TimeInstances , Traj e c t ory ) : -
tra j e c tory ( TimeI n s t a n c e s , In i t i a l C o n f
, Tr a jectory , Costs ) ,
sum ( Costs , #= , To t a l Cost s ) ,
va r i abl e _ ord e r ( T r a j ectory , Vars ) ,
minim i z e ( l a b el ing ([ lef t most , bisect ] ,
Va rs ) , Tota l C osts ) .
tra n s i tion ( Conf , Nex tConf , C o st ) : -
NextC o n f = con f (Te , De , Se , Ve , Ae ) ,
pa r a m ( vmax , Vmax ) , p a ram ( vmin , Vm in ) ,
Ve in V min .. Vmax ,
pa r a m ( amax , Amax ) , p a ram ( amin , Am in ) ,
Ae in A min .. Amax ,
ri g h t_b o u nda r y ( Se , Dmi n ) ,
lef t _ bou n d ary ( Se , Dmax ) ,
De in D min .. Dmax ,
ve h i cle _ m oti o n ( Conf , NextC o n f ) ,
findall (( ObjD , O bjRe ar , Obj F ront ,
Ob jV ) , ob j e c t (_ , Te , ObjD ,
Ob jRea r , ObjF r ont , Obj V ) , Obj e c t s
) ,
co l l is i o n_ a v oi d anc e ( Conf , NextC o nf ,
Objects ) ,
se t o f (( SLimit , Limit ) , s pee d _ l imi t (
SLimit , L i m i t ) , Vlimits ) ,
sp e e d_ l im i t _c o m pl i an c e ( Vlim its , Se ,
Ve ) ,
co s t s ( Conf , NextC onf , Cost ) .
Vehicle Motion. The most basic and important re-
lation between two vehicle configurations is given by
the motion of the vehicle. As we are not implement-
1
Labeling is the process of assigning values to constraint
variables that satisfy all present constraints. The inter-
preter’s predefined predicate labeling/2 accepts param-
eters to configure the labeling strategy (Carlsson, 2009).
ing detailed but general trajectory planning, accel-
eration of a configuration is considered to have the
meaning of a constant average acceleration for the
time period of the transition leading to the configu-
ration. Considering the already mentioned simplifica-
tions we can thus characterize vehicle motion by the
basic equations of motion for point masses with con-
stant acceleration a:
...
s
r
(t) = 0
¨s
r
(t) = a
˙s
r
(t) = at
s
r
(t) =
1
2
at
2
(1)
Listing 2 outlines a translation of these equations
into code using CLP(FD). Note that these constraints
already take into account the quantization presented
in Table 1.
Listing 2: Implementation of constraints among the vari-
ables of two consecutive vehicle configurations resulting
from the motion equations of a very simple vehicle model.
ve h i cle _ m oti o n ( c onf ( T0 , D0 , S0 , V0 , A0 ) ,
co nf ( Te , De , Se , Ve , Ae ) ) : -
pa r a m ( jmax , Jmax ) , p a ram ( jmin , Jm in ) ,
pa r a m ( aquant , AQuant ) ,
DT #= Te - T0 ,
De #= < D0 + 1, De # >= D0 - 1 ,
Ae #= < A0 + ( Jm ax / AQ u a n t ) * DT ,
Ae # >= A0 + ( Jm in / AQ u a n t ) * DT ,
Ve #= V0 + Ae * AQ u a n t * DT ,
Se #= S0 + ( V0 + ( Ae * ( AQuant / 2) *
DT ) ) * DT .
Collision Avoidance. After the application of basic
motion constraints, the configuration space of the to
be planned configuration can be narrowed down fur-
ther by imposing constraints on its position coordi-
nates. These constraints are most likely caused by ob-
stacles or objects such as other traffic participants and
therefore implement collision avoidance. An exam-
ple implementation assuming recognized objects be-
ing modeled as described in Section 3 is given in List-
ing 3. For all recognized objects, the constraints out-
lined in Listing 3 apply a static safety distance and a
safety time resulting in a dynamic velocity-dependent
safety distance to the coordinates of the vehicle con-
figuration. The value for the static safety distance
must take the vehicle dimensions into account.
Note that time discretization as explained above
can cause collisions with small objects in this im-
plementation. Therefore time instances must be cho-
sen carefully. This problem could also be solved by
adding an additional constraint regarding the coordi-
nates covered by the transition in the configuration
space.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
414

Listing 3: Implementation of constraints for the variables of
two consecutive vehicle configurations that ensure keeping
a static and dynamic safety distance to other objects.
co l l is i o n_ a v oi d anc e (_ , _ , []) .
co l l is i o n_ a v oi d anc e ( conf ( T0 , D0 , S0 , V0 , A0
) , con f (Te , De , Se , Ve , Ae ) , [( ObjD ,
Ob jRea r , Ob jFron t , Ob jV ) | Objs ]) : -
pa r a m ( s a f e t y _d is ta n ce , Ss ) , par a m (
sa f e t y _ t i m e , Ts ) ,
Sm in #= O b j R e a r - Ss - Ts * Ve ,
Sm ax #= O b j F r on t + Ss + Ts * ObjV ,
( De #= ObjD ) #= > (( Se # < Smin ) #\/ (
Se #> Smax ) ) ,
(( De #= ObjD ) # /\ ( De #\ = D0 ) ) #= > ((
S0 #< Smin ) #\/ ( S0 # > Smax ) ) ,
co l l is i o n_ a v oi d anc e ( conf ( T0 , D0 , S0 , V0 ,
A0 ) , conf ( Te , De , Se , Ve , Ae ) , O b js ) .
Speed Limits. By considering motion constraints
and collision avoidance, important requirements for
trajectory planning are satisfied. However, other con-
straints have to be taken into account as well, e.g.
the planned trajectory has to be compliant with traf-
fic rules. Listing 4 shows a possible implementation
of speed limit constraints as an example on how to
introduce traffic rules using CLP.
Listing 4: Constraints for the vehicle configuration vari-
ables S (longitudinal coordinate) and V (longitudinal veloc-
ity) implementing compliance with a list of speed limits. A
speed limit is expected to be represented by a coordinate
from where on the limit is valid and the value of the limit.
sp e e d_ l im i t _c o m pl i an c e ([] , _ , _ ).
sp e e d_ l im i t _c o m pl i an c e ([( SL imi t , V L i m i t
)] , S , V ) : -
(S # >= SLimit ) #= > ( V #= < VLimit ) .
sp e e d_ l im i t _c o m pl i an c e ([( S1 , VLimit1 ) ,
(S2 , VLimit2 ) | L i m i t s ] , S , V ) : -
(S # >= S1 # /\ S #< S2 ) #= > ( V #= <
VLimit1 ) ,
sp e e d_ l im i t _c o m pl i an c e ([( S2 , VLimit2 )
| Li m i t s ] , S , V ) .
Costs. Until now, we have specified and constrained
the relation between a number of discrete vehicle con-
figurations (represented by constraint variables over
finite domains) representing a planned trajectory (the
expected output of our general trajectory planning
module). We could now use the implemented pro-
gram to retrieve a feasible trajectory, i.e. bindings for
all the constraint variables, by using a predicate such
as labeling/2 provided by SICStus Prolog.
However, the goal of trajectory planning is to find
an optimal trajectory, not just any feasible trajectory.
Therefore we relate each vehicle configuration transi-
tion to some costs. These costs are combined to to-
tal costs which are used as the goal in the predicate
minimize/2, as it can be seen in Listing 1. On the exe-
cution of that predicate, the constraint variables repre-
senting vehicle configurations are unified with values
corresponding to the optimal solution for the queried
trajectory with respect to the specified costs. In List-
ing 5, the implementation of a predicate prescribing
the relation between costs and two consecutive dis-
crete vehicle configurations is given. This implemen-
tation considers the following costs each at which is
assigned a weight:
• C1: difference between planned velocity and de-
sired velocity. Desired velocity is assumed to be
the maximal velocity here but can of course be any
value e.g. set by the vehicle user.
• C2: acceleration
• C3: change in acceleration (jerk)
• C4: lane change
• C5: deviation from a measure representing a kind
of strategic lane advice determined by the upper
layers of decision and control. It is assumed that
this measure is represented by a value between 0
and 100 available via the predicate advice/3 for
every position that is relevant for the current plan-
ning cycle.
These costs and the weights assigned to them in List-
ing 5 serve as demonstrating examples in this paper.
In practice, they should be determined by theoretical
and empirical analysis.
Listing 5: Implementation of the predicate costs/3, giv-
ing the costs of a transition from one vehicle configuration
(indexed 0) to another vehicle configuration (indexed e).
co s t s ( con f ( T0 , D0 , S0 , V0 , A0 ) , conf ( Te , De ,
Se , Ve , Ae ) , Co s t s ) : -
advice ( De , Se , Advice ) ,
pa r a m ( vmax , V D es ir ed ) ,
C1 #= 50 * abs ( Ve - V De si re d ) ,
C2 #= 100 * abs ( Ae ) ,
C3 #= 100 * abs ( Ae - A0 ) ,
C4 #= 10 * abs ( De - D0 ) ,
C5 #= 30 * ( 1 00 - Ad v i c e ) ,
sum ([ C1 , C2 , C3 , C4 , C5 ], #= , C o s t s ).
4 EVALUATION
Functional Evaluation in Simulation. In this sec-
tion, trajectories returned by the presented general tra-
jectory planning module for two simulated traffic sit-
uations are visualized and discussed.
The first situation is visualized in Figure 2. Here,
the simulated environment is a road section with four
lanes that are separated by dashed lane markings.
Implementation of Trajectory Planning for Automated Driving Systems using Constraint Logic Programming
415

−1
0
1
2
d
r
0.8
0.5
0.2
0.0
Lane advice:
0
5
10
15
20
v[ms
−1
]
v
min
v
max
0 20 40 60 80 100 120 140
s
r
[m]
−4
−2
0
2
a[m
2
s
−1
]
a
min
a
max
Figure 2: Resulting trajectory (blue) calculated by CLPTP
for a simulated traffic situation consisting of 4 lanes, 4 other
dynamic objects with predicted movements (dark rectan-
gles) and 2 speed limits (red). Planning has been queried
for the discrete time instances 2 s, 4 s, 6 s and 8 s. At t = 0s,
the vehicle is in initial configuration.
Hence, lane changes are allowed. Two speed limits
exist at s
r
= 0m and s
r
= 50m, respectively. Further-
more, there are four dynamic objects in addition to
the ego vehicle moving with different velocities. A
simple object prediction assuming objects to continue
on their current lane with their current velocity is ap-
plied for ease of demonstration. Predicted object po-
sitions are visualized for the discrete time instances
2 s, 4 s, 6 s and 8 s, for which planning is executed.
At t = 0 s, the vehicle is in initial configuration. Val-
ues for strategic lane advice and important parameters
such as v
max
etc. are given in Figure 2 as well.
It can be seen that many requirements mentioned
in the previous section are fulfilled: Predictions of
other objects are considered. Strategic advice is taken
into account by a lane change. In general, velocity is
planned as high as possible. The second speed limit
results in an appropriate deceleration, but note that the
implementation in Listing 4 allows the vehicle to have
a velocity too high for the duration of one transition.
This could be adapted by an additional constraint for
the variable representing the velocity of the previous
configuration.
The second situation is visualized in Figure 3. It
is similar to the first situation but with the second
speed limit removed. Here, trajectory planning has
been queried for the time instances 3 s, 6 s, 9 s and 12 s
so that an overtaking maneuver can be demonstrated.
Due to the low velocity of the objects on the two
rightmost lanes, the results show that it is favourable
to change to the second leftmost lane despite its low
strategic advice in order to obtain a higher velocity.
This planning behaviour can of course be influenced
by the design of the costs that have been discussed in
−1
0
1
2
d
r
0.8
0.5
0.2
0.0
Lane advice:
0
5
10
15
20
v[ms
−1
]
v
min
v
max
0 20 40 60 80 100 120 140
s
r
[m]
−4
−2
0
2
a[m
2
s
−1
]
a
min
a
max
Figure 3: Resulting trajectory (blue) calculated by CLPTP
for a simulated traffic situation consisting of 4 lanes, 4 other
dynamic objects with predicted movements (dark rectan-
gles) and 1 speed limit (red). Planning has been queried for
the discrete time instances 3 s, 6 s, 9 s and 12 s. At t = 0 s,
the vehicle is in initial configuration.
Table 2: Execution time measurements for CLPTP (mea-
sured on a 2.5 GHz Intel
R
Core
TM
i5-2450M with SICStus
Prolog 4.0.8).
Traffic situation Execution
time
Situation 1 (Figure 2) 1427 ms
Situation 1 with a
max
= 1m
2
s
−1
360 ms
Situation 2 (Figure 3) 500 ms
Situation 2 with a
max
= 1m
2
s
−1
219 ms
Section 3.
Execution Time. Due to the dynamic environment
of real world automated vehicles, trajectories must be
planned cyclically at a high enough rate to account for
any changes in the environment. Thus execution time
is a critical characteristic for any trajectory planning
program.
Table 2 gives a summary of execution time mea-
surements for CLPTP. The results show that the com-
putational cost of our implementation is too high for
real world vehicles, where typical planning frequen-
cies lie in the range of 10 Hz to 20 Hz. However,
this does not mean that Prolog or CLP in general is
inappropriate for solving the problem of trajectory
planning, as the performance of the system is solely
determined by the labeling, search and optimization
algorithms of the underlying interpreter. For exam-
ple, if it is more appropriate to conduct a breadth-first
search (as the A* algorithm does) instead of a depth-
first search, this can be implemented in the interpreter
without modifying the declarative code it executes.
This inherent separation of logic describing a prob-
lem to solve and operational control flow can be seen
as one of the advantages of CLP over other, e.g. im-
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
416

perative, programming paradigms when solving com-
plex problems.
The results in Table 2 also illustrate the heavy in-
fluence the size of the quantized configuration space
has on execution time performance. Due to the safety-
criticality of trajectory planning, this is a significant
issue because international standards for functional
safety such as ISO 26262 demand worst-case execu-
tion time estimations for any safety-relevant software.
Worst-case execution times can only be estimated for
trajectory planning programs if upper bounds are ap-
plied for the number of lanes, dynamic objects, speed
limits etc. The automated driving system system
can then only be applied safely in traffic situations
not exceeding the estimated limits and mechanisms
(e.g. handover to a human driver) ensuring functional
safety in unexpectedly complex situations must be
implemented.
Verifiability. Two important methods are commonly
used to verify or validate safety-critical systems (ISO,
2011): On the one hand, there are formal techniques
like theorem proving. On the other hand, there is
systematic testing. Both methods can profit from the
characteristics of CLP.
Theorem proving is based on first-order
logic (Ray, 2010). Assertions on a program are
proved using logic inference. Since constraint logic
programs are also based on first-order logic, the
application of theorem proving to them is more
straightforward compared to imperative programs.
To demonstrate how CLP supports writing sys-
tematic tests efficiently, Listing 6 outlines a simple
test case for CLPTP. The interpreter executing the
test case infers whether the lateral coordinate D of the
first vehicle configuration of any trajectory calculated
by CLPTP lies within certain lane boundaries.
Listing 6: Test case for CLPTP checking that lateral coordi-
nates lie within lane boundaries. Partial data structures and
double negation are used to make the test case as generic as
possible. The predefined predicate assertz/1 is used to set
up a test scenario. fd_dom/2 is used to check the domain of
the constraint variable D.
:- ass e r t z ( o b j e c t (_ , _ , _ , _ , _ , _ )) .
:- ass e r t z ( s p eed _ l i mit ( _ , _ ) ) .
:- ass e r t z ( r igh t _ bou n d ar y (_ , -1) ) .
:- ass e r t z ( l eft _ b oun d a ry ( _ , 2) ).
:- \+( \ + ( ( tr a j e ctor y ([ _] , _ , [ conf (_ , D ,
_ ,_ , _) ] , _ ) , fd _ d o m (D , -1..2) ) ) ).
Note that the double negation used in the last di-
rective of Listing 6 is the usual Prolog method to
prove a test goal for all possible solutions and ensure
that variable bindings (in this case D) are unchanged
after executing the test goal. This test case example
uses the clause database of the interpreter for defining
a test scenario and shows how partial data structures
allow generic tests. The test scenario in Listing 6 is
generic in so far that it includes traffic situations with
arbitrary objects and speed limits by asserting facts
for the predicates object/6 and speed_limit/2 that
unify with any query. Thereby the independence of
staying within lane boundaries on the one side and
speed limits and objects on the other side is shown. In
other languages, multiple concrete test cases would
be needed to achieve an equivalent test coverage.
5 CONCLUSIONS AND FURTHER
WORK
The implementation of a general trajectory planning
module presented in this paper shows that CLP re-
duces the complexity of implementing a software
solving the problem of trajectory planning. Although
several simplifications have been applied for the ease
of demonstration, compared to imperative program-
ming languages, the translation of requirements and
constraints of the planning problem into program
code is more straightforward and easier to accomplish
for domain experts. Less operational details in the
code and the abstract, declarative way of specifying
knowledge about a problem as program code make
CLP a promising technology for the implementation
of software solving complex planning problems in au-
tomated driving systems. Compared to approaches
based on neural networks, well-known verification
methods demanded by standards such as ISO 26262
can be applied more easily.
The execution time evaluation presented in Sec-
tion 4 shows that algorithms for constraint solving
and optimization currently available in interpreters of
CLP languages such as SICStus Prolog are not capa-
ble of fulfilling the performance requirements of auto-
mated driving systems in real world situations. How-
ever, the underlying algorithms of interpreters could
be adapted and improved without having to modify
the declarative code describing the problem to solve.
Future work should include an investigation on
how to improve execution time performance, e.g. by
using parallel implementations of constraint solving
and optimization algorithms. If execution time can
be reduced considerably, the approach of this paper
could be applied to implement not just general, but
also detailed trajectory planning. Smaller quantiza-
tion step sizes, high-dimensional configuration spaces
and more accurate vehicle models could be used.
Implementation of Trajectory Planning for Automated Driving Systems using Constraint Logic Programming
417

REFERENCES
Apt, K. R. and Wallace, M. (2006). Constraint Logic Pro-
gramming Using ECLiPSe. Cambridge University
Press, Cambridge.
Arbib, J. and Seba, T. (2017). Rethinking Transporta-
tion 2020-2030: The Disruption of Transportation
and the Collapse of the Internal-Combustion Ve-
hicle and Oil Industries. Retrieved August 30,
2018, from https://www.rethinkx.com/s/RethinkX-
Report 051517.pdf.
Bauchau, O. A., editor (2011). Flexible Multibody Dynam-
ics. Solid Mechanics and Its Applications. Springer
Netherlands, Dordrecht.
Behere, S. and T
¨
orngren, M. (2015). A Functional Archi-
tecture for Autonomous Driving. In Kruchten, P., Da-
jsuren, Y., Altinger, H., and Staron, M., editors, Pro-
ceedings of the First International Workshop on Auto-
motive Software Architecture - WASA ’15, pages 3–10,
New York, New York, USA. ACM Press.
Biran, O. and Cotton, C. (2017). Explanation and
Justification in Machine Learning: A Survey.
In IJCAI-17 Workshop on Explainable AI (XAI)
Proceedings, pages 8–13. Retrieved December
3, 2018, from http://www.intelligentrobots.org/files/
IJCAI2017/IJCAI-17 XAI WS Proceedings.pdf.
Bojarski, M., Yeres, P., Choromanska, A., Choromanski,
K., Firner, B., Jackel, L. D., and Muller, U. (2017).
Explaining How a Deep Neural Network Trained
with End-to-End Learning Steers a Car. CoRR,
abs/1704.07911.
Carlsson, M. (2009). SICStus Prolog User’s Manual:
Release 4.0.8. Retrieved January 21, 2018, from
http://sicstus.sics.se/sicstus/docs/4.0.8/pdf/sicstus.pdf.
Carlsson, M. and Mildner, P. (2012). SICStus Prolog – The
first 25 years. Theory and Practice of Logic Program-
ming, 12(1-2):35–66.
Diaz, D. (2001). Design and Implementation of the GNU
Prolog System. Journal of Functional and Logic Pro-
gramming, 2001(6).
Diaz, D., Abreu, S., and Codognet, P. (2012). On the im-
plementation of GNU Prolog. Theory and Practice of
Logic Programming, 12(1-2):253–282.
Dubey, A. D., Mishra, R. B., and Jha, A. K. (2013). Path
Planning of Mobile Robot using Reinforcement Based
Artificial Neural Network. Int. J. of Advances in En-
gineering & Technology, 6(2):780–788.
Grigorescu, S. M., Glaab, M., and Roßbach, A. (2017).
From logistic regression to self-driving cars:
Chances and challenges of using machine learning
for highly automated driving. Retrieved June 6,
2018, from https://d23rjziej2pu9i.cloudfront.net/wp-
content/uploads/2017/04/12081251/EB
TechPaper
From logistic regression to self driving cars.pdf.
Gu, T. and Dolan, J. M. (2012). On-Road Motion Planning
for Autonomous Vehicles. In Su, C.-Y., Rakheja, S.,
and Liu, H., editors, Intelligent robotics and applica-
tions, volume 7508 of LNAI, pages 588–597. Springer,
Berlin.
Hart, P., Nilsson, N., and Raphael, B. (1968). A Formal Ba-
sis for the Heuristic Determination of Minimum Cost
Paths. IEEE Transactions on Systems Science and Cy-
bernetics, 4(2):100–107.
ISO (2011). International Standard ISO 26262-6:2011(E):
Road Vehicles - Functional Safety - Part 6: Product
development at the software level.
ITF (2017). ITF Transport Statistics. OECD Publishing.
Kelly, A. and Nagy, B. (2016). Reactive Nonholonomic
Trajectory Generation via Parametric Optimal Con-
trol. The International Journal of Robotics Research,
22(7-8):583–601.
Lever, J. and Richards, B. (1994). parcPlan: A planning
architecture with parallel actions, resources and con-
straints. In Ra
´
s, Z. W., editor, Methodologies for intel-
ligent systems, volume 869 of LNAI, pages 213–222.
Springer, Berlin.
McNaughton, M. (2011). Parallel Algorithms for Real-time
Motion Planning. PhD thesis, Carnegie Mellon Uni-
versity, Pittsburgh, PA.
Paden, B., Cap, M., Yong, S. Z., Yershov, D., and Frazzoli,
E. (2016). A Survey of Motion Planning and Control
Techniques for Self-Driving Urban Vehicles. IEEE
Transactions on Intelligent Vehicles, 1(1):33–55.
Piaggio, M. and Sgorbissa, A. (2000). Real-Time Mo-
tion Planning in Autonomous Vehicles: A Hybrid Ap-
proach. In Goos, G., Hartmanis, J., van Leeuwen,
J., Lamma, E., and Mello, P., editors, AI*IA 99:
Advances in Artificial Intelligence, volume 1792 of
LNCS, pages 368–378. Springer, Berlin.
Rathgeber, C. (2016). Trajektorienplanung und -
folgeregelung f
¨
ur assistiertes bis hochautomatisiertes
Fahren. PhD thesis, TU Berlin.
Ray, S. (2010). Scalable Techniques for Formal Verifica-
tion. Springer US, Boston, MA.
Werling, M. (2011). Ein neues Konzept f
¨
ur die Tra-
jektoriengenerierung und -stabilisierung in zeitkritis-
chen Verkehrsszenarien, volume 34 of Schriftenreihe
des Instituts f
¨
ur Angewandte Informatik - Automa-
tisierungstechnik, Universit
¨
at Karlsruhe (TH). KIT
Scientific Publishing, Karlsruhe.
Werling, M., Ziegler, J., Kammel, S., and Thrun, S. (2010).
Optimal trajectory generation for dynamic street sce-
narios in a Fren
´
et Frame. In 2010 IEEE International
Conference on Robotics and Automation, pages 987–
993. IEEE.
Wielemaker, J., Schrijvers, T., Triska, M., and Lager, T.
(2012). SWI-Prolog. Theory and Practice of Logic
Programming, 12(1-2):67–96.
Ziegler, J. and Stiller, C. (2009). Spatiotemporal state lat-
tices for fast trajectory planning in dynamic on-road
driving scenarios. In 2009 IEEE/RSJ International
Conference on Intelligent Robots and Systems, pages
1879–1884, Piscataway, NJ. IEEE.
Zuo, B., Chen, J., Wang, L., and Wang, Y. (2014). A rein-
forcement learning based robotic navigation system.
In 2014 IEEE Int. Conf. on Systems, Man, and Cyber-
netics (SMC), pages 3452–3457. IEEE.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
418
