
The Growing N-Gram Algorithm:
A Novel Approach to String Clustering
Corrado Grappiolo
1
, Eline Verwielen
2
and Nils Noorman
3
1
ESI (TNO), Eindhoven, The Netherlands
2
Unaffiliated, Valkenswaard, The Netherlands
3
Philips Healthcare, Best, The Netherlands
Keywords:
String Clustering, N-Grams, Operational Usage Modelling, System Verification Testing.
Abstract:
Connected high-tech systems allow the gathering of operational data at unprecedented volumes. A direct
benefit of this is the possibility to extract usage models, that is, a generic representations of how such systems
are used in their field of application. Usage models are extremely important, as they can help in understanding
the discrepancies between how a system was designed to be used and how it is used in practice. We interpret
usage modelling as an unsupervised learning task and present a novel algorithm, hereafter called Growing N-
Grams (GNG), which relies on n-grams — arguably the most popular modelling technique for natural language
processing — to cluster and model, in a two-step rationale, a dataset of strings. We empirically compare its
performance against some other common techniques for string processing and clustering. The gathered results
suggest that the GNG algorithm is a viable approach to usage modelling.
1 INTRODUCTION
Connected high-tech systems allow the gathering of
operational data at unprecedented volumes, usually
in the form of log files. These, although historically
mainly used for software debugging purposes, bring
new opportunities to understanding how end-users are
actually using a system, opposed to how they were
designed to be used, for instance during system de-
sign. To be able to extract relevant log information
and aggregate it into usage models can therefore be
extremely beneficial. Usage models can help to iden-
tify particular types of behaviour, leading to insights
which can serve as a basis for product improvements.
System verification can certainly benefit from us-
age models. During system verification, it is evalu-
ated whether the system complies to regulations, re-
quirements and specifications. System reliability ver-
ification is part of this process. The goal of reliability
verification is to drive a system with realistic clini-
cal scenarios in conditions which were not expected
beforehand, taking care that the system is not load-
and stress-tested. To evaluate the reliability of a sys-
tem, its response has to be monitored at test time. If
the response is not as expected, then the system has
made a failure which may impact the operator or the
patient. Reliability figures are usually expressed as
Figure 1: Philips Image Guided Therapy’s Azurion
interventional x-ray system https://www.philips.com.eg/
healthcare/solutions/interventional-devices-and-therapies.
mean time between failures, ranging from a few hun-
dreds to thousands of hours. Ideally, the system is
put under “average” use during reliability verification.
However, it is difficult to determine what exactly the
average use exactly is.
Our ultimate goal is the design of a computational
framework for system (reliability) verification testing
capable of distinguishing “average” usage (and other
types of usage). Ideally, the framework would lever-
age usage models to identify, from a given dataset,
logs depicting normal behaviour, and then to re-
execute them. Additionally, such framework should
52
Grappiolo, C., Verwielen, E. and Noorman, N.
The Growing N-Gram Algorithm: A Novel Approach to String Clustering.
DOI: 10.5220/0007259200520063
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 52-63
ISBN: 978-989-758-351-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Table 1: Example of an x-ray sequence.
Step Action Symbol
1 table movement start 1
2 x-ray arm movement start 2
3 table movement stop 3
4 x-ray arm movement stop 4
5 table movement start 1
6 table movement stop 3
7 table movement start 1
8 table movement stop 3
9 user-interface 5
10 user-interface 5
11 user-interface 5
12 x-ray acquisition start 6
13 table movement start 1
14 x-ray arm movement start 2
15 table movement stop 3
16 x-ray arm movement stop 4
17 x-ray acquisition stop 7
be able to continuously maintain up-to-date represen-
tations of different behaviour types. We focus our
attention on operational data of Philips Healthcare’s
Image Guided Therapy interventional systems (IGT)
— see Figure 1 — which make the task of modelling
normal behaviour far from being trivial: the flexibil-
ity of this system, the medical staff’s variety in ed-
ucational background, their familiarity with manoeu-
vring the system and the different pathologies of the
patients, result in an almost infinite amount of differ-
ent usage types. Our interest, more specifically, is on
the sequence of high-level actions performed by the
users on the x-ray system during a medical procedure,
rather than its low-level details, such as motor/sensor
readings. Table 1 depicts an example of such x-ray
sequences.
Since we hold no a-priori knowledge on how
many usage behaviours exist we interpret usage mod-
elling as an unsupervised learning task. Assuming the
successful partitioning of a given dataset into clusters,
so that the similarity of behaviours represented by the
string belonging to the same cluster is maximised,
whilst the similarity of behaviours across clusters is
minimised, the subsequent task would correspond to
the extraction of a usage model for each cluster. Nat-
ural Language Processing (NLP) techniques are par-
ticularly useful. More specifically, we aim at extract-
ing a n-gram model for each retrieved cluster. The
main key-feature of n-grams is that they can lead to
the creation of probabilistic graphs which can then be
used for classification purposes (Jurafsky and Martin,
2014). In our approach, each node of a n-gram graph
corresponds to a log action, whilst the edges connect-
ing nodes correspond to the conditional probability of
an action occurring given a finite sequence of previ-
ous actions.
Three main research questions arise: (1) how well
do existing techniques used for string/text/document
clustering perform on our data? (2) How can we com-
pare the outcome of different clustering algorithms
corresponding to a different number of clusters? (3)
Is it possible to provide an alternative clustering ap-
proach?
To answer the first research question we consid-
ered k-means and complete-link hierarchical cluster-
ing — two of the most common clustering algorithms
— in presence of raw text-data and string similar-
ity measures or given a data transformation technique
which converts the raw data into a vectorised form.
The second research question is answered by lever-
aging on our modelling approach, which essentially
aims to create probabilistic graphs for each cluster, to
retrieve probability-based metrics — entropy in our
case — to compare partitions obtained by using dif-
ferent algorithms and data transformation techniques.
Concerning the third research question, we propose a
novel algorithm, hereafter called Growing N-Grams
(GNG). GNG creates new or updates existing n-gram
models in a two-step rationale. First, given an in-
put string to cluster, the algorithm relies on the exist-
ing models’ symbols to identify the candidate models
which share most commonalities with the string. If
none are found, a new n-gram model based on that
string is created. Otherwise, the algorithm calculates,
for each candidate model, the chain probability of that
string; the string is then assigned to the model which
returned the highest probability, with the consequence
that the winner model’s n-grams and probabilities are
updated to encompass the input string. To the authors’
best knowledge, there has never been an attempt to
perform string clustering directly by means of n-gram
classification.
We conducted an empirical evaluation of string
clustering based on a dataset describing sub-
sequences of the Bolus chase procedure, a technique
in peripheral arteriography, performed on Philips
Healthcare’s IGT interventional systems
1
. Once the
set of n-gram models is built, the evaluation procedure
consists of calculating the entropy score of the chain
probabilities calculated by each n-gram model for a
given validation set of strings. The rationale is the
following: an optimal clustering partition would lead
to n-gram models which do not “overlap”, meaning
that given an input string all but one model will return
a very low chain probability, hence low entropy. On
the other hand, the worst clustering partition would
1
The dataset, algorithms and additional content can
be found using the following link: https://github.com/
bracciolo22/Growing-n-Grams.
The Growing N-Gram Algorithm: A Novel Approach to String Clustering
53

lead to n-gram models with some degree of overlap,
meaning that all models will return similar probabil-
ity values, thus resulting in a high entropy score. By
n-gram overlap we intend the existence of sub-graphs
of nodes, edges and related probabilities, which are
the same among different n-gram models, or at least
very close to each other.
The gathered results suggest that: (1) GNG can
outperform all other algorithms given appropriate hy-
perparameter setting; (2) there might be a relation-
ship between the statistical properties of the dataset
at hand and the hyperparameters leading to the op-
timal performance of GNG; (3) complete-link clus-
tering with a simple string similarity measure such
as the Levenshtein distance can lead to good results;
(4) string vectorisation does not offer straightforward
computational benefits. The investigation allows us
to conclude that not only is GNG a novel, viable ap-
proach to string clustering, but its algorithmic struc-
ture is also suitable for our goal to create a framework
for system (reliability) verification testing, given that
it can continuously create new models and update ex-
isting ones, hence maintaining up-to-date representa-
tions of system usage, without the need to perform
data pre-processing or pairwise distance matrix cal-
culations.
The remainder of this document is organised as
follows: Section 2 presents an overview of string clus-
tering approaches existing in the literature. Section 3
formalises the problem at hand and the performance
measure used for our empirical evaluation. Section 4
introduces the Growing N-Gram algorithm. Section 5
presents the experimental protocol adopted and the
details regarding the algorithms considered. Section 6
describes and discusses the obtained results. Sec-
tion 7 outlines some possible future work directions.
Section 8 concludes the research.
2 RELATED WORK
One of the most popular approaches to text and doc-
ument clustering focuses on converting the text data
into a vectorised form, so that a similarity measure
— mostly cosine similarity — can be computed and
hence used by the most generic clustering algorithms,
such as k-means (Bishop et al., 1995; Duda and
Hart, 1973) and its numerous variants, or hierarchi-
cal clustering (Anderberg, 1973), in its agglomera-
tive variation (Zhao et al., 2005; Jain and Dubes,
1988). Another term used to describe document vec-
torisation is bag-of-words (BOW). The idea is to
leverage the statistical information of words popu-
lating a document to represent data in a vectorised
Figure 2: Clustering algorithms and data processing ap-
proaches considered in our study.
form, most often retrieved by a combination of tech-
niques called Term Frequency and Inverse Document
Frequency (tf-idf), (Raghavan and Birchard, 1979;
Salton, 1989)). In essence, BOW abstracts docu-
ments as sets of words and ignores order dependen-
cies. Hornik et al. (Buchta et al., 2012) utilise BOW
and cosine similarity with spherical k-means (Dhillon
and Modha, 2001); Steinbach et al. (Steinbach et al.,
2000), instead, propose a new variant of k-means,
called bisecting k-means, to cluster vectorised doc-
uments, and compare their results against agglomer-
ative hierarchical clustering. Mahdavi and Abolhas-
sani (Mahdavi and Abolhassani, 2009) propose an-
other flavour of k-means — named harmony k-means
— with the same data transformation techniques. Fi-
nally, Cutting et al. (Cutting et al., 2017) combine
both k-means and hierarchical clustering in an algo-
rithm called Scatter/Gather, although the underlying
data processing part is very similar to the other previ-
ous work. Other related work are those of Balaban-
taray et al. (Balabantaray et al., 2015) on k-medoids
and, most relevantly, of Zhao and Karypis (Zhao et al.,
2005), which provide an extensive research on hier-
archical clustering, both agglomerative and divisive,
even by proposing a novel constrained version of it,
on vectorised documents. Our work shares with all
these the idea of using BOW with tf-idf for data vec-
torisation followed by k-means and hierarchical clus-
tering. We differ from them on the nature of the data
— strings rather than documents — and also on the
fact that we are truly unaware of how many clusters
exist, making the setting of k much more difficult.
For a broader overview of text clustering applications
please refer to (Aggarwal and Zhai, 2012) and (An-
drews and Fox, 2007) among other.
The recent raise in popularity and performance of
neural-based computing — e.g. deep learning — has
also contributed to NLP and therefore document clus-
tering. Within this field, the vectorisation of docu-
ments and words is usually referred to as word em-
beddings (Dai et al., 2015). The key concept corre-
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
54

sponds to train a neural network to predict a word
given a contextual neighbourhood of text, and sub-
sequently utilises only part of the trained network
to convert an input text into a vector of real values.
The context of a given word is mainly obtained by
two similar techniques: skip-gram (Dai et al., 2015)
and continuous-bag-of-words (Mikolov et al., 2013a),
which both rely on a window of text around the given
word, with the difference that skip-gram takes into ac-
count the order of words. Word embedding led to
a vast plethora of work, see for instance Mikolov et
al. (Mikolov et al., 2013b), Lau and Baldwin (Lau and
Baldwin, 2016), Bengio et al. (Bengio et al., 2003),
Kiros et al (Kiros et al., 2015), Kim (Kim, 2014),
Zhang et al. (Zhang et al., 2015), Xu et al. (Xu et al.,
2015), or Tai et al. (Tai et al., 2015), to name few.
Intuitively, neural computing for word embedding is
extremely popular and should not be ignored, that is
why we considered it in our empirical evaluation. On
the other hand, understanding the most consolidated
approach or even network flavour is not a trivial task
at all. We arbitrarily decided to rely on the work of
Le and Mikolov (Le and Mikolov, 2014) — primar-
ily for its popularity and practical ease of use of their
algorithm — as an alternative approach to document
vectorisation in combination with k-means and hier-
archical clustering for benchmarking purposes.
As previously said, the data in our possession
shares similarities also with sequences of strings with
a predefined vocabulary. With this respect, there ex-
ist a vast plethora of string similarity measures which
do not require any data transformation phase. Among
these, the most widely known are arguably the Leven-
shtein or edit distance (Levenshtein, 1966) and vari-
ants (Pettersson et al., 2013; Ackroyd, 1980; Marzal
and Vidal, 1993; Yujian and Bo, 2007), and the Jaro
distance (Jaro, 1989). These metrics have been used,
for instance, by Rajalingam and Ranjini (Rajalingam
and Ranjini, 2011) in combination with agglomera-
tive hierarchical clustering, albeit they pre-processed
their text data by binary encoding; by Lu and Fu (Lu
and Fu, 1978) in combination with k-nearest neigh-
bour for sentence-to-sentence clustering; by da Cruz
Nassif and Hruschka (da Cruz Nassif and Hruschka,
2013) in combination with partitional k-means, k-
medoids and agglomerative clustering for partitioning
filenames — hence strings of characters — in a foren-
sic context. Another important relevant work is done
by Wurzenberger et al. (Wurzenberger et al., 2017),
who investigated several metrics for clustering log
lines, though in a semi-supervised setting. Similarly
to these work, we will embark the task of clustering
our usage data by means of Levenshtein, normalised
Levenshtein, and Jaro metrics.
N-grams (Chen and Goodman, 1999; Jurafsky and
Martin, 2014; Kneser and Ney, 1995; Brown et al.,
1992) — i.e. sequences of n symbols — are exten-
sively used in NLP, especially when combined with
the Markov property (Markov, 1971), since they lead
to the construction of probabilistic graphs. These al-
low for e.g. character and word prediction (Lesher
and Rinkus, 2002; Lesher et al., 1998) and lan-
guage modelling (Bungum and Gamb
¨
ack, 2012; Si-
ivola and Pellom, 2005). In accordance with these
works, in fact, our ultimate goal is to model each
cluster of operational data, depicting different usage
behaviours, into a n-gram model. Attempts to lever-
age n-grams for text clustering have also been done.
Ismail and Rahman (Ismail and Rahman, 2014) use
the chain probability computed on tri-grams to calcu-
late the similarity score of word pairs, and then decide
whether to cluster them together based on a thresh-
olding rationale. Ke
ˇ
selj et al. (Ke
ˇ
selj et al., 2003),
instead, rely solely on the most frequent n-grams to
calculate the similarity between document author pro-
files; similar strategy is adopted by Miao et al. (Miao
et al., 2005), where they use most frequent n-grams as
distances to be used by k-means for document clus-
tering. Although our approach shares the use of chain
probabilities and thresholding to determine whether
a string should belong to a model, the n-grams are
used in their entirety rather than just their most fre-
quent terms, they are incrementally built through the
assignment of new strings to related clusters, and fi-
nally no other clustering algorithm such as k-means is
used.
3 PROBLEM STATEMENT
This section formally introduces the problem at hand,
the strategy to solve it, and the performance measure
used to evaluate the solutions found. In order not to
overcrowd the manuscript, only the most important
concepts are presented. Finally, in order to maintain
the mathematical notions as simple and as clear as
possible, sub- and super-script indices will be omit-
ted when not necessary.
Let D be a dataset composed of |D| = d strings
w
i
, i = 1 .. . d. Each string w is composed of a vari-
able number of characters or symbols x belonging to
a vocabulary V . V is retrieved from D. D can con-
tain more than one occurrence of a string w, and each
string can contain more than one occurrence of the
same symbol. The goal is to partition D into k clus-
ters C
i
, i = 1, . . . k and to build, for each cluster C
i
, a
n-gram G
i
solely based on the strings belonging to C
i
.
All n-gram models share the same value for n, that is
The Growing N-Gram Algorithm: A Novel Approach to String Clustering
55

the history of past events to be taken into account. No
information is known, a priori, about k. We will refer
to the set of n-gram models M = {G
1
, G
2
, . . . G
k
}
as an ensemble of models. Given a string w composed
of a sequence of m symbols w = x
1
, x
2
, . . . x
m
and
an n-gram model G, the chain probability of w given
G and n is calculated as follows:
P(w | G) = P(x
1
, x
2
, . . . x
m
| G) ≈
≈
m
∏
i=1
P(x
i
| x
i−1
, . . . x
i−n+1
, G)
(1)
therefore, the assignment of w to a n-gram model G is
obtained as follows:
G
win
= argmax
G
(P(w | G), ∀ G ∈ M) (2)
and, consequently, the corresponding cluster C
win
is
also retrieved. As we will show in Section 5, different
algorithms — or even the repeated execution of the
same algorithm — might lead to a different number
of clusters. In order to evaluate how well the parti-
tioning task is performed, given an input string w, we
calculate the entropy of the ensemble’s chain proba-
bilities:
H (w) = −
k
∑
i=1
P(w| G
i
) log P(w | G
i
) (3)
The rationale is the following: a good partition
would lead to an ensemble which, for a given w,
would return very low chain probability values for
all-but-one model G — i.e. the model obtained from
Equation 2 — which instead would return a very high
probability. Such a set of probabilities would lead
to an extremely low entropy. On the other hand, a
bad partitioning would lead to an ensemble in which
all models return chain probability values which are
close to each other, hence a high entropy score.
Given a set of ensembles M = {M
1
M
2
. . . M
m
}
resulting from a clustering-modelling task of m dif-
ferent algorithms, and a validation set W composed
of |W | = l strings, the best ensemble is defined as
follows:
M
∗
= argmin
M
1
l
l
∑
i = 1
H
M
(w
i
)
!
, ∀ M ∈ M (4)
that is, it is the ensemble which returns the lowest av-
erage entropy score (and lowest standard deviation)
calculated over the whole validation set.
4 THE GROWING N-GRAM
ALGORITHM
The GNG algorithm is presented as pseudo-code in
the next column of this page. The algorithm takes as
Algorithm 1: The Growing N-Gram Algorithm.
1 GNG(D , τ
c
, τ
u
, δ
c
, δ
u
, τ
min
c
, τ
max
u
)
2 M =
/
0
3 while |D| > 0 do
4 shu f f le(D)
5 for each w ∈ D do
6 s = set(w)
7 M
C
, M
U
=
/
0
8 for each m ∈ M do
9 if s \ m > τ
c
then
10 M
C
← M
C
∪ {m}
11 end if
12 if s \ m ≤ τ
u
then
13 M
U
← M
U
∪ {m}
14 end if
15 end for
16 if M
C
≡ M then
17 m = new n gram(w)
18 M ← M ∪ {m}
19 pop(w, D)
20 else if |M
U
| > 0 then
21 m = argmax(P(w|G), ∀ G ∈ M
U
)
22 update(m, w)
23 pop(w, D)
24 else
25 do nothing
26 end if
27 end for each
28 τ
c
← max(τ
c
− δ
c
, τ
min
c
)
29 τ
u
← max(τ
u
+ δ
u
, τ
max
u
)
30 end while
31 return M
input: (1) a dataset D of strings to be partitioned into
clusters, (2) two thresholds, namely τ
c
and τ
u
, which
regulate the creation of new models or the update of
existing ones, (3) two parameters δ
c
and δ
u
, which
modify the values of their respective τs so that the
whole dataset is processed, (4) two parameters τ
min
c
and τ
max
u
, which are used to bound the values of τ
c
and τ
u
respectively.
GNG assigns each string w ∈ D to one and only
one model m ∈ M , see lines 17 and 22. The pop
function call in lines 19 and 23 simply means that w,
once assigned to a model m, is removed from D. For
simplicity, the algorithm does not explicitly state how
to maintain the cluster composition of each model.
For each w, the algorithm first extracts the set s of
its unique symbols (line 6), then evaluates it with the
symbols of each m ∈ M. The evaluation is done via
set difference and this is compared against the two
thresholds τ
c
and τ
u
(lines 9 and 12 respectively). Two
subsets of M, M
C
and M
U
, are used to keep track of
which model satisfies which threshold condition —
lines 10 and 13 respectively. Please note that M
C
and
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
56

Table 2: Dataset Details
Feature Train Test Validation Total
Size 5301 663 662 6626
Unique Strings 1673 281 310 2019
String Intersection with Training Set 113 131
Alphabet Size 88 57 61 91
Alphabet Intersection with Training Set 56 59
Avg. String Length 7.18 7.93 7.82 7.32
Std. Dev. String Length 13.28 26.92 12.11 15.11
Median string Length 4 4 4 4
Min. String Length 2 2 2 2
Max. String Length 345 617 148 617
M
U
do not partition M, meaning that it is possible that
some model in M might belong neither to M
C
nor to
M
U
during a GNG iteration.
In essence, M
C
corresponds to the set of models
in M which are too far from w, whilst M
U
are the set
of models in M which are close enough to w. If all
existing models are too far from w (line 16), then a
new n-gram model based on w is created (line 17) and
added to the ensemble (line 18). Alternatively, and in
case there are some models which are close enough to
w (line 20), the model in M
U
which returns the highest
chain probability calculated in accordance with Equa-
tion (2) is retrieved and updated with w (lines 21 and
22). In case no creation or update is performed, the
string remains unassigned (line 25) and the algorithm
continues by processing the next string. The update
of an n-gram model simply corresponds to updating
the n-gram counts of that model given w. The con-
sequence of this is that the calculation of the model’s
chain probabilities will also become up-to-date (Ju-
rafsky and Martin, 2014; Kneser and Ney, 1995).
At the end of one dataset processing loop, some
strings might still be unassigned. This is because the
constraints based on τ
c
and τ
u
might be too strict. The
algorithm then relaxes such constraints in lines 28 and
29. τ
c
is decreased, whilst τ
u
is increased. Both are
bounded by their respective τ
min
c
and τ
max
u
. D is guar-
anteed to be fully partitioned into clusters/models if,
eventually, τ
c
= 0 or τ
c
= τ
u
.
5 EXPERIMENTAL PROTOCOL
In order to evaluate the viability of our GNG algo-
rithm we conducted an empirical investigation based
on sub-sequences of the Bolus chase procedure, a
technique in peripheral arteriography, performed on
IGT systems. For optimal handling, we represented
the log data as tokenised strings based on a vocabulary
V of actions extracted from the dataset. An example
of log tokenisation is depicted in Table 1. We gath-
ered and tokenised 6626 x-ray sequences leading to a
vocabulary of 91 symbols. It is important to remark
that each string w can only terminate with one out of
four possible symbols representing the end of an x-ray
exposure type. The statistical details of our dataset
are reported in Table 2. As it can be observed, the
dataset contains a lot of repeated sequences — only
30% of instances are unique, which indeed gives us a
hint that there must exist some usage patterns, though
the string overlap between train and test/validation set
is minor (40.21% and 46.62%). On the other hand, all
sets share most of the symbols.
Given the first research question introduced in
Section 1, and the related work presented in Section 2,
we decided to compare our GNG algorithm with sev-
eral others, based on the following:
• Data Representation: we considered both the case
in which each w ∈ D is vectorised or not;
• String Vectorisation: we considered two tech-
niques: (1) tf-idf and (2) Gensim’s implementa-
tion of the doc2vec algorithm (Rehurek and Sojka,
2010). The similarity score of vectorised strings is
calculated via cosine distance;
• Non-vectorised Data: in order to calculate the
similarity of two strings we considered: (1) the
Levenshtein distance, (2) the normalised Leven-
shtein distance, and (3) the Jaro distance;
• Clustering Algorithms: we considered k-means
and complete-link hierarchical clustering;
• Determining the Number of Clusters gor k-means:
we run k-means for k = 2, . . . k
max
and rely on
the silhouette coefficient in order to retrieve the
best k-value.
• Determining the Number of Clusters for
Complete-link: we rely on the elbow rule
calculated on the percentage of variance un-
explained for k = 2, . . . k
max
. The elbow is
retrieved by performing a two-segment curve fit-
ting task; the value k is the one which minimises
The Growing N-Gram Algorithm: A Novel Approach to String Clustering
57
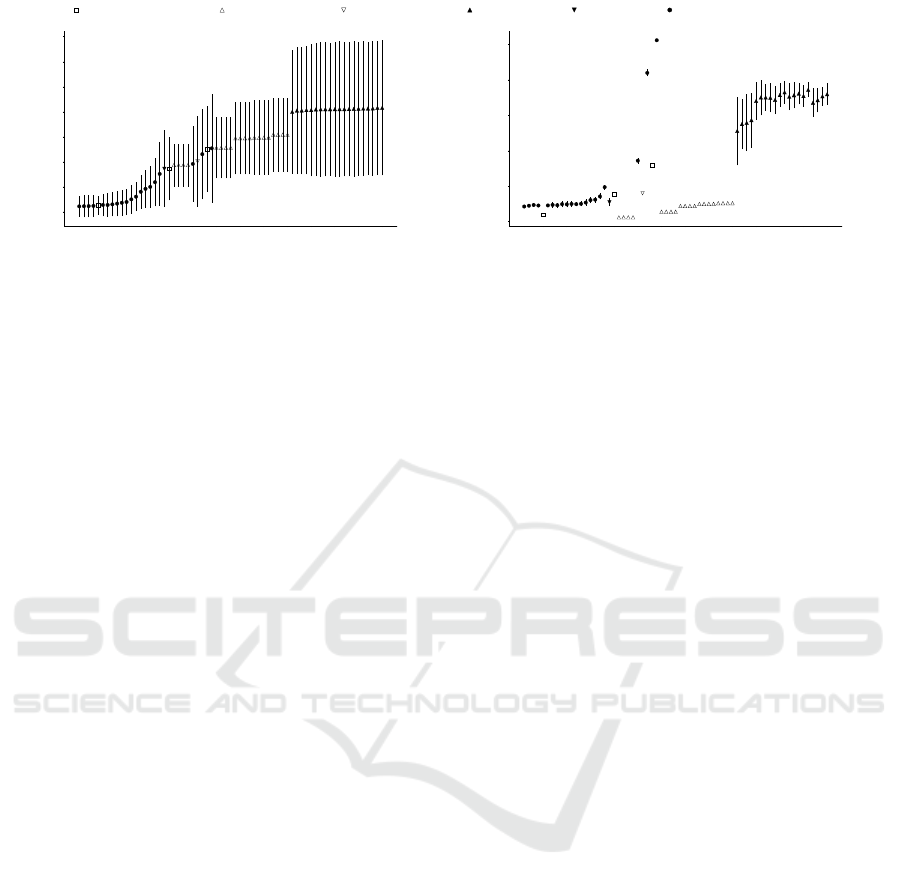
1 5 10 15 20 25 30 35 40 45 50 55 60 65
Algorithm Ran k
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
Entropy
Complete-link with string similarity Comp lete -link with doc2vec Complete-link with tf-idf
(a) Algorithm performance
1 5 10 15 20 25 30 35 40 45 50 55 60 65
Algorithm Ra nked per Entropy
0
50
100
150
200
250
Number of Clusters/Models
k-Means with doc2vec k-Means with tf-idf
Growing N-Gram
(b) Number of clusters/models per algorithm
Figure 3: Overview of the clustering algorithms considered in our investigation. Fig. (3a): average and standard deviation
entropy scores per algorithm; Fig. (3b): average number and standard deviation of clusters/models per ranked algorithm.
the mean square error between the percentage
of variance unexplained curve and the fitted
segments.
• N-Gram Modelling: we rely on Kneser-Ney
smoothing (Kneser and Ney, 1995). This is also
implemented for GNG.
We decided to rely on generic forms of k-
means and complete-link in order to have a broad
overview of the performance that these algorithms
could achieve. Similarly, Gensim’s doc2vec was cho-
sen due to its popularity in the neural computing-
based NLP community. A summary of the ap-
proaches and algorithms considered can be observed
in Figure2. Moreover:
• we partition D into train-test-validation sets —
80%, 10% and 10% of D respectively. The sets
are defined a priori and are the same for all algo-
rithms and their repetitions. The train set is used
by all algorithms to perform the clustering task. k-
means relies on the test set to identify the value for
k via silhouette score. The validation set is used
to identify the best algorithm/ensemble in accor-
dance with Equation (4);
• all k-means and GNG instantiations are repeated
30 times. The same is done for complete-link in
combination with doc2vec, whilst for the other
complete-link settings, given their deterministic
characteristics, only one repetition is performed;
• doc2vec is implemented with: train epoch 100,
vector size vs ∈ {2, 4, 6, 8, 10}, window size
ws ∈ {2, 5, 10, 20}, α = 0.025 for a total of
20 possible settings;
• for both k-means and complete-link, k
max
= 200;
• for GNG, we investigated τ
c
∈ {1, . . . 20},
τ
u
= − 1, δ
c
= 1, δ
u
= 0.5, τ
min
c
= τ
max
u
= 1;
• n = 2 for all n-gram models.
In total, therefore, we considered 20 settings for
GNG, 21 settings for k-means (20 for doc2vec), 24
settings for complete-link (20 for doc2vec), resulting
in 65 algorithmic settings.
6 RESULTS AND DISCUSSION
Figure 3a depicts the average and standard deviation
entropy scores of the 65 algorithmic settings. The al-
gorithms are ranked by average entropy score increas-
ing. Once again, the lower the entropy score, the bet-
ter the classification task, hence the clustering task.
Furthermore, Figure 3b depicts the average and stan-
dard deviation number of clusters/models returned by
each algorithm ordered in accordance with the rank of
Figure 3a.
17 out of the first 18 best ranked algorithms are in-
stances of GNG. The τ
c
values range from τ
c
= 20,
which achieves the best average entropy score of
0.1109 (Std. Dev.=0.2077), to τ
c
= 4 (18
th
), with
average score 0.7587 (Std. Dev. = 0.6311). Inter-
estingly, τ
c
= 20 resembles the average plus stan-
dard deviation string length for both train and vali-
dation set (20.46 respectively 19.93), whilst τ
c
= 4
corresponds to the median string length for both train
and validation set — see Table 2. A Welch’s t-test
with α = 0.01 under the null hypothesis that GNG
with τ
c
= 20 has the same average performance as
the other algorithms lead to a p-value which make us
reject such hypothesis from the fourth ranked algo-
rithm — i.e. GNG with τ
c
= 18 onward (the p-value
for such comparison is 0.00001675, t = − 4.3048,
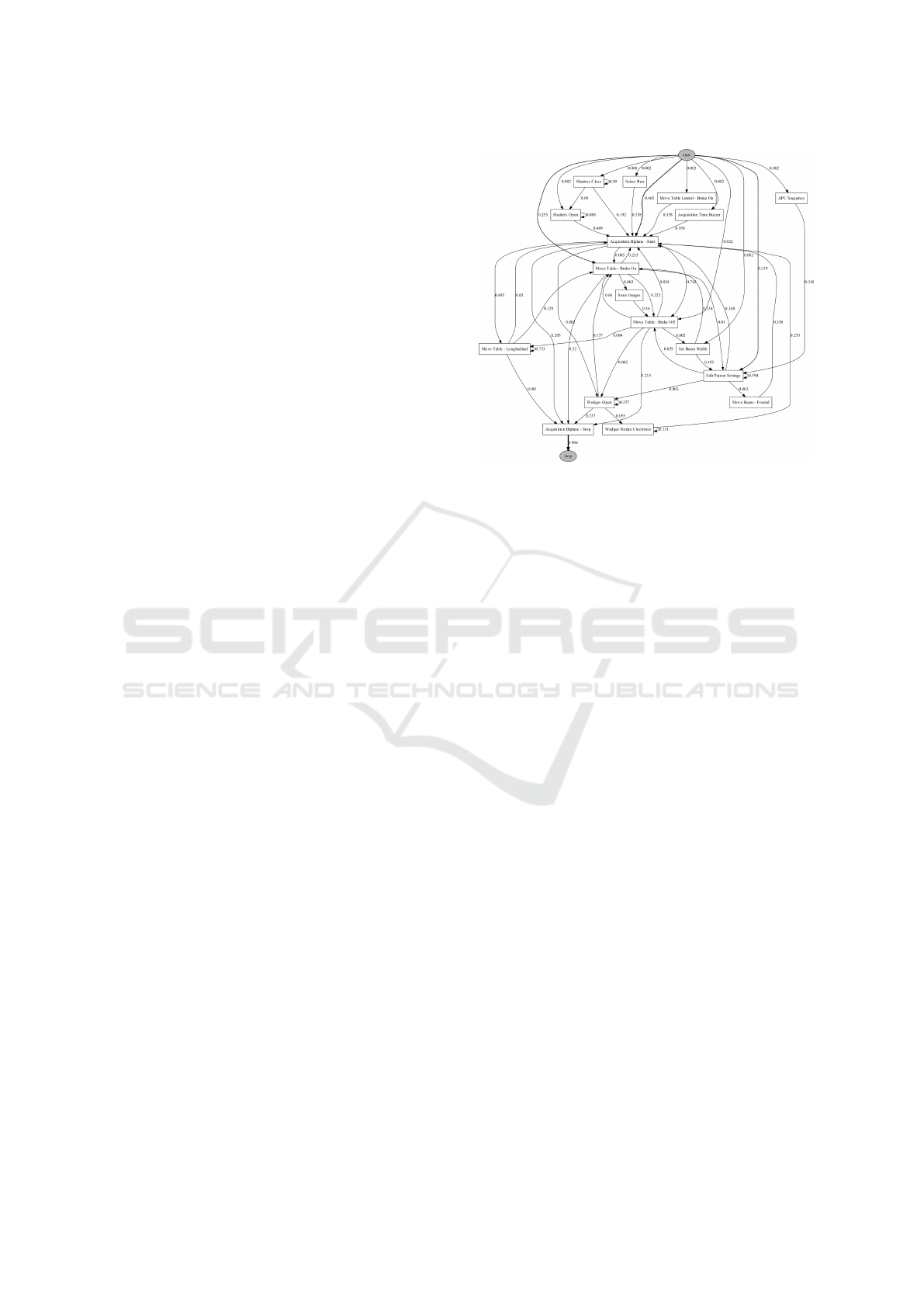
d f = 39718). An example of a mid-to-large model
obtained via GNG with τ
c
= 20 can be seen in Fig-
ure 5.
Complete-link resulted in the second best per-
forming algorithm. Strikingly, when complete-link is
combined with the Levenshtein distance, its perfor-
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
58
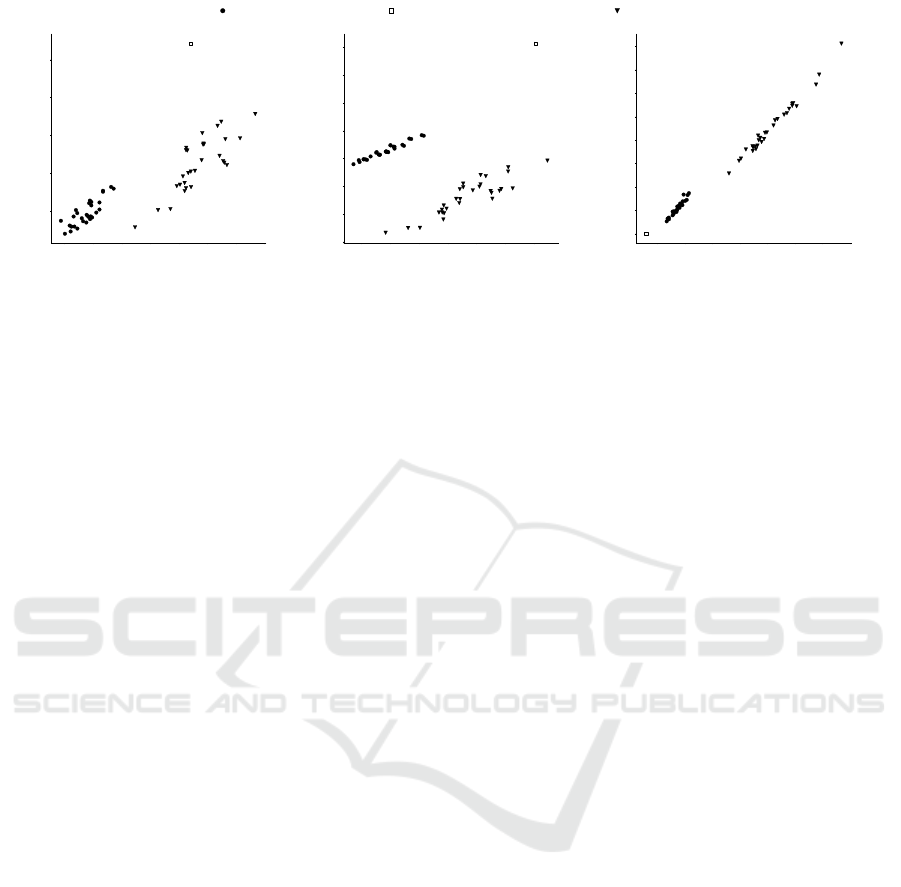
14 16 18 20 22 24 26 28
Node Avg.
14
16
18
20
22
Node Std. Dev.
GNG τ
c
= 20
(a) Number of Nodes
60 70 80 90 100 110 120
Edge Avg.
50
75
100
125
150
175
200
225
Edge Std. Dev.
Complete Link with Levenshtein
(b) Number of Edges
3 4 5 6 7 8 9 10
Edge Overlap Avg.
2
3
4
5
6
7
8
9
10
Edge Overlap Std. Dev.
k-Means with tf-idf
(c) Edge Overlap
Figure 4: Distribution details of n-gram model sizes and overlap for each of the three algorithm’s best performance: Fig.( 4a)
number of nodes, Fig. 4b number of edges, Fig. 4c edge overlap across models over 30 algorithmic iterations.
mance corresponds to the fifth best result, with an av-
erage entropy score of 0.13 (Std. Dev. = 0.1905).
Another remarkable finding is that complete-link,
when coupled with doc2vec, resulted in average (and
Std. Dev.) entropy scores which were solely de-
pendent on the vector size parameter. In other
words, given e.g. vs = 2, complete-link for all
ws ∈ {2, 5, 10, 20} scored an average entropy of
0.9349 (Std. Dev. = 0.4289). This is observed for all
vs ∈ {2, 4, 6, 18, 10}. The independence on ws for
complete-link given vs is also observed in terms of av-
erage number of clusters retrieved, see Figure 3b. It is
hard to find a plausible explanation of such behaviour.
Although one might expect results along these lines
for large ws values given the string length statistics
of our dataset, it is not clear why the same is also
achieved for ws = {2, 5} as well. Further inves-
tigations aimed at shedding light on such results are
encouraged, even beyond the case study considered
here.
Another key-finding is the poor performance that
k-means achieves when coupled with doc2vec. The
20 settings correspond to the 20 worst ranked perfor-
mances and, unlike what was observed for complete-
link, it is not possible to find correlations between vs,
ws and the entropy scores. Moreover, the recorded
standard deviations are the biggest across all algo-
rithms considered. An explanation could be that
doc2vec essentially adopts a bag-of-word vectorisa-
tion approach, hence ignores the order of symbols in
strings, which is in fact a fundamental property of our
data. This is also partly observed by the performance
of both k-means and complete-link combined with
tf-idf (ranked 19
th
and 26
th
respectively). Another
possible explanation could be that doc2vec might re-
quire many more training epochs in order to provide
reliable embeddings: the rank of complete-link with
doc2vec is in fact ordered by vs increasing, which also
corresponds to a higher number of neurons in the em-
bedding models, therefore more weights to be trained.
Along these lines, one might argue that doc2vec re-
quires much bigger datasets.
To conclude, by looking at Figure 3b, we can ob-
serve that there is no correlation between the number
of clusters and classification performance. This sup-
ports our claim that the average entropy score is a vi-
able measure for the evaluation of clusters of strings
when these can be generalised by probabilistic mod-
els.
We now centre our attention on analysing why
GNG with τ
c
= 20 has led to the best entropy
scores, as opposed complete-link with Levenshtein
distance and k-means setting with tf-idf, i.e. the two
best alternative benchmark algorithms. The perfor-
mance details can be found in Table 3. Figure 4a
depicts the average and standard deviation of nodes
of the resulting ensembles across each of the 30 it-
erated runs; Figure 4b depicts the same type of in-
formation, albeit about the number of edges compos-
ing the n-gram models, and finally Figure 4c depicts
the average and standard deviation number of edges
which are shared across models of the same ensem-
ble. Again, n-gram models can be considered as prob-
abilistic graphs, where the nodes corresponds to uni-
grams/unique symbols of the n-gram, and the edges
correspond to the probability of observing a symbol
given a previous one, since in our investigation we
consider n = 2.
By observing Figures 4a and 4b, we can see
that GNG leads to ensembles composed of generally
smaller models than complete-link and k-means, both
in terms of nodes and edges composing them. The
standard deviation values of the nodes is also smaller
than the other two algorithms, and although this is not
seen for edges, the range of GNG’s standard deviation
is much smaller than the other two algorithms. This
The Growing N-Gram Algorithm: A Novel Approach to String Clustering
59

Table 3: Algorithm Performance - Selected Details.
Rank Algorithm Parameters Avg. Entropy (Std. Dev.) Avg. Num. Clusters (Std. Dev.)
1 GNG τ
c
= 20 0.1109 (0.2077) 21.3 (2.33)
5 Complete-link Levenshtein 0.13 (0.1905) 10 (0)
19 k-means tf-idf 0.8603 (0.767) 27.3 (5.53)
also means that GNG is more robust against the ran-
domisation of the dataset, which also sets the initial
conditions of the algorithm. The high standard devi-
ation in edge distribution suggests that GNG gener-
ates ensembles where some models have many edges
and some others less. Such behaviour, although much
stronger in magnitude, is also observed for complete-
link, as opposed to the k-means setting.
By looking at Figure 4c, moreover, we can see
how little edge overlap is obtained by complete-link
and GNG, as opposed to k-means, which also sup-
ports our assumption that low model overlap leads to
low entropy scores. Strikingly, complete-link results
in ensembles with a lower edge overlap than GNG,
yet its entropy score is significantly worse. A plau-
sible explanation could be that complete-link, being
based on Levenshtein distance, calculates string sim-
ilarities solely based symbols (hence graph nodes), as
opposed to GNG, which instead takes into account
both nodes (for new model creation) and edges (for
model update).
This might make complete-link more focused on
the symbols in strings rather than sequences of sym-
bols, possibly leading to a higher degree of over-
fitting: during validation, complete-link would face
more sequences with out-of-vocabulary symbols than
GNG, hence leading to low probabilities across dif-
ferent models, hence similar chain probability values,
hence higher entropy scores than GNG. GNG with
slightly higher edge overlap, on the other hand, is
able to generate models which leave room for slightly
different sequences, hence more generic ones, which
would lead to lower entropy scores during validation.
7 FUTURE WORK
The results presented in the previous Section suggest
that our GNG algorithm is a viable approach to string
clustering and modelling. However, in order to better
understand how generic and robust our algorithm is,
a vast amount of research is still required. We here
outline what we consider being the most salient topics
of investigation.
First and foremost, GNG should be tested against
different dataset types. An immediate investigation
would correspond clustering full medical procedures
rather then their sub-sequences. GNG should also be
tested in the presence of a smaller/larger vocabulary,
and possibly even towards pure text data, rather than
sequences of symbols.
A thorough investigation on GNG’s hyperparam-
eters is due, as well as considering other settings for
the benchmark algorithms considered. We believe
that understanding the role of τ
u
and therefore its δ
u
and τ
max
u
has higher importance than the studies about
τ
c
. For instance, during preliminary investigations of
our algorithms, we understood that if τ
u
is initially
set to 1 and τ
max
u
> 1, the algorithm tends to grow
a handful of huge models encompassing most of the
strings in D and few others composed of one string
only. That is why we decided, for this investigation,
to begin with τ
u
= − 1, δ
u
= 0.5 — i.e. no up-
date actions for the first three iterations but just cre-
ations. To some extent, the behaviour we obtained by
GNG would somewhat correspond to first spawning
far away centroids, and subsequently scatter new/up-
date existing ones. Should this be the real key strength
of GNG then this could mean that τ
u
could be auto-
matically toggled (i.e. set to values greater than zero)
once a certain portion of D has been assigned to mod-
els. Moreover, as it was highlighted in Section 6, τ
c
appears to be related to the string length statistics of
the dataset at hand. Should this be also observed in
the presence of other datasets, then it could be pos-
sible to make GNG hyperparameter-free. Another
way to investigate whether GNG can indeed become
hyperparameter-free is the application of it in super-
vised learning scenarios. By adding constraints on the
returned ensemble size, GNG could autonomously set
its τ
c
, τ
u
to perform optimal clustering and modelling.
Finally, further investigations on the effect that the
size of n-grams history has on the performance of
GNG (and other algorithms) is due. Another strategy
would even correspond into making GNG, or even
each model independently, to become able to chose
their own n value.
As explained in Section 1, our ultimate goal is the
creation of a computational framework which helps
identifying “average” usage for system (reliability)
verification. The idea is to leverage usage models
to identify (i.e. classify), from a given dataset, logs
depicting normal behaviour, and then to re-execute
them. This requires a high level of self-adaptation
by the algorithm in charge of maintaining the usage
models. We claim that GNG implements a computa-
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
60
tional approach which is much more prone to self-
adaptation than those relying on pairwise distance
matrices of string vectorisation since, unlike the lat-
ter two, it does not require any form of data pre-
processing. Nevertheless, in order to achieve full
GNG’s self-adaptation, future work could focus on:
(1) understanding whether and how to re-initialise
GNG’s hyperparameters each time new strings are
to be processed; (2) re-design the algorithm to ac-
cept data-streams rather than batches; (3) allowing
the possibility to discard old models which have not
been updated in long time; (4) allowing the possibil-
ity to merge models which perhaps started far away
but after several update actions now manifest an ex-
cessively high degree of overlap; (5) allow the exis-
tence of unassigned strings (i.e. line 25 in the pseudo-
code) rather than coercively assign them to potentially
wrong models. Ultimately, we envision GNG as an
algorithm which, given a (stream) dataset, automat-
ically sets its hyperparameters — even n, or differ-
ent ns for different models — performs its cluster-
ing/modelling computation repeatedly until its inter-
nal entropy converges, is capable of merging/split-
ting/discarding models, and finally is also capable of
maintaining a genealogy of models, so that it can even
backtrack its decisions and possibly highlight how
system usage evolved through time.
The performance target of our investigation fo-
cussed on minimising average entropy scores, given
a set of algorithms and hyperparameters. While
this gives insights on the computational efficiency of
our GNG algorithm, it does not provide insights on
whether the retrieved models are semantically correct.
In order to leverage the model for the identification of
“average” system usage, we necessarily need to verify
whether or not the models make sense from the view-
point of domain experts. However, models such as
the one shown in Figure 5, let alone bigger ones, are
not easy to grasp by domain experts, as we witnessed
during early stages of our research. An alternative
approach, given the probabilistic nature of our mod-
els, is to traverse them based on such probabilities
and record traces of visited nodes. The traces, which
we would call synthetic bolus chase procedures, could
then be evaluated by domain experts. The trace eval-
uation would semantically validate the goodness of
the usage models, albeit in an indirected and par-
tial way. To pursue this investigation we launched a
crowd-sourced experiment in which experts from dif-
ferent domains (e.g. engineering, clinical, research)
are asked to observe traces — which might either be
synthetic or real ones extracted directly from raw data
— and to judge whether they would occur during clin-
ical practice of Bolus Chase, much like a Turing test
Figure 5: An example of a n-gram model obtained via GNG
with τ
c
= 20. It is composed of 20 nodes and 56 edges
and represents a cluster of 160 strings, 55 of which unique.
The values along the edges correspond to the conditional
probabilities. The values do not sum up to one because of
Kneser-Ney smoothing.
for artificial intelligence. The experiment is expected
to run until Spring 2019.
8 CONCLUSIONS
Connected high-tech systems allow the gathering of
operational data at unprecedented volumes. A direct
benefit of this is the possibility to leverage data to
draw usage models, in order to shorten the gap be-
tween how a system is designed to operate and how
it is actually used. Usage models are beneficial for
system reliability verification, part of system verifica-
tion testing, in which knowledge of “normal” system
behaviour is required. Our ultimate goal is the design
of a computational framework which helps identify-
ing “average” usage for system verification. We in-
terpreted the task of modelling usage behaviours as
string clustering/modelling task. We relied on n-gram
modelling for the representation of usage models —
one n-gram model per retrieved cluster — and con-
sidered three algorithmic approaches to string clus-
tering. The first two are based on the most commonly
used k-means and complete-link and rely on either
the transformation of the string data into vectorised
forms, or the use of pairwise string-based similar-
ity measures. We proposed a third approach and its
related algorithm, called Growing N-Grams, which
builds new or updates existing n-gram models based
on string-model similarities and chain probabilities
The Growing N-Gram Algorithm: A Novel Approach to String Clustering
61

computed given the models, hence by avoiding any
form of data pre-processing. We conducted an em-
pirical evaluation of our approach based on a dataset
representing sub-sequences of the Bolus chase pro-
cedure, a technique in peripheral arteriography, per-
formed on Philips Healthcare’s Image Guided Ther-
apy interventional systems. The gathered results sug-
gest that Growing N-Grams can return cluster com-
positions with lower entropy scores of classification,
which indicate the algorithm’s ability to retrieve dif-
ferent usage behaviours.
Growing N-Grams appears to be more prone to
self-adaptation than other algorithms considered in
our study, which also implies it could be better fit for
our ultimate goal. We also highlighted a plethora of
future work which would ultimately lead to the defi-
nition of a fully adaptive algorithm.
ACKNOWLEDGEMENTS
The research is carried out as part of the ITEA3 14035
REFLEXION project under the responsibility of the
Embedded Systems Innovation by TNO (ESI) with
Royal Philips as carrying industrial partner. The RE-
FLEXION research is supported by the Netherlands
Organisation for Applied Scientific Research TNO
and Netherlands Ministry of Economic Affairs.
REFERENCES
Ackroyd, M. (1980). Isolated word recognition using the
weighted levenshtein distance. IEEE Transactions on
Acoustics, Speech, and Signal Processing, 28(2):243–
244.
Aggarwal, C. C. and Zhai, C. (2012). A survey of text clus-
tering algorithms. In Mining text data, pages 77–128.
Springer.
Anderberg, M. R. (1973). Cluster analysis for applica-
tions. Technical report, Office of the Assistant for
Study Support Kirtland AFB N MEX.
Andrews, N. O. and Fox, E. A. (2007). Recent develop-
ments in document clustering.
Balabantaray, R. C., Sarma, C., and Jha, M. (2015). Docu-
ment clustering using k-means and k-medoids. arXiv
preprint arXiv:1502.07938.
Bengio, Y., Ducharme, R., Vincent, P., and Jauvin, C.
(2003). A neural probabilistic language model. Jour-
nal of machine learning research, 3(Feb):1137–1155.
Bishop, C., Bishop, C. M., et al. (1995). Neural networks
for pattern recognition. Oxford university press.
Brown, P. F., Desouza, P. V., Mercer, R. L., Pietra, V.
J. D., and Lai, J. C. (1992). Class-based n-gram mod-
els of natural language. Computational linguistics,
18(4):467–479.
Buchta, C., Kober, M., Feinerer, I., and Hornik, K. (2012).
Spherical k-means clustering. Journal of Statistical
Software, 50(10):1–22.
Bungum, L. and Gamb
¨
ack, B. (2012). Efficient ngram lan-
guage modeling for billion word webcorpora. In Pro-
ceedings of the 8th International Conference on Lan-
guage Resources and Evaluation, pages 6–12.
Chen, S. F. and Goodman, J. (1999). An empirical study of
smoothing techniques for language modeling. Com-
puter Speech & Language, 13(4):359–394.
Cutting, D. R., Karger, D. R., Pedersen, J. O., and Tukey,
J. W. (2017). Scatter/gather: A cluster-based approach
to browsing large document collections. In ACM SI-
GIR Forum, volume 51, pages 148–159. ACM.
da Cruz Nassif, L. F. and Hruschka, E. R. (2013). Docu-
ment clustering for forensic analysis: an approach for
improving computer inspection. IEEE transactions on
information forensics and security, 8(1):46–54.
Dai, A. M., Olah, C., and Le, Q. V. (2015). Document
embedding with paragraph vectors. arXiv preprint
arXiv:1507.07998.
Dhillon, I. S. and Modha, D. S. (2001). Concept decom-
positions for large sparse text data using clustering.
Machine learning, 42(1-2):143–175.
Duda, R. O. and Hart, P. E. (1973). Pattern classification
and scene analysis. A Wiley-Interscience Publication,
New York: Wiley, 1973.
Ismail, S. and Rahman, M. S. (2014). Bangla word clus-
tering based on n-gram language model. In Electri-
cal Engineering and Information & Communication
Technology (ICEEICT), 2014 International Confer-
ence on, pages 1–5. IEEE.
Jain, A. K. and Dubes, R. C. (1988). Algorithms for Clus-
tering Data. Prentice-Hall, Inc., Upper Saddle River,
NJ, USA.
Jaro, M. A. (1989). Advances in record-linkage methodol-
ogy as applied to matching the 1985 census of tampa,
florida. Journal of the American Statistical Associa-
tion, 84(406):414–420.
Jurafsky, D. and Martin, J. H. (2014). Speech and language
processing, volume 3. Pearson London.
Ke
ˇ
selj, V., Peng, F., Cercone, N., and Thomas, C. (2003).
N-gram-based author profiles for authorship attribu-
tion. In Proceedings of the conference pacific asso-
ciation for computational linguistics, PACLING, vol-
ume 3, pages 255–264.
Kim, Y. (2014). Convolutional neural networks for sentence
classification. arXiv preprint arXiv:1408.5882.
Kiros, R., Zhu, Y., Salakhutdinov, R. R., Zemel, R., Ur-
tasun, R., Torralba, A., and Fidler, S. (2015). Skip-
thought vectors. In Advances in neural information
processing systems, pages 3294–3302.
Kneser, R. and Ney, H. (1995). Improved backing-off for
m-gram language modeling. In icassp, volume 1, page
181e4.
Lau, J. H. and Baldwin, T. (2016). An empirical evalua-
tion of doc2vec with practical insights into document
embedding generation. CoRR, abs/1607.05368.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
62

Le, Q. and Mikolov, T. (2014). Distributed representations
of sentences and documents. In International Confer-
ence on Machine Learning, pages 1188–1196.
Lesher, G. and Rinkus, G. (2002). Leveraging word pre-
diction to improve character prediction in a scanning
configuration. In Proceedings of the RESNA 2002 An-
nual Conference, pages 90–92.
Lesher, G. W., Moulton, B. J., and Higginbotham, D. J.
(1998). Optimal character arrangements for ambigu-
ous keyboards. IEEE Transactions on Rehabilitation
Engineering, 6(4):415–423.
Levenshtein, V. I. (1966). Binary codes capable of cor-
recting deletions, insertions, and reversals. In Soviet
physics doklady, volume 10, pages 707–710.
Lu, S.-Y. and Fu, K. S. (1978). A sentence-to-sentence
clustering procedure for pattern analysis. IEEE Trans-
actions on Systems, Man, and Cybernetics, 8(5):381–
389.
Mahdavi, M. and Abolhassani, H. (2009). Harmony k-
means algorithm for document clustering. Data Min-
ing and Knowledge Discovery, 18(3):370–391.
Markov, A. (1971). Extension of the limit theorems of prob-
ability theory to a sum of variables connected in a
chain.
Marzal, A. and Vidal, E. (1993). Computation of normal-
ized edit distance and applications. IEEE transac-
tions on pattern analysis and machine intelligence,
15(9):926–932.
Miao, Y., Ke
ˇ
selj, V., and Milios, E. (2005). Document clus-
tering using character n-grams: a comparative eval-
uation with term-based and word-based clustering.
In Proceedings of the 14th ACM international con-
ference on Information and knowledge management,
pages 357–358. ACM.
Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013a).
Efficient estimation of word representations in vector
space. arXiv preprint arXiv:1301.3781.
Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and
Dean, J. (2013b). Distributed representations of words
and phrases and their compositionality. In Advances in
neural information processing systems, pages 3111–
3119.
Pettersson, E., Megyesi, B., and Nivre, J. (2013). Nor-
malisation of historical text using context-sensitive
weighted levenshtein distance and compound split-
ting. In Proceedings of the 19th Nordic Conference of
Computational Linguistics (NODALIDA 2013); May
22-24; 2013; Oslo University; Norway. NEALT Pro-
ceedings Series 16, number 085, pages 163–179.
Link
¨
oping University Electronic Press.
Raghavan, V. V. and Birchard, K. (1979). A clustering strat-
egy based on a formalism of the reproductive process
in natural systems. In ACM SIGIR Forum, volume 14,
pages 10–22. ACM.
Rajalingam, N. and Ranjini, K. (2011). Hierarchical clus-
tering algorithm-a comparative study. International
Journal of Computer Applications, 19(3):42–46.
Rehurek, R. and Sojka, P. (2010). Software framework for
topic modelling with large corpora. In In Proceedings
of the LREC 2010 Workshop on New Challenges for
NLP Frameworks. Citeseer.
Salton, G. (1989). Automatic text processing: The transfor-
mation, analysis, and retrieval of. Reading: Addison-
Wesley.
Siivola, V. and Pellom, B. L. (2005). Growing an n-gram
language model. In Ninth European Conference on
Speech Communication and Technology.
Steinbach, M., Karypis, G., Kumar, V., et al. (2000). A com-
parison of document clustering techniques. In KDD
workshop on text mining, volume 400, pages 525–526.
Boston.
Tai, K. S., Socher, R., and Manning, C. D. (2015). Im-
proved semantic representations from tree-structured
long short-term memory networks. arXiv preprint
arXiv:1503.00075.
Wurzenberger, M., Skopik, F., Landauer, M., Greitbauer, P.,
Fiedler, R., and Kastner, W. (2017). Incremental clus-
tering for semi-supervised anomaly detection applied
on log data. In Proceedings of the 12th International
Conference on Availability, Reliability and Security,
Article, number 31.
Xu, J., Wang, P., Tian, G., Xu, B., Zhao, J., Wang, F., and
Hao, H. (2015). Short text clustering via convolutional
neural networks. In VS@ HLT-NAACL, pages 62–69.
Yujian, L. and Bo, L. (2007). A normalized levenshtein dis-
tance metric. IEEE transactions on pattern analysis
and machine intelligence, 29(6):1091–1095.
Zhang, X., Zhao, J., and LeCun, Y. (2015). Character-
level convolutional networks for text classification. In
Advances in neural information processing systems,
pages 649–657.
Zhao, Y., Karypis, G., and Fayyad, U. (2005). Hierarchi-
cal clustering algorithms for document datasets. Data
mining and knowledge discovery, 10(2):141–168.
The Growing N-Gram Algorithm: A Novel Approach to String Clustering
63
