
Acceleration of Backpropagation Training
with Selective Momentum Term
Diego Santiago de Meneses Carvalho
1
and Areolino de Almeida Neto
2
1
Department of Computing, IFMA, Sao Luis, Brazil
2
Department of Informatics, UFMA, Sao Luis, Brazil
Keywords:
Artificial Neural Networks, Momentum Term, Correlation Coefficient, BP with Selective Momentum.
Abstract:
In many cases it is very hard to get an Artificial Neural Network (ANN) suitable for learning the solution, i.e., it
cannot acquire the desired knowledge or needs an enormous number of training iterations. In order to improve
the learning of ANN type Multi-Layer Perceptron (MLP), this work describes a new methodology for selecting
weights, which will have the momentum term added to variation calculus of their values during each training
iteration via Backpropagation (BP) algorithm. For that, the Pearson or Spearman correlation coefficients are
used. Even very popular, the usage of BP algorithm has some drawbacks, among them the high convergence
time is highlighted. A well-known technique used to reduce this disadvantage is the momentum term, which
tries to accelerate the ANN learning keeping its stability, but when it is applied in all weights, as commonly
used, with inadequate parameters, the result can be easily a failure in the training or at least an insignificant
reduction of the ANN training time. The use of the Selective Momentum Term (SMT) can reduce the training
time and, therefore, be also used for improving the training of deep neural networks.
1 INTRODUCTION
For decades studies are performed based on example
of intelligence. These studies, known as Artificial In-
telligence (AI), yielded some techniques that, within
its limitations, can mimic part of human intelligence.
One of the relevant features of AI techniques is the
capacity of learning, so, the capacity of acquiring new
knowledge and changing the behavior as new knowl-
edge is obtained.
Among these techniques we can mention the Arti-
ficial Neural Networks (ANNs), which have a similar
structure of human neural networks, i.e. many inter-
connections among processing units and these inter-
connections, after a training process, are able to accu-
mulate knowledge and ”learn” a desired behavior.
However, in many cases it is very hard to get an
ANN suitable for learning the solution, i.e., it cannot
acquire the desired knowledge or needs an enormous
number of training iterations.
This study aims to develop an innovation to train-
ing ANNs by introducing the momentum term in the
updating calculus of some weights, in order to accel-
erate the decrease of the mean square error and thus
reducing the learning time. That means, it is intended
to cause ANN type of multilayer perceptron (MLP)
trained with the Backpropagation (BP) algorithm to
reach the mean square error values in fewer iterations
keeping the quality of learning and without significant
computational load.
According to (Goodfellow et al., 2016), due to
the ease of training, autoencoders have been used as
building blocks to form a deep neural network, where
each level is associated with an autoencoder that can
be formed separately. The selective momentum term
can be applied to each block formed by MLP.
The next section shows the theoretical basis of the
development of this work, once it describes the learn-
ing of ANN chosen emphasizing the advantages and
disadvantages of BP algorithm. Section 3 shows some
related works. In section 4 the methodology proposed
is presented, as well as the experiments performed
and the results obtained. Concluding the article, the
last section shows relevant conclusions.
2 BACKPROPAGATION
TRAINING
The MLP, a very popular type of ANN, is used for
many different problems. However there are some
Carvalho, D. and Neto, A.
Acceleration of Backpropagation Training with Selective Momentum Term.
DOI: 10.5220/0007272004430450
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 443-450
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
443

parameters to be set up by estimate: the amount
of hidden layers, the number of neurons, the acti-
vation function, the usage of bias, initial values of
weights, the learning rate and the usage of momentum
term. The choice of these parameters has no rule and
ANN designer uses some heuristics or even a random
choice currently.
The learning process or training is an iterative pro-
cess of weights modification until the output of ANN
is close to the desired value for the given input data.
This process is usually performed by an algorithm,
which has rules for the weights adjustment.
The most used algorithm for training MLP net-
works is called Backpropagation (BP). This algorithm
implements a supervised learning and its main pur-
pose is to minimize the mean square error of the
ANN’s output. The BP algorithm applies the gradi-
ent descent method.
Each BP interaction works in two phases: forward
and backward. In the first phase, there is no change
in the value of weights, just the propagation of input
signals towards output layer for the purpose of cal-
culating the error of the network. In the backward
phase, the network output error is used to adjust the
weights. The output error travels backward, layer by
layer, from the output layer until the first hidden layer.
The error of each layer is used to adjust the weights
before this layer. The variation of each weight is per-
formed using the following equation:
∆W
i j
= η.e
i
. f
0
i
.out
j
(1)
In equation 1, ∆W
i j
is the change in the weight be-
tween the neuron i in the output layer and neuron j in
the hidden layer, η is the learning rate, e
i
corresponds
to the output error of the neuron i; f’
i
is the derivative
of the neuron i activation function with respect to its
net input, and finally, out
j
represents the output value
of neuron j in the hidden layer.
As BP algorithm provides changes in the weights,
a proper initialization of these parameters must be
done, because the success of the training is strongly
dependent on the initial values of the weights. They
are generally set randomly. If these values are not
suitable for the problem at hand, the learning pro-
cess can get stuck in a local minimum and then can
no longer reduce the ANNs output error, except if a
higher learning rate is used or another initialization
is performed, which will not necessarily guarantee a
successful training.
In practice, to get a proper level of output error,
many attempts are executed, because different weight
initializations, learning rates, amount of hidden neu-
rons, ANN topologies (layers with bias or not), activa-
tion functions in neurons and so on must be tried until
one finds a suitable set up for these items. So, one
problem faced in training via BP concerns the lack
an appropriate methodology for setting some param-
eters and other elements. Among them, the learning
rate is defined by the designer and is extremely im-
portant for ANNs learning, because it determines the
step size of each iteration, which implies to get stuck
in a local minimum or continue searching a suitable
minimum or even the global one of the ANNs output
error. Besides, high value of learning rate accelerates
the learning, but can cause instability in the learning.
As BP algorithm has a simple implementation,
low computational complexity and fast response,
many researchers try to overcome the major drawback
of MLP network, the high convergence time, consid-
ering the sum of time wasted with all attempts un-
til a suitable ANN is found. Therefore this research
presents a technique to surpass this disadvantage.
Some techniques have been developed toward im-
proving the convergence of learning. The momentum
term is one of these techniques, which can accelerate
the networks learning convergence while maintaining
its stability. Equation 2 shows this technique:
∆W
i j
= η.e
i
. f
0
i
.out
j
+ α.∆W
i j
(n − 1) (2)
In the above equation, ∆W
i j
is the change in the
weight between the neuron i in the output layer and
neuron j in the hidden layer, η is the learning rate, e
i
corresponds to the output error of the neuron i; f’
i
is
the derivative of the neuron i activation function with
respect to its net input, and finally, out
j
represents the
output value of neuron j in the hidden layer, α is the
momentum term constant and n is the current iteration
of algorithm execution.
The weights updating becomes a balance between
the current step and the previous calculated ones. This
is implemented by applying a constant α (0 < α ≤
1), called momentum constant, on the last iteration of
change in the weight vector. In this way, the next
change of weight will be roughly in the same direc-
tion of the previous one and, depending on the situ-
ation, this small acceleration can be enough to over-
come any existing local minimum.
3 RELATED WORKS
In (Xiu-Juan and Cheng-Guo, 2009), the authors im-
proved the convergence of BP algorithm increasing
the error signal by increasing the momentum constant
and self-adaptive learning rate. Thus they can avoid
updates toward regions where the error is growing,
ensuring greater accuracy and stability.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
444

In (Shi et al., 2012), the used momentum term var-
ied between 0 and 1. When the ANN output error is
dropping normally, the momentum terms value is 0,
indicating the weights updating will be based on the
normal gradient descent. When a local minimum is
reached, its value is 1, indicating the weights updat-
ing will be based on its last value update.
The work (You and Li, 2014) modifies the tradi-
tional BP in two aspects: insertion of an additional
momentum term and use of self-adaptive learning
rate. The difference between the traditional momen-
tum term and the additional one is the last one does
not consider the gradient only, but also the effects of a
possible updating of weights. The self-adaptive learn-
ing rate is based on the error, as in previous works.
Finally, work (Shao and Zheng, 2009) proposes a
new BP algorithm with a variable momentum coeffi-
cient, which is dynamically adjusted based on the er-
rors gradient and on the latest weights update. When
the angle between them is less than 90
◦
, the momen-
tum coefficient is a positive value between 0 and 10
and when the angle is more than 90
◦
, the momentum
coefficient is 0.
4 BP WITH SELECTIVE
MOMENTUM TERM
Due to the difficulties in the training process using
original BP, several techniques have been developed
in order to improve the learning. One technique very
interesting is called momentum term, which consists
of adding a term to the calculation of the variation of
the weights, as shown in equation 2. However, the
current research shows the way this technique is cur-
rently applied cannot be the most suitable for some
problems. Based on this information, in this section
a variation on original momentum term is presented,
as well how this variation can be used to accelerate
the training. This proposal uses a correlation coeffi-
cient as a rule for selecting which weights should be
updated using the momentum term.
4.1 Correlation
According to (Larson and Farber, 2003), a correlation
is a relationship between two variables, where data
may be represented by ordered pairs (x, y), with x be-
ing the independent variable (or explanatory) and y
the dependent variable (or response).
One way to analyze the correlation between two
variables is through the linear correlation coefficient.
This coefficient is limited in the range [-1, 1], and a
value close to 1 indicates a strong positive correlation
between the variables, a value close to -1 indicates a
strong negative correlation and values close to 0 indi-
cate the absence of a linear relationship between the
variables. Remember that the coefficient does not im-
ply causality.
4.1.1 Pearson Correlation Coefficient
The Pearson correlation coefficient is also called
product-moment correlation coefficient, because it
multiplies the scores (product) of two variables and
after calculates the average (time) of the product of a
group of n observations. Equation 3 summarizes this
process:
r =
n
∑
xy − (
∑
x)(
∑
y)
p
n
∑
x
2
− (
∑
x)
2
p
n
∑
y
2
− (
∑
y)
2
(3)
In above equation, r corresponds to the Pearson
coefficient, n is the number of observations, x is the
independent variable and y is the dependent variable.
The Pearson correlation coefficient is a paramet-
ric measure that performs three assumptions: the first
one is the relationship between variables is linear; the
second one is the variables should be measured in in-
tervals and the last one is the variables should have
a normal joint bivariate distribution, which means for
each given x, the variable y is normally distributed.
According (Lira, 2004), among the factors that af-
fect the intensity of the correlation coefficient, one
can list the sample size, the outliers, the restriction
on the amplitude of one or both variables and mea-
surement errors.
4.1.2 Spearman Correlation Coefficient
The Spearman correlation coefficient (ρ), or Spear-
man’s rank (intervals defined in the sample database)
correlation coefficient, is a non-parametric correla-
tion measure unlike the Pearson correlation coeffi-
cient does, because it does not make any assumptions.
Equation 4 below shows the calculation process.
ρ = 1 −
6
∑
i
d
2
i
(n
3
− n)
(4)
In the above equation, n is the number of pairs (x
i
,
y
i
) and d
i
is the difference between the rank of x
i
and
rank of y
i
.
The Spearman correlation coefficient is more ap-
propriate than the Pearson correlation coefficient in
the following cases:
• The data does not form a well-behaved data set,
with some data quite distant from the others;
• There is a nonlinear relationship;
• The amount of samples is small.
Acceleration of Backpropagation Training with Selective Momentum Term
445

In this work, equations 3 and 4 use the value of
each weight as the independent variable (x), the net-
work error value as the dependent variable (y) and the
size of the iteration interval as the number of observa-
tions (n).
4.2 Description of Developed
Methodology
Currently, most designers, who use the momentum
term, concern to choose the appropriate value for α
constant and apply it to correct all weights. However,
(Haykin, 1994) shows that learning must be acceler-
ated in weights that maintains the same algebraic sig-
nal for several consecutive training iterations. On the
other hand, weights, which often change the algebraic
sign for a certain period of consecutive iterations, in-
dicate the global minimum is near, so the acceleration
applied could destabilize the algorithm around that
point.
Based on the paragraph above, this work suggests
a way to identify the weights that should be adjusted
using the momentum term during the training. For
such identification the correlation coefficients men-
tioned above are used. The procedure is described
below:
1. A fixed number of iterations (n) for correlation
calculation is defined by the ANNs designer;
2. During ANNs training, after each n steps of itera-
tion, the correlation coefficient (Pearson or Spear-
man) between each weight and the error is calcu-
lated;
3. Correlation coefficients close to 1 or -1 indicate a
strong linear correlation between the weight and
the ANNs error and possibly a path in a steep de-
scent. So, the weights with those correlation coef-
ficient values are selected for the addition of mo-
mentum term with maximum constant (α = 1) for
the next n iterations.
For the first n iterations the momentum term is not
applied because there is not sufficient data to calculate
the correlation coefficient.
Note that the Spearman correlation coefficient is
less sensitive to outliers than Pearson coefficient. For
that reason, in this work, the momentum term was ap-
plied to weights whose Spearman coefficient in mag-
nitude is equal to 1 and Pearson coefficient in magni-
tude is greater than 0.95.
5 RESULTS
The following subsections show how the test environ-
ment was assembled and the obtained results.
5.1 Test Environment
The first stage of tests compared the traditional BP,
BP with momentum term in all weights and BP with
selective momentum term (momentum term in some
weights). The second step identifies the correlation
coefficient (Pearson or Spearman) which had the best
result. In this step it was also performed a ran-
dom weight selection for adjustment using momentum
term in order to verify if selecting proper weights is
the key for the improvement or not.
In both steps it was defined previously the num-
ber of neurons of the hidden layer, the learning rate,
the value of the mean square error of the network
output and the size of iterations range for correla-
tion coefficients calculation. It is important to men-
tion that for each approach the networks were trained
with the same architecture (MLP with the same ini-
tial values for the weights, only one hidden layer and
the same number of neurons in the hidden layer), the
same computer (i3 core processor, 4Gb of RAM and
Windows 10 operating system) and the same software
(MATLAB, v. R2015a). The results presented are the
number of iterations, the time in seconds and the suc-
cess rate of each approach.
In order to evaluate all approaches, tests were per-
formed with several quantities of neurons in the hid-
den layer, starting with seven units and going up to
105, adding seven neurons each time.
For each number of neurons in the hidden layer,
each step was performed 20 times, each one with dif-
ferent initial values of the weights. So, a total of 300
(20 initializations x 15 settings) different runs were
carried out per stage.
As the focus of this research is to improve the
training of MLP type ANN, an already solved prob-
lem of classification was chosen to validate the pro-
posal: breast cancer detection. The Wisconsin Breast
Cancer was used, which is available at the UCI repos-
itory and contains 699 associated events with nine at-
tributes. The ANNs used in this study had to classify
events as benign or malignant processing the nine at-
tributes.
Analizing the data set, one can verify there are
empty values in some attributes of 16 events, there-
fore they were discarded and not used in this research.
From the remaining data, 477 events were used for
training and 205 for generalization tests.
About the ANNs structure, all ANNs had nine
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
446

neurons in the input layer (one neuron for each value
from event), the output layer had just one neuron, rep-
resenting benign or malignant event. The characteris-
tics of the hidden layer have already been defined in
the previous section.
In order to determine the value of the learning
rate and the mean square error used in the tests,
some ANNs were trained using only the traditional
BP. From these tests, the best values for the learn-
ing rate and the mean square error were 0.0001 and
0.0145, respectively. These values indicate a success
rate around 98%, which corresponds to the percent-
age of times that the network could indicate correctly
a benign or malignant event, after training.
Concerning the size of the interval for correlation
coefficient calculation, many tests were performed in
order to define empirically the adequate amount of it-
erations. For instance, using just 10 iterations, good
results for the training iterations reduction were ob-
tained, but it wasted time as much as the traditional
BP. With 50 iterations, all local minima could not be
avoided and some tests were unsuccessful for the de-
sired knowledge. The amount of 20 iterations showed
more suitable results for all criteria, that means, good
reduction in the number of iterations, not much time
for running and successful knowledge were achieved.
Therefore, the following results were performed using
this size of iterations.
It is worth noting that only five tests using BP
with momentum term and α = 1 (momentum term con-
stant) reached the desired error, thus those cases were
deleted from the next two tables.
5.2 Results
After the first stage, some results were generated,
which are presented in Table 1, showing the average
number of iterations on the 20 trainings.
According to Table 1, using the methodology pro-
posed in this paper, the case with the largest number
of iterations was using seven neurons in the hidden
layer only, i.e. 1,523 iterations for achieving the de-
sired error. On the other hand, Table 1 shows the least
iterations were obtained with 105 neurons in the hid-
den layer, when just 195 iterations was necessary to
reach this error. Also according to the same table,
with 35 neurons in the hidden layer, there was a great
reduction in the number of iterations: from 5,814 us-
ing the traditional BP to just 363 iterations with the
proposed methodology. At the same time, for com-
parison purpose, using BP with momentum term and
α = 0.5, the number of iterations dropped to 2,988.
From the values on Table 1, Figure 1 was gener-
ated, which shows a graph of the percentage of re-
duction in the number of iterations provided by the
proposed method when compared to other methods
tested, for each amount of neurons in the hidden layer.
The graph demonstrates the best performance of BP
with Selective Momentum Term, because when com-
pared to other approaches, in all cases there was a re-
duction in the number of training iterations.
Yet in Figure 1, the average reduction provided
by this research was 92% compared to traditional BP
and 62% compared to BP with momentum term and
α = 0.9. The reduction compared to BP with max-
imum momentum term cannot be calculated, due to
the existence of training that were trapped in a local
minimum and therefore no results were obtained with
that approach. However, one can highlight that the
BP with selective momentum term was able to avoid
all existing local minima, because it was successful in
all training.
Still comparing the criteria of speed, Table 2
shows the average time in seconds of performed train-
ing. In this table, the case of the lowest average time
with the methodology proposed in this paper occurred
when the hidden layer had 14 neurons, in this case
the desired error was reached in just 2.36 s. With the
same number of neurons in the hidden layer, using
the BP with momentum term and α = 0.1, the aver-
age time was 22.79 s. In percentage, one can notice
the proposed method could reduce 79% of the time of
traditional BP and was result slightly better than the
BP with momentum term and α = 0.9.
Table 3 was also produced in the first stage. It
shows the results of generalization tests for each ap-
proach, where the average hit rate, calculated over 20
trainings (20 different weight initializations), is pre-
sented. It is noticed that the variation in hit rates is
very small, except for BP with maximum momentum
term, due to the trainings were trapped in a local min-
imum. It is worth mentioning that the results for BP
with Selective Momentum Term of the first stage were
achieved using the Pearson correlation coefficient.
After the second stage, Tables 4 and 5 were gener-
ated. All data were obtained taking into consideration
the same characteristics of ANNs used to produce the
tables 1 and 2. But now, the comparison is related
to use of correlation coefficients, not the methods of
training.
According to Table 4, the highest amount of iter-
ations using this proposal occurred when there were
seven neurons in the hidden layer and when the Pear-
son correlation coefficient was used, in this case 4,524
iterations were necessary to achieve the desired error.
The lowest number of iterations was obtained with 98
neurons in the hidden layer using Spearman correla-
tion coefficient, when just 201 iterations were neces-
Acceleration of Backpropagation Training with Selective Momentum Term
447
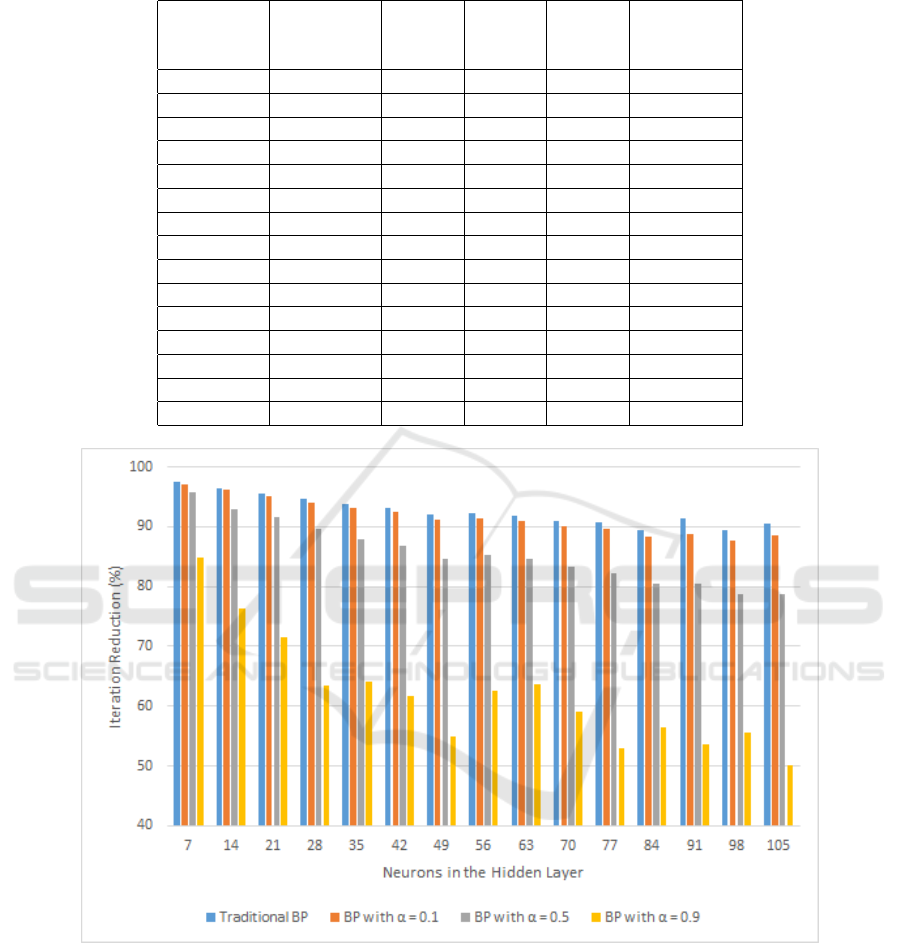
Table 1: Average number of iterations.
Neurons in Traditional BP BP BP BP
the Hidden BP with with with Selective
Layer α = 0.1 α = 0.5 α = 0.9 Momentum
7 60281 51741 36063 10038 1523
14 16944 15241 8365 2468 585
21 10544 9611 5585 1656 473
28 7516 6772 3879 1091 399
35 5814 5229 2988 1013 363
42 4681 4214 2427 836 320
49 3797 3419 1964 670 302
56 3392 3054 1766 697 261
63 3036 2738 1616 686 250
70 2673 2409 1430 587 240
77 2424 2183 1279 480 226
84 2188 1965 1169 527 229
91 2474 1908 1097 465 215
98 2026 1757 1003 483 214
105 2039 1706 918 390 195
Figure 1: Percentage reduction in the number of iterations.
sary to get the same error.
On the average, the best results were for the Spear-
man and Pearson’s correlation coefficient with 408
and 589 iterations, respectively. And as expected, the
use of random selection of weights required a higher
number of iterations than the correlation coefficients,
681 iterations on average.
Table 5 shows the average time for each number
of neurons in the hidden layer. The best results were
obtained with random selection of weights, because
it requires less time for processing the calculation,
followed by Pearson correlation coefficient. On gen-
eralization tests also does not occur big differences
among the coefficients, so the presentation of a new
table can be suppressed. In average, the Pearson cor-
relation coefficient obtained a hit rate of 98.17, the
Spearman correlation coefficient 98.15 and with ran-
dom selection of weights were obtained 98.02.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
448
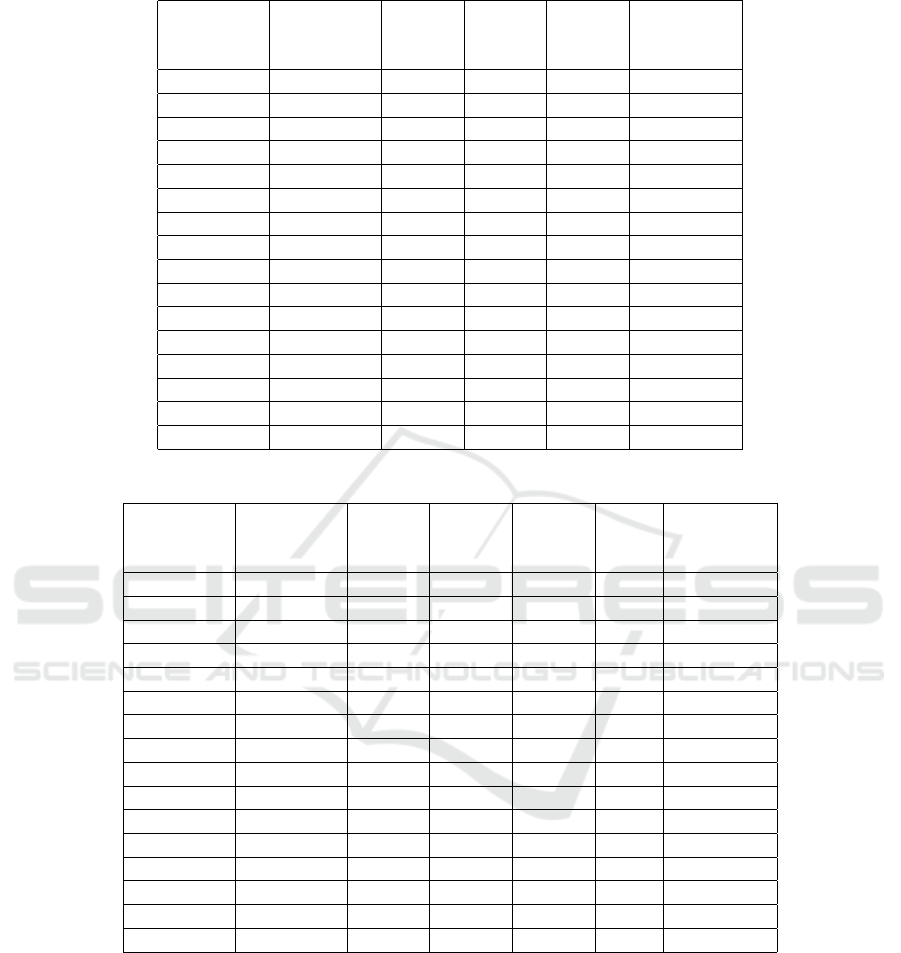
Table 2: Average time.
Neurons in Traditional BP BP BP BP
the Hidden BP with with with Selective
Layer α = 0.1 α = 0.5 α = 0.9 Momentum
7 88.27 83.47 77.93 17.89 6.28
14 21.95 22.79 12.63 3.72 2.36
21 20.73 22.53 12.71 3.79 3.09
28 18.80 20.25 11.47 3.38 3.41
35 16.06 17.24 9.81 3.40 3.63
42 14.94 16.32 9.19 3.22 3.66
49 12.30 13.00 7.66 2.65 3.54
56 12.42 13.68 7.64 3.15 3.48
63 16.78 18.46 10.81 4.65 4.85
70 16.32 17.54 10.35 4.36 5.14
77 15.88 17.19 10.15 3.81 5.32
84 14.83 16.14 9.58 4.44 5.65
91 18.21 16.91 9.72 4.18 5.65
98 13.81 13.42 7.89 3.83 4.83
105 14.41 14.35 7.69 3.27 4.72
Average 21.04 21.55 14.34 4.64 4.36
Table 3: Hit rate.
Neurons in Traditional BP BP BP BP BP
the Hidden BP with with with with Selective
Layer α = 0.1 α = 0.5 α = 0.9 α = 1 Momentum
7 98.04 98.07 98.04 98.41 63.60 97.73
14 98.31 98.29 98.31 98.14 79.12 98.09
21 98.46 98.43 98.41 98.19 84.63 98.24
28 98.36 98.39 98.41 98.39 85.34 98.31
35 98.58 98.58 98.60 98.48 82.63 98.21
42 98.48 98.46 98.46 98.46 87.34 98.26
49 98.46 98.46 98.46 98.41 83.24 98.26
56 98.24 98.24 98.19 98.34 77.26 97.92
63 98.34 98.34 98.34 98.31 83.97 97.97
70 98.43 98.43 98.58 98.51 81.48 98.07
77 98.36 98.36 98.39 98.51 82.85 98.02
84 98.53 98.58 98.43 98.43 85.82 98.21
91 98.46 98.43 98.51 98.43 88.26 98.19
98 98.31 98.36 98.41 98.43 87.56 98.26
105 98.48 98.53 98.53 98.34 81.26 98.02
Average 98.39 98.40 98.40 98.39 82.29 98.12
6 CONCLUSIONS
This paper presented an innovative methodology to
use the momentum term in Backpropagation (BP) al-
gorithm, which was able to accelerate significantly
the training and to avoid local minima more effec-
tively. The proposed methodology was called Back-
propagation with Selective Momentum Term.
The new methodology has been subjected to a
load of comparative tests with traditional BP and BP
with momentum term in all weights. In order to per-
form the tests, a well-known classification problem
(breast cancer detection) was chosen and has solved.
The test results showed a greater reduction in the
number of iterations in all cases, when compared to
training with traditional BP. The amount of iterations
reduction (50.06% to 97.70%) was obtained consider-
ing the same mean square error that was achieved by
Acceleration of Backpropagation Training with Selective Momentum Term
449

Table 4: Average number of iterations.
Neurons in the Aleatory Pearson Spearman
Hidden Layer
7 4117 4524 1772
14 1156 622 657
21 899 496 490
28 590 407 416
35 521 355 378
42 436 310 303
49 379 292 278
56 340 262 254
63 332 252 245
70 283 238 235
77 256 230 264
84 229 212 214
91 240 213 203
98 212 211 201
105 221 206 205
Average 681 589 408
Table 5: Average time.
Neurons in the Aleatory Pearson Spearman
Hidden Layer
7 3.42 9.58 5.12
14 1.45 2.37 3.49
21 1.47 2.69 3.79
28 1.18 2.81 4.10
35 1.39 3.07 4.84
42 1.22 3.08 4.31
49 1.21 3.32 4.53
56 1.27 3.47 5.00
63 3.19 8.38 11.8
70 2.94 8.59 12.5
77 2.92 8.95 15.31
84 2.88 9.14 13.40
91 3.15 9.67 13.68
98 3.95 12.42 18.53
105 1.42 4.81 6.89
Average 2.20 6.15 8.48
the other approaches.
But fewer iterations do not mean faster, so a com-
parison involving execution time of tested approaches
was performed and many times the proposed method-
ology got the best results, i.e., even with an additional
computational load (correlation coefficients calcula-
tion), the time to process the program was shorter than
one processed by other approaches. In some cases, se-
lecting weights randomly for receiving the momentum
term could be faster, because that procedure is simpler
than correlation calculation.
Besides, even using the maximum value (α =
1) for the momentum term constant, the proposed
methodology was able to avoid the local minima in all
tests, what was not possible for traditional BP and BP
with momentum term in all weights. Based on these
results, one can say that BP with Selective Momen-
tum Term is a very interesting option for the improve-
ment of BP algorithm and therefore use it in other
techniques, like stacked auto-encoded deep learning,
which has many hidden layers, each one can utilize
BP algorithm for the weights connected to them.
ACKNOWLEDGEMENTS
The authors acknowledge FAPEMA, CAPES, UFMA
and IFMA for technical and financial support to this
research. Special acknowledgements to PPGCC and
MecaNet.
REFERENCES
Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep
Learning. MIT Press. http://www.deeplearningbook.
org.
Haykin, S. (1994). Neural networks: a comprehensive foun-
dation. Prentice Hall PTR.
Larson, R. and Farber, B. (2003). Elementary statistics.
Prentice Hall.
Lira, S. A. (2004). Correlation analysis: theoretical and
construction approach (in portuguese). curitiba, 2004.
196p. Master’s thesis, Center of Exact Sciences and
Technology, UFPR.
Shao, H. and Zheng, G. (2009). A new bp algorithm with
adaptive momentum for fnns training. In Intelligent
Systems, 2009. GCIS’09. WRI Global Congress on,
volume 4, pages 16–20. IEEE.
Shi, L., Hou, W., Shi, J., and Liu, H. (2012). The intelli-
gent bit design of aviation integrated computer system
based on improved bp neural network. In Prognostics
and System Health Management (PHM), 2012 IEEE
Conference on, pages 1–6. IEEE.
Xiu-Juan, F. and Cheng-Guo, L. (2009). The research in
yarn quality prediction model based on an improved
bp algorithm. In Computer Science and Information
Engineering, 2009 WRI World Congress on, volume 2,
pages 167–172. IEEE.
You, M. and Li, Y. (2014). Automatic classification of the
diabetes retina image based on improved bp neural
network. In Control Conference (CCC), 2014 33rd
Chinese, pages 5021–5025. IEEE.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
450
