Robust Person Identiﬁcation based on DTW Distance of Multiple-Joint

Gait Pattern

Takafumi Mori

and Hiroaki Kikuchi

Graduate School of Advanced Mathematical Sciences, Meiji University, 164-8525, Japan

School of Interdisciplinary Mathematical Science, Meiji University, 164-8525, Japan

Keywords:

Gait, Biometrics, DTW, Person Identiﬁcation.

Abstract:

Gait information can be used to identify and track persons. This work proposes a new gait identiﬁcation

method aggregating multiple features observed by a motion capture sensor and evaluates the robustness against

obstacles in walking. The simplest gait identiﬁcation is to use gait statistics, but these are not a signiﬁcant

feature with regard to identifying people accurately. Hence, in this work, we use the dynamic time warping

(DTW) algorithm to calculate distances of gait sequences. DTW is a pattern-matching algorithm mainly used

in speech recognition. It can compare two sets of time series data, even when they have different lengths. We

also propose an optimal feature integration method for DTW distances. For evaluating the proposed method,

we developed a prototype system and calculated the equal error rate (EER) using 31 subjects. As a result,

we clariﬁed that the EER of the proposed method is 0.036 for normal walking, and that it is robust to some

obstacles in walking.

1 INTRODUCTION

Gait information can be used to identify and track per-

sons because there are several advantages to using a

person’s gait features. For example, the features can

be observed by outside sensors, can easily be aggre-

gated for multiple features, and target cooperation is

unnecessary. The consumer market industry has a

strong demand for automatically tracking persons and

for big-data analysis of the behavior of a large number

of customers in a store. Gait information can be used

to track customers without their consent to be tracked.

It is important to pay attention to economical cost of

security systems in modern applications (Sklavos and

Souras, 2006).

The simplest form of gait identiﬁcation is to use

statistics of human joint distance. For example, we

identify people by an average distance between hands.

However, statistics are not suitable for doing so be-

cause of the following difﬁculties:

• The dynamic distance between hands is not stable

and changes frequently, even in the same person.

• The static distance between joints does not have

a high enough resolution to distinguish between

individuals.

In order to solve the issues with regard to gait

identiﬁcation, we used the dynamic time warping

(DTW) (Berndt and Clifford, 1994) algorithm in this

work, which is a well-known pattern-matching algo-

rithm designed for time series data. With the DTW

algorithm, we can compare two time series of diffe-

rent lengths, while minimizing distances of the ﬂuc-

tuation patterns of joints in a time series. With the

DTW distance, we improve the accuracy of matching

by computing dynamic patterns, which could not be

recognized in static features.

A state-of-the-art study (Muaaz and Mayrhofer,

2017) applied the DTW algorithm to the time series

data of a smartphone-based accelerometer. However,

this work cannot be used in automatic person tracking

because of the following drawbacks:

• The subject’s cooperation is necessary to bring the

smartphone and to install the application. Hence,

the number of sensors to track is limited.

• The smartphone-based sensor detects the accele-

ration data of the center of the body but does not

detect individual movements of the hands or feet.

The time series data of the single sensor would

not provide sufﬁcient data to track a person.

• It is not robust to obstacles of walking, e.g., car-

rying a bag or box, texting, phoning, or wearing

sandals. The obstacles may interfere with the

Mori, T. and Kikuchi, H.

Robust Person Identiﬁcation based on DTW Distance of Multiple-Joint Gait Pattern.

DOI: 10.5220/0007307002210229

In Proceedings of the 5th International Conference on Information Systems Security and Privacy (ICISSP 2019), pages 221-229

ISBN: 978-989-758-359-9

221

tracking of the subject and could result in failure

of identiﬁcation.

Instead of the single sensor in the smartphone, we

will capture multiple movements of several joints of

the body by using a motion capture sensor such as

Kinect. Our proposed method does not require the

cooperation of users. Since a sensor detects many

subjects at the same time, the number of sensors is

greater than in the study by (Muaaz and Mayrhofer,

2017). The motion capture sensor allows us to de-

tect movements of multiple joints of our body. It is

thus useful for improving the robustness of identiﬁca-

tion. Even if a partial movement of a hand is blocked

by some obstacle, we can identify the person by al-

ternative joints such as the foot or the head. We can

aggregate multiple movements of joints in human bo-

dies to improve the accuracy of identiﬁcation. Our

experiment shows that the equal error rate (EER) of

our proposed method is 0.036, which is smaller than

0.13 in the above-mentioned study (Muaaz and May-

rhofer, 2017) for a single smartphone. We summarize

the comparison between this work and the previous

work in Table 1.

In our method, some research questions require

answering.

• How many features must be aggregated to mini-

mize the EER? Two features are better than one,

but it is important to deﬁne an appropriate maxi-

mum number of features because too many featu-

res may increase the false rejection rate (FRR).

• Automatic identiﬁcation should be disabled when

the subject is not willing to be tracked. Possible

ways to prevent tracking include obfuscating the

way of walking by carrying a bag or box. Which

characteristic would obfuscate the gait the most?

To answer these questions, we conducted an expe-

riment using a prototype implementation of the pro-

posed method.

The remainder of the paper is organized as fol-

lows. In Section 2, we brieﬂy describe some previous

work related to this study. In Section 3, we propose

a new gait identiﬁcation method using the DTW al-

gorithm, and an improvement that integrates multi-

ple features. With the development prototype system,

we evaluate the accuracy of the proposed method and

report the optimal parameters in Section 4. Finally,

based on the experimental results, we consider requi-

rements relating to person identiﬁcation in Section 5.

We conclude our study in Section 6.

2 RELATED WORKS

Gait authentication using an RGB camera has been

studied previously. Han et al. (Han and Bhanu,

2006) proposed the gait energy image (GEI). GEI is

an average image of gait for a cycle of walking. The

advantages of GEI are the reduction of processing

time, reduction of storage requirements, and robust-

ness of obstacles.

There are some studies using GEI. Backchy et

al. proposed a gait authentication method using Ko-

honen’s self-organizing mapping (K-SOM). In this

work, the authors used K-SOM to classify GEI and

reported a 57% recognition rate. Shiraga et al. propo-

sed the GEINet (Shiraga et al., 2016) using a convo-

lutional neural network to classify GEI images. The

best EER obtained was 0.01.

Person tracking can also be implemented using

depth sensors. A simple way of identiﬁcation is to

use statistics of human joint movement (Mori and Ki-

kuchi, 2018). In this work, 3-dimensional coordina-

tes of 25 joints of a body were captured by Microsoft

Kinect V2, and 36 features were deﬁned. In the expe-

riment, the EER was minimized to 0.25 by using the

best features in 10 subjects. This work demonstrated

that static features, such as statistics of distances, are

not useful for recognition. Preis et al. proposed a gait

recognition method using Kinect (Preis et al., 2012).

They used a decision tree and a Naive Bayes classiﬁer

to recognize the gait. In their work, a success rate of

91.0% was achieved for nine subjects.

Gender classiﬁcation using depth cameras has also

been applied. Igual et al. proposed a gender recogni-

tion method (Igual et al., 2013). In this work, they

used depth images instead of RGB images and cal-

culated the GEI from the images. The result of the

experiments showed that the accuracy of this method

is 93.90 %.

As mentioned earlier, gait authentication using

the accelerometer of mobile devices has also been

investigated. Muaaz et al.(Muaaz and Mayrhofer,

2017) proposed a person identiﬁcation method using a

smartphone-based accelerometer. They used the acce-

leration information of an Android device in a per-

son’s front pocket as data. A cycle of walking is de-

ﬁned as a template in the register phase and multiple

templates are registered. In the authentication phase,

the distances from all templates are examined and the

user is regarded as the correct person if more than half

of the templates are within the threshold. Zhang et

al. proposed a gait recognition method combining se-

veral sets of acceleration data (Zhang et al., 2015).

They showed that when the data from accelerometers

at ﬁve different body positions are used together, the

ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy

222

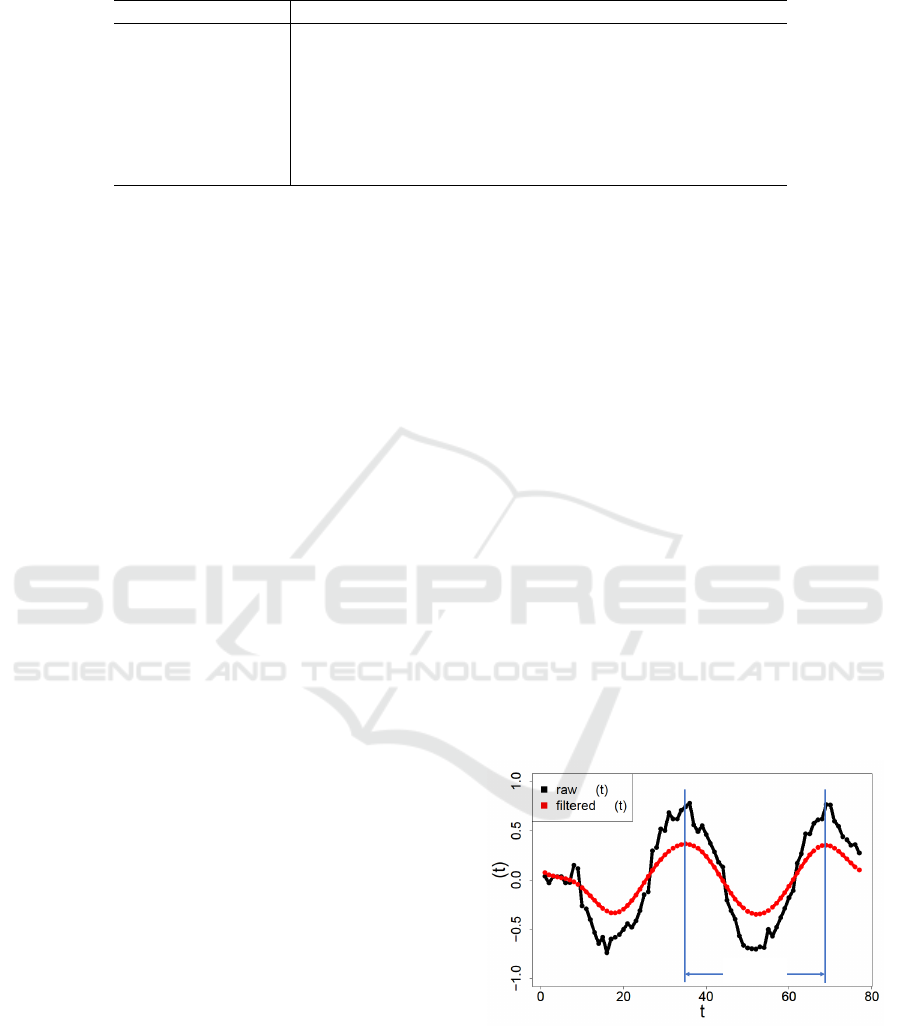
Table 1: Differences between the present work and previous works.

Muaaz GEI Mori 2018 This work

No. of features 1 1 1-36 1-24

Sensor inner outer outer outer

Observation period long short short short

No. of templates multi N/A single single

Target cooperation necessary unnecessary unnecessary unnecessary

Method DTW dist. GEI statistic feature DTW dist.

No. of subjects

35 - 10 31

rank-1 accuracy is 95.8% and the EER is 0.022.

2.1 Dynamic Time Warping

The DTW algorithm is a well-known method for pat-

tern matching and is used in speech recognition. It

quantiﬁes the distance differences between two sets

of time series data with different lengths. A DTW

distance between two sets of time series data P =

, p

,..., p

) and Q = (q

,...,q

), denoted by

d(P,Q), is deﬁned as

d(P,Q) = f (n

), (1)

where, f (i, j) is calculated recursively as

f (i, j) = ||p

− q

|| + min



f (i, j − 1), f (i − 1, j),

f (i − 1, j − 1),



(2)

f (0,0) = 0, f (i,0) = f (0, j) = ∞. (3)

The DTW algorithm also has many other uses.

Lee et al. proposed a handwritten pattern recogni-

tion method using the DTW algorithm on motion sen-

sor data generated from an accelerometer and a gy-

roscope (Lee et al., 2018). In this work, the accuracy

of the proposed method was 91.4% using a real-world

data set.

Li et al. proposed a gait recognition method based

on human electrostatic signals (Li et al., 2018). The

authors used DTW on the electric signal of walking.

From their experiment, the best correct rate achieved

was 87.5%.

3 PROPOSED METHOD

In this work, we recognize a person by using 3-

dimensional coordinates observed by motion capture

sensors, and calculate the DTW distance of the time

series data of one cycle of walking. The proposed

method consists of four steps:

1. Cycle extraction

2. Calculation of relative coordinates

3. Calculation of DTW distance

4. Person recognition.

3.1 Cycle Extraction

Let a

(t) = (x,y,z) be a time series of 3-dimensional

absolute coordinates of joint ` in time t. Skeleton data

is a set of time series data of absolute coordinates in

time t.

We extract one cycle of walking from the skeleton

data. In our environment, an observed video stream

contains about two cycles.

First, let ∆(t) be the distance between both feet in

time t, deﬁned using a

(t) and a

(t) as

∆(t) = ±||a

(t) − a

(t)||. (4)

If the right foot is in front, the sign of ∆(t) is positive,

otherwise it is negative.

Next, the Fourier transformation is applied to the

time series ∆(1),...,∆(n) and a low pass ﬁlter is ap-

plied to reduce noise and detect one cycle. The re-

sulting 1/30 low-frequency components are proces-

sed later. We deﬁne a cycle of walking as the period

between peaks. Note that the low pass ﬁlter is used

only for the purpose of cycle extraction and we use

non-ﬁltered data for the DTW algorithm. The origi-

nal data and ﬁlter-applied data are shown in Figure 1.

1 cycle

Figure 1: Distance between foot (black) and that of applied

low pass ﬁlter (red).

In the cycle extraction phase, time t is a unit cor-

responding to the frame rate of the motion capture

sensor. For example, Figure 1 shows example data

for 2.6 seconds where the frame rate is 30 fps. We

see noise-containing data (black) translated into gra-

dually changing data (red). In these example data, we

Robust Person Identiﬁcation based on DTW Distance of Multiple-Joint Gait Pattern

223

have one cycle as a series of features from the ﬁrst

peak (t = 37) to the second peak (t = 70). The data is

normalized from t

to t

3.2 Calculation of Relative Coordinates

We calculate relative coordinates of joints while wal-

king. The origin of coordinates is chosen from stable

joints in the center of the body. Note that in the expe-

riment in Section 4, c is SpineMid.

Let a

(t) be an absolute coordinate of center joints

c at time t. The relative coordinate r is deﬁned as

(t) = a

(t) − a

(t). (5)

3.3 Calculation of DTW Distance

We use a DTW algorithm to calculate a distance of

time series data. In our study, the position of a joint

is deﬁned in three axes, so we use multi-dimensional

dynamic time warping (MD-DTW) (ten Holt et al.,

2007). In MD-DTW, the 3-dimensional Euclidian dis-

tance is deﬁned as

||p

− q

|| =

i,x

− q

j,x

)

+ (p

i,y

− q

j,y

)

+ (p

i,z

− q

j,z

)

(6)

Let R

= hr

),...,r

)i and R

),...,r

)i be the time series data of joint `.

Let d(R,R

) be the distance between R and R

. When

R = R

, d(R, R

) = 0. It is not necessary to assume

that n = n

, but n is distributed in almost the same

way because the data is normalized in Section 3.1.

When several features are aggregated, the distance

is calculated as follows. Given two data sets (R

)

and (R

), and data of joints ` and m, an integra-

ted DTW distance D



),(R

)



is deﬁned

as an Euclidian distance of all DTW distances. i.e.,

d(R

)

+ d(R

)

. Likewise, given k featu-

res, distances are calculated as a k-dimensional Euc-

lidian distance.

3.4 Person Recognition

Let U be the set of all users. Let R

(u)

be time series

data of k pieces of normalized relative coordinates of

user u. Given s pieces of data (R

,...,R

), let tem-

plate data R

(u)

∗

be one of them. It is regarded that

u = v, if the integrated DTW distance D(R

(u)

(v)

)

of the two sets of time series data R

(u)

and R

(v)

is less

than θ.

Threshold θ

∗

is determined using the EER. Let

(u)

= {R

(u)

,...,R

(u)

} be a set of time series data

of u. At this time, the FRR and FAR are calculated as

FRR(θ,u) =

|{R

(u)

∈ W

(u)

|D(R

(u)

∗

) > θ}|

(u)

, (7)

FRR(θ) =

|U|

∑

u∈U

FRR(θ,u), (8)

FAR(θ,u) =

|{R ∈ W −W

(u)

|D(R,R

(u)

∗

) ≤ θ}|

(u)

. (9)

FAR(θ) =

|U|

∑

u∈U

FAR(θ,u), (10)

At this point, W is a set of time series data of all users.

The EER is an average error rate using threshold θ

∗

such that FAR(θ

∗

) = FRR(θ

∗

4 EXPERIMENT

4.1 Experiment Purposes

The purposes of our experiment are as follows:

1. To identify the best parameters (choice of num-

ber of joints k and threshold θ

∗

) for the proposed

gait identiﬁcation method using skeleton data and

DTW.

2. To evaluate the basic accuracy of the proposed

method.

3. To evaluate the accuracy of the proposed method

for walking containing some obstacles.

4. To identify the obstacle-robust joints.

4.2 Motion Capture Device

We used the Kinect V2, a motion capture device de-

veloped by Microsoft.

The Kinect device includes an RGB camera,

a depth camera, and a microphone. It identiﬁes

three-dimensional coordinates of joints of the player

to recognize the player’s movements. The three-

dimensional coordinates captured by the Kinect de-

vice are called skeleton data and can be retrieved via

the Kinect Software Development Kit.

4.3 Experimental Method

4.3.1 Experiment 1: Normal Walking

We captured walking data using Kinect V2 and eva-

luated the accuracy of the proposed method. We used

31 subjects, and each subject was assigned an ID from

ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy

224

Table 2: Information on the experiment.

1: Normal 2: Obstacles

Date April 19, 2018 March 26, 2018

Start time 12:40 19:00

End time 14:50 21:15

#subjects 31 5

Sex 26 male, 5 female 5 male

#walks 5 2

Age

18–51 21–24

Place classroom laboratory

1–31. Information regarding this experiment, Experi-

ment 1, is shown in Table 2.

We observed some skeleton data



(t),...,a

(t)



for walking straight in the

environment, as shown in Figure 2. The Kinect

device was placed horizontally 0.9 m above the ﬂoor.

The subjects each walked ﬁve times from a distance

of 5.5 m away to 1 m away from the device.

0.9m

5.5m

4.5m

2m1m

Start

Walking

Start

Recording

Finish

Recording

Finish

Walking

Kinect

Figure 2: Environment of Experiment 1.

In this experiment, we used SpineMid as the

origin c. Relative coordinates of joints from c

were calculated. We calculated the DTW distance



(u)

(v)



for each ` and detected the optimal θ

∗

for minimizing the EER.

We calculated the integrated DTW distance of the

top k joints in descending order of the EER and eva-

luated the EER.

4.3.2 Experiment 2: Obstacle-Containing

Walking

Some samples of obstacles are illustrated in Figure 3.

The information for data capture for this experiment,

Experiment 2, are shown in Table 2. We applied the

following 12 obstacles:

1. Normal (no obstacle),

2. Swinging hand and foot in a big swing (b-swing),

3. Swinging hand and foot in a small swing (s-

swing),

4. Putting hands in front pocket (pocket),

5. Walking while looking at smartphone (phone),

6. Carrying a handbag (handbag),

7. Carrying a shoulder bag (shoulder bag),

Figure 3: Sample obstacles (2 (b-swing), 4 (pocket), 5

(phone), 8 (sack), 9 (umbrella), 10 (box), 11 (sandals), 12

(suitcase)).

8. Carrying a knapsack (sack),

9. Holding an umbrella (umbrella),

10. Carrying a large box (box),

11. Wearing sandals (sandals),

12. Pulling a suitcase (suitcase).

We selected one set of template data from normal

walking and calculated the integrated DTW distance

with obstacle-containing data.

4.4 Experimental Results

4.4.1 Data Capture

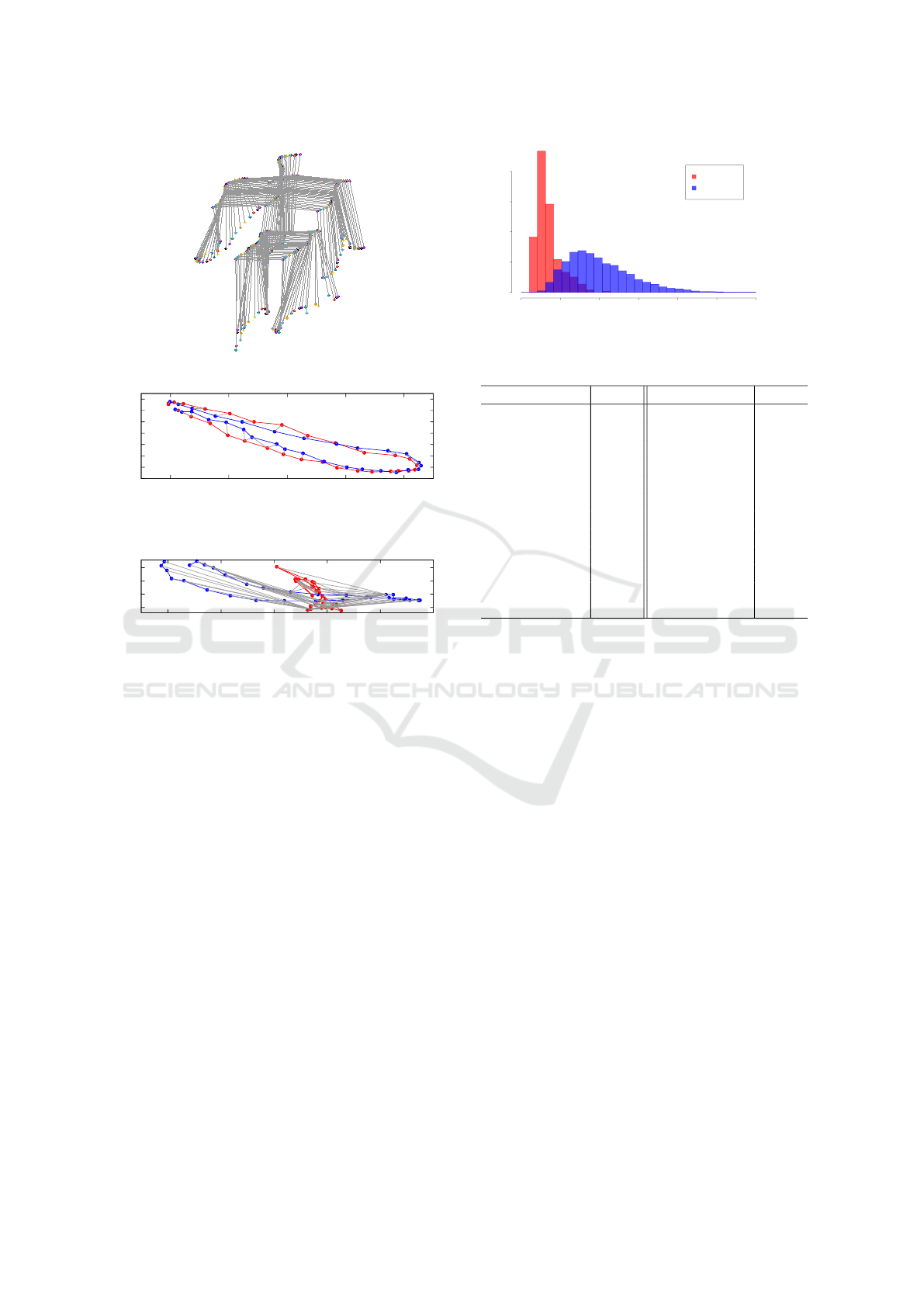
A sample of a 3D plot is shown in Figure 4. We show

the one-cycle trace of 11 principal joints (Head, Spi-

neShoulder, ShoulderRight, ShoulderLeft, HandTi-

pRight, HandTipLeft, SpineBase, HipRight, HipLeft,

FootRight, FootLeft). The subject was a 24-year old

male. He walked horizontally, swinging his head. In

this sample, one cycle had 33 frames and lasted 1.1

seconds.

4.4.2 DTW Distance

As an example, we show the sample calculation pro-

cesses of the DTW distance for HandTipLeft in Fi-

gure 5 and 6. The red line shows the trace on the x

and y axes of the movement of HandTipLeft of walk

1, and the blue line is that of walk 2. Matched coor-

dinates are indicated with gray lines. Figure 5 shows

Robust Person Identiﬁcation based on DTW Distance of Multiple-Joint Gait Pattern

225

 2 Kinect v2 



RGB  1920×1080

RGB  30fps

  512×424

 30fps

 6 

 6 

 25 

 0.54.5m

 2 Kinect v2  [9]

 3 

 

 2018/4/19

 31 

 5 

0.9m

0m 5.5m

4.5m

2m1m





Kinect

 3  1 



 3 

 3 



Kinect  0.9m 

Kinect  5.5m 1m 

 4.5m  2m 



4.3.2 

24  DTW 

0.8

1.2

1.4

1.6

1.8

2.2

2.4

2.6

2.8

-1

-0.5

0.5

-1

-0.5

0.5

 4 1  3D 

Distance

Density

0 2 4 6 8 10 12

0.0 0.2 0.4 0.6 0.8 1.0

Self

Others

 5 HAND TIP LEFT  DTW 

FAR  FRR  EER 

24  EER 

 EER 

4.4 

4.4.1 

 1  4 

4.4.2 

31  5  DTW 



 HandTipLeft  5 

Head, HandTipLeftHandTipRightFootLeft

FootRight  5 

6 

24  EER 

 4 

 4  n  EER 

 7 n =5 EER 

 0.036 n =6



 EER  5 

ROC  8 

⃝ 2018 Information Processing Society of Japan

Figure 4: Change of skeleton data a(t) of one cycle.

-0.32

-0.3

-0.28

-0.26

-0.24

-0.22

-0.2

-0.18

-0.3 -0.2 -0.1 0 0.1

Figure 5: DTW distance of HandTipLeft (genuine)



d(R

(u)

HT L

0(u)

HT L

)



-0.3

-0.25

-0.2

-0.15

-0.6 -0.4 -0.2 0 0.2 0.4

Figure 6: DTW distance of HandTipLeft (impostor)



d(R

(u)

HT L

0(v)

HT L

)



the result of the DTW process for a genuine person

and Figure 6 shows the results of an impostor.

For the genuine person, the DTW distance, deﬁ-

ned as the sum of the gray lines, d



(u)

HT L

0(u)

HT L



0.45. Thus, it implies that the trace of the left hand

differed 1.5 cm in 1/30 second because one cycle has

30 frames, as shown in Figure 5.

In contrast, for the impostor data, there is a signi-

ﬁcant difference between user u and v. In Figure 5,



(u)

HT L

(u)

HT L



= 12.0.

As examples, the distribution of DTW distances

of HandTipLeft (HTL) d



(u)

HT L

(v)

HT L



is shown in

Figure 7. In both graphs, the genuine (red) data are

distributed closer than the impostor (blue) data and

are distributed in a smaller range. The overlapped

area is equal to the sum of the FAR and the FRR.

A DTW distance is determined when both error ra-

tes are equal. According to this result, θ

∗

HT L

= 2.19.

Other joints were distributed similarly to the HTL and

SL joints. The sorted EERs of all joints are shown in

Table 3.

From Figure 3, we ﬁnd:

1. The EERs of the Neck, Head and Shoulder-

DTW Distance d(R,R)

Density

0 2 4 6 8 10 12

0.0 0.2 0.4 0.6 0.8

genuine

impostor

Figure 7: Distribution of DTW distance of HTL.

Table 3: EER of 24 Joints.

Joint EER Joint EER

ElbowLeft 0.076 HandRight 0.124

ShoulderRight 0.081 HipLeft 0.127

ShoulderLeft 0.095 WristRight 0.133

Neck 0.100 HandTipRight 0.133

SpineShoulder 0.100 FootRight 0.144

WristLeft 0.107 KneeRight 0.145

HipRight 0.107 AnkleRight 0.148

HandLeft 0.108 KneeLeft 0.155

Head 0.110 ThumbRight 0.177

HandTipLeft 0.112 ThumbLeft 0.187

ElbowRight 0.113 AnkleLeft 0.187

SpineBase 0.123 FootLeft 0.192

Right/Left tended to be stable.

2. With regard to the joints in the arms (Elbow,

Wrist, Hand), the joints in the left arm were more

stable than those in the right arm.

3. The EERs of joints in the legs (Foot, Knee, Ankle)

tended to be unstable.

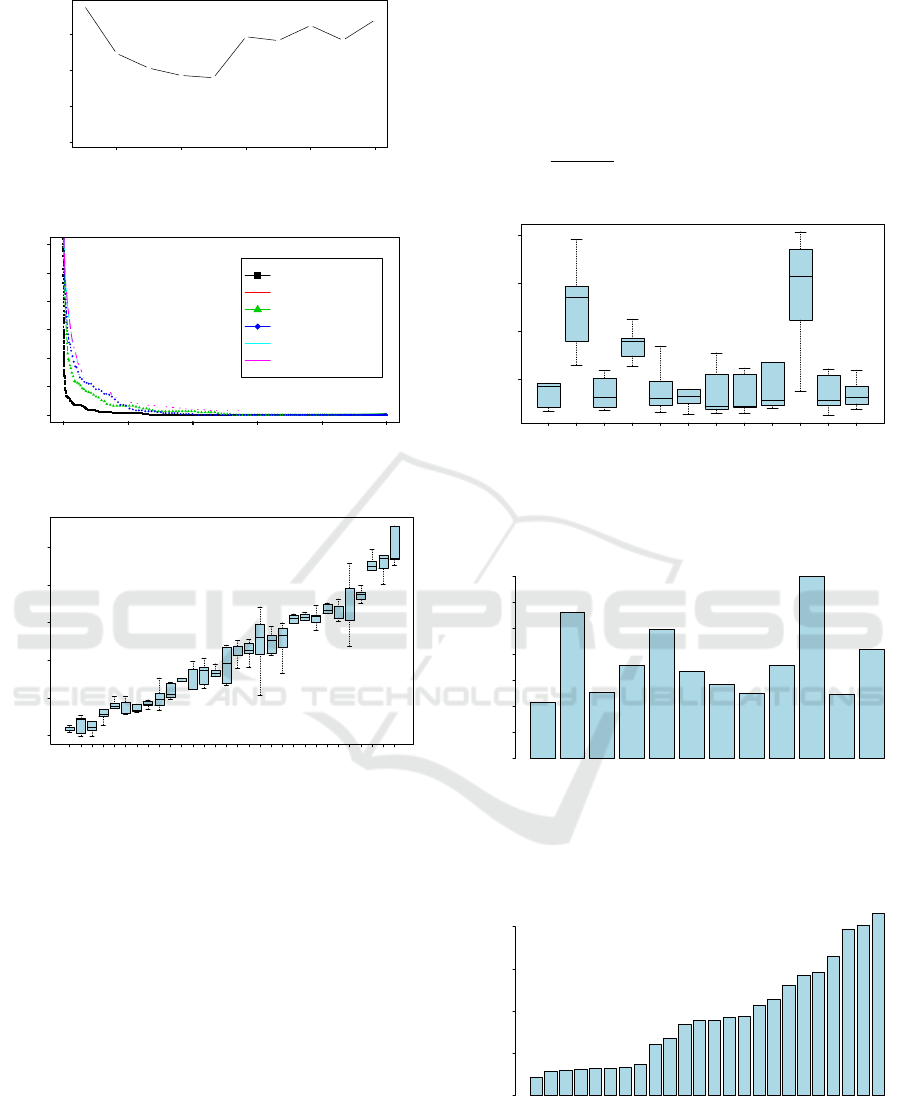
4.4.3 Calculation of Integrated DTW Distance

We aggregated the top k joints (1 ≤ k ≤ 10) in Ta-

ble 3 to improve accuracy. We show the change of the

integrated EERs in Figure 8. We ﬁnd that the EER de-

creases as the number of aggregated joints increases.

When k is ﬁve or less, the minimum EER is 0.036.

When k is six or more, the EER does not decrease.

Therefore, k = 5 is regarded as the optimum value.

Hereafter, we used the following ﬁve joints: Elbo-

wLeft (EL), ShoulderRight (SR), ShoulderLeft (SL),

Neck (NK), and SpineShoulder (SS).

We show the receiver operating characteristic

(ROC) curves of the top ﬁve joints in Figure 9. The

black line shows the ROC of the combined ﬁve joints

and the others show the ﬁve individual joints. The

diagonal line in the ﬁgure shows the EER. From this

ﬁgure, the integrated DTW distance has a lower EER

than the single joints.

We calculated the integrated DTW distance of the

ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy

226

●

2 4 6 8 10

0.00 0.02 0.04 0.06

EER

Figure 8: EER of integrated DTW distance.

0.0 0.2 0.4 0.6 0.8 1.0

0.0 0.2 0.4 0.6

FRR

FAR

●

●●

●

●●

●

●●●

●

●●●●

●●●

●●

●

●●●

●●

●●●●●●●●●●●●●●●●●●●●

●●●●●

●●●●●●●●●●●●●●●

●●●●●●●●●●●●●●●●●●●●●●●●●●●●

●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●

0.0 0.2 0.4 0.6 0.8 1.0

0.0 0.2 0.4 0.6

FRR

FAR

0.0 0.2 0.4 0.6 0.8 1.0

0.0 0.2 0.4 0.6

FRR

FAR

0.0 0.2 0.4 0.6 0.8 1.0

0.0 0.2 0.4 0.6

FRR

FAR

●

● ●

●

● ● ● ● ●

●

● ● ●

● ● ● ● ●

● ● ● ● ● ● ● ● ●

●

● ● ● ● ● ● ●

● ● ● ● ● ● ● ●

●

●● ●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●

0.0 0.2 0.4 0.6 0.8 1.0

0.0 0.2 0.4 0.6

FRR

FAR

●

● ●

●

● ● ●

● ●

●

● ● ●

● ● ● ● ● ● ● ●

●

● ● ● ●

● ● ● ● ● ●

● ●

● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●●● ● ●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●

0.0 0.2 0.4 0.6 0.8 1.0

0.0 0.2 0.4 0.6

FRR

FAR

●

Euclid

ElbowLeft

ShoulderRight

ShoulderLeft

Neck

SpineShoulder

Figure 9: ROC curves.

●

U13

U23

U21

U20

U10

U17

U26

U24

U18

U16

U30

U22

U29

U27

U25

U12

U19

U14

U11

U15

U28

1.5 2.0 2.5 3.0 3.5 4.0

DTW Dist.

Figure 10: Distribution of the integrated DTW distance of

all subjects.

top ﬁve joints between U31. We show the boxplot of

the result in Figure 10. U31 is regarded as the average

user. The range and quartiles of the integrated DTW

distance for the 30 users are sorted by the mean va-

lues. Some users have similar distances, but we can

distinguish them.

4.4.4 Obstacle Walking

We calculated the DTW distance of obstacle-

containing walking



d(R

(u)

normal

(u)

)



. The means of

the DTW distances are shown in Table 4, where the

largest value in each obstacle is underlined. We found

that all obstacles increased the EER above the nor-

mal EERs. The obstacle with the most underlined

DTW distances is the box. The B-swing affects the

Foot (FootR/L) substantially, and the suitcase affects

the Shoulder (SR/SL). The box increases the EER

from 3.46 to 14.278, which is 4.1 times greater. On

average, the box increases the EER to 1.13 (2.95 ti-

mes greater).

The distributions of the DTW distances for HTL



(u)

HT L

0(u)

HT L



for each obstacle is shown in Figures

11, respectively. In addition, the averages of the DTW

distances d(R,R

) for each obstacle and each joint are

shown in Figures 12 and 13, respectively.

●

normal

b−swing

s−swing

pocket

phone

handbag

shoulder bag

sack

umbrella

box

sandals

suitcase

5 10 15 20

DTW Dist.

Figure 11: Distribution of DTW distances for HTL



(u)

HT L

0(u)

HT L



for each obstacle.

normal

b−swing

s−swing

pocket

phone

handbag

shoulder bag

sack

umbrella

box

sandals

suitcase

Distance

0 1 2 3 4 5 6 7

Figure 12: Mean of DTW distances d



(u)

0(u)



for each

obstacle.

SpineShoulder

Neck

SpineBase

ShoulderRight

ShoulderLeft

HipLeft

HipRight

Head

KneeLeft

ElbowLeft

AnkleLeft

ElbowRight

AnkleRight

KneeRight

FootLeft

FootRight

WristLeft

HandLeft

ThumbLeft

HandTipLeft

WristRight

HandRight

ThumbRight

HandTipRight

Distance

0 2 4 6 8

Figure 13: Mean of DTW distance d



(u)

0(u)



for each

joint.

Robust Person Identiﬁcation based on DTW Distance of Multiple-Joint Gait Pattern

227

Table 4: Means of DTW distance d(R,R

) of each joint for each obstacle.

normal b-swing s-swing pocket phone handbag shoulder bag knapsack umbrella box sandals suitcase

ElbowLeft 1.83 5.41 1.83 3.06 2.36 2.18 1.86 1.88 2.48 5.61 1.68 2.28

ShoulderRight 0.97 1.76 0.99 0.96 1.06 1.31 1.33 1.14 1.12 1.60 0.99 1.63

ShoulderLeft 0.98 1.38 1.00 1.23 1.43 1.44 1.31 1.24 1.03 1.59 1.01 1.71

HipRight 0.95 1.44 1.13 1.11 1.13 1.56 1.62 1.04 1.18 1.89 1.13 1.67

Head 0.92 1.60 1.18 1.20 1.82 1.56 1.74 1.09 1.37 2.57 1.09 1.43

HandTipLeft 3.46 12.85 3.60 8.59 3.90 3.79 3.40 3.29 5.98 14.27 3.44 3.47

ElbowRight 1.84 4.55 2.28 2.92 4.20 3.17 2.76 2.47 3.52 6.90 2.15 5.83

HipLeft 1.09 1.39 1.16 1.14 1.14 1.23 1.50 1.16 1.27 2.21 1.10 1.39

HandTipRight 3.18 9.28 3.84 6.48 20.85 7.76 5.61 4.02 8.19 18.06 3.94 12.50

FootRight 3.31 6.91 4.39 3.48 3.68 3.95 4.12 4.41 4.03 4.46 4.13 4.55

FootLeft

2.96 6.32 3.89 3.15 2.88 3.27 3.21 3.70 3.69 4.14 4.06 3.80

From Figure 12, obstacles decrease the accuracy.

The most inﬂuential obstacle is carrying a box. From

Figure 13, obstacle-robust joints are the Shoulder,

Head, and Hip. In particular, the most robust joint

is the SpineShoulder.

5 DISCUSSION

In Experiment 1, stable joints have lower EERs than

variable joints. This is because the distribution of sta-

ble joints in a particular person falls in a very small

interval. Even when it is close to that of other persons,

it can be an effective feature to recognize persons. We

claim that stable joints, e.g., the head and the shoul-

ders, move periodically in a very small range.

From Table 3, in the upper half of the body, joints

on the left side have a lower EER than those on the

right side. We think the reason for this is that some

users swing their arms somewhat like the red line in

Figure 6. Joints that swing a little are more stable and

stable joints tend to be useful features.

In Figure 8, we suggest that the EER decreases as

the number of aggregated joints increases. When k is

ﬁve or less it is estimated that the dimension of the

feature is increasing and the difference between dif-

ferent persons becomes greater. However, when inte-

grated over six joints, we think the features have too

many dimensions and repeatability in the same user

decreases, which results in the EER increasing.

Big swings and carrying boxes are the largest ob-

stacles. In particular, joints in the arms are affected

by these obstacles signiﬁcantly. However, we consi-

der that big swings of arms and carrying big boxes do

not occur often in daily life. Therefore, we claim that

the proposed method is robust in terms of obstacles.

6 CONCLUSIONS

In this work, we proposed a new person identiﬁcation

method using time series data of 3-dimensional joint

coordinates, captured by a depth sensor. As a result

of our experiments, we decreased the EER to 0.03 by

using ﬁve joints including ElbowLeft, ShoulderRight,

ShoulderLeft, Neck and SpineShoulder. This is con-

siderably lower than that obtained by previous works,

such as (Mori and Kikuchi, 2018) (0.25) or (Muaaz

and Mayrhofer, 2017) (0.13).

We veriﬁed the accuracy of the proposed system

using obstacle-containing walking data. As a result,

stable joints such as the shoulder or head are not af-

fected by obstacles.

REFERENCES

Berndt, D. J. and Clifford, J. (1994). Using dynamic time

warping to ﬁnd patterns in time series. The Third In-

ternational Conference on Knowledge Discovery and

Data Mining, pages 359–370.

Han, J. and Bhanu, B. (2006). Individual recognition using

gait energy image. IEEE Trans. Pattern Anal. Mach.

Intell., 28(2):316–322.

Igual, L., Lapedriza, A., and Borr

as, R. (2013). Robust

gait-based gender classiﬁcation using depth cameras.

EURASIP Journal on Image and Video Processing,

2013(1):1–11.

Lee, W.-H., Ortiz, J., Ko, B., and Lee, R. (2018). Inferring

smartphone usersf handwritten patterns by using mo-

tion sensors. 4th International Conference on Infor-

mation Systems Security and Privacy, pages 139–148.

Li, M., Chen, X., Tian, S., Wang, Y., and Li, P. (2018).

Research of gait recognition based on human electro-

static signal. 2018 2nd IEEE Advanced Information

Management,Communicates,Electronic and Automa-

tion Control Conference (IMCEC), pages 1812–1817.

Mori, T. and Kikuchi, H. (2018). Person tracking based on

gait features from depth sensors. The 21st Internati-

onal Conference on Network-Based Information Sys-

tems (NBiS-2018), 22:743–751.

ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy

228

Muaaz, M. and Mayrhofer, R. (2017). Smartphone-

based gait recognition: From authentication to imi-

tation. IEEE Transactions on Mobile Computing,

16(11):3209–3221.

Preis, J., Kessel, M., Werner, M., and Linnhoff-Popien, C.

(2012). Gait recognition with kinect. Proceedings of

the First Workshop on Kinect in Pervasive Computing.

Shiraga, K., Makihara, Y., Muramatsu, D., Echigo, T., and

Yagi, Y. (2016). Geinet: View-invariant gait recogni-

tion using a convolutional neural network. 2016 Inter-

national Conference on Biometrics (ICB), pages 1–8.

Sklavos, N. and Souras, P. (2006). Economic models and

approaches in information security for computer net-

works. International Journal of Netowk Security,

2(1):14–20.

ten Holt, G. A., Reinders, M. J. T., and Hendriks, E. A.

(2007). Multi-dimensional dynamic time warping for

gesture recognition. Thirteenth annual conference of

the Advanced School for Computing and Imaging.

Zhang, Y., Pan, G., Jia, K., Lu, M., Wang, Y., and Wu,

Z. (2015). Accelerometer-based gait recognition by

sparse representation of signature points with clusters.

IEEE Transactions on Cybernetics, 45:1864–1875.

Robust Person Identiﬁcation based on DTW Distance of Multiple-Joint Gait Pattern

229