Scheduling on Dedicated Machines with Energy Consumption Limit

Istv

an M

odos

1,2

, Kiryl Kalodkin

1,2

, P

remysl

ucha

and Zden

ek Hanz

alek

Czech Institute of Informatics, Robotics, and Cybernetics, Czech Technical University in Prague, Czech Republic

Department of Control Engineering, Czech Technical University in Prague, Czech Republic

Keywords:

Scheduling, Dedicated Machines, Energy Consumption Limits.

Abstract:

This work studies a problem of scheduling non-preemptive independent jobs on dedicated machines while con-

sidering an energy consumption limit. The problem is motivated by energy-demanding production processes,

such as glass tempering and steel hardening, in which a material is heated to high temperature in furnaces. The

production companies have contracts with electric utilities that specify a maximum energy consumption limit.

If the heating in the furnaces is not planned carefully, the energy spikes overshoot the energy consumption

limit, and the companies must pay large penalty fees. In this paper, we propose two exact methods that ﬁnd

schedules with the minimum makespan such that the energy limit is satisﬁed. The ﬁrst proposed method is a

Constraint Programming model and the second one ﬁnds the optimal solution by iteratively re-solving a Mixed

Integer Linear Programming model with a decreasing scheduling horizon. The iterative algorithm exploits the

fact that the start times do not need to be modeled explicitly, which leads to an efﬁcient method for solving

instances with a higher number of shorter jobs. The experimental results show that our methods outperform

an adapted approach from the literature for a related problem.

1 INTRODUCTION

The motivation for this work comes from produc-

tion processes in which batches of material are heated

in furnaces to high temperature, e.g., glass temper-

ing and steel hardening. Heating of the material is

energy-demanding and causes spikes in the energy

consumption proﬁle if multiple furnaces are heating

the material at the same time. These consumption

spikes pose a problem since the production companies

have contracts with an electric utility, which specify a

maximum energy consumption limit in every 15 min-

utes metering interval. Failing to comply with the

energy consumption limit leads to substantial penalty

fees which are directly proportional to the consumed

energy over the contracted limit.

Usually, the production companies are schedul-

ing their production either manually or using special-

ized software. However, only classical scheduling

criteria and constraints such as due dates, makespan,

changeover times, etc., are considered. Consequently,

the resulting production schedules may violate the

contracted energy consumption limit. This work pro-

poses two exact scheduling methods for dedicated

machines that take into account these energy limits

alongside traditional scheduling aspects.

1.1 Related Work

A similar problem of satisfying a maximum power de-

mand was studied by (Bruzzone et al., 2012; Fang

et al., 2013). Their models try to comply with the

maximum power demand at every time instant. This

problem can be seen as a special case of our problem

in which the length of the metering interval is 1.

Another related problem to the energy consump-

tion limit is electrical load tracking (Nolde and

Morari, 2010; Ha

ıt and Artigues, 2011; Ha

ıt and

Artigues, 2011; Hadera et al., 2015; Gajic et al.,

2017), where the objective is to minimize the abso-

lute difference between the actual and contracted en-

ergy consumption over all metering intervals. In the

load tracking problem, both over-consumption and

under-consumption of the energy are penalized and

the authors usually consider minimization of the en-

ergy consumption deviation. Thus, the violation of

the contracted energy consumption is a soft constraint

in the electrical load tracking problem.

The energy consumption limits were considered in

the domain of lot sizing (Masmoudi et al., 2017; Rap-

ine et al., 2018). In contrast to scheduling, the goal of

the lot sizing problem is to determine the quantity of

the produced products by the machines in each period

so that the demand is satisﬁed.

Módos, I., Kalodkin, K., Š˚ucha, P. and Hanzálek, Z.

Scheduling on Dedicated Machines with Energy Consumption Limit.

DOI: 10.5220/0007307200530062

In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 53-62

ISBN: 978-989-758-352-0

The most similar problem to ours is the robust

scheduling problem presented in (M

odos et al., 2017).

The authors proposed algorithms for designing robust

schedules guaranteeing that the energy consumption

limits are not violated even if some jobs are delayed

due to unexpected circumstances. However, the au-

thors consider only a single machine, thus their prob-

lem is a special case of the parallel machine schedul-

ing problem. Although there is no machine alloca-

tion in the parallel scheduling problem with energy

consumption limits, the schedules on the machines in-

ﬂuence each other through the energy limit, thus the

problem cannot be solved independently on each ma-

chine.

1.2 Contribution

In this paper, we propose two exact methods for the

problem of scheduling non-preemptive independent

jobs on dedicated machines so that the makespan is

minimized. The resulting schedules must also sat-

isfy the energy consumption limit in every metering

interval. The ﬁrst method is a Constraint Program-

ming (CP) model and the second one is a Mixed In-

teger Linear Programming (MILP) based iterative al-

gorithm which exploits the fact, that the start times

of the jobs do not need to be modeled explicitly. As

shown in the experiments, both of the methods out-

perform an adapted MILP model from (Ha

ıt and Ar-

tigues, 2011; Ha

ıt and Artigues, 2011) w.r.t. the to-

tal number of solved instances to optimality. More-

over, we believe that our novel ideas for modeling the

overlap of the jobs with the metering intervals can

be used to increase the performance of the models

for scheduling with real-time energy prices (Merkert

et al., 2015; Zhao et al., 2018), where the cost of en-

ergy may change every hour.

2 PROBLEM STATEMENT

Let J = {J

, J

, . . . , J

} be a set of jobs and let

M = {M

, M

, . . . , M

} be a set of machines. For

each job J

∈ J we deﬁne its processing time p

∈ N

and dedicated machine µ

∈ M , on which the job has

to be processed without preemption. The set of jobs

that have to be processed on machine M

is denoted as

. Moreover, for each job J

we also deﬁne its power

consumption P

∈ R

that represents the power con-

sumption of machine µ

when processing job J

, i.e.,

it is the constant rate at which the energy is consumed

at every time instant. Therefore, the total consumed

energy by each job J

is p

· P

Let s

∈ N

≥0

denotes a start time of job J

∈ J .

The jobs have to be scheduled within scheduling hori-

zon H ∈ N

, i.e., the jobs must complete at most at

time H. The scheduling horizon is divided into a set

of metering intervals I = {I

, I

, . . . , I

} with equal

length of D ∈ N

(it is assumed that H is a multiple

of D). For all metering intervals, we deﬁne the same

energy limit E

max

representing the upper bound on the

total energy consumption of the jobs in each metering

interval

. We say that vector of start times s = (s

)

∈J

does not violate the energy limit in metering interval

if and only if

∑

∈J

Overlap( j, s

, i) · P

≤ E

max

, (1)

where Overlap( j, s

, i) represents the overlap length

of job J

with metering interval I

if starting at time

. Start times s are feasible if the jobs on each ma-

chine are not overlapping and the energy limit is not

violated in any metering interval. An example of a

feasible schedule of 30 jobs on four machines can be

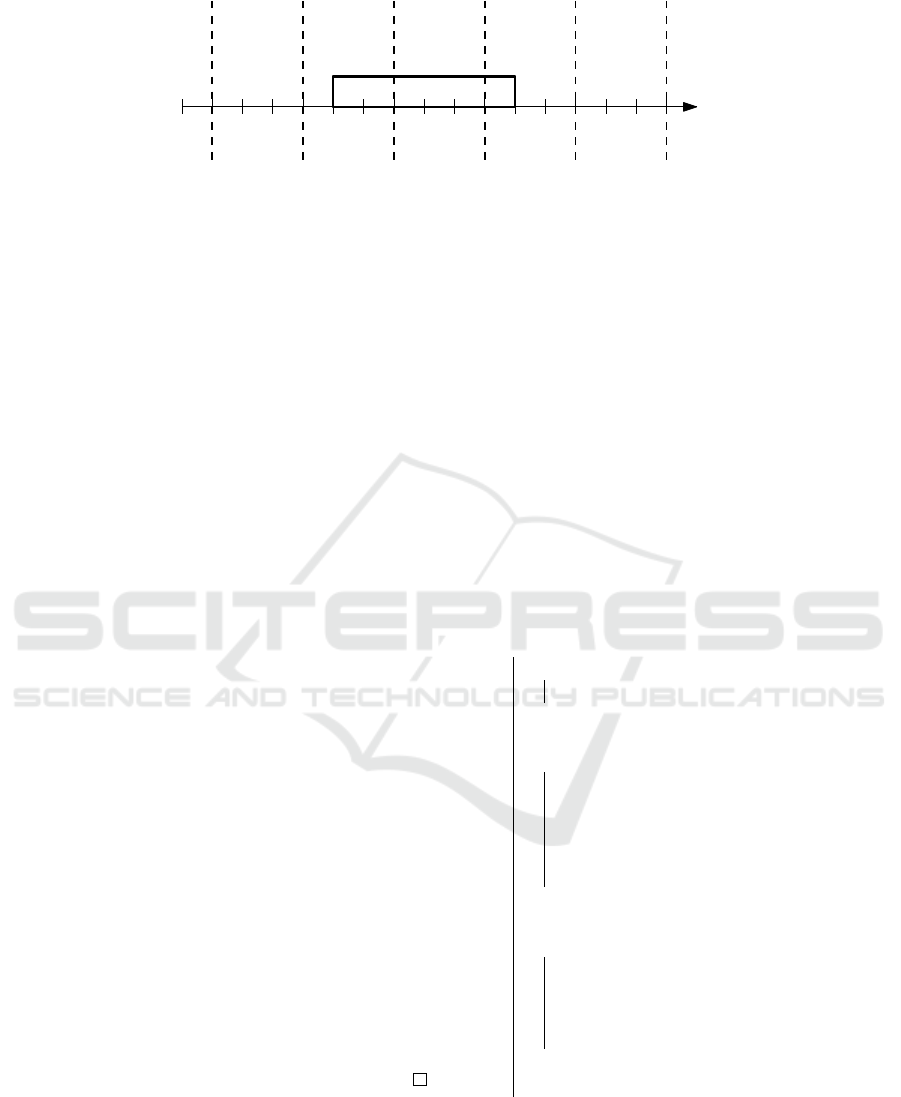
seen in Fig. 1.

The goal of our scheduling problem is to ﬁnd

feasible start times such that makespan C

max

, i.e.,

the maximum completion time of all jobs, is mini-

mized. We denote this problem in Graham’s notation

as m|E

max

The problem m|E

max

is N P -hard since we

can reduce 3-partition problem to the decision vari-

ant 1|p

= 1, E

max

|− of our scheduling problem. In

the 3-partition problem, we are given bound B and

multiset A = {a

, a

, . . . , a

3·q

} of integers such that

< a

and

∑

∈A

= q · B. In this problem we

ask the question whether there exist sets A

, . . . , A

such that (i) ∪

i=1

= A, (ii) A

∩A

0 for all i

6= i

and (iii)

∑

∈A

= B for all i. The reduction maps

each integer a

to a unit length job with power con-

sumption P

= a

. The energy limit is set to B, length

of each metering intervals to 3 and the number of me-

tering intervals is q.

3 SOLUTION APPROACHES

In this section, we propose two exact approaches to

the problem stated in Section 2: (i) a CP model (see

Section 3.1) and (ii) a MILP-based iterative algorithm

(see Section 3.2), which exploits the fact that the start

Usually, the energy consumption limit is contracted for

a longer time period such as a month. Therefore, the energy

limit is constant within the scheduling horizon. However,

our solution methods can be easily generalized to the case

where the energy limit varies, but due to the above men-

tioned reason and simplicity of the methods we consider

only one energy limit.

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

Figure 1: An example of a feasible schedule of 30 jobs on four machines. The ﬁgure below the schedule illustrates the energy

consumption of the jobs in each 15 minutes metering interval, i.e., the height of each colored box equals Overlap( j, s

, i) · P

The same color in both ﬁgures represents the same job. The energy consumption limit is denoted by the dashed horizontal red

line.

times of the jobs do not need to be modeled explicitly

(the start times from the model are obtained using an

algorithm described in Section 3.2.2).

3.1 CP Model

The ﬁrst proposed solution approach is a CP model

which will be described using IBM CP Optimizer for-

malism (Laborie et al., 2018). CP uses a notion of

interval variables representing a time interval, whose

start time, completion time and length has to be de-

cided by a solver. Our model has one interval vari-

able x

for each job J

∈ J that denotes the time in-

terval in which the job is scheduled. The idea be-

hind the model is to use CP function Overlap, which

computes the length of the overlap between a job’s

interval variable and a metering interval given by its

start and end. The overlaps in a metering interval are

multiplied by the corresponding power consumption,

added together and constrained to be at most E

max

Note that the cumulative functions cannot be used

for modeling the energy consumption since the height

of an elementary cumulative function is a constant

whereas our problem would require the height to be

a function of the overlap length with a metering inter-

val.

The complete model follows

min max

∈J

EndOf(x

) (2)

EndOf(x

) ≤ H, ∀J

∈ J (3)

LengthOf(x

) = p

, ∀J

∈ J (4)

NoOverlap({x

: J

∈ J

}), ∀M

∈ M (5)

∑

∈J

Overlap(x

, (i − 1) · D, i · D) · P

≤ E

max

∀I

∈ I

(6)

The objective (2) minimizes the maximum com-

pletion time of all the jobs. Constraint (3) guaran-

tees that the completion time of every job is bounded

by the scheduling horizon H. The following con-

straint (4) sets the length of an interval variable x

corresponding to some job J

to be p

. Global con-

straint NoOverlap in (5) ensures that the jobs on each

dedicated machine are not overlapping. Finally, the

energy limit in every metering interval is enforced by

constraint (6).

3.2 MILP-based Iterative Algorithm

In this section, we present a MILP formulation that

does not explicitly model the start times of the jobs;

we call it an implicit model. However, the implicit

model can optimize the makespan only in the last me-

tering interval of the scheduling horizon, thus it may

found suboptimal solutions to the scheduling prob-

lem presented in Section 2. This issue is mitigated by

Scheduling on Dedicated Machines with Energy Consumption Limit

wrapping the implicit model in a loop that iteratively

tightens the scheduling horizon until an optimal solu-

tion to the original problem is found.

First, we introduce the implicit MILP model, see

Section 3.2.1. The following Section 3.2.2 shows how

the start times could be reconstructed from a feasible

solution to the implicit MILP model. The last Sec-

tion 3.2.3 wraps the implicit MILP model into an it-

erative algorithm.

3.2.1 Implicit MILP Model

As noted above, the implicit model is solved itera-

tively with a decreasing horizon. Let us denote by

max

the last metering interval, which is considered

in the model. To avoid notational clutter, the set of

metering intervals in this subsection is redeﬁned to

I = {I

, I

, . . . , I

max

Similarly as the CP model, an overlap of the jobs

with metering intervals needs to be formulated. How-

ever, MILP does not contain any constructs such as

Overlap, thus we must model the overlap using linear

expressions ourselves. We observed that for “shorter”

jobs the overlap constraints can be modeled much

simpler than for “longer” jobs, thus we split the set

of jobs into non-spannable and spannable jobs, i.e.,

the set of spannable jobs is

span

= {J

∈ J : p

≥ D + 1}, (7)

while the set of non-spannable jobs is J \ J

span

For modeling purposes, we also need to determine

the maximum number of consecutive metering inter-

vals in which job J

can have non-zero overlap for any

feasible start times s; this number will be denoted as

Ω

Observation 1. The maximum number of consecu-

tive metering intervals that can have non-zero overlap

with job J

for any feasible start times s is

Ω

+ 1. (8)

Proof. See Appendix 5.1.

The implicit MILP model uses the following vari-

ables: (i) d

j,i

∈ N

≥0

denoting the length of the

overlap between job J

and metering interval I

, (ii)

j,i

∈ {0, 1} indicating whether spannable job J

starts

in metering interval I

, (iii) x

j,i

∈ {0, 1} expressing

whether job J

has non-zero overlap in metering in-

terval I

, and (iv) Z ∈ N

≥0

representing the objective

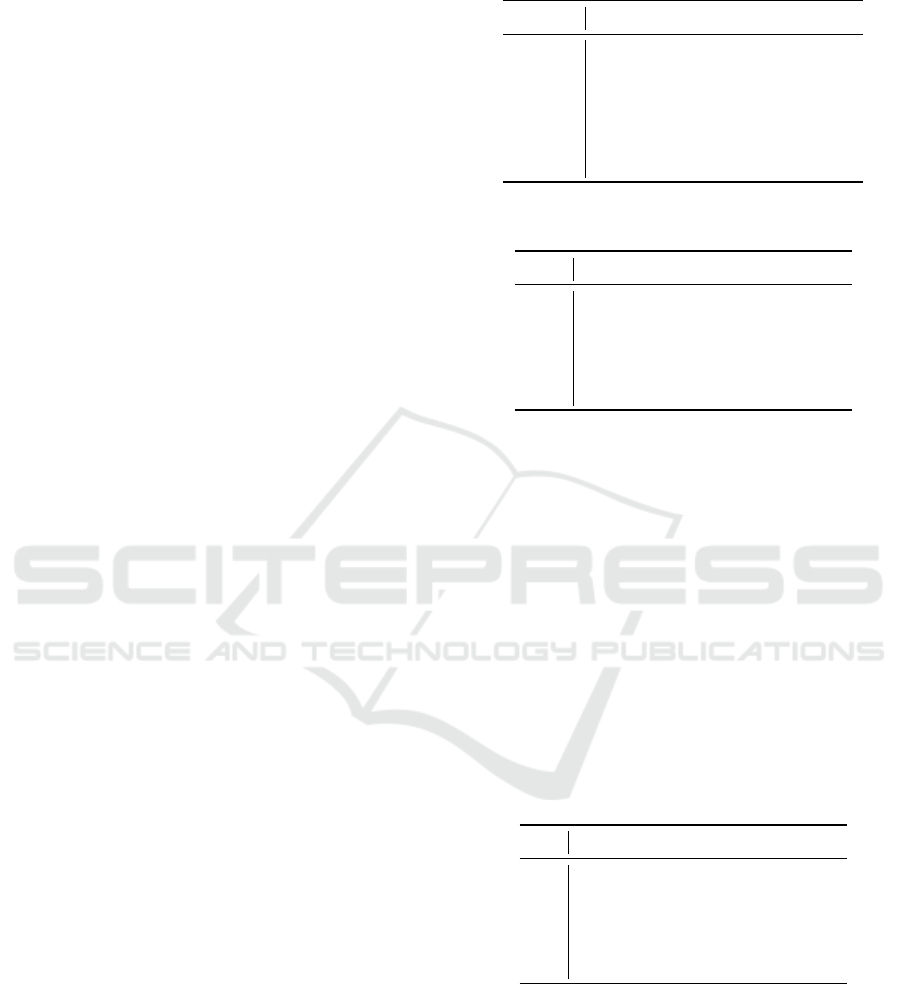
value. Fig. 2 shows an example illustrating the vari-

ables used in the implicit MILP model.

The complete model follows

min Z (9)

Z ≥

∑

∈J

j,i

max

, ∀M

∈ M (10)

∑

∈J

j,i

≤ D, ∀I

∈ I , ∀M

∈ M (11)

∑

∈J

j,i

· P

≤ E

max

, ∀I

∈ I (12)

∑

∈I

j,i

= p

, ∀J

∈ J (13)

SOS

j,1

, . . . , d

j,i

max

), ∀J

∈ J \ J

span

(14)

∑

∈I

j,i

= 1, ∀J

∈ J

span

(15)

j,i

≤ D ·

∑

=max(1,i−Ω

+1)

j,i

, ∀J

∈ J

span

, ∀I

∈ I

(16)

D · (x

j,i−1

+ x

j,i+1

− 1) ≤ d

j,i

∀J

∈ J

span

, ∀I

∈ I \ {I

, I

max

}

(17)

j,i

≤ min(D, p

) · x

j,i

, ∀J

∈ J , ∀I

∈ I (18)

+ x

,i+1

+ x

,i+1

≤ 3,

∀M

∈ M , ∀I

∈ I \ {I

max

∀J

, J

∈ J

: J

6= J

, p

≥ 2, p

≥ 2,

+ p

≤ 2 · D

(19)

In the following paragraphs, the model will be ex-

plained in detail.

The objective of the model is to minimize the

maximum total overlap in I

max

over all machines,

see Eq. (10). A simple observation is that no idle

time between two consecutive jobs on the same ma-

chine is necessary in I

max

, since the subsequent job

is fully contained in I

max

and shifting it to the com-

pletion time of the preceding job has no effect on the

consumed energy in I

max

. Therefore, minimization of

the maximum total overlap in I

max

also minimizes the

makespan in I

max

The following constraint (11) ensures, that the to-

tal overlap in every metering interval is at most the

length of the metering intervals. Constraint (12) mod-

els the energy limit and constraint (13) restricts the

sum of the overlaps of one job to be its processing

time.

Next, the continuity of the jobs over metering in-

tervals is modeled, i.e., only adjacent metering inter-

vals can have non-zero overlap with a job. The non-

preemption of the jobs is then ensured by the start

times reconstruction procedure, see Section 3.2.2. As

noted before, for non-spannable jobs this constraint

can be modeled easier than for the spannable jobs,

thus the explanation is split into two parts. We start

by handling the non-spannable jobs ﬁrst.

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

i−1

i+1

i−2

i+2

time

j;i−2

= 0

j;i−2

= 0

j;i−2

= 0

j;i−1

= 1

j;i−1

= 1

j;i−1

= 2

j;i

= 1

j;i

= 0

j;i

= 3

j;i+1

= 1

j;i+1

= 0

j;i+1

= 1

j;i+2

= 0

j;i+2

= 0

j;i+2

= 0

Figure 2: An example illustrating the values of variables for job J

that are used in the implicit MILP model. The length of

the metering intervals is 3.

Due to Observation 1, the non-spannable jobs can

overlap at most two consecutive metering intervals.

This can be exploited by modeling the continuity of

the jobs using special-ordered set (Gurobi, 2018) con-

straint of type 2 (SOS

). SOS

receives a list of or-

dered variables (can be continuous, binary or integer)

and the constraint ensures that at most two consec-

utive variables in this list can have non-zero value.

The continuity of every non-spannable job is then

achieved by passing the ordered list of overlap vari-

ables to SOS

constraint, see constraint (14).

The spannable jobs may overlap more than two

consecutive intervals, thus SOS

constraint cannot

be used. The continuity is modeled using four con-

straints (15)-(18). The ﬁrst constraint (15) requires

that the job starts in some metering interval. The sec-

ond constraint (16) ensures that at most Ω

consecu-

tive intervals have non-zero overlap with job J

. The

third constraint (17) enforces that if job J

has non-

zero overlap with metering intervals I

i−1

, I

i+1

, then

the job spans the whole metering interval I

. The last

constraint (18) pushes variable x

j,i

to be 1 if job J

has

non-zero overlap with metering interval I

Finally, the last constraint (19) of the model en-

sures that two jobs J

, J

on the same machine are

not overlapping on a boundary of two consecutive

metering intervals. Notice that due to the following

lemma this constraint has to be included only for a

pair of jobs with p

+ p

≤ 2 · D.

Lemma 1. Let J

, J

∈ J be two jobs such

that j

6= j

, µ

= µ

, p

≥ 2, p

≥ 2 and

+ p

≥ 2 · D + 1. Let d = (d

j,i

)

∈J ,I

∈I

values for some feasible solution to the MILP model

from Section 3.2. Then Eq. (19) holds for J

, J

any metering interval I

∈ I \ {I

max

Proof. See Appendix 5.1.

3.2.2 Reconstruction of the Start Times

As was noted above, the model does not include vari-

ables that represent the start times explicitly. How-

ever, a simple algorithm exists that reconstructs start

times s from the values of feasible overlap variables d.

The full pseudocode of the reconstruction algorithm is

listed in Algorithm 1.

The algorithm ﬁrst assigns the start times to the

jobs that lies on a boundary of at least two metering

intervals. For these jobs, the start time is unambigu-

ous since it equals i

· D − d

j,i

, where I

is the ﬁrst

metering interval in which the job has non-zero over-

lap.

Afterwards, the start times of the rest of the jobs,

i.e., having non-zero overlap in only one metering in-

terval, are assigned. Since the order of such jobs in

a particular metering interval is not important, their

start times are assigned in arbitrary order. The jobs are

assigned at the earliest start time in the corresponding

metering interval. After each assignment, the earliest

start time is increased by the processing time of the

assigned job.

Function ReconstructStartTimes(d):

foreach I

∈ I do

earliestStartTimes[i] ← (i −1) · D

end

foreach {J

∈ J : |{I

∈ I : d

j,i

> 0}| ≥ 2}

← argmin

i=1,...,i

max

j,i

> 0

← argmax

i=1,...,i

max

j,i

> 0

← i

· D − d

j,i

earliestStartTimes[i

] ←

earliestStartTimes[i

] + d

j,i

end

foreach {J

∈ J : |{I

∈ I : d

j,i

> 0}| = 1}

← I

∈ I : d

j,i

> 0

← earliestStartTimes[i

]

earliestStartTimes[i

] ←

earliestStartTimes[i

] + p

end

return s

Algorithm 1: Reconstruction of start times s from overlap

variables d.

3.2.3 Iterative Algorithm

Since the implicit MILP model only optimizes the

makespan in I

max

, the optimal solution found by the

Scheduling on Dedicated Machines with Energy Consumption Limit

implicit model might be suboptimal for the original

problem stated in Section 2. The idea of the itera-

tive algorithm is to progressively decrease i

max

and

re-solve the implicit model until an optimal solution

to the original problem is found. The full pseudocode

of the iterative algorithm is listed in Algorithm 2.

The algorithm starts by checking the feasibil-

ity of the given problem instance by trying to ﬁnd

any feasible solution within the whole scheduling

horizon H. If the instance is infeasible, function

SolveImplicitMILP returns an empty set instead of

a vector of start times. If the solution is feasible, the

algorithm starts iterating until the optimal solution is

found.

To determine the optimality of a feasible solution,

the algorithm tests its objective value Z. A non-zero

objective value means that the found solution is opti-

mal to the original problem since makespan is greater

than (i

max

− 1) · D. On the other hand, if the objec-

tive is zero, a shorter solution ending in the previ-

ous metering interval might exist to the original prob-

lem. Therefore, i

max

is decreased by one, the implicit

model is re-solved with the smaller horizon, and the

tests on the objective value are repeated.

Notice that in every iteration the previously found

start times are passed to SolveImplicitMILP, which

are used as an initial solution (by transformation to

the overlap variables) to reduce the running time of

the implicit model.

Function IterativeImplicitMILP():

max

←

s, Z ← SolveImplicitMILP(i

max

if s =

0 then

/* The original problem is

infeasible. */

return

end

while Z = 0 do

max

← i

max

− 1

s, Z ← SolveImplicitMILP(i

max

, s)

end

/* Found optimal solution to the

original problem. */

return s

Algorithm 2: MILP-based iterative algorithm.

4 EXPERIMENTS

In the experiments, we compare the presented ap-

proaches from Section 3 w.r.t. ﬁnding the optimal so-

lutions to a given set of generated instances and prov-

ing their optimality. Although in practice it is often

necessary to ﬁnd high-quality solutions in short time,

proving that a solution is also optimal is valuable in-

formation. The aim of the experiments is to deter-

mine, how two different parameters affect the solv-

ing time: (i) number of spannable jobs in an instance

and (ii) the energy limit tightness w.r.t. the power con-

sumption of the jobs. In addition to the proposed ex-

periments we also compare the solution approaches

w.r.t. the quality of the found solutions (which can be

sub-optimal).

For the comparison with the existing literature, we

include in the experiments a MILP model that was

adapted from a similar problem (Ha

ıt and Artigues,

2011). The model is described in Appendix 5.2, and

we will refer to this model as Disjunctive MILP.

All experiments were executed on 2x Intel(R)

Xeon(R) Silver 4110 CPU @ 2.10GHz with 188GB

of RAM (16 cores in total). For solving the MILP

and CP models, we used Gurobi 8 and IBM CP Opti-

mizer 12.8, respectively. The multi-threading settings

for each solver was set to default, i.e., the solvers can

use all the available cores for computation.

The source codes of the methods

and the generated instances are publicly

available at https://github.com/CTU-IIG/

EnergyLimitsScheduling and https://github.com/

CTU-IIG/EnergyLimitsSchedulingDatasets, respec-

tively.

4.1 Instances

The instances for the experiments were generated as

follows. The energy limit and the length of the me-

tering intervals were ﬁxed to 1000 and 15, respec-

tively. To explore how the solving time is affected

by the number of spannable jobs in an instance, we

use parameter α

α =

span

|J |

. (20)

The processing time of each spannable job is sam-

pled from discrete uniform distribution U{D +1, 60}

while the processing time of the non-spannable jobs is

sampled from discrete uniform distribution U{1, D}.

Another evaluated parameter in the experiments is

β that controls the tightness of the energy limit. Given

ﬁxed β, the power consumption of each job is then

sampled from continuous uniform distribution



β ·

max

m · D

, 2 ·

max

m · D



. (21)

To ensure that no job can violate the energy limit

by itself, the power consumption is clamped, i.e., if

min(D, p

)·P

> E

max

for some job J

, its power con-

sumption is modiﬁed to

max

min(D,p

)

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

To distribute the jobs between the machines, each

job is assigned to a random machine with uniform dis-

tribution. Finally, the length of the scheduling horizon

is set to the sum of all jobs’ processing times in an

instance. The analysis of the results shows that this

horizon is large enough to guarantee the existence of

a feasible solution.

For each n ∈ {10, 20, 30}, m ∈ {2, 4},

α ∈ {0.1, 0.25, 0.5, 0.75, 0.9} and

β ∈ {0.8, 1.0, 1.2, 1.4, 1.6} we randomly gener-

ated 10 instances using the scheme described above.

Therefore, the generated dataset has 1500 instances

in total.

4.2 Results

The results section is divided into two parts. The ﬁrst

part analyzes the ability of the proposed approaches to

prove the solutions’ optimality based on the examined

parameters n, m, α, β. The second part compares the

solution approaches w.r.t. the quality of the found so-

lutions. In the subsequent text, the following abbrevi-

ations of the solution approaches are used: (i) CP: CP

model (see Section 3.1), (ii) MILP-IMP: MILP-based

iterative algorithm (see Section 3.2) and (iii) MILP-

DIS: Disjunctive MILP model (see Appendix 5.2).

4.2.1 Finding Optimal Solutions and Proving

Their Optimality

The results are shown in Tables 1 to 3; each of the

tables provides a different view of the same results.

Each row of the table shows the number of optimally

solved instances by each approach. For example,

in Table 2 the row denoted as α = 0.25 shows the re-

sults for instances with n ∈ {10, 20, 30}, m ∈ {2, 4},

α = 0.25 and β ∈ {0.8, 1.0, 1.2, 1.4, 1.6}. To highlight

the best method in each row, the best values are shown

in bold. The time-limit given to each method for each

instance was 300s.

Table 1 shows, how the methods scale with the

increasing size of the instances. Except of the small-

est instances with n = 10, m = 2, MILP-IMP model

either outperforms or is at least as good as the other

approaches. For example, 53.2% of the instances with

n = 30, m = 4 were solved optimally by MILP-IMP,

whereas the CP approach solved 34.4% and MILP-

DIS only 14.4% of the instances.

The next Table 2 compares the approaches ac-

cording to the increasing spannable ratio α. We see

that the performance of the implicit MILP model de-

creases with increasing α. The implicit MILP model

outperforms the CP approach when the number of

shorter jobs is higher or the same; on the other hand,

CP is better for the higher spannable ratio. With

Table 1: Number of proved optimal solutions out of 250

with varying n,m.

n m CP MILP-IMP MILP-DIS

10 2 247 207 234

10 4 250 250 250

20 2 14 46 16

20 4 127 177 144

30 2 3 11 0

30 4 86 133 36

Table 2: Number of proved optimal solutions out of 300

with varying α.

α CP MILP-IMP MILP-DIS

0.1 154 239 187

0.25 165 207 157

0.5 151 163 134

0.75 134 128 113

0.9 123 87 89

exception of α = 0.9, MILP-DIS is outperformed

by MILP-IMP. The efﬁciency of MILP-IMP for the

smaller spannable ratio can be explained by break-

ing of symmetries, i.e, the solver does not have to

sequence the non-spannable jobs that are wholly pro-

cessed within one metering interval.

The following Table 3 illustrates, how the tight-

ness of the energy limit β affects the performance. We

see that MILP-IMP outperforms other approaches.

From the results we may infer that the tighter limit

leads to harder instances, which corresponds with the

intuition since our scheduling problem without the en-

ergy limit is trivially solvable (any left-shifted sched-

ule is optimal).

Table 3: Number of proved optimal solutions out of 300

with varying β.

β CP MILP-IMP MILP-DIS

0.8 185 198 150

1.0 159 181 148

1.2 144 162 136

1.4 125 152 127

1.6 114 131 119

4.2.2 Comparison of the Quality of the Found

Solutions

In addition to the previous results, we also examined

the total makespan achieved by each method within

the time limit for varying n, m, see Table 4. Instances,

for which at least one method did not ﬁnd any so-

lution, are not included (there are 5 such instances,

in all cases a solution was not found by MILP-DIS

Scheduling on Dedicated Machines with Energy Consumption Limit

Table 4: Total makespan with varying n, m.

n m CP MILP-IMP MILP-DIS

10 2 46419 46451 46425

10 4 26028 26028 26028

20 2 94673 95736 97456

20 4 49206 49284 49394

30 2 133389 136744 140814

30 4 69938 70250 71033

method). The table reveals that CP outperforms all

the other approaches, which is not surprising since

IBM CP Optimizer is primarily designed to ﬁnd good

solutions. With the exception of the instances with

n = 10, m = 2, MILP-IMP has smaller or the same

total makespan as MILP-DIS.

5 CONCLUSION

Managing the production is becoming increasingly

complex without computer-aided systems. On the

other hand, traditional scheduling constraints and ob-

jectives are not enough to design realistic produc-

tion schedules. In this work, we explored a schedul-

ing problem with a practical production constraint of

satisfying the contracted energy consumption limits.

This problem emerges in energy-demanding produc-

tion processes, such as glass tempering or steel hard-

ening, in which a material is heated in furnaces to

high temperature. The heating in the furnaces has to

be planned carefully; otherwise, the resulting energy

spikes lead to a violation of the energy limits.

We propose two exact algorithms for the studied

scheduling problem with dedicated machines: (i) a

Constraint Programming model and (ii) a Mixed In-

teger Linear Programming based iterative algorithm.

The iterative algorithm exploits the fact that the start

times do not need to be modeled explicitly, which al-

lows us to efﬁciently solve instances having a higher

number of shorter jobs. To compare the algorithms

with the approaches from literature, we adapted an ex-

isting Mixed Integer Linear Programming model for

a similar problem (Ha

ıt and Artigues, 2011; Ha

ıt and

Artigues, 2011). To summarize the experimental re-

sults on a dataset consisting of instances with 10 to

30 jobs, our best method proves the optimality for

54.9% instances, whereas the Mixed Integer Linear

Programming model inspired by the existing litera-

ture proves the optimality for 45.3% instances.

In the future, our aim is to extend our iterative al-

gorithm to the job shop scheduling problem with en-

ergy consumption limit, where the research challenge

is handling of the precedences between the operations

of the same job.

ACKNOWLEDGEMENTS

The work in this paper was supported by the Technol-

ogy Agency of the Czech Republic under the Centre

for Applied Cybernetics TE01020197.

REFERENCES

Bruzzone, A., Anghinolﬁ, D., Paolucci, M., and Tonelli,

F. (2012). Energy-aware scheduling for improving

manufacturing process sustainability: A mathematical

model for ﬂexible ﬂow shops. CIRP Annals - Manu-

facturing Technology, 61(1):459–462.

Fang, K., Uhan, N. A., Zhao, F., and Sutherland, J. W.

(2013). Flow shop scheduling with peak power con-

sumption constraints. Annals of Operations Research,

206(1):115–145.

Gajic, D., Hadera, H., Onofri, L., Harjunkoski, I., and Gen-

naro, S. D. (2017). Implementation of an integrated

production and electricity optimization system in melt

shop. Journal of Cleaner Production, 155:39 – 46.

Sustainable Development of Energy, Water and Envi-

ronmental Systems.

Gurobi (2018). Constraints. http://www.gurobi.

com/documentation/8.0/refman/constraints.html. Ac-

cessed September 18, 2018.

Hadera, H., Harjunkoski, I., Sand, G., Grossmann, I. E.,

and Engell, S. (2015). Optimization of steel pro-

duction scheduling with complex time-sensitive elec-

tricity cost. Computers & Chemical Engineering,

76:117–136.

ıt, A. and Artigues, C. (2011). A hybrid CP/MILP

method for scheduling with energy costs. European

Journal of Industrial Engineering, 5(4):471–489.

ıt, A. and Artigues, C. (2011). On electrical load tracking

scheduling for a steel plant. Computers & Chemical

Engineering, 35(12):3044–3047.

Laborie, P., Rogerie, J., Shaw, P., and Vil

ım, P. (2018).

IBM ILOG CP optimizer for scheduling. Constraints,

23(2):210–250.

Masmoudi, O., Yalaoui, A., Ouazene, Y., and Chehade, H.

(2017). Lot-sizing in a multi-stage ﬂow line produc-

tion system with energy consideration. International

Journal of Production Research, 55(6):1640–1663.

Merkert, L., Harjunkoski, I., Isaksson, A., S

aynevirta, S.,

Saarela, A., and Sand, G. (2015). Scheduling and en-

ergy – industrial challenges and opportunities. Com-

puters & Chemical Engineering, 72(0):183 – 198.

odos, I.,

ucha, P., and Hanz

alek, Z. (2017). Algo-

rithms for robust production scheduling with energy

consumption limits. Computers & Industrial Engi-

neering, 112:391 – 408.

Nolde, K. and Morari, M. (2010). Electrical load tracking

scheduling of a steel plant. Computers & Chemical

Engineering, 34(11):1899–1903.

Rapine, C., Goisque, G., and Akbalik, A. (2018). Energy-

aware lot sizing problem: Complexity analysis and ex-

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

act algorithms. International Journal of Production

Economics, 203:254 – 263.

Zhao, S., Grossmann, I. E., and Tang, L. (2018). Integrated

scheduling of rolling sector in steel production with

consideration of energy consumption under time-of-

use electricity prices. Computers & Chemical Engi-

neering, 111:55 – 65.

APPENDIX

5.1 Proofs

Observation 1. The maximum number of consecu-

tive metering intervals that can have non-zero overlap

with job J

for any feasible start times s is

Ω

+ 1. (8)

Proof. Let I

be the metering interval, where the job

starts and let I

be the metering interval, where the

job completes; thus d

j,i

∈ N

, d

j,i

∈ N

. Consider

the following two cases

1. I

= I

: This implies that the job has non-zero

overlap with only one metering interval in s. Since

Ω

≥ 1, the lemma holds.

2. I

< I

: Since the job is processed without pre-

emption, the job completely ﬁlls up each metering

interval between I

, I

, i.e., the overlap length of

the job with each metering interval between I

, I

is D. The number of such metering intervals is

q = i

− i

. The processing time can be then writ-

ten as

= q · D + d

j,i

+ d

j,i

. (22)

To ﬁnish our proof, we need to show that

Ω

≥ q + 2, (23)

i.e., the number of metering intervals with non-

zero overlap in s is at most Ω

Notice that from the deﬁnition of the ceiling func-

tion it holds that

Ω

+ 1 =

+ ε

| {z }

∈N

+1 (24)

where ε ∈ [0, 1). Therefore,

Ω

+ ε + 1

= q +

j,i

+ ε

| {z }

∈N

≥ q + 2.

The last inequality follows from

q ∈ N

≥0

, Ω

∈ N

, d

j,i

∈ N

, d

j,i

∈ N

Lemma 1. Let J

, J

∈ J be two jobs such

that j

6= j

, µ

= µ

, p

≥ 2, p

≥ 2 and

+ p

≥ 2 · D + 1. Let d = (d

j,i

)

∈J ,I

∈I

values for some feasible solution to the MILP model

from Section 3.2. Then Eq. (19) holds for J

, J

any metering interval I

∈ I \ {I

max

Proof. By contradiction. Assume that I

∈ I \ {I

max

}

is a metering interval such that Eq. (19) is violated,

i.e., d

≥ 1, d

,i+1

≥ 1, d

,i+1

≥ 1. Since

Eq. (11) holds, we know that

+ d

≤ D (25)

,i+1

+ d

,i+1

≤ D , (26)

thus

+ d

,i+1

+ d

,i+1

≤ 2 · D. (27)

For J

∈ {J

, J

}, one of the following two cases

are possible

1. d

j,i

+ d

j,i+1

= p

2. d

j,i

+ d

j,i+1

< p

. This means that the job has

non-zero overlap with either I

i−1

or I

i+2

. Due

to Eq. (17), either d

j,i

or d

j,i+1

is pushed to

be at least D, i.e., either d

j,i

≥ D, d

j,i+1

≥ 1 or

j,i

≥ 1, d

j,i+1

≥ D.

The proof is now split according to combinations

of those cases

• Case 1 holds for J

and Case 1 holds for J

: By

substitution we get

+ p

≤ 2 · D, (28)

which is a contradiction with our initial assump-

tion p

+ p

≥ 2 · D + 1.

• Case 2 holds for J

and Case 2 holds for J

: By

substitution we get

D + 1 + D + 1 ≤ 2 · D , (29)

which is an obvious contradiction.

• Case 1 holds for J

and Case 2 holds for J

W.l.o.g., assume that d

≥ D. Since d

≥ 1,

we get d

+ d

≥ D + 1, which is a contradic-

tion with d

+ d

≤ D.

• Case 2 holds for J

and Case 1 holds for J

Proof is analogous to the previous one.

Scheduling on Dedicated Machines with Energy Consumption Limit

5.2 Disjunctive MILP Model

The disjunctive MILP model uses the formulation for

computing the jobs’ overlaps with the metering inter-

vals that was presented in (Ha

ıt and Artigues, 2011;

ıt and Artigues, 2011). We adapted the model pro-

posed in (Ha

ıt and Artigues, 2011; Ha

ıt and Artigues,

2011) to the parallel machine scheduling with energy

consumption limits and makespan as an objective.

The complete model follows

min C

max

(30)

max

≥ s

+ p

, ∀J

∈ J (31)

+ p

≤ s

+ M · (1 − x

j, j

∀M

∈ M , ∀J

, J

∈ J

: j < j

(32)

+ p

≤ s

+ M · x

j, j

∀M

∈ M , ∀J

, J

∈ J

: j < j

(33)

≥ i · D · (1 − z

j,i

), ∀J

∈ J , ∀I

∈ I \ {I

} (34)

≤ i · D − 1 + M · (1 − z

j,i

∀J

∈ J , ∀I

∈ I \ {I

}

(35)

j,i+1

≥ z

j,i

, ∀J

∈ J , ∀I

∈ I \ {I

} (36)

= 1, ∀J

∈ J (37)

+ p

≥ (i − 1)· D · (1 − z

j,i

) + 1,

∀J

∈ J , ∀I

∈ I

(38)

+ p

≤ (i − 1)· D + M · (1 − z

j,i

∀J

∈ J , ∀I

∈ I

(39)

j,i+1

≥ z

j,i

, ∀J

∈ J , ∀I

∈ I \ {I

} (40)

j,i

≤ D · (z

j,i

− z

j,i

), ∀J

∈ J , ∀I

∈ I (41)

∑

∈I

j,i

= p

, ∀J

∈ J (42)

j,i

≥ D · (z

j,i−1

− z

j,i+1

∀J

∈ J , ∀I

∈ I \ {I

, I

}

(43)

j,i

≥ i · D · (1 − z

j,i−1

) − s

− D · z

j,i+1

∀J

∈ J , ∀I

∈ I \ {I

, I

}

(44)

j,i

≥ s

+ p

− i · D + D · z

j,i−1

− M · (1 − z

j,i+1

∀J

∈ J , ∀I

∈ I \ {I

, I

}

(45)

j,1

≥ D · z

j,1

− s

− D · z

j,2

, ∀J

∈ J (46)

≥ s

+ p

− H + D · z

−1

, ∀J

∈ J (47)

∑

∈J

j,i

· P

≤ E

max

, ∀I

∈ I (48)

The disjunctive MILP model uses the following

variables: (i) C

max

∈ N is the makespan of the sched-

ule, (ii) s

∈ N

≥0

denotes the start time of job J

, (iii)

j, j

∈ {0, 1} represents whether job J

is scheduled

before job J

, (iv) d

j,i

∈ N

≥0

expresses the length of

the overlap between job J

and metering interval I

, (v)

j,i

∈ {0, 1} denotes whether s

∈ [0, i ·D −1], and (vi)

j,i

∈ {0, 1} denotes whether s

+ p

∈ [0, (i − 1) · D].

The objective (30) minimizes the makespan,

which is the maximum of the completion times of the

jobs, see constraint (31). The non-overlapping of the

jobs is ensured by constraints (32) and (33). Con-

straints (34)-(47) models the overlaps of the jobs with

the metering intervals; see (Ha

ıt and Artigues, 2011)

for details. The last constraint (48) enforces the en-

ergy limit.

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems