
Visibility Forecast for Airport Operations by LSTM Neural Network
Tuo Deng
1
, Aijie Cheng
1
, Wei Han
2
and Hai-Xiang Lin
3
1
School of Mathematics, Shandong University, Jinan, Shandong, 250100, China
2
Numerical Weather Prediction Center of China Meteorological Administration, Beijing, 100081, China
3
Delft Institute of Applied Mathematics, Delft University of Technology, Mekelweg 4, 2628 CD Delft, Netherlands
Keywords:
Atmospheric Visibility, Time Series Forecast.
Abstract:
Visibility forecast is a meteorological problems which has direct impact to daily lives. For instance, timely
prediction of low visibility situations is very important for the safe operation in airports and highways. In this
paper, we investigate the use of Long Short-Term Memory(LSTM) model to predict visibility. By adjusting
the loss function and network structure, we optimize the original LSTM model to make it more suitable for
practical applications, which is superior to previous models in short-term low visibility prediction. In addition,
there is a ”time delay problem” when the number of hours time ahead we try to forecast becomes larger, this
problem is persistent given the limited amount of available training data. We report our attempt of applying
re-sampling to deal with the time delay problem, and we find that this method can improve the accuracy of
visibility prediction, especially for the low visibility case.
1 INTRODUCTION
Atmospheric visibility is the maximum horizontal
distance that a person with normal vision can distin-
guish the target with sky as the background, which
is an important indicator to reflect the degree of air
pollution (Fan et al., 2016). In the case of rain and
snow and severe smog, the visibility can be very low,
which will greatly affect the safety of aviation, na-
vigation and highway traffic. Visibility is influenced
by a variety of meteorological factors, such as tempe-
rature, wind, precipitation, pressure, etc. In particu-
lar, visibility shows strongly correlation with relative
humidity, PM2.5, PM10 and so on. Traditional pre-
diction methods relying on physical modeling are in-
effective due to the complexity and inability to fully
quantify the influence of many different factors. For
instance, Clark et al. have investigated the problem of
prediecting visibility by numerical methods with the
Operational Met Office Unified Model(Clark et al.,
2008). The results are not very accurate, especially
in case of low visibility due to insufficient spatial re-
solution of the numerical grid. Visibility can change
abruptly in a scale of 10m, whereas the current nume-
rical NWP models have a spatial resolution of 10km.
Currently, there are two main approaches to pre-
dict the visibility. The first approach is based on
the numerical forecast of other meteorological fac-
tors, and then calculates the visibility based on some
empirical relationship with those factors. Most pre-
vious researches are following such approach, and
the methods of empirical fitting the interrelation bet-
ween elements are mainly based on polynomial fitting
and traditional machine learning model. The polyno-
mial relationship between visibility, relative humidity
and aerosol concentration has been studied in the ci-
ties such as Shijiazhuang (Wang et al., 2016), Tianjin
(Song et al., 2013) and Hangzhou (Fan et al., 2016).
The visibility for highway in foggy weather is fit-
ted by temperature, wind speed and humidity through
SVM and BP neural network (Long et al., 2017) in
past studies. However, the prediction results of these
methods are not accurate, and can only predict the ge-
neral trend of visibility changes.
The second approach is to treat the visibility over
a period of time as a time series (Dietterich, 2002),
and solve the problem of time series prediction with
methods of machine learning or deep learning. For
instance, regression tree (Dietz et al., 2017) and MLP
(Zhu et al., 2017) are studied for airport visibility fo-
recast.
These two kinds of methods have their own ad-
vantages and disadvantages. The first method has bet-
ter interpretability due to the application of the actual
physical model, but it is inaccurate due to the com-
plexity and the lack of full understanding of the phe-
466
Deng, T., Cheng, A., Han, W. and Lin, H.
Visibility Forecast for Airport Operations by LSTM Neural Network.
DOI: 10.5220/0007308204660473
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 466-473
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

nomenon. Besides, this method is highly dependent
on the prediction accuracy of other meteorological
elements. The second method only uses the meteo-
rological data as input and few physical information
as prior knowledge, which makes the model much
simpler. However, it does not deliver an explanation
about the relationship between meteorological factors
and the actual physical laws.
In the past two decades, machine learning has at-
tracted much attention and established their position
as important competitors of classical statistical in the
field of prediction (Kurt and Oktay, 2010). A num-
ber of methods have been widely used, such as SVM,
KNN, Decision Trees, etc (Friedman et al., 2001).
These methods use only historical data to learn the
random dependencies between the past and the fu-
ture. Among these methods, Recurrent Neural Net-
work(RNN) can capture the characteristic of data in
sequence problems. Particularly, it has been applied
in time-series forecast problem (Yadav et al., 2013).
However, RNN models have their own shortco-
mings. Traditional RNN models can not capture long-
term dependencies in the sequence of input data. To
solve this problem, Long short-term memory(LSTM)
neural network was developed. Compared with tra-
ditional RNN models, LSTM can avoid the problem
of gradient vanishing and caputre the long-term de-
pendencies in time-series forecast problems. It has
been used in many fields, such as air pollutant pre-
diction (Li et al., 2017), earthquake prediction (Wang
et al., 2017), stock price prediction (Minami, 2018)
and internet traffic prediction (Cortez et al., 2006),
etc. LSTM has also been used for visibility prediction
in previous studies(Salman et al., 2018). However, the
result is of limited practical significance since they
focused only on overall errors(RMSE) and did not
pay attention to the accuracy of low-visibility fore-
cast, which is precisely the most relevant and difficult
part in practical application.
This paper aims to use LSTM to make visibility
predictions which is a problem with properties dif-
ferent from the aforementioned applications. Speci-
fically, we consider visibility forecast of 1 hour re-
spectively and 3 hours ahead. Compared with the
commonly used visibility prediction models in previ-
ous studies, the LSTM model has significantly impro-
ved, which is more accurate in cases of low visibility.
Because low visibility is more concerned in practice,
we design a weighted loss function to optimize the
model. In order to make predictions of many hours
more(e,g., 6 or 8 hours ahead), we find that there is
a systematic time delay in forecast result, which can
be caused by insufficient data. This also leads to the
inability of visibility prediction models to make accu-
rate predictions for 24-hour or longer like some areas
mentioned above. We try to fix it by resampling.
2 DATA AND ANALYSIS
In this section, we describe the specific information
of data, which contains the elements and distribution
of data. The spatiotemporal correlation of data is also
analyzed. Besides, we fix the missing values through
spatial correlation and normalize the data. In addi-
tion, for the particularity of time series, we need to
reconstruct the input data.
2.1 Data Description
The data that we used is provided by China Meteo-
rological Administration(CMA). Specifically, we use
the meteorological data of Beijing station ’54511’
from April 2016 to December 2017, which contains
15143 sets of data. Each set corresponds to hourly
measurements, including PM10, PM2.5, temperature,
precipitation, pressure, relative humidity, wind speed,
wind direction and visibility. We choose the first
10000 sets of data as training set while the remaining
data as test set to verify the model. Spatially, we se-
lect ten sites with relatively complete data around Bei-
jing, among which Beijing station 54511 is chosen as
experimental data to construct time series, and the re-
maining nine sites are used to interpolation missing
data. Figure 1 shows the location of all ten meteoro-
logical observation stations that we use, and Beijing
station is marked in red.
Figure 1: Location of stations in Beijing.
In order to understand the distribution of data bet-
ter, we segment the existing data into bar charts in
Figure 2, where we use intervals of 1,000 meters.
We can see that in the existing two-year data, visi-
bility is concentrated in the range of 2,000 meters to
4,000 meters. The occurrence of the visibility higher
Visibility Forecast for Airport Operations by LSTM Neural Network
467

than 3,000 meters gradually decreases. For the low-
visibility data which we are most concerned with, the
amount of existing data is also small, which makes
it difficult to obtain sufficient training for these most
interesting situations.
Figure 2: Distribution of Visibility in Beijing Station.
2.2 Spatiotemporal Correlation
Analysis
The spatial correlation of visibility among the stati-
ons is measured by Pearson’s correlation coefficient,
which is shown in Table 1. We can see that in most
cases the correlation coefficient between S0 and other
stations is above 0.5.
We use the autocorrelation function to measure the
correlation among visibility in time series at Beijing
station. For time lag k, we calculate the autocorrela-
tion coefficients with following formula:
ρ
k
=
Cov(L(t), L(t + k))
σ
L(t)
σ
L(t+k)
(1)
where L(t) and L(t + k) represent the meteorological
observation data of the same station with k time steps
difference. Cov(.) stands for covariance and σ stands
for standard deviation.
Figure 3: Autocorrelation coefficient in Beijing Station.
The autocorrelation coefficient of visibility in Bei-
jing station is shown in Figure 3. As the time lag
increases, the autocorrelation of time series shows a
clear downward trend, which agrees with the com-
mon sense that the closer events have greater influ-
ence. From Figure 3 we can see that autocorrelation
is above 0.8 for visibility values within 3 hours, and
then drops rapidly until it reaches 0.4 for visibility be-
tween 12 hours. After that, autocorrelation slowly de-
creases, reaching about 0.3 at 24 hour. We find that
the meteorological information after 24 hours is basi-
cally not related to the current stage. Therefore, we
decide to use the data of the past 24 hours as a single
input item for the model.
2.3 Fixing Missing Values
Due to failures of measure instruments and other dis-
turbances, there are often missing values in the obser-
vation data. The missing rate of all features is sum-
marized in Table 2. One way to handle the missing
data is to omit the missing values directly in time se-
ries prediction (Fan et al., 2017). However, compared
to other factors, the missing rate of PM10 and wind
direction is higher. For this part of data, if we neg-
lect the missing value directly, we may lose important
information. In this paper, we use the method of spa-
tially nearest neighbour interpolation to complement
the data, which almost does not affect the autocorre-
lation of time series itself, but supplement the infor-
mation by data from different sites.
Let L(t) = {x
1
,x
2
,x
3
,··· ,x
t
} be a sequence with
missing values. Each observation x
i
(i = 1, 2, · · · ,t)
has nine features. We traverse the time series in order
and mark the missing data, which will replaced by the
values from nearest neighbour. If there is a missing
data, select the next adjacent site to fill the data. To
summarize, the missing values can be fixed through
following steps.
Step1: Use Nearest Neighbour interpolation as a
replacement of a missing data and skip if a vacancy
still exists in the chosen site.
Step2: Remove used sites and repeat step 1 until
the data is completely filled
2.4 Data Normalization
Since the range of various meteorological elements is
different, we normalize all data to values between 0
and 1. In Table 3, we can see the statistical characte-
ristics of each meteorological element.
A feature x
i
is normalized as follows
x
i
=
x
i
− min(x
i
)
max(x
i
) − min(x
i
)
(2)
Through normalization, we can effectively avoid nu-
merical problems in gradient calculation. For itera-
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
468
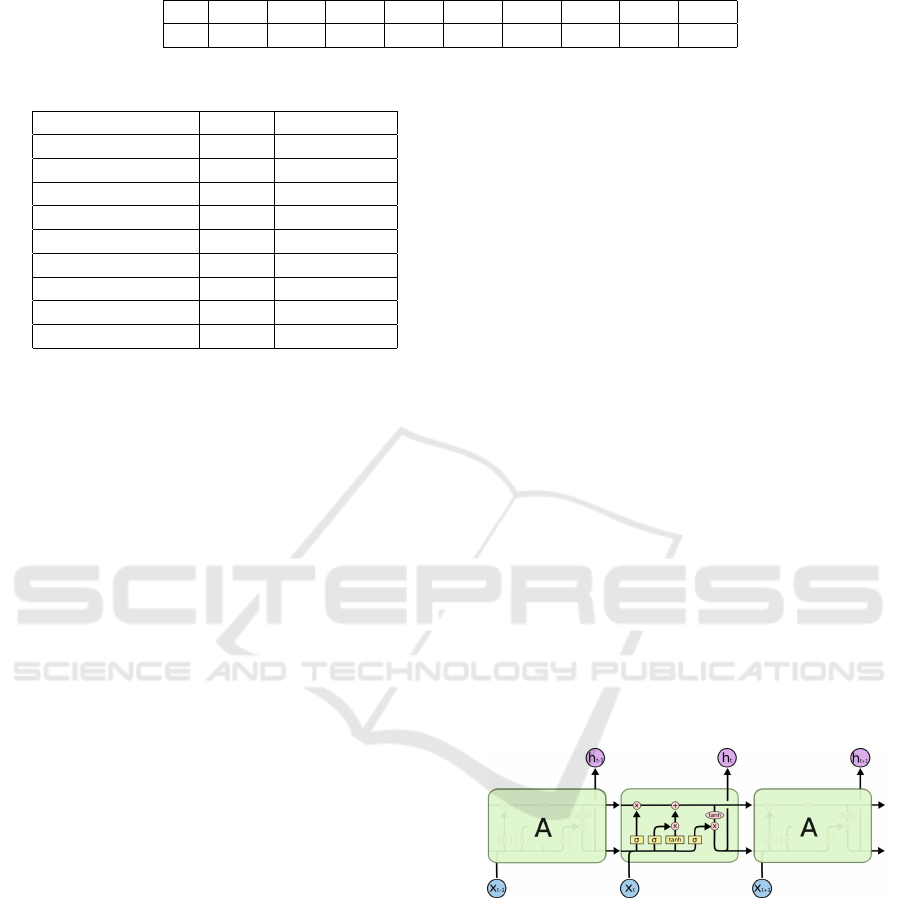
Table 1: Corr of visibility between stations.
L S1 S2 S3 S4 S5 S6 S7 S8 S9
S0 0.66 0.74 0.42 0.83 0.71 0.62 0.66 0.42 0.19
Table 2: Missing rate of measurement values.
Factor Unit Missing rate
PM10 ug/ml 1.72%
PM2.5 ug/ml 0.16%
Pressure hPa 0.03%
Temperature
◦
C 0.03%
Relative humidity % 0.03%
Precipitation mm 0.03%
Wind direction (
◦
) 3.78%
Wind speed m/s 0.03%
Visibility m 0.04%
tive algorithms in neural networks, normalized data
can also converge faster.
2.5 Data Configuration
For time series prediction problems, the input and out-
put of the model have special forms (Bontempi et al.,
2012). Without loss of generality, we will summarize
the time series prediction model as follows
x
t+d
= f (x
t
,x
t−1
,··· ,x
t−n+1
) + ε (3)
where {x
1
,x
2
,x
3
,··· ,x
t+d
} is time series data we al-
ready have and f is the model we build. ε is the irre-
ducible error. In equation (3), we use the data from
the past n time steps to predict the state after d time
steps.
Before building the model, we need to confi-
gure the input and output. For the time series pre-
diction problem, our input is a matrix and the out-
put is a vector. More specifically, the time series
{x
1
,x
2
,x
3
,··· ,x
t+d
} forms a [(t −n+1)∗n] input ma-
trix as in equation (4) and a [(t − n + 1) ∗ 1] output
vector as in equation (5)
x
t
x
t−1
··· x
t−n+1
x
t−1
x
t−2
··· x
t−n
.
.
.
.
.
.
.
.
.
.
.
.
x
n
x
n−1
··· x
1
(4)
x
t+d
x
t+d−1
.
.
.
x
n+d
(5)
where d is the time step we want to predict in the fu-
ture.
3 LSTM MODEL
In this section, we introduce the basic principles of the
LSTM model and describe resampling. At the end of
this section, we define the evaluation criteria of the
model.
3.1 LSTM
As it is known, RNN is sensitive to short-term in-
formation and insensitive to long-term information,
which is caused by the gradient vanishing problem. In
order to solve this problem, the LSTM model was pro-
posed in 1997 (Hochreiter and Schmidhuber, 1997)
and has been improved since (Greff et al., 2016).
Roughly speaking, LSTM model is a special RNN
neural network structure controlled by gates, which
is widely used in time series prediction. Figure 4 is
an illustration of LSTM.
The LSTM model has a chain structure which is
similar to the RNN model. The neurons in RNN are
replaced by memory blocks which have three units:
input gate,output gate and forget gate. The gate struc-
ture of LSTM solves the gradient vanishing problem,
thus enables the long-term dependence of time series.
Similar to RNN, the parameters of the LSTM
model are fitted by back propagation through
time(BPTT).
Figure 4: LSTM.
3.2 Resampling
The resampling method can be traced back to the
randomization test proposed by Fisher in the 1930s
(Simon, 1992). According to the original resampling
idea, when the two sample sets were merged, there
should be no difference between the resampled statis-
tical indicators and the original sample statistical indi-
cators unless they came from different natural models
(Bi et al., 2009).
In recent years, resampling methods are gradually
being applied in the field of machine learning, among
Visibility Forecast for Airport Operations by LSTM Neural Network
469

Table 3: Statistical characteristics of facors.
Factor Range Mean Std
PM10 [3,1000] 110.36 89.57
PM2.5 [1,1000] 81.88 75.16
Pressure [989.8,1037.5] 1011.82 10.12
Temperature [-9.9,38.2] 15.73 11.20
Relative humidity [5,98] 53.10 24.39
Precipitation [0,52.7] 0.08 0.99
Wind direction [0,360] 162.89 99.96
Wind speed [0,9.5] 2.03 1.32
Visibility [23,35000] 13454.64 11487.26
which bagging method and boosting method are po-
pular (James et al., 2013). In these methods, new data
sets are obtained by resampling, and these data sets
are applied to ensemble algorithm. In some cases, we
also verify the model with a random subset, which is
commonly known as cross-validation.
In this paper, we will use the resampling idea to
supplement the training set in the case of insufficient
data volume. We obtain new data by sampling with
replacement. The new data are combined with the ori-
ginal data to supplement the training set.
3.3 Evalution Criterion
We use the Root Mean Squared Error (RMSE) to eva-
luate the model
RMSE =
s
1
N
N
∑
i=1
( ˆy
i
− yi)
2
(6)
where ˆy
i
is the predicted value and y
i
is the true value.
Consider the impact of low visibility to safety ope-
rations, we focus on low visibility forecast, which we
will evaluate separately. After the predicted results
are obtained, we will take out the data below 1600
meters and 800 meters and calculate their RMSE re-
spectively. These two dividing lines are the common
visibility standards for airports operations regarding
safe aircraft taking-off and landing.
4 EXPERIMENT AND ANALYSIS
In this section, we will introduce the detail of experi-
ments. First, we predict the visibility after one hour,
and improve forecast accuracy in low visibility situ-
ations by weighted RMSE. After that, we predict the
visibility after three hours. As the forecast time incre-
ases, the error becomes larger, and the result shows
clearly there is delay between the predicted and the
actual time series. We try to solve this problem by ad-
justing the structure of the model and by resampling.
4.1 One-hour Visibility Forecast
In this case, we build models for one-hour visibility
forecast with very simple neural network structure.
Since the prediction time is short and information be-
tween input and output is more correlated, the sim-
ple structure can reduce the model complexity and the
calculation time without suffering too much.
As described in Section 2.5, we select 24 hours
of meteorological information as input and the visibi-
lity for the next hour as output. For each set of inputs,
we select all nine meteorological elements as features,
and we also add the difference in visibility to provide
trend information for visibility changes in advance.
Therefore we have ten features in one set of data: tem-
perature, precipitation, pressure, wind speed, wind
direction, relative humidity, PM2.5, PM10, visibility
and difference value between visibilities.
We construct our model by a neural network with
two hidden layers. The first hidden layer is the LSTM
layer containing 200 neurons and the second is the
fully connected layer with one neuron, as shown in
Figure 5. For other parameters, we choose the tanh
function as activation function and adam as optimizer.
In order to get better forecast for situation of low
visibility, we design a weighted RMSE (Eq.(7)) as
loss function. In the loss function, we add a hyperpa-
rameter α to adjust the weight of different data. The
weight e
−α∗y
i
is larger for lower visibility y
i
.
W RMSE =
s
1
N
N
∑
i=1
e
−α∗y
i
( ˆy
i
− yi)
2
(7)
Table 4 shows the RMSE for all test set becomes
larger when the value of α increases. RMSE is 4390
when α = 0, which means the weight for all error
term is 1, and increases to 5208 when α grows to
5. However, as the α increases, the RMSE of low
visibility part will first decrease and then increase,
which is easy to understand since we give the error
term of low visibility part a higher weight. A furt-
her increase of α makes the weighted term in the loss
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
470

Figure 5: LSTM structure.
function (Eq.(7)) close to zero, and the model optimi-
zation stops. When α = 2, the RMSE of low visibility
part is minimal. The result of α = 2 is shown in Fi-
gure 6. The first 200 time steps from the test set are
shown, where the blue line is the predicted value and
the black is the true value.
Table 4: RMSE by different α.
α 0 1 2 3 5
all data 4390 4572 4708 5107 5208
< 1600 1564 1118 933 1321 1373
< 800 1251 993 756 1233 1391
Figure 6: 1 hour visibility forecast with α = 2.
We can see that in Table 4 the weighted loss
function has a significant improvement effect on the
forecast model. The improved model has higher pre-
diction accuracy for low visibility whereas the overall
prediction accuracy becomes worse, which is not the
focus in this specific application though. It can be
seen in Figure 6 that when α = 2, the overall trend
of the model’s prediction results is consistent with the
observation data.
In order to evaluate the performance of LSTM, we
compare the prediction results of LSTM model with
other commonly used forecast models in previous stu-
dies, namely, polynomial fitting model (Fan et al.,
2016), regression tree model (Dietz et al., 2017) and
MLP model (Zhu et al., 2017). Polynomial fitting is
used for the relationship between real-time elements,
and the latter two models are used for time series pre-
diction with similar data configuration as in Section
2.5. In previous works mentioned above, limited by
the number of features used and models themselves,
these methods are usually used for short-term visibi-
lity prediction, such as one hour or even shorter. The
prediction results of the models in the following table.
Table 5: RMSE of different model.
RMSE Poly RF MLP LSTM
all data 6393 4432 4732 4708
< 1600 2113 1362 1517 933
< 800 2579 1811 2087 756
As can be seen from Table 5, compared with other
three methods, the overall error of the LSTM model
for visibility prediction has not been reduced, but the
prediction results for the low visibility part have been
significantly improved, which is also the most rele-
vant in practical applications.
4.2 Three-hours Visibility Forecast
It is shown in the previous section that the LSTM mo-
del is effective for 1-hour visibility prediction. Re-
latively accurate predictions can be obtained with a
simple neural network structure. In the following,
we consider prediction of 3 hours with more complex
neural network structure, because the increase of pre-
diction time will lead to the loss of relevant informa-
tion in time series.
For the 3-hour visibility prediction model, we take
the same input dimension, which is the meteorologi-
cal data of the past 24 hours. Each set of data inclu-
des the ten elements. We change the complexity of
the model by adjusting the network structure. In the
previous section we use the structure with two hidden
layers, and now we will add more LSTM layers and
investigate the effects. In the experiment, we add one
LSTM layer each time, while each layer contains 200
neurons. For computational efficiency considerations,
we limit to add up to the model with four LSTM lay-
ers. Between multiple LSTM layers, we add dropout
to prevent overfitting. Before the output layer, we still
add a fully connected layer with one neuron.
In the experiments, we add more hidden layers
while keeping other parameters unchanged. We use
the weighted loss function with α = 2.
Visibility Forecast for Airport Operations by LSTM Neural Network
471
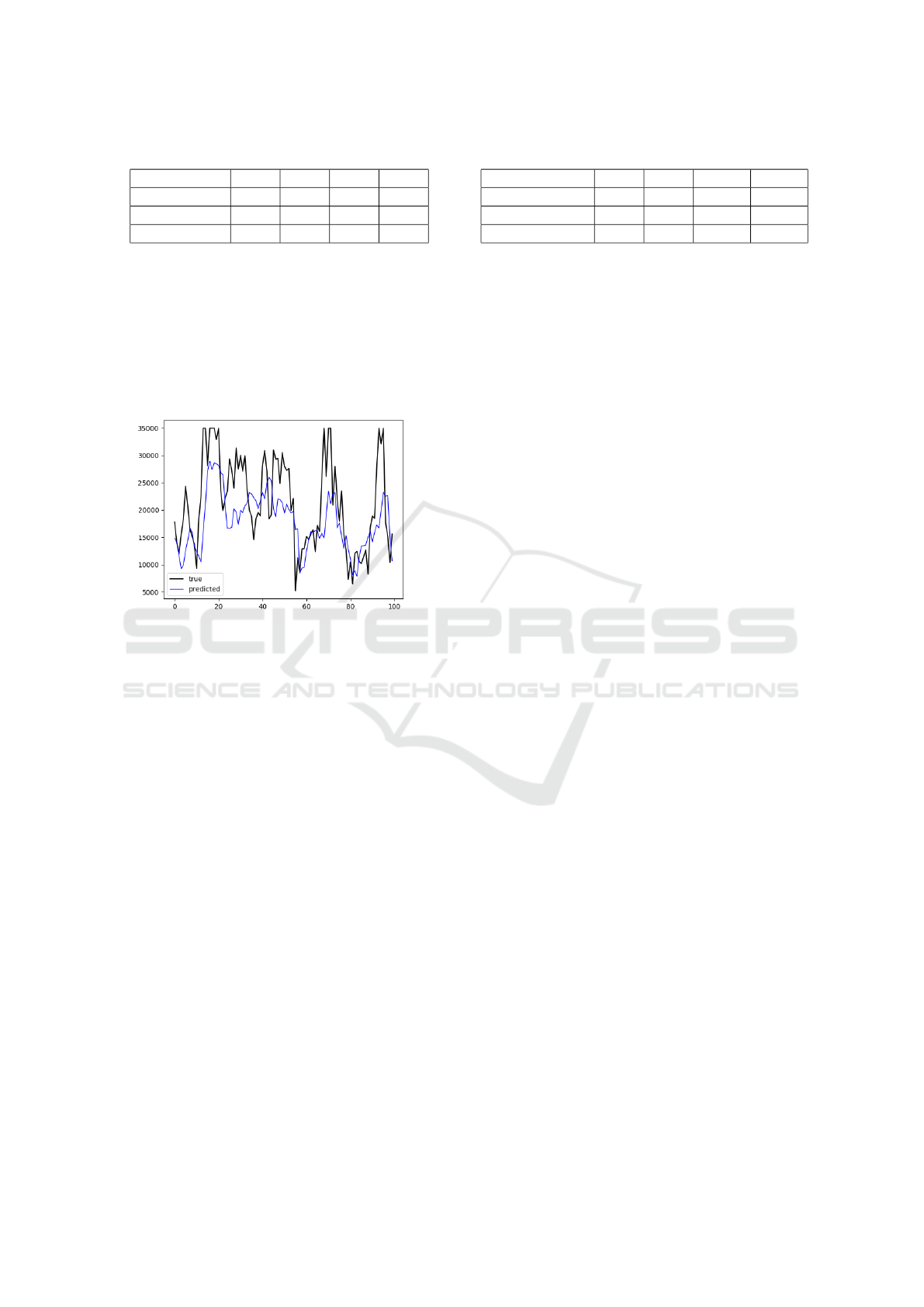
Table 6: RMSE by different number of layers.
LSTM layers 1 2 3 4
all data 7006 7013 7063 7710
< 1600 2149 1906 1685 1159
< 800 2702 2249 2159 1763
From Table 6 we can see that when the neural net-
work structure has fewer layers, the prediction results
are more accurate for the whole data. Neural network
structure with more layers obtains more accurate pre-
diction for low visibility situation. Figure 7 illustrates
the results of the 3-hour visibility forecast model with
only one LSTM layer, only the first 100 time steps in
the test set is shown.
Figure 7: 3 hour visibility forecast with 1 LSTM layer.
Although the prediction accuracy of low visibi-
lity cases is improved by sacrificing that for the high
visibility cases, Figure 7 shows there is a signifi-
cant ”time delay” between the predicted result and
the actual value for 3-hour visibility forecast model.
By constructing a simple experiment with a periodic
function, we find that this result is partly due to the
lack of data volume. Through experiments of trigono-
metric functions and other periodic functions that we
construct randomly, we find that this phenomenon is
not only in the visibility prediction problem, but also
ubiquitous in the LSTM model applied to time series
problems, which can be solved when the amount of
data is sufficient.
To solve this problem, we try to generate more
data by resampling. Specifically, after obtaining the
input matrix through data configuration, sampling
with replacement is carried out by row, that is, res-
ampling by group. These data sets are added to the
input matrix after the resampling. Without loss of ge-
nerality, we choose the simplest neural network struc-
ture to study the resampling modeling. The results are
shown in Table 7.
After data configuration, we randomly selected
5,000 to 15,000 groups of data as new data to supple-
ment the training set. It can be seen from the table that
Table 7: RMSE of resmapling model.
Added samples 0 5000 10000 15000
all data 7006 6824 6653 6844
< 1600 2149 1360 1628 1516
< 800 2702 1663 2291 2009
appropriate resampling can improve the model. When
the data volume of resampling is 5000, we can see
that RMSE is significantly reduced. However, when
more data are added, the RMSE increases rather than
decreases, which is due to the problem of overfitting.
More specifically, beyond a certain point of adding
data via resampling, the loss function is still decreas-
ing, while the RMSE of the test set is increasing. In
summary, proper resampling can reduce errors in the
original model. However, constraint by the limited
amount of data, the ”time delay” problem cannot be
solved.
5 CONCLUSIONS
In this paper, we transform the traditional visibility
prediction problem into time series prediction pro-
blem, and predict the visibility by LSTM model.
Compared with previous studies mainly use simple
polynomial fitting and MLP, the LSTM model per-
forms better in the overall trend and the accuracy. By
introducing a weighted loss function, we can improve
the accuracy of low visibility prediction. Specifically,
with appropriate hyperparameters, the RMSE of visi-
bility is reduced by 37% for cases of less than 1600
meters and by 21% for cases of less than 800 meters.
For short-term visibility prediction, our study shows
that the LSTM model can be used to aid airport opera-
tions in decision about suitability of take-off and lan-
ding of aircraft.
In the 3-hour visibility prediction model, we find
that with complex LSTM structure, the overall error
of the model will become larger, but the RMSE of
the low visibility part will decrease, which is what we
hope to see. In predictions of many hours ahead(e,g.
6 or 8 hours), we encountered a systematic time delay
in LSTM forecast result. We investigated the causes
of this problem with a periodic function amplified by
a time dependent factor that we randomly construct, it
is shown that the LSTM model has a significant time
delay for the prediction of multiple time steps when
the amount of data is insufficient. This phenomenon
not only appears in the visibility prediction, but also
widely exists in time series prediction problems with
LSTM. We find this is partly due to insufficient me-
asurement data and try to solve it by resampling. In
our experiment, resampling can effectively reduce the
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
472

error, but constraint by the limited amount of data the
”time delay” phenomenon is not completely elimina-
ted.
REFERENCES
Bi, H., Liang, H., and Wang, W. (2009). Resampling
method and machine learning. Journal of Computer,
32(5):862–877.
Bontempi, G., Taieb, S. B., and Le Borgne, Y.-A. (2012).
Machine learning strategies for time series forecas-
ting. In European Business Intelligence Summer
School, pages 62–77. Springer.
Clark, P. A., Harcourt, S. A., Macpherson, B., Mathison,
C. T., Cusack, S., and Naylor, M. (2008). Prediction of
visibility and aerosol within the operational met office
unified model. i: Model formulation and variational
assimilation. Quarterly Journal of the Royal Meteo-
rological Society, 134(636):1801–1816.
Cortez, P., Rio, M., Rocha, M., and Sousa, P. (2006). Inter-
net traffic forecasting using neural networks. In Neu-
ral Networks, 2006. IJCNN’06. International Joint
Conference on, pages 2635–2642. IEEE.
Dietterich, T. G. (2002). Machine learning for sequential
data: A review. In Joint IAPR International Works-
hops on Statistical Techniques in Pattern Recognition
(SPR) and Structural and Syntactic Pattern Recogni-
tion (SSPR), pages 15–30. Springer.
Dietz, S. J., Kneringer, P., Mayr, G. J., and Zeileis, A.
(2017). Forecasting low-visibility procedure states
with tree-based statistical methods. Pure and Applied
Geophysics, pages 1–14.
Fan, G., Ma, H., Zhang, X., and Liu, Y. (2016). Effects
of relative humidity and pm2.5 concentration on at-
mospheric visibility: a multi station comparative ana-
lysis based on hourly data. Journal of Meteorology,
74(6):959–973.
Fan, J., Li, Q., Hou, J., Feng, X., Karimian, H., and Lin,
S. (2017). A spatiotemporal prediction framework for
air pollution based on deep rnn. ISPRS Annals of the
Photogrammetry, Remote Sensing and Spatial Infor-
mation Sciences, 4:15.
Friedman, J., Hastie, T., and Tibshirani, R. (2001). The
elements of statistical learning. Springer series in sta-
tistics New York, NY, USA:.
Greff, K., Srivastava, R. K., Koutnik, J., Steunebrink, B. R.,
and Schmidhuber, J. (2016). Lstm: A search space
odyssey. IEEE Transactions on Neural Networks &
Learning Systems, 28(10):2222–2232.
Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. Neural Computation, 9(8):1735–1780.
James, G., Witten, D., Hastie, T., and Tibshirani, R. (2013).
An introduction to statistical learning, volume 112.
Springer.
Kurt, A. and Oktay, A. B. (2010). Forecasting air pollu-
tant indicator levels with geographic models 3 days in
advance using neural networks. Expert Systems with
Applications, 37(12):7986–7992.
Li, X., Peng, L., Yao, X., Cui, S., Hu, Y., You, C., and
Chi, T. (2017). Long short-term memory neural net-
work for air pollutant concentration predictions: Met-
hod development and evaluation. Environmental Pol-
lution, 231:997–1004.
Long, K., Li, C., Mao, X., and Hu, Y. (2017). Highway
foggy visibility prediction method. Journal of Xuzhou
Institute of Technology: Natural Sciences Edition, pa-
ges 31–37.
Minami, S. (2018). Predicting equity price with corporate
action events using lstm-rnn. Journal of Mathematical
Finance, 8(01):58.
Salman, A. G., Heryadi, Y., Abdurahman, E., and Suparta,
W. (2018). Weather forecasting using merged long
short-term memory model (lstm) and autoregressive
integrated moving average (arima) model. Journal of
Computer Science.
Simon, J. L. (1992). Resampling: the new statistics. arling-
ton, va: Resampling stats.
Song, M., Han, S., Zhang, M., Yao, Q., and Zhu, B. (2013).
Relationship between visibility and relative humidity
and pm10 and pm2.5 in tianjin. Journal of Meteoro-
logy and Environment, 29(2):34–41.
Wang, Q., Guo, Y., Yu, L., and Li, P. (2017). Eart-
hquake prediction based on spatio-temporal data mi-
ning: An LSTM network approach. IEEE Transacti-
ons on Emerging Topics in Computing, PP(99):1–1.
Wang, X., Han, J., Chen, J., Yan, W., and Yue, Y. (2016).
Variation characteristics of atmospheric visibility and
their relationship with relative humidity and particle
concentration in shijiazhuang of hebei. Journal of
Arid Meteorology, 34(4):648–655.
Yadav, A. P., Kumar, A., and Behera, L. (2013). Rnn ba-
sed solar radiation forecasting using adaptive learning
rate. In International Conference on Swarm, Evoluti-
onary, and Memetic Computing, pages 442–452.
Zhu, L., Zhu, G., Han, L., and Wang, N. (2017). The ap-
plication of deep learning in airport visibility forecast.
Atmospheric and Climate Sciences, 7(03):314.
Visibility Forecast for Airport Operations by LSTM Neural Network
473
