Extended Colored Traveling Salesperson for Modeling Multi-Agent
Mission Planning Problems
Branko Miloradovi
´
c, Baran C¸
¨
ur
¨
ukl
¨
u, Mikael Ekstr
¨
om and Alessandro Vittorio Papadopoulos
Division of Intelligent Future Technologies, M
¨
alardalen University, H
¨
ogskoleplan 1, 721 23 V
¨
aster
˚
as, Sweden
Keywords:
Multi-Agent Mission Planning, Colored Traveling Salesperson (CTSP), Genetic Algorithms.
Abstract:
In recent years, multi-agent systems have been widely used in different missions, ranging from underwater to
airborne. A mission typically involves a large number of agents and tasks, making it very hard for the human
operator to create a good plan. A search for an optimal plan may take too long, and it is hard to make a time
estimate of when the planner will finish. A Genetic algorithm based planner is proposed in order to overcome
this issue. The contribution of this paper is threefold. First, an Integer Linear Programming (ILP) formulation
of a novel Extensive Colored Traveling Salesperson Problem (ECTSP) is given. Second, a new objective
function suitable for multi-agent mission planning problems is proposed. Finally, a reparation algorithm to
allow usage of common variation operators for ECTSP has been developed.
1 INTRODUCTION
In recent years, multi-agent systems have been widely
used in different missions, ranging from underwater
to airborne. It can be very challenging for a human
operator to devise a good plan if a mission involves a
large number of agents and tasks. Given a global mis-
sion objective, resources, and constraints, the plan-
ning problem consists of assigning appropriate tasks
to a set of agents in such a way that the plan is physi-
cally feasible. We assume that agents are not homoge-
neous: velocity and equipment may vary. Tasks have
Precedence Constraints (PC) as well as equipment, or
sensor requirements. Thus, the optimization problem
may also include choosing the optimal set of agents
for the mission. Tasks have precedence constraints
(PC) as well as equipment, or sensor requirements.
This type of a combinatorial problem can be
solved by an exact method or with a meta-heuristic
approach. Exact methods guarantee to output op-
timal solution, usually by mapping a problem into
a tree or a graph and searching through the nodes,
pruning unfeasible branches and backtracking from
dead-ends. Meta-heuristics solve problems differ-
ently, which sometimes leads to a sub-optimal solu-
tion. On the other hand, as the search space increases,
exact methods fail to produce a plan within a reason-
able time. In the general case, the time taken for an
initial plan to be produced is less critical compared to
that of re-planning. If re-planning takes too long, the
state of the system may have changed while the plan-
ning process is being done. Thus, it might be better
to have a fast solution even if it is sub-optimal. The
planner proposed in this work is based on GA (Hol-
land, 1992), and has been adapted to the problem of
multi-agent mission planning, described in Sect. 3.
The main contributions of this paper are to (i) give
a formal problem formulation of a novel Extended
Colored Traveling Salesperson Problem (ECTSP); (ii)
Propose a new optimization criterion useful for multi-
agent mission planning problems; and (iii) Develop a
reparation algorithm to allow usage of common vari-
ation operators for ECTSP.
2 RELATED WORK
A domain-independent taxonomy describing multi-
robot task allocation (MRTA) problems has been pro-
posed by (Gerkey and Matari
´
c, 2004). Later, extended
with temporal and ordering constraints (Nunes et al.,
2017). The TSP variation that will be described in this
paper can be labeled as Single-Task robots, Single-
Robot tasks, Time-Extended Assignments (ST-SR-
TA) with precedence constraints and heterogeneous
robots.
Plans that are to be executed in a distributed fash-
ion can nonetheless be produced by a centralized
planner. A planner breaks a mission plan into smaller
pieces that are sent to the appropriate agent for execu-
Miloradovi
´
c, B., Çürüklü, B., Ekström, M. and Papadopoulos, A.
Extended Colored Traveling Salesperson for Modeling Multi-Agent Mission Planning Problems.
DOI: 10.5220/0007309002370244
In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 237-244
ISBN: 978-989-758-352-0
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
237

tion. A multi-objective harmony search algorithm is
used to solve a mission planning problem for a swarm
of Autonomous Underwater Vehicles (AUVs) with-
out PCs between tasks (Landa-Torres et al., 2017). A
research framework on mission planning for swarms
of Unmanned Aerial Vehicles (UAVs) has been pro-
posed by (Zhou et al., 2017). In general, most of the
approaches used for UAV mission planning can be
used in different scenarios, such as swarms of AUV
in the underwater application or for swarms of ter-
restrial vehicles. The problem of mission planning
for a swarm of UAVs can be solved using evolution-
ary approaches (Ramirez-Atencia et al., 2017a). The
problem is modeled as a constraint satisfaction prob-
lem and solved using multi-objective GA. This work
has been further extended by (Ramirez-Atencia et al.,
2017b) to utilize re-planning and analysis of operator
training in the control center. For a similar problem of
a mission planning for cooperative UAV teams, a so-
lution was proposed by (Bello-Orgaz et al., 2016) that
uses GA to optimize a weighted linear combination of
mission’s makespan and fuel consumption. This ap-
proach is further improved by (Cristian et al., 2018)
by using weighted random generator strategies for the
creation of new individuals. An overview of the most
common optimization criteria in MRTA problems is
given by (Nunes et al., 2017).
TSP expressed as an ILP was introduced by
Dantzig and colleagues (Dantzig et al., 1954). Many
different approaches were developed and proposed
in order to solve TSP. The Lin-Kernighan approach
(Keld, 2009) and GA with Edge Assembly Crossover
(Yuichi and Shigenobu, 2013), are among the best
perfroming approaches. The original problem def-
inition of TSP is later extended to an mTSP (Bek-
tas, 2006). An approach using sub-tours was pro-
posed by (Giardini and Kalm
´
ar-Nagy, 2011) to solve
multiple TSP (mTSP). The idea is to divide a graph
into subgraphs which are solved using GA. Each sub-
graph represents a tour for one of the salesperson. An-
other extension of the original TSP is done by adding
Precedence Constraint (TSPPC) (Kubo and Kasugai,
1991). mTSP and TSPPC were later combined into an
mTSPPC (Zhong, 2014), although a formal problem
formulation was not given. Recently, a Colored TSP
formulation (CTSP) has been given by (Meng et al.,
2018) in order to model and solve multiple bridge ma-
chine planning in industry.
In this paper, their approach has been further ex-
tended by the addition of PC, that is formally de-
scribed as an inter-schedule dependency by (Korsah
et al., 2013), multi-depots (with different source and
destination depots), and heterogeneous salespersons.
salesperson s
city v
i
ordering
constraint
destination
depot
corresponding
colors c
s
1
1
1
2
2
σ
1
σ
2
σ
2
Figure 1: An Illustration of the ECTSP.
3 EXTENDED COLORED TSP
Before introducing the theoretical background of the
ECTSP, the connection between the theoretical model
and real-world mission will be explained.
A city corresponds to a task, a salesperson to an
agent
1
, and a color to an equipment type (Camera,
Gripper, etc.). The colors associated with an agent
represent the agent’s equipment, while the colors as-
sociated with a task indicate the equipment required
for its successful completion (see Fig. 1).
The need for PC is apparent, as explained in this
example: An agent has two tasks, e.g., scan an area
for data collection, and send data back. Obviously, the
data cannot be sent before it is acquired, thus the only
possible ordering between the two tasks is to gather
data first, and then send that data. Also, equipment
heterogeneity is not the sole determinant for the dif-
ferences between the agents. Every agent may have a
different velocity, therefore the duration of every task
depends on the selected agent.
In Fig. 1 three salespersons are shown starting
from three different source depots (σ
1
to σ
3
). Each of
them visits a certain number of tasks and goes to the
destination depot. Cities that have precedence con-
straints are marked with numbers (1 has to be vis-
ited before 2). Now the theoretical background of the
ECTSP will be presented.
3.1 Problem Formulation
Suppose that an ECTSP has m salespersons, s ∈ S :=
{s
1
,s
2
,...,s
m
}, n cities, v ∈ V := {v
1
,v
2
,...,v
n
} and
k colors, c ∈ C := {c
1
,c
2
,...,c
k
} where m,n,k ∈ N.
Each salesperson s starts from a source depot σ,
where σ ∈ Σ := {σ
1
,...,σ
z
}, and finishes its tour at
a destination depot δ, where δ ∈ ∆ := {δ
1
,...,δ
w
}.
The superset containing all of the cities V and depots
is defined as
e
V := V ∪ {Σ,∆}. This problem can be
formulated over a directed graph G = (
e
V , E), where
1
Terms agent and robot are used interchangeably
throughout this work.
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
238

E :
e
V ×
e
V 7→ R
+
0
. An edge e ∈ E, connecting ver-
texes i, j ∈
e
V can be expressed as
e(i, j) =
(
ω
i j
, if i is connected to j
0, otherwise,
where ω
i j
≥ 0 represents the cost of edge e(i, j). The
decision variable x
i js
∈ {0, 1} can be defined as
x
i js
=
(
1, if s travels from i to j,
0, otherwise.
Every city i ∈
e
V \ ∆ has a weight ξ(i), with ξ :
e
V \
∆ 7→ R
+
0
(with ξ(i) = 0 when i ∈ Σ). Also, every city
i ∈ V is associated with a color f
c
(i), with f
c
: V 7→
C. Each salesperson s ∈ S has a set of colors C
s
⊆ C
assigned to it. In contrast to city color matrix that
was defined by (Li et al., 2015), here a color matrix
of a salesperson s, A
s
∈ {0, 1}
n×n
, shows openness of
cities towards a salesperson s, and is defined as A
s
:=
[a
i js
], with
a
i js
=
(
1, f
c
(v
i
) ∈ C
s
∧ f
c
(v
j
) ∈ C
s
∧ π
i j
= 1
0, otherwise,
where Π = [π
i j
]
n×n
is the adjacency matrix indicating
the precedence relations among the cities. If a certain
city i needs to be visited before a city j, precedence
constraints can be defined as
∑
l∈V
x
ils
≤
∑
k∈
e
V \Σ
x
jks
, ∀s,∀i, j ∈ V : π
i j
= 1, π
ji
= 0,
(1)
and, in order to disallow a salesperson s omitting com-
pletely city j, and going directly to a destination depot
from city i, a following constraint is imposed:
∑
l∈∆
x
ils
≤ 0, ∀s, ∀i, j ∈ V : π
i j
= 1, π
ji
= 0. (2)
The definition of the color matrix A
s
can be extended
to include the depots as:
a
i js
=





a
i js
, i, j ∈ V ,
1, (i ∈ Σ, j ∈
e
V \ Σ) ∨ (i ∈
e
V \ ∆, j ∈ ∆),
0, (i, j ∈ Σ) ∨ (i, j ∈ ∆).
A salesperson s is allowed to only visit the cities spec-
ified in its extended color matrix A
s
:
x
i js
≤ a
i js
, ∀s ∈ S,∀i ∈
e
V \ ∆, ∀ j ∈
e
V \ Σ, i 6= j. (3)
Furthermore, a salesperson s must enter (Eq. 4) and
leave (Eq. 5) each city exactly once.
∑
s∈S
∑
i∈
e
V \∆
x
i js
= 1, ∀ j ∈ V , i 6= j (4)
∑
s∈S
∑
j∈
e
V \Σ
x
i js
= 1, ∀i ∈ V ,i 6= j. (5)
The final destination of a salesperson s is always a
destination depot δ:
∑
i∈
e
V \∆
∑
j∈∆
x
i js
= 1, ∀s ∈ S. (6)
It is important to note that it is allowed for some sales-
persons to go directly from a source depot σ to a des-
tination depot δ, i.e., x
i js
= 1, i ∈ Σ, j ∈ ∆.
The starting location of a salesperson s is always
a source depot σ:
∑
i∈Σ
∑
j∈
e
V \Σ
x
i js
= 1, ∀s ∈ S. (7)
The number of salespersons B
σ
in each source depot
σ is given, and it is such that
∑
i∈Σ
B
i
= |S |, and:
∑
s∈S
∑
j∈
e
V \Σ
x
i js
= B
i
, ∀i ∈ Σ. (8)
To eliminate the sub-tours, it is required that for each
nonempty subset M ⊆ V , the number of edges be-
tween the nodes of M must be at most |M | − 1:
∑
i∈M
∑
j∈M
x
i js
≤ |M | − 1, ∀s ∈ S,∀M ⊆ V ,M 6=
/
0.
(9)
A salesperson s cannot travel from a city i to the same
city i:
x
iis
= 0, ∀i ∈
e
V , ∀s ∈ S. (10)
3.2 Objective Function
In multi-agent systems a mission can involve an op-
timization of many different parameters. Commonly,
mission duration is minimized, however a duration of
a mission can be defined in various ways. (Maoudj
et al., 2015) defined mission duration as the sum of
all tasks in a mission (minSUM), where (Bello-Orgaz
et al., 2016) describe mission duration as the time in-
terval from the start time of the first task to the end
time of the last task (minMAX). Neither of these ap-
proaches is suitable for the problem presented in this
paper. The former approach can produce a plan where
one agent is doing much more work than the other
agents. In an actual AUV mission, this can mean that
the extraction vessels and the crew have to stay in the
open sea much longer increasing the overall cost of
the mission. The latter approach minimizes the max-
imum cost of an agent over all the agents. This ap-
proach works well if tasks are instantaneous or have
the same duration. However, if there is a task that
Extended Colored Traveling Salesperson for Modeling Multi-Agent Mission Planning Problems
239

dominates the duration of the other tasks
2
, then the
mission would not be optimized at all. This issue
is partly mitigated in the work of (Alighanbari et al.,
2003) where a linear aggregation function is used to
minimize the maximum and average task completion
times, as well as total idle times. This approach fa-
vors the usage of as many agents as possible, and it
might lead to an increased cost, if agent needs to be
deployed to the environment. In order to avoid afore-
mentioned problems, a weighted combination of min-
MAX
f
m
= min
x
max
s
∑
i∈
e
V \∆
∑
j∈
e
V \Σ
(ω
i j
+ ξ(i))x
i js
and minSUM
f
s
= min
x
∑
i∈
e
V \∆
∑
j∈
e
V \Σ
(ω
i j
+ ξ(i))x
i js
, ∀s
is proposed as objective function:
J = w
1
f
m
+ w
2
f
s
(11)
subject to constraints (1), (2), (3), (4), (5), (6), (7),
(8), (9), where w
1
,w
2
> 0 are user defined weights.
4 GENETIC MISSION PLANNER
(GMP)
In addition to TSP, GA and its numerous variations
have been widely used to solve other combinato-
rial optimization problems like Vehicle Routing Prob-
lem (VRP) (Baker and Ayechew, 2003), Job Shop
Scheduling problems (Nisha and Nathi Ram, 2015),
as well as Resource Constrained problems (Brie and
Morignot, 2005). Although the initial plan making is
not bounded by time, the re-planning is. Re-planning,
in this case, can be seen as planning again with new
initial conditions. Since multi-agent missions are usu-
ally costly and autonomy of agents is limited as well,
the re-planning process should be very fast. This is
one of the reasons for the use of a metaheuristic ap-
proach over exact methods.
Chromosome encoding is done in the same way
as it done by (Miloradovi
´
c et al., 2017), thus two
arrays of integers, representing the genes, are used.
2
Its duration is larger than the makespan of any other
agent’s plan
A1 T3 T5 T2 A2 T7 T7 T4
0 P1 P0 P1 0 P1 P2 P1 0 0 0
Agent Task Parameter Inactive
Figure 2: An example of an individual in the population.
The first array consists of integers representing tasks
and agents, whereas the second array represents task
parameters (PC, equipment requirements, duration of
the task, and location) as shown in the Fig. 2. Chro-
mosome length can be fixed a priori if the length of a
plan (number of tasks + number of agents involved )
is known. However, if a planner can introduce a new
task or optimize the number of agents (some agents
might not be used even if they are available for a
mission) then a variable chromosome length is pre-
ferred. In this paper a mix of these two approaches
is used - chromosome length is fixed, in addition, be-
sides active genes (AG), a certain number of inactive
genes is introduced. The reason for this is that al-
though the number of tasks in a mission is fixed, the
planner is allowed to optimize the number of agents
involved. This implies that the number of AG is
n + 1 ≤ AG ≤ n + m thus the chromosome length is
fixed to the size of n + m.
The initial population is created at random with
the respect to given constraints. As a start, the mini-
mum number of agents and agent types (with appro-
priate equipment) are determined. Then a number of
agents in the chromosome is randomly picked in the
range of the bare minimum and the maximum num-
ber of available agents. For example, if all agents
have the same equipment, then the number of agents
in a chromosome would be in a range of 1 to m. Af-
ter this step, a list of possible tasks for every agent is
created. The number of tasks per agent is randomly
determined based on the previously created list. Two
or more agents may have the ability to do the same
task, e.g., a task requires a sonar, and there are three
agents with sonar available. In this specific case, a
task is randomly assigned to one of the valid agents.
Task assignment is repeated until there are no more
tasks left to assign and the whole process is repeated
for every individual in the population.
4.1 Precedence Reparation Algorithm
In a classical implementation of a GA for TSP, chro-
mosomes are arrays consisting of genes (city identi-
fiers). In this case, crossover operators can mix indi-
viduals in many possible ways and produce feasible
solutions. The only thing that has to be taken into
account is to disallow city duplicates in a potential
solution. In contrast to the TSP, implementation of
the crossover operators for ECTSP is not trivial, since
there are PCs that need to be taken into account, in
order to avoid the creation of infeasible solutions.
Since variation operators (crossover and mutation)
do not have the ability to preserve or guarantee to
create offspring with a valid ordering, a Precedence
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
240

Constraint Reparation (PCR) operator has been devel-
oped. The PCR is applied after the creation of the ini-
tial population, crossover (when used), and mutation
operator.
The algorithm starts by iterating through each task
gene of each individual. When a task gene with incor-
rect PC is found, the algorithm searches for the other
inter-related task. Two cases can be distinguished. In
the first case (case 1) both tasks are allocated to the
same agent, while in the second case (case 2) both
tasks are not allocated to the same agent.
In case (1) task genes are simply swapped. In case
(2) there are three different sub-cases. In sub-case (1)
both tasks are allocated to agents able to handle de-
fined constraints, then a uniform random mechanism
is used to determine which of the tasks will be re-
allocated and which one will retain the previous allo-
cation. In sub-case (2) one of the tasks is allocated to
an agent that cannot fulfill task’s constraints. In that
case, the invalid task is allocated to the agent of the
task with valid constraints. In sub-case (3) both of the
tasks are allocated to agents that cannot fulfill their
constraints. In this case, a search is performed to find
if there is an agent available that can fulfill both of the
A1
T2
T5
T8
A2
T1
T7
A3
T9
T4
T6
A1
T2
T8
T5
A2
T1
T7
A3
T9
T4
T6
A1
T2
T5
T7
A4
T8
T7
A3
T9
T4
T6
A1
T2
T7
A4
T5
T8
T7
A3
T9
T4
T6
A1
T2
T5
T7
A2
T1
T8
A3
T9
T4
T6
A1
T2
T5
T7
T8
A2
T1
A3
T9
T4
T6
A1
T2
T1
T7
A2
T5
T9
A3
T8
T4
T6
A1
T5
T2
T1
T7
A2
T9
A3
T8
T4
T6
A1
T5
T2
T8
T1
T7
A2
T9
A3
T4
T6
case (1)
case (2); sub-case(1)
case (2); sub-case(2)
case (2); sub-case(3)
Figure 3: An example of the mechanism of PCR, showing
both cases and all three possible sub-cases of case (2).
tasks. If that agent exists, both tasks are re-allocated
to that agent. In every case, the location of the re-
allocated task within an agent is randomly determined
with respect to the PC. An example of aforementioned
cases is given in Fig. 3. Let’s assume that task T8 has
to be done after task T5. Only agents A1 and A4 have
the necessary equipment to fulfill these tasks. In case
(1) both tasks are allocated to the proper agent (A1)
and simple task swap is done. The first sub-case of
case(2) shows the problem when each task is allocated
to a different agent, however, both the A1 and A4 are
able to fulfill the allocated task. Options here are to
move either T8 to A1 after T5 or T7, or to move T5
to A4 before T8. In Fig. 3 the latter option is shown.
In the sub-case (2) of case (2) T8 is allocated to A2
and A2 does not meet the requirements of T8. The
solution is to move T8 to A1, either after T5 or T7.
In Fig. 3 the latter option is shown. The last sub-case
of case (2) shows a problem when both of the tasks
are allocated to the agents that do not meet the tasks’
requirements. In this case, first the pre-Task (task T5)
is re-allocated to A1. T5 can be allocated to any po-
sition in the A1’s plan. In Fig. 3 the 1st position is
chosen, right after gene A1. After this is done T8 is
re-allocated to A1. Possible options are after T5, T2,
T1 or T7. In Fig. 3 T8 is shown to be re-allocated
after T2. As already mentioned, when making a de-
cision of where to re-allocate certain task a uniform
random function is used.
4.2 Mutation
Mutation is the source of variability as it allows ge-
netic diversity in the population. Every individual has
a low probability to be selected for mutation. In this
paper, two types of mutation schemes are introduced.
One operates on the task genes through swapping
tasks and inserting new genes (Alg. 1), whereas the
other mutates agent genes through growing (adding
Algorithm 1: Task Swap/Insert Mutation.
1: procedure TASKMUTATION(population)
2: Select random chromosome i from the pop.
3: Select random task gene from i
4: case (1) - Task Swapping
5: Create a list of valid tasks for swapping
6: Choose a task gene randomly from that list
7: Swap tasks
8: case (2) - Task Insertion
9: Create a list of suitable agents for chosen task
10: Randomly select agent and position and insert
gene from step 3.
11: return modified chromosome
Extended Colored Traveling Salesperson for Modeling Multi-Agent Mission Planning Problems
241

Algorithm 2: Agent Growth/Shrink Mutation.
1: procedure AGENTMUTATION(population)
2: Select random chromosome i from the pop.
3: case (1) - Agent Growth
4: If there are available agents
5: Select random position to insert new agent
6: Validate that no constraint is violated
7: Add new agent
8: Check if new agent’s plan is valid
9: If not, reassign invalid tasks to other agents
10: case (2) - Agent Shrink
11: If the minimum is not reached
12: Select random agent gene for removal
13: Remove that gene
14: Reassign its tasks to other agents with the
respect to constraints
15: return modified chromosome
agents) and shrinking (removing agents) from the
chromosome as shown in (Alg. 2).
Task swap mutation swaps two task genes in a
chromosome, meaning that it can both swap tasks
within a single agent or between two agents. Insert
mutation chooses a task and inserts it in a new lo-
cation in a chromosome, same as in previously ex-
plained mutation, the insertion can be within the same
agent or different one.
Agent shrink mutation removes one agent from a
chromosome, reassigning its tasks to other agents if
possible (Alg. 2). If such action would cause an
invalid plan the action is skipped. For example, re-
moving the only agent from a plan or removing the
only agent with the required equipment for a specific
task. Growth agent mutation adds a new agent to the
plan if the limit of available agents is not reached in
that specific chromosome. The new agent gene is ran-
domly inserted, acquiring tasks from that location in
the chromosome up to the next agent gene or end of
the chromosome. If there are conflicting (a task not
supported by assigned agent) tasks, they are randomly
reassigned to other agents. Both algorithms take into
account color constraints ensuring that the mutation
process does not produce infeasible solutions.
4.3 Fitness Function
The fitness function evaluates the individuals, in the
population, by calculating a quantitative measure, i.e.,
fitness or cost. Depending on the design of the GA
and its operators, population might consist of both
feasible and infeasible or only feasible solutions.
In the first case, where operators are not bound to
always produce valid chromosomes, the fitness func-
tion has a penalty/award system in order to deal with
invalid chromosomes (Miloradovi
´
c et al., 2016). The
second approach, used in this paper, is to define vari-
ation operators in such a way only feasible solutions
can be produced. The former approach has the ad-
vantage of variation operators being simpler to imple-
ment, whereas in the latter approach the search space
is reduced.
In the fitness function, the candidate solution that
is being evaluated is first divided into agent’s plans,
i.e., sub-plans per each agent. Each plan is evaluated
separately and results are combined afterward to form
an overall chromosome fitness. The objective func-
tion that is being minimized is given in Eq. (11).
5 SIMULATION RESULTS
The proposed approach is tested in the use case of un-
derwater mission planning (SWARMs
3
project). In
order to ease the process of a mission preparation, a
special Mission Management Tool (MMT) is devel-
oped. This tool allows a human operator an intuitive
way of creating complex missions involving different
types of robots with non-overlapping abilities, e.g.,
due to different sensory modalities, and configura-
tions, as well as tasks. When the operator has pre-
pared the mission, it is translated into a formal model
(see Sect. 3) which is forwarded to the GMP (see
Sect. 4). After this step, the result is presented to the
operator on the map and with a Gantt chart.
The experimental platform was i5-7200U @
2.4GHz CPU with 8GB of DDR4 RAM. The GMP
is implemented in the C++ programming language.
Four different underwater scenarios are used for eval-
uating the proposed planning algorithm. Tasks can
have 3 different equipment requirements (colors)
(Camera, Sonar, and Salinity). All AUVs are hetero-
geneous. Each of the scenarios has a certain num-
ber of precedence constraints that need to be fulfilled.
The objective function (Eq. 11) is used with W
1
and
W
2
being 1 and 0.1, respectively. Complete scenario
settings are presented in Table 1. Due to the paper
length limitations, GA parameters will be given with-
out giving simulation results. A number of generation
was set to 5000, with a population consisting of 200
individuals. Crossover probability was 65%, mutation
probability was 10%, and elitism 20%. Three types of
crossover operator were tested—One Point, Partially
Mapped (PM), and Edge Recombination. Since re-
sults showed no statistically significant difference be-
tween them, all simulations including crossover oper-
ator were done with the PM crossover.
3
http://swarms.eu
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
242

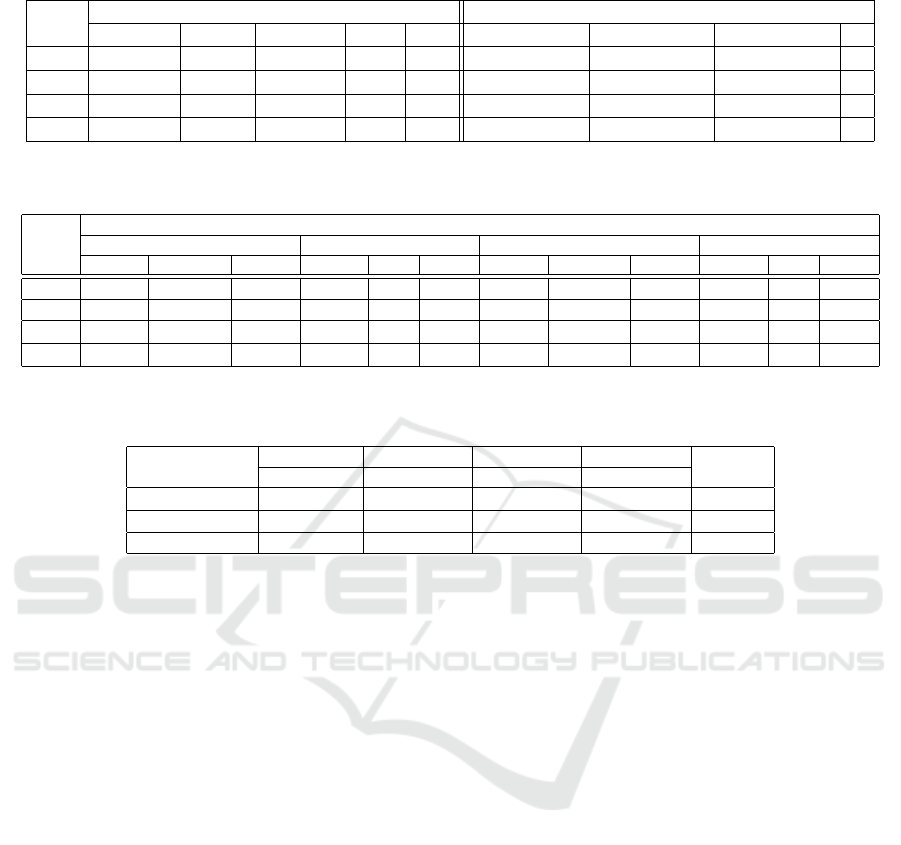
Table 1: Settings for different simulation scenarios.
Sim. Task’s settings AUV’s settings
Camera Sonar Salinity #PC # Camera Sonar Salinity #
1 4 3 3 3 10 AUV 2 AUV 1 AUV 1,2 2
2 7 6 6 5 19 AUV 2,3 AUV 1,3 AUV 1,2 3
3 17 16 16 10 49 AUV 2,3,4,5 AUV 1,3,4 AUV 1,2,4 5
4 33 27 40 14 100 AUV 2,3,4,5 AUV 1,3,4,6 AUV 1,2,4,7 7
*(Sim. - Simulation scenario; #PC - Number of precedence constraints; # - Total number of tasks (or AUVs) in a scenario)
Table 2: Simulation results for 4 different scenarios.
Sim. Different Variation Operators Settings
Mutation Mut. & PC X & Mut. X, Mut. & PC
mdn. std. best mdn. std. best mdn. std. best mdn. std. best
1 3041 0 3041 3041 0 3041 3041 0 3041 3041 0 3041
2 4231 278 4047 4047 37 4047 4202 252 4047 4047 41 4047
3 7793 1.4 · 10
5
6102 5871 280 5490 7761 1.7 · 10
5
6063 5956 252 5506
4 13795 3.1 · 10
5
10961 10738 550 9378 13331 2.8 · 10
5
10895 10797 594 9612
*(Mut. - Mutation; X - Crossover, PC - Precedence Constraint Reparation; mdn. - median; std. - standard deviation; best -
best solution found)
Table 3: Statistical tests of the gathered results from 4 different simulations using different variation operators settings.
Mut. & PC Scenario 1 Scenario 2 Scenario 3 Scenario 4 Critical
vs. p - value p - value p - value p - value value
Mutation 1 6.76 · 10
−26
8.77 · 10
−33
3.62 · 10
−33
0.0033
X & Mut. 1 2.03 · 10
−26
8.99 · 10
−32
5.50 · 10
−32
0.0067
X, Mut. & PC 1 0.0034 0.2350 0.2350 0.0100
Results of the planning process are shown in Table
2 for 4 different variation operator’s settings. All sce-
narios had 1 starting depot for all the vehicles, while
scenario 1 had 2 exit depots and each next scenario
had plus one exit depot, making it finally to 5 exit de-
pots in scenario 4. For every scenario, the algorithm
was run 100 times.
A series of statistical tests were conducted to see if
the null hypothesis: ”Using different variation oper-
ator settings makes no difference on the final result”
is true. It is assumed that the samples used in these
experiments are random and independent.
Since the sample data can be highly skewed and
have extended tails, an average of that data can pro-
duce a value that behaves non-intuitively, thus me-
dian was used instead of the mean. This means that
the non-parametric Mann-Whitney-Wilcoxon test is
used. Since multiple comparisons are performed,
Benjamini-Hochberg (B-H) procedure is applied in
order to adjust the false discovery rate. The B-H criti-
cal value is calculated as (i/m)· Q, where i is the rank,
m number of tests and Q false discovery rate set to
0.01. The variation operator settings that had the best
median value is compared to all other setups in all
4 scenarios. Since there is a statistically significant
difference between the results (Table 3), the null hy-
pothesis is rejected.
Results show that in every scenario, a mutation
with PC reparation algorithm produces equally good
or better results than other setups. From scenario 3
and 4, it can be concluded that a crossover operator is
not needed since it doesn’t help to improve the final
result. Moreover, in scenario 2, the use of crossover
leads to worse results than in the setup without it. Sce-
nario 1 is solved equally good with all tested variation
operators settings.
6 CONCLUSION
In this paper, the mission planning problem is mod-
eled as a novel variation of TSP, referred to as Ex-
tended Colored TSP. The problem formulation was
given in a form of an ILP problem in Sect. 3. It is
concluded that ECTSP can be applied to model dif-
ferent real-world problems in addition to being rele-
vant from a theoretical point of view. In this work,
GA is adapted to be used for ECTSP’s objective func-
tion optimization with a few improvements in varia-
tion operators in order to handle given constraints. As
demonstrated, the objective function presented in this
work is more suitable for the intended mission plan-
ning domain than other specific solutions found in the
literature. In addition, a precedence constraint repa-
Extended Colored Traveling Salesperson for Modeling Multi-Agent Mission Planning Problems
243

ration algorithm is presented. This algorithm makes
the use of crossover operator unnecessary, thus saving
valuable computation time, which is of major impor-
tance in the context of the population-based search.
Presented results show the usefulness of using GMP
for solving ECTSP.
ACKNOWLEDGEMENT
The research leading to the presented results has been
undertaken within the Smart and Networking Under-
water Robots in Cooperation Meshes (SWARMs) Eu-
ropean project, under Grant Agreement n. 662107-
SWARMs-ECSEL-2014-1, and Aggregate Farming
in the Cloud (AFarCloud) European project, with
project number 783221 (Call: H2020-ECSEL-2017-
2). Both projects are supported by ECSEL JU and the
VINNOVA. Special thanks to Afshin E. Ameri for de-
veloping GUI for the MMT.
REFERENCES
Alighanbari, M., Kuwata, Y., and How, J. P. (2003). Co-
ordination and control of multiple UAVs with timing
constraints and loitering. In ACC, pages 5311–5316.
Baker, B. M. and Ayechew, M. A. (2003). A genetic algo-
rithm for the vehicle routing problem. Computers and
Operations Research, 30(5):787 – 800.
Bektas, T. (2006). The multiple traveling salesman prob-
lem: an overview of formulations and solution proce-
dures. Omega, 34(3):209–219.
Bello-Orgaz, G., Ramirez-Atencia, C., Fradera-Gil, J., and
Camacho, D. (2016). GAMPP: Genetic algorithm for
uav mission planning problems. In Intelligent Dis-
tributed Computing IX, pages 167–176.
Brie, A. H. and Morignot, P. (2005). Genetic planning using
variable length chromosomes. In ICAPS, pages 320–
329.
Cristian, R.-A., Javier, D. S., and David, C. (2018).
Weighted strategies to guide a multi-objective evo-
lutionary algorithm for multi-UAV mission planning.
Swarm and Evolutionary Computation.
Dantzig, G., Fulkerson, R., and Johnson, S. (1954). Solu-
tion of a large-scale traveling-salesman problem. JS-
TOR, 2(4):393–410.
Gerkey, B. P. and Matari
´
c, M. J. (2004). A formal analysis
and taxonomy of task allocation in multi-robot sys-
tems. The International Journal of Robotics Research,
23(9):939–954.
Giardini, G. and Kalm
´
ar-Nagy, T. (2011). Genetic algo-
rithm for combinatorial path planning: The subtour
problem. Mathematical Problems in Engineering.
Holland, J. H. (1992). Genetic algorithms. Scientific amer-
ican, 267(1):66–73.
Keld, H. (2009). An effective implementation of k-opt
moves for the lin-kernighan tsp heuristic. Mathemati-
cal Programming Computation, 1:119–163.
Korsah, G. A., Stentz, A., and Dias, M. B. (2013). A
comprehensive taxonomy for multi-robot task alloca-
tion. The International Journal of Robotics Research,
32(12):1495–1512.
Kubo, M. and Kasugai, H. (1991). The precedence con-
strained traveling salesman problem. Journal of the
Operations Research Society of Japan, 34:152–172.
Landa-Torres, I., Manjarres, D., Bilbao, S., and Del Ser,
J. (2017). Underwater Robot Task Planning Using
Multi-Objective Meta-Heuristics. Sensors, 17(4):762.
Li, J., Zhou, M., Sun, Q., Dai, X., and Yu, X. (2015). Col-
ored traveling salesman problem. IEEE Trans. on Cy-
bernetics, 45(11):2390–2401.
Maoudj, A., Bouzouia, B., Hentout, A., and Toumi, R.
(2015). Multi-agent approach for task allocation and
scheduling in cooperative heterogeneous multi-robot
team: Simulation results. In IEEE Int. Conf. on Indus-
trial Informatics (INDIN), pages 179–184.
Meng, X., Li, J., Dai, X., and Dou, J. (2018). Variable
Neighborhood Search for a Colored Traveling Sales-
man Problem. IEEE Trans. on Int. Transp. Systems,
19(4):1018–1026.
Miloradovi
´
c, B., C¸
¨
ur
¨
ukl
¨
u, B., and Ekstr
¨
om, M. (2016). A
genetic planner for mission planning of cooperative
agents in an underwater environment. In IEEE Sym-
posium Series on Computational Intelligence (SSCI),
pages 1–8.
Miloradovi
´
c, B., C¸
¨
ur
¨
ukl
¨
u, B., and Ekstr
¨
om, M. (2017). A
genetic mission planner for solving temporal multi-
agent problems with concurrent tasks. Lecture Notes
in Computer Science, 10386 LNCS:481–493.
Nisha, B. and Nathi Ram, C. (2015). Genetic algorithm
applications on Job Shop Scheduling Problem: A re-
view. In ICSCTI, pages 7–14.
Nunes, E., Manner, M., Mitiche, H., and Gini, M. (2017). A
taxonomy for task allocation problems with temporal
and ordering constraints. Robotics and Autonomous
Systems, 90:55–70.
Ramirez-Atencia, C., R-Moreno, M. D., and Camacho, D.
(2017a). Handling swarm of UAVs based on evolu-
tionary multi-objective optimization. Progress in Ar-
tificial Intelligence, 6(3):263–274.
Ramirez-Atencia, C., Rodriguez-Fernandez, V., Gonzalez-
Pardo, A., and Camacho, D. (2017b). New artificial
intelligence approaches for future UAV ground con-
trol stations. In CEC, number June, pages 2775–2782.
Yuichi, N. and Shigenobu, K. (2013). A powerful genetic
algorithm using edge assembly crossover for the trav-
eling salesman problem. Informs Journal on Comput-
ing, 25:346–363.
Zhong, W. (2014). Multiple Traveling Salesman Prob-
lem with Precedence Constraints Based on Modi-
fied Dynamic Tabu Artificial Bee Colony Algorithm.
Journal of Information and Computational Science,
11(4):1225–1232.
Zhou, X., Wang, W., Wang, T., Li, X., and Li, Z. (2017). A
research framework on mission planning of the UAV
swarm. In System of Systems Engineering Conf.
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
244