
A Stochastic Optimization Approach of Flow Shop Sequencing
Problem for On-time Delivery of Precast Components
Mohamed Mamdouh Yusuf
1
, Ahmed Karam
2
and Amr B. Eltawil
1
1
Industrial Engineering and Systems Management, Egypt-Japan University of Science and Technology (E-JUST),
PO box 179, New Borg Elarab City, Alexandria 21934, Egypt
2
Mechanical Engineering Department, Faculty of Engineering at Shoubra, Benha University, 108, Cairo, Egypt
Keywords: Precast Industry, Discrete Event Simulation, Flow Shop Sequencing, Stochastic Processing Times,
Simulation-based Optimization, Optquest
®
for Arena
®
.
Abstract: Recently, the flow shop sequencing problem in precast plants has been witnessing remarkable interest from
many researchers. This paper contributes to recent literature by providing a simulation-based optimization
approach to solve the precast flow shop sequencing problem taking into account the uncertainty of processing
times of precast production operations. The proposed approach is developed by integrating a Discrete Event
Simulation (DES) model, which is built to capture the realistic features of precast production activities, and
OptQuest
®
to find the optimum sequencing of Precast Components (PCs). The proposed approach is validated
against another approach from literature. In addition, its practicability is put to the test by applying the
proposed approach to a real case study. The obtained results indicated that pre-casters can use this approach
to attain better PCs sequences than that based on a rule of thumb.
1 INTRODUCTION
Precasting is a kind of industrialized building system
which refers to the process of shifting some
construction operations from the field to off-site
workshops, where construction components can be
produced with higher quality, in less time, lower
prices and in a leaner and greener way than the
traditional construction practice (Sacks et al., 2004).
By virtue of their advantages, Precast Components
(PCs) were used by 56% of construction projects in
Finland, and by 28% in Germany, 26% in Britain, and
about 20% in Spain (Sacks et al., 2004).
However, the precast industry faces many
challenges which can be cushioned by proper
management of its multi-echelon supply chain,
starting from material supplying and ending with
installation at construction sites (Wang et al., 2018b).
This paper focuses only on production scheduling in
precast plants where production managers shoulder
ordering of PCs to be processed through a number of
sequential operations to ensure on-time delivery of
PCs to the construction sites. So, it is a typical
flowshop sequencing problem. Early delivery of PCs
leads to higher inventory costs and double handling
of PCs at the construction site. However, lateness of
PCs causes higher direct and indirect costs due to
project delay. The problem is worsened by the fact
that each type of PC has different processing times on
the different production operations, and the managers
only depend on know-how and hands on experience
to tackle this problem, which in turn leads to
suboptimal PCs sequences (Wang et al., 2018a). So,
there exists a need to provide the production
managers with a decision support tool to help them in
scheduling of PC production efficiently in order to
meet due dates and maximize resource utilization to
achieve satisfactory return on investment.
until now, a plethora of researchers addressed the
precast production scheduling problem by using
different techniques such as mathematical
programming methods and simulation models. Most
of these studies considered the processing times of PC
production operations as deterministic times.
Recently, the stochastic nature of precast processing
times was claimed to be considered in the precast
flow shop sequencing problem only by (Wang et al.,
2018a). They developped a two-phase sequential
approach which firstly generates near optimal PCs
schedules obtained by a Genetic Algorithm (GA), and
then a DES model is used to evaluate performance of
these PCs schedules under stochastic processing
Yusuf, M., Karam, A. and Eltawil, A.
A Stochastic Optimization Approach of Flow Shop Sequencing Problem for On-time Delivery of Precast Components.
DOI: 10.5220/0007309602450252
In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 245-252
ISBN: 978-989-758-352-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
245

times. In other words, it is a simulation based
evaluation approach which does not guarantee full
integration between simulation and optimization, as
explicitly mentioned by (Wang et al., 2018a). To
improve, this paper presents a simulation-based
optimization approach to obtain optimum PCs
production schedules with consideration of the
stochastic nature of the problem to achieve just in
time delivery of PCs. In doing so, a DES model is
integrated with an optimization module. After
verification and validation of the proposed approach,
it is used to find the near optimum PCs production
schedules in a real case study.
The rest of the paper is organized as follows,
previous studies of precast production planning are
reviewed and related research gaps are identified in
section 2. Section 3 illustrates the operations to
produce and deliver PCs to construction sites while
section 4 provides a detailed explanation of the
developed simulation-based optimization approach.
Numerical experiments are elaborated in section 5.
Finally, conclusions are discussed in section 6.
2 LITERATURE REVIEW
The literature on precast production planning is
plentiful, and previous researchers dealt with it by
using either mathematical programming methods or
discrete event simulation models as will be illustrated
later in sections 2.1 and 2.2, respectively. Finally,
research gaps are identified in section 2.3.
2.1 Precast Production Scheduling
using Mathematical Programming
Despite that literature is riddled with many studies on
production scheduling (Yenisey and Yagmahan,
2014), these studies did not fit the precast production
scheduling problem (Chan and Hu, 2001). So,
numerous academics are avid for solving this problem
by means of mathematical modeling. (Chan and Hu,
2001) was the first to model the precast sequencing
problem as a flow shop sequencing problem with the
objective of minimizing the makespan or Tardiness
and Earliness (T&E) penalty cost. They made it more
realistic by distinguishing between daily working and
non-working hours, and classifying production
activities into interruptible or uninterruptible and
sequential or parallel activities, as will be illustrated
in section 3. Their model was deemed to be a
stepping-stone because subsequent researchers
enhanced it by considering ignored resources or
adding other objectives. For example, moulds were
considered by the same authors in (Chan and Hu,
2002), however, the competition between PCs on
limited moulds was simulated by (Benjaoran et al.,
2005) who calculated the PC waiting times due to
mould scarcity; they used a multi-objective function
to minimize the total flow time, machine idle time and
T&E penalty cost. Moreover, mould planning was
addressed carefully by (Hu, 2007), who sought for
minimizing the number of required moulds and
levelling its usage. To improve the models, the buffer
capacity between production processes as a limited
resource was added by (Ko and Wang, 2011), who
used a multi-objective function to minimize the
makespan and T&E penalty cost. By the same token,
(Yang et al., 2016) not only considered the previous
resources but also included pallets, capacity of the
curing chamber and the number of production lines to
the model. Their objective was to reduce idle time,
T&E penalty cost, inventory cost, makespan and PC
changeover, simultaneously. Recently, (Wang and
Hu, 2017) expanded this model by including three
ignored stages in the precast supply chain which are,
mould manufacturing, storage and transportation to
construction sites, with the objective of cutting T&E
penalty costs.
With respect to the applied optimization
algorithm, a Genetic Algorithm (GA) was used in the
previous studies, by virtue of its performance to find
near-optimal solution for such nondeterministic
polynomial (NP)-hard problems, except (Chan and
Hu, 2002) who applied constrained programming
method.
2.2 Discrete Event Simulation-based
Approaches Applied to Precast
Production
Simulation modelling is preferred over mathematical
modelling in analysing large problems of real and
complex systems characterized with uncertainty
(Law, 2007). Moreover, the ability to conduct
different scenarios and check their performance is
another advantage over analytical methods (Law,
2007). This fact conduced to the adoption of
simulation modelling to tackle precast production
planning issues in many studies. Based on the purpose
of using simulation, these studies can be categorized
into two types: studies applied simulation based
evaluation approach and others used simulation based
optimization approach.
In the first type, simulation models were used to
evaluate some predetermined scenarios and as a result
a conclusion can be drawn according to the purpose
of study. For instance, (Chen et al., 2016) used a DES
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
246

model, as an evaluation tool, to validate the
advantages of a proposed precast production method
over the traditional one in terms of minimizing the
makespan and maximizing resource utilization. A
DES model was used by (Wang et al., 2018a) to
compare between ten PCs production schedules pre-
generated by optimizing a mathematical model using
GA. The same authors enhanced their model to
simulate different risks which disturb the precast
supply chain, (Wang et al., 2018b). By using an
applied simulation based evaluation approach, they
prioritized the identified risks based on their
detrimental impact.
In the second type of these studies, the researchers
fully integrated simulation with search techniques, to
generate a new set of solutions after evaluating an
objective function defined in the simulation model.
This process continues until a predefined stopping
criteria is met. For example, (Cheng and Yan, 2009)
coupled a messy GA and CYCLic Operation
NEtwork (CYCLONE), a simulation language, to
search for optimum resource allocation in order to
both minimize hiring cost and maximize production
rate of a precast plant. Different kinds of production
resources were simulated in this study such as molds,
labors, trucks, cranes, hydraulic jacks and truck
mixers. Also, (Al-Bazi and Dawood, 2018) integrated
GA and simulated annealing, respectively with
Arena
®
simulation model; the purpose was to find the
optimum allocation of multi skilled labors in a precast
plant with the objective of reducing crew allocation
costs. Arena
®
is a simulation software enables both
discrete and continuous simulation simultaneously.
Moreover, (Arashpour et al., 2016) used Tabu search
and Arena
®
model to meet contracted due dates of
PCs by finding the optimum PCs production sequence
while considering multi-skilled resources and wasted
time due to switching from one PC type to another.
However, the realistic nature of the precast
production activities, identified by (Chan and Hu,
2001) and mentioned in section 2.1, was not
considered in their model.
2.3 Research Gaps
After reviewing the aforementioned studies, some
research gaps can be deduced and discussed along the
following fronts.
Despite the superiority of simulation modelling
over mathematical modelling in capturing the
characteristics of complex systems and incorporating
uncertainty, precast production planning issues
addressed by using mathematical models were more
diverse than that addressed by simulation models. So,
a research gap needs to be filled by applying
simulation modelling not only to consider uncertainty
but also to regard other important factors in the
precast industry such as inventory management,
logistics, multiple production lines, buffer space
between workstation, materials supply, coordination
with contractors at construction sites, risk
management, incorporation of valuable assets such as
trucks, cranes and steamers.
In addition to that, the realistic nature of precast
production activities was simulated only by (Wang et
al., 2018a), who built their model based on the
mathematical formulation illustrated in (Chan and
Hu, 2001) and (Wang and Hu, 2017). This
formulation does not reflect other realistic conditions
in precast production such as waiting time due to
shared resources like moulds, cranes and multi-
skilled labours, hiring additional crews at each
process, limited capacity of curing and storing
processes, limited production space between
processes and specifying failure data for each type of
production resources. So, there exists a need to
develop a more general model to enable practitioners
to experience the different production conditions
without the need to reformulate the mathematical
model to suit each condition.
Besides, reviewing the studies in section 2.2
shows that researchers used only metaheuristics in
their simulation based optimization methodology due
to their advantages. However, other simulation
optimization methods may be more beneficial than
metaheuristics to deal with noisy functions and
correlated decision variables in case of applying
cross-entropy methods, or to reduce computational
time by using the Response Surface Methodology
(RSM) which will be of great importance in case of
more complex models of precast production planning
in the future. In a similar vein, commercial
optimization toolboxes can be used due to its
capability, credibility and usability.
To bridge these gaps, this paper is intended to
develop a more general simulation model to reflect
the nature of precast production activities without the
need to use case dependent mathematical equations.
This model is linked with an optimizer to solve the
precast flow shop sequencing problem with
considering uncertainty in processing times of precast
production activities.
A Stochastic Optimization Approach of Flow Shop Sequencing Problem for On-time Delivery of Precast Components
247

3 DESCRIPTION OF THE
PRECAST PRODUCTION
PROCESS
To be ready for installation on the construction site,
PCs have to be processed through nine sequential
operations (from M1 to M9), (Wang and Hu, 2017).
M1- Mould manufacturing: Due to lack of
standardization, pre-casters may receive PC orders
inconsistent with their own moulds. If that is the case,
new moulds should be manufactured.
M2- Mould assembling: assemblers have to prepare
moulds by fastening, cleaning and oiling its sides to
ensure smooth PCs surface and effortless
demoulding.
M3- Reinforcement setting: reinforcement and other
predetermined parts are placed in their locations
according to shop drawings.
M4- Casting: ready mix concrete is poured,
compacted and levelled.
M5- Curing: PCs are either transferred to the steam
curing chamber or covered by water proof membrane,
to ensure its strength development and durability.
M6- Demoulding: stripping moulds and extracting
PCs.
M7- Finishing and repairing: after taking out PCs,
they should be checked and any imperfections have
to be fixed.
M8- Storing: the PCs are stored at the stockyard to
ensure delivery strength.
M9- Transportation: in this process, the PCs are
transferred to the construction sites by using trucks.
These nine processes can be classified into
interruptible and sequential (M1, M2, M3, M6 and
M7), uninterruptible and sequential (M4),
uninterruptible and parallel activities (M5, M8 and
M9), (Wang and Hu, 2017). With respect to
interruptible activities, it is not permitted that
working on the PCs exceeds an allowable working
time denoted by H
w
. If working on a PC needs time
beyond H
w
, it will be continued on the next day, as
shown in Figure 1.a. However, in case of
uninterruptible activities, labors are allowed to work
overtime hours denoted by H
A
if they can finish
working on a PC. If they cannot, the whole working
on this PC is delayed to the next day, as shown in
Figure 1.b. In parallel activities, more than one PC
can be processed, simultaneously. On the contrary,
only one PC can be processed in sequential activities.
Moreover, PC curing and storing can be extended
overnight in case of requiring time beyond H
w
in
contrast to transportation activity, as shown in
Figures 2.c and 2.d, respectively.
4 THE PROPOSED
SIMULATION-BASED
OPTIMIZATION APPROACH
The proposed approach is based on iterative
interaction between a DES model and OptQuest
®
which is a commercial optimization software fully
integrated with Arena
®
. The integration mechanism is
as follows: OptQuest
®
finds trial schedules for the
simulation model. The quality of the schedules is
evaluated through running the simulation model. The
evaluation of the schedules is feedback to OptQuest
®
in order to search for new trial schedules. Once, a
termination condition is held true, the iterative
process is stopped and the best schedule is output. In
Figure 1: Completion Time (CT) in different classes of precast production activities.
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
248
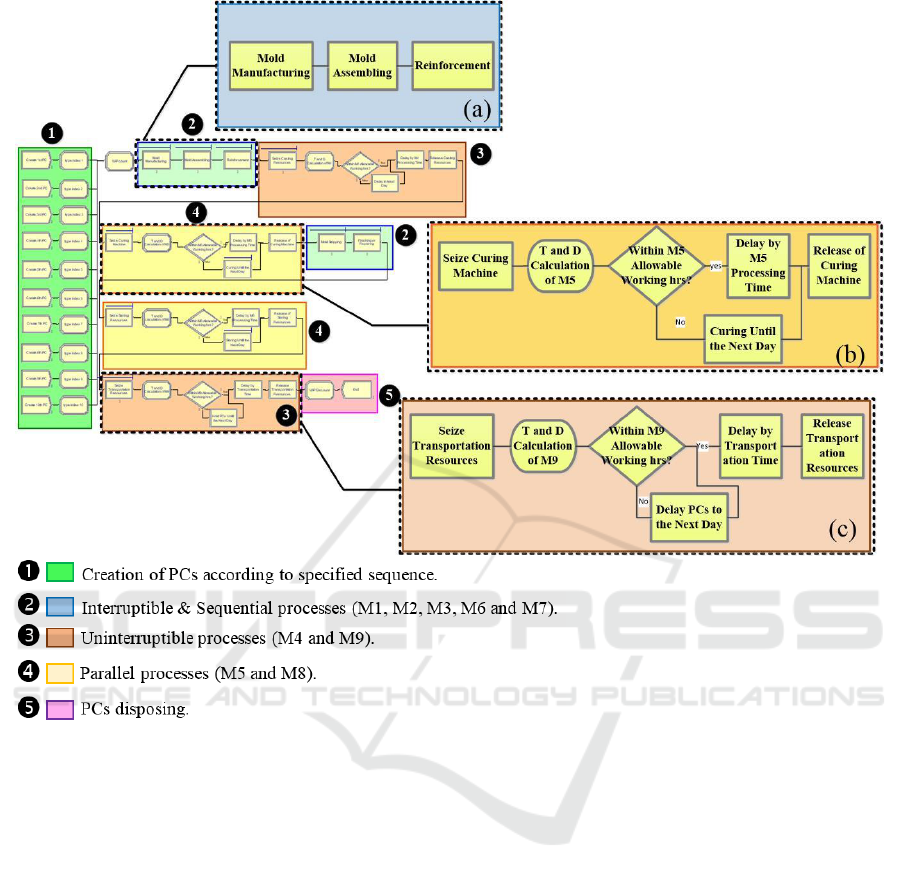
the following sections, the simulation model and the
optimization procedure are described in detail.
4.1 The Simulation Model of the
Precast Production Activities
The realistic nature of each precast production
activity is simulated in a more general model than that
of (Wang et al., 2018a), as shown in Figure 2. For
instance, interruptible and sequential activities such
as mold manufacturing (M1), mold assembling (M2),
reinforcement (M3), mold stripping (M6) and
finishing/repairing (M7) can be modeled by using
only Arena
®
’s “Process” modules, as shown in Figure
2.a, and identify a resource schedule with unit
capacity and “Preempt Rule”, available during
normal working hours (H
w
). Regarding the parallel
activities (curing M5 and storing M8) and the
uninterruptible activity (casting M4), they are
modeled by using “Seize”, “Delay” and “Release”
modules, as shown in Figures 3.b and 3.c. After
seizing the respective resources, the completion time
of each PC until this stage must be examined to decide
whether this PC can be processed during the
remaining hours of a typical working day (normal
working hours (H
w
) for M5 and M8; normal working
hours (H
w
) + allowable overtime (H
A
) for M4). If it is
not the case, the PC is delayed to the next day for the
casting process, as shown in Figure 2.c. As for the
curing or storing processes, the PC is left in the curing
machine or the storage yard until the next day, as
depicted in Figure 2.b. The resources’ schedules with
unlimited capacity during 24 hours are identified for
the M5 and M8 processes, but only a unit resource
Figure 2: Arena simulation model of precast workshop; (a) The representation of the interruptible and sequential activity
by using Arena
®
’s “Process” module; (b) The representation of the parallel activity by using Arena
®
’s “Seize”, “Decide”,
“Delay” and “Release” modules; (c) The representation of the uninterruptible activity by using Arena
®
’s “Seize”, “Decide”,
“Delay” and “Release” modules.
A Stochastic Optimization Approach of Flow Shop Sequencing Problem for On-time Delivery of Precast Components
249

capacity is available during (H
W
+ H
A
) hours for the
M4 process. It is worth mentioning that all the
scheduling rules are set to “Preempt” for all activity
types. Finally, the transportation process (M9) is an
uninterruptible activity with unlimited capacity.
The developed simulation model is built on some
assumptions illustrated through the following points:
1- Every PC has to be processed throughout all of the
operations starting from mold manufacturing (M1)
and ending with transportation (M9).
2- It is not possible that a PC is processed on more
than one operation simultaneously.
3- Every process can work only on one PC within a
time period except curing (M5) and storing (M8)
which have an unlimited capacity.
4- Rescheduling of PCs is not allowable. In other
words, the PCs processing sequence will not be
manipulated until the exit of the last PC even if it
could improve objective function.
5- The considered resources are the molds and labors
only, and there are no shared resources. To clarify,
each process has its own crew and each PC has its
specific mold.
6- The storing and transportation processes (M8 and
M9) are considered under daytime scenario, as
illustrated in (Wang and Hu, 2017).
7- Ramifications of resources breakdown are not
taken into consideration.
8- First-In-First-Out (FIFO) is adopted as a priority
rule at each task.
4.2 The Optquest® Optimization
Module
OptQuest
®
depends mainly on scatter search, and
Tabu search as a secondary algorithm. In addition, it
uses neural network to speed up searching process.
By using these techniques, OptQuest
®
establishes a
new set of decision variables after evaluating value of
objective function retrieved from Arena
®
simulation
model (Bradley, 2007). This process is iterated in a
cyclic manner until a predefined stopping criteria is
achieved; more details on how it works can be found
in (Laguna and Marti, 2003). In order to commence
the optimization process, decision variables,
constraints and objective function need to be
identified to OptQuest
®
. As for the constraints, they
are formulated to guarantee that each PC has a unique
ordering. For more clarification, suppose that there a
number of PCs and each PC must be processed with
a sequence number where . We define
a bianry variable,
which is one if the PC , where
, is processed in
th
order and zero
otherwise.
(1)
Constraint set (1) ensures that in any
th
order, one
and only one PC is processed.
(2)
Constraint set (2) ensures that each PC must be
processed in only one
th
order.
OptQuest
®
generates new sets of feasible
sequences of PCs after evaluating the objective
function though running the simulation model. The
objective function aims at minimizing tardiness and
earliness penalty cost, as defined in equation (3).
(3)
Where
is the total tardiness and earliness
penalty costs for PCs of sequence of precast
components ;
is completion time of each PC at
the last process;
is contracted due date for each PC
;
and
are tardiness and earliness penalties for
each PC .
5 NUMERICAL EXPERIMENTS
In this section, numerical experiments are carried out
to investigate the performance of the proposed
approach. Firstly, section 5.1 shows the validation of
the proposed approach by making a comparison with
an approach existing in literature. In section 5.2, the
proposed approach is applied to a case study.
5.1 Validation of the Proposed
Approach
The developed approach was validated by comparing
its results with that provided by (Chan and Hu, 2001).
In their work, they proposed a GA to solve the precast
flow shop sequencing problem. The objective was to
minimize makespan by sequencing six PCs on six
operations, starting from mold assembling (M2) and
ending with finishing/repairing (M7), and compared
their results with heuristic rules from literature. In
order to compare our approach with the approach of
(Chan and Hu, 2001), we modified our objective
function into theirs and also, we conducted a purely
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
250
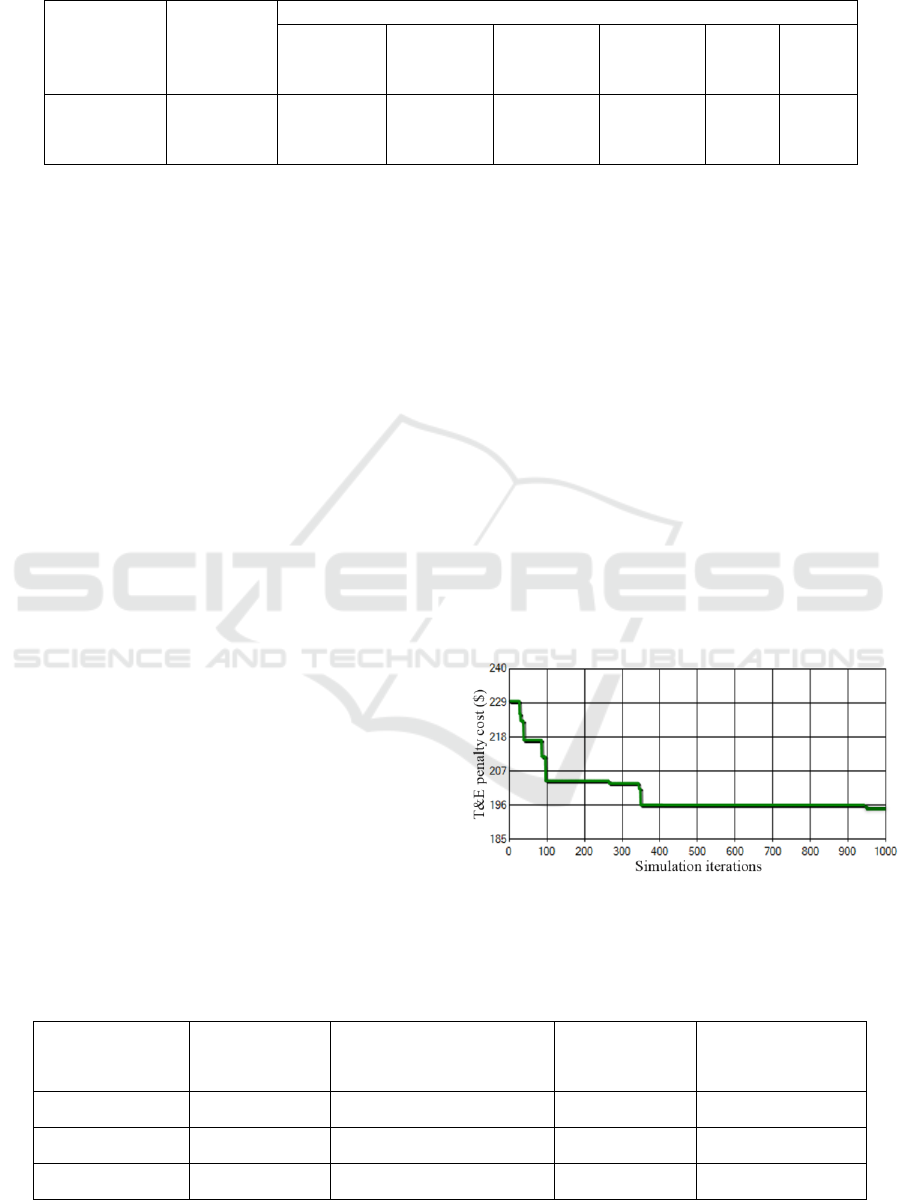
Table 1: Comparison of our approach with the results reported by (Chan and Hu, 2001).
deterministic run of our approach by considering the
deterministic times as in the work of (Chan and Hu,
2001). In other words, their example is replicated by
using the proposed approach and a comparison is
made between the results, as shown in Table 1. It can
be noticed that the proposed approach could obtain
optimal solution that is as good as that provided by
the GA proposed by (Chan and Hu, 2001). In
addition, the optimal solution of the proposed
approach outperforms the other heuristic rules.
5.2 Case Study
The purpose of this section is to test the performance
of the proposed approach within a realistic problem
taken from literature (Wang et al., 2018a). In this case
study, it was required to order ten PCs on nine
processes (from M1 to M9) with the objective of
minimizing T&E penalty costs. Since the processing
times of the production operations are stochastic (the
processing times obey triangular distribution), ten
replications are used based on preliminary analysis to
achieve reasonable half-width of the 95% confidence
intervals of the resulted penalty cost. Before starting
the optimization process, the initial solution is
selected to be 7-9-2-5-4-10-8-6-3-1. This solution is
based on a heuristic rule often used by pre-casters in
reality, (Chan and Hu, 2001). The penalty cost that
resulted from applying this heuristic sequence is
229.6$. Table 2 lists the optimum solutions of the
case study obtained by applying the proposed
approach under different number of simulation
iterations, accompanied by the average penalty costs
and the half-width of the 95% confidence intervals.
These simulation experiments were conducted by
using a laptop with Intel(R) Core(TM) i7-6500U 2.50
GHz processor, 8.00 GB of RAM and running a
Windows 10 Education 64-bit operating system.
Obviously, the adoption of the proposed approach can
lead to better PCs production sequences than that
based on the heuristic rule. Interestingly, the proposed
approach took only four minutes to provide a PC pro-
duction sequence (sequence obtained after 100
iterations) that saves about 11% of penalty costs in
comparison with the heuristic sequence, which in turn
proves the practicability of the proposed approach in
case of making such urgent operational decisions like
PCs sequencing. Figure 3 shows the fast convergence
of the proposed approach after 1000 simulation
iterations. This figure indicates that the penalty cost
was plunged during the first hundred iterations and
there was no improvement in the objective function
after 400th iteration.
Figure 3: Convergence of the proposed approach to solve
the case study.
Objective
function
The
proposed
approach
Heuristic algorithms used in (Chan and Hu, 2001)
Palmer’s
heuristic
Gupta’s
heuristic
CDS
heuristic
RA
heuristic
EDD
rule
GA
Minimize
Makespan
(Hours)
48.5
50.6
50
50
49.4
51
48.5
Table 2: Results of the case study after applying the proposed approach.
No. of
simulation
iterations
Solution time
(Min)
Optimum PCs sequence
Average
penalty cost
($)
Half-width
penalty cost ($)
1000
32
3-2-9-7-4-5-10-8-6-1
195.2
1.35
500
16
2-1-9-7-4-5-8-10-3-6
196
0.17
100
4
1-9-2-4-7-5-8-10-3-6
203.9
0.22
A Stochastic Optimization Approach of Flow Shop Sequencing Problem for On-time Delivery of Precast Components
251

6 CONCLUSION
Previous studies addressed precast production
planning by using either mathematical programming
methods or simulation models. However, the
uncertainty of processing times when determining
optimum PCs schedules to achieve on-time delivery
of PCs was seldom addressed. To fill this gap, a
simulation-based optimization approach is developed
in which a discrete event simulation model was
developed by using Arena
®
software based on precast
flow shop sequencing formulation. Then, the
developed model is linked with OptQuest
®
(an
optimization package) to search for optimum PCs
sequences that minimize deviation from the
contracted due dates of PCs. Thereafter, the proposed
approach was validated by comparing its results with
a published approach from literature. To test its
practicality, the developed approach was applied on a
case study with the objective of minimizing the
tardiness and earliness penalty costs. The obtained
results indicated that the optimum sequence can save
about 15% of penalty costs in comparison with the
results of a heuristic rule.
In future work, multi-objective function to
minimize both the penalty cost and production costs
can be applied while considering other realistic
features of the precast production such as buffer space
between production stages and multiple production
lines. However, the computation time will be longer
due to the complexity of the simulation model. This
might call for using other simulation optimization
methods such as the response surface methodology to
reduce the time needed to make urgent operational
decisions in precast plants such as PCs sequencing.
REFERENCES
Al-Bazi, A., and Dawood, N., 2018. Simulation-based
optimisation using simulated annealing for crew
allocation in the precast industry. Architectural
Engineering and Design Management, 14(1–2), 109–
126. https://doi.org/10.1080/17452007.2017.1313721
Arashpour, M., Wakefield, R., Abbasi, B., Lee, E. W. M.,
and Minas, J., 2016. Off-site construction optimization:
Sequencing multiple job classes with time constraints.
Automation in Construction, 71(Part 2), 262–270.
https://doi.org/10.1016/j.autcon.2016.08.001
Benjaoran, V., Dawood, N., and Hobbs, B., 2005. Flowshop
scheduling model for bespoke precast concrete
production planning. Construction Management and
Economics, 23(1), 93–105.
https://doi.org/10.1080/0144619042000287732
Bradley, A., 2007. OptQuest for Arena User’s Guide. RS
Inc., Ed., Ed.
Chan, W.-T., and Hu, H., 2001. An application of genetic
algorithms to precast production scheduling.
Computers and Structures, 79(17), 1605–1616.
Chan, W. T., and Hu, H., 2002. Constraint programming
approach to precast production scheduling. Journal of
Construction Engineering and Management, 128(6),
513–521.
Chen, J. H., Yang, L. R., and Tai, H. W., 2016. Process
reengineering and improvement for building precast
production. Automation in Construction, 68, 249–258.
https://doi.org/10.1016/j.autcon.2016.05.015
Cheng, T. M., and Yan, R. Z., 2009. Integrating messy
genetic algorithms and simulation to optimize resource
utilization. Computer-Aided Civil and Infrastructure
Engineering, 24(6), 401–415.
https://doi.org/10.1111/j.1467-8667.2008.00588.x
Hu, H., 2007. A study of resource planning for precast
production. Architectural Science Review, 50(2), 106–
114. https://doi.org/10.3763/asre.2007.5016
Ko, C. H., and Wang, S. F., 2011. Precast production
scheduling using multi-objective genetic algorithms.
Expert Systems with Applications, 38(7), 8293–8302.
https://doi.org/10.1016/j.eswa.2011.01.013
Laguna, M., and Marti, R., 2003. The OptQuest callable
library. In Optimization Software Class Libraries (pp.
193–218). Springer.
Law, A. M., 2007. Simulation modeling and analysis,
McGraw-Hill New York, 4
th
edition.
Sacks, R., Eastman, C. M., and Lee, G., 2004. Process
model perspectives on management and engineering
procedures in the precast/prestressed concrete industry.
Journal of Construction Engineering and Management,
130(2), 206–215.
Wang, Z., and Hu, H., 2017. Improved Precast Production
– Scheduling Model Considering the Whole Supply
Chain. Journal of Computing in Civil Engineering,
31(4), 1–12. https://doi.org/10.1061/(ASCE)CP.1943-
5487.0000667.
Wang, Z., Hu, H., and Gong, J., 2018a. Framework for
modeling operational uncertainty to optimize offsite
production scheduling of precast components.
Automation in Construction, 86(April 2017), 69–80.
https://doi.org/10.1016/j.autcon.2017.10.026
Wang, Z., Hu, H., and Gong, J., 2018b. Simulation based
multiple disturbances evaluation in the precast supply
chain for improved disturbance prevention. Journal of
Cleaner Production, 177(March), 232–244.
https://doi.org/10.1016/j.jclepro.2017.12.188
Yang, Z., Ma, Z., and Wu, S., 2016. Optimized flowshop
scheduling of multiple production lines for precast
production. Automation in Construction, 72, 321–329.
https://doi.org/10.1016/j.autcon.2016.08.021
Yenisey, M. M., and Yagmahan, B., 2014. Multi-objective
permutation flow shop scheduling problem: Literature
review, classification and current trends. Omega, 45,
119–135.
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
252
