
An Investigation on the Data Mining to Develop Smart Tire
Jae-Cheon Lee
1
, Hao Liu
1
, Young Gi Seo
2
, Seong Woo Kwak
2
, Ho Seung Lee
1
, Hae Jun Jo
1
and
Sangsu Park
2
1
Department of Mechanical and Automotive Engineering, Keimyung University, 1095 Dalgubeol-daero, Daegu, S. Korea
2
Department of Electronic and Electrical Engineering, Keimyung University, 1095 Dalgubeol-daero, Daegu, S. Korea
Keywords: Data Mining, Smart Tire, Tire Built-in Sensor, Strain Gage, Tire Deformation Value, Vehicle Load.
Abstract: A smart tire is required to improve driving safety for an intelligent vehicle especially for automated driving
electric vehicles. It is necessary to provide information of tire contact forces (vertical, longitudinal, and lateral
directions) to control velocity and steering angle of the autonomous vehicle so as to ensure driving stability.
This study presents a smart tire system with the data mining to estimate the vertical load by using the tire
deformation data in particular. Firstly, the hardware system construction of the smart tire in which tire
deformation on driving by using strain gauge is described. And then the test condition is set up and total 27
sets of experimental data are processed to perform correlation analysis for specifications of measured waves.
Next, the estimation algorithm of smart tire vertical load is derived by considering the area of tire-ground
contact patch and also by introducing compensate coefficient of transverse direction length of contact area.
The experimental results show the proposed estimation algorithm is feasible and precise. The advanced
adaptive and precise estimation algorithm with artificial neural network will be developed further.
1 INTRODUCTION
As the fourth industrial revolution approaches, the
development of automated driving vehicles has been
undertaken by major car manufactures with supplier
companies and various research institutes. While
electric powered complete autonomous car is final
goal, its safety and reliability issues must be solved
for commercialization.
Conventional vehicle motion control systems
estimate the grip force between the tire and the road
as well as the coefficient of road friction, the rigidity
and the slip angle based on the mathematical vehicle
dynamics model. However, the dynamic power
transfer rate from the power pack to the wheels of an
electric car is over 10ms faster than that of the internal
combustion engine’s vehicle. And the driving safety
of automated driving cars need immediate response
on the current road-vehicle situation. Therefore, in
order to reduce the time to calculate the grip force
between the tire and the road, sensors must be built
into the tire and be directly measured in real time. As
such, tires built-in sensors are referred to smart tires
(Park and Gerdes, 2015).
Measurement of the real-time deformation of a
tire has been a challenge in the field of smart tire
development (Matsuzaki and Todoroki, 2008). This
study used strain gauge sensor incorporated inside the
tire to measure the deformation of a tire. Then, a
unique algorithm was proposed to estimate the
vehicle load on each tire based on the time-varying
deformation data obtained by data mining technique
in real time. A method was also developed to
accurately calculate the ground area with the road
surface. To verify the proposed algorithm, a sensor-
driven electrical circuit was designed and a load
measurement experiment was conducted using the
vehicle tester. In addition, the measurement system
was implemented to detect the deformation of the tire
in real time.
The composition of this paper is as follows:
Section 2 describes the real-time instrumentation
system for detecting the deformation of a tire, and the
experimental conditions and data analysis are given
in Section 3. Section 4 proposes an algorithm to
obtain the vertical load using the measured
deformation data. It also describes how the
parameters needed for the proposed algorithm are
extracted. Section 4 shows the accuracy of proposed
algorithm by comparing the experimental actual load
and estimated load. Finally, Section 5 draws
conclusion.
480
Lee, J., Liu, H., Seo, Y., Kwak, S., Lee, H., Jo, H. and Park, S.
An Investigation on the Data Mining to Develop Smart Tire.
DOI: 10.5220/0007311104800487
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 480-487
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
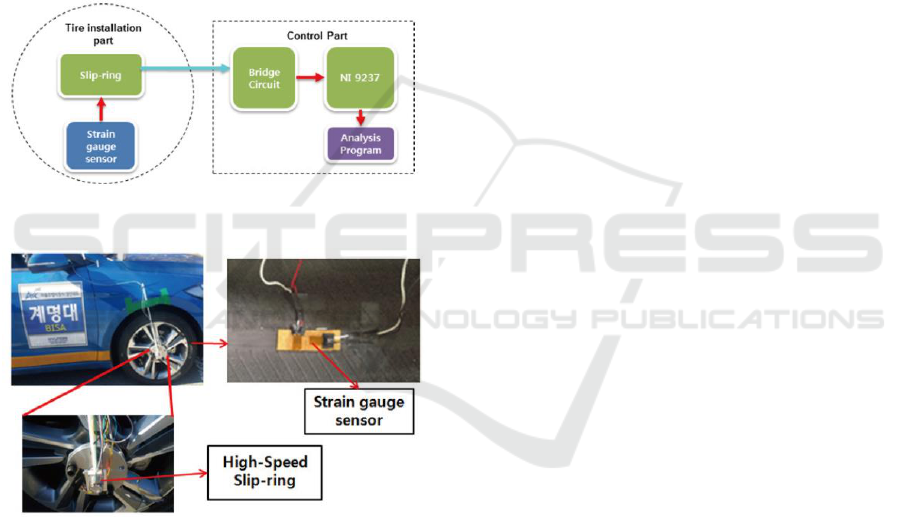
2 SMART TIRE SYSTEM
Strain gauge sensor is a sensor that measures load by
using the properties that change resistance depending
on the force applied. The compression and length
variation of the strain gauge results in a change in
resistance, which is indicated by a change in voltage
(Ahn, Bae and Kim, 2003). This study has used a
strain gauge with a wire length of 150mm and a
resistance of 120Ω. NI 9237 module with built-in
Wheatstone Bridge circuit was also used to measure
the output voltage signal of the strain gauge. Figure 1
and Figure 2 show the schematic and photos of the
smart tire instrumentation system composed by the
strain gauge, NI 9237 module and a slip-ring
respectively.
Figure 1: Schematic of a smart tire system.
Figure 2: Strain gauge sensor and slip-ring mounted on a
tire and wheel.
3 EXPERIMENT AND DATA
PROCESSING
3.1 Experiment Description
After the acquisition system using the strain gauge is
constructed test experiment should be design. Only
vertical load acting on the tire is firstly considered. It
is well known that there are lots of factors which can
effect tire deformation in vertical direction.
Therefore, the objective of test experiment is to
collect information which contains relation between
tire deformation reflected by the strain gauge and
these factors.
Three main factors, i.e. tire vertical load, tire air
charging pressure, and tire center speed (vehicle
speed), are considered in the test experiment. They
are set as following values:
Vertical load: 285kgf, 300kgf, 315kgf. The total
weight of the test vehicle is about 1.2Ton and the
vertical load acting on each tire is 300kgf with ±
5% variations (±15kgf);
Pressure: 33psi, 35psi, 37psi. The standard tire air
charging pressure is 35 psi and variation with ±
2psi is set;
Speed: 25kph, 30kph, 35kph. Low speed is tested
at first to ensure experiment success.
As a result, there are 27 different experimental
conditions totally. In order to keep tire constant speed
all experiments were performed on a tire test rig.
3.2 Data Processing and Specification
Extraction
The raw signal (red dotted line) measured by the
strain gauge is shown in Figure 3, which obviously
contains lots of noise. Noise contained in the original
strain gauge is mainly eliminated by using a wavelet
decomposition at the level 3 with a symlet wavelet.
The two waveforms in Figure 3 mean that the tire part
where the strain gauge adheres contacts with the
ground as the tire rolls while the period between two
waveforms imply that the part rolls out from the
ground and hasn’t other deformation but deformation
due to tire pressure. The strain gauge signal during
this period shows the normal deformation of the tire.
Accordingly, the value of the strain gauge signal
during this period is selected as a base line (green
dashed line in Figure 3) of the waveform. Because
most of measured voltage value distributes around the
base line it is easy to determine its value by using
histogram distribution. Figure 3 shows the measured
strain gauge signal with the vertical load of 285kgf,
the speed of 25kph, and the pressure of 33psi.
In order to extract features of the strain gauge
waveform the following five specifications are
defined as shown in Figure 4.
Base line value: the distance between the base line
and the zero horizontal axis;
Max peak value: the peak value from the base line;
Min peak value: the trough peak value from the
base line;
Peak duration: the time length of a waveform;
An Investigation on the Data Mining to Develop Smart Tire
481
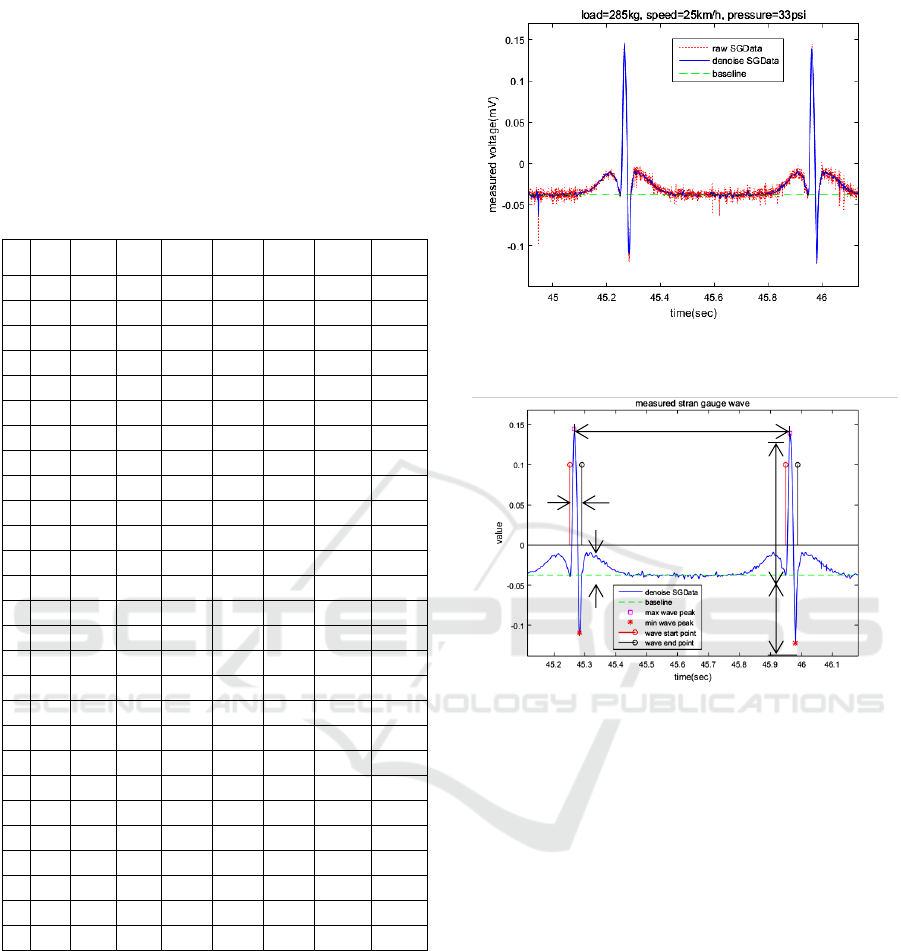
Peak-peak interval: the time interval between two
neighboring waveform peaks.
Base on above definitions the five specifications
of all acquired strain gauge signal for one
experimental condition can be calculated and then the
average value of them is obtained, which is shown in
the Table1.
Table 1: Calculated specifications for different
experimental conditions.
No.
Load
(kgf)
Speed
(kph)
Pres.
(psi)
Base
line
Max
peak
Min
peak
Duration
PP
interval
1
285
25
33
-0.038
0.179
0.079
0.038
0.692
2
300
25
33
-0.031
0.163
0.077
0.038
0.688
3
315
25
33
-0.027
0.151
0.074
0.038
0.681
4
285
30
33
-0.035
0.183
0.083
0.032
0.576
5
300
30
33
-0.030
0.170
0.086
0.032
0.573
6
315
30
33
-0.027
0.157
0.080
0.032
0.573
7
285
35
33
-0.033
0.188
0.085
0.028
0.494
8
300
35
33
-0.029
0.175
0.085
0.028
0.494
9
315
35
33
-0.026
0.164
0.080
0.028
0.493
10
285
25
35
-0.061
0.207
0.072
0.047
0.694
11
300
25
35
-0.049
0.199
0.070
0.046
0.694
12
315
25
35
-0.043
0.192
0.070
0.045
0.693
13
285
30
35
-0.054
0.215
0.078
0.040
0.578
14
300
30
35
-0.048
0.212
0.076
0.038
0.578
15
315
30
35
-0.042
0.204
0.077
0.038
0.578
16
285
35
35
-0.051
0.225
0.081
0.034
0.496
17
300
35
35
-0.045
0.221
0.081
0.032
0.494
18
315
35
35
-0.040
0.209
0.079
0.031
0.492
19
285
25
37
-0.108
0.312
0.104
0.049
0.695
20
300
25
37
-0.086
0.241
0.079
0.050
0.692
21
315
25
37
-0.072
0.224
0.071
0.049
0.695
22
285
30
37
-0.094
0.276
0.092
0.041
0.579
23
300
30
37
-0.078
0.242
0.080
0.042
0.579
24
315
30
37
-0.066
0.232
0.082
0.042
0.579
25
285
35
37
-0.086
0.274
0.090
0.038
0.497
26
300
35
37
-0.074
0.251
0.081
0.037
0.496
27
315
35
37
-0.062
0.240
0.084
0.036
0.496
Figure 3: Filtered strain gauge wave by using wavelet
transform.
Figure 4: Definitions of specifications of the measured
strain gauge wave.
3.3 Specification Analysis
In order to investigate how the three factors (the
vertical load, the tire air pressure, and the speed)
effect the five specifications the calculated
specifications are represented in Figure 5 to Figure 9.
Two horizontal axes are the vertical load and the
pressure, respectively, in these figures and the vertical
axis represents variation of specifications with three
different speeds.
The following conclusions can be drawn from
each figure:
Base line value: shows the normal state when the
local part of the tire does not contact with the
ground. The higher the tire air pressure is, the
further the base line deviates from zero, which
means tire deformation is more serious.
Max peak value: increases with increasing of
pressure and decreasing of vertical load. The
higher air pressure leads to the greater
deformation of the tire. The higher speed causes
peak-peak interval
peak duration
base line value
max peak
value
min peak
value
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
482
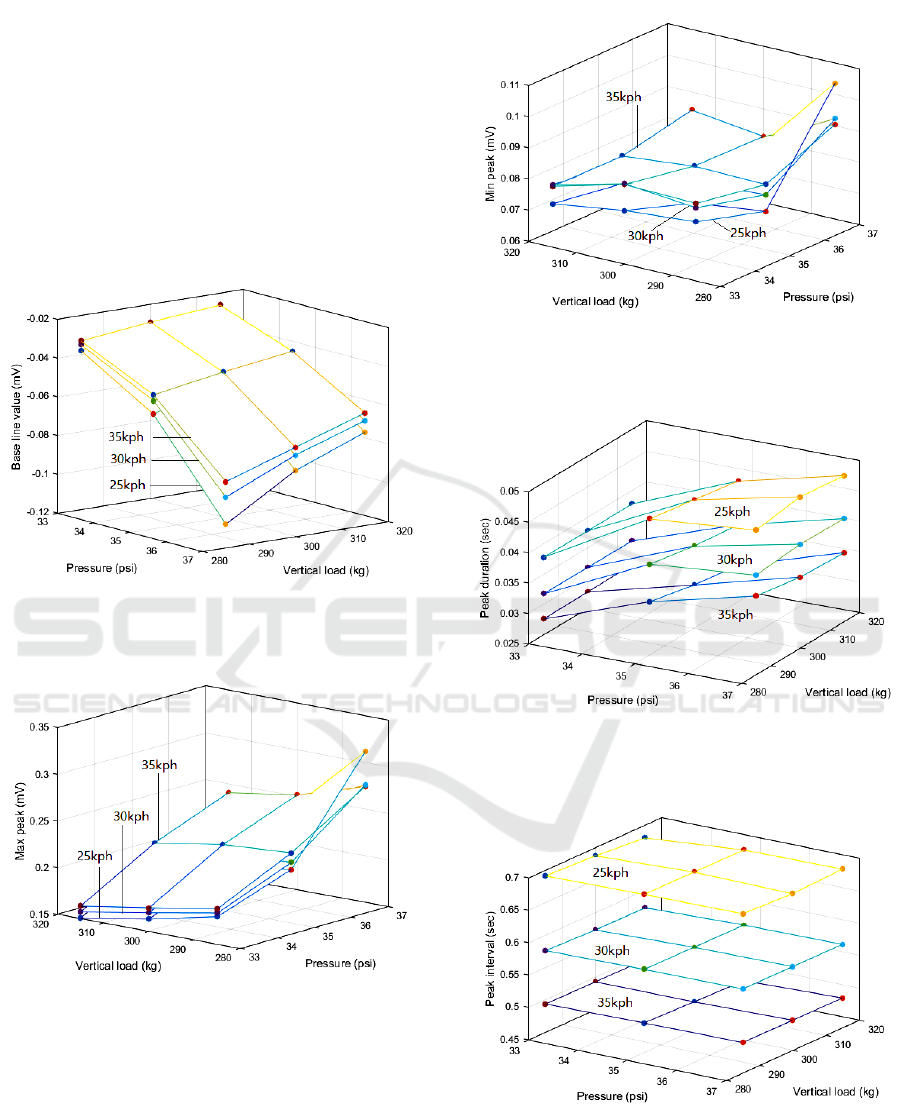
the greater peak value, however it is inverse in
high pressure and low vertical force.
Min peak value: indicates almost same trend as
the max peak value.
Peak duration: obviously increases with
decreasing of speed. Meanwhile it rises up in high
tire pressure but is not sensitive to the vertical load.
Peak-peak interval: shows the same behaviors
with the speed as peak duration. And it keeps
almost constant value regardless of the vertical
load and the pressure.
Figure 5: Base line variation VS. vertical load, pressure, and
speed.
Figure 6: Max peak variation VS. vertical load, pressure,
and speed.
Figure 7: Min peak variation VS. vertical load, pressure,
and speed.
Figure 8: Peak duration variation VS. vertical load,
pressure, and speed.
Figure 9: Peak-Peak interval variation VS. vertical load,
pressure, and speed.
An Investigation on the Data Mining to Develop Smart Tire
483
4 LOAD ESTIMATION
ALGORITHM
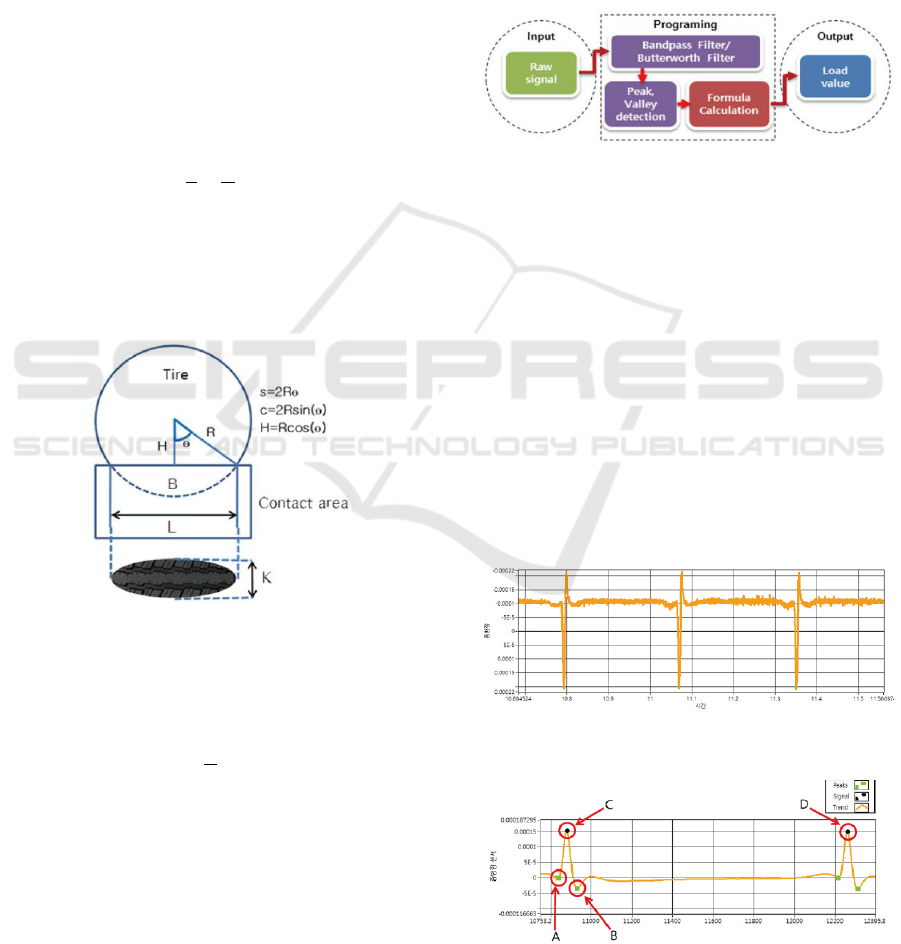
4.1 Tire Tread Area and Vertical Load
The tread area between the actual tire and the road
surface may vary with steering and speed. The shape
of the grounding area was assumed as an ellipse to
simplify the load estimation algorithm for real-time
processing. Measure the starting and end points of the
strain gauge sensor output waveform as shown in
Figure 10 to obtain an elliptical length L and measure
the longitudinal length of the tire K and , and
calculate the ground area with the road surface. The
following equation (1) is to obtain the tire-slope tread
area.
(1)
Where, is the tread correction factor for
considering the area where the tire does not touch the
tire the road surface because of the tread. The
horizontal length L of the ellipse can be obtained by
measuring the strain gauge sensor.
Figure 10: Tire contact patch.
The loads delivered to each tire using the section
A obtained previously can be obtained in the
following manner.
(2)
(3)
Where is the load, P is the air pressure, and W
is the vertical drag. The load is the opposite of the
vertical force W.
4.2 Tire-road Longitudinal Contact
Length
Figure 11 shows a data processing diagram using a
strain gauge sensor signals. Figure 12 shows the
output waveform of the strain gauge sensor attached
to the tire. A secondary Butterworth filter was used to
eliminate voltage noise from sensor signal in which
the cut-off frequencies are 50 Hz and 1 Hz and a
sampling frequency (
) is 5 kHz. Figure 13 shows the
typical output waveform through the filter.
Figure 11: Data processing flow chart.
After going through the filter, the peak and the
valley of the signal were found and the contact
grounding time and speed were calculated. In the
signal waveform shown in Figure 13, the two peaks
of A and B are the points at which the tire deformation
(contact with the road surface) begins and ends (Kim,
Lee, Heo and Kim, 2014). Points C and D are the
points at which the highest load is applied. Equation
(4) is to obtain the ground contacting time(s), and
equation (5) is to obtain the tire's rotational speed (v).
The ground time was calculated by dividing the
sampling frequency (
). The rotational
speed was obtained using the difference in the
number of samples at the peak points C and D and the
circumference of the tire (T).
Figure 12: An example of strain gauge sensor signal.
Figure 13: strain gauge sensor signal after the filter to
longitudinal deformation of a tire.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
484
(4)
(5)
The lateral length of the tire contact surface L can
be calculated using the tire's ground contacting time
and the road surface's speed of rotation as follows.
(6)
4.3 Tire-Road Lateral Contact Length
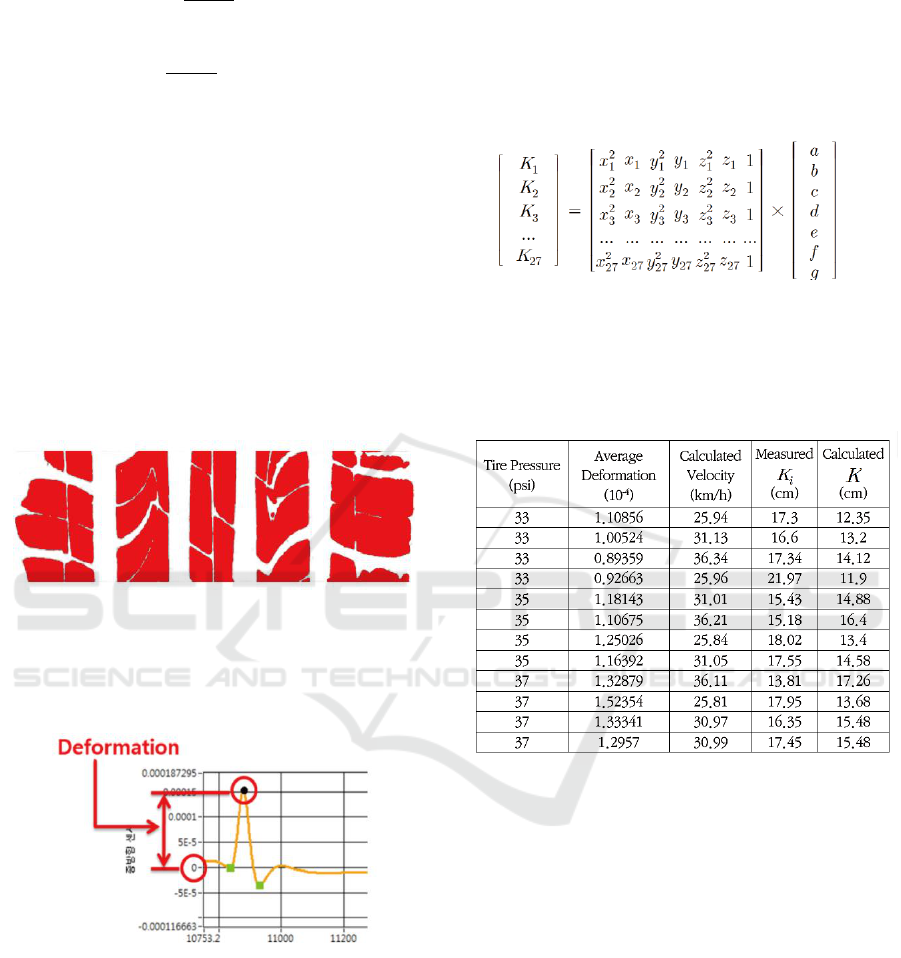
The tire-road lateral ground length K in equation (1)
was experimentally extracted from the tread samples
on the tires and on the road, as shown in Figure 14.
As a result, the K-value is determined to vary
depending on the tire air pressure, tire distortion and
speed.
Figure 14: A sample of the K length under load.
The tire deformation corresponds to the y-axis
value of the graph obtained through the strain gauge
sensor as shown in Figure 15 below.
Figure 15: Longitudinal deformation data of a tire.
Table 2 shows the value of the sample
for the
experimentally extracted lateral ground length for
part of experimental results. The generalized
relationship between K and tire pressures,
deformation and vehicle speed, was found when tire
pressures are 33, 35, and 37 (psi), loads are 285, 300,
and 315 (kgf) and vehicle speeds are 25, 30 and 35
(kph) respectively to yield the equation (7). Where
constants a~g were obtained by substituting 27 data
into the equation (8). The final results are shown in
the equation (9), where x is the tire pressure (psi), y is
the strain, and z is the vehicle speed (kph).
(7)
(8)
(9)
Table 2: The sample of the transverse K length between the
tire and the road surface.
4.4 Tire-Tread Correction Factor
Looking at the tread between the tire and the road
surface in Figure 16, it can be seen that there are areas
where the tread of the tire does not cause direct
contact with the road surface. Therefore, the effect of
the track should be considered in order to obtain an
accurate ground area. The track correction factor is
introduced to compensate for the change in the
ground surface due to the track.
The tread correction factor was calculated
experimentally using image pre-processing by
printing the ground area between the tire and the road
surface as shown in Figure 16 (Kang, Jung, Bae and
Park, 1995). The tread correction factor, is the ratio
between the non-contact empty area of a tire caused
by the tread and the total elliptical contact area
defined by the equation (10). actual
An Investigation on the Data Mining to Develop Smart Tire
485
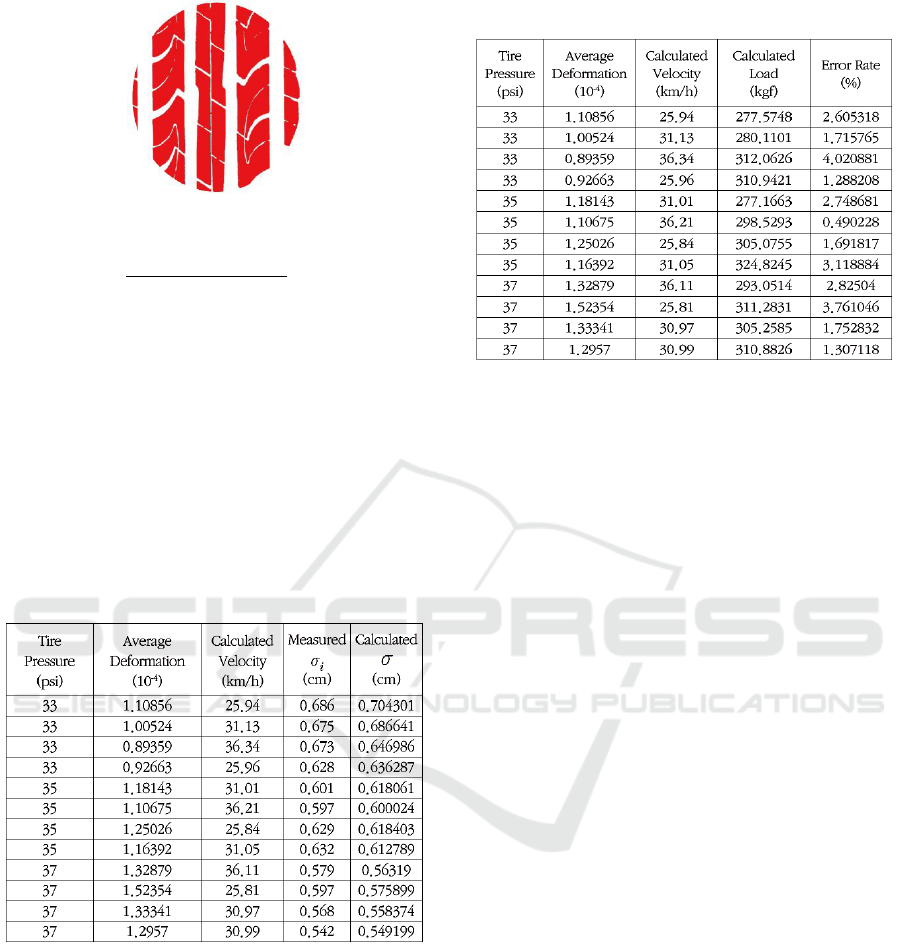
Figure 16: An example of tire-road contact area.
(10)
Measured in the same 27 situations as measuring
K length previously, the tracking correction factor
was also found to vary with the pressure, strain and
vehicle speed, as like in K length. Therefore, it was
possible to obtain the calculation using Equation (11)
in the same way as when the K-length was obtained.
This is shown in Table 3.
Table 3: Estimated results of tread correction factor.
5 TEST RESULTS
Using the tread correction factor obtained in the
previous section, and the lateral ground length K,
longitudinal length L, the tire-road ground area A was
obtained. The load was calculated using equation (2)
and multiplied by 0.073 to express the tire pressure P
by kgf Table 4 shows the strain, estimated load from
equation (2) and the error. As shown in the table, load
estimates revealed very close to the experimental
loads as a margin of error within 5%.
Table 4: Load error rate.
6 CONCLUSIONS
In this paper, we proposed a method for measuring
tire deformation through strain gauges and estimating
the load applied to tires using them. Tire variations
are closely related to the tread area between the tire
and the road surface. To accurately calculate the
ground area of a tire, a track correction factor was
introduced and a correction factor value was derived
experimentally. The contact time between the tire and
the road surface was also calculated using a strain
gauge sensor waveform. The results of the
experiment showed that the difference between the
estimated load value and the actual load was within
5%. The load estimation algorithm proposed in this
study could be used to improve the chassis control
system and to enhance the stability of automated
driving of electrical vehicles
The next work is to perform more experiments
with combination of diverse vertical loads, tire air
pressures, and driving speeds to collect more
information about the tire deformation. Based on
these measured signal from stain gauge and diverse
test conditions, a surrogate model or an artificial
neural network could be constructed to further
precisely descript the relation between tire load
(vertical, longitudinal, and lateral directions) and
measure signal. Finally, the tire contact force with the
ground could be estimated based on the developed
model.
ACKNOWLEDGEMENTS
This research was supported by The Leading Human
(11)
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
486

Resource Training Program of Regional New
industry through the National Research Foundation of
Korea(NRF) funded by the Ministry of Science and
ICT (2016H1D5A1910019).
REFERENCES
Ahn, B.-H., Bae, C.-H., Kim, H.-S., 2003. A study on the
contact seam tracking sensor by using strain gauges,
The Journal of the Kore Institute of Maritime
Information & Communication Sciences, vol. 7, no. 5.
Kang, Y.-K., Jung, S.-W., Park, G.-T., 1995. Tire tread
pattern classification using Fuzzy clustering algorithm,
Journal of Korean Institute of Intelligent Systems. vol.
5, no. 2, pp. 44-57.
Kim, I.-H., Lee, J.-H., Heo, S.-J., Kim, J. G., 2014. A study
of road friction coefficient estimation algorithm using
intelligent tire system, Autumn Conference and
Exhibition of the Korean Society of Automotive
Engineers, pp. 321-326.
Matsuzaki, R, Todoroki, A., 2008. Wireless monitoring of
automobile tires for intelligent tires, Sensors, vol. 8, no.
12., pp. 8123-8138.
Park, H., Gerdes, J. C., 2015. Optimal tire force allocation
for trajectory tracking with an over-actuated vehicle,
2015 IEEE Intelligent Vehicles Symposium.
An Investigation on the Data Mining to Develop Smart Tire
487
