
Uncertain Formal Concept Analysis for the Analyze of a Course
Satisfaction Questionnaire
Guillaume Petiot
CERES, Catholic Institute of Toulouse, 31 rue de la Fonderie, Toulouse, France
Keywords:
Formal Concept Analysis, Possibility Theory, Natural Language Processing, Neural Network, Data Mining.
Abstract:
The Formal Concept Analysis (FCA) is a method of data analysis often used in data mining. This method pro-
poses to build a collection of formal concepts from a set of objects and their properties. These formal concepts
can be ordered to provide a concept lattice. Several researches have demonstrated a link between the possi-
bility theory and the formal concept analysis. Thus, it is possible to take into account the uncertainties of the
properties by using the possibility theory before propagating them during the computation of the formal con-
cepts. We propose in this paper an experimentation of the uncertain formal concept analysis for the extraction
of knowledge in a satisfaction questionnaire for a course of professionalization in bachelor. Some questions
can be open questions where the answers provided by students are given freely. For this purpose, we perform
a text mining processing in order to categorize and classify the answers. During this processing, uncertainties
can appear. In this research, we will handle these uncertainties by using the uncertain formal concept analysis.
Then, we will extract the uncertain formal concepts from the concept lattice by using queries and represent the
reduced lattice concepts with a visualization tool.
1 INTRODUCTION
The realization of a satisfaction questionnaire at the
end of a course at the university allows us to know bet-
ter the students’ expectations. It gives us also a quality
evaluation of our pedagogy, our course resources and
so on. Many universities have already proposed this
kind of evaluation by using for example the learning
management system such as Moodle. It contributes to
the continuous improvement of the courses.
It is easy to build a quiz but the processing of an-
swers is often complex. Closed questions can be de-
fined as questions where the answer is in a set of pos-
sible answers, for example yes or no. This kind of
question sometimes presents difficulties for analysis.
The second category of questions is called open ques-
tions. These are questions where answers are pro-
vided freely and the student needs to give his opinion
or express his feelings. These free answers increase
even more the difficulty of processing. The process-
ing of answers often uses data mining or natural lan-
guage processing to analyse the syntax, semantics or
to extract information by text mining. For open ques-
tions, the goal of processing is to categorize and clas-
sify answers in order to provide the synthesis of the
answers which can help in decision making.
For our experimentation we would like to extract
the answers given by the majority of the students.
As presented in (Belohlavek et al., 2007), the Formal
Concept Analysis (FCA) can be used to do this. A
formal concept is described in (Bedek et al., 2015)
as a set of objects which have the same properties.
Several researches have been published for educa-
tional application (Bedek et al., 2015; Fernandez-
Manjon and Fernandez-Valmayor, 1998; Kickmeier-
Rust et al., 2016) or social network (Sn
´
a
ˇ
sel et al.,
2008). We can also find several studies which pro-
pose to use fuzzy logic for imprecise properties as in
(Belohlavek, 2004; Zou and Deng, 2017; Cross et al.,
2010). Nevertheless, we rarely found applications of
the formal concept analysis taking into account un-
certainty. It is however possible. Authors in (Dubois
and Prade, 2009; Dubois and Prade, 2012; Dubois and
Prade, 2015; Dubois et al., 2007; Navarro et al., 2012;
Miclet et al., 2011) propose a generalization of the
formal concept analysis by using the possibility the-
ory.
We propose in this paper an experimentation of
the uncertain formal concept analysis. Our applica-
tion consists in analysing a satisfaction questionnaire
for a course of PPP (Professional Personal Project) in
bachelor.
488
Petiot, G.
Uncertain Formal Concept Analysis for the Analyze of a Course Satisfaction Questionnaire.
DOI: 10.5220/0007311504880495
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 488-495
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Our questionnaire consists of closed questions and
open questions. For our open questions we must per-
form a processing to classify the answers of the stu-
dents. Unfortunately, this processing generates un-
certainties because an answer can belong, though in
different measure, to several classes at the same time.
The uncertainties must be propagated in the formal
concept analysis to avoid losing information.
Our study will first propose the description of
the formal concept analysis and show how it can be
generalized by the possibility theory. Then we will
present our application and the processing of the an-
swers to open questions. Finally, we will show several
results which illustrate our approach.
2 THE POSSIBILITY THEORY
The possibility theory was developed in 1978 by L.A.
Zadeh after the fuzzy set theory in the paper (Zadeh,
1978). This theory proposes to take into account im-
precision and uncertainty often attached to knowl-
edge. Knowledge can be modeled by a possibility dis-
tribution. For example, if Ω is the universe and π
x
a
possibility distribution of the variable x defined from
Ω in [0, 1], then if π
x
(u) = 0 then x = u is impossible.
If π
x
(u) = 1 then x = u is possible. In the possibility
theory there are two fundamental measures, the pos-
sibility measure noted Π and the necessity measure
noted N (Dubois and Prade, 1988) defined from the
set of parts of Ω, P(Ω) in [0,1]. These measures can
be defined as below:
∀A ∈ P(Ω),Π(A) = sup
x∈A
π(x). (1)
∀A ∈ P(Ω),N(A) = 1 − Π(¬A) = in f
x /∈A
1 − π(x ). (2)
The possibility theory is not additive but maxitive.
This very important characteristic explains why the
properties of the probability theory cannot be applied
to the possibility theory. The possibility theory is a
non-additive theory of the uncertain:
∀A,B ∈ P(Ω),Π(A ∪ B) = max(Π(A),Π(B)). (3)
We can present two other operators of the possibil-
ity theory. The first one is the measure of guaranteed
possibility:
∀A ∈ P(Ω),∆(A) = in f
x∈A
π(x). (4)
And the second one is the measure of potential
necessity:
∀A ∈ P(Ω),∇(A) = 1 − in f
x /∈A
π(x). (5)
As we will see in the next section, all these op-
erators can be used to generalize the formal concept
analysis.
3 FORMAL CONCEPT ANALYSIS
The formal concept analysis is a data analysis ap-
proach introduced by R. Wille (Wille, 1982). It con-
sists in analysing concepts by using a concept lattice.
The concept can be viewed as a basic component of
human thinking.
There are two notions to define the concept
present in philosophy: the intent and the extent. The
intent is the definition of the concept and the extent
denotes the elements to which it applies. Mathemat-
ically, a formal context is a triple (O,P,ℜ) where
O =
{
o
1
,...,o
n
}
is the set of objects, P =
{
p
1
,..., p
m
}
is the set of properties, and ℜ is a relation such as
ℜ ⊆ O × P.
In fact if (o, p) ∈ ℜ, then the object o has the prop-
erty p. It can also be noted oℜp. Generally, we repre-
sent this in a table where the lines are the objects and
the columns are the properties. The relation is rep-
resented by a 0 if (o, p) /∈ ℜ or by a 1 if (o, p) ∈ ℜ.
These values correspond to the values of the table.
We can define a valuation ϑ(o, p) which returns
the value of the table for object o and property p.
A formal concept of (O, P,ℜ) is a pair (X,Y ) such
that X ∈ O and Y ∈ P where Y is the set of prop-
erties shared by all objects of X . We can use as
in (Belohlavek et al., 2007) the notation X
↑
= Y or
Y
↓
= X. For example, in the formal context below the
sets ({o
2
,o
3
,o
5
},{p
2
, p
3
}) and ({o
4
,o
5
},{p
1
, p
2
})
are two formal concepts.
Table 1: Example of a formal context.
Object p
1
p
2
p
3
o
1
0 1 0
o
2
0 1 1
o
3
0 1 1
o
4
1 1 0
o
5
1 1 1
The set of all formal concepts of (O,P,ℜ) is
noted β(U,V,ℜ) =
(X,Y )|X
↑
= Y,Y
↓
= X
. If ≤
is a partial order such that for (X
1
,Y
1
),(X
2
,Y
2
) ∈
β(X,Y,ℜ), then (X
1
,Y
1
) ≤ (X
2
,Y
2
) si X
1
⊆ X
2
ou Y
2
⊆
Y
1
. Then we can build a concept lattice based on
the partial order ≤. A concept lattice can be vi-
sualized by using a Hasse diagram. For exam-
ple, we can show the concept lattice of the previ-
Uncertain Formal Concept Analysis for the Analyze of a Course Satisfaction Questionnaire
489

ous example performed by using the tool ConExp
(http://sourceforge.net/projects/conexp):
Figure 1: Concept lattice of the example.
We can see that the notation is reduced because
we use the legacy of properties and objects. When
the properties are many-valued, it is necessary to per-
form a transformation of the context into a binary for-
mal context. We can take as an example the following
many-valued context:
Table 2: Example of a many-valued context.
Object Score Quality
o
1
5 low
o
2
15 high
o
3
15 medium
o
4
12 low
o
5
18 medium
We can see that the score is numerical with a range
in [0,20], so we must propose a categorization of the
values by defining for example three classes. The
first one is low for the values in [0,7], the second is
medium for the values in [8, 14], and the last class is
high for the values in [15,20]. It can be transformed
into the following binary formal context:
Table 3: The transformation of the many-valued context
into a binary formal context.
Object S
low
S
medium
S
high
Q
low
Q
medium
Q
high
o
1
1 0 0 1 0 0
o
2
0 0 1 0 0 1
o
3
0 0 1 0 1 0
o
4
0 1 0 1 0 0
o
5
0 0 1 0 1 0
So far, the properties were perfectly known but if
the properties are uncertain, it is interesting to propa-
gate the uncertainty to the lattice concept. We propose
to use the possibility theory (Zadeh, 1978) to take
into account uncertainty as proposed by the authors
in (Dubois et al., 2007). Thus, we obtain the pos-
sibility distribution π
o
p
(u) defined for u ∈ Ω, which
is the possibility that the property p of the object o
is u. This possibility distribution must be normal-
ized. The authors propose also to extend the for-
mal concept analysis by defining four operators in-
spired from the possibility theory. If ℜ is a relation,
then we can define R(o) = {p ∈ P|(o, p) ∈ ℜ} and
R
t
(p) = {o ∈ O|(o, p) ∈ ℜ}. If S is a subset of O, we
obtain the following operators:
• (S)
Π
= {p ∈ P|R
t
(p) ∩ S 6= }
• (S)
N
= {p ∈ P|R
t
(p) ⊆ S}
• (S)
∆
= {p ∈ P|R
t
(p) ⊇ S}
• (S)
∇
= {p ∈ P|R
t
(p) ∪ S 6= O}
As an example, we propose to show the results of
these operators for Table 1 and for different sets of
objects:
Table 4: Example of the application of the four operators.
S (S)
Π
(S)
N
(S)
∆
(S)
∇
(o
1
,o
2
,o
3
) (p
2
, p
3
) () (p
2
) ()
(o
2
) (p
2
, p
3
) () (p
2
, p
3
) (p
1
, p
3
)
(o
4
,o
5
) (p
1
, p
2
, p
3
) (p
1
) (p
1
, p
2
) (p
1
, p
3
)
(o
1
,o
2
,o
3
,o
4
) (p
1
, p
2
, p
3
) () (p
2
) ()
(S)
Π
is the set of properties possessed by at least
one object of S. (S)
N
is the set of properties possessed
only by the objects of S. In other words, if the prop-
erty is in (S)
N
, it is not possible that another object
not present in S should have this property. (S)
∆
is
a set of properties shared by all objects of S. (S)
∇
is a set of properties that are not satisfied by at least
one object in
¯
S. The behaviour of the operator (.)
∆
corresponds to the formal concept analysis. In our
research, we will use this operator. The authors in
(Dubois et al., 2007) remark that the four operators
have already been proposed in scientific works with-
out reference to the possibility theory. These opera-
tors can be presented in the cube of oppositions for
formal concept analysis (AffIrmo nEgO):
Figure 2: Cube of oppositions.
These operators are defined for a set of objects S
but we can easily propose equivalent operators for the
sets of properties noted (.)
−1Π
, (.)
−1N
, (.)
−1∆
, (.)
−1∇
as in (Dubois et al., 2007). It is possible to use fuzzy
sets to model imprecise properties as in (Belohlavek,
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
490

2004) but there is less research taking into account
uncertainty and ignorance which can be partial or full.
Certainty is associated with the necessity measure in
the possibility theory. This measure can be used in
the table of the formal context. As a result, the for-
mal context can be viewed as a weighted family of
formal contexts obtained by the threshold of uncer-
tain values of the table. The authors in (Dubois and
Prade, 2015) propose to use a pair of necessity mea-
sures (α(o, p), β(o, p)) with α(o, p) = N((o, p) ∈ ℜ)
and β(o, p) = N((o, p) /∈ ℜ) which represents the cer-
tainty that the object has the property (resp. does not
have the property). Moreover, we must satisfy the
property min(N((o, p) ∈ ℜ),N((o, p) /∈ ℜ)) = 0 of
the possibility theory. The pairs (1, 0) and (0, 1) rep-
resent the fact that the object has the property or not.
On the other hand, if 1 > max(α(o, p), β(o, p)) > 0,
the ignorance is partial, and if we have (0,0), the ig-
norance is total. We can define the uncertain formal
context in the following formula:
ℜ
0
=
{
(α(o, p), β(o, p))|o ∈ O, p ∈ P
}
(6)
For this first experimentation, we propose to con-
sider only the simple case where the uncertain val-
ues (α(o, p),0) and (0, β(o, p)) are changed into sure
values. So (α(o, p),0) is changed in (1,0) and
(0,β(o, p)) is changed in (0,1). For example, (0.5,0)
can be transformed into (1,0) in the table and (0,0.7)
can be transformed into (0,1). As a result, we obtain
a formal context noted ℜ
0
+
and we can now extract all
formal concepts. We can provide below an example
of an uncertain context:
Table 5: Example of an uncertain context.
Object p
1
p
2
p
3
o
1
(0,1) (1,0) (0.2,0)
o
2
(0,0.5) (1,0) (1,0)
o
3
(0.5,0) (1,0) (1,0)
o
4
(1,0) (1,0) (0.8,0)
o
5
(1,0) (1,0) (1,0)
In this example, we can see that
({o
1
,o
2
},{p
2
, p
3
}) and ({o
3
,o
4
,o
5
},{p
1
, p
2
, p
3
})
are formal concepts. We have come up with the
following formula in order to compute the certainty
degree of a formal concept C = (X,Y ):
N(C) = min
o∈X,p∈Y
N((o, p) ∈ ℜ) (7)
In the previous example, the certainty of
({o
1
,o
2
},{p
2
, p
3
}) is 0.2 and the certainty of
({o
3
,o
4
,o
5
},{p
1
, p
2
, p
3
}) is 0.5. This indicates that
there is one or more properties which are uncertain in
these formal concepts. The interest of this approach
is to take into account uncertain properties and to pro-
vide a concept lattice where the formal concept can
be weighted by the degree of certainty. If we per-
form a purely binary reasoning, in which an object
has the property or not, we can fail to discover the
core knowledge. Among the existing algorithms de-
scribed in (Kuznetsov and Obiedkov, 2003) for com-
puting formal concepts, we have chosen Ganter Al-
gorithm Next Closure (Ganter, 1987) for our experi-
mentation. This algorithm finds all intents or extents.
We have adapted this algorithm to compute uncertain
formal concepts. To do this, we propose to modify
the previous function R for a certainty threshold s:
R
s
(o) = {p ∈ P|N((o, p) ∈ ℜ) > s} and R
t
s
(p) = {o ∈
O|N((o, p) ∈ ℜ) > s}, and to define two new opera-
tors based on these functions (.)
∆
s
and (.)
−1∆
s
:
(S)
∆
s
= {p ∈ P|R
t
s
(p) ⊇ S} (8)
(S)
−1∆
s
= {o ∈ O|R
s
(o) ⊇ S} (9)
We also have to define the closure operator ⊕
s
:
X ⊕
s
i = ((X ∩ {p
1
,..., p
i−1
}) ∪ {p
i
})
−1∆
s
∆
s
(10)
And finally we have to present the comparison op-
erator <
i
(lexicographic order). If X ∈ P and Y ∈ P
then X <
i
Y if:
p
i
∈ Y −X and
X ∩ {p
1
,..., p
i−1
} = Y ∩ {p
1
,..., p
i−1
}
(11)
Moreover, we have X < Y if an i exists such that
X <
i
Y is verified. If s = 0 then we perform the com-
putation of the formal concepts for the formal context
ℜ
0
+
. The algorithm for the computation of uncertain
formal concepts is the following:
Algorithm 1: Uncertain NextClosure.
Input : R is an uncertain context
Output: The set of intents noted I
1 begin
2 V =
−1∆
0
∆
0
3 Save(V )
4 while V 6= P do
5 for i ← |P| to 1 do
6 V
+
= V ⊕
0
i
7 if V <
i
V
+
Exit of the loop.
8 Save(V
+
)
9 V ←− V
+
If we use a comparison operator between all con-
cepts then we build the lattice concept.
Uncertain Formal Concept Analysis for the Analyze of a Course Satisfaction Questionnaire
491
4 NATURAL LANGUAGE
PROCESSING
In the satisfaction questionnaire of our experimenta-
tion we have an open question which requires a free
answer. However, it is possible to provide a set of
classes for the possible answers. So, if we have a set
of samples for each class, then it is possible to do a
supervised classification of the students’ answers. To
do this, we must perform the processing of the sam-
ples to extract the key words and eliminate useless
characters and words. The training set can be the pro-
vided samples of the classes. Then, we have to per-
form the supervised learning before the classification
of all answers. A neural network can be used for this
classification. The processing of the samples of the
classes and of the students’ answers consists at first in
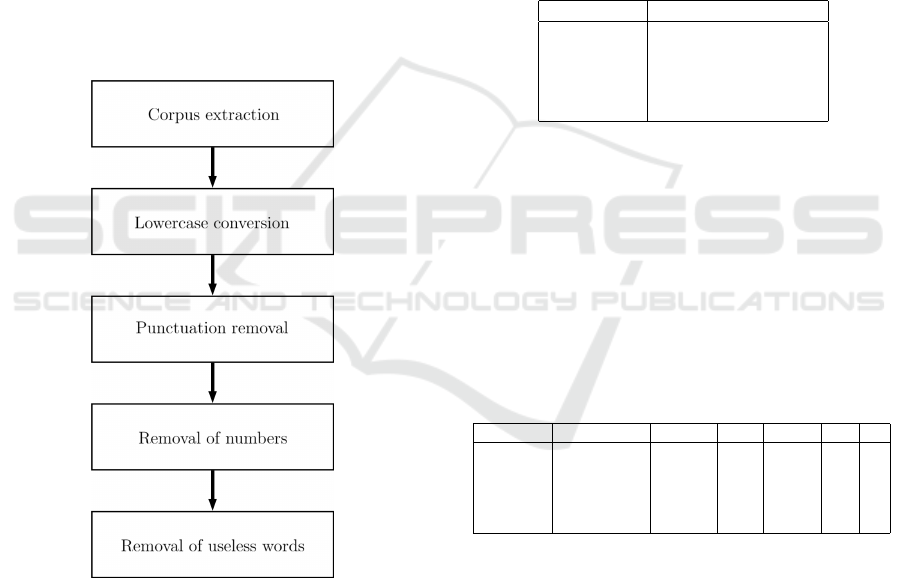
constructing the corpus. Then we change the case, we
eliminate undesired characters, punctuation, numbers
and useless words. We resume below the processing:
Figure 3: Processing of the corpus.
After this processing, we perform the computa-
tion of the Document Term Matrix for the samples
of the classes and the students’ answers. The clas-
sification will use for the training set the DTM of the
samples of the classes. Then the students’ answers are
classified. A significant problem in natural language
processing is the problem of a spelling mistake. Our
idea is to use a measure of resemblance between the
words during the computation of the DTM and dur-
ing the classification. We propose to use a fuzzy mea-
sure in [0,1]. Several string metrics exist to measure
the resemblance of two strings (Christen, 2006; Jaro,
1989). The most famous are the distance of Leven-
shtein, Jaccard, Damerau-Levenshtein, hamming, the
longest common subsequence, Smith-Waterman and
Jaro-Winkler (Winkler, 1999).
All these metrics didn’t return measures in [0,1]
except the distance of Jaro-Winkler. This measure has
also been positively evaluated by the author of (Chris-
ten, 2006). So we will use this measure for our study.
If we consider the following example which concerns
several spellings of the word intelligence and if we
calculate for each word the Jaro-Winkler distance, we
obtain:
Table 6: Comparison of the Jaro-Winkler distance for the
word intelligence.
Word Jaro-Winkler distance
Intelligence 1.0
Inteligence 0.95
Inelligence 0.89
Intelijence 0.92
Hazard 0
We can notice that if the words are very close to
the word intelligence, then the Jaro-Winkler distance
returns a value close to 1. If the measure is not close
enough to 1, then we can consider that the words are
different. So if d
JW
(word 1, word 2) < η, then the
word 1 is different from the word 2.
In the previous example, if η = 0.8 then the word
hazard is different from intelligence. The next step
is the construction of the DTM. For example for the
students’ answers the result is the following:
Table 7: Example of DTM matrix for the students’ answers.
student intelligences gardner quiz proust cv ...
student 1 1.0 0.96 0.0 0.0 0.0 ...
student 2 0.0 0.0 0.0 0.82 0.0 ...
student 3 1.0 1.0 0.0 0.0 0.0 ...
... ... ... ... ... ... ...
student N 0.0 0.0 0.0 0.0 0.0 ...
When the DTM are computed for the students’ an-
swers and the samples of the classes, we can perform
the classification of the students’ answers by a neural
network. The learning of the coefficient of the neural
network is performed by using a backpropagation of
the gradient. The algorithm is presented below:
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
492
Algorithm 2: Backpropagation of the gradient.
Input : E: Sets of samples, N: Number of neurons, NM: Number
of values in input, NC: Number of classes, µ: a constant,
E
max
: maximum error, I
max
: maximum number of
iterations.
Output: ω
1
,ω
2
1 begin
2
∑
Error
←− +∞
3 count ←− 0
4 while
∑
Error
> E
max
∧ count < I
max
do
5
∑
Error
←− 0
6 count ←− count + 1
7 forall the x ∈ E do
8 for i ← 0 to NC do
9 RC1 ←− NeuronsLayer(ω
1
,x
i
,N, NM)
10 RF ←− NeuronsLayer(ω
2
,RC1,NC, N)
11 for j ← 0 to NC do
12 η ←− ErrorComputation(RF,i)
13 e
j
= RF
j
× (1 − RF
j
) × η
14 for k ← 0 to N do
15 ω
j,k
2
←− ω
j,k
2
+ µ × e
j
× RC1
k
16
∑
Error
=
∑
Error
+
|
η
|
17 for j ← 0 to N do
18 for k ← 0 to NM do
19 s ←− 0
20 for l ← 0 to NC do
21 s ←− s + ω
l , j
2
× e
l
22 ω
j,k
1
←− ω
j,k
1
+ µ × RC1
j
(1 − RC1
j
) × s × x
i,k
The result of the classification can be interpreted
as a possibility measure after normalization for each
class. We can also compute a necessity measure
which is in fact certainty. This necessity measure can
be taken into account in the formal concept analysis.
5 EXPERIMENTATION
The experimentation concerns the analysis of a sat-
isfaction questionnaire for a course of bachelor. 144
students have answered the questionnaire which con-
sisted of closed questions and open questions. To sim-
plify the processing, we take into account only one
open question, the one which is the most important
for us. There are 32 other closed questions where the
answers are many-valued. We have transformed these
many-valued data accordingly to the proposed solu-
tion of part 3 (as in the example of table 3) and per-
formed a processing of the open question by using the
method presented in the previous section. The result
is an uncertain formal context where the columns are
the possible answers (the properties of the FCA) and
the lines are the students (the object of the FCA). Con-
cerning the open question, we have as many columns
as possible classes. The values of the table are the
necessity measures. When an answer is certain, the
value is 1. The uncertain values are between 0 and 1.
Finally, we have a table of 158 columns and 144 lines.
To simplify the computation of the lattice, we can ap-
ply a filter on the formal concepts by using the cri-
teria such as the number of students, the certainty of
the formal concept, the score, the properties, and the
presence of one student or a group of students in the
formal concepts. We present below several examples
of results in order to illustrate some of these criteria.
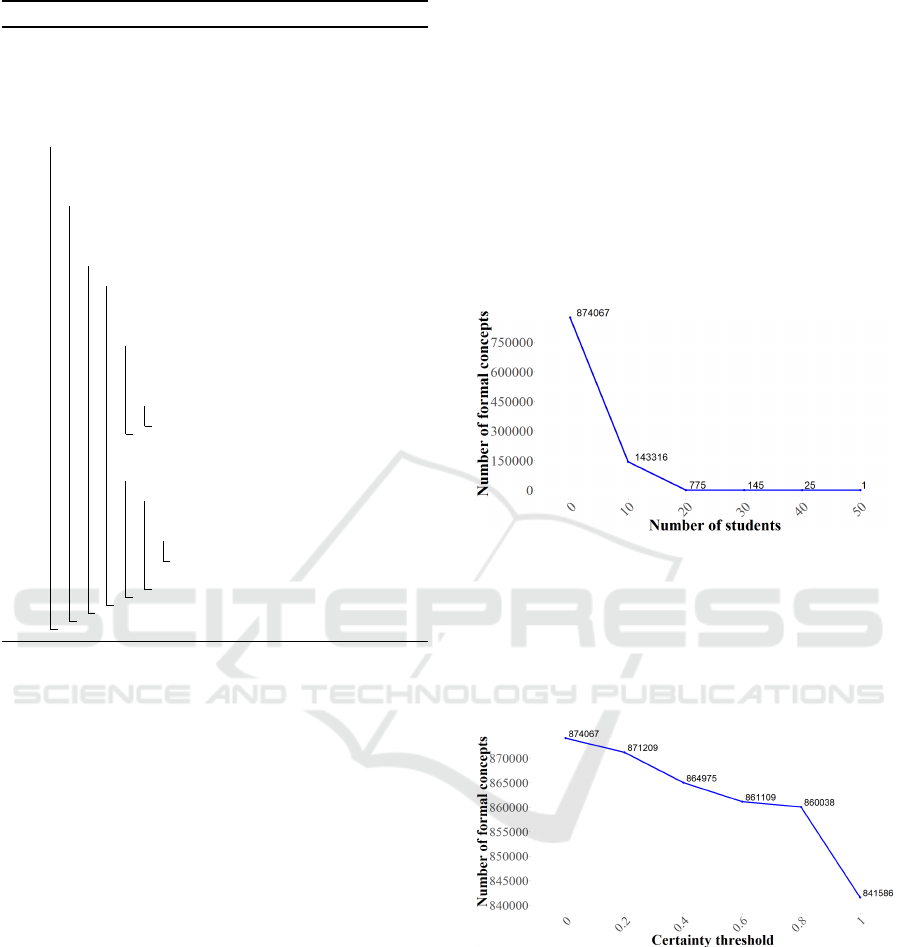
The first one is an example of filtering depending on
the number of students:
Figure 4: Filtering of the formal concepts according to the
number of students.
We can see as expected that more there are stu-
dents, fewer there are formal concepts. The second
criterion is to filter the formal concept by making vary
the threshold of certainty between 0 and 1. The ob-
tained result is as follows:
Figure 5: Filtering of the formal concepts according to the
threshold of certainty.
We can see that the number of formal concepts
is still high for the certainty equal to 1. These pre-
vious filters are not sufficient to extract the concepts
representing the students’ most frequent answers. So
we have imagined to use a score representing the stu-
dents’ most common answers. If β(U,V,ℜ) is the set
of formal concepts and C = (X,Y ) a formal concept
with X the extent and Y the intent, then the score can
be the following:
Uncertain Formal Concept Analysis for the Analyze of a Course Satisfaction Questionnaire
493
Score(C) =
|X| + |Y |
max
(u,v)∈β(U,V,ℜ)
|u| + |v|
(12)
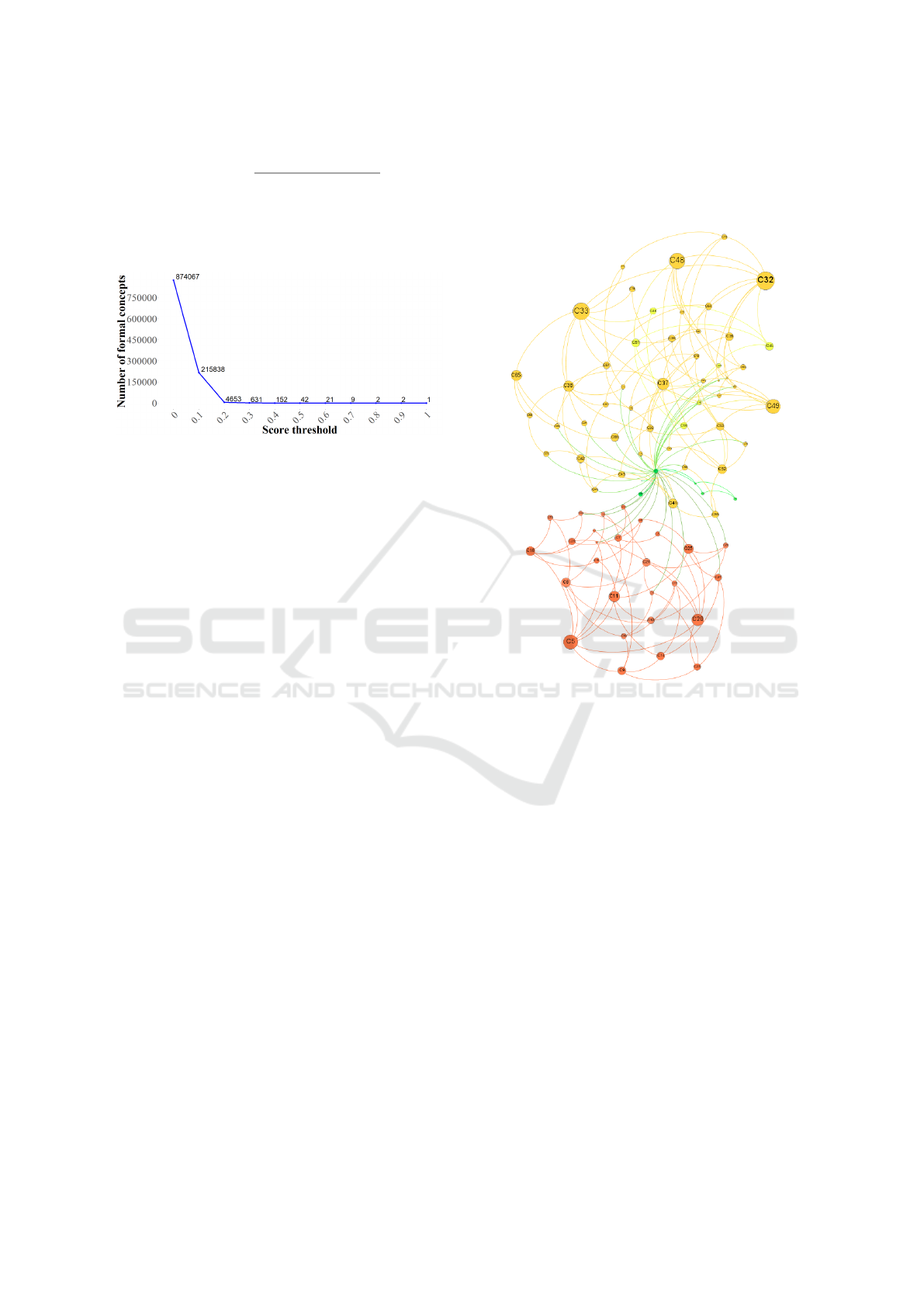
We have filtered the formal concepts by using the
score and we obtain the following result:
Figure 6: Filtering of the formal concepts by using the
score.
We can also define filters on the properties or ob-
jects. All these criteria can be used in a query on
formal concepts. The aim of the query is to per-
form complex filtering of the formal concepts to ex-
tract only those which are interesting. The query is a
multi-criteria filtering of the formal concepts. Most of
the papers concerning the formal concept analysis are
focused on two topics: performance computation or
visualization of information. After the computation,
the results of the queries can be visualized to high-
light the best results. We might have build a Hasse
diagram but we have preferred to present a person-
alized visualisation of the information. For example,
if a formal concept represents a lot of students’ an-
swers, then it can be displayed as a circle with a ra-
dius proportional to its significance. If it represents
few answers then the radius is smaller. The uncer-
tainty of the formal concept can be represented by a
colour gradation (red, yellow and green) from red for
less certain formal concepts to green for certain for-
mal concepts. Several visualization tools exist. We
have chosen Gephi because it is free and has a lot of
functionalities. The results of the queries are trans-
formed in a format compatible with Gephi and can be
easily imported. For example, we can extract the con-
cepts for a given score, with a set of properties and
at least 20 students. The query can be seen as a set
of criteria B
φ
= (φ
1
∧ ... ∧ φ
n
) which must be all satis-
fied. Then we have B
φ
B
C
with B
C
the set of formal
concepts which verify all criteria of B
φ
. We present
below an example of a query:
B
φ
=
P
1
∨ P
2
∨ P
3
∨ P
4
∨ P
5
∨ P
6
∨ P
7
∨ P
8
Score(C) ≥ 0.1
Card(X ) ≥ 20
(13)
With C = (X,Y ) a formal concept, Card the num-
ber of properties or objects of the concept and P
i
the
classes of the open question. In our experimentation
we obtain for this query the result below:
Figure 7: Example of a query result.
In the above figure, we can see the uncertainty of
the formal concepts and the formal concepts which
represent a lot of students’ answers. The formal con-
cept C5 seems to be a good solution but it is too un-
certain because it is marked in red. There are several
formal concepts with a certainty medium which can
be a good compromise because we have no good re-
sults with a big green circle. For example, the formal
concept C33 is interesting. We can deduce from this
concept that the majority of the students have appre-
ciated the co-facilitating of the course and found use-
ful the topic concerning the theory of multiple intel-
ligences. We can also define a score of relevance for
a query in order to present the ranking of the results
from the best solution to the less pertinent one.
6 CONCLUSIONS
The formal concept analysis can be extended by us-
ing the possibility theory leading to the uncertain for-
mal concept analysis. We have applied the uncertain
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
494

formal concept analysis to the analysis of a satisfac-
tion questionnaire for a course of bachelor. To do
this, we have performed a natural language process-
ing for open questions before extracting formal con-
cepts. The goal was to extract the lattice concepts by
taking into account uncertainty generated by the pro-
cessing of open questions. We have proposed to use
queries to extract interesting formal concepts. In or-
der to improve the presentation of the results of the
queries, we have proposed a visualization which high-
lights the uncertainty of the formal concept by using
a colour gradation and a circle with a radius propor-
tional to the number of answers. In future, we would
like to improve our experimentation in order to ob-
tain more experimental results and comparative eval-
uations. Particularly, we have to evaluate better the
query on the lattice concept and the use of the score
of relevance. In this study, we have limited our ap-
proach to a simple case of the certainty computation
of a formal concept but we wish to propose a general
frame for certainty computation. On the other hand,
we also need to improve the performance of the lattice
concept computation. We have explored only the use
of the guaranteed possibility operator, so we would
like to explore the interest of the use of the other op-
erators.
REFERENCES
Bedek, M. A., Kopeinik, S., Pr
¨
unster, B., and Albert, D.
(2015). Applying the formal concept analysis to in-
troduce guidance in an inquiry-based learning envi-
ronment. In IEEE 15th International Conference on
Advanced Learning Technologies, pages 285–289.
Belohlavek, R. (2004). Concept lattices and order in fuzzy
logic. In Annals of Pure and Applied Logic, volume
128, pages 277–298.
Belohlavek, R., Sklen
´
a
ˇ
r, V., Zacpal, J., and Sigmund, E.
(2007). Evaluation of questionnaires by means of for-
mal concept analysis. In In J. Diatta, P. Eklund, M.
Liquiere (Eds.): CLA 2007, Int. Conference on Con-
cept Lattices and Their Applications, pages 100–111.
Christen, P. (2006). A comparison of personal name match-
ing: Techniques and practical issues. In Proceedings
of the Sixth IEEE International Conference on Data
Mining - Workshops, ICDMW ’06, pages 290–294,
Washington, DC, USA. IEEE Computer Society.
Cross, V., Kandasamy, M., and Yi, W. (2010). Fuzzy con-
cept lattices: Examples using the gene ontology. In
2010 Annual Meeting of the North American Fuzzy
Information Processing Society, pages 1–6.
Dubois, D., de Saint-Cyr, F. D., and Prade, H. (2007). A
possibility-theoretic view of formal concept analysis.
volume 75, pages 195–213, Amsterdam, The Nether-
lands. IOS Press.
Dubois, D. and Prade, H. (1988). Possibility theory: An
Approach to Computerized Processing of Uncertainty.
Plenum Press, New York.
Dubois, D. and Prade, H. (2009). Possibility theory and
formal concept analysis in information systems. pages
1021–1026.
Dubois, D. and Prade, H. (2012). Possibility theory and
formal concept analysis: Characterizing independent
sub-contexts. volume 196, pages 4–16. On Advances
in Soft Computing Applied to Databases and Informa-
tion Systems.
Dubois, D. and Prade, H. (2015). Formal concept analysis
from the standpoint of possibility theory. In Baixeries,
J., Sacarea, C., and Ojeda-Aciego, M., editors, Formal
Concept Analysis, pages 21–38, Cham. Springer Inter-
national Publishing.
Fernandez-Manjon, B. and Fernandez-Valmayor, A. (1998).
Building educational tools based on formal concept
analysis. volume 3, pages 187–201.
Ganter, B. (1987). Algorithmen zur formalen begriffsanal-
yse. pages 241–255.
Jaro, M. A. (1989). Advances in record linking method-
ology as applied to the 1985 census of tampa florida.
volume 84, pages 414–420.
Kickmeier-Rust, M. D., Bedek, M., and Albert, D. (2016).
Theory-based learning analytics: Using formal con-
cept analysis for intelligent student modelling. pages
97–100, Las Vegas, Nevada, USA.
Kuznetsov, S. O. and Obiedkov, S. A. (2003). Comparing
performance of algorithms for generating concept lat-
tices. volume 14, pages 189–216.
Miclet, L., Prade, H., and Guennec, D. (2011). Looking
for analogical proportions in a formal concept analysis
setting. pages 295–307, Nancy, France.
Navarro, E., Prade, H., and Gaume, B. (2012). Clustering
sets of objects using concepts-objects bipartite graphs.
In H
¨
ullermeier, E., Link, S., Fober, T., and Seeger,
B., editors, Scalable Uncertainty Management, pages
420–432, Berlin, Heidelberg. Springer Berlin Heidel-
berg.
Sn
´
a
ˇ
sel, V., Hor
´
ak, Z., and Abraham, A. (2008). Under-
standing social networks using formal concept anal-
ysis. In 2008 IEEE/WIC/ACM International Confer-
ence on Web Intelligence and Intelligent Agent Tech-
nology, volume 3, pages 390–393.
Wille, R. (1982). Restructuring lattice theory: An approach
based on hierarchies of concepts. In Rival, I., edi-
tor, Ordered Sets, pages 445–470, Dordrecht. Springer
Netherlands.
Winkler, W. E. (1999). The state of record linkage and cur-
rent research problems. Technical report, Statistical
Research Division, U.S. Bureau of the Census.
Zadeh, L. A. (1978). Fuzzy sets as a basis for a theory of
possibility. volume 1, pages 3–28.
Zou, C. and Deng, H. (2017). Using fuzzy concept lattice
for intelligent disease diagnosis. In IEEE Access, vol-
ume 5, pages 236–242.
Uncertain Formal Concept Analysis for the Analyze of a Course Satisfaction Questionnaire
495
