
Accelerate Performance for Elliptic Curve Scalar Multiplication based
on NAF by Parallel Computing
Mohammad Anagreh
1,2
, Eero Vainikko
1
and Peeter Laud
2
1
Institute of Computer Science, University of Tartu, J. Liivi 2, Tartu, Estonia
2
Cybernetica, M
¨
aealuse 2/1, Tallinn, Estonia
Keywords:
ECC, NAF, Hamming Weight, Parallel Computing, Signed Binary Representation.
Abstract:
The aim of Elliptic Curve Cryptosystems (ECC) is to achieve the same security level as RSA but with shorter
key size. The basic operation in the ECC is scalar multiplication which is an expensive operation. In this paper,
we focus on optimizing ECC scalar multiplication based on Non-Adjacent Form (NAF). A new algorithm
is introduced that combines an Add-Subtract Scalar Multiplication Algorithm with NAF representation to
accelerate the performance of the ECC calculation. Parallelizing the new algorithm shows an efficient method
to calculate ECC. The proposed method has sped up the calculation up to 60% compared with the standard
method.
1 INTRODUCTION
Elliptic curve cryptosystems (ECC) are powerful
cryptosystem to encrypt data because they have a
high-level of security but shorter key sizes compared
with other existing algorithms such as RSA (Rivest
et al., 1978). For example, the elliptic curve cryp-
tosystems with 160-bit keys are considered to have
comparable security to 1024-bit RSA (Gura et al.,
2004). Several application fields of elliptic curve
cryptosystems such as RFIDs, smart mobile, and
smart cards, as the shorter key length also makes ECC
better to be used on portable devices. There are diffe-
rent reasons that enable them to be used widely.
The most important operations in the ECC are
the time-consuming scalar multiplications. There-
fore, many researchers have focused to enhance and
improve this area.
Elliptic curve cryptosystems (ECC) were indepen-
dently proposed by two researchers, Koblitz (Koblitz,
1987) and Miller (Miller, 1986). The security of ECC
is based on the Elliptic curve Discreet logarithm Pro-
blem (ECDLP), two given points in the elliptic curve
P and Q, the equation is Q = d.P, where d is an inte-
ger converted to the binary or signed binary, while a
given P is a point in elliptic curve.
The number of adding and doubling operations on
an elliptic curve are based on length n of the scalar d.
It is an integer which, for the purposes of the compu-
tation, is represented in binary — d =
∑
n−1
i=0
2
i
d
i
, d
i
∈
{0,1} —, or in signed binary — d =
∑
n−1
i=0
2
i
d
i
, d
i
∈
{
¯
1,0,1}, where
¯
1 is a ’-1’. Several ECC researchers
have been working to accelerate the performance of
the ECC scalar multiplication by introducing new
conversion algorithms to give low-Hamming-weight
representations of d. Hamming Weight (HW) is the
number of non-zero bits in the scalar representation
d. Reducing the number of the bits ’1’ (or ’
¯
1’) in the
scalar representation will reduce the number of addi-
tion operations in the ECC scalar multiplication. The-
refore, lower HW is preferred.
Several researchers have proposed new methods
to convert the binary representation to the signed bi-
nary representation in order to reduce the Hamming
Weight of the scalar d. These methods are Mutual
Opposite Form (MOF) (Okeya et al., 2004), Joint
Sparse Form (JSF) (Solinas, 2001), Non-Adjacent
Form (NAF) (Booth, 1951). As well as, Comple-
mentary Recoding Technique (CRT) is proposed (Ba-
lasubramaniam and Kathikeyan, 2007) which enhan-
ced to be Direct Recoding method (DRM) (Pathak
and Sanghi, 2010) and other methods (Huang et al.,
2010). Also, there are several methods proposed to re-
duce calculation time of the ECC scalar multiplication
by parallel computing (Azarderakhsh and Reyhani-
Masoleh, 2015) (Asif and Kong, 2017) (Gutub and
Arabia, 2010).
In this paper, acceleration of the performance of
the ECC scalar multiplication is proposed by paral-
lelizing scalar multiplication algorithm (Add-subtract
238
Anagreh, M., Vainikko, E. and Laud, P.
Accelerate Performance for Elliptic Cur ve Scalar Multiplication based on NAF by Parallel Computing.
DOI: 10.5220/0007312702380245
In Proceedings of the 5th International Conference on Information Systems Security and Privacy (ICISSP 2019), pages 238-245
ISBN: 978-989-758-359-9
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

scalar multiplication algorithm) and transforming the
scalar from binary representation to the signed binary
representation using the non-adjacent form (NAF) al-
gorithm. Scalar multiplication performance can be
improved by parallelizing the NAF algorithm.
This paper is organized as follows: Section 2
briefly introduces the ECC and scalar multiplication
algorithms. Section 3 gives the preliminaries. Section
4 is the related work. Section 5 presents our appro-
ach. Section 6 is the results and discussion. The last
section concludes the proposed method and discusses
future works.
2 ELLIPTIC CURVE
CRYPTOSYSTEM OVERVIEW
For cryptographic applications, elliptic curves are
considered over two main kinds of finite fields: the
binary fields F
2
m
and the prime fields F
p
, as described
below.
2.1 Binary Fields F
2
m
The finite field F
2
m
consists of 2
m
elements, which
are at most (m − 1)-th degree polynomials over Z
2
=
{0,1}, taken modulo an irreducible m-th degree poly-
nomial. An elliptic curve over this field is determined
by two elements a,b ∈ F
2
m
(Nichols, 1998). It con-
sists of all pairs (x,y) of elements of F
2
m
satisfying
the following cubic equation:
y
2
+ xy = x
3
+ ax
2
+ b
(1)
Additionally, there is one more element called the
point at infinity.
2.2 Prime Fields F
p
In this paper, we focus on the prime curves over F
p
.
The prime curves over F
p
make use of the cubic equa-
tion as identified in Equation (2) with Cartesian coor-
dinate variables (x,y) and coefficients (a, b) as ele-
ments of F
p
. All the values can be considered in-
tegers that are computed modulo the prime number
p (Stallings, 2005). The cubic equation with coeffi-
cients (a,b) and variables (x, y) for the elliptic curves
over F
p
is the following:
y
2
mod = (x
3
+ ax + b) mod p
(2)
let the point P = (x
1
,x
2
) and point Q = (x
2
,y
2
)
be in the elliptic curve over F
p
, defined by the coeffi-
cients (a,b). In addition, let O be the point at infinity.
The rules for addition operation in the EC is as fol-
lows:
P + O = P
(3)
Given point P and point Q, if x
1
= x
2
and y
2
= −y
1
then
P + Q = 0
(4)
In general, R = Q + P, where the result R = (x
3
,y
3
) is
defined as follows:
x
2
= λ
2
− x
1
− x
2
mod p
(5)
y
3
= λ(x
1
− x
3
) − y
2
mod p
(6)
λ =
y
2
−y
1
x
2
−x
1
mod p, if P 6= Q
3x
2
1
+a
2y
1
mod p, if P = Q
(7)
3 PRELIMINARIES
3.1 Non-Adjacent Form (NAF)
This representation of integers was proposed by
Reitwiesner (Reitwiesner, 1960). In Non-Adjacent
Form (NAF), a third digit with the value −1 (sub-
sequently denoted
¯
1) is added to the representation
of integers, beside the binary digits 0 and 1. The
NAF representation corresponds to the same value as
the binary representation but the difference appears
in the representation itself. The goal of using such
algorithms in the ECC is to reduce the Hamming
Weight which is the number of non-zero bits in
the key. Therefore, reducing the Hamming Weight
will reduce the number of addition operations in
the calculation of the scalar multiplication. So,
calculating the scalar multiplication based on the
signed binary representation will the reduce the total
execution time of an ECC operation.
Example : d = 958, converting d to the binary re-
presentation is (1110111110)
2
. The converting bi-
nary representation to the NAF is (1000
¯
10000
¯
10). To
prove the solution, let us convert the NAF to the deci-
mal, d = 1024-64-2 = 958.
The hamming weight of 958 is reduced from 8 to 3.
As known, one addition operation requires 2 squaring,
2 multiplications and 1 inversion. Using the NAF re-
presentations will save 10 squarings, 10 multiplicati-
ons and 5 inversions.
Accelerate Performance for Elliptic Curve Scalar Multiplication based on NAF by Parallel Computing
239

Data: n-bit integer K
Result: NAF Representation
(d
0
,d
1
,...,d
n−1
)
begin
C ← K, j ← 0
1 while C > 0 do
if C is odd then
d
j
← 2 - (C mod 4)
C ← C - d
j
else
d
j
← 0
end
C ← C/2
j ← j + 1
end
return NAF
end
Algorithm 1: NAF Representation Algorithm.
Algorithm 1 is the NAF Representation Algo-
rithm. The input must be an integer and the output is
the signed binary representation (d
0
,...,d
n−1
), where
d
i
∈ {
¯
1,0,1}. This representation will be used in fin-
ding the scalar multiplication of the ECC.
3.2 ECC Scalar Multiplication
The scalar multiplication is the main operation in the
ECC. Scalar multiplication is built up from two main
operations — addition of points, and the doubling of
a point. The scalar d — an integer — has to be con-
verted to a bit-string. The occurrence of bit ’1’ in the
representation corresponds to the operation of adding
two points. There are approximately n/2 such additi-
ons in a scalar multiplication. On the other hand, the
number of doubling operations is n − 1. In case of
signed binary representation, the third digit which is
¯
1 will be processed by the subtracting operations.
Algorithm 2 is an Adding-Subtracting Scalar mul-
tiplication algorithm, which is used to compute the el-
liptic curve scalar multiplication based on a scalar d =
∑
n−1
i=0
2
i
d
i
, represented either in binary — d
i
∈ {0,1}
— or in signed binary — d
i
∈ {
¯
1,0,1}
4 RELATED WORK
The improvement of the scalar multiplication can be
achieved by improving or proposing some related al-
gorithms in the scalar multiplication. Applying the
signed binary representation algorithms to find the
scalar multiplication is an efficient way to reduce the
number of non-zero bits in the key. Hamming Weight
is a big player to reduce the number of addition ope-
rations in computing the scalar multiplication.
Data: Point on EC P, a non-zero string
(d
0
,...,d
n−1
) representing d
Result: Q = dP
begin
Q ← 0, R ← P
1 for i = 0 to n-1 do
if (d
i
= 1) then
Q ← Q + R
else if (d
i
=
¯
1) then
Q ← Q - R
end
R ← 2R
end
return Q
end
Algorithm 2: Adding-Subtracting Scalar Multiplication Al-
gorithm.
There are many methods to represent integers in
signed binary such as NAF, JSF and MOF, Also in
2003 a new method to compute general multiplication
was proposed by Change et al (Chang et al., 2003)
which is the result of using the NAF, MOF and JSF.
Different researchers proposed methods to calcu-
late the scalar multiplication in parallel computing
using the binary or signed binary representation.
Ansari et al (Ansari and Wu, 2005), proposed a
parallel method based on task decomposition, to pa-
rallelize the ECC scalar multiplication. The binary
representation and double-and-add algorithm are used
to compute the ECC scalar multiplication.
In different fields of the applications such as
in a cloud computing need high-speed applications,
Chung et al (Chung et al., 2012) proposed a new
elliptic curve cryptography (ECC) processor archi-
tecture. The proposed processor requires much fe-
wer execution cycles than that of previous methods
which includes a 3 pipelined-stage full-word Mont-
gomery multiplier. As well as, the time-cost pre-
computation steps of Montgomery modular multipli-
cation are achieved by the processor to reach real-
time requirement. To improve hardware performance,
parallelization techniques and hardware sharing are
used. The results show that by using the proposed
elliptic curve cryptosystem processor in comparison
with relative works is 25% faster.
Pabbuleti et al (Pabbulti et al., 2013), proposed
vector processing techniques to accelerate modular
multiplications in prime fields. They implemented
their proposed work on two different embedded com-
puting platforms which are Intel Atom N2800 and
Qualcomm Snapdragon APQ8060. As well as, they
used a NIST- standard Prime filed curve. The re-
sult shows the proposed technique is faster than the
OpenSSL versions of the same ECC operations two
ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy
240

times.
Anagreh et al (Anagreh et al., 2014), proposed
a parallel method to compute scalar multiplication
based on the mutual opposite form (MOF). They
extracted a new algorithm that combined Adding-
Subtracting Algorithm and mutual opposite form
(MOF). The Method calculates the doubling opera-
tion and addition operation at the same time without
performing the MOF conversion. The proposed met-
hod is performing the comparison operation of the
bit-string to decide that the second processor has to
perform the addition operation in case of non-zero
bits. Robert (Robert, 2014) proposed different soft-
ware implementations for finding the elliptic curve
scalar multiplication. He tested the implementations
within two threads, and four threads algorithms on va-
rious elliptic curves over the prime F
p
and the binary
fields F
2
m
. The scalar multiplication is performed by
using the Double-and-add and Halve-and-add algo-
rithms.
This work talks about putting doubling operations
into one thread (producer) while additions and sub-
tractions into another thread (consumer). His met-
hod was to avoid using the mutex synchronization as
much as possible by using one single mutex at the
beginning of the computation. The goal of using the
mutex is to keep the thread which is responsible for
performing the addition or subtraction in an inactive
state. At the same time, the first batch of doubling
operations is computed by the producer thread.
The method shows some violation of the read-
after-write dependency. The memory violation may
happen because the size of the first batch of points
which is before releasing the mutex was too small.
As well as, in the case of the long sequence of zeros
in the binary or NAF scalar representation. The re-
sults have shown that this error rate is limited to less
than 1%, but is not acceptable because that causes the
corruption of the calculation.
The variable which is stored in the global memory
as the loop counter is used to eliminate this problem,
this allows the checking if the addition operation uses
a point which has already been produced to the shared
memory from the producer thread. The test which
is used on the addition-thread is an extra operation
that will reduce the parallel time. Computing the sca-
lar multiplication is based on the NAF representation
which is already given. The conversion method is not
a part of the proposed work. The software implemen-
tations achieved an enhancement 15% in the compa-
rison with their sequential case.
New parallel approaches are proposed by Negre
et al (Negre and Robert, 2015), they introduced pa-
rallel approaches which split the scalar multiplication
based on NAF into two parts for the prime field F
p
,
and three parts for the binary field F
2
m
. In this ap-
proaches, both operations (doubling and addition) or
subtraction will be performed in each thread, the split-
ting is for finding scalar multiplication itself. In the
case of the prime field, they divided the scalar multi-
plication into two parts, the first part Q
1
= k
1
P will be
performed in a thread and the second part Q
2
= 2
s
k
2
P
will be performed in another thread. Then at the end,
the two points Q
1
and Q
2
are added to get the sca-
lar multiplication Q = Q
1
+Q
2
. Computing the scalar
multiplication by parallel calculation is based on the
window size of Non-Adjacent Form (w-NAF). The re-
sult shows, that the proposed approaches achieved an
improvement by at least 10% the computation time of
the scalar multiplication.
Liu et al (Liu et al., 2016), proposed ECC soft-
ware implementation based on the NIST curve for
wireless sensor nodes and similar devices equipped
with an 8-bit AVR processor. The paper includes
a thorough evaluation of different protocols, tools,
and platforms. They demonstrated that the perfor-
mance of their elliptic curve cryptosystem implemen-
tation through three widely-used protocols, ECDH,
ECDSA, and ECMQV. In comparison to the state-of-
the-art, the proposed ECC implementation which uses
the ECDH and ECDSA achieve an enhancement by
factors of 1.35 and 2.33, respectively.
An optimal representation for right-to-left paral-
lel elliptic curve scalar multiplication is introduced by
Phalakarn et al (Phalakarn et al., 2018). They devised
a mathematical model that will reduce the calculation
time. As well as, proposed algorithms that will ge-
nerate the representations which will reduce the exe-
cution time of the model. The optimal representation
which is generated for multi-scalar point multiplica-
tion is under a condition. That a three processor will
perform the calculations, two for doubling P, Q and
the third processor for addition operation using two
binary representation n, m. They improved the paral-
lel double-and-add model by defining the time which
used in the model when performing the calculation.
Anyway, the issue of the communication time bet-
ween the processors in the model is still opened and
is not considered yet. That might affect the proposed
optimal representation especially in the case of using
three processors or more.
5 PROPOSED WORK
The minimum key size of the ECC is 160 bits, this
size can ensure same security level as 1024-bits key
size of the RSA. Therefore, reducing the execution
Accelerate Performance for Elliptic Curve Scalar Multiplication based on NAF by Parallel Computing
241

Data: Integer k, Point in EC P
Result: Q = kP, based on (NAF)
Processor 1 performs Doubling Operations
(DBL):
begin
R ← P
1 for i = 0 to n-1 do
R ← 2R
A
i
← R
end
end
Processor 2 performs NAF conversion,
followed by Addition Operations (ADD):
begin
C ← k, j ← 0
2 while C > 0 do
if C is odd then
d
j
← 2 - (C mod 4)
C ← C - d
j
else
d
j
← 0
end
C ← C / 2, j ← j + 1
end
3 for y = 0 to n-1 do
T ← A
y
m ← d
y
if m = 1 then
Q ← Q + T
else if m = -1 then
Q ← Q - T
end
end
return Q
end
Algorithm 3: Parallel Scalar Multiplication based on NAF
(PECC-NAF) Algorithm.
time of scalar multiplication by applying some an effi-
cient method is desired. In that case, we can increase
the size of the key that will increase the security le-
vel of the ECC with the same execution time. In this
work, we propose a parallel method that calculates
the ECC scalar multiplication based on signed binary
representation algorithm which is the NAF. We cal-
culate the scalar multiplication by applying the add-
subtract scalar multiplication algorithm. The propo-
sed method combines add-subtract scalar multiplica-
tion algorithm with the non-adjacent form algorithm.
We extracted a new algorithm (PECC-NAF) to per-
form the proposed scheme, see Algorithm 3.
Our parallel method strategy in this work is to pa-
rallelize the algorithm 3. Task decomposition strategy
is used to perform the parallel calculation by splitting
the adding-subtracting scalar multiplication algorithm
into two parts.
Part 1 will be processed by Processor-1 which
computes the n −1 doubling operations and saves that
doubled points in the shared array A. We can recog-
nize that there is no dependency between the kind
of bits {
¯
1,0,1} and doubling operations. Processor-
1 has to perform the doubling operations based on the
length of the key n−1, regardless of whether the bit is
’1’, ’0’ or ’
¯
1’. In this case, if the key size is 160-bits,
Processor-1 has to perform the doubling operations
159 times. Also, Processor-1 has to save the doubled
point in the shared array A, see Algorithm 3. The size
of the array A is the same size of n.
Part 2 of the algorithm, is to find the NAF repre-
sentation by applying NAF algorithm. Performing the
addition operations in the part 3 of the algorithm (both
part 2 and part 3 will be performed in the processor-
2). The total number of addition operations is equal
to the Hamming weight (the number of non-zero bits)
of the key. Processor-2 has to find the NAF repre-
sentation before performing the addition operations.
According to the kind of the bits (1 or
¯
1) in the NAF
representation, Processor-2 has to perform the addi-
tion or subtraction operations.
In case the bit is ’1’, Processor-2 perform the ad-
dition operation and saves the result in accumulator
Q, while if the bit is ’
¯
1’, performs the subtracting
operations and saves the result in the Q. If the bit is
’0’, Processor-2 does not have to perform any elliptic
curve operations.
Processor-2 performs addition or subtraction ope-
rations by reading the saved points (2P,4P,...,2
n−1
P)
in the shared array A, see Figure 1. Both processors
Figure 1: General Framework of Scheme.
have the ability to access the shared array A which is
located in the shared memory. Processor-1 perform
the writing in the array A, while Processor-2 perform
ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy
242

the reading in the array. We should carefully ma-
nage the reaching to the shared array. Processor-1
should be able to write only, while Processor-2 should
only be able to read. Also, Processor-2 should read
only from the locations which already contain dou-
bled points. We achieve this by making Processor-1
write the doubled points in the shared array A,
Processor-2 computes the NAF representation be-
fore performing the addition operations, in order to
avoid the bugs or reading some rubbish data from
the memory, while processor-1 performs the doubling
operation and save the result in the array A. In our
scheme, Processor-2 perform the NAF conversion be-
fore starting to perform the addition operations. Af-
ter performing the doubling operations, Processor-1
will save the results (doubled points) in the shared
array A. In this case, doubled points are already sa-
ved in the memory and ready to be read by Processor-
2. So, we can say that our method is managed au-
tomatically without adding some extra code or pro-
tocols to manage the synchronization of the memory
accesses. During the execution time of finding the
NAF representation by Processor-2, Processor-1 per-
forms the doubling operations and save the points in
the shared memory. So, some doubled points stored
already in the array A by Processor-1 to be reada-
ble by Processor-2 once finish the converting to the
NAF. Processor-1 will write the points in location d
i
,
while Processor-2 will read the points from location
d
j
, where d
i
> d
j
.
6 RESULTS AND DISCUSSION
We can summarize that the proposed method is ex-
tracting a new algorithm that combines two algo-
rithms: Add-Subtract Scalar Multiplication, and Non-
Adjacent Form. It performs the parallel computing on
the extracted algorithm (PECC-NAF), given in Algo-
rithm 3. In Figure 2, we can recognize clearly the
performance result we get from the real implementa-
tion of our proposed scheme. In the implementation,
we tested three different key sizes: 160-bits, 256-bits,
and 522-bits. Each key size is represented with two
fractions of occurrence of the non-zero bits in the key
given by N = Total of non-zero bits / key-size.
The result shows that the best case is when the
number of non-zero bits is close to the key size. The
the best difference time (between parallel and serial
versions) we got in case of key-size is 256-bits and
522-bits in case of N = 1. Its important to note, we
tested our implementation when N = 1 to get the va-
riance time between the parallel version and standard
version to test the parallel method, not to get the best
Figure 2: The Performance Results.
result. In the Figure 3, we can see that the execution
time is high cost in the case N = 1. In the real-time,
the number of hamming weight in the NAF represen-
tation is less than in the binary representation, it’s ra-
rely to be N = 1.
As with almost all parallel applications, it’s impor-
tant to produce the best sequential code before star-
ting to parallelize the code. Task decomposition is
used to divide the work into two Processors to per-
form the overall scheme to get the best result as shown
in Figure 2. We wrote both the sequential and the
parallel code in Visual C++.Net. We use the Open
MP Library that is supported in the Visual C++.Net
package in order to write the parallel section in the
parallel version. It’s important to note that we use
Intel Dual-Core machine to test both versions using
Windows 7. The specification of the machine is Intel
Dual core with 1 MB L2 cache memory. We perfor-
med each key size in both N cases 10 times and the
average execution time is taken as shown in Figure 3.
The execution of the code for both serial and pa-
rallel versions show that the result of the scalar mul-
tiplication is the same in both cases. The scalar mul-
tiplication in the parallel version (proposed method)
is the same as the scalar multiplication in the serial
version (standard method), meaning that Processor-2
reads the doubling point from the location in the ar-
ray correctly to perform the addition operation. In
such cases, we have to organize the reading and wri-
ting operations correctly to avoid reading rubbish data
from the memory.
In our proposed method as we can see in Algo-
rithm 3, Processor-1 has to write the doubled point
R
i
in the shared array A each round n
i
in the whole
rounds of the key size n. The writing is always per-
formed in a different location of the array A respecti-
vely. Each point has a unique location that will be
readable from Processor-2. There is no possibility
to write two points at the same location because the
doubling operation is done serially. Processor-2 per-
form the NAF conversion before performing the ad-
dition or subtraction operations. while at the same
Accelerate Performance for Elliptic Curve Scalar Multiplication based on NAF by Parallel Computing
243
time Processor-1 performs the doubling operations
and writes the doubled points in the array. Processor-
2 reads the doubled points from the shared array A and
performing either addition operation in case the d
i
is
1 or performing the subtraction operation in case the
d
i
is
¯
1. In case the d
i
is 0, Processor-2 ignores perfor-
ming the addition or subtraction in that location, see
in Figure 1.
We tested our implementation several times, we
did not record any occurrence of error. The main point
in our implementation is that Processor-1 writes the
doubled point in location d
i
while Processor-2 reads
the doubled point from location d
j
, while d
i
> d
j
. As
well as, Processor-2 starts reading the doubled points
after finding the NAF conversion.
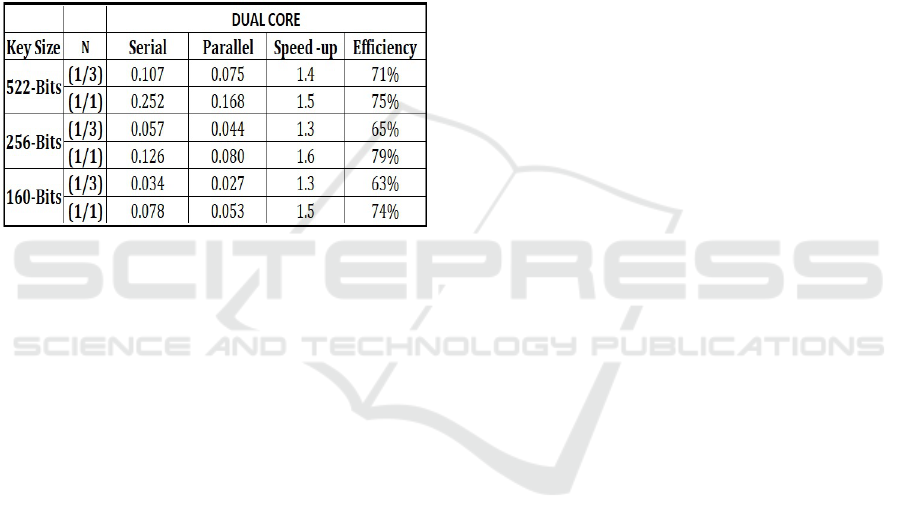
Figure 3: The time in milliseconds.
The aim of our scheme is to reduce the execution
time of computing the ECC scalar multiplication.
Therefore, we can exploit the time variance between
the parallel execution and the standard case to
increase the key size of the ECC. The execution time
of the expanded key size will be the same as the
execution time of the sequential version.
For example, consider the key size of 160-bits and
N = 1/3. Both the serial and parallel time (in milli-
seconds) can be looked up from Figure 3. Assuming,
the key size is 160-bits, the execution time of the se-
rial version as shown in Figure 3 is 0.034 ms and pa-
rallel time is 0.027 ms. The difference between them
is 0.007 ms. The execution time for each iteration in
parallel time is around 0.027 ms/160 = 0.00016 ms.
Therefore, we can increase the key size according to
the difference among serial and parallel time as fol-
lows: 0.007 / 0.00016 = 43.3 iterations, thus we can
expand the key size to 43 bits higher than 160-bits.
We can summarize, that by applying our scheme the
execution time of the scheme with a key size of 203-
bits gives us the same execution time as the serial ver-
sion with 160-bits. And therefore, the security level
of the ECC with 203-bits key size is more than the
security level of the ECC with 160-bits key size.
In the best cases of our method as 256-bits while
N = 1, the speed-up is around 1.6 times. Let us
test another best case of our method which is 160-
bits while N = 1, the speed-up is around 1.5x. The
time difference between serial time and parallel time
is 0.025ms. The execution time for one iteration
in the case of parallel version is 0.053 ms/160 =
0.00033 ms. Therefore, we can increase the key size
by 0.025/0.00033 = 75.7 bits, then we can expand the
size of the ECC key 75-bits more and of course, that
will increase the security level of the scheme. As we
mentioned above, the security level of the ECC with
160-bits key size is the same security level of the RSA
with 1024-bits key size. In case the RSA has a key
size 2048-bits, it’s considered as the same security le-
vel of the ECC which has 224-bits key size. There-
fore, our method will decrease the execution time in
the best cases around 50% to 60%. So, we can incre-
ase the security level of the standard scheme by ap-
plying our proposed method. Increasing the security
level by expanding the key size 160 + 75 = 235 bits
which have the same execution time of the standard
method.
We can summarize, the execution time of finding
the ECC scalar multiplication with a key size 235- bits
in the parallel version is the same execution time of
finding the ECC scalar multiplication with key size
160-bits in the serial version. Therefore, the security
level of the proposed method is reached to the 235-
bits which is more than the security level of 2048-bit
key size of the RSA (235-bits > 224-bits), and that is
the significance of the proposed method.
7 CONCLUSIONS
In this work, we extracted a new algorithm that com-
bines the adding-subtracting scalar multiplication al-
gorithm with non-adjacent form (NAF). We paralleli-
zed the proposed algorithm using two processors. The
first processor performs the doubling operations while
the second processor performs the NAF conversion
and adding or/and subtracting operations. We tes-
ted our proposed method with different key sizes. In
Processor-2, finding the NAF conversion organized to
be before performing the addition and/or subtraction
to avoid any error occurrence. Processor-1 supports
the doubled point to the Processor-2. The difference
in hamming weight can affect the execution time in
both parallel and serial versions.
The future work is testing almost signed binary
representation algorithms such as MOF, JSF comple-
mentary method, and other signed binary represen-
tation methods. Testing our proposed method is by
using two processors and passing the data among two
processors using a shared memory. We assume that
ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy
244

using three processors will reduce the execution time
more, especially in performing the addition operati-
ons.
REFERENCES
Anagreh, M., Samsudin, A., and Omar, M. (2014). Paral-
lel method for computing elliptic curve scalar mul-
tiplication based on mof. Int. Arab J. Inf. Technol,
11(6):521–525.
Ansari, B. and Wu, H. (2005). Parallel scalar multiplication
for elliptic curve cryptosystems. In Proceedings of In-
ternational Conference on Communications, Circuits
and Systems, vol. 1, pages 71–73.
Asif, A. and Kong, Y. (2017). Highly parallel modular mul-
tiplier for elliptic curve cryptography in residue num-
ber system. Circuits, Systems, and Signal Processing,
36(3):1027–1051.
Azarderakhsh, R. and Reyhani-Masoleh, A. (2015). Pa-
rallel and high-speed computations of elliptic curve
cryptography using hybrid-double multipliers. IEEE
Transactions on Parallel and Distributed Systems,
26(6):1668–1677.
Balasubramaniam, P. and Kathikeyan, E. (2007). Ellptic
curve scalar multiplication algorithm using comple-
mentary recoding. Applied mathematics and compu-
tation, 190(1):51–56.
Booth, A. (1951). A signed binary multiplication technique.
Journal of Applied Mathematics, 4:236–240.
Chang, C., Kuo, Y., and Lin, C. (2003). Fast algorithms for
common-multiplicand multiplication and exponentia-
tion by performing complements. In Advanced In-
formation Networking and Applications, 2003. AINA
2003. 17th International Conference on, pages 807–
811. IEEE.
Chung, S., Lee, J., chang, C., and Lee, C. (2012). A
high-performance elliptic curve cryptographic proces-
sor over gf(p) with spa resistance. In Circuits and Sy-
stems (ISCAS), 2012 IEEE International Symposium
on, pages 1456–1459.
Gura, N., Patel, A., Wander, A., Eberle, H., and Shantz, S.
(2004). Comparing elliptic curve cryptography and
rsa on 8-bit cpus. In Proceedings of the International
workshop on cryptographic hardware and embedded
systems, pages 119–132. Springer.
Gutub, A. and Arabia, S. (2010). Remodeling of elliptic
curve cryptography scalar multiplication architecture
using parallel jacobian coordinate system. Internati-
onal Journal of Computer Science and Security (IJ-
CSS), 4(4):409–ff.
Huang, X., Shah, G., and Sharma, D. (2010). Minimizing
hamming weight based on 1’s complement of binary
numbers over gf (2 m). In Advanced Communica-
tion Technology (ICACT), 2010 The 12th Internatio-
nal Conference on, pages 1226–1230.
Koblitz, N. (1987). Elliptic curve cryptosystems. Mathe-
matics of computation, 48(177):203–209.
Liu, Z., Seo, H., Großsch
¨
adl, J., and Kim, H. (2016). Ef-
ficient implementation of nist-compliant elliptic curve
cryptography for 8-bit avr-based sensor nodes. IEEE
Transactions on Information Forensics and Security,
11(7):1385–1397.
Miller, V. (1986). Use of elliptic curves in cryptography. In
Advances in Cryptology, Proceedings of CRYPTO85
(LNCS 218), pages 417–426. Springer.
Negre, C. and Robert, M. (2015). Parallel approaches for
efficient scalar multiplication over elliptic curve. In
SECRYPT: International Conference on Security and
Cryptography, pages 202–209.
Nichols, R. K. (1998). Biometric Encryption, chapter 22.
McGraw-Hill.
Okeya, K., Schmidt-Samoa, K., Spahn, C., and Takagi, T.
(2004). Signed binary representations revisited. In An-
nual International Cryptology Conference, CRYPTO
2004, pages 123–139. Springer.
Pabbulti, K., Mane, H., Desai, A., Albert, C., and
Schaumont, P. (2013). Simd acceleration of modu-
lar arithmetic on contemporary embedded platforms.
In High Performance Extreme Computing Conference
(HPEC), pages 1–6. IEEE.
Pathak, K. and Sanghi, A. (2010). Speeding up computation
of scalar multiplication in elliptic curve cryptosystem.
International Journal on Computer Science and Engi-
neering, 2(4):236–240.
Phalakarn, K., Phalakarn, K., and Suppaktpaisarn, V.
(2018). Optimal representation for right-to-left paral-
lel scalar and multi-scalar point multiplication. In-
ternational Journal of Networking and Computing,
8(2):166–185.
Reitwiesner, G. (1960). Binary arithmetic. Advances in
Computers, 1:231–308.
Rivest, R., Shamir, A., and Adleman, L. (1978). A method
for obtaining digital signatures and public-key cryp-
tosystems. Communications of the ACM, 21(2):120–
126.
Robert, M. (2014). Parallelized software implementation of
elliptic curve scalar multiplication. In International
Conference on Information Security and Cryptology,
pages 445–462. Springer.
Solinas, J. (2001). Low-weight binary representations for
pairs of integers. Technical Report CORR 2001-41,
Center for Applied Cryptographic Research, Univer-
sity of Waterloo.
Stallings, W. (2005). Cryptography and Network Security
Principles and Practices. Prentice Hall, 4th edition.
Accelerate Performance for Elliptic Curve Scalar Multiplication based on NAF by Parallel Computing
245
