
Dynamic Path Planning with
Stable Growing Neural Gas
Carsten Hahn, Sebastian Feld, Manuel Zierl and Claudia Linnhoff-Popien
Mobile and Distributed Systems Group, LMU Munich, Munich, Germany
Keywords:
Path Planning, Autonomous Agents, Robots, Machine Learning, Collision Avoidance, Neural Networks.
Abstract:
This paper considers the problem of path planning under dynamic aspects. We propose ”Neural Gas Dynamic
Path Planning” (NGDPP), a novel algorithm that continuously provides a valid path between two points inside
an environment that transforms in an unpredictable manner. These transformations can occur due to both,
changes in the environment’s shape and moving collision objects. The algorithm incorporates several tech-
niques: Neural Gas, a dynamic discretization method; the A* Algorithm, a path planning algorithm for graphs;
and the Potential Field method, which facilitates the avoidance of collisions. We empirically evaluate the pro-
posed algorithm under various aspects providing performance information and guidance about situations and
applications benefiting from the algorithm. The evaluation reveals that NGDPP is a solid algorithm for path
planning in dynamic environments. Yet, the algorithm is based on heuristic information, i.e. a optimal result
in term of the path length cannot be guaranteed.
1 INTRODUCTION
Autonomous path planning is an important topic in
artificial intelligence research. From an evolutionary-
biological point of view there is the assumption that
the brain in living beings has arisen, among other
things, from the need to move (Legendre et al.,
1994). It is therefore logical that one goal in the field
of Artificial Intelligence is to make purposeful and
meaningful movements automatically, i.e. computer-
controlled. A meaningful movement is only possible
if it has been planned beforehand, which leads to the
path planning problem.
We consider a problem domain consisting of an
autonomous agent that is able to move freely in a two
dimensional floor plan. The agent’s goal is to navigate
to given targets. Besides, an agent can either locate
itself inside the floor plan or knows at least its starting
position. We also allow that the walkable area can
change dynamically. These changes may occur due to
new areas that are made available or due to blockades
that separate the previously walkable area. The agent
shall adapt its plan to these changes. Finally, the agent
should neither collide with static obstacles nor with
dynamic obstacles like other agents.
In the following, the problem domain will be split
into three subproblems: a) Discretization of the con-
tinuous domain into a graph structure to ease compu-
tation , b) Path planning on the previously generated
graph structure, and c) Deployment of a suitable col-
lision avoidance strategy.
We propose a complete solution (namely NGDPP)
to the described problem domain that combines ex-
isting methods for the individual subtasks. We show
the benefits arising by the combination of the chosen
methods. Furthermore we propose improvements for
the method chosen to discretize the continuous do-
main, namely Stable Growing Neural Gas (SGNG).
The paper is structured as follows. In Section II
common related approaches are outlined. Our ap-
proach as well as the used methods are presented in
Section III. This is followed by an evaluation in Sec-
tion IV. The paper is concluded in Section VI, where
also clues for future work are given.
2 RELATED WORK
There are multiple existing approaches that solely
treat one of the named subproblems. We focus on two
of the most common approaches for the discretization
and path planning in a continuous domain.
The Probabilistic Roadmap (PRM) (Kavraki et al.,
1996) method is a path planning algorithm for con-
tinuous spaces. The algorithm quantizes the space
by randomly setting nodes and connecting all exist-
138
Hahn, C., Feld, S., Zierl, M. and Linnhoff-Popien, C.
Dynamic Path Planning with Stable Growing Neural Gas.
DOI: 10.5220/0007313001380145
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 138-145
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ing nodes within a predefined distance with an edge,
if the space allows it. Disjoint graphs, that possibly
occur, are connected in a posterior step. The pro-
cedure might produce many redundant edges which
densely cover certain areas of the space. Since the
graph created by the Probabilistic Roadmap is only
a snapshot of space in time, the question arises of
how to deal with dynamically changing spaces. In
this case, it is necessary to recalculate the roadmap
unless one has specific information about the nature
of the changes. Such a complete recalculation is very
inefficient. However, there are procedures that make
the replanning of Probabilisic Roadmaps more effi-
cient (Belghith et al., 2006). These are essentially
based on accelerating the path planning phase by us-
ing dynamic graph-based path planning algorithms
that do not require a complete recalculation of the
path (Likhachev et al., 2005).
Similar to the Probabilistic Roadmap, so-called
Rapidly Exploring Random Trees (RRT) (LaValle,
1998) are also based on the random generation of
waypoints. The intention behind RRT was to include
physical phenomena that influence real path planning
directly into the planned path. The path calculated
by a Probabilistic Roadmap may have sudden turns at
a certain angle: a path that a real agent (e.g. a car)
with properties such as speed, acceleration or braking
distance may not be able to drive. RRT is therefore
particularly suitable for non-holonomic systems. As
described, Probabilistic Roadmaps may return several
disjoint graphs that can only be connected after a high
number of iterations. The RRT procedure solves this
problem by using a different data structure. A sin-
gle tree is created from the starting position of the
agent, to which each node that is generated must be
connected. One can easily trace back from the target
node to its topological parent node until the root of
the tree is reached, i.e. the position of the agent. The
inversion of this path then corresponds to the path the
agent has to move. Advantageous is the possibility
to define conditions for new nodes during generation
that take properties such as speed, acceleration, etc.
into account. A drawback, however, is the fact that a
new tree must be generated for each agent when con-
trolling several agents.
3 NEURAL GAS DYNAMIC PATH
PLANNING
The algorithm proposed in this paper – Neural Gas
Dynamic Path Planning (NGDPP) – tries to solve the
path planning problem in a very general way by ap-
plying to dynamic spaces, both in the form of spa-
tial changes and dynamic obstacles. Several agents
should be able to approach any target inside a con-
tinuous space without colliding with walls, collision
objects or each other.
NGDPP uses a matrix in form of a bitmap to rep-
resent the original space, whereby individual pixels
can be either free or occupied. However, in order to
maintain the continuous property of space, the bitmap
can be as large or as fine as necessary. We call the set
of all free pixels in space the signal space. Although
the signal space is finite, it can be enlarged and thus
retains its continuous character.
Basically, the algorithm is divided into three paral-
lel running parts. These are discretization, path plan-
ning and collision avoidance.
3.1 Discretization through Stable
Growing Neural Gas
The discretization creates a waypoint graph from
the signal space. The graph consists of nodes and
edges, whereas nodes represent positions in space
and edges represent collision-free transitions between
them. Since sporadic changes in space can occur,
it is necessary to choose a method for discretization
that also can dynamically co-develop a representa-
tion of this space. For this dynamic discretization
we use the Stable Growing Neural Gas (SGNG) al-
gorithm (Tenc
´
e et al., 2013), which is an iterative un-
supervised learning technique that learns the underly-
ing topology of an n-dimensional space in quantized
form. It is an extension of the neural gas (Martinetz
et al., 1991) and the growing neural gas algorithm
(GNG) (Fritzke, 1995) for dynamic scenarios which
is more stable in respect to the number of nodes that
are created.
The term “gas” refers to the fact that the nodes
of the formed topology evenly distribute in space,
similarly to gas molecules. GNG has been used be-
fore for waypoint graph generation in a static fashion
(Dellinger et al., 2017). However, the key feature of
the SGNG, that we use, is that it continuously evolves
with the space as it changes. Furthermore, the algo-
rithm can be executed continuously as it converges to
a stable state in regard to the number of nodes.
We understand sporadic changes as modifications
in the matrix of space forming the signal space and as-
sume that these changes have a relatively large surface
area. In addition, the changes should not occur too
dynamically as the neuronal gas would fail due to its
latency to remedy erroneous edges or nodes (likewise
Figure 1a). Therefore, small or fast dynamic changes
have to be treated in a different manner with the help
of collision avoidance, as explained later on.
Dynamic Path Planning with Stable Growing Neural Gas
139

The SGNG algorithm is continuously executed in
order to build up a topological representation that can
develop dynamically with the space. If a certain area
of the space becomes unaccessible, no more signals
are generated there. This in turn means that the nodes
at this location are no longer selected by the algorithm
and thus the “age” of the connected edges increases
until they are finally removed. If all edges of a node
have been removed, also the node is removed. If a
new area is added to the space, signals are also gen-
erated there and nodes are pulled in their direction.
Due to the usually longer distances between existing
nodes and the signal, the “error” property of the node
increases and thus new nodes are more likely to form
which fill the newly created space. The high level
pseudocode of NGDPP is shown in Algorithm 1. The
agent uses the created waypoint graph in its step()-
Method which is further explained in Section 3.3.
The discretization of the environment with SGNG
might not be optimal. This error also strongly de-
pends on a “maxError” variable which steers the cre-
ation of new nodes and with which the precision of
the SGNG can be controlled. A comparison of two
different settings of this “maxError” variable can be
seen in Figure 1.
Algorithm 1: NGDPP.
Req.: graph ← GRAPH(nodes ← [], edges ← [])
area ← LOADINITIALAREA()
agents ← LOADAGENTS()
collisionObjs ← LOADCOLLISIONOBJS()
1: nodes ← [n
1
,n
2
]
2: i ← 0
3: while True do
4: i ← i + 1
5: # get a random free position in the area
6: s ← GETSIGNAL(area)
7: # find the nearest two nodes in the graph to s
8: n
1
,n
2
← NEARESTNODES(s, graph)
9: n
1
.error ← n
1
.error + DISTANCE(s, n
1
)
2
10: # moves node n
1
and its neighbors towards s
11: ATTRACTNODES(s, n
1
)
12: # new edge between n
1
and n
2
if not existing
13: NEWEDGECONNECTION(n
1
, n
2
)
14: # delete edges according to Section 3.1
15: AGESELECTION(i)
16: # heuristic creation of new nodes
17: SPLITNODES()
18: DECREASEALLERRORS()
19: for each agent in agents do
20: agent.STEP(area, collisionObjs, graph)
21: end for
22: end while
(a) • (b) •
Figure 1: In the comparison of the SGNG with low (a) and
high precision (b), it is noticeable that in the first case wrong
(not collision-free) edges can be formed (colored in red).
In order to allow the agents to navigate to any des-
tination in space, we propose to integrate the targets
as nodes into the routing graph. Target nodes do not
have to be defined at the beginning, but can be in-
serted at runtime. This is especially useful if not all
targets are known at the beginning. Unlike a normal
node, a target node has the following three properties:
1. Directly after a target node has been created, it
must be connected with the node having the short-
est distance to it. Else it would be immediately
deleted.
2. If the target node has got only one edge and this
edge exceeds the “maxAge”, its “age” variable
must be reduced by at least one in order to keep
the edge.
3. Targets should be static. If the algorithm tries to
move a target node, because it is the next node to
a signal (or the topological neighbour of such a
signal), this is not permitted and is therefore not
executed.
From these properties it follows that it is not possible
for the SGNG algorithm to remove a target node and
they have to be removed otherwise for example, if an
agent has reached its target.
Nearest Neighbor Problem. A large part of the
SGNG’s computational cost is caused by the need
to find the nodes with the shortest distance to a cer-
tain position in every iteration. This search could be
done simply by measuring the distance between each
node in the graph and the position and then sorting
the nodes accordingly. However, this is quite ineffi-
cient, especially with a high number of nodes. We
therefore strive to optimize this search. Due to the
highly dynamic character of SGNG, in which nodes
move in space in every iteration, we do not consider
advanced space-partitioning data structures like k-d
Trees (Bentley, 1975) as suitable for our approach as
these data structures had to be costly rebuilt or up-
dated in every iteration.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
140

We pursue a simpler approach and divide the
graph space into a grid. Each node is stored in a two-
dimensional array at the position where it is located
within this grid. A node located at the position (x,y)
can then be stored in the array at position g
i, j
with
(i, j) = (b(x/a)c,b(y/a)c), where a indicates the ac-
curacy of the grid and b. . .c rounds the result off to
integers. The accuracy must be defined in the begin-
ning and must not be changed during the runtime of
the algorithm. If we now save all nodes according to
this scheme, we can use this to find the next node in
the graph much more efficiently. Whenever a node
is moved, its position within the array must also be
checked and possibly updated. This is not a major
problem, as the formula for g
i, j
is evaluated very fast.
Sorted List for Edges. Another factor that in-
creases the calculation effort of the algorithm is the
calculation of the “edge age”. In principle, the SGNG
algorithm requires that each edge receives an “age”
property, which is increased by one at each iteration.
In addition, it must be checked for each edge whether
it has exceeded a “maxAge”. We propose a more ad-
vanced strategy:
Each edge receives a property “birth” instead of
an “age”. This specifies the iteration step of the al-
gorithm for which the edge was created. The edges
are now stored in a list. The oldest edge, whose birth
property is the lowest, comes first. As soon as a new
edge is created, it has an age of zero (“birth” = current
iteration step) and it is simply added at the tail of the
list. The resulting list is naturally sorted as the itera-
tion counter is strictly monotonically increasing. For
the deletion of outdated edges the algorithm no longer
has to check all edges in every iteration, but can sim-
ply inspect the last edge in the list. Subtracting its
“birth” from the current iteration step gives its age. If
this value exceeds the “maxAge”, it is deleted from
the list and from the graph. Then the following edge
(from direction of the tail) also has to be checked as
it might be the same age. If it has not exceeded the
maximum age, it can be calculated when it exceeds
it at the earliest time by subtracting the “birth” value
from the current iteration count. By storing this value,
we know for how many iterations it is not necessary
to check whether an edge is too old. Thus, the algo-
rithm does not only save iterating over all edges, but
also does not have to check the edges at all for several
iterations of the main loop.
It also happens in SGNG that the age of edges is to
be reset to zero. In this case we remove the edge from
the list, no matter at which position it is located, set
its “birth” variable to the current iteration count and
add it at the tail of the list.
3.2 Path Planning with A*
Parallel to the waypoint graph, a path for the agent
must be calculated. Due to the dynamic property of
the graph, planned paths do not have to necessarily be
valid over time. This problem can be solved by a con-
tinuous recalculation of the path. Of course, in case
of multiple agents, each agent must calculate its own
path in parallel using the globally available waypoint
graph.
We use the A*-algorithm (Hart et al., 1968) for
path planning, because the formed waypoint graph is
located in Euclidean space and thus heuristic informa-
tion can easily be extracted which provides a perfor-
mance advantage compared to the Dijkstra algorithm
(Dijkstra, 1959). For the A* algorithm, it is neces-
sary to know the cost of the edges. In our case, these
are described by the distance between nodes in space.
The cost of an edge between two nodes can be calcu-
lated using the Euclidean distance. Since this calcu-
lation must be applied to all edges that are examined
during path planning, it accounts for a large part of
the calculation effort of path planning.
However, the SGNG algorithm spanning the graph
has a crucial property that the NGDPP can take advan-
tage of to save itself these calculations. The SGNG al-
gorithm is designed in such a way that the nodes con-
verge to a state in which they are evenly distributed
within the space, similar to a gas on a molecular level,
which implies that edges formed between nodes level
off quite exactly to the same length. This property
results from the fact, that the generated signals are
uniformly distributed over the space and nodes are ac-
cordingly generated or displaced.
The fact that all edge lengths are almost the same
makes the calculation of their exact length obsolete.
It is sufficient to set the edge costs equal to one. The
performance advantage resulting from this methodol-
ogy and the fact that there is no deterioration of the
path is one of our contributions and further evaluated
in Section 4.
3.3 Collision Avoidance through the
Potential Field Approach
A collision object, i.e. an object that moves within the
space, does not directly alter the original space. Ob-
viously, the agent cannot enter the area where a colli-
sion object is located, although this area is part of the
space. In principle, the collision object could also be
defined as a change in space. However, such an inter-
pretation is not sensible due the following properties
of a collision object.
A collision object does not change its size, is
Dynamic Path Planning with Stable Growing Neural Gas
141
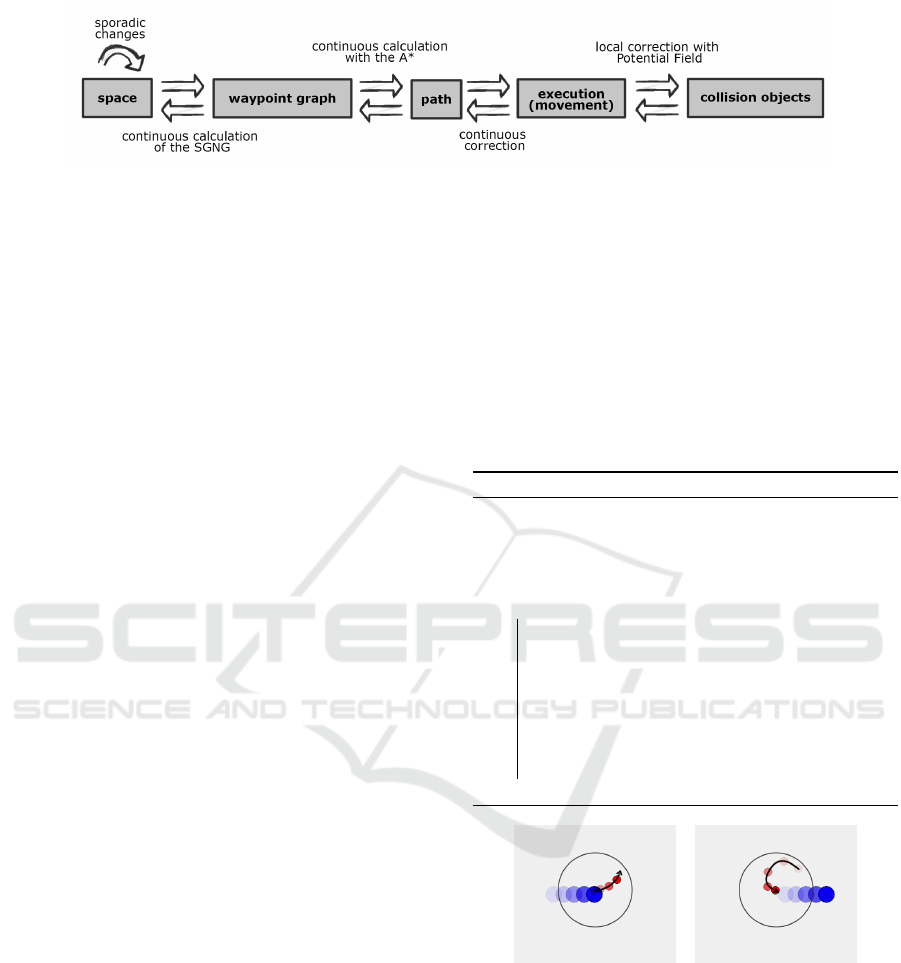
Figure 2: Structure of the NGDPP.
mostly in motion and it is usually much smaller than
the sporadic changes that might occur to the space. As
the neuronal gas takes some time to adapt to changes,
it is not practical to apply it directly to small fast mov-
ing objects. The much more important reason is, that
the graph should represent a globally valid topology
of the space. If we assume an area in which two
agents are to move independently, from an agent’s
point of view, the other agent is nothing more than
a collision object that moves relatively unpredictable.
If we applied the neural gas directly to avoid colli-
sion objects, it would be necessary to create a separate
SGNG graph for each individual agent as the graph
would no longer be globally valid. However, a glob-
ally valid graph yields the great advantage that it can
be calculated by one central processing unit, while it
can be used by multiple agents concurrently.
Therefore, we use the potential field approach
(Koren and Borenstein, 1991) for collision objects. In
order to move several objects in the same space with-
out collisions, the phenomenon of electromagnetism
is copied from nature. It describes mathematically
the fact that two particles with the same charge re-
pel each other. This concept is applied to collision
objects. Objects within space are in principle treated
like particles with the same charge, so that in the event
of an impending collision they are repeled from each
other and thus prevent a collision.
On its own, the potential field is not enough for
planning the route. However, it is very effective at
avoiding collisions between objects in local space.
Therefore it is used in our NGDPP algorithm. In or-
der to apply the “Potential Field” and allow an agent
to leave its planned path locally, we extend the ba-
sic agent which was only defined by its position to a
“force field agent” which is defined by the three prop-
erties position of the force field, detection radius and
position of the agent.
The agent is surrounded by a force field within
which collision objects are detected. As a result, the
agent no longer has an absolute position in space, but
receives relative coordinates to the center of its force
field. So instead of moving the agent directly along
its path, now the agent’s force field is moved along
the path, with the agent normally located in the center
of the force field (x = 0,y = 0). If a collision with
another agent is imminent, so if one enters the agent’s
force field radius, the agent can move within its force
field (see Figure 3). Because an attracting force is
constantly applied to the agent towards the center of
the force field, the agent returns to its relative zero
position when no collision object is within its detec-
tion radius. Some more insight in the movement of
the agent is given in algorithm 2. The entire NGDPP
process is summarized in Figure 2.
Algorithm 2: agent.STEP( ).
Precon.:graph ← GRAPH(nodes ← [], edges ← [])
area ← LOADINITIALAREA()
collisionObjs ← LOADCOLLISIONOBJS()
target ∈ graph.nodes
1: function STEP(area, collisionObjs, graph)()
2: # move agent according to Section 3.3
3: MOVEAGENTINFORCEFIELD(collisionObjs)
4: # find nearest node in the graph to s
5: n ← NEARESTNODE(agent.position, graph)
6: path ← PATHPLANNING(n, target)
7: # execute one step of the path
8: MOVEFORCEFIELD(path)
9: end function
(a) • (b) •
Figure 3: An agent (red) evades a collision object (blue)
within its force field. After the collision object leaves the
detection radius, the agent returns to the center.
4 EVALUATION
In this section we will empirically evaluate the as-
sumption about the evenly distributed edge lengths
that we proposed and other properties of NGDPP, like
occurring collisions. Also, NGDPP is compared to
related work methods.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
142

4.1 Simplification for the Usage of A*
In Section 3.2 the assumption was made, that the
SGNG algorithm produces a graph with equal-sized
edges. This simplifies the path planning as the real
edge lengths do not have to be calculated, which
yields a performance advantage. In Figure 4 both
the mean values and the variances of the edge lengths
over 100,000 iterations are shown. There is a strong
rash in the variance at the beginning, but it converges
quickly towards zero. Also the mean value converges
against a certain value after a few thousand iterations
of the algorithm. That means, that it is sensible to
assume all edge lengths to be the same, i.e. to be one.
Figure 4: Mean and variance of all actual edge lengths over
more than 100,000 iterations of NGDPP.
The above assumption was used to compare the
performance of four different path planning algo-
rithms. Figure 5 shows, that the “simple” procedures,
which utilize the assumption, dominate the others in
terms of performance. In addition, it was checked for
more than 1 million iterations whether the methods
calculate a different path length. This could theo-
retically happen due to inaccurate edge lengths, but
also due to the heuristic mode of operation of the A*.
However, not a single deviation in the length of the
path was found. Not only does this improve perfor-
mance, it is also highly likely that the calculated path
Figure 5: Performance comparison of path planning algo-
rithms with and without the assumed simplification.
will retain its quality.
4.2 Collisions
NGDPP is a heuristic algorithm and Collisions can
occur between agents as well as between agents and
their environment.
As mentioned in Section 3.1 the discretization of
the environment with SGNG is not perfect as the pre-
cision is bound to parameters of the algorithm and
also due to the fact that it iteratively adapts to changes
in the environment. That is why we measured the
number of wrong edges, that means, edges that in-
tersect with the environment (see Figure 1), after a
change of the map over time. The experiment shows
that the proportion for wrong edges (or nodes) de-
creases significantly over time after a map change
(Figure 6).
Figure 6: Percentage of wrong edges over time.
Figure 7 shows the evaluation of occurring colli-
sions between agents. A number of 1-20 agents col-
lected random targets over 100,000 iterations in a free
space. Since collisions are probabilistic, the exper-
iment was repeated eight times for each number of
agents. The curve shows the average number of col-
lision per agent amount. It can be seen that a larger
number of agents leads more frequently to collisions.
Figure 7: Evaluation of the collision of multiple agents.
Dynamic Path Planning with Stable Growing Neural Gas
143
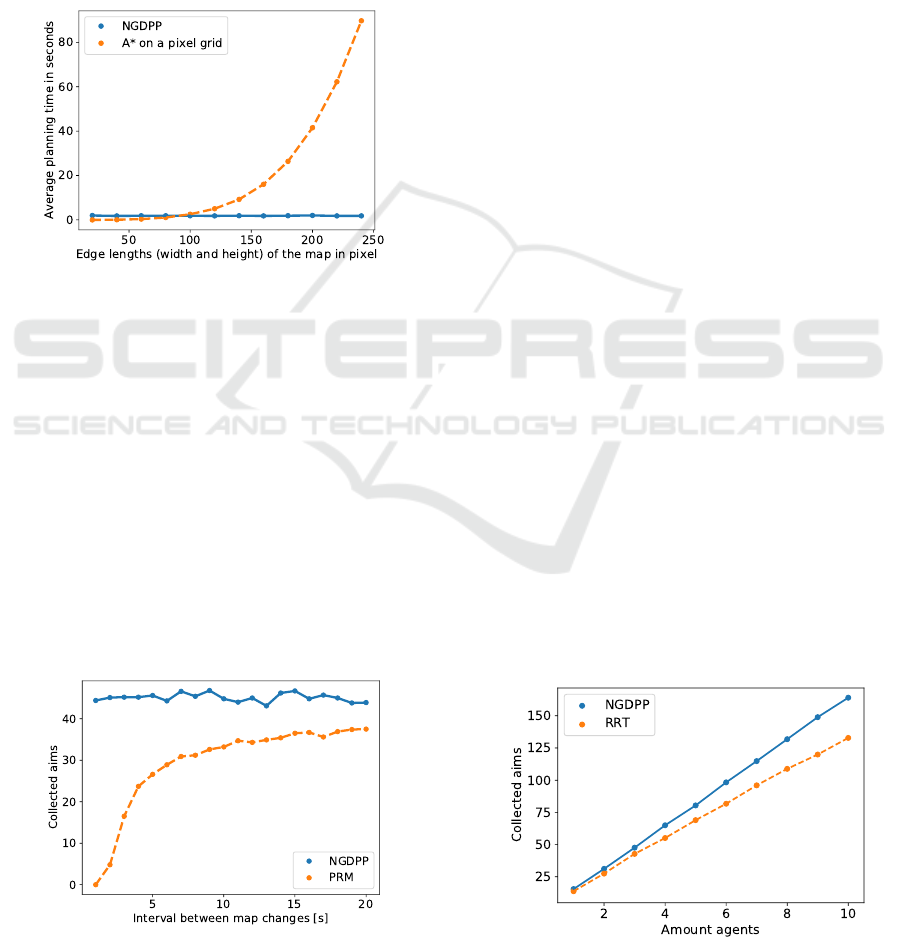
4.3 Comparison with Other Methods
In Figure 8 the NGDPP algorithm is compared with
another, very simple pathfinding procedure to show
its efficiency. The method used for comparison uti-
lizes the A* algorithm for path finding, however, the
underlying graph results from the fact, that every
walkable pixel of the spatial plan is transformed into a
node, with edges between adjacent nodes. With larger
spaces, the runtime of this method increases quadrat-
ically while the NGDPP algorithm increases linear.
Figure 8: Performance comparison of NGDPP to A* rout-
ing on a graph that results from interpreting every pixel of
the input floor plan as node.
Comparison with PRM
In Section 2 the PRM approach was mentioned with
the point of criticism that the Probabilistic Roadmap
has to be completely rebuild after every change in
the space. During this reconstruction of the waypoint
graph no routing can be executed. In comparison, our
NGDPP approach dynamically adapts to changes and
continuously allows routing queries (with the restric-
tion that edges might collide with obstacles during the
adaption of changes and with inappropriate parameter
settings as mentioned in Section 3.1).
Figure 9: Performance comparison of NGDPP to a simple
PRM implementation (adapted from (Sakai et al., 2018)).
In the experiment both approaches were used for
the navigation of a single agent which had to collect
targets, that were spawned at random positions on the
map over the course of 5 minutes. In those 5 minutes
changes of the map occurred at different rates. The
changes had the character, that parts of the map be-
came accessible and were blocked again. The exper-
iment was repeated 10 times for each algorithm and
map change rate. The mean of the results is plotted in
Figure 9.
The results show that the agent using NGDPP col-
lects an almost constant amount of targets over the
course of 5 minutes as the adaption of the waypoint
graph to map changes and the path planning of the
agent are interleaved. On the other hand the agent us-
ing the PRM approach has to wait for the completion
of the waypoint graph before navigation can start. If
the interval between map changes is low, for example
2 second, the generation of the graph takes up most of
the time, leaving the agent no time to move before the
next change occurs and the graph as to be recreated.
Comparison with RRT
As mentioned in Section 2, one problem with RRT, a
method often used for path planning, is that a separate
graph (tree) has to be created for each agent. The con-
sideration here was that with an increasing number of
agents our method (NGDPP) should be superior to the
RRT method. This is based on the fact that in our case
all agents can use the same waypoint graph. In order
to verify this thesis empirically, we have carried out
an experiment.
We have used the two algorithms to let a number
of 1 - 10 agents collect randomly placed targets (but
the same for both) for 3 minutes in 10 different envi-
ronments. The results of this experiment can be seen
in Figure 10.
The experiment shows that the NGDPP is superior
to the RRT approach. Agents using NGDPP collect
more targets in the same time which is attributable to
Figure 10: Performance comparison of NGDPP to a simple
RRT implementation (adapted from (Sakai et al., 2018)).
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
144

the higher planning time of RRT while the NGDPP
waypoint graph can continuously be used. This dif-
ference increases, as already assumed, with a higher
number of agents.
5 CONCLUSION AND FUTURE
WORK
In this paper, a new holistic method for path planning
in dynamic environments was presented: the NGDPP
algorithm. The sub problems of the problem domain
mentioned in the introduction, discretization, path
planning and collision avoidance, were dealt with sep-
arately. The dynamic discretization of the space was
solved using the SGNG algorithm. The resulting way-
point graph could then be used by the A* algorithm
to plan a valid path. During execution, this path is
locally adjusted using the “Potential Field” method,
so that collisions with dynamic obstacles are avoided.
Section 3 explains how these methods work together
to form the new NGDPP algorithm and which syner-
gies arise by the combination of them. In the evalua-
tion, the proposed changes that can be made to meth-
ods for the subproblems in order to obtain compu-
tational advantages, particularly the observation that
the used SGNG algorithm produces edges of equal
length, which accelerates the path planning, yield the
anticipated performance improvements. Overall, the
algorithm shows good performance compared to re-
lated work.
Up until now, our algorithm has only been applied
in simulations of holonome systems. However, most
real agents cannot take sudden turns through a 90
◦
an-
gle, for example. Such agents would probably not be
able to execute most paths planned by the NGDPP al-
gorithm. A possible solution for this could be smooth-
ing the path using Splines (Catmull and Rom, 1974)
respectively through the De-Casteljau algorithm (Alt
et al., 1997). To what extent this can be applied to
a path calculated by the NGDPP algorithm has to be
examined.
We assume, that our algorithm can be straightfor-
wardly adapted for three-dimensional spaces, since
all used methods, i.e. both neural gas and the “Po-
tential Field” as well as our proposed improvements,
would be possible in a three-dimensional application.
The algorithm could then be used e.g. for the move-
ment planning of flying drones. However, the appli-
cability of our algorithm and its performance in three-
dimensional spaces has not been tested and leaves
room for further investigation.
REFERENCES
Alt, H., Welz, E., and Wolfers, B. (1997). Piecewise lin-
ear approximation of b
´
ezier-curves. In Proceedings
of the thirteenth annual symposium on Computational
geometry, pages 433–435. ACM.
Belghith, K., Kabanza, F., Hartman, L., and Nkambou, R.
(2006). Anytime dynamic path-planning with flex-
ible probabilistic roadmaps. In IEEE International
Conference on Robotics and Automation, 2006. ICRA
2006., pages 2372–2377. IEEE.
Bentley, J. L. (1975). Multidimensional binary search
trees used for associative searching. Commun. ACM,
18(9):509–517.
Catmull, E. and Rom, R. (1974). A class of local interpo-
lating splines. In Computer aided geometric design,
pages 317–326. Elsevier.
Dellinger, B., Jenkins, R., and Walton, J. (2017). Auto-
mated waypoint generation with the growing neural
gas algorithm.
Dijkstra, E. W. (1959). A note on two problems in connex-
ion with graphs. Numerische mathematik, 1(1):269–
271.
Fritzke, B. (1995). A growing neural gas network learns
topologies. In Advances in neural information pro-
cessing systems, pages 625–632.
Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A for-
mal basis for the heuristic determination of minimum
cost paths. IEEE transactions on Systems Science and
Cybernetics, 4(2):100–107.
Kavraki, L. E., Svestka, P., Latombe, J.-C., and Overmars,
M. H. (1996). Probabilistic roadmaps for path plan-
ning in high-dimensional configuration spaces. IEEE
transactions on Robotics and Automation, 12(4):566–
580.
Koren, Y. and Borenstein, J. (1991). Potential field methods
and their inherent limitations for mobile robot naviga-
tion. In IEEE International Conference on Robotics
and Automation, 1991. Proceedings., pages 1398–
1404. IEEE.
LaValle, S. M. (1998). Rapidly-exploring random trees: A
new tool for path planning.
Legendre, P., Lapointe, F.-J., and Casgrain, P. (1994). Mod-
eling brain evolution from behavior: a permutational
regression approach. Evolution, 48(5):1487–1499.
Likhachev, M., Ferguson, D. I., Gordon, G. J., Stentz, A.,
and Thrun, S. (2005). Anytime dynamic a*: An any-
time, replanning algorithm. In ICAPS, pages 262–271.
Martinetz, T., Schulten, K., et al. (1991). A ”neural-gas”
network learns topologies.
Sakai, A., Ingram, D., Dinius, J., Chawla, K., Raffin, A.,
and Paques, A. (2018). Pythonrobotics: a python code
collection of robotics algorithms.
Tenc
´
e, F., Gaubert, L., Soler, J., De Loor, P., and Buche,
C. (2013). Stable growing neural gas: A topology
learning algorithm based on player tracking in video
games. Applied Soft Computing, 13(10):4174–4184.
Dynamic Path Planning with Stable Growing Neural Gas
145
