
Analogy-based Matching Model for Domain-specific Information
Retrieval
Myriam Bounhas
1,2
and Bilel Elayeb
1,3
1
Emirates College of Technology, Abu Dhabi, United Arab Emirates
2
LARODEC Research Laboratory, ISG of Tunis, Tunis University, Tunisia
3
RIADI Research Laboratory, ENSI, Manouba University, Tunisia
Keywords:
Information Retrieval, Analogical Proportions, Similarity, Agreement, Disagreement, Analogical Relevance.
Abstract:
This paper describes a new matching model based on analogical proportions useful for domain-specific Infor-
mation Retrieval (IR). We first formalize the relationship between documents terms and query terms through
analogical proportions and we propose a new analogical inference to evaluate document relevance for a given
query. Then we define the analogical relevance of a document in the collection by aggregating two scores:
the Agreement, measured by the number of common terms, and the Disagreement, measured by the number
of different terms. The disagreement degree is useful to filter documents out from the response (retrieved doc-
uments), while the agreement score is convenient for document relevance confirmation. Experiments carried
out on three IR Glasgow test collections highlight the effectiveness of the model if compared to the known
efficient Okapi IR model.
1 INTRODUCTION
Reasoning by analogy (Prade and Richard, 2010),
which straddles the fields of artificial intelligence and
linguistics, is the basis of psychological foundations
of human behaviour, in which an inference is applied
to analyze and categorize new problems by highlight-
ing their resemblance to problems already solved.
Analogical proportions are recognized as useful tools
to perform comparisons between situations expressed
by differences that are equated to other differences.
More precisely, they are statements of the form: x is
to y as z is to t, often denoted x : y :: z : t that express
that “x differs from y as z differs from t”, as well as “y
differs from x as t differs from z” (Miclet and Prade,
2009). In terms of pairs, we can consider that the pair
(x,y) is analogous to the pair (z,t) (Hesse, 1959). Ana-
logical proportions are based on the assumption that
if four objects x, y, z, t are making an analogical pro-
portion on a set of given features, it may also continue
holding on another sign related to them. The problem
is then to predict this sign for t based on the known
signs for x, y and z in case the signs make an analogi-
cal proportion.
Analogical proportions have been recognized as
an interesting direction in the last two decades (Lep-
age, 2001; Yvon et al., 2004; Stroppa and Yvon,
2005b; Miclet and Prade, 2009; Prade and Richard,
2013). They have demonstrated their ability to pro-
vide operational and effective models for morpholog-
ical linguistic analysis (Stroppa and Yvon, 2005a) and
classification tasks developed first by (Bayoudh et al.,
2007; Miclet et al., 2008) and extended by (Prade
et al., 2012) and (Bounhas et al., 2017a) and has led
to encouraging results in terms of accuracy and com-
plexity. In classification case, the predicted sign is the
label of the class.
IR problems are founded on the idea of assigning
relevant documents for a given query. It is natural to
think that dissimilar queries should lead to a very dis-
tinct set of relevant documents. In contrary, the set of
relevant documents for too similar queries should not
be distinguishable. From an analogical point of view,
this is can be expressed as a matter of comparisons
between queries and the corresponding set of relevant
documents. Starting from this assumption, this leads
us to wonder if what is successfully working in classi-
fication may be applied to information retrieval. The
problem in this case is no longer to predict the class
for a new example but rather the relevance of a docu-
ment to a new query.
In this paper, we mainly focus on information re-
trieval based on the idea of analogy between queries
and documents and we propose a new Analogical
496
Bounhas, M. and Elayeb, B.
Analogy-based Matching Model for Domain-specific Information Retrieval.
DOI: 10.5220/0007342104960505
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 496-505
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Proportion-based Matching Model (APMM). Given
two queries q
1
and q
2
with their corresponding set
of relevant documents rel(q
1
) and rel(q
2
), this model
assumes that q
1
differs from q
2
as rel(q
1
) differs
from rel(q
2
). This means that the difference be-
tween the two queries may considerably affect the
difference between their corresponding relevant docu-
ments. Based on this logic and given a new query, the
idea of APMM is to guess the relevance/irrelevance
of any document in the collection to this new query,
based on other existing queries. The matching model
that we propose is dedicated for domain-specific in-
formation retrieval as a sub-domain of IR in which
queries and document collection are issued from a
specific domain, such as social science, medical in-
formation, aeronautic, etc. Given a domain-specific
IR test collection, we exploit the idea of analogy be-
tween a “test” query (new query), “training queries”
(past queries) along with their corresponding docu-
ments to search for relevant documents to this new
test query.
This paper is organized as follows. Section 2 re-
calls the basic definitions and properties of analog-
ical proportions. In Section 3, we describe how to
exploit analogical proportions to evaluate document
relevance. For this purpose, we propose new Agree-
ment and Disagreement scores. This forms the basis
for defining the final Analogical Relevance measure
for documents. In Section 4, we present the analogy-
based IR matching model and we propose a new al-
gorithm for this purpose. Section 5 details the exper-
iments carried out on three IR Glasgow test collec-
tions and compares the effectiveness of the model to
the known efficient Okapi IR model.
2 BACKGROUND ON
ANALOGICAL PROPORTIONS
As already said, an Analogical proportion denoted as
a : b :: c : d, can be read: a is to b as c is to d or more
informally as “a differs from b as c differs from d
and vice versa”. It is considered as a special case of
logical proportion and defined as (Prade and Richard,
2012):
a : b :: c : d = (a ∧ ¬b ≡ c ∧ ¬d) ∧ (¬a ∧ b ≡ ¬c ∧ d)
(1)
Analogical proportion satisfies diverse properties,
usually expected from numerical proportion such as:
• Symmetry: a : b :: c : d ⇒ c : d :: a : b and
• Central permutation: a : b :: c : d ⇒ a : c :: b : d.
• Thanks to the central permutation property, a third
property requires that the two following implica-
tions also hold: a : b :: a : x ⇒ x = b and a : a :: b :
x ⇒ x = b
• Transitivity: a : b :: c : d ∧c : d :: e : f ⇒ a : b :: e :
f .
Let u,v be two distinct values in a finite set
U, an analogical proportion always holds for the
three following patterns: (u,u, u,u), (u, u,v,v) and
(u,v, u,v). All other possible patterns with two dis-
tinct values disagree with the idea of analogical
proportions. More precisely, (u, u, u,v), (u,u, v,u),
(u,v,u,u), (v,u,u,u), and (u, v,v,u) are invalid pat-
terns. In fact, assuming that “u is to u as u is to v”
for u 6= v seems strange.
The above definition of analogical proportions can
easily be extended to items represented as vectors of
values. In the Boolean setting, let S be a set of vec-
tors ∈ {0, 1}
n
, each vector
−→
x ∈ S is represented by
n features as
−→
x = (x
1
,· ·· , x
n
). Given four vectors
−→
a ,
−→
b ,
−→
c and
−→
d ∈ S. For each feature i ∈ [1,n], there
are only eight possible combinations of values of
−→
a ,
−→
b and
−→
c (see Table 1). We can see that in two situa-
tions among eight, the equation can not be solved.
Table 1: Solving analogical proportion for Boolean vectors.
−→
a 0 0 0 0 1 1 1 1
−→
b 0 0 1 1 0 0 1 1
−→
c 0 1 0 1 0 1 0 1
−→
d 0 1 1 ? ? 0 0 1
Let us consider the analogical equation
−→
a :
−→
b ::
−→
c :
−→
d between four Boolean vectors. To solve this
equation, it is common to apply the following exten-
sion of the previous definitions to Boolean vectors in
{0,1}
n
:
−→
a :
−→
b ::
−→
c :
−→
d iff ∀i ∈ [1,n], a
i
: b
i
:: c
i
: d
i
which supposes that analogical proportion between
four vectors holds true iff the analogical proportion
holds componentwise between all their features.
The above equation solving property forms the ba-
sic to define an inference principle for binary classifi-
cation problems applied to Boolean datasets in (Bay-
oudh et al., 2007; Bounhas et al., 2017a). Based
on the continuity principle, the authors assumed that
if the analogical equation holds componentwise for
all features of four Boolean instances, this analogi-
cal equation should still holds for their classes. Hav-
ing four Boolean instances
−→
a ,
−→
b ,
−→
c and
−→
d , the first
three instances are in the training set with known
classes cl(
−→
a ), cl(
−→
b ), cl(
−→
c ) and the last one whose
class is unknown (to be classified). The inference
principle is defined as:
∀i ∈ [1, n],a
i
: b
i
:: c
i
: d
i
cl(
−→
a ) : cl(
−→
b ) :: cl(
−→
c ) : cl(
−→
d )
Analogy-based Matching Model for Domain-specific Information Retrieval
497

To classify the new instance
−→
d , the equation cl(
−→
a ) :
cl(
−→
b ) :: cl(
−→
c ) : x should be solvable and then assign
its solution to cl(
−→
d ).
3 EVALUATING DOCUMENT
RELEVANCE USING
ANALOGICAL INFERENCE
In this section, we investigate the ability of analogical
proportions to model the relationship between queries
and documents. Let us consider a set of n queries
Q = (q
1
,q
2
,..., q
n
) and their corresponding sets of
relevant documents D = (rel(q
1
),rel(q
2
),...,rel(q
n
)),
s.t: rel(q
i
) = {d
1
,d
2
,..., d
w
} is the set of relevant doc-
uments for a query q
i
.
Based on analogical proportions, the “query-
document” relationship may have a new meaning
based on linking pairs of queries. Namely, q
i
dif-
fers from q
j
as rel(q
i
) differs from rel(q
j
). More
precisely, the extent to which queries q
i
and q
j
are similar/dissimilar should strongly affect the iden-
tity/difference of sets rel(q
i
) and rel(q
j
) in terms of
the relevance or irrelevance of each document from
the collection D. Given a new query (unseen before),
the basic idea is to guess the relevance/irrelevance of
any document d ∈ D to this new query based on ex-
isting queries.
In order to understand better the above idea, we
need to represent in a more precise way the link be-
tween queries and documents. We assume here that
both queries and documents are indexed in the same
way and can be represented through a set of index-
ing terms. Let us consider two queries q
i
, q
j
and a
document d
k
denoted as:
q
i
= (t
i
1
,t
i
2
,...,t
i
p
),q
j
= (t
j
1
,t
j
2
,...,t
j
p
0
) and
d
k
= (t
k
1
,t
k
2
,...,t
k
p
00
)
If we consider a particular term t, we define a
predicate q(t)(resp. d(t)) as a boolean value which is
equal to 1 if the term t exists in the query q (resp. doc-
ument d) and 0 otherwise. We also define the predi-
cate rel
ik
(t) which is evaluated to 1 if, according to
the term t, the document d
k
is relevant to the query
q
i
and 0 otherwise (we assume here that each term
t provides us a bit of knowledge about the relevance
or irrelevance of this document). Following this logic,
one may represent query-document relationship using
analogical proportion in two different ways:
• (i) Term existence: In a first level, we aim to repre-
sent the existence or non existence of a particular
term in a query or document. For this purpose,
we propose to consider the following analogical
proportion:
q
i
(t) : q
j
(t) :: d
k
(t) : q
j
(t) (2)
This proportion states that the term t exists/not ex-
ists in queries q
i
and q
j
in the same way as it ex-
ists /not exists in document d
k
and query q
j
. This
means that, for a particular term t, the difference
between two queries is the same as the difference
between a document and one of the two queries.
• (ii) Document relevance: In a second level, we
wonder about the relevance/irrelevance of a doc-
ument for a given query. The analogical propor-
tion:
q
i
(t) : q
j
(t) :: rel
ik
(t) : rel
jk
(t) (3)
states that the difference in terms of
existence/non-existence of a term between
two queries and a document implies the dif-
ference in terms of relevance/irrrelevance of
the given document, satisfying term existence
proportion (eq. 2), for these queries.
It is clear that, the second analogical proportion
(eq. 3) can only be applied if the first one holds. In
fact, we assume here that the existence/non existence
of a term in a query and a document may be a good in-
dicator of the relevance/irrelevance of this document
to this query, which means that we may induce docu-
ment relevance from the existence of the term in both
query and document. This leads to the following ana-
logical inference:
q
i
(t) : q
j
(t) :: d
k
(t) : q
j
(t)
q
i
(t) : q
j
(t) :: rel
ik
(t) : rel
jk
(t)
Since in IR, queries and documents are previously
indexed with terms in a preliminary step, the first type
of analogical proportion (eq. (2)) is known from the
training set. If this first equation holds, it helps to
infer the second type of analogical proportion (eq.(3))
which helps to induce document relevance.
The analogical inference that we propose seems
close to that stated first in classification problems
(Bayoudh et al., 2007). However, the logic is differ-
ent: in classification, if the analogical equation be-
tween the four components holds for all features, the
classification inference is applied to guess the final
class of the instance to be classified. In our model,
since we treat indexing terms independently, the
above analogical inference is applied for each term
in the query to induce document relevance according
to this particular term. Then, the final document rele-
vance is guessed by aggregating individual document
relevance induced from each term in the query. This
will be explained in the next subsections.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
498

Table 2: Relevance truth values.
q
r
(t) q
x
(t) d
k
(t) rel
rk
rel
xk
(i) 1 1 1 −
(ii) 1 1 1 1 y= 1 |A
t
(i) 1 0 1 −
(ii) 1 0 1 1 y=0 |D
t
The search process for relevant documents is
based on the resolution of analogical equations de-
scribed above. This process assumes that: if the two
queries q
i
and q
j
are in analogical proportion (with
some documents d), it should be the case for their cor-
responding relevance/irrelevance predicates with re-
gard to the same document. In next subsection, we
describe how this inference process can be applied to
evaluate the relevance /irrelevance of each document
in the collection.
3.1 Agreement and Disagreement
Scores
Let us consider the query-document matching prob-
lem in IR where a query q
r
is in the training set hav-
ing its known corresponding relevant document set
rel(q
r
) = {d
r
1
,d
r
2
,..., d
r
w
}. A second query q
x
is ex-
tracted from the test set and whose rel(q
x
) is un-
known. Starting from the training set, the equation
q
r
(t) : q
x
(t) :: d
k
(t) : q
x
(t) is solvable. To build the
set of relevant documents rel(q
x
) for the new query
q
x
, one may start by looking at each document d
k
∈
rel(q
r
) for each known query q
r
. If the analogical pro-
portion given in equation (3): q
r
(t) : q
x
(t) :: rel
rk
(t) : y
has a solution, we assign to rel
xk
(t) its solution for
each document d
k
∈ rel(q
r
). In the following, we first
analyze the truth table for the two proposed equations
(2) and (3) introduced before. Then, we propose an
agreement/disagreement scores that help to evaluate
document relevance. Table 2 provides the truth val-
ues of the predicate rel
xk
as a solution of equation (3).
In each line of this Table, only bold truth values are to
be considered appropriately to solve each analogical
eq.(2) and (3).
To solve the above analogical equation, it is clear
that only two different situations (see Table 2) are
important to consider. In terms of generic patterns,
we can see that the analogical proportion (2), for ex-
ample, always holds for the two following patterns:
u:u::u:u (two first rows in Table 2) and u:v::u:v (two
last rows) where u and v are distinct values. However
and as introduced in Section 2, analogy should also
hold for the pattern u:u::v:v. Nevertheless, this sit-
uation is meaningless in our inference process since
in equation (2), the second and last predicates are as-
sumed to be the same. Moreover, for the two used
patterns we only consider the case where the predi-
cate q
r
(t) (or u) is true since when it is false it does not
help for predicting the relevance of a document: we
focus on terms existing in the query q
r
not on those
that are not existing.
Based on the patterns in Section 2, there are
two indicators of document relevance: The pattern
u:u::u:u states for a total agreement between the two
queries and the document according to the existence
of term t. This agreement should also be applied to
guess document relevance in equation (3) and thus
may be considered as a good indicator that the stud-
ied document is also relevant for q
x
(i.e: y = 1). In
contrary, the pattern u:v::u:v states for a disagreement
between the two queries according to term existence
(eq. (2)). Applying this disagreement in the same way
to equation (3) reinforce the idea that this document
is rather irrelevant for q
x
(i.e: y = 0). We define the
agreement and disagreement scores by:
• Term Agreement: According to term t, a document
d
k
is relevant for a test query q
x
if this query agree
with both query q
r
and its relevant document d
k
on
the existence of this term.
• Term Disagreement: According to term t, a doc-
ument d
k
is irrelevant for a test query q
x
if this
query do not agree with query q
r
and with its rel-
evant document d
k
on the existence of this term.
Let us now state the previous ideas with formal
notations. Given a particular term t, in the following
we define two scores A
t
and D
t
to evaluate the ex-
tent to which a query q
x
is in agreement/diagreement
with another query q
r
, and a document d
k
as:
A
t
(q
r
,q
x
,d
k
) = q
r
(t) ∧ q
x
(t) ∧ d
k
(t) ∧ rel
rk
(t) (4)
D
t
(q
r
,q
x
,d
k
) = q
r
(t) ∧ ¬q
x
(t) ∧ d
k
(t) ∧ rel
rk
(t) (5)
We can easily check that A
t
and D
t
appropriately
rewrite the analogical proportions (2) and (3). In fact,
we assign to rel
xk
= A
t
∧ ¬D
t
the solution of (q
r
(t) :
q
x
(t) :: d
k
(t) : q
x
(t)) ∧ (q
r
(t) : q
x
(t) :: rel
rk
(t) : y). The
two proposed scores will be used to define a global
agreement/disagreement scores between queries and
documents with regard to all terms.
3.2 Global Agreement and
Disagreement Scores
It is known in IR that queries and documents can sim-
ply be represented by a set of indexing terms. The in-
dexing process of queries and documents can be done
in a preliminary step before applying the matching
model. Starting from the previously defined agree-
ment/disagreement scores related to one term t, we
have to define a global score suitable for a set of
Analogy-based Matching Model for Domain-specific Information Retrieval
499

terms. The agreement and disagreement scores de-
fined by equations (4) and (5) are used to evaluate
the extent to which a test query agrees or disagrees
with other seen queries and their corresponding rele-
vant documents if we only look to one particular term
t. Given a set of terms for each query and assum-
ing independence of indexing terms, one may esti-
mate the global agreement/disagreement of a query
q
x
with a query q
r
= (t
1
,t
2
,...,t
m
) as the sum of agree-
ment/disagreement of each term t
i
,i ∈ [1,m] as fol-
lows:
Ag(q
r
,q
x
,d
k
) =
1
m
m
∑
i=1
A
t
i
(q
r
,q
x
,d
k
)
Dis(q
r
,q
x
,d
k
) =
1
m
m
∑
i=1
D
t
i
(q
r
,q
x
,d
k
)
where m is the number of terms in q
r
. For a given
test query q
x
, the matching model aims to evalu-
ate each distinct pair (query, document) i.e: (q
r
,d
k
),
where q
r
is in the training set and d
k
is among its
relevant documents. This enables to select relevant
documents for q
x
among those relevant for other seen
queries. Combining each pair (q
r
,d
k
) with q
x
forms
a set of triples (q
r
,q
x
,d
k
). To compute the agree-
ment/disagreement for each triple in this set, we can
estimate Ag(q
r
,q
x
,d
k
) for the set of terms where they
agree (i.e. the term t exists) and Dis(q
r
,q
x
,d
k
) for the
set of terms where they disagree (i.e. the term t exists
in q
r
and d
k
and does not exist in q
x
).
To understand better this idea, in Table 3 we rep-
resent term predicates for each element of the triple to
show the Ag/Dis situations.
Table 3: Ag/Dis scores with regard to all indexing terms.
Ag Dis
t
1
... t
k−1
t
k
... t
m
rel
q
r
1 ... 1 1 ... 1
q
x
1 ... 1 0 ... 0
d
k
1 ... 1 1 ... 1 rel
xk
=?
After reordering q
r
terms in Table 3, we can see
that q
r
and q
x
agree on terms t
1
to t
k−1
and disagree
on terms t
k
to t
m
. Consider now the document d
k
known to be relevant for q
r
and agree with q
x
in the
same way as q
r
. It is clear that the equations (2) and
(3) hold componentwise between the three elements
of the triple. The aim is thus to guess the relevance
of document d
k
for q
x
based on the amount of agree-
ment/ disagreement terms with both q
r
and q
x
.
It is natural to consider a document d
k
(known to
be relevant for q
r
) as likely to be also relevant for a
query q
x
if it contains as much as agreement terms
and no disagreement terms. To select the best doc-
uments with high relevance, it is recommended to
choose those having high value of Ag and small value
of Dis. High value of Ag means that for large number
of terms, the document agrees with the test query. On
the opposite, small value of Dis guarantee a reduced
number of terms for which the document disagrees
with the test query. In the very optimistic case, one
wants a document d
k
to agree with the query q
x
with
respect to all terms (Ag close to 1) and to disagree on
no term (Dis close to 0). We define the Analogical
Relevance of a document d
k
for a query q
x
as:
AR(q
r
,q
x
,d
k
) = min(Ag(q
r
,q
x
,d
k
),1−Dis(q
r
,q
x
,d
k
))
(6)
It is natural to assume that any document d
k
in the
collection D may be relevant for different training
queries at the same time (d
k
∈ rel(q
r
) and d
k
∈ rel(q
0
r
)
with q
r
6= q
0
r
). This means that, for each candidate
document d
k
, we have to evaluate its analogical rele-
vance AR with regard to each training query q
r
where
d
k
∈ rel(q
r
). Then, the final Analogical Relevance of
document d
k
is obtained by aggregating all these AR’s
evaluations on all training queries using the max:
AnalogicalRelevance(q
x
,d
k
) =
n
max
r=1
(AR(q
r
,q
x
,d
k
))
(7)
The analogy-based matching model that we propose
combines the two scores of agrement and disagree-
ment to guess document relevance. In fact, the dis-
agreement indicator, measured by the number of dif-
ferent terms, removes from the list of returned doc-
uments, for a given query, those that are not rele-
vant, while the agreement indicator, measured by the
number of common terms, reinforces the relevance of
the remaining documents which are not eliminated by
the disagreement indicator. The proposed matching
model has its counter part in classification problems.
In fact, the analogy-based classification approach of
Bounhas et al. (Bounhas et al., 2014) treats the sim-
ilarity and dissimilarity sequently in separate levels.
In their approach, they first look for the most similar
pairs (a,b) having the maximum number of similar at-
tributes. This enables to filter the candidate voters for
classes. Then check the analogical equation on the re-
maining dissimilar attributes between pairs (a,b) and
(c,d) to solve the analogical equation for classes. The
authors have proven the efficiency of this approach to
reduce the average number of used triples for classifi-
cation.
4 ANALOGICAL
PROPORTION-BASED
MATCHING MODEL
In this section, we detail the proposed matching
model, denoted here APMM, based on the previously
defined Analogical Relevance measure.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
500

4.1 Methodology
Let Q = (q
r
,rel(q
r
)) be a training set of queries
with their known corresponding relevant documents.
Given a new query q
x
/∈ Q, a first option to re-
trieve its relevant documents is to start by a force
brute method in which all queries q
r
in the training
set Q along with their corresponding relevant doc-
uments are considered in the search process. Each
document in each pair (q
r
,d
k
) (where d
k
∈ rel(q
r
))
is assumed to be a candidate relevant document for
q
x
. Retrieved documents are simply the solution of
the equation (3). Based on the analogical relevance
function defined by equation (7), we first compute
AnalogicalRelevance(q
x
,d
k
) for each document, then
choose the best ones as a final set of relevant docu-
ments for q
x
. As can be seen, the complexity of this
force brute approach is quadratic due to the search
space for pairs of (query, document). This process
may become time consuming for large number of
queries and/or relevant documents for each query. To
optimize this first approach, we have chosen to use
only the nearest neighbors queries to the new query
q
x
in the search process of relevant documents. This
will considerably reduce the search space to be lin-
ear. In fact, we wonder if the study of the set of rel-
evant documents of the nearest neighbors queries q
r
to q
x
are enough to retrieve the most relevant docu-
ments to this new query. Similar approaches, based
on the idea of nearest neighbors applied to classifi-
cation, has been developed and achieved successful
results for Boolean or numerical data (Bounhas et al.,
2017b; Bounhas et al., 2018).
In practice, our implementation can be summa-
rized by the following steps:
• Given a new query q
x
in the test set, find its k near-
est neighbors queries in the training set q
r
∈ Q.
• Build the set of candidate relevant documents.
This set is simply the union of all relevant doc-
uments corresponding to the k-nearest neighbors
queries.
• In a filtering step, compute the
AnalogicalRelevance for each candi-
date document then remove those whose
AnalogicalRelevance(q
x
,d
k
) is less than a fixed
threshold.
The proposed matching model can be described
by the following algorithm.
4.2 Algorithm
Let CosineSim(q
x
,q
r
) be a function that returns the
cosine similarity between the two queries q
x
and q
r
(Amit, 2001). This function enables to order train-
ing queries q
r
according to their similarity to the test
query and then select the k-nearest neighbors (k is a
given value). The computation of the NN
k
(q
x
)’s can
be done offline in a pre-processing step, which helps
to speed up the matching process. The previous ex-
planation can now be described with Algorithm 1. It
is important to know that, contrary to other matching
models, the proposed APMM looks only for a small
subset of documents from the collection D thanks to
the study of selected set of documents i.e: those rele-
vant for the nearest neighbors queries to q
x
. This will
considerably speed up the search process and thus im-
prove the response time.
Algorithm 1: Analogical Proportion-based Matching Model
APMM.
1: Input: a set Q = {q
r
,rel(q
r
)}, a test query q
x
/∈ Q, a
threshold θ, k ≥ 1
2: CandidateRelDoc(q
x
)=null, RetrDoc(q
x
)=
/
0
3: for each q
r
∈ Q do compute CosineSim(q
x
,q
r
) end for
4: sort by increasing order the list L of values
{CosineSim(q
x
,q
r
)|q
r
∈ Q}
5: build up the set NN
k
(q
x
) = {q
r
∈ Q
s.t. rank(CosineSim(q
x
,q
r
)) in L ≤ k}
//Document search
6: CandidateRelDoc =
S
{rel(q
r
) s.t. q
r
∈ NN
k
(q
x
)}
// Document Filter
7: for each document d ∈ CandidateRelDoc do
8: Compute AnalogicalRelevance(q
x
,d)
9: if AnalogicalRelevance(q
x
,d) < θ then
10: CandidateRelDoc(q
x
).Remove(d)
11: end if
12: end for
13: RetrDoc(q
x
) = CandidateRelDoc(q
x
)
14: return (RetrDoc(q
x
))
5 EXPERIMENTATIONS AND
DISCUSSION
In this section, we first provide the detail of the ex-
perimental results of the proposed algorithm. Then,
we discuss a comparative study between our approach
and the most known efficient model Okapi-BM25
(available in the Terrier platform
1
) to show the rele-
vance of the training step in the IR matching model.
For this purpose, we conduct a variety of evalua-
tion scenarios of the APMM following the TREC
protocol applied to three IR test collections (CRAN,
CACM and CISI)
2
. These collections have been se-
lected among other known standards due to the high
1
http://terrier.org/
2
http://ir.dcs.gla.ac.uk/resources/test -collections/
Analogy-based Matching Model for Domain-specific Information Retrieval
501

Table 4: The degree of similarity between queries in the
three test collections.
CRAN
MinSim 0.5 0.54 0.58 0.62 0.66 0.72 0.76 0.78
#test queries 43 33 24 20 14 12 8 6
CACM
MinSim 0.28 0.3 0.32 0.34
#test queries 8 7 6 4
CISI
MinSim 0.5 0.54 0.56
#test queries 4 3 2
similarity between their topics. To figure out the de-
gree of similarity between queries in the three test
collections, we first compute the cosine similarity be-
tween each pair of queries as described in Algorithm
1. Then, queries q
x
are grouped into subsets S such
that:
q
x
∈ S iff CosineSimilarity(q
x
,NN
1
(q
x
)) ≥ MinSim,
for a given MinSim value. Table 4 provides a sum-
mary of the number of queries in each subset corre-
sponding to a given MinSim value. This table shows
that queries from the CRAN test collection reveal a
higher degree of similarity between them than for
those of CACM and CISI.
For all the following experiments, we run Algo-
rithm 1 with θ = 0 and k = 5 to benefit from larger set
of nearest neighbor queries. Then, we use the same
test queries to run the Okapi model.
5.1 Main Results of the CRAN Test
Collection
The first two rows in Figure 1 present a set of recall-
precision curves that compare the APMM to Okapi
for the CRAN test collection for different similari-
ties’ scores (MinSim) between queries. The second
two rows in Figure 1 present the precision values at
different top documents (e.g. P@5, P@10,..., P@30),
the MAP and the R-Precision. For instance, the preci-
sion at point 30, namely P@30, is the ratio of relevant
documents among the top 30 retrieved documents.
Figure 1, shows that the APMM recall-precision
curves outperform the Okapi on the majority points
of recall for all similarity levels.
In the second two rows of Figure 1, we can also
see that the APMM is clearly better than the Okapi
in terms of precision at top returned documents, the
MAP and the R-Precision for all similarity levels. The
proposed model is largely better with a significant gap
for the first values of precision corresponding to the
first selected documents (P@1-P@5). It is also im-
portant to note that, for the CRAN test queries having
similarity greater or equal to 72% (MinSim = 0.72),
the APMM achieves the best results in terms of MAP
and R-Precision with the largest gap to Okapi.
5.2 Main Results of the CACM and
CISI Test Collections
As noted before (see Table 4), the two test collections
CACM and CISI have a reduced number of similar
queries if compared to the CRAN. This limits their ef-
fectiveness for testing our approach. If we analyze the
recall-precision curves provided for the CACM test
collection (see: first row in Figure 2), we remark that
the APMM still outperforms the Okapi on the major-
ity points of recall. However, the Okapi is slightly
better between the points of recall 0.5 and 0.8.
For the third test collection CISI (see: second row
of Figure 2), we note that the APMM is better than the
Okapi especially for low-level points of recall (less or
equal to 0.4). However, for the high-level points of
recall, the reverse is true. The two models achieve
similar results on the point of recall 1.
In Figure 2, we also provide a comparison in terms
of precision at different top documents, MAP and R-
Precision metrics for the two test collections CACM
and CISI.
From results of the CACM (see: third row in Fig-
ure 2), it is clear that the APMM is more efficient, if
compared to Okapi, in terms of precision at the first
top returned documents from P@1 until P@10, the
MAP and the R-Precision and for all similarity lev-
els.
Regarding the CISI test collection (see: last row
in Figure 2), we can draw the following conclusions:
• For test queries having MinSim = 0.5 or 0.54, the
APMM outperforms Okapi in terms of precision
at all top returned documents (except at P@5) and
especially the R-Precision.
• When the similarity is increased to 56%, the
Okapi seems better than APMM in terms of preci-
sion at top returned documents (P@4,..., P@20)
and the MAP, while APMM performs clearly bet-
ter in terms of P@3 and R-Precision. Both match-
ing models have close results at P@1, P@2 and
P@30.
5.3 Improvement Percentage
In order to investigate more the effectiveness of the
APMM, we compare its results to the Okapi still us-
ing the previous evaluation metrics but in a different
way. In Table 5, we assess and present the best im-
provement percentages of the APMM if compared to
Okapi for the three datasets using the precision at dif-
ferent top documents, the MAP and the R-Precision.
For each dataset, we only present the detail of the im-
provement at different precision metrics for the sim-
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
502
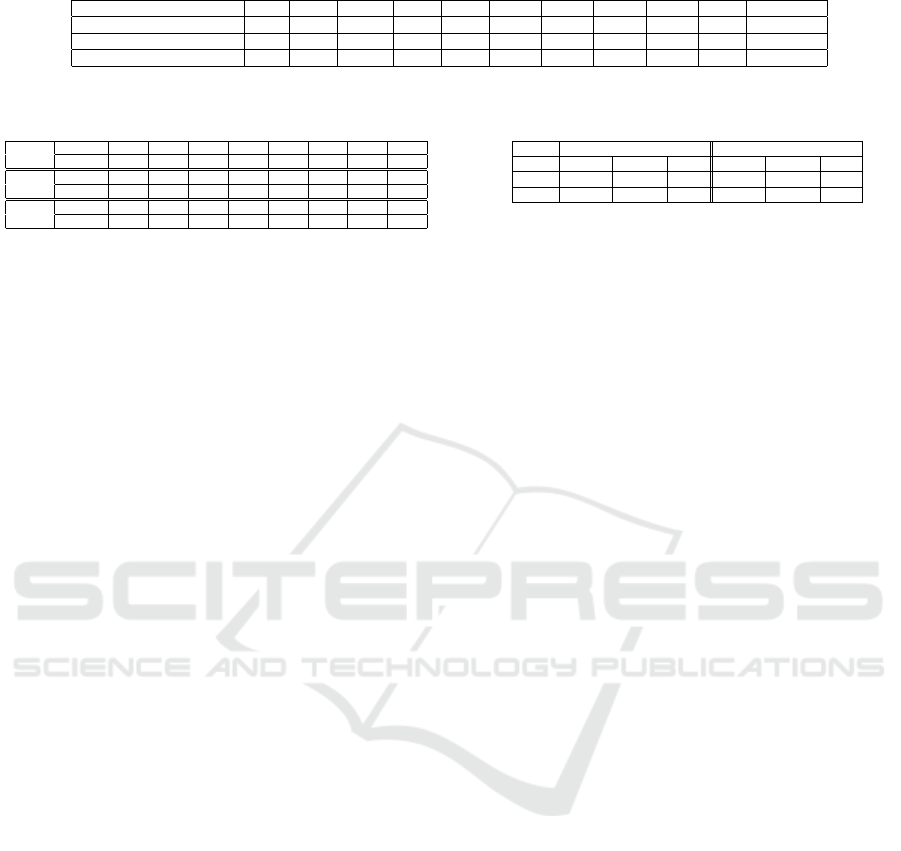
Table 5: The best improvement percentages of APMM compared to Okapi for the three test collections.
Dataset (Best MinSim) P@1 P@2 P@3 P@4 P@5 P@10 P@15 P@20 P@30 MAP R-precision
CRAN(Best MinSim=0.72) 200 168 130.38 63.75 67.35 41.45 58.81 46.37 65.59 53.59 73.13
CACM(Best MinSim=0.34) 300 65.33 34 71.43 40 12.94 -8.81 -14.48 1.24 33.81 16.67
CISI(Best MinSim=0.5) 0 24 50 10.22 -9.09 30 25.44 17.14 26.67 -7.8 28.11
Table 6: The p-value for the Wilcoxon matched-pairs
signed-ranks test for the three test collections.
CRAN
MinSim 0.5 0.54 0.58 0.62 0.66 0.72 0.76 0.78
p-value 0.003 0.002 0.003 0.003 0.003 0.002 0.002 0.003
CACM
MinSim 0.28 0.3 0.32 0.34
p-value 0.013 0.015 0.055 0.011
CISI
MinSim 0.5 0.54 0.56
p-value 0.009 0.028 0.312
ilarity level that provides us the best improvement
percentage. If we analyze the results of the CRAN
test collection, we notice an average improvement
of APMM if compared to Okapi of about 94% (if
we consider all the top returned documents P@1,...,
P@30). We also registered an improvement respec-
tively about 54% for the MAP and 73% for the R-
Precision.
Overall, the APMM also highlights an improve-
ment if compared to Okapi for the two other test
collections CACM and CISI. The average improve-
ment on all the top returned documents is respectively
about 56% for the CACM and 20% for the CISI.
These conclusions confirm our first observations
presented above about the efficiency of the APMM if
compared to Okapi especially for the IR collections
having large similarity between their test queries as in
the case of CRAN.
5.4 Statistical Evaluation of APMM
It is important to know if the previously observed
improvement of the APMM over Okapi is statisti-
cally significant. This is can be checked using the
Wilcoxon Matched-Pairs Signed-Ranks Test as pro-
posed by Demsar (Demsar, 2006). Table 6 summa-
rizes the results of the computed p-values comparing
the APMM to Okapi in terms of precision at different
top documents, the MAP and the R-Precision scores
for respectively the CRAN, CACM and CISI test col-
lections. The null hypothesis (stating that the two
compared models perform equally) has to be rejected
when the p-value is less than the threshold 0.05.
The computed p-values show that:
• In case of the CRAN test collection (see: Ta-
ble 6), the improvement of the APMM compared
to Okapi in terms of precision at different top
documents, the MAP and the R-Precision scores,
is statistically significant for all similarity lev-
els between test queries (all p − values < 0.05).
The best registered p − value = 0.002 < 0.05
corresponds to MinSim = 0.54 (33 test queries),
Table 7: A comparative study between APMM and (Fuhr
and Buckley, 1991).
APMM (Fuhr and Buckley, 1991)
CRAN CACM CISI CRAN CACM CISI
P@15 0.30 0.38 0.46 0.37 0.33 0.17
MAP 0.46 0.30 0.22 0.38 0.29 0.20
MinSim = 0.72 (12 test queries) and MinSim =
0.76 (8 test queries).
• If we consider the CACM test collection, we can
see that the improvement of the APMM com-
pared to Okapi is still statistically significant in
different levels of similarity between test queries
(p − value < 0.05 in the most cases). Except for
similarity score at least equal to 32%, for which
we have registered a borderline p-value = 0.05.
As can be noted in Figure 2, the Okapi outper-
forms APMM in some precisions at different top
documents such as P@15, P@20 and P@30.
• Regarding the CISI test collection and when the
similarity between queries is not less than 50%,
a statistically significant improvement of APMM
over Okapi can clearly be observed (p − value =
0.009). We can also see a significant improve-
ment when we extend the similarity between the
test queries to 54% (p − value = 0.028 < 0.05).
However if we restrict the minimum similarity
to 0.56%, the improvement of the APMM over
Okapi is not statistically significant since the p −
value = 0.312 > 0.05. This confirms what we pre-
viously noted above.
5.5 Further Comparison and Discussion
In this sub-section, we aim to provide further compar-
isons of the APMM to the state-of-the-art approaches.
To the best of our knowledge, there are no previ-
ous works applying analogical proportions in the IR
context. For this reason, we compare our model
to the work proposed by Fuhr and Buckley (Fuhr
and Buckley, 1991). First, because the authors have
applied a kind of learning in their model and sec-
ond because they have tested their approach on the
same IR Glasgow test collections (CRAN, CACM
and CISI) and they have used the same indexing tech-
nique (TFxIDF). Table 7 summarizes experimental
results of Fuhr and Buckley (Fuhr and Buckley, 1991)
and APMM for the three test collections. These re-
sults show an improvement of APMM if compared to
Fuhr and Buckley (Fuhr and Buckley, 1991) model
Analogy-based Matching Model for Domain-specific Information Retrieval
503

except in P@15 for the CRAN dataset for which their
approach outperformed the APMM (see bold values
in Table 7).
6 CONCLUSION
The success of analogical proportions in a variety of
domains, such as in classification and language pro-
cessing, led us to wonder whether it may be a suc-
cessful tool for building an IR matching model. We
are mainly interested to this last field in this paper. We
have first studied the way to apply analogy between
queries and documents. Then, given a particular in-
dexing query term, we formalize two logical propor-
tions linking queries and their corresponding relevant
documents for an analogical inference. These propor-
tions form the basis for our matching model.
The two proposed analogical proportions help to
define agreement and disagreement scores useful to
estimate to what extent any document, from the col-
lection, is to be accepted or rejected given a new
query. The agreement score is calculated according
to the common terms between the query and the doc-
ument while the disagreement is computed using the
number of terms they differ. The two scores treat doc-
uments differently: the disagreement allows you to
exclude irrelevant documents from the returned list,
while the agreement score strengthen the relevance of
the remaining documents not eliminated by the dis-
agreement. Based on these two scores, we have pro-
posed and tested a new analogy-based IR matching
model on three IR Glasgow test collections. The ex-
perimental results highlighted the effectiveness of the
model compared to the well known efficient Okapi IR
model.
The analogy-based IR matching model can be ap-
plied in different IR/CLIR tasks such as in query
expansion, disambiguation and translation tasks that
will be our future interest.
REFERENCES
Amit, S. (2001). Modern information retrieval: A brief
overview. Bulletin of the IEEE Computer Society
Technical Committee on Data Engineering, 24:35–43.
Bayoudh, S., Miclet, L., and Delhay, A. (2007). Learning
by analogy: A classification rule for binary and nomi-
nal data. In Proc. IJCAI 2007, pages 678–683.
Bounhas, M., Prade, H., and Richard, G. (2014). Analogical
classification: A new way to deal with examples. In
Proc. ECAI, pages 135–140.
Bounhas, M., Prade, H., and Richard, G. (2017a). Analogy-
based classifiers for nominal or numerical data. IJAR,
91:36–55.
Bounhas, M., Prade, H., and Richard, G. (2017b).
Oddness/evenness-based classifiers for boolean or nu-
merical data. IJAR, 82:81–100.
Bounhas, M., Prade, H., and Richard, G. (2018). Oddness-
based classification: A new way of exploiting neigh-
bors. IJIS, 33(12):2379–2401.
Demsar, J. (2006). Statistical comparisons of classifiers
over multiple data sets. Journal of Machine Learning
Research, 7:1–30.
Fuhr, N. and Buckley, C. (1991). A probabilistic learning
approach for document indexing. ACM Trans. on Inf.
Sys., 9(3):223–248.
Hesse, M. (1959). On defining analogy. Proceedings of the
Aristotelian Society, 60:79–100.
Lepage, Y. (2001). Analogy and formal languages. In Proc.
FG/MOL 2001, pages 373–378.
Miclet, L., Bayoudh, S., and Delhay, A. (2008). Analog-
ical dissimilarity: Definition, algorithms and two ex-
periments in machine learning. Journal of Artificial
Intelligence Research, 32:793–824.
Miclet, L. and Prade, H. (2009). Handling analogical pro-
portions in classical logic and fuzzy logics settings. In
Proc. ECSQARU’09, pages 638–650. Springer, LNCS
5590.
Prade, H. and Richard, G. (2010). Reasoning with logical
proportions. In Proc. KR 2010, pages 545–555.
Prade, H. and Richard, G. (2012). Homogeneous logi-
cal proportions: Their uniqueness and their role in
similarity-based prediction. In Proc. KR 2012, pages
402–412.
Prade, H. and Richard, G. (2013). From analogical pro-
portion to logical proportions. Logica Universalis,
7(4):441–505.
Prade, H., Richard, G., and Yao, B. (2012). Enforcing regu-
larity by means of analogy-related proportions-a new
approach to classification. Int. J. of Comp. Inf. Sys.
and Indus. Management App., 4:648–658.
Stroppa, N. and Yvon, F. (2005a). An analogical learner for
morphological analysis. In Proc. CoNLL 2005, pages
120–127.
Stroppa, N. and Yvon, F. (2005b). Analogical learning and
formal proportions: Definitions and methodological
issues. Technical report.
Yvon, F., Stroppa, N., Delhay, A., and Miclet, L.
(2004). Solving analogical equations on words.
Technical report, Ecole Nationale Sup
´
erieure des
T
´
el
´
ecommunications.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
504

Figure 1: Main results of the CRAN test collection: APMM vs. Okapi.
Figure 2: Main results of the CACM and CISI test collection: APMM vs. Okapi.
Analogy-based Matching Model for Domain-specific Information Retrieval
505
