
A Comparative Assessment of Ontology Weighting Methods in
Semantic Similarity Search
Antonio De Nicola
1
, Anna Formica
2
, Michele Missikoff
2
, Elaheh Pourabbas
2
and Francesco Taglino
2
1
Italian National Agency for New Technologies, Energy and Sustainable Economic Development (ENEA),
Casaccia Research Centre, Via Anguillarese 301, I-00123, Rome, Italy
2
Istituto di Analisi dei Sistemi ed Informatica (IASI) “Antonio Ruberti”, National Research Council,
Via dei Taurini 19, I-00185, Rome, Italy
Keywords:
Weighted Reference Ontology, Semantic Similarity, Information Content, Probabilistic Approach.
Abstract:
Semantic search is the new frontier for the search engines of the last generation. Advanced semantic search
methods are exploring the use of weighted ontologies, i.e., domain ontologies where concepts are associated
with weights, inversely related to their selective power. In this paper, we present and assess four different
ontology weighting methods, organized according to two groups: intensional methods, based on the sole
ontology structure, and extensional methods, where also the content of the search space is considered. The
comparative assessment is carried out by embedding the different methods within the semantic search engine
SemSim, based on weighted ontologies, and then by running four retrieval tests over a search space we have
previously proposed in the literature. In order to reach a broad audience of readers, the key concepts of this
paper have been presented by using a simple taxonomy, and the already experimented dataset.
1 INTRODUCTION
Search engines represent today the killer application
of the Web and can be found in every and all pos-
sible Web applications. For instance, if you need to
find a place on Google Maps, or you are looking for
a friend on Facebook, or you want to discover the last
song of your preferred singer on YouTube or Spo-
tify, you always go through a search facility. Since
the first appearance of general purpose search engines
on the Web, such as Yahoo! and AltaVista in the
Nineties, followed a few years later by Google and,
almost a decade afterwards, by Bing (just to name the
popular ones), their technology has been constantly
evolving. Such an evolution brought continuous en-
hancements of search strategies, algorithms, and, last
but not least, indexes, directories, vocabularies, and
other supporting metadata. Among metadata, seman-
tic annotation has emerged as an important enrich-
ment of digital resources, necessary to support the
evolution of search engines towards semantic similar-
ity search. A semantic annotation consists of a set
of concepts, taken from an ontology, that character-
ize a resource. In (Formica et al., 2008), (Formica
et al., 2013), (Formica et al., 2016), the authors ad-
dressed the semantic annotation and retrieval in accor-
dance to a probabilistic approach, based on a Vector
Space Model proposed in the context of text mining
and retrieval, where text documents are represented
by feature vectors. In our case, we deal with any kind
of digital resources (not only text documents), and
the features that characterize a resource correspond
to concepts in a reference ontology. Therefore we re-
fer to such a vector of features as an Ontology Feature
Vector (OFV). The adoption of ontologies is the base
of semantic search, representing a marked evolution
from the traditional keyword based retrieval methods.
In an ontology based search engine, the matchmaking
process can take place between a user request vector
and the annotation vectors associated with the digital
resources in the search space. A significant enhance-
ment of semantic search consists in the use of prob-
abilistic similarity reasoning methods. Within these
approaches, concept similarity is computed consider-
ing the contextual knowledge represented by the on-
tology, with its (topo)logical structure (essentially, the
ISA hierarchy). This approach requires each concept
in the ontology be associated with a weight related to
the level of specificity of the concept in the resource
space. The introduction of concept weights yields a
new breed of weighted ontologies, see for instance
(Abioui et al., 2018), (S
´
anchez et al., 2011). The
506
De Nicola, A., Formica, A., Missikoff, M., Pourabbas, E. and Taglino, F.
A Comparative Assessment of Ontology Weighting Methods in Semantic Similarity Search.
DOI: 10.5220/0007342805060513
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 506-513
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

majority of them share the idea that the weight of a
concept corresponds to the probability that selecting
at random a resource, it is characterized by a set of
features including one representing such a concept,
or one of its descendants in the ontology. Then, the
higher the weight of a concept the lower its specificity.
For instance, the concept student has a smaller weight
than person since the former is more specific than the
latter. Therefore, in formulating a query, the lower
the weights of the concepts, the higher their selective
power, and a more focused answer set is returned.
The performance of a semantic search engine de-
pends on the semantic matchmaking method and the
approach used to weigh the reference ontology. In this
paper, we focus on the analysis of four different ap-
proaches for weighting the concepts of an ontology,
and we carry out an experiment in order to asses the
analyzed ontology weighting methods.
The presented methods are divided according to
two groups (S
´
anchez et al., 2011): (i) extensional
methods (also known as distributional methods),
where the concept weights are derived by taking into
account both the topology of the ISA hierarchy and
the content of the resource space, also referred to as
dataset, (ii) intensional methods (also known as in-
trinsic methods), where the concept weights are de-
rived on the basis of the sole topology of the ISA hi-
erarchy.
In this paper, we selected the semantic similar-
ity method SemSim (Formica et al., 2013) in order to
evaluate the assessment of the four methods. In the
mentioned paper, the authors illustrate that SemSim
outperforms the most representative similarity meth-
ods proposed in the literature, i.e., Dice, Cosine, Jac-
card, and Weighted Sum. The SemSim method re-
quires: i) a dataset consisting of a set of resources
annotated according to a given ontology, and ii) a
method for associating weights with the concepts of
the ontology. Then, SemSim has been conceived to
compute the semantic similarity between a given user
request and any annotated resource in the dataset.
With respect to this work, in the mentioned paper
we considered only two weighting methods, i.e., the
frequency and the probabilistic approaches. In this
paper, they correspond to the Annotation Frequency
Method and the Top Down Topology Method, respec-
tively. Note that, in order to be coherent with the re-
sults given in (Formica et al., 2013), in this paper we
keep the same experimental setting, in particular, the
reference ontology and the dataset presented in the
mentioned work.
The next section gives a brief overview about on-
tology weighting. Section 3 provides the basic no-
tions concerning weighted ontologies and ontology
based feature vectors and proposes a probabilistic
model for weighted ontologies. Section 4 describes
in detail the four methods. Section 5 illustrates the
assessment of the methods and, finally, Section 6 con-
cludes.
2 RELATED WORK
According to the extensional methods, also referred
to as distributional (S
´
anchez et al., 2011), the infor-
mation content of a concept is in general estimated
from the frequency distribution of terms in text cor-
pora. Hence, this type is based on the extensional
semantics of the concept itself as its probability can
be derived on the basis of the number of occurrences
of the concept in the text corpora. This approach was
used in (Jiang and Conrath, 1997), (Resnik, 1995),
and (Lin, 1998) to assess semantic similarity between
concepts. Other proposals include the inverse docu-
ment frequency (IDF) method, and the method based
on the combination of term frequency (TF) and the
IDF (Manning et al., 2008). In our work, we de-
rived the concept frequency method and the annota-
tion frequency method, respectively, from those used
in (Resnik, 1995) and the IDF.
According to the intensional methods, also re-
ferred to as intrinsic (S
´
anchez et al., 2011), informa-
tion content is computed starting from the conceptual
relations existing between concepts and, in particular,
from the taxonomic structure of concepts. With this
regard, one of the most relevant methods is presented
in (Seco et al., 2004). This is based on the number
of concepts’ hyponyms and the maximum number of
concepts in the taxonomy. In (Meng et al., 2012), the
authors present a method derived from (Seco et al.,
2004) but they also consider the degree of generality
of concepts and, hence, their depth in the taxonomy.
In (S
´
anchez et al., 2011), the authors claim that the
taxonomical leaves are enough to describe and dif-
ferentiate two concepts because ad-hoc abstractions
(e.g., abstract entities) rarely appear in a universe of
discourse, but have an impact on the size of the hy-
ponym tree. In (Hayuhardhika et al., 2013), the au-
thors propose to use the density factor to estimate con-
cept weights on the basis of the sum of inward and
outward connections with other concepts against the
total number of connections in the ontology. Finally,
just to mention one more example, (Abioui et al.,
2018) takes into account both the taxonomic structure
and other semantic relationships to compute weights
of concepts.
In this work, first of all we focus on a tree-shaped
taxonomy organized as an ISA hierarchy and, within
A Comparative Assessment of Ontology Weighting Methods in Semantic Similarity Search
507
the above mentioned classification, we investigate
two extensional and two intensional methods. In par-
ticular, with regard to the extensional methods, we
address semantic annotations of resources rather than
text corpora.
3 A WEIGHTED ONTOLOGY AS
A PROBABILISTIC MODEL
In line with (Formica et al., 2013), (Formica et al.,
2016), an ontology Ont is a taxonomy defined by the
pair:
Ont =< C ,ISA >
where C = {K
i
} is a set of concepts and ISA is the
set of pairs of concepts in C that are in subsumption
(subs) relation:
ISA = {(K
i
,K
j
) ∈ C × C |subs(K
i
,K
j
)},
where subs(K
i
,K
j
) means that K
i
is a child of K
j
in the
taxonomy. In this work, we assume that the hierarchy
is a tree. A Weighted Reference Ontology (W RO) is
then defined as follows:
W RO =< Ont,w >
where w, the concept weighting function, is a proba-
bility distribution defined on C , such that given K ∈ C ,
w(K) is a decimal number in the interval [0.. .1].
The W RO is then used to annotate each resource
in the Universe of Digital Resources (U DR) by means
of an OFV. An OFV is a vector that gathers a set of
concepts of the ontology Ont, aimed at capturing the
semantic content of the corresponding resource. The
same also holds for a user request, and is represented
as follows:
o f v = (K
1
,...,K
n
), where K
i
∈ C ,i = 1,...,n
A normalized OFV is an OFV where if a concept ap-
pears, none of its ancestors appears. Note that, when
an OFV is used to represent a user request, it is re-
ferred to as semantic Request Vector (RV) whereas,
if it used to represent a resource, it is referred to as
semantic Annotation Vector (AV). They are denoted,
respectively, as follows:
rv = (R
1
,. .. ,R
n
), av = (A
1
,. .. ,A
m
),
where {R
1
,. .. ,R
n
} ∪ {A
1
,. .. ,A
m
} ⊆ C . We assume
that also AVs and RVs are normalized OFVs.
In the following, consider an ontology Ont =<
C ,ISA > and a dataset defined as a set of annotated
resources, where different resources can also have
the same annotations. For each K
i
∈ C , let X
K
i
be a
boolean variable, where 1 ≤ i ≤ q and q = |C |. Ac-
cording to the semantics of the ISA relationship, we
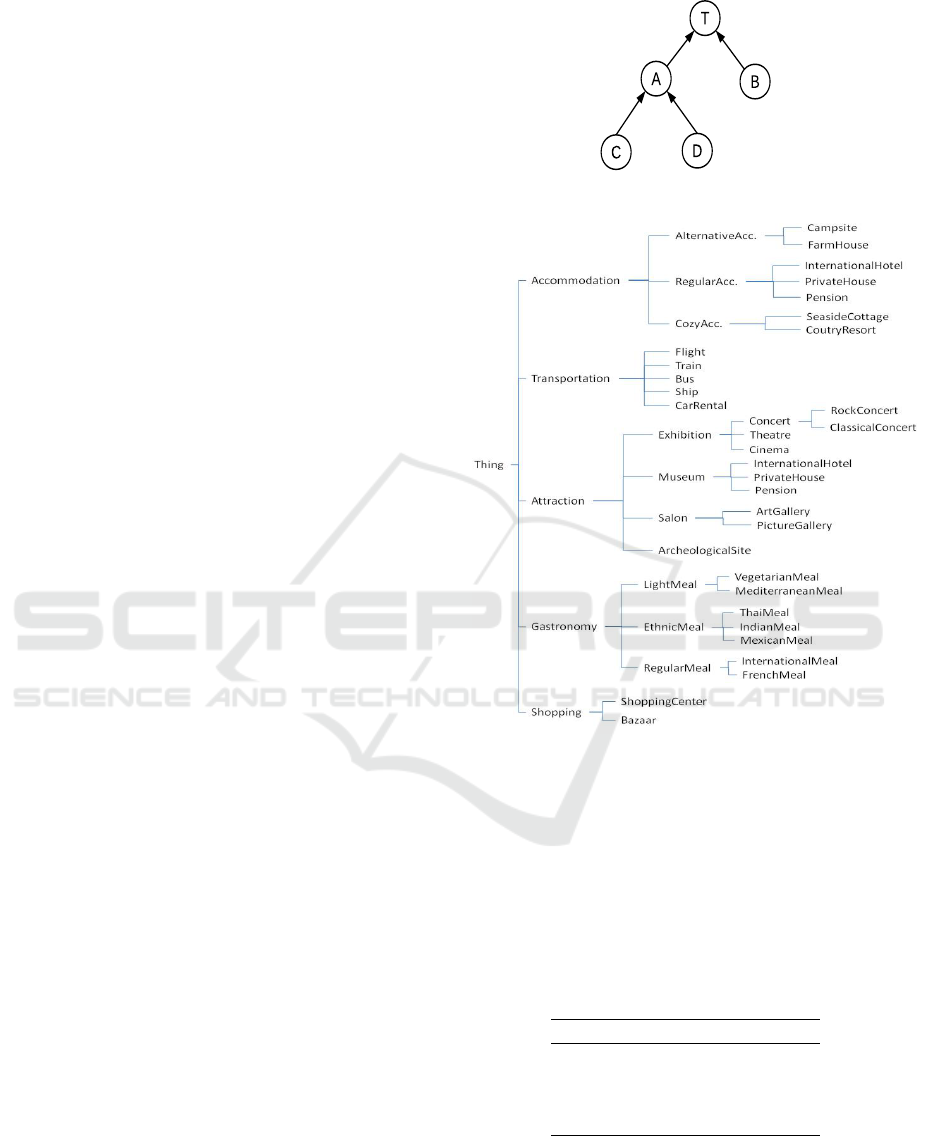
Figure 1: The simple taxonomy.
Figure 2: The Reference Ontology.
assume that the set of variables associated with the
concepts of the ontology are dependent. Each annota-
tion av = (A
1
,. .. ,A
m
) in the dataset can also be rep-
resented as:
[X
A
i
= 1,...,X
A
m
= 1] (1)
Analogously, any OFV can also be represented ac-
cording to the above notation.
Table 1: Simple dataset.
Resource Annotation Vector
r
1
av
1
= (A,B)
r
2
av
2
= (C)
r
3
av
3
= (B)
r
4
av
4
= (C,D)
In order to better illustrate this point, let us consider
the very simple taxonomy shown in Figure 1. Accord-
ing to this taxonomy, we have the following boolean
variables: X
T
, X
A
, X
B
, X
C
, X
D
, corresponding to the
concepts T , A, B, C, D, respectively. For example,
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
508

the variables X
C
and X
A
are dependent because C is a
child of A. Therefore X
C
= 1 implies X
A
= 1, accord-
ing to the semantics of the ISA hierarchy. Further-
more, with regard to the dataset, we assume the UDR
is composed by the four resources r
1
, r
2
, r
3
, and r
4
,
annotated as shown in Table 1. According to the no-
tation given in (1), for instance av
1
= (A,B) can also
be represented as [X
A
= 1,X
B
= 1].
In the literature, there are several definitions about
the notion of probability (Papoulis, 1965). In this
paper, we focus on the axiomatic and classical ap-
proaches. With respect to the axiomatic approach for
which a dataset is not required, in the classical ap-
proach a dataset has to be defined in order to identify
the bag of all possible outcomes, here indicated as S .
An outcome corresponds to an OFV . For instance,
the outcome corresponding to the o f v = (X
K
i
,X
K
j
) is:
[X
K
i
= 1,X
K
j
= 1] and we assume: X
K
h
= 0 for h 6= i, j,
1 ≤ h ≤ q, q = |C |.
Note that, the same dataset can determine different
bags of all possible outcomes. It may vary from a bag
of concepts to a bag of annotations, according to the
methods we consider in the next sections.
An event corresponds to a bag of outcomes (a
subset of S ) a probability is associated with. Accord-
ing to our approach, an event is a valued subset of
the q boolean variables enclosed in angular brackets.
In particular, the event defined by the single variable
X
K
= 1 is defined as follows:
< X
K
= 1 >
S
=
[X
H
1
,. .. ,X
H
q
] ∈ S |H
1
,. .. ,H
q
∈ C ,
∃X
H
j
= 1,1 ≤ j ≤ q, H
j
∈ K
+
where:
• K
+
= {K} ∪ desc(K),
and desc(K) is the set of the descendants of the
concept K in Ont
• double curly brackets denote a bag.
Finally, the probability of an event is given as follows:
p(< X
K
= 1 >
S
) =
| < X
K
= 1 >
S
|
|S |
(2)
We assume that, given a bag of possible outcomes S ,
the probability p
S
associated with a concept K in the
taxonomy is defined as the probability of the corre-
sponding event < X
K
= 1 >
S
, i.e.:
p(K) = p(< X
K
= 1 >
S
) (3)
4 WEIGHTING METHODS
In this section, we illustrate four methods for com-
puting the probability of concepts (weights) in a
tree-shaped taxonomy, by adopting the probabilistic
framework described in the previous section. In order
to better illustrate these methods, we use a running ex-
ample based on the ontology shown in Figure 1 and,
in the case of the methods based on the classical ap-
proach, we refer to the dataset shown in Table 1. For
this reason, for each classical method, we introduce
outcomes and events.
4.1 Extensional Methods
Concept Frequency Method (CF). The CF method
is based on the standard approach for computing the
relative frequency of a concept from a taxonomy in a
corpus of documents (Resnik, 1995).
According to this approach, given a concept K, its
relative frequency is the number of occurrences of K
+
divided by the number of occurrences of all concepts
in the set of all annotation vectors (AVs). In formal
terms, we have:
p(K) =
n(K
+
)
N
(4)
where n(K
+
) is the total number of occurrences of the
concepts in K
+
(K and its descendants in the taxon-
omy, as defined previously), and N is the number of
occurrences of all the concepts in the AVs.
Therefore, the bag of all possible outcomes S is
formed by all the occurrences of the concepts in the
AV s defined in the dataset, and an event < X
K
= 1 >
S
corresponds to the occurrences of the concept K and
its descendants in S .
Let us consider the running example, defined ac-
cording to Figure 1 and Table 1. In this case, the set
S is defined as follows:
S = {[X
A
= 1],[X
B
= 1],[X
C
= 1],
[X
B
= 1],[X
C
= 1],[X
D
= 1]}.
For instance, consider the event < X
A
= 1 >
S
. We
have:
< X
A
= 1 >
S
= {[X
A
= 1],[X
C
= 1],
[X
C
= 1],[X
D
= 1]}
As a result, according to Eq. (2), we have:
p(A) = p(< X
A
= 1 >
S
) = 4/6 = 2/3.
Similarly, in the other cases:
p(T ) = p(< X
T
= 1 >
S
) = 1
p(B) = p(< X
B
= 1 >
S
) = 1/3
p(C) = p(< X
C
= 1 >
S
) = 1/3
p(D) = p(< X
D
= 1 >
S
) = 1/6.
Annotation Frequency Method (AF). The AF
method is also referred to as frequency in (Formica
et al., 2013). In the AF method, given a concept K, its
relative frequency is the number of annotation vectors
A Comparative Assessment of Ontology Weighting Methods in Semantic Similarity Search
509

containing K, or a descendant of it, divided by the to-
tal number of annotation vectors. Therefore we have:
p(K) =
|AV
K
+
|
|AV |
(5)
where AV is the set of all the annotation vectors in the
dataset, and AV
K
+
is the subset of AV containing the
concept K or a descendant of it.
The bag of all possible outcomes S is represented
by the bag of the outcomes corresponding to the AVs
in the UDR, and an event < X
K
= 1 >
S
corresponds
to the occurrences of the AVs containing a concept in
K
+
.
Consider the running example:
S = {[X
A
= 1,X
B
= 1],[X
C
= 1],[X
B
= 1],
[X
C
= 1,X
D
= 1]}.
For instance, in the case of the event < X
A
= 1 >
S
we
have:
< X
A
= 1 >
S
= {[X
A
= 1,X
B
= 1],
[X
C
= 1],[X
C
= 1,X
D
= 1]}
and:
p(A) = p(< X
A
= 1 >
S
) = 3/4.
Similarly, in the other cases, we have:
p(T ) = p(< X
T
= 1 >) = 1
p(B) = p(< X
B
= 1 >) = 1/2
p(C) = p(< X
C
= 1 >) = 1/2
p(D) = p(< X
D
= 1 >) = 1/4.
4.2 Intensional Methods
With respect to the previous methods, the intensional,
or topology-based, methods illustrated in this sec-
tion follow an axiomatic approach, and therefore do
not require a dataset and a set of possible outcomes S .
Top-Down Topology-based Method (TD). The TD
method has been introduced in (Formica et al.,
2008), and successively extensively experimented in
(Formica et al., 2013) (where it has been referred to
as probabilistic). Here, we briefly recall it for reader’s
convenience. In order to compute the probabilities
of concepts in the reference ontology, this method
adopts a uniform probabilistic distribution along the
ISA hierarchy following a top-down approach. In par-
ticular, the root of the hierarchy has the probability
equal to 1, and the probability of a concept K of the
ontology is computed as follows:
p(K) =
p(parent(K))
|children(parent(K))|
(6)
In our running example, according to this approach,
the probabilities of the concepts in Figure 1 are
defined as follows:
p(T ) = 1, p(A) = 1/2, p(B) = 1/2
p(C) = 1/4, p(D) = 1/4.
Intrinsic Information Content Method (IIC). The
IIC method is based on an axiomatic approach, which
has been conceived in order to compute the informa-
tion content of concepts (Seco et al., 2004). The au-
thors define the information content of a concept in
a taxonomy as a function of its descendants. In par-
ticular, they claim that the more descendants a con-
cept has the less information it expresses. Therefore,
concepts that are leaves are the most specific in the
taxonomy, and their information is maximal.
Formally, they define the intrinsic information
content (iic) of a concept K as follows:
iic(K) = 1 −
log(|desc(K)| + 1)
log(|C |)
(7)
where the desc(K) is the set of the descendants of the
concept K, and C is the set of the concepts in Ont.
Note that the denominator assures that the iic values
are in [0,. ..,1]. The above formulation guarantees
that the information content decreases monotonically.
Moreover, the root node of the taxonomy yields an
information content value equal to 0.
For instance, consider the taxonomy shown in Fig-
ure 1. The information contents of the concepts are:
ic(T ) = 0, ic(A) = 1 −
log(2+1)
log(5)
= 0.32
ic(B) = 1, ic(C) = 1, ic(D) = 1.
5 ASSESSMENT OF METHODS
In this section, in order to carry out an assessment of
the four methods illustrated in the previous section,
we first recall the SemSim method.
5.1 Semsim
The SemSim method has been conceived to search for
the resources in the resource space that best match the
RV, by contrasting it with the various AV, associated
with the searchable digital resources (Formica et al.,
2013). This is achieved by applying the semsim func-
tion, which has been defined to compute the semantic
similarity between OFV. In SemSim, the probabilities
of concepts are used to derive the information content
(ifc) of the concepts that, according to (Lin, 1998),
represents the basis for computing the concept simi-
larity. In particular, according to the information the-
ory, the ifc of a concept K, is defined as:
ifc(K) = −log(w(K))
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
510

Table 2: Annotation Vectors (dataset).
av
1
= (InternationalHotel, FrenchMeal, Cinema, Flight)
av
2
= (Pension, VegetarianMeal, ArtGallery, ShoppingCenter)
av
3
= (CountryResort, MediterraneanMeal, Bus)
av
4
= (CozyAccommodation, VegetarianMeal, Museum, Train)
av
5
= (InternationalHotel, ThaiMeal, IndianMeal, Concert, Bus)
av
6
= (SeasideCottage, LightMeal, ArcheologicalSite, Flight, ShoppingCenter)
av
7
= (RegularAccommodation, RegularMeal, Salon, Flight)
av
8
= (InternationalHotel, VegetarianMeal, Ship)
av
9
= (FarmHouse, MediterraneanMeal, CarRental)
av
10
= (RegularAccommodation, EthnicMeal, Museum)
av
11
= (RegularAccommodation, LightMeal, Cinema, Bazaar)
av
12
= (SeasideCottage, VegetarianMeal, Shopping)
av
13
= (Campsite, IndianMeal, Museum, RockConcert)
av
14
= (RegularAccommodation, RegularMeal, Museum, Bazaar)
av
15
= (InternationalHotel, PictureGallery, Flight)
av
16
= (Pension, LightMeal, ArcheologicalSite, CarRental, Flight)
av
17
= (AlternativeAccommodation, LightMeal, RockConcert, Bus)
av
18
= (CozyAccommodation, VegetarianMeal, Exhibition, ArcheologicalSite, Train)
av
19
= (CountryResort, VegetarianMeal, Concert, Bus)
av
20
= (Campsite, MediterraneanMeal, ArcheologicalSite, Attraction, CarRental)
av
21
= (AlternativeAccommodation, LightMeal, Concert, Bus)
av
22
= (FarmHouse, LightMeal, RockConcert, Train)
Table 3: Request Vectors.
rv
1
= (Campsite, EthnicMeal, RockConcert, Bus)
rv
2
= (InternationalHotel, InternationalMeal, ArtGallery,
Flight)
rv
3
= (Pension, MediterraneanMeal, Cinema,
ShoppingCenter)
rv
4
= (CountryResort, LightMeal, ArcheologicalSite,
Museum, Train)
The semsim function is based on the notion of similar-
ity between concepts (features), referred to as consim.
Given two concepts K
i
, K
j
, it is defined as follows:
consim(K
i
,K
j
) =
2 × IC(lub(K
i
,K
j
))
IC(K
i
) + IC(K
j
)
where the lub represents the least abstract concept of
the ontology that subsumes both K
i
and K
j
. Given an
instance of RV and an instance of AV , say rv and av re-
spectively, the semsim function computes the consim
for each pair of concepts belonging to the set formed
by the Cartesian product of the rv, and av.
However, we focus on the pairs that exhibit high
affinity. In particular, we adopt the exclusive match
philosophy, where the elements of each pair of con-
cepts do not participate in any other pair. The method
aims to identify the set of pairs of concepts of the rv
and av that maximizes the sum of the consim similar-
ity values. In particular, given rv = {R
1
,..., R
n
} and
av = {A
1
,..., A
m
} as defined in Section 3, let S be the
Cartesian Product of rv and av, i.e., S = rv × av, then,
P (rv,av) is defined as follows:
P (rv,av) = {P ⊂ S | ∀ (R
i
, A
j
), (R
h
, A
k
) ∈ P, R
i
6=
R
h
, A
j
6= A
k
, |P| = min{n, m}}.
Table 4: Results of SemSim about rv
1
.
AV
Extensional Intensional
HJ CF AF TD IIC
av
1
0.10 0.49 0.16 0.54 0.47
av
2
0.10 0.30 0.03 0.34 0.29
av
3
0.25 0.45 0.26 0.50 0.45
av
4
0.18 0.47 0.08 0.49 0.44
av
5
0.51 0.64 0.54 0.64 0.59
av
6
0.14 0.39 0.07 0.40 0.36
av
7
0.16 0.47 0.08 0.51 0.48
av
8
0.10 0.33 0.04 0.37 0.34
av
9
0.10 0.41 0.19 0.46 0.42
av
10
0.21 0.48 0.28 0.49 0.45
av
11
0.15 0.42 0.11 0.45 0.38
av
12
0.10 0.21 0.01 0.25 0.20
av
13
0.89 0.72 0.73 0.71 0.69
av
14
0.10 0.33 0.03 0.38 0.33
av
15
0.10 0.33 0.07 0.33 0.31
av
16
0.10 0.39 0.07 0.39 0.36
av
17
0.93 0.85 0.69 0.87 0.84
av
18
0.26 0.45 0.17 0.46 0.42
av
19
0.50 0.68 0.45 0.73 0.66
av
20
0.34 0.51 0.28 0.51 0.50
av
21
0.77 0.82 0.63 0.85 0.80
av
22
0.46 0.70 0.44 0.72 0.70
Corr 1.00 0.92 0.96 0.90 0.92
Therefore, semsim(rv,av) is given below:
semsim(rv,av) =
max
P∈P (rv,av)
∑
(R
i
,A
j
)∈P
consim(R
i
,A
j
)
max{n,m}
A Comparative Assessment of Ontology Weighting Methods in Semantic Similarity Search
511

Table 5: Results of SemSim about rv
2
.
AV
Extensional Intensional
HJ CF AF TD IIC
av
1
0.72 0.59 0.52 0.80 0.76
av
2
0.21 0.41 0.35 0.55 0.50
av
3
0.16 0.24 0.05 0.35 0.31
av
4
0.10 0.34 0.07 0.49 0.42
av
5
0.10 0.39 0.26 0.47 0.46
av
6
0.20 0.36 0.22 0.49 0.43
av
7
0.71 0.67 0.60 0.90 0.86
av
8
0.10 0.36 0.28 0.49 0.47
av
9
0.10 0.23 0.05 0.35 0.31
av
10
0.40 0.30 0.18 0.46 0.39
av
11
0.10 0.29 0.18 0.44 0.39
av
12
0.10 0.10 0.00 0.23 0.18
av
13
0.10 0.19 0.02 0.34 0.27
av
14
0.44 0.30 0.18 0.55 0.49
av
15
0.86 0.69 0.66 0.70 0.68
av
16
0.25 0.40 0.29 0.54 0.48
av
17
0.10 0.35 0.07 0.48 0.43
av
18
0.10 0.28 0.06 0.39 0.35
av
19
0.10 0.34 0.08 0.46 0.42
av
20
0.10 0.28 0.06 0.41 0.35
av
21
0.10 0.36 0.08 0.48 0.45
av
22
0.10 0.32 0.07 0.46 0.42
Corr 1.00 0.81 0.87 0.83 0.82
5.2 Validation
In order to analyze the four methods illustrated in
the previous sections, we refer to the experiment pre-
sented in (Formica et al., 2013). In that experiment,
the taxonomy shown in Figure 2 has been considered,
and four request vectors, namely rv
i
, i = 1, ...4, which
are recalled in Table 3. In the same experiment, 22 an-
notated resources have been defined, which are repre-
sented by their annotation vectors av
1
, av
2
, .. ., av
22
as recalled in Table 2. In our approach they repre-
sent the dataset. In the experiment, the SemSim val-
ues were computed against the 22 annotation vectors,
and the correlation index (Corr) against human judg-
ment (HJ) scores was calculated. The HJ scores were
computed by asking to a group of 21 people to eval-
uate the similarity among each request vector and the
annotation vectors defined in Table 2. In the same
work, the authors demonstrated that the Annotation
Frequency Method (AF) (referred to as frequency in
the mentioned paper) outperforms some of the most
representative similarity methods defined in the liter-
ature (i.e., Dice, Jaccard, Cosine, and Weighted Sum).
In our work, for each request vector, we apply Sem-
Sim by using the four weighting methods illustrated
above. In Tables 4, 5, 6, 7 the results about rv
1
, rv
2
,
rv
3
, rv
4
are shown. In particular, we observe that the
AF method still achieves a higher correlation with HJ
with respect to all the other considered methods, i.e.,
Table 6: Results of SemSim about rv
3
.
AV
Extensional Intensional
HJ CF AF TD IIC
av
1
0.10 0.50 0.35 0.55 0.50
av
2
0.62 0.73 0.58 0.80 0.76
av
3
0.29 0.34 0.25 0.36 0.34
av
4
0.10 0.36 0.08 0.44 0.37
av
5
0.10 0.34 0.18 0.38 0.32
av
6
0.31 0.49 0.28 0.56 0.51
av
7
0.10 0.38 0.15 0.45 0.40
av
8
0.10 0.30 0.15 0.38 0.34
av
9
0.12 0.34 0.25 0.36 0.34
av
10
0.18 0.39 0.15 0.45 0.39
av
11
0.78 0.79 0.61 0.85 0.83
av
12
0.38 0.45 0.25 0.52 0.48
av
13
0.10 0.35 0.11 0.39 0.31
av
14
0.42 0.58 0.31 0.63 0.56
av
15
0.10 0.24 0.11 0.28 0.24
av
16
0.31 0.42 0.28 0.47 0.43
av
17
0.10 0.44 0.18 0.51 0.45
av
18
0.18 0.35 0.16 0.43 0.37
av
19
0.10 0.41 0.18 0.49 0.42
av
20
0.22 0.38 0.23 0.40 0.38
av
21
0.10 0.45 0.20 0.53 0.47
av
22
0.10 0.42 0.18 0.50 0.43
Corr 1.00 0.85 0.88 0.81 0.85
Concept Frequency (CF), Top-Down Topology-based
(T D), Intrinsic Information Content (IIC). Table 8
summarizes the results about the four request vectors.
First of all note that, in most cases, the extensional
methods outperform the intensional ones. This con-
firms the intuition that semantic methods work bet-
ter if a dataset representing the application domain is
considered. In the case of the intensional methods, the
IIC achieves higher correlations with respect to the
TD method. In order to better clarify, let us consider
two sibling concepts A and B in the taxonomy, where
A is a leaf and the B has some descendants. Accord-
ing to the TD method A and B have the same weights,
whereas according to the IIC method their weights
are different because the descendants contribute to
the weights of the concept B. Furthermore, the IIC
method outperforms the other intensional method be-
cause it also considers the total number of concepts
in the ontology. Concerning the extensional methods,
as mentioned above, the AF method outperforms the
other one (and all the others).
6 CONCLUSION
In this paper, we presented a comparative assessment
of the performances of four different methods for on-
tology weighting. The results of this work reveal
that, in general, the extensional methods outperform
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
512

Table 7: Results of SemSim about rv
4
.
AV
Extensional Intensional
HJ CF AF TD IIC
av
1
0.10 0.36 0.06 0.39 0.33
av
2
0.10 0.31 0.11 0.36 0.31
av
3
0.45 0.44 0.30 0.48 0.47
av
4
0.88 0.72 0.63 0.75 0.73
av
5
0.10 0.38 0.07 0.38 0.34
av
6
0.50 0.65 0.55 0.66 0.65
av
7
0.10 0.39 0.07 0.43 0.38
av
8
0.10 0.32 0.12 0.37 0.34
av
9
0.10 0.31 0.10 0.37 0.34
av
10
0.14 0.41 0.21 0.42 0.40
av
11
0.14 0.38 0.22 0.40 0.36
av
12
0.16 0.30 0.20 0.34 0.31
av
13
0.18 0.46 0.23 0.48 0.43
av
14
0.20 0.40 0.21 0.42 0.39
av
15
0.10 0.26 0.05 0.29 0.25
av
16
0.31 0.58 0.44 0.59 0.58
av
17
0.10 0.48 0.26 0.49 0.46
av
18
0.84 0.83 0.66 0.86 0.82
av
19
0.32 0.56 0.35 0.57 0.55
av
20
0.36 0.63 0.34 0.71 0.65
av
21
0.21 0.49 0.26 0.50 0.47
av
22
0.29 0.56 0.42 0.58 0.54
Corr 1.00 0.87 0.91 0.88 0.90
Table 8: Summary of correlations.
RV
Extensional Intensional
CF AF TD IIC
rv
1
0.92 0.96 0.90 0.92
rv
2
0.81 0.87 0.83 0.82
rv
3
0.85 0.88 0.81 0.85
rv
4
0.87 0.91 0.88 0.90
Mean 0.86 0.91 0.86 0.87
the intensional ones. Furthermore, among the ex-
tensional methods, the AF method exhibits the best
correlation with human judgment. However, there
are cases where the extensional methods may require
more elaboration, e.g., when the resource space is
highly dynamic, and then it is more appropriate to rely
on intensional methods.
REFERENCES
Abioui, H., Idarrou, A., Bouzit, A., and Mammass, D.
(2018). Towards a novel and generic approach for
owl ontology weighting. Procedia Computer Science,
127:426 – 435.
Formica, A., Missikoff, M., Pourabbas, E., and Taglino, F.
(2008). Weighted ontology for semantic search. In
Proc. of the OTM 2008 Confederated International
Conferences, CoopIS, DOA, GADA, IS, and ODBASE
2008. Part II on On the Move to Meaningful Internet
Systems, OTM ’08, pages 1289–1303, Berlin, Heidel-
berg. Springer-Verlag.
Formica, A., Missikoff, M., Pourabbas, E., and Taglino, F.
(2013). Semantic search for matching user requests
with profiled enterprises. Comput. Ind., 64(3):191–
202.
Formica, A., Missikoff, M., Pourabbas, E., and Taglino, F.
(2016). A bayesian approach for weighted ontolo-
gies and semantic search. In Proc. of the 8th Int.
Joint Conf. on Knowledge Discovery, Knowledge En-
gineering and Knowledge Management (IC3K 2016)
- KEOD, Porto - Portugal, November 9 - 11, 2016.,
pages 171–178.
Hayuhardhika, W., Purta, N., Sugiyanto, R., S., and Sidiq,
M. (2013). Weighted ontology and weighted tree
similarity algorithm for diagnosing diabetes mellitus.
In 2013 International Conference on Computer, Con-
trol, Informatics and Its Applications (IC3INA), pages
267–272.
Jiang, J. and Conrath, D. (1997). Semantic similarity based
on corpus statistics and lexical taxonomy. In Proc.
of the Int’l. Conf. on Research in Computational Lin-
guistics, pages 19–33.
Lin, D. (1998). An information-theoretic definition of sim-
ilarity. In Proceedings of the 15th International Con-
ference on Machine Learning, ICML ’98, pages 296–
304, San Francisco, CA, USA. Morgan Kaufmann
Publishers Inc.
Manning, C. D., Raghavan, P., and Schutze, H. (2008). In-
troduction to Information Retrieval. Cambridge Uni-
versity Press, New York, NY, USA.
Meng, L., Gu, J., and Zhou, Z. (2012). A new model of
information content based on concepts topology for
measuring semantic similarity in wordnet 1. Inter-
national Journal of Grid and Distributed Computing,
5(3):81–94.
Papoulis, A. (1965). Probability, Random Variables, and
Stochastic Processes. McGraw Hill, New York, NY,
USA.
Resnik, P. (1995). Using information content to evaluate se-
mantic similarity in a taxonomy. In Proceedings of the
14th International Joint Conference on Artificial In-
telligence - Volume 1, IJCAI’95, pages 448–453, San
Francisco, CA, USA. Morgan Kaufmann Publishers
Inc.
S
´
anchez, D., Batet, M., and Isern, D. (2011). Ontology-
based information content computation. Know.-Based
Syst., 24(2):297–303.
Seco, N., Veale, T., and Hayes, J. (2004). An intrinsic infor-
mation content metric for semantic similarity in word-
net. In Proceedings of the 16th European Conference
on Artificial Intelligence, ECAI’04, pages 1089–1090,
Amsterdam, The Netherlands, The Netherlands. IOS
Press.
A Comparative Assessment of Ontology Weighting Methods in Semantic Similarity Search
513
