
Efficient SAT Encodings for Hierarchical Planning
Dominik Schreiber
1,2
, Damien Pellier
2
, Humbert Fiorino
2
and Tom
´
a
ˇ
s Balyo
1
1
Karlsruhe Institut f
¨
ur Technologie, Karlsruhe, Germany
2
Universit
´
e Grenoble-Alpes, Grenoble, France
Keywords:
HTN Planning, SAT Planning, Incremental SAT Solving.
Abstract:
Hierarchical Task Networks (HTN) are one of the most expressive representations for automated planning
problems. On the other hand, in recent years, the performance of SAT solvers has been drastically improved.
To take advantage of these advances, we investigate how to encode HTN problems as SAT problems. In
this paper, we propose two new encodings: GCT (Grammar-Constrained Tasks) and SMS (Stack Machine
Simulation), which, contrary to previous encodings, address recursive task relationships in HTN problems. We
evaluate both encodings on benchmark domains from the International Planning Competition (IPC), setting a
new baseline in SAT planning on modern HTN domains.
1 INTRODUCTION
HTN (Hierarchical Task Network) planning
(Georgievski and Aiello, 2015) is one of the
most efficient and widely used planning techniques
in practice. It is based on expressive languages
allowing to specify complex expert knowledge for
real world domains. Unlike classical planning (Fikes
and Nilsson, 1971), in HTN planning, the goal is
expressed as a set of tasks to achieve, and to which it
is possible to associate different kinds of constraints:
the set of constraints and tasks is a Task Network.
Boolean satisfiability (SAT) solving is a generic
problem resolution method which has already been
successfully applied to classical planning before, e.g.,
(Rintanen, 2012). Given a propositional logic for-
mula F, the objective of SAT solving is to find an
assignment to all occurring Boolean variables such
that F evaluates to true, or to report unsatisfiability if
no such assignment exists. When applying SAT solv-
ing to planning problems, the full procedure features
four steps: (1) enumerating and instantiating all the
possible actions, (2) encoding the instantiated plan-
ning problem into propositional logic, (3) finding a
solution with a SAT solver, e.g., (E
´
en and S
¨
orensson,
2003a; Audemard and Simon, 2009; Biere, 2013),
and (4) decoding the found variable assignment back
to a valid plan. In conventional SAT planning (Kautz
and Selman, 1992; Kautz et al., 1996), each fact and
each action at each step is commonly represented by
a Boolean variable. The logic of how actions are ex-
ecuted and how they transform the world state is en-
coded with general clauses, while the initial state and
the goal are provided as single literals (unit clauses).
As the number of necessary actions is generally un-
known in advance, the planning problem is iteratively
re-encoded for a growing amount of steps, until a so-
lution is found or the computation timed out. The
SAT approach to planning is appealing because all
planning is performed by SAT solvers using very ef-
ficient domain-independent heuristics; thus, any ad-
vances towards more efficient SAT solvers can also
improve SAT-based planning.
The technique of incremental SAT solving has
recently gained popularity for planning purposes
(Gocht and Balyo, 2017). While conventional SAT
solving processes a single formula in an isolated
manner, incremental SAT solving allows for multiple
solving steps while successively modifying the for-
mula (E
´
en and S
¨
orensson, 2003b): New clauses can
be added between steps, and single literals can be as-
sumed, i.e. they are enforced for a single solving at-
tempt and dropped afterwards. A central advantage of
incremental SAT solving is that SAT solvers can learn
conflicts in assignments from past solving attempts
and thus find a solution more efficiently (Nabeshima
et al., 2006).
Compared to classical planning, significantly less
research has been done on using SAT solvers for HTN
planning (Mali and Kambhampati, 1998). One of the
reasons is that enumerating and instantiating methods
in HTN planning is challenging. Recently, efficient
Schreiber, D., Pellier, D., Fiorino, H. and Balyo, T.
Efficient SAT Encodings for Hierarchical Planning.
DOI: 10.5220/0007343305310538
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 531-538
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
531

instantiation procedures in HTN planning have been
proposed (Ramoul et al., 2017), which allows us to
investigate effective SAT-based approaches.
In this paper, our contributions are two new
SAT encodings for HTN problems: GCT (Grammar-
Constrained Tasks) and SMS (Stack Machine Sim-
ulation). Contrary to previous encodings (Mali and
Kambhampati, 1998), GCT and SMS fully address re-
cursive task relationships in HTN problems, and SMS
is specifically designed for incremental SAT solving.
2 HTN PLANNING
In this section we introduce the foundations of HTN
planning. A fact is an atomic logical proposition.
A state s is a consistent set of positive facts. An
operator o is a tuple o = (name(o), pre(o), eff (o))
where: name(o) is a syntactic expression of the form
n(x
1
,. ..,x
n
) with n being the name of the operator
and x
1
,. ..,x
n
its parameters; and pre(o) and eff (o)
are two sets of facts which define respectively the pre-
conditions that must hold to apply the operator and the
effects that must hold after the application of o.
An action is a ground operator, i.e. it has no free
parameters. Action a is applicable to a state s if
pre(a) ⊆ s. The resulting state s
0
of the application
of a in a state s is defined as follows: s
0
= γ(s,a) =
(s \ eff
−
(a)) ∪ eff
+
(a), where eff
+
(eff
−
) represent the
positive (negative) facts in eff. The application of a se-
quence of actions is recursively defined by γ(s,hi) = s
and γ(s,ha
0
,a
1
,. ..,a
n
i) = γ(γ(s,a
0
),ha
1
,. ..,a
n
i).
A method m = (name(m),pre(m),subtasks(o)) is
a tuple where: name(m) is a syntactic expression of
the form n(x
1
,. ..,x
n
) with n being the name of the
method and x
1
,. ..,x
n
its parameters; pre(m) defines
the preconditions, i.e., facts that must hold to apply
m, and subtasks(m) is the sequence of subtasks that
must be executed in order to apply m. A reduction
is a ground method. A reduction r is applicable in a
state s if pre(r) ⊆ s.
A task t is a syntactic expression of the form
t(x
1
,. ..,x
n
) where t is the task symbol and x
1
,. ..,x
n
its parameters. A tasks is primitive if t is the name of
an operator; otherwise the task is non-primitive.
An action a accomplishes a primitive task t in a
state s if name(a) = t and a is applicable in s. Simi-
larly, a reduction r accomplishes a non-primitive task
t in a state s if name(r) = t and r is applicable in s.
Moreover, tasks can have different reductions.
An HTN planning problem is a 5-tuple P =
(s
0
,g,T,O,M) where s
0
and g are respectively the ini-
tial state and the goal defined by logical propositions,
T is an ordered list of tasks ht
0
,. ..,t
k−1
i, O is a set
of operators, and M is a set of methods defining the
possible reductions of a task.
A solution plan for a planning problem P =
(s
0
,g,T,O,M) is a sequence of actions π =
ha
0
,. ..,a
n
i such that g ⊆ γ(s
0
,π). Intuitively, it
means that there is a reduction of T into π such that
π is executable from s
0
and each reduction is appli-
cable in the appropriate state of the world. The re-
cursive formal definition has three cases. Let P =
(s
0
,g,T,O,M) be an HTN planning problem. A plan
π = ha
0
,. ..,a
n
i is a solution for P iff:
Case 1. T is an empty sequence of tasks. Then the
empty plan π = hi is the solution for P if g ⊆ s
0
.
Case 2. The first task t
0
of T is primitive. Then
π is a solution for P if there is an action a
0
ob-
tained by grounding an operator o ∈ O such that
(1) a
0
accomplishes t
0
, (2) a
0
is applicable in s
0
and (3) π = ha
1
,. ..,a
n
i is a solution plan for the
HTN planning problem:
P
0
= (γ(s
0
,a
0
),g,ht
1
,. ..,t
k−1
i,O, M)
Case 3. The first task t
0
of T is non-primitive.
Then π is solution if there is a reduction d =
subtasks(t
0
) obtained by grounding a method m ∈
M such that d accomplishes t
0
and π is a solution
for the HTN planning problem:
P
0
= (s
0
,g,hsubtasks(t
0
),t
1
,. ..,t
k−1
i,O, M)
3 GCT ENCODING
As Mali et al. (Mali and Kambhampati, 1998) already
noted, their general encoding approach is equivalent
to supplementing a classical planning encoding with
HTN-specific constraints, which essentially enforce a
valid grammar over the sequence of actions. A note-
worthy restriction of their encoding is that each task is
assumed to have some fixed maximal amount of prim-
itive actions when fully reduced. Under this assump-
tion, it is easily possible to “allocate” a fixed amount
of propositional variables to each initial task in the
plan, knowing exactly the point where a task, and ul-
timately the entire plan, will certainly have finished.
In contrast, many common HTN problems can expand
indefinitely due to recursive relationships. As such, it
is difficult to decide in advance how many actions a
given task will take, depending on which reductions
are chosen and which facts hold before. The GCT en-
coding overcomes this limitation. For each step of the
plan to be found, we assign one Boolean variable to
the execution of some action as well as to the begin-
ning and the end of some task or reduction. Then, we
express all logical constraints which the occurrence of
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
532

a certain action, task, or reduction will imply at some
step, such as the preconditions of an action or the pos-
sible reductions of a task. The encoding generally al-
lows for recursive task relationships, as we do not set
any upper limit on a single task’s amount of primitive
actions (except for the total plan length).
3.1 Rules of Encoding
All facts from the specified initial state hold at the
beginning:
^
p∈s
0
holds(p,s
0
) ∧
^
p/∈s
0
¬holds(p,s
0
) (1)
Likewise, all facts of the goal hold in the last state s
n
:
^
p∈g
holds(p,s
n
) (2)
The preconditions of an action a must hold for it to be
executed at s
i
, and the execution of that action implies
its effects at the next state s
i+1
:
execute(a,s
i
) ⇒
^
p∈pre(a)
holds(p,s
i
) (3)
execute(a,s
i
) ⇒
^
p∈add(a)
holds(p,s
i+1
) ∧
^
p∈del(a)
¬holds(p,s
i+1
)
(4)
Facts only change their logical value if an action is
executed which has this change as an effect:
¬holds(p,s
i
) ∧ holds(p,s
i+1
) ⇒
_
p∈add(a)
execute(a,s
i
)
(5)
holds(p,s
i
) ∧ ¬holds(p,s
i+1
) ⇒
_
p∈del(a)
execute(a,s
i
)
Exactly one action is executed. For each distinct pair
of actions a and b, b 6= a we have:
¬execute(a,s
i
) ∨ ¬execute(b,s
i
) (6)
The following clauses ensure the ordering and se-
quential execution of initial tasks. The first task t
0
begins at s
0
. When a task t
j
ends, then the next task
t
j+1
begins at the next state. The last task t
k
ends at
state s
n−1
(such that its final effects hold in s
n
):
taskStarts(t
0
,s
0
) (7)
taskEnds(t
j
,s
i
) ⇔ taskStarts(t
j+1
,s
i+1
) (8)
taskEnds(t
k
,s
n−1
) (9)
Clauses in (10) essentially provide a grammar for
valid start and end points of tasks. Any start point
of a task must precede a corresponding end point and
vice versa.
taskStarts(t,s
i
) ⇒
_
i
0
≥i
taskEnds(t,s
i
0
) (10)
taskEnds(t,s
i
) ⇒
_
i
0
≤i
taskStarts(t,s
i
0
)
The following clauses are added only for non-
primitive tasks t. They define reduction variables in
order to uniquely refer to some particular task reduc-
tion beginning or ending at some computational step.
Remember, D(t) is the set of all the possible reduc-
tions of t:
taskStarts(t,s
i
) ⇒
_
d∈D(t)
reducStarts(t,d,s
i
) (11)
taskEnds(t,s
i
) ⇒
_
d∈D(t)
reducEnds(t,d,s
i
)
To provide a meaning to the newly defined variables,
it is enforced that the first subtask begins whenever
the reduction begins, and the last subtask ends when-
ever the reduction ends:
reducStarts(t,ht
0
,. ..i,s
i
) ⇒ taskStarts(t
0
,s
i
) (12)
reducStarts(t,ha,. .. i,s
i
) ⇒ execute(a,s
i
)
reducEnds(t,h.. .,t
0
i,s
i
) ⇒ taskEnds(t
0
,s
i
)
reducEnds(t,h.. ., ai,s
i
) ⇒ execute(a,s
i
)
All subtasks (both primitive (13) and non-primitive
(14)) of any occurring non-primitive task t need to be
completed within the execution of t.
reducStarts(t,h.. ., a,...i, s
i
) ⇒
_
i
0
≥i
execute(a,s
i
0
)
(13)
reducEnds(t,h.. ., a,...i, s
i
) ⇒
_
i
0
≤i
execute(a,s
i
0
)
reducStarts(t,h.. .,t
0
,. ..i,s
i
) ⇒
_
i
0
≥i
taskStarts(t
0
,s
i
0
)
(14)
reducEnds(t,h.. .,t
0
,. ..i,s
i
) ⇒
_
i
0
≤i
taskEnds(t
0
,s
i
0
)
The preconditions of a reduction need to hold.
reducStarts(t,d,s
i
) ⇒
^
p∈pre(d)
holds(p,s
i
) (15)
Again, an additional set of variables is introduced de-
noting that some task t
0
at step i
0
is part of some reduc-
tion of task t at step i. They are required in order to
reference the subtask relationship between two tasks
in an unambiguous manner in the following subtask
Efficient SAT Encodings for Hierarchical Planning
533

ordering constraints.
reducStarts(t,h.. .,t
0
,. ..i,s
i
) ⇒
⇒
_
i
0
≥i
subtaskStarts(t,s
i
,t
0
,s
i
0
) (16)
subtaskStarts(t,s
i
,t
0
,s
i
0
) ⇒ taskStarts(t
0
,s
i
0
)
subtaskStarts(t,s
i
,a, s
i
0
) ⇒ execute(a,s
i
0
)
reducEnds(t,h.. .,t
0
,. ..i,s
i
) ⇒
⇒
_
i
0
≤i
subtaskEnds(t,s
i
,t
0
,s
i
0
) (17)
subtaskEnds(t,s
i
,t
0
,s
i
0
) ⇒ taskEnds(t
0
,s
i
0
)
subtaskEnds(t,s
i
,a, s
i
0
) ⇒ execute(a,s
i
0
)
Now, the following clauses enforce that the subtasks
of any given task are totally ordered. Assume that a
reduction of t is d = ht
0
1
,. ..,t
0
k
i and 1 ≤ j < k:
reducStarts(t,d,s
i
) ∧ subtaskEnds(t,s
i
,t
0
j
,s
i
0
) ⇒
⇒ subtaskStarts(t,s
i
,t
0
j+1
,s
i
0
+1
) (18)
reducStarts(t,d,s
i
) ∧ subtaskStarts(t,s
i
,t
0
j+1
,s
i
0
+1
) ⇒
⇒ subtaskEnds(t,s
i
,t
0
j
,s
i
0
) (19)
At this point, if one would just use variables
taskStarts(t
0
,s
i
0
) instead of the more explicit
subtaskStarts(t,s
i
,t
0
,s
i
0
), then the clauses may lead to
unresolvable conflicts. This is because some task t
0
may then in fact not belong to the reduction of task t
at step i, but still impose restrictions on some actual
subtask of t. This problem is avoided by introducing
explicit variables for the subtask relationship between
tasks.
3.2 Complexity
In the following, a brief analysis of the complexity
of the GCT encoding is provided. Hereby, T , F,
and A correspond to the respective amount of tasks,
facts, and actions. Let r = max
|D(t)|
t ∈ T
be the maximal amount of reductions per task and
e = max
|subtasks(d)|
d ∈ D(t)
be the maximal
amount of subtasks per task reduction.
The GCT encoding features O(S · T ) variables for
the starts and ends of tasks, O(S · T · r) variables for
the starts and ends of task reductions, and O(S
2
· T
2
)
variables for modelling the subtask relationship be-
tween tasks. In addition, O(S · F) variables for the
encoding of facts, O(S · A) variables for the exe-
cution of actions and O(S · A log A) helper variables
for the “at most one action” rule (see rule 6) are
added. This leads to a total variable complexity of
O
S
2
T
2
+ S(Tr + A log A + F)
which in practice is
clearly dominated by the term S
2
T
2
.
Similarly, the clause complexity of the GCT is
asymptotically dominated by rules 18 and 19 which
results in a total of O(S
2
·T
2
·r · e) clauses. The length
of each clause is linear either in the amount of tasks,
reductions, or steps.
The Linear Bottom-Up Forward (LBF) encoding
(Mali and Kambhampati, 1998) can be compared to
GCT due to its state-based nature. LBF featured a
variable complexity of O (S
2
· TA · r
2
· e) and a clause
complexity of O (S
3
· TA · r
2
· e). The T
2
factor in
GCT’s complexity is fundamentally caused by the ad-
mission of recursive task definitions, while the r
2
fac-
tor in the complexity of LBF comes from the arbitrary
constraints that can be specified between reductions.
However, the LBF encoding has a clause complexity
which is cubic, not quadratic, in the number of en-
coded steps.
4 SMS ENCODING
The GCT encoding has various shortcomings. Most
significantly, it has a quadratic complexity of vari-
ables and clauses, rendering it inefficient both for the
encoding process and for the solving stage, and a
complete re-encoding has to be performed for each
additional computational step considered.
To improve this encoding, an initial idea has been
to adjust the encoding in order to make it eligible for
incremental SAT solving. This way, an abstract en-
coding is created only once and is then handed to the
solver without any given limit on the maximal num-
ber of computational steps to consider. The solver can
instantiate the clauses as needed and will remember
conflicts learned from previous solving steps, there-
fore reducing run times (Gocht and Balyo, 2017).
However, to achieve an incremental SAT encod-
ing for HTN planning, a number of challenges need
to be considered. Specifically aiming at a separated
encoding as proposed in (Gocht and Balyo, 2017), it
is necessary to reformulate all clauses such that each
clause only contains variables from the computational
steps i and i + 1, for some clause-specific i, and that
for each time step, all of the encoded clauses follow a
single, general “construction scheme”. In the follow-
ing, such an encoding is presented.
4.1 Encoding Principle
The Stack Machine Simulation (SMS) encoding sim-
ulates a stack of tasks which is transformed between
computational steps, always checking the task on top
of the stack and either pushing its subtasks if it is
non-primitive, or executing the corresponding action
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
534
get_soil_data(w1)
bottom empty_store()
send_soil_data(w1)
sample_soil(w1)
bottom
push(4) move(w0,w1)
bottom
pop()
bottom
Execute action: Preconditions + effects
empty_store()
send_soil_data(w1)
sample_soil(w1)
move(w0,w1) empty_store()
send_soil_data(w1)
sample_soil(w1)
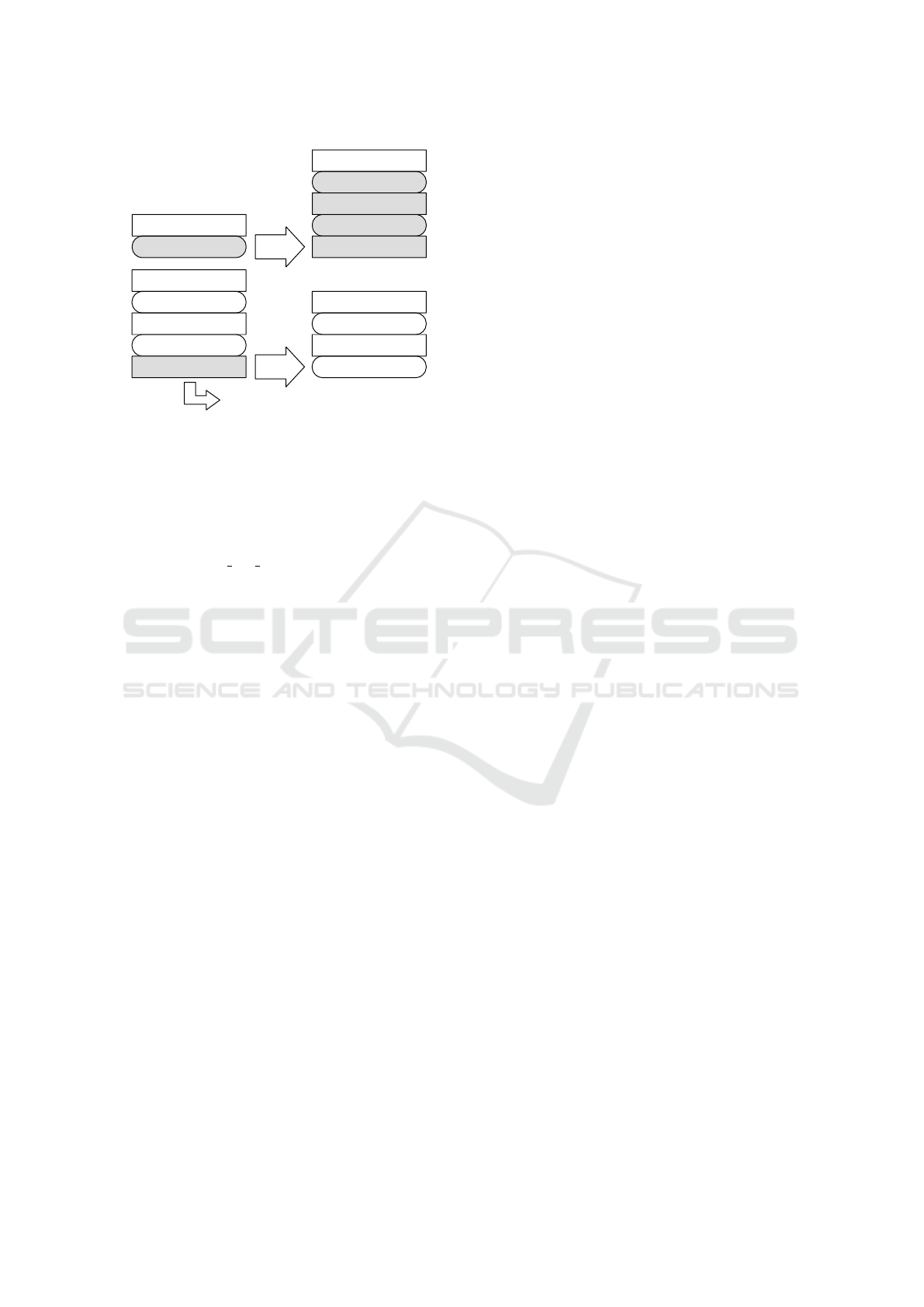
Figure 1: Illustration of the two central transitions between
computational steps in the SMS encoding: processing a
non-primitive task (top) and a primitive task (bottom).
if it is primitive. This central idea is illustrated in
Fig. 1 with a simplified example from the IPC domain
“Rover”. Non-primitive tasks have rounded corners
and primitive tasks are rectangular. First, the non-
primitive task get soil data(w1) is reduced to some
valid subtask sequence. In the next step, the primitive
task move(w0,w1) is processed and removed. Using
a stack memory and such transitions, the entire cur-
rently considered task hierarchy can be manipulated
in a step-by-step manner, eliminating the necessity of
linking steps that are further apart.
At the initial step, the first k positions of the stack
are enforced to contain the k initial tasks, followed by
an explicit bottom symbol. The goal is defined by the
requirement of bottom to be on top of the stack, or in
other words, of the stack being empty.
With this procedure, the initial tasks and their sub-
tasks will be sequentially processed and broken down
into subtasks until all tasks are removed and only bot-
tom remains. Thereby, the SAT solver decides which
cell of the stack contains which element at which step
such that all constraints are satisfied.
The SMS encoding is inherently incremental: To
extend an encoding with n computational steps into an
encoding with n + 1 computational steps, new clauses
are added and the goal assertions (rules 21, 23) are
updated. Apart from these simple operations, the pre-
vious formula can be reused without any changes.
4.2 Rules of Encoding
All facts specified in the initial state must hold:
^
p∈s
0
holds(p,s
0
) ∧
^
p/∈s
0
¬holds(p,s
0
) (20)
At the end, all facts from the goal must hold:
^
p∈g
holds(p,s
n
) (21)
The initial stack contains the initial tasks T and a bot-
tom symbol afterwards. Let T = ht
0
,. ..,t
j
,. ..,t
k
i:
stackAt( j,t
j
,s
0
) (22)
stackAt(k + 1, bottom,s
0
)
The stack must be empty in the end:
stackAt(0,bottom,s
n
) (23)
The execution of an action implies its preconditions
to hold:
execute(a,s
i
) ⇒
^
p∈pre(a)
holds(p,s
i
) (24)
The execution of an action implies its effects to hold
in the next step.
execute(a,s
i
) ⇒
^
p∈add(a)
holds(p,s
i+1
) ∧
^
p∈del(a)
¬holds(p,s
i+1
)
(25)
Facts only change if a supporting action is executed.
¬holds(p,s
i
) ∧ holds(p,s
i+1
) ⇒
_
p∈add(a)
execute(a,s
i
)
(26)
holds(p,s
i
) ∧ ¬holds(p,s
i+1
) ⇒
_
p∈del(a)
execute(a,s
i
)
At each step, all the push(k) and pop operations are
mutually exclusive. Let a and b be two operations in
{push(k) | 1 ≤ k ≤ maxPushes} ∪ {pop}. For each
distinct operation a and b, we have:
¬do(a,s
i
) ∨ ¬do(b, s
i
) (27)
If no pop operation is done, then no action is executed,
enforced by a virtual action noAction which does not
have any preconditions or effects.
¬do(pop, s
i
) ⇒ execute(noAction,s
i
) (28)
If an action a is on top of the stack, then it is executed
(and only this action); additionally, a pop operation is
done.
stackAt(0,a,s
i
) ⇒ execute(a,s
i
) ∧ do(pop,s
i
) (29)
execute(a,s
i
) ⇒ stackAt(0,a, s
i
)
If a non-primitive task t is on top of the stack, then
one of its possible reductions d must be applied.
stackAt(0,t,s
i
) ⇒
_
d∈D(t)
reduc(t,d,s
i
) (30)
Efficient SAT Encodings for Hierarchical Planning
535

If a non-primitive task t on top of the stack is re-
duced by some specific reduction d = ht
0
1
,. ..,t
0
k
i, then
a push by the amount of subtasks in the reduction is
performed, and all of its preconditions must hold.
stackAt(0,t,s
i
) ∧ reduc(t,d,s
i
) ⇒
⇒
do(push(k),s
i
) ∧
^
p∈pre(d)
holds(p,s
i
)
(31)
The stack content moves according to the performed
operation at a given step. Let t be any task or bottom,
and j > 0:
do(push(k),s
i
) ∧ stackAt( j,t,s
i
) ⇒
⇒ stackAt( j+k − 1,t, s
i+1
) (32)
do(pop, s
i
) ∧ stackAt( j,t,s
i
) ⇒
⇒ stackAt( j−1,t,s
i+1
) (33)
A non-primitive task and a reduction together de-
fine the corresponding subtasks as the new stack con-
tent at the positions which are freed by the occurring
push operation. Assuming that a reduction of t is
d = ht
0
0
,. ..,t
0
k−1
i:
stackAt(0,t,s
i
) ∧ reduc(t,d,s
i
) ⇒
⇒
k−1
^
j=0
stackAt( j,t
0
j
,s
i+1
) (34)
4.3 Variants
In addition to this encoding, which we will refer to
as SMS-ut (unary tasks) from now on, two additional
encodings of SMS have been considered.
The variant SMS-ur (unary reductions) does not
encode tasks, but instead reductions as the content of
the stack. This leads to transitional clauses of a differ-
ent kind, and the set of variables deciding the chosen
reduction are no more necessary.
In the variant SMS-bt (binary tasks), the stack
content is encoded not with one variable for each pos-
sible task at each position, but instead with one vari-
able for each binary digit of a number representing the
task at that position. This reduces the total variable re-
quirement for the stack content at each cell from O(T )
to O (logT ) per computational step, but complicates
some transitional clauses.
4.4 Complexity
In the following, the asymptotic complexity of clauses
and variables of the encoding is discussed. The en-
coding variant SMS-ut is chosen for this purpose. As-
sume that after n computational steps, a plan π of
length |π| ≤ n is found.
The amount of variables is dominated by the en-
coding of the stack itself: if a stack of size σ has been
encoded, then O (n·σ ·T ) variables are used to encode
the stack. Additionally, the action executions gener-
ate O (n· A) variables and the state encoding generates
O(n · F) variables. Moreover, O(n · r) variables rep-
resenting the chosen reduction of the current task are
needed for r = max
|D(t)|
t ∈ T
. This leads to a
total of O
n · (σT + A + F + r)
variables. With some
σ ∈ O(n), this measure implies a quadratic term n
2
T .
Regarding the amount of clauses: the classic plan-
ning clauses include O (n · A) clauses for precondi-
tions and effects of actions, and O(n · F) clauses
for frame axioms (rule 26). To uniquely specify
the content of the stack at each computational step,
O(n · σ · T · e) transitional clauses (for each push(k),
1 ≤ k ≤ e, and for pop) are needed, where e =
max
|subtasks(d)|
d ∈ D(t)
. O(n·A) clauses link
the stack operations with the execution of actions. As
e is usually a small constant, a pairwise “at most one
action” rule is added by introducing O(n · e
2
) clauses
(rule 27). For the actual transitions, each task which
can be on top of the stack causes O(r · e) clauses; con-
sequently, O(n · T · re) clauses are needed. In total,
O
n · (A + F + σTe + e
2
+ Tre)
clauses are added.
Again assuming σ ∈ O (n), the dominating factor be-
comes n
2
Te.
5 EXPERIMENTAL EVALUATION
We evaluate the proposed encodings on a set of plan-
ning benchmarks. Due to the significant differences
regarding recursion in the HTN models (recursion is
not supported in (Mali and Kambhampati, 1998)), we
cannot directly compare the performances of our dif-
ferent encodings. However, the encodings proposed
by (Mali and Kambhampati, 1998) have been a start-
ing point for the ideas implemented in the GCT en-
coding. GCT is then used as baseline in our experi-
ments for the SMS encodings that are build on a dif-
ferent approach.
A total of 120 instances from six domains have
been considered. The instances have been gener-
ated by using problem generators from the Interna-
tional Planning Competition (IPC). All experiments
have been conducted on a server with 24 cores of In-
tel Xeon CPU E5-2630 clocked at 2.30 GHz and with
264 GB of RAM, running Ubuntu 14.04. Each run has
been cut off after five minutes or when its RAM us-
age exceeded 12 GB. Glucose (Audemard and Simon,
2009) has been used as the primary SAT solver and
as a standalone application to efficiently solve non-
incremental formulae produced by GCT. The applica-
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
536
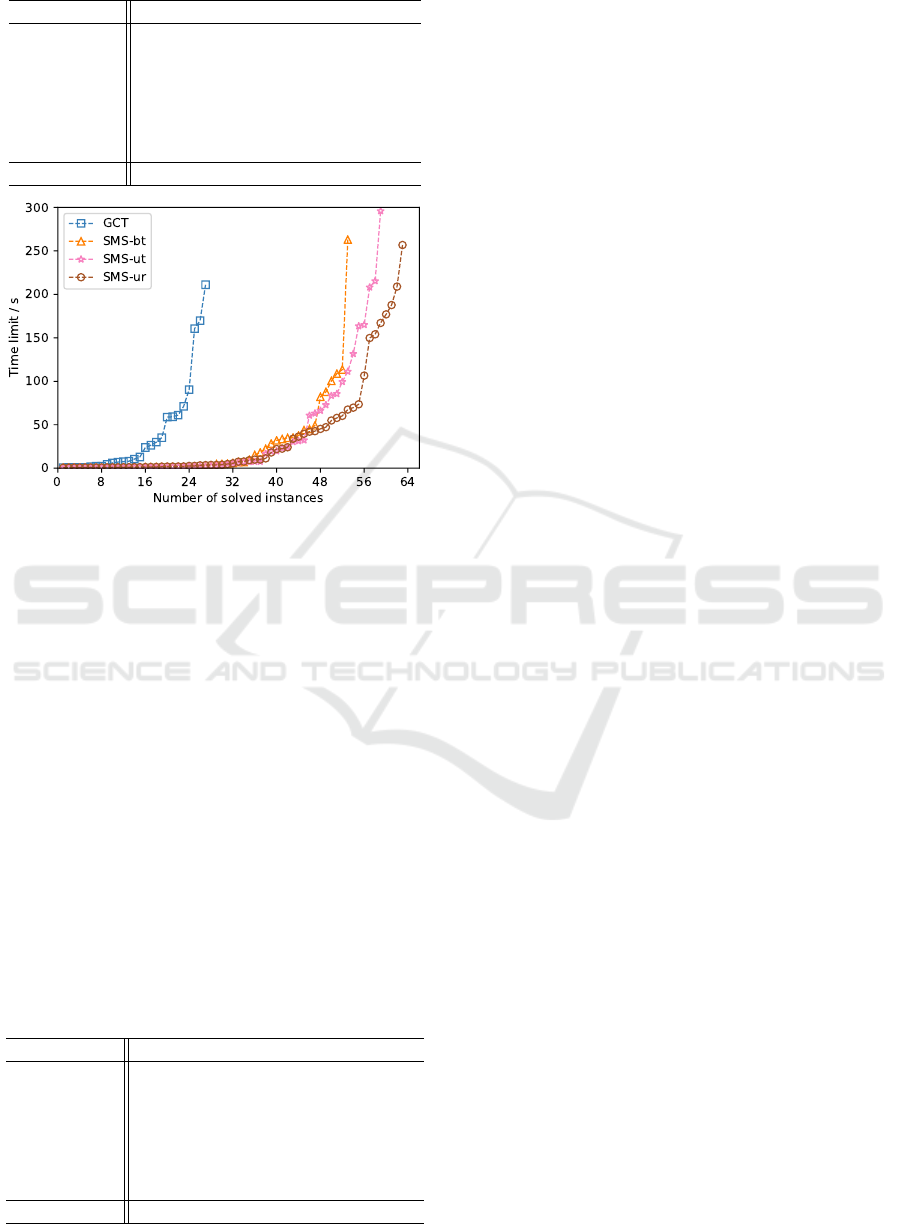
Table 1: Run time scores of encodings.
Domain GCT SMS-bt SMS-ut SMS-ur
Barman 0.09 1.90 1.96 4.68
Blocksworld 0.08 9.22 10.94 6.74
Childsnack 0.98 3.90 9.95 4.50
Elevator 4.21 14.86 13.32 10.29
Rover 0.44 6.17 5.40 5.58
Satellite 0.96 7.08 7.17 16.08
Total 6.75 43.13 48.74 47.88
Figure 2: Amount of instances solved by each encoding ap-
proach relative to the time limit.
tion Incplan (Gocht and Balyo, 2017) has been used
as a unified approach to solve the incremental plan-
ning problems produced by SMS.
Fig. 2 illustrates the number of instances solved by
each competing approach relative to the set time limit.
With the GCT encoding, 27 instances have be solved
within the maximum time limit. SMS significantly
outperformed this baseline: the variant bt solved 53
instances, ut solved 59 instances, and ur solved 63
instances.
A domain-specific comparison of run time perfor-
mances is provided in Table 1. For each tested in-
stance, a score of 1 is attributed to the competitor with
the lowest run time t
∗
, and a score of t
∗
/t is attributed
to each further competitor with a run time t. Unfin-
ished computations lead to a score of 0. For each
domain, the scores of all instances are then summed
up. Overall, the variant ur performed best on the
Table 2: Plan length scores of encodings.
Domain GCT SMS-bt SMS-ut SMS-ur
Barman 0.85 2.72 2.00 5.00
Blocksworld 2.00 10.00 13.00 11.00
Childsnack 3.00 6.00 10.00 8.00
Elevator 13.00 16.00 15.00 15.00
Rover 3.86 6.62 6.55 6.62
Satellite 4.00 9.61 11.79 16.77
Total 26.70 50.96 58.33 62.40
Barman and Satellite domains whereas the task-based
variants ut and bt generally performed better on the
Blocksworld and Elevator domains. The binary en-
coding variant bt only lead to small improvements on
some domains while significantly worsening the run
times on other domains. This result is consistent with
the general belief that SAT constraints encoded in a
binary manner can actually hinder the propagation of
variable assignments and conflicts and, as a result, in-
crease the execution time of SAT planning (Ghallab
et al., 2004). The length of the plans found with the
different encodings are compared in Table 2, with the
scores being computed analogously to the run time
scores. By design, the GCT encoding generally leads
to the shortest possible plan, as the amount of possible
primitive actions is increased one by one until a solu-
tion is found. The only exception for this is if nop ac-
tions are involved, which do not account for the plan
length, but still cause additional solving iterations.
Yet, the SMS encoding variants lead to plans which
are nearly as short as the plans found with GCT.
6 RELATED WORKS
In his pioneering work, Sacerdoti (Sacerdoti, 1975)
proposed a planner called NOAH (Nets of Action Hi-
erarchies). The system was built up on a data struc-
ture called procedure net. This data structure intro-
duced for the first time the concept of tasks network
and reduction. These two concepts are today part of
all the modern HTN planners. Mali (Mali and Kamb-
hampati, 1998; Mali, 2000) proposed to use classi-
cal SAT solvers by encoding HTN planning problems
into satisfiability problems. Recent and modern HTN
planners such as SHOP (Simple Hierarchical Ordered
Planner) (Nau et al., 1999; Ramoul et al., 2017) main-
tain states during the search process and explore a
space of states. Each task network contains a repre-
sentation of the state in addition to the tasks. A re-
duction is applicable if and only if some constraints
expressed as precondition of the reduction hold in the
state. A comprehensive comparison of these different
works is given in (Georgievski and Aiello, 2015) and
a complexity analysis of HTN planning in (Erol et al.,
1994; Alford et al., 2015).
SAT solving has been successfully applied in the
classical STRIPS planning context (Fikes and Nils-
son, 1971) since the initial proposal (Kautz and Sel-
man, 1992; Kautz et al., 1996). As a significant im-
provement, more efficient action encodings based on
the execution of multiple actions in parallel (as long
as some valid ordering on the actions exists) have
been proposed (Rintanen et al., 2004; Rintanen et al.,
Efficient SAT Encodings for Hierarchical Planning
537

2006). Recently, incremental SAT solving has been
shown to significantly speed up the planning proce-
dure of Madagascar (Gocht and Balyo, 2017), based
on the observation that reusing conflicts from previ-
ous solving attempts can lead to a much faster solving
process (Nabeshima et al., 2006).
7 CONCLUSION
In the work at hand, we have presented new efficient
approaches of totally ordered HTN planning by mak-
ing use of SAT solvers. Previous SAT encodings for
HTN planning problems had many shortcomings re-
stricting their practical usage. We proposed two new
encodings, GCT and SMS, which mend these short-
comings and thus can exploit efficient existing HTN
grounding routines. SMS is specifically designed for
incremental SAT solving and works reliably on all
kinds of special cases which may occur in the consid-
ered planning domains. We experimentally evaluated
both encodings and showed their practical applicabil-
ity by running our planning framework on problem
domains from the International Planning Competition
(IPC). With the SMS encoding significantly outper-
forming GCT regarding overall run times while find-
ing plans of comparable length, we have defined a
new baseline of SAT planning on totally ordered HTN
domains.
In future work, we will investigate alternative SAT
encodings based on the general idea of SMS in or-
der to further improve the overall performance of the
approach. While the SMS encoding works reliably,
its performance is limited by the amount of primi-
tive actions in the shortest possible plan, and the stack
size must be provided as parameter. Enhancements of
SMS which function without any external parameters
and which require less incremental iterations in order
to find a solution may significantly speed up the plan-
ning process.
REFERENCES
Alford, R., Bercher, P., and Aha, D. (2015). Tight bounds
for HTN planning with task insertion. In Proceedings
of the International Joint Conference on Artificial In-
telligence, pages 1502–1508.
Audemard, G. and Simon, L. (2009). Predicting learnt
clauses quality in modern SAT solvers. In IJCAI, vol-
ume 9, pages 399–404.
Biere, A. (2013). Lingeling, plingeling and treengeling en-
tering the SAT competition 2013. Proceedings of SAT
competition, 51.
E
´
en, N. and S
¨
orensson, N. (2003a). An extensible SAT-
solver. In International conference on theory and
applications of satisfiability testing, pages 502–518.
Springer.
E
´
en, N. and S
¨
orensson, N. (2003b). Temporal induction by
incremental SAT solving. Electronic Notes in Theo-
retical Computer Science, 89(4):543–560.
Erol, K., Hendler, J., and Nau, D. (1994). UMCP: A sound
and complete procedure for hierarchical task-network
planning. In Proceedings of the Artificial Intelligence
Planning Systems, volume 94, pages 249–254.
Fikes, R. and Nilsson, N. (1971). STRIPS: A new approach
to the application of theorem proving to problem solv-
ing. Artificial Intelligence, 2(3-4):189–208.
Georgievski, I. and Aiello, M. (2015). HTN planning:
Overview, comparison, and beyond. Artifical Intel-
ligence, 222:124–156.
Ghallab, M., Nau, D., and Traverso, P. (2004). Automated
Planning: theory and practice. Elsevier.
Gocht, S. and Balyo, T. (2017). Accelerating SAT based
planning with incremental SAT solving. Proceedings
of the International Conference on Automated Plan-
ning and Scheduling, pages 135–139.
Kautz, H., McAllester, D., and Selman, B. (1996). Encod-
ing Plans in Propositional Logic. In Proceedings of the
International Conference on Knowledge Representa-
tion and Reasoning, pages 374–384.
Kautz, H. and Selman, B. (1992). Planning as Satisfiabil-
ity. In Proceedings of the European Conference on
Artificial Intelligence, pages 359–363.
Mali, A. (2000). Enhancing HTN planning as satisfability.
In Artificial Intelligence and Soft Computing, pages
325–333.
Mali, A. and Kambhampati, S. (1998). Encoding HTN
planning in propositional logic. In Proceedings In-
ternational Conference on Artificial Intelligence Plan-
ning and Scheduling, pages 190–198.
Nabeshima, H., Soh, T., Inoue, K., and Iwanuma, K. (2006).
Lemma reusing for SAT based planning and schedul-
ing. In Proceedings of the International Conference
on Automated Planning and Scheduling, pages 103–
113.
Nau, D., Cao, Y., Lotem, A., and Munoz-Avila, H. (1999).
SHOP: Simple hierarchical ordered planner. In Pro-
ceedings of the international joint conference on Arti-
ficial intelligence, pages 968–973.
Ramoul, A., Pellier, D., Fiorino, H., and Pesty, S. (2017).
Grounding of HTN planning domain. International
Journal on Artificial Intelligence Tools, 26(5):1–24.
Rintanen, J. (2012). Planning as satisfiability: Heuristics.
Artificial Intelligence Journal, 193:45–86.
Rintanen, J., Heljanko, K., and Niemel
¨
a, I. (2004). Parallel
encodings of classical planning as satisfiability. In Eu-
ropean Workshop on Logics in Artificial Intelligence,
pages 307–319.
Rintanen, J., Heljanko, K., and Niemel
¨
a, I. (2006). Planning
as satisfiability: parallel plans and algorithms for plan
search. Artificial Intelligence, 170(12-13):1031–1080.
Sacerdoti, E. (1975). A structure for plans and behavior.
Technical report, DTIC Document.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
538
