
The Impact of Environmental and Evolutionary Factors on the
Emergence of Cooperation among Evolved Mobile Agents
Maud D. Gibbons, Josephine Griffith and Colm O’Riordan
Discipline of Information Technology, National University of Ireland, Galway, Ireland
Keywords:
Evolutionary Game Theory, Contingent Mobility, Evolution of Cooperation.
Abstract:
This paper presents work investigating the influence of various environmental and evolutionary factors on
the evolution of cooperation in a spatial game theoretical setting. These include agent mobility, population
density, agent lifespan, and the placement mechanism. In the model considered, a population of agents inhabit
a toroidal lattice grid, in which they participate in the Prisoner’s Dilemma game. The agents have the ability to
respond to, and learn from, environmental stimuli. In particular, agents learn movement strategies to compete
with other agents in the game, which may result in improved payoffs by increasing the number of beneficial
interactions. We compare the levels of cooperation and the corresponding movement strategies evolved under
the various environmental and evolutionary settings. We present results indicating that, given suitable densities
and evolutionary settings, cooperators in well-mixed populations develop a suitable movement strategy to
promote the evolution of cooperation. Additionally, we show that cooperation may emerge without significant
aid from mobile strategies given a placement mechanism conducive to the formation of cooperator clusters.
1 INTRODUCTION
The role of agent mobility has grown in recognition
and importance as a factor in solving the puzzle of
the evolution of cooperation. Mobility was originally
perceived as a hindrance to cooperators by allowing
highly mobile defectors go unpunished, leading to the
‘free rider’ effect (Enquist and Leimar, 1993). Ho-
wever, it has since been demonstrated that simple
movement rules (Aktipis, 2004) and mobility rates
(Vainstein et al., 2007) significantly curb this pheno-
menon allowing self-preserving, or evasive, coopera-
tor clusters to form, which in turn allows for coope-
ration to proliferate. Mobile strategies now play a
vital role as mechanisms for the emergence, promo-
tion, and sustainability of cooperation. In this paper,
we investigate the influence of some environmental
and evolutionary factors on the evolution of these mo-
bile strategies. We hypothesize that effective mobility
strategies lead to the creation of evasive cooperator
clusters, thereby facilitating the evolution of coopera-
tion.
Contingent, or non-random, mobility has the ca-
pacity to be proactive, whereby individual agents de-
liberately seek out better environments. However,
many of these models (Helbing and Yu, 2008; Bu-
esser et al., 2013) suffer from incurring high memory
requirements and complexity costs. In this paper, we
present a reactive mobility model to imbue agents
with a simple, yet expressive, range of actions: fol-
low, flee, and stay still. The action to ‘follow’ ena-
bles an agent to maintain connections with others in
their neighbourhood on the grid, conversely the action
to ‘flee’ severs such connections. These actions are
dependent on the strategies (cooperate or defect) and
positions of an agent’s neighbours, and are evolved
through a process of selection and duplication. We
encode each action into an 8-bit binary array, and in-
clude an option to move randomly. Agents determine
where to move by ranking the free grid locations in
their neighbourhood according to their chosen action.
We hypothesize that mobility directly influences the
evolution of cooperation by utilizing movement pat-
terns, which allows for the formation of cooperative
clusters which increase the number of beneficial inte-
ractions for cooperators.
Much of the contingent mobility strategies in
the literature are heuristically guided and imbued to
agents at the outset of a simulation. There has been
less focus on the explicit evolution of these strate-
gies by agents over the course a simulation. The
use of evolutionary models may provide some insight
into how mobility strategies may have originated in
nature, and more generally allow for the investiga-
Gibbons, M., Griffith, J. and O’Riordan, C.
The Impact of Environmental and Evolutionary Factors on the Emergence of Cooperation among Evolved Mobile Agents.
DOI: 10.5220/0007344500690079
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 69-79
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
69

tion of the co-evolution of agent traits. In this sense,
despite the possibility of adapting the traditional ge-
netic algorithm-like approach, i.e. tournament se-
lection, crossover, and mutation to be limited to the
local interactions of each agent, it would add another
layer of complexity to the model, which is not the aim
of this work. In particular, considering this traditional
evolutionary approach at a global level, i.e. building
the next generation based on the best fittest agents of
the entire population, which would negate the mecha-
nism of network reciprocity (Nowak, 2006). Thus,
this work adopts a simplified birth-death mechanism
to keep the complexity of the procedures of selection
and replacement at a minimum.
Agent mobility is not the only factor impacting the
emergence of cooperation, population density and the
specific settings of the evolutionary model also have
considerable influence. These include: agent lifespan,
generation length, and the means of placement of new
agents. Population density has been shown to have
a significant influence on the evolution of coopera-
tion in spatial environments, particularly in a diluted
lattice (Vainstein and Arenzon, 2001). On the other
hand, fewer studies have focused on the effects of va-
rying particular evolutionary settings, or on the im-
pact that different placement mechanisms have on the
outcome of a simulation. In this paper, we also in-
vestigate the influence of these factors on the emer-
gence of cooperation using the proposed mobility mo-
del. We will begin by identifying the evolutionary and
environmental settings conducive to the evolution of
cooperation, and then attempt to accurately explain
these phenomena through analysis of the evolved ge-
notypes present in the final stage of a simulation. We
hypothesize that the factors that influence cluster gro-
wth, and the number of interactions cooperators have
with defectors, directly impact the evolution of coope-
ration.
The paper outline is as follows: we review the re-
lated work of mobility in the Spatial Prisoners Di-
lemma in the next section. Section 3 outlines our
methodology, including a description of our agent re-
presentation, the evolutionary mechanism, and details
of the movement function. In Section 4, we discuss
a number of experiments and present results regar-
ding the relative influence of factors on the emergence
of cooperation, and the movement strategies evolved
therein. Finally, we present our conclusions and sug-
gest future avenues for this research.
2 RELATED WORK
Questions relating to cooperation and its emergence
have been studied in a range of domains including
economics, psychology, theoretical biology, and com-
puter science. Researchers explore the conditions
necessary for cooperation to emerge among groups
using social dilemmas due to their usefulness in cap-
turing the conflict between individual and collecti-
vely rational behaviours. Evolutionary game theory
has been studied since the 1980s when John May-
nard Smith incorporated ideas from evolutionary the-
ory into game theory (Maynard Smith, 1982). Howe-
ver, these ideas become increasingly relevant as they
expand into new fields, such as evolutionary robotics
(Andr
´
e and Nolfi, 2016).
The Prisoner’s Dilemma (Axelrod, 1984), and its
extensions in the iterated form, is the game most of-
ten studied in this domain. It has attained such popu-
larity due to its succinct representation of the conflict
between individually rational choices and those made
for the common good. It is described as follows: two
players make a choice simultaneously to either coope-
rate or defect. Mutual cooperation yields a reward R
for both participants. However, unilateral defection
results in a greater payoff, T , for the defector and a
worse payoff, S, for the cooperator (the sucker’s pa-
yoff). If both players chose to defect, both receive P
as a payoff such that: T > R > P > S.
Spatial models promote the evolution of coopera-
tion by constraining agent interactions to a particu-
lar static topology. Previous work has investigated
structures such as lattices (Nowak and May, 1992),
small-world graphs (Santos et al., 2006), and scale-
free graphs (Poncela et al., 2009). However, the in-
clusion of movement creates a more realistic model
by allowing agents to respond to their current neig-
hbourhood by moving within their environment.
Mobility is a form of network reciprocity (Nowak,
2006), which has been garnering increased attention
in the literature due to its direct application in robotics
(Floreano and Keller, 2010), and human behaviour
(Antonioni et al., 2015). It has gone from being per-
ceived as a hindrance to the emergence of cooperation
to a key concept in its promotion. While unrestrained
movement can, and does, lead to the ‘free-rider’ ef-
fect (Enquist and Leimar, 1993), allowing highly mo-
bile defectors to go unpunished, using simple strategy
rules (Aktipis, 2004; Ichinose et al., 2013) or using
mobility rates (Meloni et al., 2009; Vainstein et al.,
2007) significantly curbs the free-rider phenomenon
allowing self-preserving cooperator clusters to form,
and cooperation to proliferate.
Several mechanisms for the emergence of coope-
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
70

ration exist, but all essentially express a need for
cooperators to either avoid interactions with defectors
or increase and sustain interactions with other coope-
rators. Research in this domain is largely divided into
two categories based on authors’ definitions of mobi-
lity; all movement should be random (Meloni et al.,
2009; Sicardi et al., 2009; Antonioni et al., 2014), or
should be purposeful or strategically driven, but may
indeed contain random elements (Cong et al., 2012;
Droz et al., 2009; Jiang et al., 2010; Yang et al., 2010;
Tomassini and Antonioni, 2015). Random mobility
can be used to describe the minimal conditions for
the evolution of cooperation. However, their expres-
siveness and applications to real-world problems are
limited. Alternatively, contingent mobility has the ca-
pacity to be proactive. Agents can deliberately seek
better environments, rather than simply react to sti-
muli and randomly relocate.
Aktipis (Aktipis, 2004) presents a simple contin-
gent movement strategy, ‘Walk Away’. In this set
up, agents form pairs and repeatedly interact together
when they meet in the spatial environment. The po-
pulation evolves using a birth-death process, in which
agents require certain energy levels to live and repro-
duce, and acquire this energy from interactions in the
game. Following interaction, agents disconnect from
defecting partners by relocating to a local random
cell, and continue cooperative partnerships by staying
still. The main strength of this strategy is its sim-
plicity; agents are memoryless but cooperation can
spread and dominate. However, one major criticism
of this model is that it does not attempt to maintain
those crucial mutually cooperative pairings.
The works by Helbing and Yu (Helbing and Yu,
2008; Helbing and Yu, 2009) describe a form of con-
tingent movement called Success Driven Migration
SDM, which forms one of the most influential models
within the scope of mobility. In this model, agents
can test potential sites for migration in order to dis-
cover neighbourhoods with the highest expected pa-
yoff. However, this model suffers from incurring high
memory and information requirements; testing po-
tential sites, regardless of a successful outcome, co-
mes at a cost to an agent’s payoff, and agents require
complete knowledge of their environment. These re-
quirements can prove to be cumbersome in instances
where perfect global information may be incorrect or
impossible to obtain. A small memory is a require-
ment that also comes from the robotics field, and has
been well studied (Nguyen et al., 2018). Additionally,
recent work has shown that cooperation can emerge
from mobility models using only local information in
both explicitly spatial (Burgess et al., 2017), and non-
spatial (Joshi et al., 2017) environments.
There has been some research (Perc and Szolnoki,
2010; Joyce et al., 2006) indicating that evolutionary
models may be used to evolve movement strategies
that are conducive to the emergence of cooperation.
Ichinose et al. (Ichinose et al., 2013) use an evolutio-
nary model to investigates the co-evolution of migra-
tion and cooperation. Agents play an N-player Pri-
soner’s Dilemma game after which they move locally
according to an evolved probability vector. Agents
evolve to move collectively in the same direction de-
termined by cooperators. This model uses separate
probability functions for the birth and death proces-
ses, which allows the population level to fluctuate.
However, while this may be more realistic, it vastly
complicates any investigation into the influence of po-
pulation density. In previous work (Gibbons et al.,
2016), we demonstrated that intelligent mobility stra-
tegies could be evolved for populations playing both
the 2-Player and N-Player Prisoner’s Dilemma to pro-
mote the evolution of cooperation in a wide range of
sparse environments. However, the impact of varying
the evolutionary setting of the genetic algorithm was
not considered, and we were unable to demonstrate
significant rates of cooperation using an unseeded po-
pulation.
3 METHODOLOGY
This work considers a population of agents inhabiting
a toroidal shaped diluted lattice with L × L cells, each
of which can be occupied by up to one agent. The
interaction and movement radii of agents are deter-
mined using a Moore neighbourhood of radius one.
This comprises the eight cells surrounding an agent
in a cell on the lattice. The agents can only perceive
and play with those within this radius.
A single simulation consists of a population of
N = 100 agents placed randomly on a L × L torus.
The population density is defined as D = N/L
2
. A
simulation consists of agents taking s steps per gene-
ration, using the replacement rate, r, over 5000 time
steps. The game strategies (whether to cooperate or
to defect) are assigned in equal proportion, and the
movement strategies are assigned randomly. A total
of 3000 simulations are performed for each configu-
ration of density and evolutionary settings.
Each agent in the population is characterized by
two different attributes: game strategy and a set of
movement actions. The classical version of the Pri-
soner’s Dilemma game is adopted as the interaction
model for the agents in our population, in this way,
an agent can either cooperate (C) or defect (D). Ac-
cordingly, an agent may receive a reward R = 3 for
The Impact of Environmental and Evolutionary Factors on the Emergence of Cooperation among Evolved Mobile Agents
71

mutual cooperation, T = 5 for successful defection, a
punishment P = 1 for mutual defection or S = 0 for
exploited cooperation.
At each time step, agents participate in a single
round of the Prisoner’s Dilemma game with each of
their neighbours, if any. Agents play using pure stra-
tegies; either always cooperate or always defect. We
implement pure strategies in order to reduce the stra-
tegy space allowing us to examine the effect of mo-
bility in these experiments more clearly. Agents are
aware of the actions taken by their neighbours in a
single round, but these memories do not persist. This
is done to allow agents to accurately identify the stra-
tegies of their neighbours when determining their next
movement. The payoffs agents receive from playing
the game are accumulated and used as their score.
This fitness function used in this work is based on
these accumulated payoffs within a generation, as we
wish to capture both the payoffs and frequency of in-
teraction for individual agents.
Following the interaction phase, agents then have
the opportunity to respond to those interactions by
moving to a position in their neighbourhood determi-
ned by their mobility strategy. In this model, each
agent has an 8-bit genotype, which encodes the acti-
ons it can preform. Each action is represented by a
2-bit gene capturing the following four behaviours:
remain where they are i.e. stay still (00), follow a
neighbour (01), flee from a neighbour (10), and move
randomly (11). Given the bit positions from left to
right, the agents will perform one of these actions in
each of the following scenarios, i.e. when it meets:
• only cooperator(s) (bit position 0 and 1);
• only defector(s) (bit position 2 and 3);
• cooperator(s) in a neighbourhood with defector(s)
present (bit position 4 and 5);
• defector(s) in neighbourhoods with cooperator(s)
present (bit position 6 and 7);
If an agent has no neighbours it explores by moving
to an adjacent free location at random.
An agent’s chosen action determines how each lo-
cation in its neighbourhood is evaluated. Each loca-
tion is assigned a score, based on the number and type
of neighbouring agents, which in turn is used to rank
those available locations. In this way, if the choice is:
• ‘stay still’ (00), the current cell location sums
zero, while the other cell locations subtract one;
• ‘follow’ (01), the cell locations adjacent to each
neighbour sum one, while the other cell locations
sum zero;
• ‘flee’ (10), the cell locations adjacent to each neig-
hbour sum zero, while the other cell locations sum
Table 1: An illustration of the calculation used to determine
the move performed by an agent where: all neighbours are
cooperators (left); all neighbours are defectors (middle) and
neighbours are both cooperators and defectors (right).
C 1 0 1 1 1 C 2 1
1 X (1) 0 0 X (0) 0 1 X (1) 0
0 0 0 0 D 0 0 D 0
one;
• ‘random’ (11), all cell locations sum randomly;
based on the total score obtained for each cell, the
agent moves to the highest ranking location and ties
are broken by choosing a tied location at random.
For example, given an agent X with the genotype
{0,1,1,0,0,1,1,0}, which translates to ‘follow coope-
rators and flee from defectors’, Table 1 outlines the
results of agent X’s movement locations being scored
in each of the non-trivial scenarios.
In Table 1(left), agent X sees a cooperator C and
adjacent cells are rewarded. The current location is
treated as an adjacent cell, thus staying still, or not
moving, is a valid option. The opposite is true in Ta-
ble 1(middle), where agent X sees a defector D, adja-
cent cells score nothing and distant cells are rewarded.
In Table 1(right), agent X sees both C and D, multiple
neighbours are handled by first calculating a score set
for each individual and then combining them. Agent
X will then move to the location represented by the
highest scoring cell, and in the case of a tie, a location
is chosen at random from the highest scoring cells.
At the end of each generation, s steps of inte-
raction and movement, the population of agents is
ranked according to their fitness score. The highest
scoring agents duplicate themselves, and the lowest
scoring agents die. In this way the population den-
sity remains constant throughout a simulation. The
number of agents replaced in this way is controlled
by the replacement rate, r. At the end of each ge-
neration, the fitness score of the whole population is
reset. No other genetic operators are utilized. This
evolutionary approach preserves the spatial structure
of clusters present, in the population, across generati-
ons.
In this work, we consider two mechanisms for pla-
cing agent offspring in the environment. The first,
‘random’ placement, chooses a location at random
from the available free spaces on the grid. Similar
methodologies are present in other works (Aktipis,
2004; Burgess et al., 2017). The second placement
mechanism investigated places offspring in the neig-
hbourhood of their parent. In the case where the pa-
rent’s neighbourhood is full, they are randomly placed
on the grid instead. This ‘nearby’ placement approach
should further strengthen the structure of clusters cre-
ated between generations.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
72
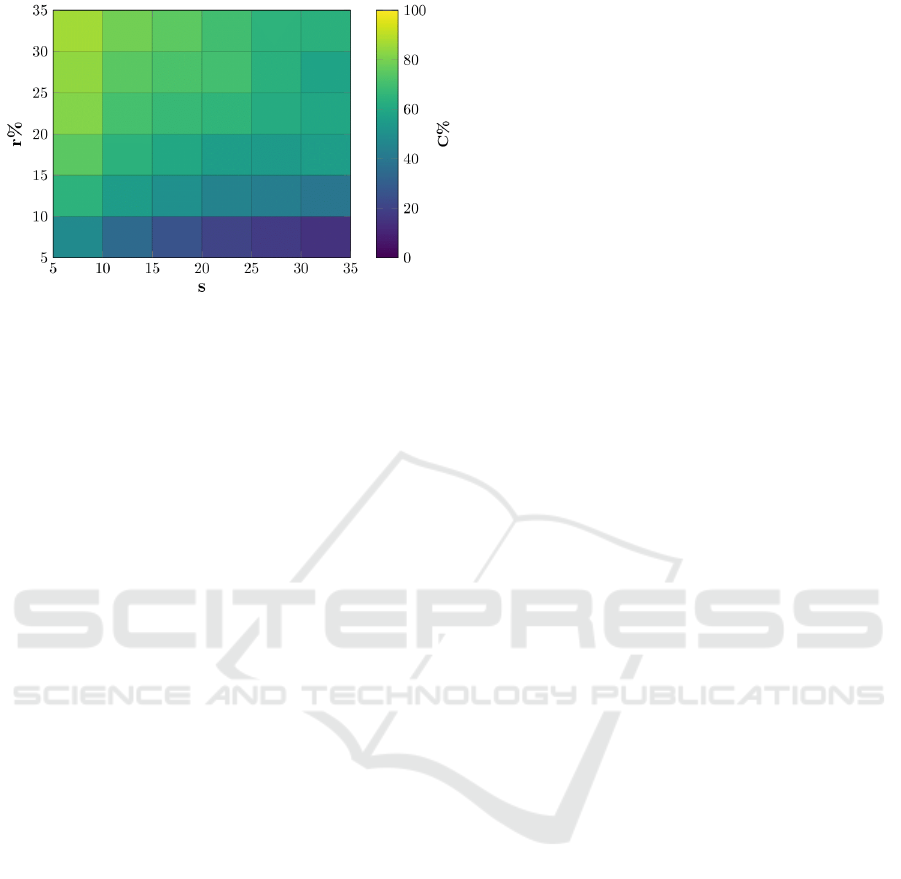
Figure 1: Average percentage of cooperators victories for
grid size L = 40 as a function of replacement rate r, and the
steps per generation s.
4 SIMULATION RESULTS
In this section, we present some of the relevant ex-
perimental results of the simulations of the Prisoner’s
Dilemma game on a diluted toroidal lattice grid. The
first set of experiments comprise variations in the pa-
rameters r and s; the second set of experiments com-
prise variations in the parameters r and s at diffe-
rent density levels (varying L); the third set of expe-
riments compare results across the two replacement
mechanisms (‘random’ or ‘nearby’) and the fourth
section presents an analysis of the genotypes of agents
in a specific evolutionary setting with ‘random’ pla-
cement. The distribution of spatial strategies, level
of cooperation, the time taken for the simulation to
converge on cooperation (or defection), and the total
number of interactions are recorded.
4.1 Varying the Evolutionary Settings
We start by investigating the scenarios in which a
well-mixed population of agents playing the Priso-
ner’s Dilemma game evolve movement behaviours
conducive to the evolution of cooperation by identi-
fying optimal evolutionary settings. The generation
length s and replacement rate r, which constitute the
lifespan of agents, are both varied from the values 5
to 35, while the population density remains fixed at
L = 40. The ‘random’ placement mechanism is used.
In Figure 1, we see the percentage of simulati-
ons that end with total adoption of cooperation, this
will be referred to henceforth as cooperator victories.
Simulations always converge on either total coope-
ration or defection, ‘draws’ are very rare, and only
occur when the convergence for a particular evoluti-
onary setting is slow. We see that the settings that
lead to the most cooperative outcomes, on average,
are hight replacement rates, r, coupled with low ge-
neration lengths, s. Using these settings, cooperators
dominate the population in 93% of randomly initiali-
zed simulations. We note that the value of r has a big-
ger influence on the emergence of cooperation than
s. In practice, this indicates that cooperation emerges
more readily when fewer agents are replaced per ge-
neration, than when agents have longer to interact du-
ring a single generation and potentially be exploited
by ‘free riders’ (Enquist and Leimar, 1993). Howe-
ver, the best results are achieved when these scena-
rios are combined. This suggests that the replacement
process should be tuned in order for cooperation to
emerge with the greatest probability.
Figure 2, shows a snapshot sequence of a popula-
tion during a single, though typical, simulation. We
observe the decline in the number of defectors over
time as cooperator clusters form and expand.
4.2 Varying Environment Density
We investigate the influence of density on the evolu-
tion of cooperation by repeating the previous experi-
ment across a range of grid sizes: L = 20 to L = 60.
In Figure 3, we observe the percentages of coope-
rator victories across a range of both evolutionary set-
tings and density levels. In the high density graphs,
Figure 3(a), we observe that extremely low levels of
cooperation emerge despite the variation in evolutio-
nary settings. These results are unsurprising as this
environment is close to being fully connected. In this
setting, we would expect defectors to easily invade
cooperators as described by the ‘free-rider’ effect.
Figure 3(b)-(h) shows an increase in the level of
cooperation emerging. We observe the evolutionary
settings’ growing effect on the emergence of coope-
ration. It becomes clear that as the population density
decreases, the percentage of simulations resulting in
a cooperative outcome increases, as agents have the
space to learn and deploy their movement strategies.
In the low density environments, i.e. Figure 3(i),
the trend becomes most pronounced. We see that
cooperation is able to emerge in almost 100% of si-
mulations for a wide range of evolutionary settings.
In randomly initialized simulations, cooperators have
enough time and space to learn the movement strate-
gies capable of dominating the defectors.
Figure 4 more clearly demonstrates the impact of
density on the evolution of cooperation. In the graph,
the most extreme values for the evolutionary settings,
r and s, are directly observed across the density va-
lues, from very low to very high. Again, it is clear
that cooperation emerges most readily for high values
The Impact of Environmental and Evolutionary Factors on the Emergence of Cooperation among Evolved Mobile Agents
73
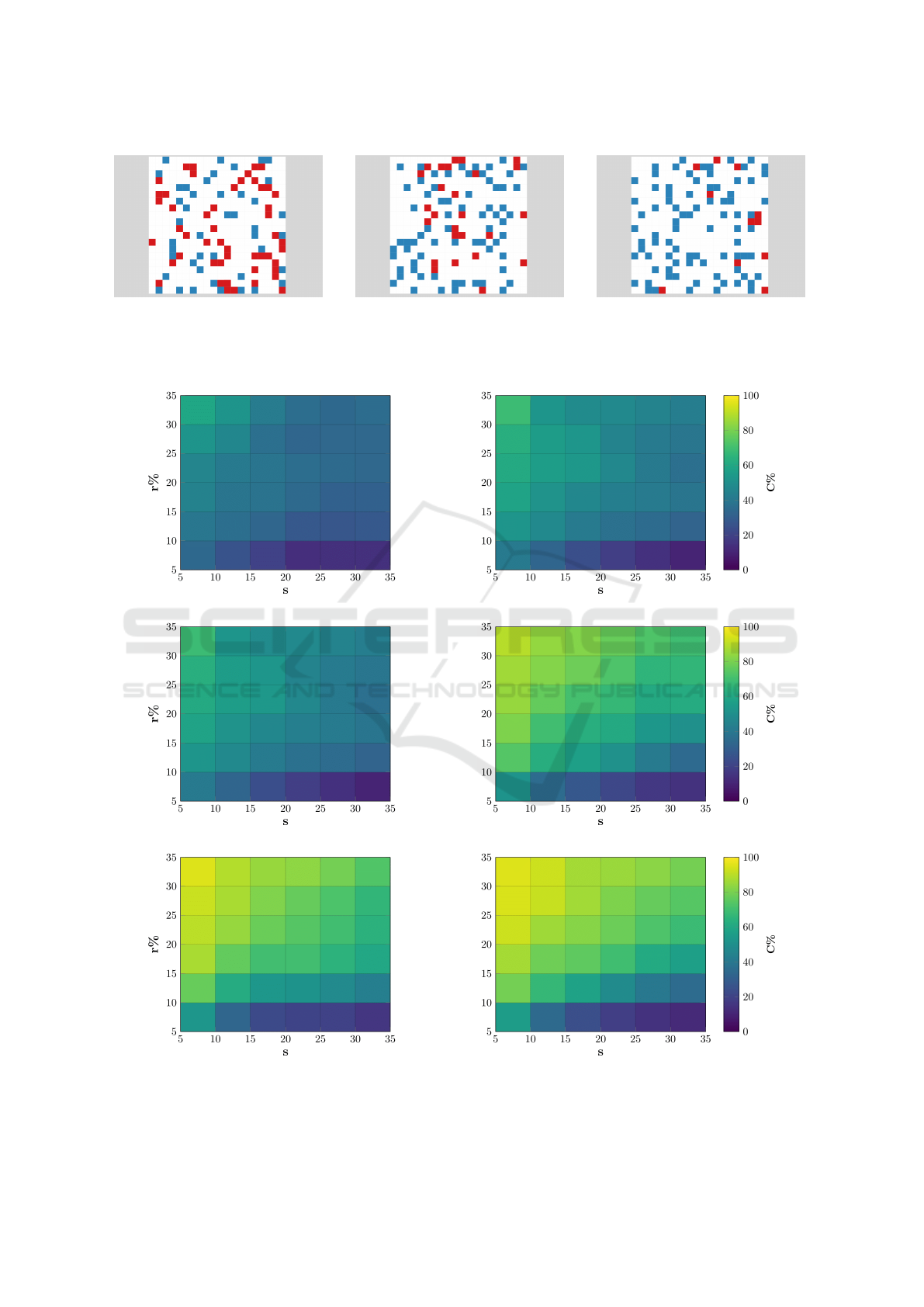
(a) t = 1 (b) t = 20 (c) t = 60
Figure 2: Typical distributions of agents, cooperators (blue) and defectors (red), at various timesteps (t) in a single simulation,
using r = 35 and s = 5, on a L = 20 diluted lattice grid. Screenshots generated using Evolpex (Cardinot et al., 2018).
(a) L=25 (b) L=30
(c) L=35 (d) L=45
(e) L=50 (f) L=55
Figure 3: Average percentage of cooperator victories, C, for a variety of different values for the grid size L, as a function of
replacement rate r, and the number of steps per generation s.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
74
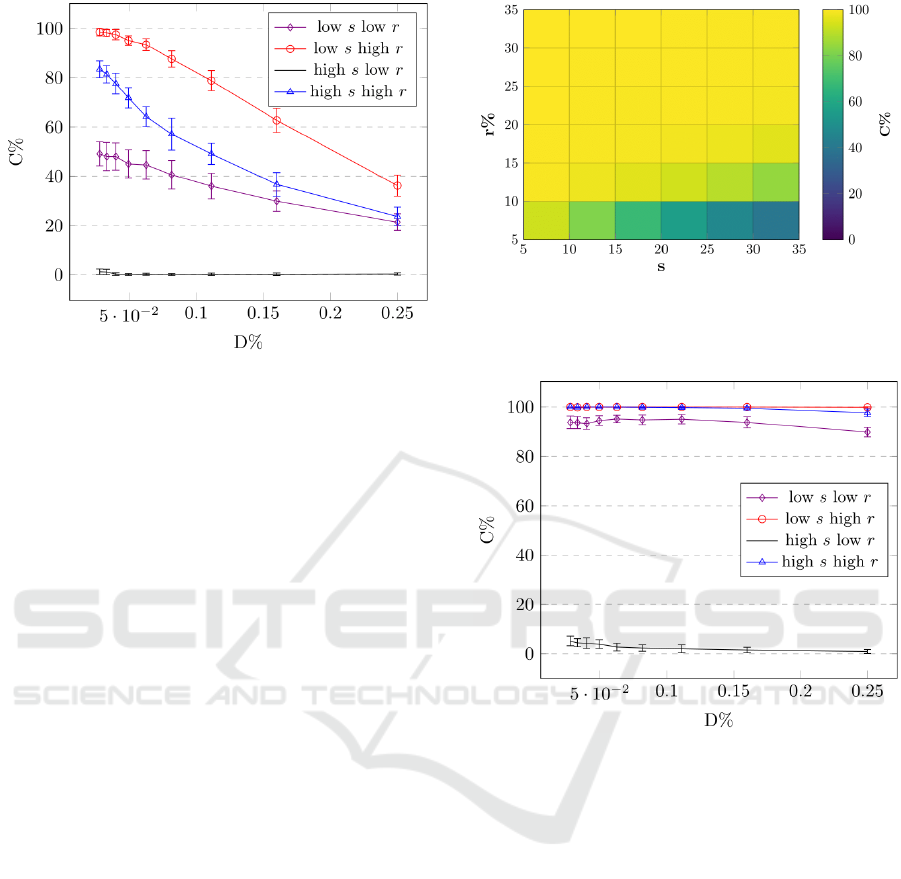
Figure 4: Average percentage of cooperator victories, C, for
a number of evolutionary settings as a function of density,
D. The low and high values are r = 5,35 and s = 5, 35. The
error bars show the standard deviation for each value of C.
of r and low values of s. However, it is also clear that
for certain evolutionary settings, i.e. low r and high
s, it is close to impossible for cooperation to emerge,
regardless of any variation in density.
4.3 Comparing Placement Mechanisms
In this section, we repeat again our central experi-
ment, co-evolving agent strategy and movement pat-
tern, using the ‘nearby’ placement mechanism. In the
previous two sets of experiments, new agents were
placed in a ‘random’ free cell in the environment, wit-
hout regard to the location of their parent, to the agent
they were replacing, or to other agents. The ‘nearby’
placement mechanism locates new agents in the neig-
hbourhood (i.e. the surrounding 8 cells) of their pa-
rent, if a free space exists, and otherwise places them
randomly as before. This mechanism is more lifelike
and realistic, and we hypothesise that it can promote
cluster formation.
In Figure 5, we observe the percentages of
cooperator victories across the range of evolutionary
settings using the ‘nearby’ placement mechanism.
Cooperation emerges in almost 100% of simulations
for the vast majority of scenarios, and is only hindered
in the most restrictive of evolutionary settings. These
results are replicated across the density levels without
significant variation, as seen in Figure 6.
4.4 Genotype Consistency
In order to better understand the reasons for obtaining
higher levels of cooperation in specific evolutionary
settings (the replacement rate r, the number of steps
Figure 5: Average percentage of cooperator victories for
grid size L = 40 as a function of replacement rate r, and the
steps per generation s using the ‘nearby’ placement mecha-
nism.
Figure 6: Average percentage of cooperators victories, C,
for a number of evolutionary settings as a function of den-
sity, D, using ‘nearby’ placement. The low and high values
are r = 5, 35 and s = 5, 35. The error bars show the standard
deviation for each value of C.
in a generation s) and the grid size L (which deter-
mines the population density), we investigate the ge-
notypic consistency across a number of simulations
using ‘random placement’. We only consider this pla-
cement mechanism as there is insufficient variation in
agent behaviour when using ‘nearby’ placement (see
Figure 5). Considering that all simulations are rand-
omly initialised, in all scenarios, each agent could be
assigned any combination of genes with equal proba-
bility. In other words, any of the 2
8
genotypes could
be expressed in the population.
Thus, based on the outcomes generated in previ-
ous sections, we now are interested in looking speci-
fically at the evolved movement behaviours of coope-
rative populations under the aforementioned evolutio-
nary settings. To achieve this, at the end of each simu-
lation, we record the game strategy and the most com-
The Impact of Environmental and Evolutionary Factors on the Emergence of Cooperation among Evolved Mobile Agents
75

(a) Evolved Cooperator Genotypes
(b) Evolved Defector Genotypes
Figure 7: Percentage distribution of the most frequently
evolved genotypes (the 8-bit set of actions) expressed in
a population where (a) cooperation dominates and (b) de-
fection dominates. The extruded segments represent the
most commonly evolved genotypes. The ‘Other’ segment
represents the combined total of the ten remaining set of
genotypes that are less frequently evolved.
monly occurring genotypes that emerge in the popu-
lation. The majority of simulations will result in con-
vergence on either cooperation or defection. A small
minority of simulations will result in a ‘draw’ using
evolutionary settings with a slow convergence rate.
The genotypes are recorded at the end of the simu-
lations, despite the potential for genetic drift, because
the convergence point can vary depending on many
different factors including initialisation, the particular
evolutionary settings, population density, and which
strategy is undergoing convergence.
Figure 7 shows the percentage break down of the
top ten most prevalent emergent genotypes (the 8-
bit set of actions) from both (a) cooperator dominant
and (b) defector dominant populations. It was ob-
served that independently of the given evolutionary
settings and population densities, the simulations re-
sulting in widespread cooperation exhibit ‘01100110’
as the most commonly evolved behaviour, with the
critical segment, ‘****0110’, being produced in 35%
of all evolved behaviours, as shown in Figure 7 (a).
This genetic pattern corresponds to ‘follow coopera-
tors and flee defectors’. We focus our analysis on this
gene section because it is critical both in terms of the
evolutionary pressure it undergoes, and the major im-
pact on the potential fitness it generates.
In other words, it is more important, from an evo-
lutionary perspective, for an individual cooperator to
move optimally in the scenario where both strate-
gies are present than when just interacting with ot-
her cooperators. This is because there are fewer gene
combinations that would lead to being punished in the
latter scenario. For example, the ‘stay still’ behavi-
our, ‘00******’, in the gene segment corresponding
to ‘only cooperators present’, is almost functionally
equivalent to the ‘follow’ behaviour, ‘01******’, be-
cause both result in actions that lead to a continuation
of the beneficial interactions with cooperators. Howe-
ver, the ‘stay still’ behaviour, ‘****00**’, in the gene
segment corresponding to ‘cooperators with defectors
present’ is significantly worse than the ‘follow’ beha-
viour, ‘****01**’, as it results in continual harmful
interactions with defectors.
Additionally, we see in Figure 7 (a) that the se-
cond most frequently occurring set of genotypes in
simulations resulting in the emergence of cooperation
is ‘****1110’. These genotypes are genetically si-
milar, and constitute a reasonable approximation of
the optimal solution, because they often produce acti-
ons that are phenotypically identical. For example,
the ‘random’ behaviour, ‘****11**’, in the above ge-
notype produces the more beneficial action, ‘follow’,
in a significant percentage of interactions.
Moreover, due to the lack of genetic mutation in
the evolutionary process, once a population reaches
the point of convergence, meaning that agents are no
longer subject to the same level of evolutionary pres-
sure, it may settle on a sub-optimal solution. These
results indicate that the ‘follow-flee’ pattern is usually
the most beneficial mobility strategy for the creation
of cooperative clusters which leads to the evolution of
cooperation. These patterns are not found in the simu-
lations resulting in defector dominance. As shown in
Figure 7 (b), the ‘follow-flee’ movement pattern does
not appear among the most commonly evolved ge-
notypes. It is clear that defectors are subject to much
less evolutionary pressure to optimise their mobility.
The genotypic consistency of populations using
‘nearby’ placement is also investigated. As shown in
Figure 8, the results are largely similar, but one no-
teworthy deviation is that the ‘follow-flee’ movement
pattern is less pronounced. It’s clear that cooperators
are under less pressure to be optimally mobile.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
76
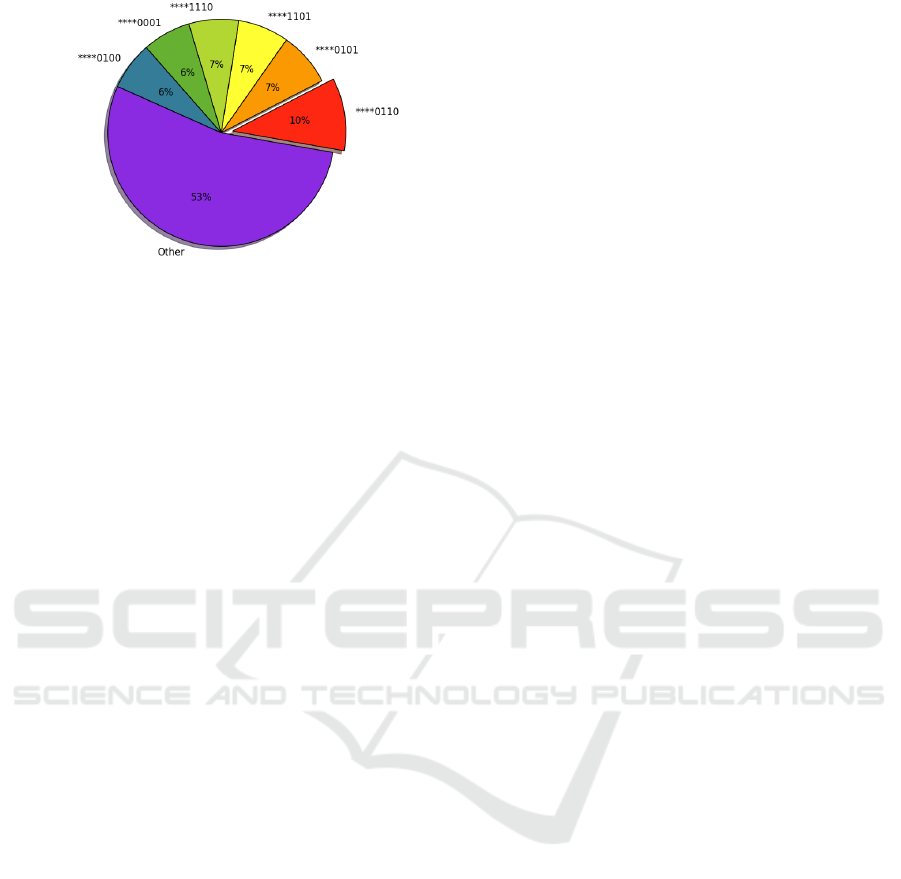
Figure 8: Percentage distribution of the most frequently
evolved genotypes (the 8-bit set of actions) expressed in a
population where cooperation dominates using the ‘nearby’
placement mechanism. The extruded segments represent
the most commonly evolved genotypes. The ‘Other’ seg-
ment represents the combined total of the ten remaining set
of genotypes that are less frequently evolved.
5 DISCUSSION
We have observed a number of environmental and
evolutionary factors governing the emergence of
cooperation within populations of mobile agents. Po-
pulation density, agent lifespan, and the choice of pla-
cement mechanism all distinctly impact the formation
of cooperator clusters, which is the most critical factor
in the evolution of cooperation among agents using
pure strategies. These clusters emerge as a conse-
quence of the agents’ evolved mobile strategies.
Agent lifespans consisting of short generations
and high replacement rates favour, and often promote,
the evolution of cooperation. These evolutionary set-
tings curb the ‘free rider’ effect once the cooperators
have learned good movement strategies, which form
clusters, allowing agents to avoid repeated exploita-
tion by defectors. If, in the initial generations of a
simulation, cooperators have not learned to cluster by
following neighbouring cooperators and fleeing from
neighbouring defectors, defection will emerge. We
have shown that in every simulation in which coope-
ration emerges some approximation of the ‘follow-
flee’ movement strategy is evolved.
Population density has a major impact on the
emergence of cooperation in spatial environments
with a mobile population, because it directly impacts
the interaction rate with defectors. Cooperation is
most likely to emerge when clusters of cooperators,
with appropriate genes, are formed and allowed to
grow unimpeded in the initial timesteps of a simula-
tion. The chance of this occurring is significantly hig-
her in sparse environments. In dense environments,
cooperators have a higher chance of being exploited
by defectors, as a result neither the evolved movement
strategies nor the evolutionary settings can ignite the
evolution of cooperation, unless the initial conditi-
ons are particularly favourable. On the other hand, a
sparse environment almost guarantees the emergence
of cooperation. Clusters in sparse environments have
a higher chance of avoiding exploitation, thus allo-
wing its members to the learn beneficial movement
patterns, and obtain a high fitness score.
There is a clear interplay between the population
density and the evolutionary settings in this work. In
general, the more time and space agents have to learn
‘good’ movement strategies, the more likely coopera-
tion is to emerge. It is even possible to construct a set
of parameters to ensure that cooperation emerges in
the vast majority of simulations. However, unsympat-
hetic agent lifespans will result in total defector do-
mination, regardless of the population density. These
aggressive evolutionary settings favour defectors be-
cause the movement strategies, which give coopera-
tors the competitive edge over the defectors, are not
learned in sufficient time to be effective.
The scenarios discussed thus far assume the use of
the ‘random’ placement mechanism, however we ob-
serve a substantial decline in influence of both agent
lifespan and population density when the ‘nearby’
placement mechanism is in effect. In fact, these fac-
tors become almost irrelevant (see Figure 5 and 6).
Furthermore, the ‘follow-flee’ genotype doesn’t occur
with the same frequency in evolved cooperator popu-
lations as with ‘random’ placement. We hypothesise
that this is due to there being significantly less pres-
sure to learn clustering behaviours as ‘nearby’ place-
ment ensures, where possible, that clusters grow.
6 CONCLUSION
In this paper, we presented a novel mobility model, in
which agent proactively seek out better locations by
moving in response to their local environment. We
demonstrated the influence of several environmental
and evolutionary factors on the emergence of coope-
ration among mobile agents using this mobility mo-
del.
We show that appropriately tuning the evolutio-
nary process in conjunction with a favourable popu-
lation density and sufficiently mobile agents can al-
most guarantee cooperation to emerge from a rand-
omly initialized population. Additionally, we present
results indicating that cooperation may emerge in a
population with sub-optimal mobility strategies given
a placement mechanism that promotes the growth of
cooperator clusters.
The Impact of Environmental and Evolutionary Factors on the Emergence of Cooperation among Evolved Mobile Agents
77

Finally, we have shown that the impact of cer-
tain environmental and evolutionary settings can sub-
stantially diminish others. The ‘nearby’ placement
mechanism creates cooperator clusters with such ef-
ficiency that the agents are under considerably less
pressure to evolve the clustering behaviours.
Future work will involve modifying our agent re-
presentation to allow for the inclusion of noise in the
model. A noise variable would be introduced that
would cause agents to incorrectly identify interacti-
ons with their neighbours for some percentage of inte-
ractions. This would allow us to test the robustness of
the evolved mobile strategies. In addition, we wish to
investigate the impact on the evolution of cooperation
when agents are given the ability to teleport, i.e. move
to a location outside their neighbourhood, within their
own lifespan. This ability would incur a cost to their
fitness and allow them to randomly, or deterministi-
cally, jump to a distant location on the grid in a limited
set of circumstances. Currently, both placement me-
chanisms allows for some amount of random reloca-
tion, however this only occurs with newborn agents.
Additionally, other work has shown benefits of this
type of mobility (Helbing and Yu, 2008). Finally, we
may also consider other types of network topology to
evaluate our proposed model in more realistic situati-
ons.
ACKNOWLEDGEMENT
This work is funded in full by the Hardiman Research
Scholarship, National University of Ireland Galway.
REFERENCES
Aktipis, C. A. (2004). Know when to walk away: Con-
tingent movement and the evolution of cooperation.
Journal of Theoretical Biology, 231(2):249–260.
Andr
´
e, J.-B. and Nolfi, S. (2016). Evolutionary robotics
simulations help explain why reciprocity is rare in na-
ture. Scientific reports, 6:32785.
Antonioni, A., Tomassini, M., and Buesser, P. (2014).
Random diffusion and cooperation in continuous two-
dimensional space. Journal of theoretical biology,
344:40–48.
Antonioni, A., Tomassini, M., and S
´
anchez, A. (2015).
Short-range mobility and the evolution of cooperation:
an experimental study. Scientific reports, 5:10282.
Axelrod, R. M. (1984). The Evolution of Cooperation. Ba-
sic Books.
Buesser, P., Tomassini, M., and Antonioni, A. (2013). Op-
portunistic migration in spatial evolutionary games.
Physical Review E - Statistical, Nonlinear, and Soft
Matter Physics, 88(4).
Burgess, A. E., Lorenzi, T., Schofield, P. G., Hubbard, S. F.,
and Chaplain, M. A. (2017). Examining the role of in-
dividual movement in promoting coexistence in a spa-
tially explicit prisoner’s dilemma. Journal of theoreti-
cal biology, 419:323–332.
Cardinot, M., O’Riordan, C., Griffith, J., and Perc, M.
(2018). Evoplex: A platform for agent-based mo-
deling on networks. ArXiv e-prints.
Cong, R., Wu, B., Qiu, Y., and Wang, L. (2012). Evolution
of cooperation driven by reputation-based migration.
PLoS One, 7(5):e35776.
Droz, M., Szwabi
´
nski, J., and Szab
´
o, G. (2009). Motion
of influential players can support cooperation in pri-
soners dilemma. The European Physical Journal B,
71(4):579.
Enquist, M. and Leimar, O. (1993). The evolution of
cooperation in mobile organisms. Animal Behaviour,
45(4):747–757.
Floreano, D. and Keller, L. (2010). Evolution of adaptive
behaviour in robots by means of darwinian selection.
PLoS biology, 8(1):e1000292.
Gibbons, M. D., O’Riordan, C., and Griffith, J. (2016). Fol-
low flee: A contingent mobility strategy for the spatial
prisoners dilemma. In International Conference on
Simulation of Adaptive Behavior, pages 34–45. Sprin-
ger.
Helbing, D. and Yu, W. (2008). Migration as a mechanism
to promote cooperation. Advances in Complex Sys-
tems, 11(4):641–652.
Helbing, D. and Yu, W. (2009). The outbreak of cooperation
among success-driven individuals under noisy condi-
tions. Proceedings of the National Academy of Scien-
ces of the United States of America, 106(10):3680–
3685.
Ichinose, G., Saito, M., and Suzuki, S. (2013). Collective
Chasing Behavior between Cooperators and Defec-
tors in the Spatial Prisoner’s Dilemma. PLoS ONE,
8(7):28–31.
Jiang, L.-L., Wang, W.-X., Lai, Y.-C., and Wang, B.-H.
(2010). Role of adaptive migration in promoting
cooperation in spatial games. Physical Review E,
81(3):036108.
Joshi, J., Couzin, I. D., Levin, S. A., and Guttal, V. (2017).
Mobility can promote the evolution of cooperation via
emergent self-assortment dynamics. PLOS Computa-
tional Biology, 13(9):1–19.
Joyce, D., Kennison, J., Densmore, O., Guerin, S., Barr, S.,
Charles, E., and Thompson, N. S. (2006). My way
or the highway: a more naturalistic model of altruism
tested in an iterative prisoners’ dilemma. Journal of
Artificial Societies and Social Simulation, 9(2):4.
Maynard Smith, J. (1982). Evolution and the theory of ga-
mes. Cambridge University Press, Cambridge; New
York.
Meloni, S., Buscarino, A., Fortuna, L., Frasca, M., G
´
omez-
Garde
˜
nes, J., Latora, V., and Moreno, Y. (2009). Ef-
fects of mobility in a population of prisoner’s dilemma
players. Physical Review E - Statistical, Nonlinear,
and Soft Matter Physics, 79(6):3–6.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
78

Nguyen, P., Akiyama, T., and Ohashi, H. (2018). Expe-
rience filtering for robot navigation using deep rein-
forcement learning. In Proceedings of the 10th In-
ternational Conference on Agents and Artificial In-
telligence - Volume 2: ICAART,, pages 243–249. IN-
STICC, SciTePress.
Nowak, M. A. (2006). Five rules for the evolution of coope-
ration. Science, 314(5805):1560–3.
Nowak, M. A. and May, R. M. (1992). Evolutionary games
and spatial chaos. Nature, 359(6398):826–829.
Perc, M. and Szolnoki, A. (2010). Coevolutionary gamesa
mini review. BioSystems, 99(2):109–125.
Poncela, J., G
´
omez-Garde
˜
nes, J., Flor
´
ıa, L. M., Moreno,
Y., and S
´
anchez, A. (2009). Cooperative scale-free
networks despite the presence of defector hubs. EPL
(Europhysics Letters), 88(3):38003.
Santos, F., Rodrigues, J., and Pacheco, J. (2006). Graph
topology plays a determinant role in the evolution of
cooperation. Proceedings of the Royal Society B: Bi-
ological Sciences, 273(1582):51–55.
Sicardi, E. A., Fort, H., Vainstein, M. H., and Arenzon, J. J.
(2009). Random mobility and spatial structure often
enhance cooperation. Journal of theoretical biology,
256(2):240–246.
Tomassini, M. and Antonioni, A. (2015). L
´
evy flights and
cooperation among mobile individuals. Journal of the-
oretical biology, 364:154–161.
Vainstein, M. H. and Arenzon, J. J. (2001). Disordered
environments in spatial games. Physical review. E,
Statistical, nonlinear, and soft matter physics, 64(5 Pt
1):051905.
Vainstein, M. H., Silva, A. T. C., and Arenzon, J. J. (2007).
Does mobility decrease cooperation? Journal of The-
oretical Biology, 244(4):722–728.
Yang, H.-X., Wu, Z.-X., and Wang, B.-H. (2010). Role of
aspiration-induced migration in cooperation. Physical
Review E, 81(6):065101.
The Impact of Environmental and Evolutionary Factors on the Emergence of Cooperation among Evolved Mobile Agents
79
