The Price of Anarchy: Centralized versus Distributed Resource

Allocation Trade-offs

Jinhong K. Guo

, Alexander Karlovitz

, Patrick Jaillet

and Martin O. Hofmann

Lockheed Martin Advanced Technology Laboratories, 3 Executive Campus, Suite 600, Cherry Hill, NJ 08002, U.S.A.

Department of Mathematics, Rutgers University, Piscataway, NJ 08854, U.S.A.

Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology,

Cambridge, MA 02139, U.S.A.

Keywords:

Resource Allocation, Resource Optimization, Auction-based Approach, Decentralized Resource Allocation.

Abstract:

Optimizing decision quality in large scale, distributed, resource allocation problems requires selecting the

appropriate decision network architecture. Such resource allocation problems occur in distributed sensor net-

works, military air campaign planning, logistics networks, energy grids, etc. Optimal solutions require that de-

mand, resource status, and allocation decisions are shared via messaging between geographically distributed,

independent decision nodes. Jamming of wireless links, cyber attacks against the network, or infrastructure

damage from natural disasters interfere with messaging and, thus, the quality of the allocation decisions. Our

contribution described in the paper is a decentralized resource allocation architecture and algorithm that is

robust to signiﬁcant message loss and to uncertain demand arrival, and provides ﬁne-grained, many-to-many

combinatorial task allocation. Most importantly, it enables a conscious choice of the best level of decentraliza-

tion under the expected degree of communications denial and quantiﬁes the beneﬁts of approximating status

of peer nodes using proxy agents during temporary communications loss.

1 OVERVIEW

Teams of autonomous sensor assets are expected to

self-organize to perform a variety of spatially dis-

tributed sensing tasks, such as search and rescue,

surveillance and environmental monitoring. Chal-

lenging characteristics of these applications include

incomplete and uncertain status (current tasks, as-

set status, etc.), time-sensitive objectives (re-direction

during mission execution, failed asset replacement),

and limited and varying communication topologies

between assets and command and control nodes. De-

centralized command and control promises greater

agility and resilience in communication contested en-

vironment. To decentralize safely, one has to under-

stand the trade-offs between agility and quality.

The contribution of this work is in characteriz-

ing the trade-off of decentralization using a robust,

probabilistic, auction-based resource allocation archi-

tecture with a variable number of distributed auc-

tioneer nodes, each responsible for optimally allocat-

ing a subset of tasks to a subset of assets. We use

a many-to-many, combinatorial task allocation and

scheduling algorithm that is robust to uncertain fu-

ture demand and uses expressive cost formulations

to model mobile sensors with variable costs that de-

pend in travel distance and sensor quality that varies

with environmental conditions. Our algorithm is ro-

bust against communication interruptions and mini-

mizes ripple effects due to unexpected tasks and re-

source failures. To further reduce the effect of in-

termittent communication failures, we employ proxy

agents which bid on behalf of their remote assets. Our

experiments show that proxy agents improve alloca-

tion success rates. Due to the complexity of our prob-

lem, unmatched in other published work, a rigorous

and tractable mathematical analysis is impossible. In-

stead, we derived theoretical bounds on a simpliﬁed

version and validated our algorithm’s performance.

2 RESOURCE ALLOCATION

We assume m heterogeneous agents, each represent-

ing an asset that can possess multiple capabilities. n

tasks arrive dynamically over time and are located in

a given geographical region G. In each area G, one

of the agents assumes the role of auctioneer. Upon

146

Guo, J., Karlovitz, A., Jaillet, P. and Hofmann, M.

The Price of Anarchy: Centralized versus Distributed Resource Allocation Trade-offs.

DOI: 10.5220/0007345701460153

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 146-153

ISBN: 978-989-758-350-6

arrival of a task, the auctioneer announces the task

and agents bid to perform the task. The auctioneer

determines the winner and assigns the task to one or

several bidders. A task is assigned to multiple agents

when the task requires the combined capabilities of

multiple agents. The completion of an assigned task

incurs a cost and earns a reward for the agent. The

goal is to maximize net revenue, the sum of reward

minus cost for all agents and tasks, over time.

Task: A task requires a number of capabilities

to be fulﬁlled by one or more agents. Each ca-

pability has an associated timeline and a minimum

proﬁciency, which allowes suboptimal but accept-

able use of less capable resources. For shared ca-

pabilities, the proﬁciency requirement is used to in-

dicate the minimum capacity needed, e.g., the por-

tion of bandwidth needed from a communication

channel. Therefore, we represent task j as a tuple

,req

,Pr

0 j

), where, t

∈ R

is the

release time of task j and l

∈ G is the location of task

j. req

∈ [0,1]

3×k

is a 3 × k matrix, describing the re-

quired capabilities for performing task j. k is the to-

tal number of capabilities deﬁned for the application,

and each speciﬁc capability is identiﬁed by its column

position in the matrix. The values in the ﬁrst row in-

dicates the required proﬁciency level for the required

capabilities. The second row is a boolean, 0 (false) or

1 (true), that indicates if the capability is shared. If

it is shared, then the corresponding value in the third

row represents the minimum required capacity level.

∈ R

is a k-vector of time durations for task j along

its k dimensional requirements req

. r

∈ R

is the

reward for the completion of task j. Pr

∈ R

is the

priority of task j, T

∈ R

is a k-vector of deadlines

before which task j’s requirements must be assigned,

0 j

∈ R

is a k-vector of the requested earliest starting

times for task j’s required capabilities.

Agent: m agents, each possessing a set of capabili-

ties, are assigned to one or more groups. An agent

is deﬁned by (l

,cap

), where l

∈ G is the loca-

tion of agent i, g

is the group identiﬁer of agent i, and

cap

∈ [0,1]

3×k

is a 3 × k matrix with values of 0 to 1

describing the qualiﬁcation of agent i along k capabil-

ity dimensions, similar to the capability requirement

in the task representation, with the third row repre-

sents an agent’s capability capacity. s

is the speed of

the agent.

Objective: The completion of task j requires that the

set of agents i

,... assigned to it collectively

have qualiﬁcations that meet req

. The objective of

the optimization problem is to maximize total net rev-

enue (reward minus cost) over the n tasks. The re-

source allocation problem can be written as a mixed-

integer program:

max

x,τ

∑

j=1

∑

i=1

∑

p=1

∑

q=1

i j

s.t.H(x,τ) ≤ d

x ∈ {0,1}

n,m,k,k

,τ ∈ {R

}

n,m,k,k

where x ∈ {0, 1}

n,m,k,k

, is a set of binary decision

variables x

i j

with x

i j

= 1 indicates that the capability

p of agent i will serve the capability requirement q of

task j. τ ∈ {R

}

n,m,k,k

is the set of real-positive deci-

sion variables that indicates when agent i capability p

will serve task j requirement q. R

i j

is the revenue of

serving task j requirement q with agent i capability p.

Assuming the total reward associated with the com-

pletion of task j is r

and the cost of performing task

j by agent i is c

i j

, R

i j

= r

i j

−c

i j

with r

i j

and c

i j

de-

ﬁned as a fraction of r

and c

i j

. H(x,τ) deﬁnes a set

of linear and possibly non-linear constraints that cap-

tures transition dynamics, resource, spatial and tem-

poral limitation, etc., that are bounded by some crite-

ria d. The constraint functions depend on both of the

decision variables x and τ, making this mixed-integer

problem even more difﬁcult to solve.

Our algorithm enforces both soft and hard con-

straints. The hard constraints include the following.

Capability: an agent is only considered for a task if it

has the required capability, sufﬁcient proﬁciency, and

the required capacity, if it is a shareable capability.

Therefore, this deﬁnes three constraints, such that

(req

∧ I

) · (cap

∧ I

) > 0

(req

∧ I

) − (cap

∧ I

) ≤ 0

(req

∧ I

) − (cap

∧ I

) ≤ 0 i f req

2,q

= 1

req

is the c

row of matrix req

and cap

the c

row of matrix cap

. I

is a vector with

the d

element being 1 while the other elements

are 0. q

2,q

is the q

element of the second row of req

Temporal and spatial: an agent can perform differ-

ent tasks concurrently only if these tasks ( j

and j

)

are geographically collocated (within a radius), i.e.,

− l

k ≤ radius

An agent can bid for a task only if it can reach the

requested location before the task starts, i.e., there is

sufﬁcient time (T ) between the schedule of j

and j

by agent i. Note that T is determined by both the task

locations and the speed of the agent.

|τ

i,j1

− τ

i,j2

| > T, i f kl

− l

k > radius

The Price of Anarchy: Centralized versus Distributed Resource Allocation Trade-offs

147

Dependency (hard): if some of the requirements

(possibly across multiple tasks) are deemed depen-

dent, all those capability requirements must be allo-

cated together or none at all. Let Ψ be the set of pairs

( j, q) (task j, capability requirement q) deﬁning such

a dependency set,

∑

i=1

∑

p=1

i j

∑

i=1

∑

p=1

i j

∀pairs ( j, q),( j

) ∈ Ψ

Same Agent: a set of capabilities (possibly across

multiple tasks) has to be performed by the same agent.

Let Ψ deﬁne the set of pairs ( j, q) (task j, capability

requirement q) to be performed by the same agent,

∑

( j,q)∈Ψ

i j

≤ 1

Soft constraints are implemented as adjustments

to the revenue function. To enforce a soft constraint,

the revenue is adjusted to be

i j

= r

i j

− c

i j

+ ∆

i j

where ∆

i j

is calculated depending on the constraints.

The soft constraints are designed for:

Honoring Priority: higher priority tasks have a bet-

ter chance of being assigned by increasing revenue.

Therefore, ∆

i j

is chosen to be proportional to a level

of priority Pr

, i.e., ∆

i j

∝ Pr

Anticipating Future Needs: reserve assets for future

high priority tasks based on an estimated distribution

of future task arrivals. The adjustment on the revenue

i j

uses an expectation E(y) of future high priority

tasks, i.e., ∆

i j

∝ −E(y)

Minimizing Ripple Effects: cost of anticipated addi-

tional allocation changes due to the allocation change

under consideration. Assuming E(z) quantiﬁes the an-

ticipated changes, ∆

i j

∝ −E(z)

Dependencies (soft): increasing the chances of the

assignment of associated capabilities if some of them

are assigned i.e., ∆

i j

∝

∑

( j,q)∈Ψ

i j

As illustrated above, the mixed-integer problem is

very difﬁcult to solve. We employ a single-round auc-

tion where one or more auctioneers announce tasks to

their respective groups of agents, agents with appro-

priate capabilities bid (whether they are already busy

or not), the auctioneers optimize many-to-many as-

signments of task capabilities to agent capabilities,

and announce the allocation. We use a greedy win-

ner determination algorithm that is based on a con-

strained clustering algorithm (Tung et al., 2001), sim-

ilar to the greedy approach developed in (Greene and

Hofmann, 2006), but allowing resource sharing over

time. Each agent deﬁnes a cluster of its capabilities.

An additional cluster consists of all the unallocated

capability requirements (of all tasks). Task require-

ments are moved among agent clusters based on rev-

enue improvement, but honoring constraints, until a

local optimum is achieved.

Group membership is dynamically determined by

geographic proximity within the range of communi-

cation. When an agent moves beteween groups, it

gives up its unfulﬁlled previous assignments so that

the previous auctioneer can attempt to reassign them

to other agents in its group.

3 PROXY AGENTS

Limited ad-hoc and varying communication topolo-

gies between assets (agents) and command and con-

trol nodes (auctioneer) signiﬁcantly affect resource

allocation performance for both centralized and dis-

tributed architectures. To lessen the effect of failed

communication preventing agents from participating

in an auction, we employed proxy agents. The proxy

agents, which reside within the auctioneer, keep sta-

tus of the agents they represent. The auctioneer tracks

the connectivity status of the real agents such that if an

agent has repeatedly failed to communicate with the

auctioneer, its proxy agent will not be allowed to par-

ticipate in future auctions until the agent is heard from

again. In the experiments described in this paper, the

agents send pings every t

wait

= 100 ms. The auction-

eer counts every t

wait

ms if it does not receive a ping

from an agent. If this count gets above maxCnt = 20

for some agent, the auctioneer does not include that

proxy agent in any bids until it receives another ping.

1 2 3 4 5

0.1

0.2

0.3

0.4

0.5

0.6

0.7

Number of groups

% Capabilities Completed

Communications Denial (Level 1)

With proxies

Without proxies

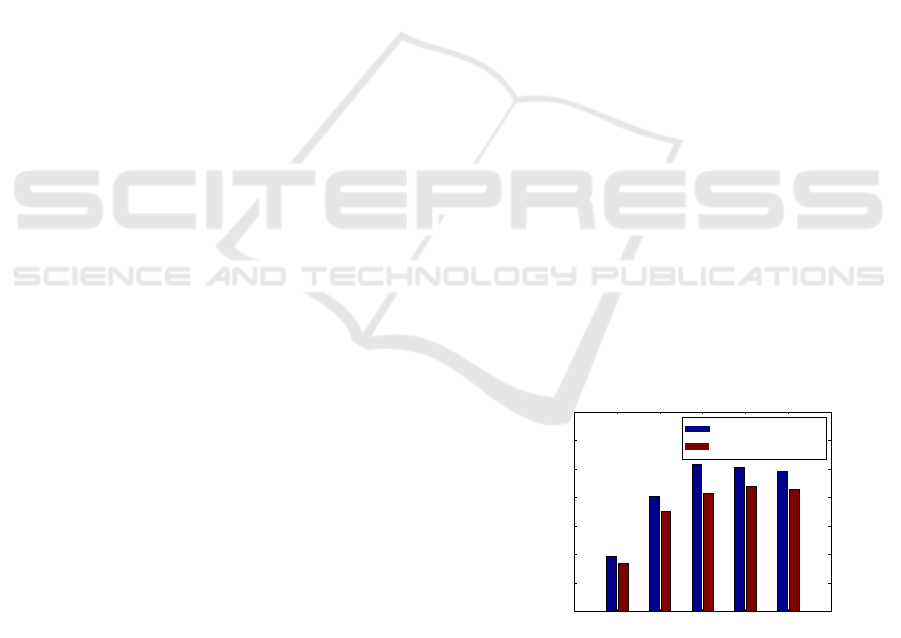
Figure 1: Capability allocation success with and without

proxy agents: number of agents = 30, number of pre-

assigned tasks = 30, number of new tasks = 30, Task du-

ration = 1000ms, New task arrival Poisson mean = 50ms.

Experiment results have shown (Figure 1) that

when probability of communication failure is high,

proxy agents improve the performance of task allo-

cation rates. This is implemented by incorporating

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

148

the expectation of successful communication into the

utility function (for simplicity denoted by R, omitting

the indices for tasks and agents): R

= p·R, where p is

the probability that agent i will receive the assignment

should it win the bid for performing capability j. p is

calculated using the latest n pings between the proxy

agent and its agent. p =

∑

k=1

× p

∑

k=1

= 1,

with α

k+1

= f ×α

,k = 1,. .. ,n−1 to favor the lastest

ping.



1 if k

ping succeeded

0 otherwise

In our experiments, α

= 0.2, f = 0.8, and n = 20.

4 THEORETICAL BOUNDS

Due to the complexity of the problem addressed in

this paper, a mathematical formulation is impossi-

ble except for a simpliﬁed version which we used

to derive theoretical bounds and validate algorithms.

Theoretical bounds help us understand empirical re-

sults and design systems with consideration of per-

formance bounds.

First, given some task arrival intervals and task

durations over a given geographical area, we would

like to know the smallest number of agents needed

for the system to work properly. We consider the sim-

plest possible analytical framework within our overall

problem setting.

In particular we will assume that: (1) Task re-

quirements (req

’s) and agent qualiﬁcations (cap

’s)

are unidimensional (i.e., k = 1). (2) Release times

of the tasks are random and follow a Poisson pro-

cess of parameter λ. (3) The duration of the tasks

are i.i.d. exponential with parameter µ (Model 1), or

uniform over the interval [0, 2/µ] (Model 2) [expected

task duration is 1/µ under both models]. (4) There are

m agents, initially distributed at random over a unit

square. (5) At any time, an agent is either busy or

available. (6) Upon arrival of a task, if no agents are

available then the task is dropped, otherwise it is as-

signed to one of the free agents uniformly at random.

(7) A free agent, upon assignment of a task, can start

working on it immediately, irrespective of his/her lo-

cation. (8) We observe the system over a long period

of time so that the observed number of tasks n is very

large (the system is in a “steady-state”).

Result 1: The probability that all agents are busy

when a new task arrives is given by

Due to space limitation, a detailed proof is omitted.

Note that this is closely related to the classical Erlang’s loss

formula, developed during the ﬁrst decade of the 20th cen-

(λ/µ)

/m!

∑

i=0

(λ/µ)

/i!

For a given λ and µ, this formula allows us to ﬁnd

the minimum number of agents so that the fraction of

tasks being allocated is above a given level of service.

Result 1 remains valid, under some scaling of the pa-

rameters, e.g., for a given ratio λ/µ, the region can

be any compact region, and not just the unit square.

More interestingly, Result 1 can also be shown to re-

main valid even when the duration of serving a task

also includes moving to the location of the task, as

long as it is driven by independent (between tasks)

random variables following any general distribution.

with mean 1/µ (not necessarily exponential). For ex-

ample, this would be the case when the task is allo-

cated at random uniformly among any free agents, ir-

respective of their geographical location. In that case,

under the assumption that the overall region of inter-

est is the square [0,l]

, and assuming that any agents

move at constant speed s, the previous formula be-

comes

(λ(0.52l/s + 1/µ))

/m!

∑

i=0

(λ(0.52l/s + 1/µ))

/i!

Result 1 provides a valid upper bound if an alloca-

tion based on shortest distance will lead to a smaller

number of agents for the same level of service.

Result 2 (ﬁrst generalizations): Now assume that in-

stead of being dropped, a new task, ﬁnding all agents

busy, is put on a waiting list and then assigned to the

ﬁrst available agent. Then under Model 1, the system

will reach steady-state if λ/mµ < 1. We have:

a) The probability p

that there are j tasks in the sys-

tem at any time is given by



(λ/µ)

/ j! for 0 ≤ j ≤ m − 1

(λ/µ)

/(m

j−m

m!) for j ≥ m

where

= [

m−1

∑

j=0

(λ/µ)

/ j!+(λ/µ)

/(m!(1−λ/mµ))]

−1

b) The average number of tasks waiting in the system

is:

n = p

(λ/µ)

(λ/mµ)/(m!(1 − λ/mµ)

)

c) The average waiting time of a task is

w = n/λ = p

(λ/µ)

(λ/mµ)/(m!(1−λ/mµ)

)/λ

tury by Erlang, a Danish engineer who was working on siz-

ing up telephone systems.

The Price of Anarchy: Centralized versus Distributed Resource Allocation Trade-offs

149

From b), for a given λ and µ, we can choose m so

that the average number of tasks waiting in the system

at any time is below a desired level and/or the average

waiting time of a task is below a prescribed level.

Result 3 (second generalizations): We now consider

the case where the allocation of a new task to a given

agent is done proportionally to the shortest distance

among all free agents. A new task, ﬁnding all agents

busy, is put on a waiting list and then assigned to the

closest available agent. In that case,

d) Under heavy-trafﬁc approximation, when

λ/mµ → 1, the average waiting time of a task is

given by

w ≈ (1/λ + λσ

/m)/2(1 − λ/mµ)

where σ

is the variance of the service time under

the chosen policy (i.e. travel time plus execution

time of the task).

Assuming a uniform spatial distribution of free

agents and unit speed over the unit square, we would

have σ

≈ 0.07. The value in d) shows that the av-

erage waiting time is dominated by the term (1 −

λ/mµ)

−1

as λ/mµ → 1.

We conducted experiments to co-validate the the-

oretical bounds and our constraint resource allocation

algorithm (setting the conﬁguration to match the sim-

ple framework).

0 5 10 15 20 25 30 35

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Number of Agents

% Tasks Completed

Exponential Task Duration, Mean 60 Seconds,

InterArrival Mean 3 Seconds

Theoretical

Algorithm 1

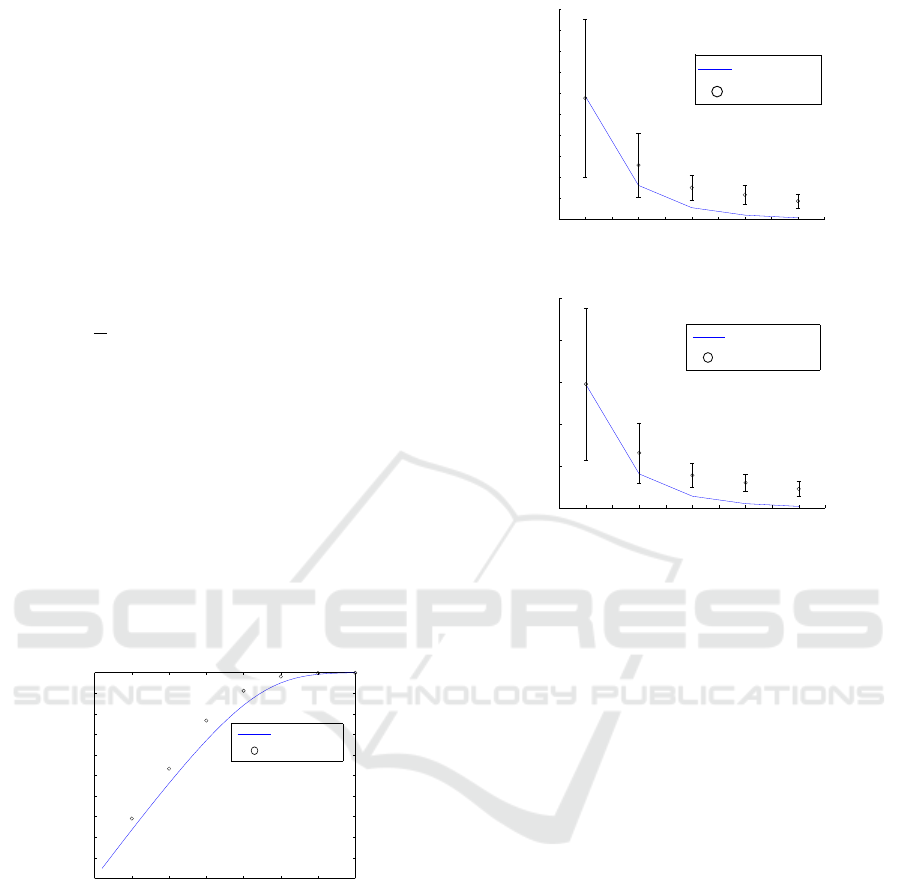
Figure 2: Empirical results and theoretical bound on mini-

mum number agents needed to ensure the fraction of tasks

being allocated (i.e. not dropped) is above a given level

of service with task duration exponentially distributed with

mean 60s; task arrival with Poisson mean 3s and λ/µ = 20.

Figure 2 shows results of empirical runs (labeled

Algorithm 1) overlaid over theoretical curves of Re-

sult 1. As illustrated, the empirical results ﬁt well

with the theoretical lower bound. A relaxation of the

time threshold in our algorithm implementation after

which a task was dropped if not assigned may have

contributed to the slightly better performance than the

theoretical analysis suggests.

Figure 3 shows the empirical results overlaid over

the theoretical curves for Result 2. For empirical data

6 7 8 9 10

0.5

1.5

2.5

3.5

4.5

Number of Agents

Average Number of Waiting Tasks

Theoretical

Algorithm 1

(a) λ = 1/500,µ = 1/2500

6 7 8 9 10

500

1000

1500

2000

2500

Number of Agents

Average Task Wait Time (ms)

Theoretical

Algorithm 1

(b) λ = 1/500,µ = 1/2500

Figure 3: Empirical and theoretical results on (a) average

number of waiting tasks; (b) average waiting time per task.

points, the vertical bars show standard deviation about

the mean over multiple runs. Note that for the system

to reach a steady-state, λ/mµ < 1 must hold. Also

note that the closer to the boundary condition (m =

1), the larger the standard deviation is.

5 RELATED RESEARCH

Most work on distributed systems focuses on collab-

oration algorithms and strategies (Spall, 2012), such

as routing and positioning UAVs to perform a spe-

ciﬁc task (Bednowitz et al., 2014). Only a few re-

searchers have investigated the trade-offs of decen-

tralization, (Cicalo et al., 2011), and, in contrast to our

work, the performance tradeoff is generally analyzed

without considering communications degradation or

adversary interference (Tsitsiklis and Xu, 2011). A

key reason is that it is extremely difﬁcult to mathe-

matically model the complex aspects of the problem.

In this paper, we speciﬁcally address communication

failure and empirically explore trade-offs.

A number of market-based algorithms for collab-

orative multi-agent planning have been developed,

beneﬁting from their simplicity and low computa-

tion and communication costs ((Zheng and Koenig,

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

150

2009)(Zheng and Koenig, 2010)(Hong and Gordon,

2011)). However, most existing market-based al-

gorithms cannot re-evaluate the existing allocations

when new tasks need to be inserted (Mauadi et al.,

2011). In contrast to algorithms for homogeneous

agents (Amador et al., 2014), our algorithm also ap-

plies to heterogeneous agents. Uniquely, our agents

are modeled by a set of capabilities with individu-

ally variable proﬁciencies. Their bids are relative

to spatial and temporal constraints and dependencies

of the roles to be fulﬁlled. Most research consid-

ers only assignments of one agent to one task, one

agent to multiple tasks (Liu and Shell, 2011), or many

agents to one task (Zhang et al., 2012), while our ap-

proach handles many-to-many task assignments with

different capability mixes with varying proﬁciencies.

Also, unlike most techniques (Roggendorf and Bel-

tran, 2006)(Bonacquisto et al., 2014) the bidding

agents in our auction algorithm represent unselﬁsh

agents that share the common goal of achieving over-

all maximum revenue. Our agents do not lower their

bids for highly contended resources, e.g., caching

(Wang and Martinez, 2015). Instead, our robust win-

ner determination algorithm accounts for such reﬁne-

ments. Similar to the consensus-based approach in

Choi et al. (Choi et al., 2009), our approach is robust

to network changes, but also adds proxy agents. Un-

like more analytical work (Lagoudakis et al., 2004),

our algorithm does not provide a guarantee on the

quality of its allocations. Instead, we provided the-

oretical bounds.

6 EMPIRICAL ANALYSIS

The goal of this empirical analysis is to explore

the trade-off between centralized and distributed ar-

chitectures without the simpliﬁcation that theoretical

analysis is forced to make. To achieve this goal, we

simulated various experiment settings under different

communication conditions. We varied the given max-

imum number of different capability types M, collec-

tively required by the tasks (and collectively offered

by the agents), and randomized task characteristics,

the number of groups that the agents are divided into,

and varied communication conditions. We imple-

mented agent communications using the Java Agent

Development Framework (JADE) (Bellifemine et al.,

2007) and developed a module to add interference to

the communication between the agents using a com-

munication model described below.

Our assumption is that the farther a message has

to travel, the more likely the message is to fail. So

is the closer the sender is to a communication jam-

Table 1: Exemplar parameters used in deﬁning different

communication levels.

Level a

1 0.8 0.001 0.1 0.001 0.5 0.01 0.5 0.01

2 0.7 0.001 0.2 0.001 0.5 0.01 0.6 0.01

3 0.6 0.001 0.3 0.001 0.4 0.0075 0.6 0.0075

4 0.5 0.001 0.5 0.001 0.3 0.005 0.6 0.005

5 0.5 0.01 0.5 0.01 0.3 0.005 0.7 0.005

6 0 0 1 0 0 0 1 0

mer. We model communication failures with a two

stage Gilbert-Elliott channel (Kong, 2002). The chan-

nel either stays put or transitions between a “good”

and a “bad” state. We assume that when the channel

is in a bad state, the agent cannot send or receive its

message. The agent will repeatedly resend the mes-

sage until either the message is sent successfully or

the message times out (upon which it is dropped). In

our experiment, in addition to the reliability of the

communication channel, we need to consider adver-

sary interference. Therefore, the communication be-

tween the two agents will have to be in a compounded

“good” state both in terms of the normal communica-

tion channels as well as adversary interference. This

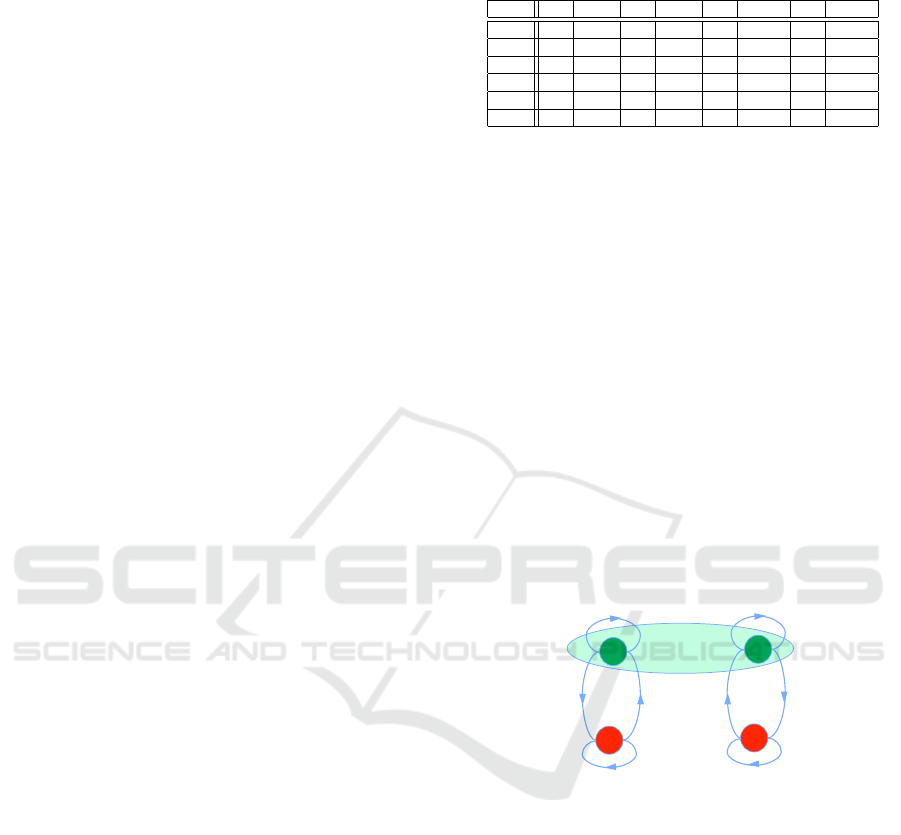
is illustrated in Figure 4, with green being good state

and red being bad state. The transition probabilities

α and β are parameterized with distances d

and d

which are distances to the closest jammer and of the

sender-receiver distance, respectively.

"(!

"('

)

"(!

)

"('

)

Figure 4: Communication model between two agents.

In the current experiment, the following parame-

ters are used.

) = a

− b

∗ d

, β

) = e

+ f

∗ d

) = a

+ b

∗ d

, β

) = e

− f

∗ d

We divided the communication levels into 1,2, .. ., 6,

with 6 indicating perfect communications. The corre-

sponding parameters are shown in Table 1.

The experiment results shown below are averaged

over at least 100 runs of the same parameter setup to

get statistically signiﬁcant results. Our experiments

have shown that above 80 repetitions, the results reach

a stable state.

As communication degrades, messages - includ-

ing those with task requirements, bidding requests,

acknowledgments, etc - are being dropped, affecting

The Price of Anarchy: Centralized versus Distributed Resource Allocation Trade-offs

151

the quality of the results. For the following set of ex-

periments, we used the following set of parameters

unless otherwise stated. The number of agents is 60.

There were 30 preassigned tasks before 100 pop-up

tasks started to arrive in sequence. Each task has a

duration requirement of 1000ms, and the pop-up ar-

rival times follow a Poisson distribution with mean

50ms. The axis labeled “comms level” represents the

communication condition divided into 6 levels as de-

scribed above. The other horizontal axis represents

the number of groups that the 60 agents are divided

into. The vertical axis represents the percentage of

tasks (out of all 130) that are successfully allocated.

Figure 5 shows the result of task completion under

different communication conditions with different de-

grees of decentralization. As illustrated in Figure 5, a

centralized system works best under perfect and rel-

atively good communication conditions, and perfor-

mance degrades as the number of groups increases.

However, as communication conditions worsen, dis-

tributed systems start to outperform the centralized

system. It is further clear that an optimal point of de-

centralization exists beyond which, as the group num-

ber increases, the performance starts to degrade again.

0.2

0.4

0.6

0.8

Number of Groups

Cap Types: 5, Max Caps Per Agent: 5

Comms Level

% Tasks Totally Completed

Figure 5: Tasks that were completely executed (all capabil-

ities fulﬁlled).

Due to capability mismatches of and scheduling

conﬂicts, agents can be idle at times. Communica-

tion failures also cause agents to be idle even when

their capabilities are needed. Some agents either fail

to participate in the auction or fail to receive the win-

ner announcement. Our experiment results show that

with imperfect communication, a lower percentage of

agents are either assigned to (scheduled to execute)

or busy with (executing) tasks. It is further illustrated

that the drop in the number of agents that are assigned

or busy is larger in centralized systems than in dis-

tributed systems when communication failures are in-

troduced.

In the experiments, we placed the agents, tasks,

etc. on an N × N grid, where N ∈ R

. If we vary

N, but keep all else constant, smaller N will corre-

spond to better results. This is because communica-

tions success depends on distance. Our experiments

conﬁrm that, given a ﬁxed communication level, the

larger grid (larger N) results in a greater optimal point

of decentralization. For example, the optimal point

is 3 groups for Comms Level 2 when N = 100, but

7 groups when N = 200. This trend is clear for all

communication levels. The main conclusion is that

the message drop rate dictates the optimal decentral-

ization point. Similarly, our experiments also showed

that the number of agents will not affect the opti-

mal decentralization point, since it does not affect the

message success rate.

To simulate adversaries attempting to block com-

munications, we included jammers in the software.

jammers have a location on the grid, and they inter-

fere with communications in their vicinity.

We conjectured that the more jammers there are,

the higher the optimal point of decentralization would

be. The argument is that the more groups there are,

the more likely it is that there are some auctioneers -

as well as some of their agents - far away from jam-

mers. This will increase the number of successful

communications attempts. We again compute the av-

erage percentage of capabilities completed over thou-

sands of runs. The results conﬁrm our hypothesis.

There is a marked change in the optimal points of de-

centralization, since the jammers affect the communi-

cations signiﬁcantly. According to our initial analysis,

this should signiﬁcantly shift the optimal point along

the group axis. However, we note that with smaller

groups, each group has fewer capabilities it can pro-

vide, lessening the effects of message drops on the

optimal point of decentralization. We see that on aver-

age, the optimal point of decentralization is about one

group more when there are ﬁve jammers than when

there are none.

Another interesting result we found when consid-

ering jammers is how well the algorithm performed in

the contested-communications environment. At the

optimal point of decentralization (4 groups), about

80% of communication attempts get through. At the

optimal point with jammers (5 groups), between 0.5%

and 1% of communication attempts are successful.

Despite this huge loss in communications, the agents

still manage to complete just over 30% of the capabil-

ities.

7 CONCLUSION

In this paper, we presented an empirical analysis of

the trade-offs between centralized and distributed re-

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

152

source allocation in communication contested envi-

ronments. The results show that there is an optimal

degree of decentralization that depends on the level

of communications disruption, which opens the pos-

sibility of actively managed distributed regimes. We

have extended the distributed auctioneer architecture

with asset proxy agents and have shown that this ex-

tension improves performance by 10 to 20%. To per-

form empirical analysis, we developed a distributed

auction architecture and winner determination algo-

rithm that optimizes a global objective function with

constraints. The set of these constraints enables us

to apply the algorithm to many problems where typ-

ical combinatorial auction algorithms fail to capture

the details and nuances of the application. We derived

theoretical bounds and conducted experiments to both

validate the theoretical analysis and, using the theo-

retical analysis, to validate the algorithm. Our results

show close correspondence between experimental re-

sults from our algorithm and the theoretical bounds.

Our next step is to enhance asset sharing among dis-

tributed auctioneers, modeling probabilistic resource

allocation by incorporating knowledge, e.g., a proﬁle

of asset capabilities and expected geolocations.

ACKNOWLEDGEMENTS

This research was supported by ONR contract

N00014-12-C-0162.

REFERENCES

Amador, S., Okamoto, S., and Zivan, R. (2014). Dynamic

multi-agent task allocation with spatial and tempo-

ral constraints. In Proceedings of the Twenty-Eighth

AAAI Conference on Artiﬁcial Intelligence.

Bednowitz, N., Batta, R., and Nagi, R. (2014). Dispatch-

ing and loitering policies for unmanned aerial vehicles

under dynamically arriving multiple priority targets.

Journal of Simulation, 8(1):9–24.

Bellifemine, F. L., Caire, G., and Greenwood, D. (2007).

Developing Multi-Agent Systems with JADE. Wiley.

Bonacquisto, P., Modica, G. D., Petralia, G., and Tomar-

chio, O. (2014). A strategy to optimize resource allo-

cation in auction-based cloud markets. In Proceeding

of 2014 IEEE International Conference on Services

Computing.

Choi, H., Brunet, L., How, J. P., and Member, S. (2009).

Consensus-based decentralized auctions for robust

task allocation. IEEE Transactions on Robotics.

Cicalo, S., Tralli, V., and Perez-Neira, A. (2011). Cen-

tralized vs distributed resource allocation in multi-cell

ofdma systems. In Proceeding of 2011 IEEE 73rd Ve-

hicular Technology Conference (VTC Spring).

Greene, K. and Hofmann, M. O. (2006). Coordinating busy

agents using a hybrid clustering-auction approach. In

Proceeding of AAAI 06, Workshop on Auction Mecha-

nisms for Robot Coordination, Boston, MA.

Hong, S. A. and Gordon, G. J. (2011). Decomposition-

based optimal market-based planning for multi-agent

systems with shared resources. In Proceeding of

the 13th International Conference on Artiﬁcial Intelli-

gence and Statistics (AISTSTS), Chia Laguna Resort,

Sardinia, Italy.

Kong, P. (2002). Performance of queue in impaired wireless

channel. Electronic letters, 38(22).

Lagoudakis, M. G., Berhault, M., Koenig, S., Keskinocak,

P., and Kleywegt, A. J. (2004). Simple auctions with

performance guarantees for multi-robot task alloca-

tion. In Proceedings of the IEEE/RSJ International

conference on Intelligent Robots and Systems (IROS).

Liu, L. and Shell, D. A. (2011). Assessing optimal as-

signment under uncertainty: An interval- based algo-

rithm. International Journal of Robotics Research,

30(7):936–953.

Mauadi, M., Li, W., and Murata, T. (2011). Combinato-

rial auction method for decentralized task assignment

of multiple-loading capacity agv based on intelligent

agent architecture. In Proceeding of the Second In-

ternational Conference on Innovations in Bio-inspired

Computing and Applications (IBICA), pages 207–211.

Roggendorf, M. and Beltran, F. (2006). Flow-based

resource allocation in a multiple-access wireless

market-setting using an auction. In Proceeding of the

26th IEEE International Conference on Distributed

Computing Systems Workshops (ICDCSW06).

Spall, J. C. (2012). Cyclic seesaw process for optimiza-

tion and identiﬁcation. Journal of Optimization The-

ory and Applications, 154(1):187–208.

Tsitsiklis, J. and Xu, K. (2011). On the power of (even a

little) centralization in distributed processing. In Pro-

ceeding of SIGMETRICS’11.

Tung, A. K. H., Ng, R. T., Lakshmanan, L., and Han, J.

(2001). Constraint-based clustering in large databases.

In den Bussche, J. V. and Vianu, V., editors, Database

Theory ICDT 2001, pages 405–419. Springer Berlin

Heidelberg.

Wang, X. and Martinez, J. F. (2015). Xchange: A market-

based approach to scalable dynamic multi-resource

allocation in multicore architectures. In Proceeding

of 2015 IEEE 21st International Symposium on High

Performance Computer Architecture (HPCA).

Zhang, K., Collins, Jr., E. G., and Shi, D. (2012). Cen-

tralized and distributed task allocation in multi-robot

teams via a stochastic clustering auction. ACM Trans.

Auton. Adapt. Syst., 7(2):21:1–21:22.

Zheng, X. and Koenig, S. (2009). K-swaps: Cooperative

negotiation for solving task-allocation problems. In

Proceeding of the International Joint Conference on

Artiﬁcial Intelligence (IJCAI), pages 373–379.

Zheng, X. and Koenig, S. (2010). Sequential incremental

value auctions. In Proceeding of AAAI Conference on

Artiﬁcial Intelligence (AAAI).

The Price of Anarchy: Centralized versus Distributed Resource Allocation Trade-offs

153