Dual SVM Training on a Budget

Sahar Qaadan, Merlin Sch¨uler and Tobias Glasmachers

Department of Neural Computing, Ruhr University Bochum, 44801, Bochum, Germany

Keywords:

Dual Subspace Algorithm, Kernel SVM, Budget Maintenance, Merging Method.

Abstract:

We present a dual subspace ascent algorithm for support vector machine training that respects a budget con-

straint limiting the number of support vectors. Budget methods are effective for reducing the training time

of kernel SVM while retaining high accuracy. To date, budget training is available only for primal (SGD-

based) solvers. Dual subspace ascent methods like sequential minimal optimization are attractive for their

good adaptation to the problem structure, their fast convergence rate, and their practical speed. By incorpo-

rating a budget constraint into a dual algorithm, our method enjoys the best of both worlds. We demonstrate

considerable speed-ups over primal budget training methods.

1 INTRODUCTION

Support Vector Machines (SVMs) introduced by

(Cortes and Vapnik, 1995) are popular machine learn-

ing methods, in particular for binary classiﬁcation.

They are supported by learning-theoreticalguarantees

(Mohri et al., 2012), and they exhibit excellent gener-

alization performance in many applications in science

and technology (Son et al., 2010; Shigeo, 2005; Byun

and Lee, 2002; Quinlan et al., 2003).They belong to

the family of kernel methods, applying a linear algo-

rithm in a feature space deﬁned implicitly by a kernel

function.

Training an SVM corresponds to solving a large-

scale optimization problem, which can be cast

into a quadratic program (QP). The primal prob-

lem can be solved directly with stochastic gradi-

ent descent (SGD) and accelerated variants (Shalev-

Shwartz et al., 2007; Glasmachers, 2016), while the

dual QP is solved with subspace ascent, see (Bottou

and Lin, 2006) and references therein.

The computational complexity of each stochastic

gradient or coordinate step is governed by the cost of

evaluating the model of a training point. This cost is

proportional to the number of support vectors, which

grows at a linear rate with the data set size (Steinwart,

2003). This limits the applicability of kernel meth-

ods to large-scale data. Efﬁcient algorithms are avail-

able for linear SVMs (SVMs without kernel) (Shalev-

Shwartz et al., 2007; Fan et al., 2008). Parallelization

can yield considerable speed-ups (Wen et al., 2017),

but only by a constant factor. For non-linear (kernel-

ized) SVMs there exists a wide variety of approaches

for approximate SVM training, many of which aim to

leverage fast linear solvers by approximating the fea-

ture space representation of the data. The approxima-

tion can either be ﬁxed (e.g., random Fourier features)

(Lu et al., 2016; Le et al., 2016; Nguyen et al., 2017)

or data-dependent(e.g., Nystr¨om sampling) (Lu et al.,

2016; Rahimi and Recht, 2008; Yang et al., 2012; Ca-

landriello et al., 2017).

Several online algorithms ﬁx the number of SVs to

pre-speciﬁed value B ≪ n, the budget, and update the

model in a greedy manner. This way they limit the

iteration complexity. The Stoptron (Orabona et al.,

2009) is a simple algorithm that terminates when the

number of SVs reaches the budget B. The Forgetron

algorithm (Dekel et al., 2008) removes the oldest SV

when the number of SVs exceeds the budget. Un-

der some mild assumptions, convergence of the al-

gorithm has been proven. The Projectron (Orabona

et al., 2009) projects the SV to be removed on the

remaining SVs to minimize the weight degradation.

While the latter outperforms the Forgetron, it requires

O(B)

time to compute the projection. Recently, (Lu

et al., 2018) have implemented an efﬁcient stochas-

tic sampling strategy based on turning the incoming

training example into a new support vector with prob-

ability proportional to the loss suffered by the exam-

ple. This method aims to convert the online classiﬁers

for batch classiﬁcation purposes.

The above approach can be based on stochastic

gradient descent and combined with more elaborate

budget maintenance techniques (Dekel and Singer,

2007). In particular with the popular budget main-

tenance heuristic of merging support vectors (Wang

Qaadan, S., Schüler, M. and Glasmachers, T.

Dual SVM Training on a Budget.

DOI: 10.5220/0007346400940106

In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 94-106

ISBN: 978-989-758-351-3

et al., 2012), it goes beyond the above techniques by

adapting the feature space representation during train-

ing. The technique is known as budgeted stochastic

gradient descent (BSGD).

In this context we design the ﬁrst dual SVM train-

ing algorithm with a budget constraint. The solver

aims at the efﬁciency of dual subspace ascent as used

in LIBSVM, ThunderSVM, and also in LIBLINEAR

(Chang and Lin, 2011; Fan et al., 2008; Wen et al.,

2017), while applying merging-based budget mainte-

nance as in the BSGD method (Wang et al., 2012).

The combination is far from straight-forward, since

continually changing the feature representation also

implies changing the dual QP, which hence becomes

a moving target. Nevertheless, we provide guarantees

roughly comparable to those available for BSGD.

In a nutshell, our contributions are:

• We present the ﬁrst dual decomposition algorithm

operating on a budget,

• we analyze its convergence behavior,

• and we establish empirically its superiority to pri-

mal BSGD.

The structure of the paper is as follows: In the next

section we introduce SVMs and existing primal and

dual solvers, including BSGD. Then we present our

novel dual budget algorithm and analyze its asymp-

totic behavior. We compare our method empirically

to BSGD and validate our theoretical analysis. We

close with our conclusions.

2 SUPPORT VECTOR MACHINE

TRAINING

A Support Vector Machine is a supervised kernel

learning algorithm (Cortes and Vapnik, 1995). Given

labeled training data (x

),. ..,(x

) ∈ X ×Y and

a kernel function k : X × X → R over the input space,

the SVM decision function f(x) 7→ hw,φ(x)i (we drop

the bias, c.f. (Steinwart et al., 2011)) is deﬁned as the

optimal solution w

∗

of the (primal) optimization prob-

lem

min

w∈H

P(w) =

kwk

∑

i=1



, f(x

)



, (1)

where λ > 0 is a regularization parameter, L is a loss

function (usually convex in w, turning problem (1)

into a convex problem), and φ : X → H is an only im-

plicitly deﬁned feature map into the reproducing ker-

nel Hilbert space H , fulﬁlling hφ(x),φ(x

′

)i = k(x,x

′

The representer theorem allows to restrict the solution

to the form w =

∑

i=1

φ(x

) with coefﬁcient vector

α ∈ R

, yielding f(x) =

∑

i=1

k(x,x

). Training

points x

with non-zero coefﬁcients α

6= 0 are called

support vectors.

We focus on the simplest case of binary classi-

ﬁcation with label space Y = {−1, +1}, hinge loss

L(y, f(x)) = max{0,1 − yf(x)}, and classiﬁer x 7→

sign( f(x)), however, noting that other tasks like

multi-class classiﬁcation and regression can be tack-

led in the exact same framework, with minor changes.

For binary classiﬁcation, the equivalent dual problem

(Bottou and Lin, 2006) reads

max

α∈[0,C]

D(α) =

α−

Qα, (2)

which is a box-constrained quadratic program (QP),

with

= (1,...,1)

and C =

λn

. The matrix Q con-

sists of the entries Q

= y

k(x

Kernel SVM Solvers. Dual decomposition solvers

like LIBSVM (Chang and Lin, 2011; Bottou and Lin,

2006) are the method of choice for obtaining a high-

precision non-linear (kernelized) SVM solution. They

work by decomposing the dual problem into a se-

quence of smaller problems of size O(1), and solv-

ing the overall problem in a subspace ascent manner.

For problem (2) this can amount to coordinate ascent

(CA). Keeping track of the dual gradient ∇

D(α) =

− Qα allows for the application of elaborate heuris-

tics for deciding which coordinate to optimize next,

based on the violation of the Karush-Kuhn-Tucker

conditions or even taking second order information

into account. Provided that coordinate i is to be op-

timized in the current iteration, the sub-problem re-

stricted to α

is a one-dimensional QP, which is solved

optimally by the truncated Newton step

←



1− Q



, (3)

where Q

is the i-th row of Q and [x]

max



0,min{C,x}



denotes truncation to the box

constraints. The method enjoys locally linear conver-

gence (Lin, 2001), polynomial worst-case complexity

(List and Simon, 2005), and fast convergence in prac-

tice.

In principle the primal problem (1) can be solved

directly, e.g., with SGD, which is at the core of the

kernelized Pegasos algorithm (Shalev-Shwartz et al.,

2007). Replacing the average loss (empirical risk)

in equation (1) with the loss L(y

, f(x

)) on a single

training point selected uniformly at random provides

an unbiased estimate. Following its (stochastic) sub-

gradient with learning rate 1/(λt) = (nC)/t in itera-

tion t yields the update

α ← α−

+ 1

f(x

)<1}

, (4)

Dual SVM Training on a Budget

where e

is the i-th unit vector and 1

{E}

is the indicator

function of the event E. Despite fast initial progress,

the procedurecan take a long time to produce accurate

results, since SGD suffers from the non-smooth hinge

loss, resulting in slow convergence.

In both algorithms, the iteration complexity is

governed by the computation of f(x) (or equivalently,

by the update of the dual gradient), which is linear in

the number of non-zero coefﬁcients α

. This is a lim-

iting factor when working with large-scale data, since

the number of support vectors is usually linear in the

data set size n (Steinwart, 2003).

Linear SVM Solvers. Specialized solvers for lin-

ear SVMs with X = R

and φ chosen as the iden-

tity mapping exploit the fact that the weight vector

w ∈ R

can be represented directly. This lowers the

iteration complexity from O(n) to O(d) (or the num-

ber of non-zero features in x

), which often results in

signiﬁcant savings (Joachims, 2006; Shalev-Shwartz

et al., 2007). This works even for dual CA by keep-

ing track of the direct representation w and the (re-

dundant) coefﬁcients α, however, at the price that the

algorithm cannot keep track of the dual gradient any

more, which would be an O(n) operation. Therefore

the LIBLINEAR solver resorts to uniform coordinate

selection (Fan et al., 2008), which amountsto stochas-

tic coordinate ascent (SCA) (Nesterov, 2012).

Linear SVMs shine on application domains like

text mining, with sparse data embedded in high-

dimensional input spaces. In general, for moderate

data dimension d ≪ n, separation of the data with a

linear model is a limiting factor that can result in se-

vere under-ﬁtting.

SVMs on a Budget. Lowering the iteration com-

plexity is also the motivation for introducing an upper

bound or budget B ≪ n on the number of support vec-

tors. The budget B is exposed to the user as a hyper-

parameter of the method. The proceeding amounts to

approximating w with a vector ˜w from the non-trivial

ﬁber bundle

(

∑

j=1

φ( ˜x

)



,. .., β

∈ R ; ˜x

,. .., ˜x

∈ R

)

⊂ H .

Critically, W

is in general non-convex, and so are

optimization problems over this set. Each SGD step

(eq. (4)) adds at most one new support vector to the

model. If the number of support vectors exceeds B

after such a step, then the budgeted stochastic gradi-

ent descent (BSGD) method applies a budget mainte-

nance heuristic to remove one support vector. Merg-

ing of two support vectors has proven to be a good

compromise between the induced error and the re-

sulting computational effort (Wang et al., 2012). It

amounts to replacing β

φ( ˜x

)+β

φ( ˜x

) (with carefully

chosen indices i and j) with a single term β

′

φ( ˜x

′

aiming to minimize the “weight degradation” error

kβ

φ( ˜x

) + β

φ( ˜x

) − β

′

φ( ˜x

′

. For the widely used

Gaussian kernel k(x, x

′

) = exp(−γkx− x

′

) the opti-

mal ˜x

′

lies on the line spanned by ˜x

and ˜x

, and it is a

convex combination if merging is restricted to points

of the same class. The coefﬁcient h of the convex

combination ˜x

′

= (1− h) ˜x

+ h˜x

is found with golden

section search, and the optimal coefﬁcient β

′

is ob-

tained in closed form. This procedure was deﬁned by

(Wang et al., 2012). We use it throughout the rest of

the paper. For completeness sake, the pseudo-code

of the procedure is found in Algorithm 1. It selects

two points from the model with an O(B) heuristic

that aims to minimize the squared weight degradation.

First the point with the smallest coefﬁcient is selected.

The second point is chosen to minimize the squared

weight degradation when merged with the ﬁrst. These

two points are then merged, i.e., removed from the

model and replaced with the best single-point approx-

imation. We refer to (Wang et al., 2012) for details on

the efﬁcient calculation of the squared weight degra-

dation, as well as on the golden section search proce-

dure used to obtain the coefﬁcient h.

Algorithm 1: Procedure Budget Maintenance for a

sparse model M.

Input/Output: model M =



(β

, ˜x

)



i∈I

(β

min

, ˜x

min

) ← argmin



|β|



(β, ˜x) ∈ M



∗

← ∞

for (β, ˜x) ∈ M \ {(β

min

, ˜x

min

)} do

m ← β/(β + β

min

)

κ ← k( ˜x, ˜x

min

)

h ← argmax



mκ

(1−h

′

)

+(1−m)κ

′2



′

∈

[0,1]



← β

min

· κ

(1−h)

+ β· κ

WD ← β

min

+ β

− β

+ 2· β

min

· β· κ

if (WD < WD

∗

) then

∗

← WD

(β

∗

, ˜x

∗

,κ

∗

) ← (β, ˜x,h,κ)

end

z ← h

∗

· ˜x

min

+ (1− h

∗

) · ˜x

∗

← β

min

· (κ

∗

)

(1−h

∗

)

+ β

∗

· (κ

∗

)

∗

)

M ← M \ {(β

min

, ˜x

min

),(β

∗

, ˜x

∗

)} ∪{(β

,z)}

In effect, merging allows BSGD to move support

vectors around in the input space. This is well jus-

tiﬁed since restricted to W

the representer theorem

does not hold. (Wang et al., 2012) show that asymp-

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

totically the performance is governed by the approx-

imation error implied by w

∗

6∈ W

(see their Theo-

rem 1).

BSGD aims to achieve the best of two worlds,

namely a reasonable compromise between statistical

and computational demands: fast training is achieved

through a bounded computational cost per iteration,

and the application of a kernel keeps the model sufﬁ-

ciently ﬂexible. This requires that B ≪ n basis func-

tions are sufﬁcient to represent a model ˜w that is suf-

ﬁciently close to the optimal model w

∗

. This assump-

tion is very reasonable, in particular for large n.

3 DUAL COORDINATE ASCENT

WITH BUDGET CONSTRAINT

In this section we present our novel approximate

SVM training algorithm. At its core it is a dual de-

composition algorithm, modiﬁed to respect a budget

constraint. It is designed such that the iteration com-

plexity is limited to O(B) operations, and is hence

independent of the data set size n. Our solver com-

bines components from decomposition methods (Os-

una et al., 1997), dual linear SVM solvers (Fan et al.,

2008), and BSGD (Wang et al., 2012) into a new al-

gorithm. Like BSGD, we aim to achieve the best of

two worlds: a-priori limited iteration complexity with

a budget approach, combined with fast convergence

of a dual decomposition solver. Both aspects speed-

up the training process, and hence allow to scale SVM

training to larger problems.

Introducing a budget into a standard decomposi-

tion algorithm as implemented in LIBSVM (Chang

and Lin, 2011) turns out to be non-trivial. Work-

ing with a budget is rather straightforward on the pri-

mal problem (1). The optimization problem is uncon-

strained, allowing BSGD to replace w represented by

α transparently with ˜w represented by coefﬁcients β

and ﬂexible basis points ˜x

. This is not possible for

the dual problem (2) with constraints formulated di-

rectly in terms of α.

This difﬁculty is solved by (Fan et al., 2008) for

the linear SVM training problem by keeping track of

w and α. We follow the same approach, however, in

our case the correspondence between w represented

by α and ˜w represented by β

and ˜x

is only approx-

imate. This is unavoidable by the very nature of the

problem. Luckily, this does not impose major addi-

tional complications.

Algorithm 2: Budgeted Stochastic Coordinate As-

cent (BSCA) Algorithm.

Input: training data (x

),. ..,(x

k : X × X → R , C > 0, B ∈ N

α ← 0, M ←

while not happy do

select index i ∈ {1,. ..,n} uniformly at

random

f(x

) =

∑

(β, ˜x)∈M

βk(x

, ˜x)

δ =





1− y

f(x

)





− α

if δ 6= 0 then

← α

+ δ

M ← M ∪ {(δ,x

)}

if |M| > B then

trigger budget maintenance, i.e.,

merge two support vectors

end

return β

The pseudo-code of our Budgeted Stochastic Co-

ordinate Ascent (BSCA) approach is detailed in algo-

rithm 2. It represents the approximate model ˜w as a

set M containing tuples (β, ˜x).

Critically, in line 2

the approximate model ˜w is used to compute

f(x

) =

h ˜w,x

i, so the complexity of this step is O(B). This is

in contrast to the computation of f(x

) = hw,x

i, with

effort linear in n. At the target iteration cost of O(B) it

is not possible to keep track of the dual gradient, sim-

ply because it consists of n entries that would need

updating with a dense matrix row Q

. Consequently,

and in line with (Fan et al., 2008), we resort to uni-

form variable selection in an SCA scheme, and the

role of the coefﬁcients α is reduced to keeping track

of the constraints.

For the budget maintenance procedure, the same

options are available as in BSGD. It is usually imple-

mented as merging of two support vectors, reducing

a model from size |M| = B+ 1 back to size |M| = B.

It is understood that also the complexity of the budget

maintenance procedure should be bounded by O(B)

operations. Furthermore, for the overall algorithm

to work properly, it is important to maintain the ap-

proximate relation ˜w ≈ w. For reasonable settings of

the budget B, this is achieved by non-trivial budget

maintenance procedures like merging and projection

(Wang et al., 2012).

We leave the stopping criterion for the algorithm

open. A stopping criterion akin to (Fan et al., 2008)

based on thresholding KKT violations is not viable,

Note that summing over an empty index set simply

yields zero.

Dual SVM Training on a Budget

as shown by the subsequent analysis. We therefore

run the algorithm for a ﬁxed number of iterations (or

epochs), as is common for BSGD.

4 ANALYSIS OF BSCA

BSCA is an approximate dual training scheme.

Therefore two questions of major interest are how

quickly it approaches w

∗

, and how close it gets. To

simplify matters somewhat, we make the assumption

that the matrix Q is strictly positive deﬁnite. This

ensures that the optimal coefﬁcient vector α

∗

corre-

sponding to w

∗

is unique. For a given weight vector

w =

∑

i=1

φ(x

), we write α(w) when referring to

the corresponding coefﬁcients, which are also unique.

Let w

(t)

and α

(t)

= α(w

(t)

), t ∈ N, denotethe sequence

of solutions generated by an iterative algorithm, using

the labeled training point (x

(t)

) for its update in

iteration t. The indices i

(t)

∈ {1,... ,n} are drawn i.i.d.

from the uniform distribution.

Optimization Progressof BSCA. We start by com-

puting the single-iteration progress.

Lemma 1. The change D(α

(t)

) − D(α

(t−1)

) of the

dual objective function in iteration t operating on the

coordinate index i = i

(t)

∈ {1,..., n} equals



(t−1)

, i, α

(t)

− α

(t−1)







1− Q

(t−1)

−



(t)

− α

(t−1)



−

1− Q

(t−1)





Proof. Consider the function s(δ) = D(α

(t−1)

+ δe

It is quadratic with second derivative −Q

< 0 and

with its maximum at δ

∗

= (1− Q

(t−1)

)/Q

. Repre-

sented by its second order Taylor series around δ

∗

reads s(δ) = s(δ

∗

) −

(δ − δ

∗

)

. This immediately

yields the result.

The lemma is in line with the optimality of the

update (3). Based thereon we deﬁne the relative ap-

proximation error

E(w, ˜w) := 1− max

i∈{1,...,n}













α(w), i,

(w) +

1−y

h ˜w,φ(x

− α

(w)





α(w), i,

(w) +

1−y

hw,φ(x

− α

(w)













(5)

The margin calculation in the numerator is based on

˜w, while it is based on w in the denominator. Hence

E(w, ˜w) captures the effect of using ˜w instead of w

in BSCA. Informally, we interpret it as a dual quan-

tity related to the weight degradation error k ˜w− wk

Lemma 1 implies that the relative approximationerror

is non-negative, because the optimal step is in the de-

nominator, which upper bounds the fraction by one.

It is continuous (and in fact piecewise linear) in ˜w,

for ﬁxed w. Finally, it fulﬁlls ˜w = w ⇒ E(w, ˜w) = 0.

The following theorem bounds the suboptimality of

BSCA, and it captures the intuition that the relative

approximation error poses a principled limit on the

achievable solution precision.

Theorem 1. The sequence α

(t)

produced by BSCA

fulﬁlls

D(α

∗

) − E

D(α

(t)

)

≤



D(α

∗

) +



∏

τ=1

1−

2κ



1− E(w

(τ−1)

, ˜w

(τ−1)

)



(1+ κ)n

where κ is the smallest eigenvalue of Q.

Proof. Theorem 5 by (Nesterov, 2012) applied to the

non-budgeted setting ensures linear convergence

E[D(α

∗

) − D(α

(t)

)] ≤



D(α

∗

) +





1−

2κ

(1+ κ)n



and in fact the proof establishes a linear decay of

the expected suboptimality by the factor 1 −

2κ

(1+κ)n

in each single iteration. With a budget in place, the

improvement is further reduced by the difference be-

tween the actual dual progress (the numerator in eq. 5)

and the progress in the non-budgeted case (the de-

nominator in eq. 5). By construction (see lemma 1

and eq. 5), this additive difference, when written as

a multiplicative factor, amounts to 1− E(w, ˜w) in the

worst case. The worst case is reﬂected by taking the

maximum over i ∈ {1,.. ., n} in eq. 5.

We conclude from Theorem 1 that the behavior

of BSCA can be divided into an early and a late

phase. For ﬁxed weight degradation, the relative ap-

proximation error is small as long as the progress

is sufﬁciently large, which is the case in early iter-

ations. Then the algorithm is nearly unaffected by

the budget constraint, and multiplicative progress at

a ﬁxed rate is achieved. Progress gradually decays

when approaching the optimum, which increases the

relative approximation error, until BSCA stalls. In

fact, the theorem does not witness further progress

for E(w, ˜w) ≥ 1. Due to w

∗

6∈ W

, the KKT violations

do not decay to zero, and the algorithm approaches a

limit distribution.

The precision to which the opti-

mal SVM solution can be approximated is hence lim-

ited by the relative approximation error, or indirectly,

by the weight degradation.

BSCA does not converge to a unique point. It does not

become clear from the analysis provided by (Wang et al.,

2012) whether this is also the case for BSGD, or whether

the decaying learning rate allows BSGD to converge to a

local minimum.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

Budget Maintenance Rate. The rate at which bud-

get maintenance is triggered can play a role, in partic-

ular if the procedure consumes a considerable share

of the overall runtime. In the following we highlight

a difference between BSGD and BSCA. For an algo-

rithm A let

= lim

T→∞





t ∈ {1,. .. ,T}



(t)

(t−1)

,φ(x

(t)

)i < 1





denote the expected fraction of optimization steps in

which the target margin is violated, in the limit t → ∞

(if the limit exists). The following lemma establishes

the fraction for primal SGD (eq. (4)) and dual SCA

(eq. (3)), both without budget.

Lemma 2. Under the conditions (i) α

∗

∈ {0,C} ⇒

∂D(α

∗

)

∂α

6= 0 and (ii)

∂D(α

(t)

)

∂α

6= 0 (excluding only a zero-

set of cases) it holds p

SGD

∑

i=1

∗

and p

SCA

|{i|0 < α

∗

< C}|.

Proof. The lemma considers the non-budgeted case,

therefore the training problem is convex. Then the

condition

∑

∞

t=1

= ∞ for the learning rates ensures

convergence α

(t)

→ α

∗

with SGD. This can happen

only if the subtraction of α

(t−1)

and the addition of

nC with learning rate

cancel out in the update equa-

tion (4) in the limit t → ∞, in expectation. Formally

speaking, we obtain

lim

T→∞

∑

t=1

{

(t)

}

{

(t)

(t−1)

,φ(x

(t)

)i<1

}

nC− α

(t−1)

= 0 ∀i ∈ {1,.. ., n},

and hence lim

T→∞

∑

t=1

{

(t)

}

{

(t)

(t−1)

,φ(x

(t)

)i<1

}

∗

. Summation over i completesthe proof of the result

for SGD.

In the dual algorithm, with condition (i) and the

same argument as in (Lin, 2001) there exists an it-

eration t

so that for t > t

all variables fulﬁlling

∗

∈ {0,C} remain ﬁxed: α

(t)

= α

)

, while all other

variables remain free: 0 < α

(t)

< C. Assumption

(ii) ensures that all steps on free variables are non-

zero and hence contribute 1/n to p

SCA

in expectation,

which yields p

SCA

|{i|0 < α

∗

< C}|.

A point (x

(t)

) that violates the target margin

of one is added as a new support vector in BSGD

as well as in BSCA. After the ﬁrst B such steps, all

further additions trigger budget maintenance. Hence

Lemma 2 gives an asymptotic indication of the num-

ber of budget maintenance events, provided ˜w ≈ w,

i.e., if the budget is not too small. The different rates

for primal and dual algorithm underline the quite dif-

ferent optimization behavior of the two algorithms:

while (B)SGD keeps making non-trivial steps on all

training points corresponding to α

∗

> 0 (support vec-

tors w.r.t. w

∗

), after a while the dual algorithm oper-

ates only on the free variables 0 < α

∗

< C.

5 EXPERIMENTS

In this section we compare our dual BSCA algorithm

on the binary classiﬁcation problems ADULT, COD-

RNA, COVERTYPE, IJCNN, and SUSY, covering a

range of different sizes. Moreover, we run BSCA

on a smaller budget. The regularization parameter

C =

n·λ

and the kernel parameter γ were tuned with

grid search and cross-validation, see table 1. The C++

implementation of our algorithm is published on the

third author website.

Table 1: Data sets used in this study, hyperparameter set-

tings, test accuracy, number of support vectors, and training

time of the full SVM model (using LIBSVM).

data set size features C γ accuracy #SVs training time

SUSY 4,500,000 18 2

−7

80.02% 2,052,555 504h25m38s

COVTYPE 581,012 54 2

−3

75.88% 187,626 10h5m7s

COD-RNA 59,535 8 2

−3

96.33% 9,120 53.951s

IJCNN 49,990 22 2

98.77% 2,477 46.914s

ADULT 32,561 123 2

−7

84.82% 11,399 97.152s

Data Sets and Hyperparameters. The test prob-

lems were selected according to the following criteria,

which taken together imply that applying the budget

method is a reasonable choice:

• The feature dimension is not too large. Therefore

a linear SVM performs rather poorly compared to

a kernel machine.

• The problem size is not too small. The range of

sizes spans more than two orders of magnitude.

The hyperparameters C and γ were log

encoded and

tuned on an integer grid with cross-validation using

LIBSVM, i.e., aiming for the best possible perfor-

mance of the non-budgeted machine. The budget was

set to B = 500 in all experiments, unless stated other-

wise. This value turns out to offer a reasonable com-

promise between speed and accuracy on all problems

under study.

5.1 Primal vs. Dual Solver

The ﬁrst step is to compare dual BSCA to its closest

sibling, the primal BSGD method. Both algorithms

maintain the budget by means of merging of pairs of

support vectors.

Optimization Performance. BSCA and BSGD are

optimization algorithms. Hence it is natural to com-

pare them in terms of primal and dual objective func-

Dual SVM Training on a Budget

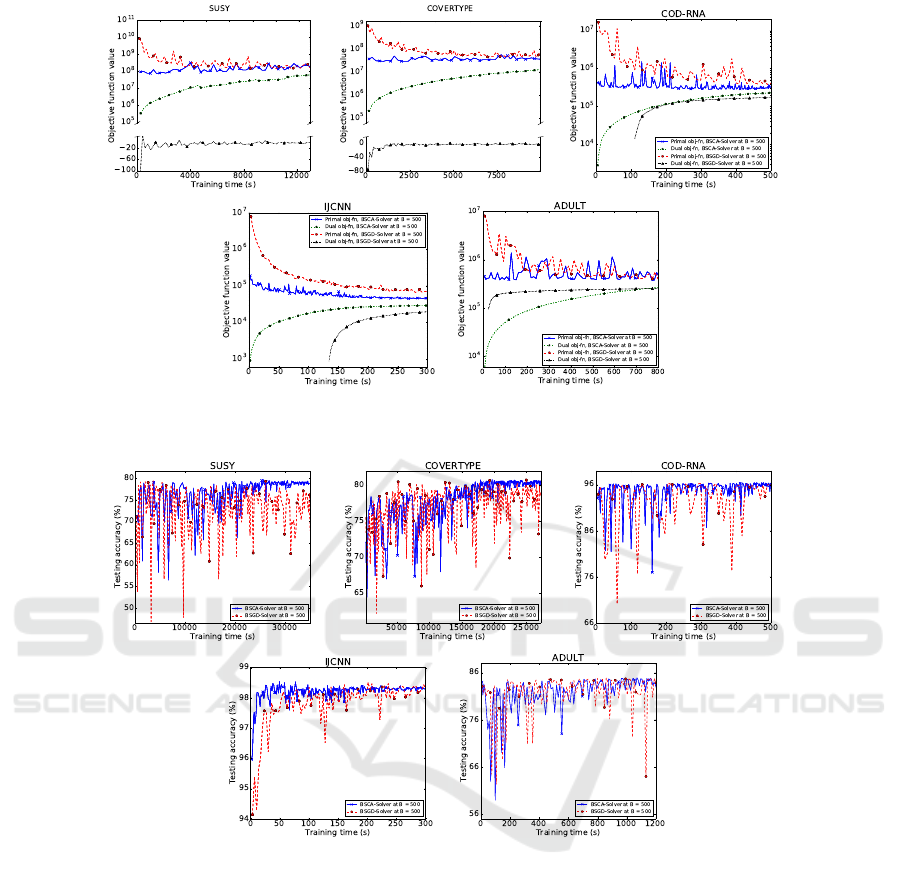
Figure 1: Primal and dual objective function curves of BSGD and BSCA solvers with a budget of B = 500. We use a mixed

linear and logarithmic scale where the dual objective stays negative, which happens for BSGD on two problems.

Figure 2: Test accuracy for the primal and dual solvers at a budget of B = 500 over training time.

tion, see equations (1) and (2). Since the solvers opti-

mize different functions, we monitor both. However,

we consider the primal as being of primary interest

since its minimization is the goal of SVM training,

by deﬁnition. Convergence plots are displayed in ﬁg-

ure 1. Overall, the dual BSCA solver clearly outper-

forms the primal BSGD method across all problems.

While the dual objective function values are found

to be smooth and monotonic in all cases, this is not

the case for the primal. BSCA generally oscillates

less and stabilizes faster (with the exception of the

ADULT problem), while BSGD remains somewhat

unstable and is hence at risk of delivering low-quality

solutions for a much longer time when it happens to

stop at one of the peaks.

Learning Performance. Figure 2 shows the corre-

sponding evolution of the test error. In our experi-

ment, all budgeted models reach an accuracy that is

nearly indistinguishable from the exact SVM solu-

tion. The accuracy converges signiﬁcantly faster for

the dual solver. For the primal solver we observe a

long series of peaks corresponding to signiﬁcantly re-

duced performance. This observation is in line with

the observed optimization behavior. The effect is par-

ticularly pronounced for the largest data sets SUSY

and COVERTYPE. Moreover, we conduct extensive

experiments to check if the learning performance re-

sults vary in different runs depending upon the order

of data-point considered in the algorithm 1. There-

fore, a variance plot for each data set is shown in ﬁg-

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

100

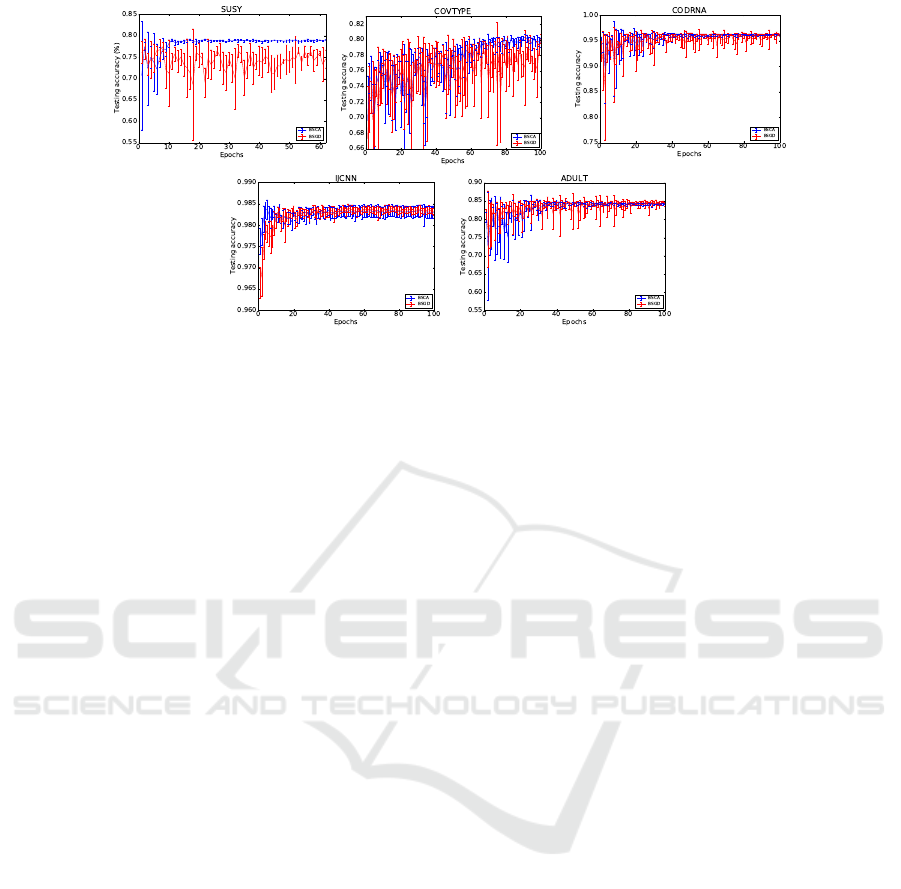
Figure 3: Stability of the test accuracy for the primal and dual solvers at a budget of B = 500. The plots indicate mean and

standard deviation of the test accuracy over 10 independent runs.

ure 3. The plots provide variance curves for the aver-

age over 10 set of experiments.

Convergence Behavior. The next experiment vali-

dates the predictions of Lemma 2 when using a bud-

get. Figure 8 displays the fraction of mergingsteps for

different budget sizes applied to the dual and primal

solvers. We ﬁnd the predictions of the lemma being

approximately valid also when using a budget. The

ﬁgure highlights an interesting difference in the opti-

mization behavior between BSGD and BSCA: while

the former makes non-zero steps on all support vec-

tors (training points with a margin of at most one), the

latter manages to ﬁx the dual variables of margin vio-

lators (training points with a margin strictly less than

one) at the upper bound C.

5.2 Impact of the Budget

In this section we investigate the impact of the budget

and its size on optimization and learning behavior. We

start with an experiment comparing primal and dual

solver without budget. The results are presented in

ﬁgure 4. It is apparent that the principal differences

between BSGD and BSCA remain the same when run

without budget constraint, i.e., the most signiﬁcant

differences stem from the quite different optimization

behavior of stochastic gradient descent and stochas-

tic coordinate ascent. The SGD learning curves are

quite noisy with many downwards peaks. The results

are in line with experiments on linear SVMs by (Fan

et al., 2008; Hsieh et al., 2008). To investigate the

effect of the budget size, Figure 5 provides test ac-

curacy curves for a reduced budget size of B = 200.

For some of the test problems this budget it already

rather small, resulting in sub-optimal learning behav-

ior. Generally speaking, BSCA clearly outperforms

BSGD. However, BSCA fails on the IJCNN data set,

while BSGD fails to deliver high quality solutions

on SUSY and COVERTYPE. Figure 7 aggregates the

data in a different way, comparing the test accuracy

achieved with different budgets on a common time

axis. In this presentation it is easy to read off the

speed-up achievable with a smaller budget. Unsur-

prisingly, BSCA with budget B = 200 is much faster

than the same algorithm with budget B = 500 when

run for the same number of epochs. However, when

it comes to achieving a good test error quickly, the re-

sults are mixed. While the small budget apparently

sufﬁces on COVERTYPE and SUSY, the provided

number of epochs does not sufﬁce to reach good re-

sults on IJCNN, where the solver with B = 500 is sig-

niﬁcantly faster. Figure 6 presents a similar analysis,

but with primal and dual objective function. Overall

it underpins the learning (test accuracy) results, how-

ever, it also reveals a drift effect of the dual solver

in particular for the smaller budget B = 200, with

both objectives rising. This can happen if the weight

degradation becomes large and the gradient computed

based on the budgeted representation does not prop-

erly reﬂect the dual gradient any more.

5.3 Comparison of BSCA with

Alternative Budgeted Solvers

In this section, we conduct an extensive set of experi-

ments to examine the efﬁciency of the proposed algo-

rithm in comparison to state-of-the-art approaches for

online kernel learning. To make a fair comparison of

algorithms with different parameters, the RBF kernel

parameter γ and the regularization parameter C were

optimized with 5-fold cross validation on the training

Dual SVM Training on a Budget

101

Figure 4: Test accuracy results of solvers based directly on SCA and SGD, without budget. The results are monitored every

300,000 iterations for SUSY and COVERTYPE, and every 10,000 iterations for all other data sets.

Figure 5: Test accuracy results for BSCA and BSGD at a budget of 200.

dataset using LIBSVM. The budget size B and learn-

ing rate η in NOGD and Pegasos and the feature di-

mension D and learning rate η in FOGD are set in-

dividually for different datasets according to the rec-

ommendation of (Lu et al., 2016). For each dataset,

the model is trained in a single pass through the data.

For comparison, we employ 11 state-of-the-art online

kernel learning methods:

• perceptron (Freund and Schapire, 1998),

• online gradient descent (OGD) (Kivinen et al.,

2003),

• randomized budget perceptron (RBP) (Cavallanti

et al., 2007),

• forgetron (Dekel et al., 2008),

• projectron and projectron++ (Orabona et al.,

2009),

• budgeted passive-aggressive simple (BPAS)

(Wang and Vucetic, 2010),

• bounded OGD (BOGD) (Zhao et al., 2012),

• budgeted SGD using merging strategy (BSGD)

(Wang et al., 2012),

• Fourier OGD (FOGD) and Nystrom OGD

(NOGD) (Lu et al., 2016).

Their implementations are published as a part of the

LIBSVM

and LSOKL5 toolboxes.

The results are

summarized in Table 2.

Our ﬁrst observation is that the budgeted online

approaches demonstrate their effectiveness with sub-

stantially shorter runtimes than the ones without bud-

http://www.csie.ntu.edu.tw/ cjlin/libsvm/

http://lsokl.stevenhoi.org

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

102

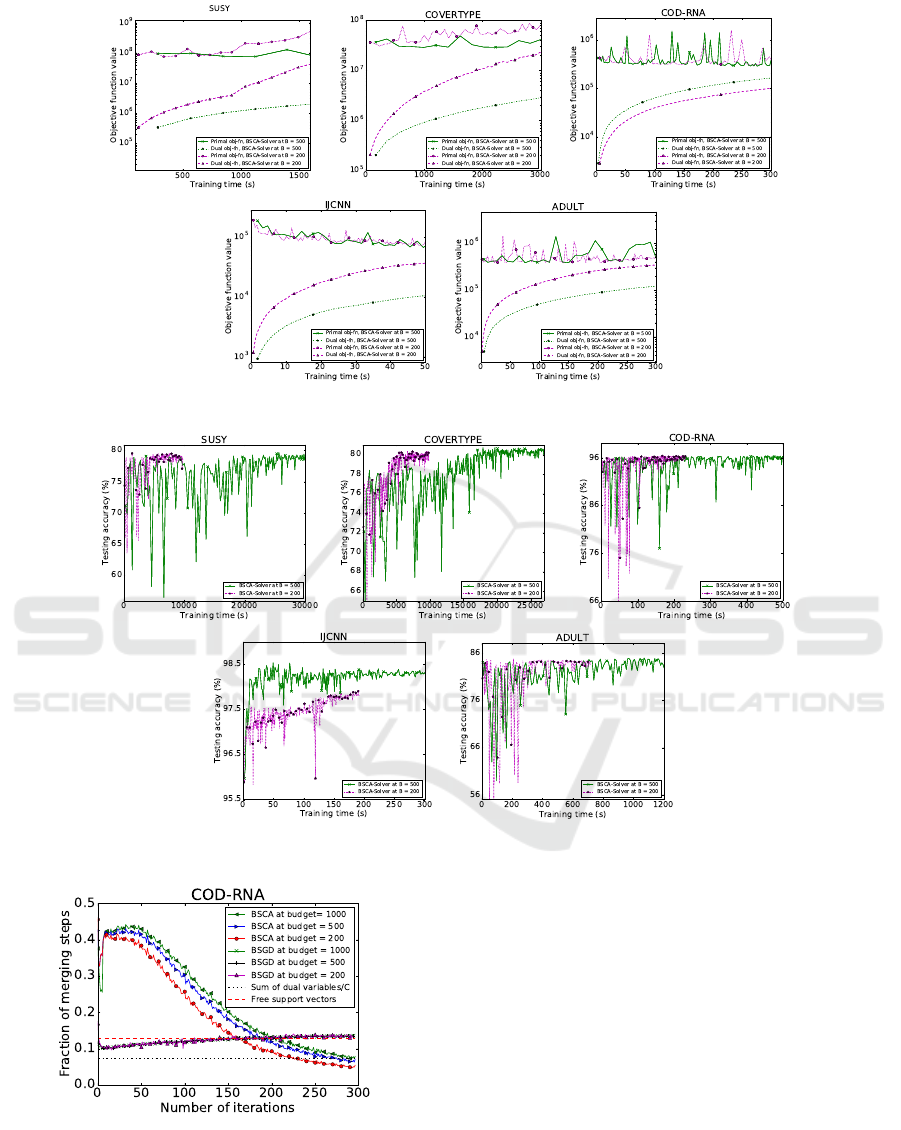
Figure 6: Primal and dual objective function over time for BSCA at budgets B ∈ {200,500}.

Figure 7: Test accuracy over time for BSCA at budgets B ∈ {200,500}.

Figure 8: Fraction of merging steps over a large number of

epochs at budgets B ∈ {200,500,1000}.

gets. More speciﬁcally, the execution time of our

proposed model BSCA is much faster than that of

alternative online algorithms and the recent fast al-

gorithms FOGD and NOGD. BCDA is only slightly

slower than the fastest methods which, with the no-

table exception of BPAS, achieve signiﬁcantly worse

results.

In terms of accuracy, the BSCA method performs

best on IJCNN, and more importantly, it performs

consistently well across all problems. Only the rather

slow online gradient descent approach achieves sim-

ilar performance, but using 8 to 33 times as much

training time, which would allow BSCA to perform

many epochs.

We excluded the SUSY and COVTYPE data sets

from table 2 due to the effort of tuning the param-

eter D for the FOGD method. For example, an ex-

periment using D = 10,000 for FOGD was running

for approximately two hours, achieving a test accu-

Dual SVM Training on a Budget

103

Table 2: Training time (seconds) and testing error (%) comparison between BSCA algorithm and all approaches implemented

by (Lu et al., 2016). The budget size B is ﬁxed to 500 for consistency with the previous experiment. The number of random

features D for FOGD is selected depending on the settings in (Lu et al., 2016), where D is set to 4000, 1600 and 1000 for

ADULT, CODRNA and IJCNN, respectively. For better readability, column-wise best values are highlighted.

ADULT CODRNA IJCNN

Algorithm training time test accuracy training time test accuracy training time test accuracy

Perceptron 53.37 83.35% 60.04 88.12% 25.31 95.75%

OGD 107.02 84.50% 227.25 95.77% 92.90 94.59%

RBP 7.21 76.38% 6.42 95.31% 8.04 91.74%

Forgetron 9.31 83.39% 7.24 92.55% 9.06 92.74%

Projectron 38.80 25.65% 61.79 33.31% 11.98 96.24%

Projectron++ 36.00 82.59% 46.89 71.95% 51.02 96.77%

BPAS 7.69 83.44% 6.76 94.12% 8.86 95.01%

BOGD 8.02 76.38% 6.59 80.77% 8.66 91.01%

BSGD 8.48 80.74% 4.37 89.85% 11.28 96.68%

FOGD 18.00 82.00% 9.17 72.20% 26.13 90.50%

NOGD 37.10 83.15% 38.17 95.62% 40.30 90.50%

BSCA 9.84 83.18% 6.85 95.68% 11.53 97.27%

racy of 49.98% (guessing performance), where BSCA

achieved 77.03%. This observation further validates

the effectiveness and efﬁciency of our proposed tech-

nique. Thus, we believe that our BSCA algorithm is a

promising technique for building large kernel learning

algorithms for large-scale classiﬁcation tasks.

5.4 Discussion

Our results do not only indicate that the optimization

behavior of BSGD and BSCA is signiﬁcantly differ-

ent, they also demonstrate the superiority of the dual

approach for SVM training, in terms of optimization

behavior as well as in terms of test accuracy. We at-

tribute its success to the good ﬁt of coordinate ascent

to the box-constrained dual problem, while the pri-

mal solver effectivelyignores the upper bound (which

is not represented explicitly in the primal problem),

resulting in large oscillations. Importantly, the im-

proved optimization behavior translates directly into

better learning behavior. The introduction of budget

maintenance techniques into the dual solver does not

change this overall picture, and hence yields a viable

route for fast training of kernel machines.

The BSCA method does not only clearly outper-

form the primal BSGD method, but it also performs

very well when compared with alternative fast train-

ing schemes for training kernelized SVMs. The fast

epoch times indicate a low overhead over the margin

computation, which is at the heart of every iterative

method. At the same time our new approach achieves

excellent accuracy.

6 CONCLUDING REMARKS

We have presented the ﬁrst dual decomposition algo-

rithm for support vector machine training honoring a

budget, i.e., an upper bound on the number of sup-

port vectors. This approximate SVM training algo-

rithm combines fast iterations enabled by the budget

approach with the fast convergence of a dual decom-

position algorithm. Like its primal cousin, it is fun-

damentally limited only by the approximation error

induced by the budget. We demonstrate signiﬁcant

speed-ups over primal budgeted training, as well as

increased stability. Overall, for training SVMs on a

budget, we can clearly recommend our method as a

plug-in replacement for primal methods. It is rather

straightforward to extend our algorithm to other ker-

nel machines with box-constrained dual problems.

ACKNOWLEDGEMENTS

We acknowledge support by the Deutsche

Forschungsgemeinschaft (DFG) through grant

GL 839/3-1.

REFERENCES

Bottou and Lin, 2006Bottou, L. and Lin, C.-J. (2006). Support

vector machine solvers.

Byun and Lee, 2002Byun, H. and Lee, S.-W. (2002). Applica-

tions of Support Vector Machines for Pattern Recogni-

tion: A Survey, pages 213–236. Springer Berlin Hei-

delberg, Berlin, Heidelberg.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

104

Calandriello et al., 2017Calandriello, D., Lazaric, A., and

Valko, M. (2017). Efﬁcient second-order online ker-

nel learning with adaptive embedding. In Guyon, I.,

Luxburg, U. V., Bengio, S., Wallach, H., Fergus, R.,

Vishwanathan, S., and Garnett, R., editors, Advances

in Neural Information Processing Systems 30, pages

6140–6150. Curran Associates, Inc.

Cavallanti et al., 2007Cavallanti, G., Cesa-Bianchi, N., and

Gentile, C. (2007). Tracking the best hyperplane

with a simple budget perceptron. Machine Learning,

69(2):143–167.

Chang and Lin, 2011Chang, C.-C. and Lin, C.-J. (2011). LIB-

SVM: A library for support vector machines. ACM

Trans. Intell. Syst. Technol., 2(3).

Cortes and Vapnik, 1995Cortes, C. and Vapnik, V. (1995).

Support-vector networks. Machine learning,

20(3):273–297.

Dekel et al., 2008Dekel, O., Shalev-Shwartz, S., and Singer,

Y. (2008). The forgetron: A kernel-based perceptron

on a budget. SIAM J. Comput., 37(5):1342–1372.

Dekel and Singer, 2007Dekel, O. and Singer, Y. (2007). Sup-

port vector machines on a budget. MIT Press.

Fan et al., 2008Fan, R.-E., Chang, K.-W., Hsieh, C.-J., Wang,

X.-R., and Lin, C.-J. (2008). Liblinear: A library for

large linear classiﬁcation. J. Mach. Learn. Res., pages

1871–1874.

Freund and Schapire, 1998Freund, Y. and Schapire, R. E.

(1998). Large margin classiﬁcation using the percep-

tron algorithm. In Proceedings of the Eleventh An-

nual Conference on Computational Learning Theory,

COLT’ 98, New York, NY, USA. ACM.

Glasmachers, 2016Glasmachers, T. (2016). Finite sum accel-

eration vs. adaptive learning rates for the training of

kernel machines on a budget. In NIPS workshop on

Optimization for Machine Learning.

Hsieh et al., 2008Hsieh, C.-J., Chang, K.-W., Lin, C.-J.,

Keerthi, S. S., and Sundararajan, S. (2008). A dual co-

ordinate descent method for large-scale linear SVM.

In Proceedings of the 25th International Conference

on Machine Learning, pages 408–415. ACM.

Joachims, 2006Joachims, T. (2006). Training linear SVMs in

linear time. In Proceedings of the 12th ACM SIGKDD

international conference on Knowledge discovery and

data mining, pages 217–226. ACM.

Kivinen et al., 2003Kivinen, J., Smola, A. J., and Williamson,

R. C. (2003). Online learning with kernels. volume 52,

pages 2165–2176.

Le et al., 2016Le, T., Nguyen, T., Nguyen, V., and Phung, D.

(2016). Dual space gradient descent for online learn-

ing. In Lee, D. D., Sugiyama, M., Luxburg, U. V.,

Guyon, I., and Garnett, R., editors, Advances in Neu-

ral Information Processing Systems 29, pages 4583–

4591. Curran Associates, Inc.

Lin, 2001Lin, C.-J. (2001). On the convergence of the decom-

position method for support vector machines. IEEE

Transactions on Neural Networks, 12(6):1288–1298.

List and Simon, 2005List, N. and Simon, H. U. (2005). Gen-

eral polynomial time decomposition algorithms. In

International Conference on Computational Learning

Theory, pages 308–322. Springer.

Lu et al., 2016Lu, J., Hoi, S. C., Wang, J., Zhao, P., and Liu,

Z.-Y. (2016). Large scale online kernel learning. Jour-

nal of Machine Learning Research, 17(47):1–43.

Lu et al., 2018Lu, J., Sahoo, D., Zhao, P., and Hoi, S.

C. H. (2018). Sparse passive-aggressive learning for

bounded online kernel methods. ACM Trans. Intell.

Syst. Technol., 9(4).

Mohri et al., 2012Mohri, M., Rostamizadeh, A., and Tal-

walkar, A. (2012). Foundations of Machine Learning.

MIT press.

Nesterov, 2012Nesterov, Y. (2012). Efﬁciency of coordinate

descent methods on huge-scale optimization prob-

lems. SIAM Journal on Optimization, 22(2):341–362.

Nguyen et al., 2017Nguyen, T. D., Le, T., Bui, H., and Phung,

D. (2017). Large-scale online kernel learning with

random feature reparameterization. In Proceedings of

the 26th International Joint Conference on Artiﬁcial

Intelligence.

Orabona et al., 2009Orabona, F., Keshet, J., and Caputo, B.

(2009). Bounded kernel-based online learning. J.

Mach. Learn. Res., pages 2643–2666.

Osuna et al., 1997Osuna, E., Freund, R., and Girosi, F. (1997).

An improved training algorithm of support vector ma-

chines. In Neural Networks for Signal Processing VII,

pages 276 – 285.

Quinlan et al., 2003Quinlan, M. J., Chalup, S. K., and Mid-

dleton, R. H. (2003). Techniques for improving vi-

sion and locomotion on the Sony AIBO robot. In In

Proceedings of the 2003 Australasian Conference on

Robotics and Automation.

Rahimi and Recht, 2008Rahimi, A. and Recht, B. (2008).

Random features for large-scale kernel machines. In

Advances in neural information processing systems,

pages 1177–1184.

Shalev-Shwartz et al., 2007Shalev-Shwartz, S., Singer, Y., and

Srebro, N. (2007). Pegasos: Primal estimated sub-

gradient solver for SVM. In Proceedings of the

24th International Conference on Machine Learning,

pages 807–814.

Shigeo, 2005Shigeo, A. (2005). Support Vector Machines for

Pattern Classiﬁcation (Advances in Pattern Recogni-

tion). Springer-Verlag New York, Inc., Secaucus, NJ,

USA.

Son et al., 2010Son, Y.-J., Kim, H.-G., Kim, E.-H., Choi, S.,

and Lee, S.-K. (2010). Application of support vec-

tor machine for prediction of medication adherence

in heart failure patients. Healthcare Informatics Re-

search, pages 253–259.

Steinwart, 2003Steinwart, I. (2003). Sparseness of support

vector machines. Journal of Machine Learning Re-

search, 4:1071–1105.

Steinwart et al., 2011Steinwart, I., Hush, D., and Scovel, C.

(2011). Training SVMs without offset. Journal of

Machine Learning Research, 12(Jan):141–202.

Wang et al., 2012Wang, Z., Crammer, K., and Vucetic, S.

(2012). Breaking the curse of kernelization: Budgeted

stochastic gradient descent for large-scale SVM train-

ing. J. Mach. Learn. Res., 13(1):3103–3131.

Wang and Vucetic, 2010Wang, Z. and Vucetic, S. (2010). On-

line passive-aggressive algorithms on a budget. In

Dual SVM Training on a Budget

105

Proceedings of the Thirteenth International Confer-

ence on Artiﬁcial Intelligence and Statistics, vol-

ume 9, pages 908–915. PMLR.

Wen et al., 2017Wen, Z., Shi, J., He, B., Li, Q., and Chen, J.

(2017). ThunderSVM: A fast SVM library on GPUs

and CPUs. To appear in arxiv.

Yang et al., 2012Yang, T., Li, Y.-F., Mahdavi, M., Jin, R., and

Zhou, Z.-H. (2012). Nystr¨om method vs. random

fourier features: A theoretical and empirical compar-

ison. In Advances in neural information processing

systems, pages 476–484.

Zhao et al., 2012Zhao, P., Wang, J., Wu, P., Jin, R., and Hoi,

S. C. H. (2012). Fast bounded online gradient descent

algorithms for scalable kernel-based online learning.

In Proceedings of the 29th International Coference on

International Conference on Machine Learning, USA.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

106